A methodology for the fast identification and monitoring of microplastics in environmental samples using random decision forest classifiers

Abstract

A new yet little understood threat to our ecosystems is microplastics. These microscopic particles accumulate in our oceans and in the end may find their way into the food chain. Even though their origin and the laws governing their formation have become ever more clear fast and reliable methodologies for their analysis and identification are still lacking or at an early stage of development. The first automatic approaches to analyze μFTIR images of microplastics which have been enriched on membrane filters are promising and provide the impetus to put further effort into their development. In this paper we present a methodology which allows discrimination between different polymer types and measurement of their abundance and their size distributions with high accuracy. In particular we apply random decision forest classifiers and compute a multiclass model for the polymers polyethylene, polypropylene, poly(methyl methacrylate), polyacrylonitrile and polystyrene. Further classification results of the analyzed μFTIR images are given for comparability. The study also briefly discusses common issues that can arise in classification such as the curse of dimensionality and label noise.

---

1 Introduction

The pollution of aquatic environments by microplastics^1–3 (MPs) is a topic that receives ever more attention both from scientists and the general public. To better understand the impact of this novel contaminant it is indispensable to quantify the abundance of MPs in their respective habitats. Therefore many approaches to monitor MPs have been proposed⁴ and though these methodologies shed light on the complexity of the dilemma a generally applicable procedure which truly handles the problem of quickly and accurately identifying MPs remains yet to be found.

Chemical analysis of environmental samples is usually limited to bulk features such as the overall abundance of polymer types. In order to assess the size distribution of MPs micro Fourier-transform infrared (μFTIR) and μRaman spectroscopy^5,6 have become ever more popular as these methods also allow an analysis of particles that are too small for manual sorting and single spectroscopic measurements.² After mandatory purification⁷ MPs are enriched on membrane filters which are then measured to obtain hyperspectral images (HSIs). While these technologies open the gates towards far smaller scales they also introduce further challenges such as large amounts of spectroscopic data.

Even though most instrument software packages include algorithms to analyse HSIs current solutions still do not yield high accuracy⁴ or are computationally expensive. Currently the common approach is to perform MP identification in a semi-automatic manner where a spectroscopy expert compares selected pixel spectra to a reference database.⁸

At first glance the obvious solution to speed up this process is to automatically compare each pixel to the database without any human intervention. However, this approach is not only slow but also results in high error rates as current database search routines often either do not recognize certain MP spectra or falsely assign them to a different type of polymer. Nevertheless attempts have been made to improve the shortcomings of current algorithms.

Primpke et al.⁹ proposed an algorithm which relies on a dual database search using two different similarity measures. A class affiliation is considered as correct only if both measures yield the same polymer type. Though the use of two different measures certainly reduces the error rate the detected MPs still have blurred contours, gaps and holes. The authors attributed this problem to effects caused by weathering processes or insufficiently removed biofilms and post-processed the class affiliation image using a closing algorithm that smoothens particle contours based on neighboring polymer pixels.

Renner et al.¹⁰ proposed to use a database search to identify MP spectra based on a spectral feature selection algorithm which can also deal with weathered MPs. In the first step vibrational bands are detected using the 1^st derivative of the spectra. In the second step a curve fitting of the derived spectra allows a de-noised estimation of the MP spectra to be produced. Using the peak areas the MPs are then identified using a database search. While this study applied the algorithm to MP spectra obtained from attenuated total reflection FTIR (ATR-FTIR or FTIR ATR) spectroscopy the authors stated that the method might require only a little alteration to be applicable to μFTIR images.

While database searches can be considered to be pioneering methods in this field we believe that future routine analyses will require faster approaches as the throughput demand will certainly rise. In this paper we propose to use model-based classification for a fast identification of MPs in large HSI datasets. In particular we use a combination of spectral descriptors¹¹ and random decision forest¹² (RDF) classifiers to obtain our preliminary results for the polymers polyethylene (PE), polypropylene (PP), poly(methyl methacrylate) (PMMA), polyacrylonitrile (PAN) and polystyrene (PS).

This work is intended to provide a faster alternative to current database algorithms but should not be considered a full evaluation of classification with respect to MP identification as only one type of algorithm is considered. However, as many issues which are discussed in this study are independent of the used classifier we hope that the given references may also be helpful when other approaches are considered.

The rest of this article is organized as follows: section 2 discusses some aspects of μFTIR images that are particularly problematic for classification and related approaches. In section 3 we give a brief introduction into classification and the algorithms used. A discussion on the differences and benefits of classification with respect to current solutions is given in section 3.1 and a description of the involved algorithms and mathematics in sections 3.2 and 3.3. The most important aspects of the methodology are summarized in section 3.4 and the used software is described in section 3.5. The experimental assessment is described in section 4 leading to some considerations regarding the throughput rate in section 4.5. The article concludes with a discussion of the experiments in section 5 and final remarks in section 6. Readers who are new to machine learning might also be interested in further reading given in section 7.

2 μFTIR images from the viewpoint of chemometrics

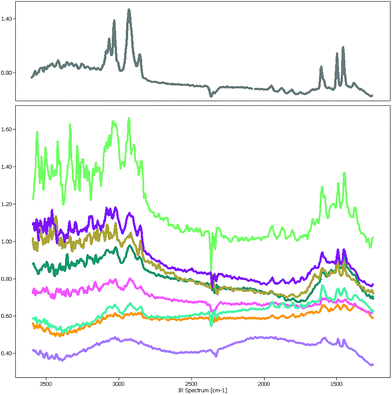
The focal plane array-based μFTIR images⁵ (FPA-based μFTIR) used in this study were measured in the wavenumber range between 1249.6 cm⁻¹ and 3594.5 cm⁻¹ with a spectral resolution of 609 bands. The image size varies around 1000 × 1000 pixels so that each image contains about 10⁶ spectra. Even though the lateral resolution is high enough to capture polymer particles as small as 10 μm the chemometric analysis of these images is far from trivial.

One major obstacle is the Mie scattering effect, a phenomenon that occurs if electromagnetic waves are in the size range of the measured particles. In the case of μFTIR the infrared radiation is diffracted at the edges of the MPs and other materials which results in a distorted baseline. Fig. 1 depicts a collection of PS spectra which were sampled at various positions of a μFTIR image. The spectrum in the upper chart was extracted from the center of a particle whereas the others originate from particle edges. While the characteristic PS bands are still recognizable in these spectra the signal-to-noise ratio worsens to a degree where they are barely visible. However, if our goal is to correctly measure the number of MPs and their size distribution the identification of these low quality spectra is of crucial importance for determining the particle contour.

Fig. 1 Polystyrene spectra of varying quality sampled at the center of a particle (upper chart) and at particle edges (lower chart). As particle sizes can be as low as 10 μm Mie scattering distorts the baselines of the spectra.

Another problem that has to be overcome is the so-called curse of dimensionality,^13,14 a phenomenon which is due to the high dimensionality of the datasets. In the case of spectroscopic data only a few spectral wavelengths contain information which is relevant for the identification of MPs whereas the largest part of the spectrum contains mostly noise. Similarity measures, such as the Euclidean distance or the Pearson correlation coefficient, are therefore dominated by noise rather than characteristic vibrational bands which negatively impacts the performance of many distance-based chemometric techniques.

Less evident but also problematic for MP identification is the resonant Mie scattering effect which alters the intensity and position of vibrational bands. This phenomenon is not addressed in this paper; however, for further reading we here refer to Bassan et al.¹⁵

3 Methodology

3.1 Motivation

In their extensive review about monitoring MPs Renner et al.⁴ stressed the need to develop more robust database search algorithms and to standardize the different methodologies to increase their comparability. In this context we propose to use model-based classification as an alternative to the common database approach. Classification or supervised learning is the task of learning a function from labeled training data so that the class affiliations of unknown data can be predicted. The key difference between model-based classification and database searches is that instead of using reference data for deciding the class affiliation we use a multivariate model of the actual data.

The typical use case of databases is when we have an unknown spectrum and require a ranking of similar spectra in order to help the researcher in the identification. In the case of monitoring MPs the situation is very different as the associated spectra of certain polymer types are already known. Therefore, our motivation of proposing classification as an alternative is that the mathematical problem that underlies database searches makes them ill-suited for the task of identifying large numbers of spectra for the following reasons:

• The classification of n unknown spectra using a database of m reference spectra requires n × m computations of a similarity measure in order to determine the hit quality, which is an expensive task.

• Database reference spectra are often measured under ideal laboratory conditions which decreases the similarity to the actual MP spectra as these may be distorted by Mie scattering, have very low signal-to-noise ratios, show total absorption or contain a mixture of artifacts originating from biofilms. Further we have to consider that polymers are often not pure with respect to their chemical composition as they can appear as blends and usually will contain various additives such as fillers and pigments. One may argue that this problem can simply be solved by adding further reference spectra to the database but this significantly increases the computational load per spectrum as stated above.

• The decision of class affiliation is usually based on the highest hit quality which as seen from the viewpoint of machine learning is closely related to a 1-nearest-neighbor (1NN) classification. While the k-nearest neighbor (kNN) classifier for k > 1 is a well-established benchmark technique, the 1NN classifier is known to require large sample sizes in order to be stable enough for most applications.

In chemometric classifiers such as the RDF,¹² partial least squares discriminant analysis¹⁶ (PLS-DA) and support vector machine¹⁷ (SVM) have long found their way into the analysis of hyperspectral images.^18–20 In order to identify an unknown spectrum we simply have to compute the model output which is orders of magnitude faster than a similarity search. Another advantage of using classifiers is that they are readily available through open source libraries such as scikit-learn²¹ or WEKA²² and thus allow an easy comparison and evaluation of research results.

While one classification algorithm might be preferable over the other depending on the structural characteristics of the data we chose the RDF because it is a fast algorithm with respect to the training and application step. Another advantage of RDFs is that they can solve problems where the decision boundary is non-linear which we found to be a useful property for some polymer types. However, before the RDF can be applied to the problem of classifying MPs a preprocessing step is necessary to boost its performance which will be discussed in the following section.

3.2 Spectral descriptors

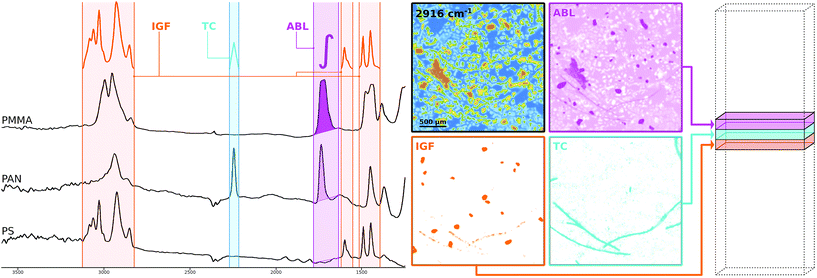
The conclusions that can be drawn from section 2 regarding the spectra in μFTIR images are that we have to deal with both a distorted baseline and high dimensionality of the dataset. While there exist many algorithms for baseline correction and dimensionality reduction²³ those methods tend to be computationally expensive and may also introduce artifacts into the data. Here we propose to preprocess the data using spectral descriptors^11,24 (SPDCs). This concept allows a spectroscopy expert to apply his or her knowledge to the data to extract the features that are descriptive for certain chemical compounds thereby making baseline correction obsolete and reducing the dimensionality at the same time.

SPDCs are simple mathematical functions that map one or more spectral bands into one descriptive variable. By creating an entire set of SPDCs which is tailored to certain polymer types the spectroscopist can concentrate the chemical information into a descriptor space of much reduced dimensionality and improved data structure. In other words if we use q SPDCs on a hyperspectral datacube of p layers, where q ≪ p, we create a descriptor cube of q layers where each individual layer represents the output of a certain descriptor. The process of designing a set of SPDCs can also be seen as a manual method of building a model for dimensionality reduction as in the end the SPDCs are reused to preprocess other datasets.

The methodology is illustrated schematically in Fig. 2 where a selection of three different kinds of SPDCs is applied to polymer spectra (left side) sampled from μFTIR data. Probably the most straightforward descriptor is the ABL§ whose mathematical definition is to compute the baseline-corrected peak area within a defined wavenumber range. The resulting descriptor image (pink) highlights mainly PMMA particles as this polymer has a prominent peak in that region. The PAN fibers are visible as well though their contribution is poor.

Fig. 2 Descriptor images generated using the ABL, TC and IGF descriptors. The spectra (left) correspond to three types of common polymers. By using the stated spectral descriptors on certain ranges of the hypercube the corresponding descriptor images (middle) can be computed which are then reassembled as a descriptor cube of reduced dimensionality and improved data quality (right).

As can be guessed from that image one descriptor alone doesn't do the job. Due to the overlapping peaks further SPDCs will be necessary. However, the ABL is not always the best way to go. A more sophisticated way which is less prone to noise¹¹ and achieves an even better separation from the background is the TC§ descriptor. Here we compute the Pearson correlation between a simple triangular template peak and the spectrum. If the correlation is significant the resulting value is multiplied with the base-line corrected area of that region. The introduction of correlation makes the descriptor more robust against background noise which can be seen in the corresponding descriptor image (cyan) where the PAN fibers clearly stand out.

Taking the concept of templates a step further we can also use characteristic peak patterns instead of a simple triangle to compute a correlation. The IGF§ descriptor embeds this concept by multiplying the correlation coefficients of multiple ranges that each apply an individual peak pattern. In Fig. 2 this specific IGF uses the patterns of PS and thus selects the PS beads from the background as can be seen in the orange image.

While the IGF seems the most appealing descriptor it is also the most cost intensive to compute and in some cases too strict with respect to certain low quality spectra from particle edges. In our experience the TC is the most generally applicable descriptor and also significantly faster to compute. For this reason we mostly used that type to design our SPDC sets for our experiments and reduced the dimensionality from 609 spectral bands to 50 baseline corrected descriptor variables.

3.3 Random decision forest

The RDF is a binary tree-based ensemble learner that combines the concept of the random subspace method²⁵ and bagging²⁶ (bootstrap aggregating). Its theory is based on decision trees which have long been used as models both in classification and regression. A common trait of decision trees is their tendency to overfit the training data which causes a low bias but high variance. While the former is beneficial for a model the latter causes a poor general performance. The RDF addresses this issue by averaging the output of an entire forest of decision trees thereby retaining the low bias while compensating for the high variance. However, a basic requirement for this approach to work is that the trees are uncorrelated which necessitates some form of randomization in the process of model creation.

Ho²⁷ introduced the idea that each tree is grown on its own randomly selected subspace of the feature space spanned by a dataset. This concept was then enhanced by Breiman¹² who used bagging to further decorrelate the decision trees. Here each tree is grown on its own randomly sampled subset of the training data. By combining both randomization strategies we arrive at the modern version of the RDF.

In short the growth of each tree starts with the initial node splitting its bootstrap sample using a randomly sampled subset of variables. The split is determined by a threshold on the variable which achieves the best separation of the training data. This process repeats recursively for each child node using its own set of variables to determine the optimal split. In the end we arrive at a forest of trees where each leaf node represents a class.

For an object of unknown class affiliation the prediction is then determined in the following way: starting from the root the object traverses the trees where each node determines (through the use of the threshold) the next branch that is to be followed. In the end the object reaches the leaf nodes where the final class affiliation may then be determined using an average vote of the trees which results in a value in the interval [0,1] or a majority vote yielding either 0 or 1. Please note that in this scenario we only discriminate between two classes which is called a binary classification problem. In brief multiple classes can be treated by creating a set of binary classifiers for each polymer type. How these outputs can be treated will be discussed in more detail in sections 3.5 and 4.4.

Regardless of which classification algorithm is used a trained model should always be validated to assess how well it generalizes on independent test data. A common approach is to separate a test dataset from the training data which is then classified using the RDF model. By comparing the known labels to the predicted labels we can thus draw conclusions about the model performance. Here the RDF has the special trait that the separation of a test dataset is not strictly necessary. As only the bootstrap samples determine the model the omitted samples form a kind of test dataset that can be used in the validation by computing different out-of-bag (OOB) estimates. For better comparability to other classification algorithms we will use both approaches in this paper.

3.4 Implementation strategy

In summary the concept of classifying μFTIR images uses a combination of SPDCs and RDFs and is based on the following steps:

• Decide on the polymer classes that would be identified using the RDF. The background and the matrix have to be considered as well and thus also form at least one class. While the distinction between polymers may be simple the matrix is by far more complex because it contains a mixture of IR active substances both of biologic or inorganic origin.

• Create a training set of labeled spectra drawn from different μFTIR images, which contains a sufficient number of representatives from all classes (including the background and matrix). Here it is important to include low-quality spectra from particle edges so that their contours can be correctly estimated.

• Design a set of SPDCs which is tailored towards the detection of the polymers. The goal is to enhance the separation of classes in the descriptor space. Therefore, if certain matrix spectra are very similar to those of polymers this set may be enhanced by SPDCs that cover their features as well.

• Train the classifier. At this stage we use the RDF though other algorithms can be considered as well.

• Validate the classifier on test data.

• Reiterate this process from an earlier stage if the model validation proves unsatisfactory.

The above process requires the knowledge of a spectroscopy expert in two phases: the sampling of the spectra establishes our ground truth and thus should not contain any errors. Further the quality of the SPDCs may be higher if an expert applies his or her domain knowledge.

Whether a machine learning expert is required depends on the used software and classification algorithm. When tuning classification models the determination of the model order is of crucial importance. Underfitting the training data increases the model bias whereas overfitting leads to increased variance. In this context the RDF might be easier to handle than other algorithms as choosing a too high number of trees will not lead to overfitting. On the other hand underfitting is possible if the number of trees is set too low.

3.5 Software

In this study we used the general purpose imaging software Epina ImageLab (imagelab.at) to implement the described strategy. This software facilitates sampling of the training set, the design of SPDCs and the training of the RDF in an easy-to-use graphical user interface. ImageLab handles multiclass problems by using a one-vs-all (OVA) scheme. This means that in order to discriminate between N classes we create N binary classifiers where each RDF separates one class from all others. In this implementation of the RDF the model creates an output in the range [0,1] with the decision boundary at 0.5. By applying each binary classifier to our data we thus get N class maps. Subsequent analysis of these images is then performed using a built-in particle detection tool which will not be covered in this paper.

4 Experimental

In the following sections we will cover the training, validation and application of a RDF classifier set for the polymers PE, PP, PMMA, PAN and PS. The background, matrix and other polymers will be denoted as ‘NonPolymer’.

For this preliminary assessment we chose PE, PP, PS and PMMA as these are among the 10 most important polymer resins with respect to the demand in the EU.²⁸ PAN on the other hand allows us to determine whether the proposed method can deal with fibers.

4.1 Data acquisition

Sampling polymer spectra from real-world environmental samples is a cumbersome task as most images will only contain a few if any particles of the polymer types that we want to detect. As a workaround we created artificially enhanced samples where selected MPs of varying sizes were added to a freshwater plankton sample as the matrix before filtering. The justification for this procedure lies in the need to sample spectra which show the same effects that were discussed in section 2.

In particular the microplastics were either produced by abrasion from a larger polymer material or directly bought as powder. By using a round surface aluminum oxide filter (Anodisc 0.2 μm pore size, 10 mm diameter) the spiked environmental samples were then filtered and dried at room temperature overnight. The subsequent imaging was conducted using a Bruker Hyperion 3000 FTIR microscope (https://www.bruker.com) equipped with a 60 × 64 pixel FPA detector in conjunction with a Tensor 27 spectrometer. Each sample was placed on a CaF₂ filter and measured in transmission mode with a 15× IR objective. The FTIR measurement was performed at a resolution of 8 cm⁻¹ and a coaddition of 6 scans. 4 × 4 binning was applied to the measured data resulting in a pixel size of ca. 11 μm. The measurement of the whole sample surface takes around 10 hours. Further the background was acquired on a blank filter material. For a more detailed description of this procedure see Löder et al.⁵ The subsequent chemometric analysis was conducted in ImageLab by exporting the data as ENVI files.

4.2 Training

For this preliminary study about 100 spectra were sampled for each of the polymer classes by three spectroscopy experts. To ensure enough variability in the matrix and the background 2770 spectra were sampled from both the artificially enhanced datasets and from two environmental samples published by Primpke et al.⁸ which sums up to a total of 3270 spectra. As stated above the validation of the RDF does not require separate test data though for reasons of better comparability to other classification algorithms we further divided each class into a randomly sampled training and test set of equal size.

For the final training of the RDF a set of 50 SPDCs was built to overcome the effects discussed in section 2. As illustrated in Fig. 2 the SPDC set was designed to enhance the separability of the polymer and matrix spectra in the descriptor space. For the most part this was done by using TC and ABL descriptors which are well suited to describe the presence of single peaks. For more complex peak patterns such as the ones observed in PS we used IGF descriptors. Each binary classifier was then trained on the transformed spectra using 75 trees and a bootstrap sample size of 50%.

4.3 Validation

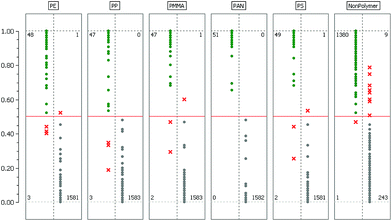
The model validation results for each binary classifier are given in Table 1. Here ‘OOB-RelCls’ is the OOB relative classification error which is defined as the ratio of incorrectly classified cases. ‘OOB-RMS’ refers to the OOB root mean square error when estimating posterior probabilities.

Table 1 Validation results using OOB estimates and true/positive and false/negative rates of the test dataset

Class name	OOB-RelCls	OOB-RMS	TP rate	FN rate
PE	0.0012	0.0361	0.9412	0.0006
PP	0.0006	0.0335	0.9400	0.0000
PMMA	0.0006	0.0353	0.9592	0.0006
PAN	0.0006	0.0317	1.0000	0.0000
PS	0.0024	0.0531	0.9608	0.0006
NonPolymer	0.0037	0.0881	0.9993	0.0357

---

The last two columns show the true/positive (TP) and false/negative (FN) rate when the RDF model is used to predict the labels of the test dataset. A more detailed assessment of this result is given in Fig. 3 where the confusion matrices for each binary classifier are illustrated.

Fig. 3 Confusion matrices for the classes PE, PP, PMMA, PAN, PS and NonPolymer. Here the test dataset is classified using the RDF model. The scale to the left indicates the ratio of trees that agree on the positive classification. The default decision boundary at 0.5 is highlighted in red. The green dots represent the true/positives whereas the gray dots represent the true/negatives. The cases where the known and the predicted labels differ are marked using a red ‘×’. The numbers in each confusion matrix specify the absolute number of cases for each quadrant.

4.4 Application

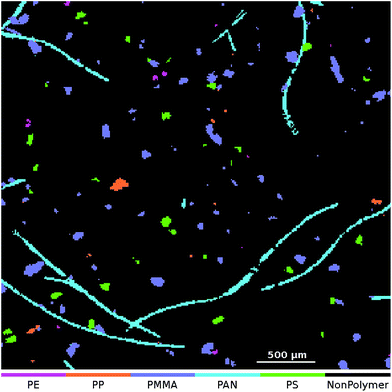
At the application stage the μFTIR image that is to be analyzed is transformed using the set of 50 SPDCs. The resulting descriptor cube is then classified using the binary classifiers. For each class the model output is assembled as a class map where each pixel indicates the result of the averaged vote. For the final particle count analysis we require dichotomized images which can be obtained in two ways: one approach is to apply a threshold to each class map and post-process it individually. Here we can either use the default threshold at 0.5 or an arbitrary selection in the range [0,1]. (For example we might set the threshold to 0.8 which means that at least 80% of the decision trees have to agree for a positive classification.) The other would be to create a combined class affiliation image where each pixel receives the class number of the binary classifier which yields the highest output value. This approach is known as an OVA scheme. For a discussion of other possibilities for handling multiclass problems we here refer to Rifkin and Klautau.³⁰

An OVA result of one of our artificially enhanced datasets is given in Fig. 4. In Fig. 5 we further show the upper right part of the result as an overlay with the optical image of the sample.

Fig. 4 OVA image of the ‘Microplastic’† (ref. 31) dataset.

Fig. 5 Zoomed-in overlay of the classification result obtained from the ‘Microplastic’† (ref. 31) dataset. The NonPolymer class is transparent so that the underlying image is visible.

In order to assess the performance of the RDF on untreated natural data we also classified the dataset ‘RefEnv1’† which was published by Primpke et al.⁸ The result of the lower left part of the μFTIR image is given in Fig. 6.

Fig. 6 Zoomed-in overlay of the lower left part of the ‘RefEnv1’† dataset. The original μFTIR data and the optical image were published by Primpke et al.⁸ under a Creative Commons Attribution 4.0 International License and is accessible through DOI: 10.1007/s00216-018-1156-x.

Please note that the ESI‡ includes a link to a short video³¹ which shows the application of the RDF using the datasets ‘Microplastic’²⁹ and ‘RefEnv1’.†

4.5 Throughput rate

Even though the performance of modern day computer systems evolves very quickly we want to give a rough estimation of the throughput rate. As a reference dataset we chose ‘RefEnv1’† (1024 × 1024 pixels) which was tested on two different PCs. The first PC was equipped with an Intel Core i5-8400 CPU @ 2.80 GHz and 8 GB RAM (speed: 2400 MHz, form factor: DIMM) running MS Windows 10. Here the time required for all six binary RDF classifiers was 4 min 10 s, which yields an approximate rate of 4195 spectra per s. If we disregard the time required for computing the descriptor cube we thus get an average rate of 25 165 spectra per s for a single class. From there we estimate the time required for an image of 10⁶ pixels and 20 polymer classes to be in the range of 15 min.

To assess the performance of the RDF on different operating systems we also conducted a test on a PC running Arch Linux (https://www.archlinux.org) and Windows 10 using dual booting. Though ImageLab is an MS Windows application it can be run on GNU/Linux distributions using Wine (https://www.winehq.org). The system was equipped with an Intel Core i5-7400 CPU @ 3 GHz and 32 GB RAM (speed: 2133 MHz, form factor: DIMM). On this setup we measured 4 min 45 s for Arch Linux and 5 min 30 s for Windows 10. Due to the better memory management of GNU/Linux the performance here increases by approximately 15%.

Please note that all computations were done using one CPU core. For parallel computations on multi-core systems these rates have to be adapted accordingly.

5 Discussion

Considering Table 1 and Fig. 3 we find that the most challenging binary problem appears to be the separation of the NonPolymer spectra from those of the polymers. An explanation for this behavior might be that in this particular case the RDF has to encapsulate multiple dispersed classes whereas with respect to the polymer classes we have the comparatively simple task of separating one class from all others. As stated in section 3.4 it might therefore be a better approach to separate the matrix and background into more than one class. However, whether the additional effort really improves the overall classification result has yet to be determined experimentally.

The confusion matrices in Fig. 3 allow a deeper insight into the mechanics of the decision process while the error rates in Table 1 only give an overall result. For almost all polymer classes we find a few instances where the RDF's decision deviates from the labels of the test dataset. We investigated these instances and found that the spectra in question are all rather extreme cases of very low quality where the spectroscopy experts had difficulties in deciding on the class affiliation. In the literature this phenomenon is referred to as label noise or class noise and often arises if either low quality data have to be labeled or the task of labeling is in itself very difficult and requires a lot of experience. Another source of label noise can also be attributed to the fact that the three spectroscopy experts each labeled their own training data independently. Consequently, their biased opinions on certain rare cases thus become visible in the confusion matrices. We can therefore conclude that these misclassifications are not a sign of poor model quality but are a result of human bias.

Nonetheless the question arises to what extent the label noise affects the training of the RDF and classification in general. Though we did not investigate this topic in our experimental setting, simulations conducted by Folleco et al.³² on eleven different classification algorithms show that the RDF seems to be very robust against label noise. A more general discussion on handling label noise can found in Frénay and Verleysen³³ and Nettleton et al.³⁴

From visual inspection of the classification results shown in Fig. 4 and 6 we conclude that the RDF model performs satisfactorily within certain bounds. By closely assessing polymer particles both in the lateral and the spectral domain we found some instances in the datasets RefEnv1† and RefEnv2† where certain MP spectra were not detected. A closer assessment of these spectra revealed that the reason for the failed identification is strong total absorbance effects. As our training data did not contain spectra which exhibit total absorbance of this magnitude the model has difficulties in assigning these spectra to the correct polymer class. In particular PE and PP are most affected because they have only a few characteristic vibrational bands. Contrary to that we find that PMMA is quite robust against this phenomenon because of its rather broad peaks.

One approach to address this problem would be to also sample such spectra where total absorbance is very prominent and include them in the training of the RDF. However, we question whether this is a reasonable approach because the class assignment thus also contains a high uncertainty of whether the underlying particle is truly of that polymer type. Another idea could be that an RDF model is used to flag spectra which show strong total absorption effects after the initial polymer identification has been performed. In this way a researcher can be warned that the automatic result requires a manual reassessment or that the sample should be remeasured altogether. We here conclude that this issue is less a technical problem but more a matter of discussion of how much total absorption can be tolerated to still allow an accurate analysis of FPA-based μFTIR images.

As for the throughput rate of the method we find that the RDF facilitates a relatively fast analysis and as dataset sizes can be expected to rise in the future we can assume that the additional demand can be met. In the case that much shorter analysis times are necessary there are also linear classification algorithms such as PLS-DA and linear SVM at hand which are even faster and can be trained in parallel using the same methodology.

6 Conclusion

In this paper we presented a preliminary study of the application of the RDF classifier for the fast detection of MPs in FPA-based μFTIR images. While many questions regarding best practices for the design of classifiers in this research field are still open our experimental results show that the development of classifiers is both feasible with a reasonable amount of effort and yields high accuracy while retaining a high throughput rate.

7 Further reading

For readers who are new to machine learning and are interested in the mathematical background of the paper we would like to provide some guiding citations to the literature. We recommend the book of Hastie et al.³⁵ for an introduction to machine learning. Further the paper by Domingos³⁶ summarizes the main challenges we face when trying to create classifiers. Rich course material and code examples may also be found on https://www.scikit-learn.org and https://www.cs.waikato.ac.nz/ml/weka/. Readers more interested in the details of the RDF should start with Biau and Scornet³⁷ before they proceed to Breiman.¹²

Conflicts of Interest

There are no conflicts to declare.

Acknowledgements

Research funding was provided by Deutsche Forschungsgemeinschaft (DFG) – project number 391977956 – SFB 1357 and the German Federal Ministry of Education and Research (project PLAWES, grant 03F0789A). We thank Epina GmbH for providing the software for this research. Many thanks also go to Gabriel Gruber for proof reading and his suggestions to improve the quality of this paper. Further the authors acknowledge the TU Wien University Library for financial support through its Open Access Funding Programme.

References

1. D. Eerkes-Medrano, R. C. Thompson and D. C. Aldridge, Water Res., 2015, 75, 63–82.
2. V. Hidalgo-Ruz, L. Gutow, R. C. Thompson and M. Thiel, Environ. Sci. Technol., 2012, 46, 3060–3075.
3. P. Kay, R. Hiscoe, I. Moberley, L. Bajic and N. McKenna, Environ. Sci. Pollut. Res., 2018, 25, 20264–20267.
4. G. Renner, T. C. Schmidt and J. Schram, Current Opinion in Environmental Science & Health, 2017, 55–61.
5. M. G. J. Löder, M. Kuczera, S. Mintenig, C. Lorenz and G. Gerdts, Environ. Chem., 2015, 12, 563–581.
6. A. Käppler, D. Fischer, S. Oberbeckmann, G. Schernewski, M. Labrenz, K.-J. Eichhorn and B. Voit, Anal. Bioanal. Chem., 2016, 408, 8377–8391.
7. M. G. J. Löder, H. K. Imhof, M. Ladehoff, L. A. Löschel, C. Lorenz, S. Mintenig, S. Piehl, S. Primpke, I. Schrank, C. Laforsch and G. Gerdts, Environ. Sci. Technol., 2017, 51, 14283–14292.
8. S. Primpke, M. Wirth, C. Lorenz and G. Gerdts, Anal. Bioanal. Chem., 2018, 410, 5131–5141.
9. S. Primpke, C. Lorenz, R. Rascher-Friesenhausen and G. Gerdts, Anal. Methods, 2017, 9, 1499–1511.
10. G. Renner, T. C. Schmidt and J. Schram, Anal. Chem., 2017, 89, 12045–12053.
11. H. Lohninger and J. Ofner, Spectrosc. Eur., 2014, 26, 6–10.
12. L. Breiman, Mach. Learn., 2001, 45, 5–32.
13. R. Bellman, Adaptative Control Processes, 1961.
14. M. Radovanović, A. Nanopoulos and M. Ivanović, J. Mach. Learn. Res., 2010, 11, 2487–2531.
15. P. Bassan, H. J. Byrne, F. Bonnier, J. Lee, P. Dumas and P. Gardner, Analyst, 2009, 134, 1586–1593.
16. S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109–130.
17. C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297.
18. C. Ferrari, G. Foca, R. Calvini and A. Ulrici, Chemom. Intell. Lab. Syst., 2015, 146, 108–119.
19. M. Imani and H. Ghassemian, IEEE Geosci. Remote Sens. Lett., 2014, 11, 1325–1329.
20. A. Plaza, J. A. Benediktsson, J. W. Boardman, J. Brazile, L. Bruzzone, G. Camps-Valls, J. Chanussot, M. Fauvel, P. Gamba, A. Gualtieri, M. Marconcini, J. C. Tilton and G. Trianni, Remote Sens. Environ., 2009, 113, S110–S122.
21. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
22. I. H. Witten, E. Frank, M. A. Hall and C. J. Pal, Data Mining: Practical machine learning tools and techniques, Morgan Kaufmann, 2016.
23. L. van Der Maaten, E. Postma and J. van den Herik, J. Mach. Learn. Res., 2009, 10, 66–71.
24. J. Ofner, K. A. Kamilli, E. Eitenberger, G. Friedbacher, B. Lendl, A. Held and H. Lohninger, Anal. Chem., 2015, 87, 9413–9420.
25. T. K. Ho, IEEE Trans. Pattern Anal. Mach. Intell., 1998, 20, 832–844.
26. L. Breiman, Mach. Learn., 1996, 24, 123–140.
27. T. K. Ho, Proceedings of 3rd International Conference on Document Analysis and Recognition, 1995, pp. 278–282.
28. Plastics – the Facts 2018, An analysis of European plastics production, demand and waste data, https://www.plasticseurope.org/download_file/force/2387/319, 2019.
29. B. Hufnagl, D. Steiner, E. Renner, M. G. J. Löder, C. Laforsch and H. Lohninger, Microplastic, Zenodo, 2019, supplementary hyperspectral image dataset,  DOI:10.5281/zenodo.2555732.
30. R. Rifkin and A. Klautau, J. Mach. Learn. Res., 2004, 5, 101–141.
31. B. Hufnagl, D. Steiner, E. Renner, M. G. J. Löder, C. Laforsch and H. Lohninger, A Methodology for the Fast Identification and Monitoring of Microplastics in Environmental Samples using Random Decision Forest Classifiers, Zenodo, 2019, supplementary video,  DOI:10.5281/zenodo.2541745.
32. A. Folleco, T. M. Khoshgoftaar, J. Van Hulse and L. Bullard, IEEE International Conference on Information Reuse and Integration, 2008, pp. 190–195.
33. B. Frénay and M. Verleysen, IEEE Transactions on Neural Networks and Learning Systems, 2014, 25, 845–869.
34. D. F. Nettleton, A. Orriols-Puig and A. Fornells, Artif. Intell. Rev., 2010, 33, 275–306.
35. T. Hastie, R. Tibshirani and J. H. Friedman, The elements of statistical learning, Springer, New York, 2nd edn 2009.
36. P. M. Domingos, Commun. ACM, 2012, 55, 78–87.
37. G. Biau and E. Scornet, Test, 2016, 25, 197–227.

---

Footnotes

† A short video showing the application of the RDF model using the datasets ‘Microplastic’ and ‘RefEnv1’ is available through DOI: 10.5281/zenodo.2541745

‡ Electronic supplementary information (ESI) available: Classification results of the datasets ‘Microplastic’, ‘RefEnv1’ and ‘RefEnv2’ (data not shown) are provided as *.png and MATLAB*.mat files. See DOI: 10.1039/c9ay00252a

§ This is a software specific abbreviation. See http://www.imagelab.at/help/spectral_descriptors.htm for further information.

---