Thermal degradation in methylammonium–formamidinium–guanidinium lead iodide perovskites†
F. B.
Minussi
 *a,
R. M.
Silva
Jr
*a,
R. M.
Silva
Jr
 b,
J. F.
Carvalho
c and
E. B.
Araújo
b,
J. F.
Carvalho
c and
E. B.
Araújo
 a
a
aDepartment of Physics and Chemistry, São Paulo State University, 15385-007, Ilha Solteira, SP, Brazil. E-mail: fbminussi@gmail.com
bDepartment of Electrical Engineering, São Paulo State University, 15385-007, Ilha Solteira, SP, Brazil
cInstitute of Physics, Federal University of Goiás, 74690-900, Goiânia, GO, Brazil
First published on 6th March 2024
Abstract
The stability of hybrid halide perovskites (HPs) is one of the main factors hindering their potential commercial application. Numerous environmental agents are known to degrade HPs and their devices, including temperature, which can cause chemical modifications even at operational temperatures. Thermal degradation has been the subject of major studies in pure and HP-related compounds that have paved the way for a deep understanding of the phenomenon. However, thermally induced modifications in mixed-cation HPs have not been addressed in detail yet. In the present work, we report a systematic study of thermal degradation over a wide range of compositions of methylammonium lead iodide (MAPbI3) partially substituted by guanidinium (GA+) and formamidinium (FA+), using diverse experimental techniques and thermal treatment conditions. The results indicated that mixed-cation HPs were more stable than pure MAPbI3. Thermal degradation followed the volatilization of MA+ and MA+-related chemical species with PbI2 consequently appearing; however, GA+-rich compositions could suffer from an additional degradation pathway by the segregation of non-perovskite GAPbI3, reducing the material's thermal stability. This process also provoked a change in the degradation kinetic law. Remarkably, the simultaneous substitution with FA+ inhibited the formation of GAPbI3, even in compositions with high GA+ contents. Our work advances the crucial understanding of thermal degradation processes and how to increase the thermal stability of halide perovskites.
1. Introduction
Hybrid halide perovskites have been intensively studied in the last decade and have emerged as a revolutionary semiconductor with several outstanding properties for optoelectronic and photovoltaic applications. Despite the high performance of perovskite-based photovoltaic devices, several barriers must be overcome for large-scale commercial deployment. The degradation of the physical properties of devices based on halide perovskites is a complex problem and a real obstacle to overcome. Profoundly understanding these degradation mechanisms remains a significant challenge.Halide perovskites have the general chemical formula of the type ABX3, where A denotes a monovalent cation, B a divalent cation, and X a halide anion composed of a tridimensional arrangement of corner-sharing PbX6 octahedra, and have found many applications in optoelectronic and electrochemical devices, including solar cells, LEDs, lasers, X-ray and nuclear radiation detectors, sensing, photocatalysis, and organic synthesis.1–9 Despite the unprecedented success in inexpensive laboratory applications, the low stability of halide perovskite materials and devices is one of the main bottlenecks for their definitive commercial usage.10–12 Among the possible degradation stressors are humidity, oxygen, light, high temperatures and thermal stresses, bias voltages, and interfacial reactions between layers in perovskite devices.13–15 At present, the longest-lasting halide perovskite solar cell possesses a predicted lifetime of about five years under continuous operation at 35 °C,16 much lower than the desired times of at least 10 years, without even considering that humidity, light, and temperature fluctuations in real conditions could reduce this value. Furthermore, the solar cell in question is all-inorganic, much more stable but less efficient than the state-of-the-art organic–inorganic halide perovskite solar cells,17–21 for which retentions of initial efficiencies are generally lower than 80% after less than one year, even in strictly controlled environmental conditions. In this sense, to develop commercially competitive solar cells and other perovskite optoelectronic devices, efforts should be directed toward increasing the efficiency of inorganic perovskite devices and increasing the stability of hybrid perovskite devices. For such, one of the main strategies is the formulation of mixed compositions.22,23
Generally, mixed compositions possess higher stabilities24 due to the positive entropy of mixing leading to free energy reduction. It was experimentally found that entropy is the main stabilizing factor in MAPbX3 (MA+ = methylammonium, CH3NH3+) perovskites.25 Although this often happens,22–24 it has been observed, for example, that solid solutions containing guanidinium (or GA+) may display time,26 light,27 and temperature28 dependent segregation of guanidinium-related non-perovskite phases (possibly GAPbI3) even below the solubility limit of GA+ in the host perovskite. This segregation could be expected in compositions of guanidinium concentrations above the solubility limit.29 The segregation of imidazolium and dimethylammonium-related non-perovskite phases may also appear under light-induced degradation.27 On the other hand, this phenomenon seems less common in compositions containing formamidinium (or FA+) cations, possibly due to the closer MA+ and FA+ radii and the fact that FA+ is also a perovskite-forming cation. Despite this, the segregation of the non-perovskite δ-FAPbI3 phase coexisting with δ-CsPbI3 was observed in some compositions of the type CsxMAyFA1−x−yPbI3 submitted to different light, thermal, and humidity conditions.30 This secondary phase segregation may negatively affect the stability and efficiency of materials and devices.31
Regarding the thermal stability of halide perovskites, initial studies32–34 reported that methylammonium lead iodide, MAPbI3, decomposes by the reaction MAPbI3(s) → CH3NH2(g) + HI(g) + PbI2(s). A general thermal decomposition reaction of the type CH3NH3PbX3(s) → CH3NH2(g) + HX(g) + PbX2(s), where CH3NH3 = MA+, was considered to interpret the thermal degradation kinetics and phase evolution in MAPbCl3, MAPbBr3, and MAPbI3, which may happen even at temperatures as low as 60 °C.34 At the same time, it was experimentally and theoretically demonstrated that MAPbI3 decomposes following the reaction CH3NH3PbI3(s) → CH3I(g) + NH3(g) + PbI2(s).35 Later, it was proposed that the actual degradation path depends on the thermal degradation conditions,36–38 so that the preferential formation of CH3I(g) and NH3(g) occurs at temperatures below 350 °C.38 For all purposes, computational methods, such as density functional theory (DFT) and molecular dynamics (MD) calculations, are valuable tools for predictions and mechanistic insights related to the degradation and stability of halide perovskites and related materials.39–43 Although the thermal stability and thermal degradation kinetics have been studied in other perovskites and perovskite-like materials with different A-site cations, such as Cs+, formamidinium (or FA+), and tetramethylammonium,44–47 and some mixed-systems,28,30,48,49–53 studies on the systematized effects of A-site solid solutions containing different cations and concentrations on the thermal stability of halide perovskites are still scarce. It was recently noted that, chemically, the thermal degradation induction of a secondary phase segregation acts as an additional perovskite degradation route, which provokes a change from first to second-order degradation kinetics and an unexpectedly higher thermal degradation rate.28 This phenomenon was observed at 150 °C in GA0.10MA0.90PbI3 and indicated that the sole substitution by guanidinium led to a decrease in the thermal stability of the resulting material in comparison to MAPbI3. On the other hand, the compositions FA0.10MA0.90PbI3 and GA0.05FA0.05MA0.90PbI3 showed lower thermal degradation kinetics than pure MAPbI3. This intriguing scenario suggests that not all mixed-cation compositions are more stable than their analog pure compounds, as observed elsewhere.30
From a thermally induced degradation perspective, although much information is available, mostly on how devices behave with time under thermal stress, fundamental insights, for example, on activation energies for thermal degradation in mixed-cation compositions, microstructural aspects, and differences in volatiles eliminated between different compositions, have not been adequately explored. This information is crucial for better understanding which compositions and characteristics of the substituent cations lead to the greatest stabilities to allow the best chemical design of halide perovskites for reliable long-term application in devices. Nevertheless, despite the greater focus of the current literature on FA+-based perovskite solar cells, the top efficiency solar cells today still contain the less stable MA+ cations.54,55 Considering this scenario, in the present work we used a combination of different experimental techniques, including X-ray diffraction, scanning electron microscopy, energy-dispersive X-ray spectroscopy, and mass spectrometry-coupled thermogravimetry analysis, to systematically investigate the degradation conditions with time and temperature considering a robust set of compositions of the GAxFAyMA1−x−yPbI3 system. The results show that mixed-cation halide perovskites generally exhibit higher thermal stability with lower degradation rate constants. However, guanidinium-rich compositions show increased rate constants due to GAPbI3 segregation triggered by the volatilization of MA+ and related molecules. The formation of this secondary phase can be severely mitigated by partial substitution with FA+. Unexpectedly, the activation energies for thermal degradation were found to decrease with increasing the radius of the substituting cations. Our findings provide insights on the essential compositional design principles for achieving high thermal stability in halide perovskites.
2. Experimental
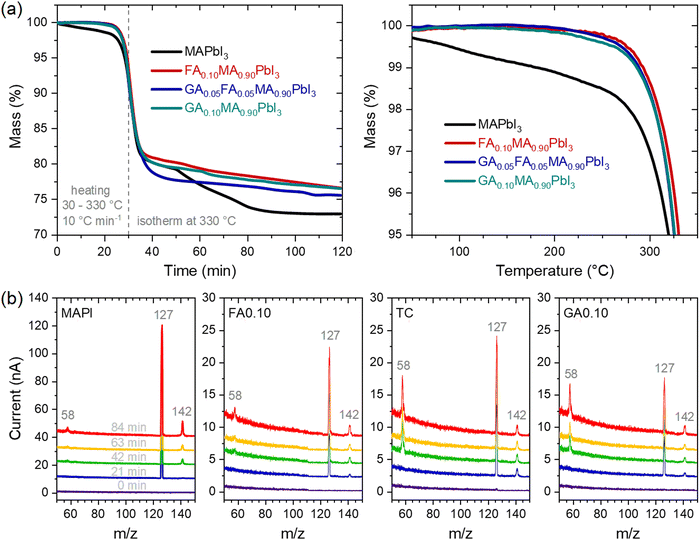
For the present study, different samples of the GAxFAyMA1−x−yPbI3 system in the composition range 0 ≤ x + y ≤ 0.3 were prepared from the precursors lead iodide (PbI2, Sigma-Aldrich, 99%), methylammonium iodide (CH3NH3I or MAI, Sigma-Aldrich, 98%), formamidinium iodide (CH(NH2)2I or FAI, Sigma-Aldrich, 99%), and guanidinium iodide (C(NH2)3I or GAI, Sigma-Aldrich, 99%). The precursors were manually mixed and ground to react in a natural agate mortar for about 1 h under ambient conditions in a controlled temperature room (∼25 °C) and in relative humidity below 30%. The resulting black powders of perovskites were sieved in a 250 μm aperture sieve (60 mesh), dried, and annealed for 6 h at 60 °C in a laboratory oven with periodic (once an hour) stirring. Pelletized powders were produced with 150–160 mg of the powders uniformly spread into a 10 mm diameter circular cavity of a metallic mold and compacted with a pressure of about 250 MPa. Lastly, the pellets were sintered in an electric furnace at 120 °C for 2 h and slowly cooled to room temperature inside the electric furnace. Several pellets of each composition were synthesized and used in the present study.The crystalline structure of the materials was characterized by X-ray diffraction (XRD) using a Rigaku Ultima IV diffractometer with CuKα1 radiation (λ = 1.5406 Å), under 40 kV and 20 mA, with continuous scanning (2° min−1), under controlled conditions (dark, at approximately 22 °C and relative humidity below 30%), in the range of 2θ from 10° to 16°. The microstructure images of the samples were obtained using a Zeiss EVO LS15 scanning electron microscopy (SEM) system, with a tungsten beam operating in the voltage range between 10 and 20 kV, by secondary electron analysis. Coupled energy-dispersive X-ray spectroscopy (EDS) analysis was performed using an Oxford Instruments INCA x-act system. Iodine and lead elemental composition estimations were based on EDS analyses in regions of 1278 × 684 μm. Thermogravimetric analysis (TGA) was performed using a Netzsch STA 449 F3 Nevio analyzer under nitrogen flux, using an open 85 μL alumina crucible filled with powdered perovskite masses of about 15 mg, from 30 °C to 330 °C at a heating rate of 10 °C min−1 proceeded by a 90 min isotherm at 330 °C. Coupled mass spectroscopy (MS) analysis was performed using a QMS 403 C Aëolos spectrometer using an electron multiplier detector, under nitrogen flux, in an m/z ion scanning range of 0.02, integration time per m/z of 200 ms, detector voltage of 2500 V, and analyzed m/z range from 40 to 160.
For the thermal degradation experiments, the pellets were placed in a 60 × 15 mm glass Petri dish and heated for up to 110 h at 150–200 °C in an electric oven under ambient air in the dark. After predefined intervals, the samples were removed from the oven and rapidly cooled to ∼22 °C and XRD, SEM, and EDS data were collected. Precautions were taken so that the same faces of the samples were always exposed to air during the heat treatment in the oven. Except when intentionally desired, the XRD data were always collected on those same faces, with care always taken to position the samples in the same arrangement in the sample holder.
3. Results and discussion
To understand the degradation behavior of different mixed-cation compositions, possible temperature-induced GAPbI3 segregation in GA+-containing compositions and its consequences, the first set of experiments aimed to track time-temperature phase changes and determine the rate constants (k) at different temperatures for MAPbI3 (MAPI), FA0.10MA0.90PbI3 (FA0.10), GA0.05FA0.05MA0.90PbI3 (TC), and GA0.10MA0.90PbI3 (GA0.10) compositions. We estimated the degradation rate constants by tracking the time-dependent vanishing of XRD peaks related to the perovskite crystalline phase when submitted to the thermal treatments at different temperatures. For this study, the degradation extent is described by the expression α(t) = 1 − A(t)/A0, where A(t) is the perovskite XRD peak area (integrated intensity) after a given degradation time t, and A0 is the initial perovskite peak area, which has been previously used to model the different effects of mixed A-site compositions of HPs.28 The foregoing analysis of the XRD data was based on the 10° to 15° range, which contains the signature peaks of relevant phases related to the studied materials. Ideally, the complete diffractograms should be used for such; however, due to the number of diffractograms needed for the present work (more than 400), it would have been unfeasible to collect the complete diffractograms for all composition-time-temperature conditions. Extensive elaborations of the limitations of the use of areas in this type of study, and how to deal with them, can be found elsewhere.47,57 Despite that, other similar studies were based in the area of the selected XRD peaks.48–50 Potential quantitative errors are clear and so making direct comparisons between the various results present in the literature is difficult as the results are highly sensitive to experimental conditions, material architecture, and the methods used in data analysis. This is exemplified by the number of different models that can be employed to interpret results.47 However, the results presented here were obtained using the same methodology, so a self-comparison is quite reasonable. That said, the time and temperature-dependent XRD data used in this study are summarized in Supplementary Note 1 (ESI†), while details of the modeling used are given in Supplementary Note 2 (ESI†).Fig. 1a shows the degradation extent as a function of time, α(t), for the MAPbI3, FA0.10MA0.90PbI3, GA0.05FA0.05MA0.90PbI3, and GA0.10MA0.90PbI3 samples at different temperatures in the 150–200 °C range. In addition to the fact that the degradation rate increased with temperature for all compositions, the most important observation was that the time-dependent degradation extent profiles of the compositions MAPI, FA0.10, and TC were similar, but different from those observed for GA0.10. Similarly, as recently observed,28 in the present work, the thermal degradation in the first three compositions seemed to follow a first-order kinetics since it followed a linear behavior in a plot of ln(1−α) versus t. In contrast, the latter followed a second-order reaction kinetics according to linearization of the data in a plot of 1/(1 − α) versus t. In fact, in the respective diffractograms, at all temperatures between 150 °C and 200 °C, increasing the thermal treatment time for the composition GA0.10 was accompanied not only by the intensification of the peak associated with PbI2 simultaneously with the decrease in peak associated with perovskite but also a concurrent emergence and peak intensification associated with GAPbI3. On the other hand, in MAPI, FA0.10, and TC, only the signs of the emergence and increase of the PbI2 and the vanishing of the perovskite were present. Again, two simultaneous thermal degradation pathways led to the change from a first to a second-order reaction kinetics in the studied mixed-cation halide perovskites.
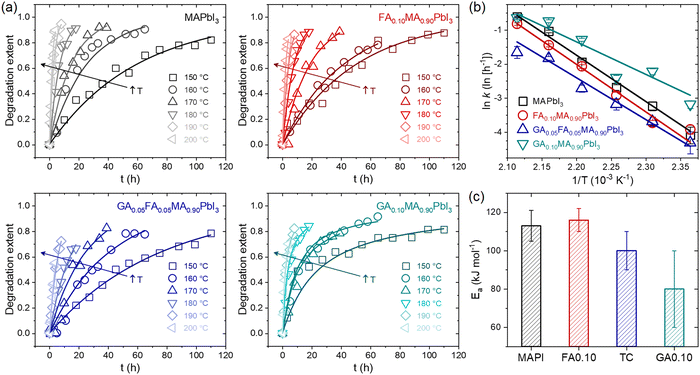 | ||
| Fig. 1 (a) Degradation extent α(t) of the MAPbI3 (MAPI), FA0.10MA0.90PbI3 (FA0.10), GA0.05FA0.05MA0.90PbI3 (TC), and GA0.10MA0.90PbI3 (GA0.10) compositions as a function of time at different temperatures. Dots are the data obtained from XRD measurements. Lines are reconstructed curves using the rate constants extracted from respective linear fits (details in Supplementary Note 2, ESI†). (b) Temperature dependency of the rate constants in the form of linearized Arrhenius plots. Lines are linear fits using an Arrhenius model. (c) Activation energies for thermal degradation obtained from linear fits for the Arrhenius plot data. | ||
Fig. 1b shows plots of 1n(k) versus 1/T to compare the relative thermal stabilities of the studied compositions. The results, in the form of a linearized Arrhenius plot, are given in the rate constant perspective, whereby the thermal stability of the studied compositions followed the order GA0.10 < MAPI < FA0.10 < TC over the entire temperature range. To obtain the activation energies for thermal degradation (Ea), we modeled the temperature dependency of the rate constant with an Arrhenius equation of the form k = k0 exp(−Ea/RT), where k0 is a constant, R is the universal gas constant, and T is the temperature. The results are given in Fig. 1c. The MAPbI3 activation energy was about 110 kJ mol−1, in agreement with values from 80 to 120 kJ mol−1 reported in the literature.34,35,56,57 Considering the error bars, there seemed to be a trend of the activation energies lowering with the average size of the A-site cations. The commonly used effective ionic radii of MA+, FA+, and GA+ are 217, 253, and 278 pm,58 respectively. Hence, the average A-site cation size increased in the order MAPI < FA0.10 < TC < GA0.10. When the substituting and host cations have different radii, a lattice distortion is accompanied by a crystal strain, which should increase the system's accumulated elastic energy. In other words, the enthalpy of mixing was possibly positive for all the mixed-cation compositions, as expected from the theoretical results.59 Hence, with the increasing difference between the cations, the greater the enthalpy of mixing. Since the activation energy is related to the enthalpy changes between the reactants and the transition state, it was unsurprising that the activation energy decreased with the average size of the substitute cation. Although contradictory at first glance, the compositions FA0.10 and TC had lower k values than pure MAPI because they were entropically stabilized (which reduces the k0 term) and did not have additional degradation pathways, as was the case for GA0.10. This hypothesis is corroborated by the fact that, among the studied compositions, the highest mixing entropy occurred for TC, which was the one with the lowest k value. The difficulties in assigning the significance of activation energies in solid-state decomposition reactions is worth pointing out.60 Also, depending on the methods used, one of more activation energies could be obtained, indicating reactions with multiple steps.46 With the employed analysis, we could not distinguish processes with several steps, hence the results may reflect an average of more than one step or of the rate-limiting step. This would complicate the scenario if compositions had more than one volatile component. But, as will be shown, the thermally induced mass loss was largely due to the elimination of MA+-related species. Hence, whatever the significance of the decomposition activation energy for the MAPbI3-based materials, it was clear that the composition effects were solely based on the kinetics of MA+-related decomposition and not on other volatiles.
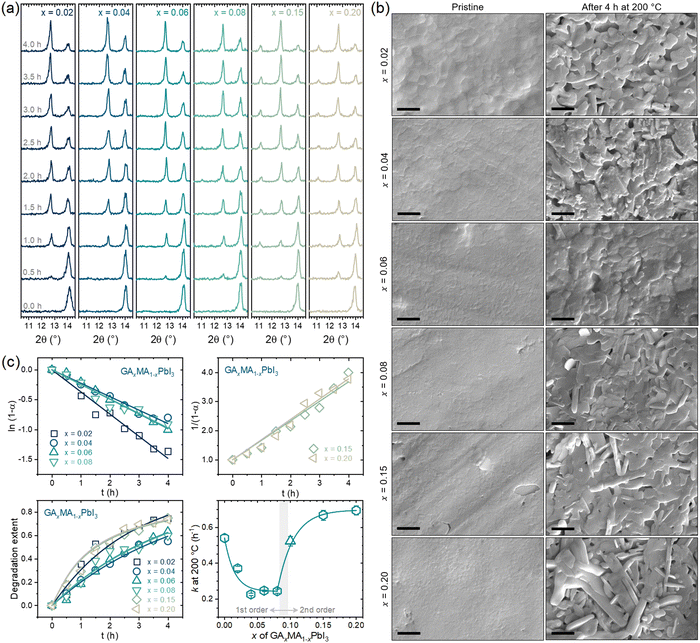
A critical aspect of processes in solid-state materials is the microstructural changes that occur during the reactions. To track these changes, we collected SEM images of samples of the studied compositions submitted to thermal treatment at 200 °C for up to 4 h. Fig. 2a shows the SEM microstructure images of the studied samples as prepared and after thermally treated at different times at 200 °C. For all compositions, we observed a general behavior of appearance and increasing volume fraction of secondary phases from the initially dense and homogeneous microstructures. At later stages, voids started to appear, resulting in a completely modified surface. One interesting aspect was that the formation of voids was severely delayed in the mixed-cation compositions. For pure MAPI, voids could be clearly identified after 90 min of thermal treatment. For the other compositions, these voids were only present after at least 120 min, with the extreme case being that for TC, where voids could only be identified after 240 min (4 h). Not surprisingly, this was the composition with the lowest thermal degradation rate constant. Another interesting aspect was that for MAPI, FA0.10, and TC, the first secondary phases appeared to be round-shaped and somewhat bright, possibly related to the PbI2 phase identified in the XRD data. On the other hand, for GA0.10, the first secondary phase appeared to have an elongated shape, which was only later followed by the presence of the round-shaped segregates. This elongated microconstituent had the same aspect as the secondary phases present in GAxMA1−xPbI3 compositions above the solubility limit of GA+.61 Hence, as expected, we conclude that these different segregates that appeared in GA0.10MA0.90PbI3 were due to GAPbI3. The appearance of PbI2 in the microstructure of lead iodide-based perovskites is a common feature when the materials eliminate volatiles from the reactions mentioned earlier. It suggests that these processes start at the surface, giving rise to the formation of PbI2 segregates, while, at later stages, the internal layers start to degrade as well, forming the voids. This observation agrees with the demonstration that the degradation of MAPbI3 is initiated at the surfaces and progresses toward the bulk of the material.62 For GA0.10MA0.90PbI3, the fact that GAPbI3 segregates appeared before or simultaneously to PbI2, not after, was also observed in the XRD data and suggests that both degradation pathways occur somewhat independently, as will be discussed ahead.
Fig. 2b summarizes the SEM cross-section images of the as-prepared sample and after being thermally treated at 200 °C for 240 min. These images were obtained to understand how deep the thermally induced formation of voids was across the bulk. At the deeper layers away from the surface, the only microstructural change appeared to be due to continued sintering, i.e., densification and grain growth processes. In this sense, microstructural changes indicative of thermal degradation processes, the formation of secondary phases, and voids appeared to be restricted to only a few microns at the surface of the samples. This expected behavior is typical of the inherent diffusional restrictions of solid-state materials. To be released, the volatiles must reach the surface. The initial components at the surface are readily prompted to react, but the deeper components must diffuse over increasing distances to react. On the other hand, the role the local atmosphere and its dynamics play in the rate of degradation must be questioned. It is known that molecular oxygen contributes to the decomposition of MAPbI3.63 As shown in Supplementary Note 3 (ESI†), the comparison between the visual aspects and diffractograms of the sample′s directly exposed and non-exposed surfaces shows that thermal degradation was severely reduced at the non-exposed surface. This could be mainly attributed to the continuous convection of oxygen and moisture and the impossibility of achieving equilibrium at the exposed surface. In turn, on the non-exposed surface, a state of equilibrium could be reached as the gases released by the material might be trapped in the grooves between the sample and the sample holder (glass), preventing the progression of thermal decomposition reactions. This exemplifies why encapsulation should be necessary for halide perovskite devices whenever possible.
In addition to modifying the phase composition and microstructure of the materials under heat treatment, it is also essential to understand the chemical changes that result from thermal degradation. As emphasized, it is notable that hybrid perovskites based on lead iodide leave solid PbI2 as one of the degradation products through the elimination of volatiles. To understand these transformations, we performed EDS measurements of the surface of the samples, as shown in Fig. 2, to estimate the iodine-to-lead ratio as a function of time. Fig. 3 shows the EDS iodine/lead molar ratio quantification as a function of heat treatment time.
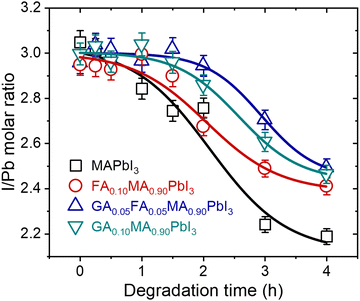 | ||
| Fig. 3 Surface EDS iodine-to-lead molar ratio quantification as a function of time for samples treated at 200 °C. Lines were added as guides for the eyes. | ||
For all compositions, the iodine-to-lead molar ratio varied from an initial value of 3 to values theoretically tending to 2. Although the quantitative limitations of estimating the chemical composition through EDS results are recognized, it is notable in our results that the mixed-cation compositions presented a lower I/Pb molar ratio reduction rate than pure MAPbI3. After 4 h of heat treatment, the I/Pb molar ratio in the mixed-cation samples was 2.4 to 2.5, while in MAPbI3 it was 2.2. These results suggest that entropic stabilization in mixed-cations compositions strongly mitigates the elimination of volatiles by the materials. This was true even for GA0.10, even though it was the composition with the highest thermal degradation rate constants. This is a robust indication that the thermal degradation in this composition is strongly affected by the concomitant segregation of GAPbI3 and is not only due to the elimination of volatiles.
Considering the above results, we also tracked the correlated mass changes during the thermal treatments. The results from thermogravimetric analyses under two heating regimes, shown in Fig. 4a, clearly corroborated that the mass loss rate in MAPbI3 was much higher than in the other compositions. Not surprisingly, the relative mass loss was also the highest for MAPbI3 after the experiment.
With the clear perspective of gases being released from the materials, it must be asked if there are differences in the gas profile with time/temperature and from one composition to another. The mass spectra were periodically collected during the thermogravimetric experiments. The results are shown in Fig. 4b. For all the compositions, the main relevant peaks to appear had the same m/z values of 58, 127, and 142. It is also clear that no other peaks appeared within the time/temperature of the thermal treatment; the only variations corresponded to the intensities of the peaks. Noteworthy, the peak at m/z = 127 was the most intense in all compositions, but in the guanidinium-containing ones, the relative intensity of the peak at m/z = 58 was higher than the others. These peaks could all be attributed, directly or indirectly, to the initial decompositions of methylammonium cations to NH3 and CH3I.35 The peaks at m/z = 127 and 142 were respectively due to I+ and CH3I+ ions formed from CH3I, while the peak at m/z = 58 was due to C3H8N+ ions, attributed to the presence of (CH3)3N formed from the reaction of trapped NH3 molecules with the host methylammonium cations of the perovskite. A corroboration of this pathway was given by observing the peak at m/z = 42 (Supplementary Note 4, ESI†) associated with C2H4N+ ions, also arising from (CH3)3N. The changes in the relative intensities between the peaks in the different compositions may be due to the observed ions coming from other sources, for example, I+ from I2, and from kinetic/thermodynamic modifications that lead to certain pathways and products being preferred over others. One corroboration for such is that MAPI presented a two-step mass loss attributed to the sequential release of CH3I and NH3,35 while the mixed-cation compositions displayed a single-step mass loss regime. Although the present results do not allow establishing these distinctions, it is clear that even though the nature of the FA+ and GA+ cations present differently affected the thermal stability of the material, there was no evidence, at least in the temperature range studied and the detection limit of the equipment, that these cations were degraded or eliminated during the thermal treatment. For example, the thermal degradation of formamidinium cations has been reported to lead to the formation of sym-triazine, for which related peaks would be present at m/z = 54 and 81,44 both of which were absent in our results. With that in mind, it is quite likely that the mass loss resulting from thermal degradation in our materials was largely due to the elimination of methylammonium. In fact, methylammonium is very well known to be volatile, while formamidinium and guanidinium could be expected to be much less susceptible to being released from the halide perovskites because they are larger, less acidic, and capable of forming more hydrogen bonds than methylammonium. It should be noted that the final mass of MAPI was 73% of the initial mass, which was close to the theoretical remaining mass of 74.3% considering the complete release of organic molecules. For the other compositions, between 75% and 77% of the initial masses remained after the thermal treatment. Simple mass balances indicate that this difference was due to non-volatile GA+- and FA+-related molecules.
Regarding, again, the segregation of GAPbI3 in the composition GA0.10, one of the outcomes of the previous results pointed toward the following scenario. When the material is subjected to thermal degradation, there is a major volatilization of MA+ and derived molecules but much less, if any, of GA+. When this occurs, the mole fraction of GA+ increases. Although the extent of the damage, that is, the volume of material subject to thermal degradation, is small, there may not be the time necessary for the redistribution of GA+ cations, such that in the degraded layers, the concentration of GA+ becomes much higher than that in the bulk of the material. If the proper conditions were to be achieved, i.e., a local supersaturation, there may be GAPbI3 segregation. In this case, for compositions with high initial GA+ concentrations, a smaller degradation extent would be required to reach local GA+ supersaturation and trigger GAPbI3 segregation. Also, it must be considered that the higher the concentration of GA+, the greater the mitigation of ion transport64,65 therefore, the more difficult (slow) the redistribution of ions would be, translating into the local concentration of GA+ increasing quicker. Given this plausible scenario, we studied the thermal degradation behavior of GAxMA1−xPbI3 compositions with x up to 0.20.
Fig. 5a presents the XRD results of the compositions subjected to a thermal treatment of up to 4 h. For all compositions, there was a clear vanishing of the perovskite peak at ∼14° with the appearance and intensification of the PbI2 peak at ∼12.5° with the thermal treatment time. For the compositions with x = 0.15 and 0.20, there was also a prompt appearance and intensification of the peak at ∼11° attributed to GAPbI3. This is the same behavior previously observed for x = 0.10. For x = 0.06 or lower, no GAPbI3 peaks could be identified, while for x = 0.08, the GAPbI3 peak appeared, but only at later degradation times. These results indicate a GA+ concentration threshold, around x = 0.08, below which there appears to be no segregation of GAPbI3. The same conclusions can be drawn from the surface SEM images of the pristine and fully degraded samples, as shown in Fig. 5b, where it can be noted that for compositions with x up to 0.06 there were no elongated microconstituents indicative of GAPbI3, which could be seen for compositions with x = 0.08 or higher. This follows the proposed idea of its formation being because of volatilizing MA+ cations and aligns with GAPbI3 being formed concomitantly to PbI2, not consequently to it. The two phases are formed simultaneously but independently, starting from the same chemical phenomenon. We obtained the degradation extent with the XRD data as a function of time and respective rate constants. The results are given in Fig. 5c.
One of the most important aspects to note is that for the compositions with low GA+ concentration (x ≤ 0.08), the degradation was found to follow a first-order kinetics while a second-order kinetics was followed for the compositions with high GA+ concentration (x ≥ 0.15). Hence, as a general rule, it can be concluded that the segregation of GAPbI3 provokes a change from a first- to a second-order reaction kinetics. From our results, this was not true only for the composition with x = 0.08, which might be due to the comparatively low GAPbI3 segregation or because it was formed only at later stages of degradation. When we include the previous results for x = 0.10, we also noted a clear and expected trend of larger rate constants for compositions where GAPbI3 was extensively formed, leading to second-order reaction kinetics.
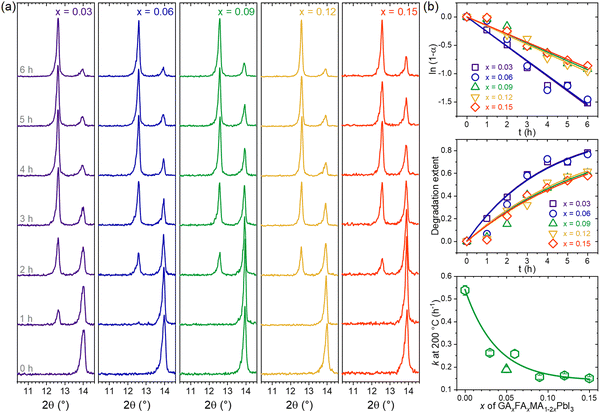
Now, following earlier results with the TC composition, which showed the highest thermal stability (lowest rate constant), we wanted to further explore the behavior of the thermal degradation kinetics in other compositions with equal amounts of GA+ and FA+ (GAxFAxMA1−2xPbI3 system). From the XRD results shown in Fig. 6a, we note that all compositions displayed the same behavior of vanishing perovskite peaks with the appearance and intensification of PbI2 peaks. One surprising feature was that compositions with GA+ = FA+ up to 0.15 did not segregate GAPbI3. Other compositions of the type GAxFAyMA1−x−yPbI3, with x = 2y and y = 2x, were tested using the same approach (see details in Supplementary Note 5, ESI†). Surprisingly, none of the compositions, even the ones with a total substitution content of up to 0.30, showed any signals for GAPbI3 segregation. This remarkable result suggests that FA+ strongly inhibits the formation of GAPbI3. We wonder if this also holds for other compositions with large cations, such as ethylammonium and dimethylammonium. This will be the subject of future work.
Fig. 6b shows the thermal degradation extents and rate constants of GAxFAxMA1−2xPbI3 compositions obtained from the XRD data. The results for the other GAxFAyMA1−x−yPbI3 compositions are given in Supplementary Note 5, (ESI†). In all cases, the degradation behavior could be modeled assuming first-order reaction kinetics, which is consistent with the fact that none showed the segregation of GAPbI3. Also, increasing the substitution contents decreased the rate constants, as observed in the literature,48 when no secondary phases other than PbI2 were formed.
Lastly, to better understand the effect of composition on the thermal stability of the halide perovskite system under study, we constructed a ternary diagram to correlate the guanidinium and formamidinium contents with the rate constant of thermal degradation. To do so, we organized all the previous results at 200 °C and complemented the data with additional experiments in FAxMA1−xPbI3 compositions at the same temperature (Supplementary Note 6, ESI†). The results, in the form of a heat map, are summarized in Fig. 7.
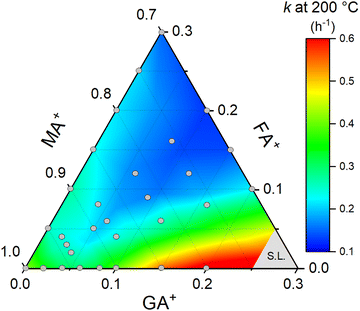 | ||
| Fig. 7 Composition map for the thermal degradation rate constants at 200 °C for GAxFAyMA1−x−yPbI3 perovskites. Gray circles are the compositions for which we obtained experimental rate constants. The data are presented in Supplementary Note 7 (ESI†). The region denoted as S.L. were compositions above the solubility limit,29 not considered in this work. To construct the heat map, a smoothing parameter of 0.5 and total points increase factor of 1 were used to highlight the composition-dependent trends of the rate constants. | ||
The general trend observed was a lowering of the rate constant with increasing the substitution contents. This can be explained based on the entropic stabilization of mixed-cation compositions aligned with the reduced molar fraction of the volatile component, i.e., the methylammonium cations. This effect was intensified in the compositions with close to equimolar fractions of guanidinium and formamidinium, which showed the lowest rate constant values and, thereby, highest thermal stabilities, possibly due to increased entropic stabilization contributions. On the other hand, the guanidinium-rich compositions had higher rate constants. This may derive from the fact that guanidinium cations are large and destabilize the system through highly endothermic mixing, but certainly, the main reason for this is the segregation of GAPbI3 in compositions with high guanidinium contents. Lastly, it should be stressed that even though this study was conducted in thick samples, the trends in Fig. 7 would possibly be the same in thin films since the degradation processes are restricted to the surface.
4. Conclusions
Using a broad range of time and temperature conditions for thermal degradation, experimental techniques, and compositions based on the system GAxFAyMA1−x−yPbI3, we showed that, in general, mixed-cation halide perovskites possess lower degradation rate constants, indicative of higher thermal stabilities. However, guanidinium-rich compositions tend to display higher rate constants. Mass loss processes seem localized at the surfaces and vastly controlled by the release of methylammonium and related chemical species, leaving solid-state PbI2. For some guanidinium-rich compositions, the volatilization of methylammonium triggered the segregation of GAPbI3, acting as an additional thermal degradation pathway that led to lower thermal stability. Contrary to expectations, the activation energies for thermal degradation seemed to decrease with substitution by cations larger than methylammonium, possibly due to endothermic mixing. In this sense, higher thermal stabilities might be controlled by the positive entropy of mixing, which also explains why the compositions with equimolar substitution degrees possessed lower degradation rate constants. Noteworthy, compositions with both FA+ and GA+ tended to be much less prone to segregate GAPbI3, even for high GA+ contents. This work provides a conceptual basis for the important design variables that need to be considered to achieve high thermal stabilities in halide perovskites.Author contributions
F. B. Minussi: conceptualization, methodology, validation, formal analysis, investigation, writing – original draft, writing – review and editing, and visualization. R. M. Silva Jr.: investigation, writing – review and editing. J. F. Carvalho: conceptualization, methodology, validation, investigation, resources, writing – review and editing, and funding acquisition. E. B. Araújo: conceptualization, methodology, resources, writing – review and editing, supervision, project administration, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP Project: 2017/13769-1), the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES-PRINT Project: 88881.310513/2018-01), and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (151319/2023-5). The authors thank Mr Elton José de Souza for supporting SEM experiments and CRTI for the measurements of TGA coupled to mass spectroscopy.References
- W. Zhang, G. E. Eperon and H. J. Snaith, Nat. Energy, 2016, 1, 1 Search PubMed.
- C. He and X. Liu, Light: Sci. Appl., 2023, 12, 15 CrossRef CAS PubMed.
- L. Chouhan, S. Ghimire, C. Subrahmanyam, T. Miyasaka and V. Biju, Chem. Soc. Rev., 2020, 49, 2869 RSC.
- M. J. Seol, S. H. Hwang, J. W. Han, H. W. Jang and S. Y. Kim, ACS Appl. Electron. Mater., 2023, 5, 5261 CrossRef CAS.
- F. Temerov, Y. Baghdadi, E. Rattner and S. Eslava, ACS Appl. Energy Mater., 2022, 5, 14605 CrossRef CAS PubMed.
- H. Huang, B. Pradhan, J. Hofkens, M. B. J. Roeffaers and J. A. Steele, ACS Energy Lett., 2020, 5, 1107 CrossRef CAS.
- X. Zhu, Y. Lin, J. San Martin, Y. Sun, D. Zhu and Y. Yan, Nat. Commun., 2019, 10, 2843 CrossRef PubMed.
- H. Wei and J. Huang, Nat. Commun., 2019, 10, 1066 CrossRef PubMed.
- G. Kakavelakis, M. Gedda, A. Panagiotopoulos, E. Kymakis, T. D. Anthopoulos and K. Petridis, Adv. Sci., 2020, 7, 2002098 CrossRef CAS PubMed.
- T. Huang, S. Tan and Y. Yang, J. Phys. Chem. C, 2021, 125, 19088 CrossRef CAS.
- N. Li, X. Niu, Q. Chen and H. Zhou, Chem. Soc. Rev., 2020, 49, 8235 RSC.
- S.-P. Feng, Y. Cheng, H.-L. Yip, Y. Zhong, P. W. K. Fong, G. Li, A. Ng, C. Chen, L. A. Castriotta, F. Matteocci, L. Vesce, D. Saranin, A. D. Carlo, P. Wang, J. W. Ho, Y. Hou, F. Lin, A. G. Aberle, Z. Song, Y. Yan, X. Chen, Y. (Michael) Yang, A. A. Syed, I. Ahmad, T. Leung, Y. Wang, J. Lin, A. M. C. Ng, Y. Li, F. Ebadi, W. Tress, G. Richardson, C. Ge, H. Hu, M. Karimipour, F. Baumann, K. Tabah, C. Pereyra, S. R. Raga, H. Xie, M. Lira-Cantu, M. V. Khenkin, I. Visoly-Fisher, E. A. Katz, Y. Vaynzof, R. Vidal, G. Yu, H. Lin, S. Weng, S. Wang and A. B. Djurišić, J. Phys. Mater., 2023, 6, 032501 CrossRef.
- J. Zhuang, J. Wang and F. Yan, Nano-Micro Lett., 2023, 15, 84 CrossRef CAS.
- F. Baumann, S. R. Raga and M. Lira-Cantú, APL Energy, 2023, 1, 011501 CrossRef.
- S. Kundu and T. L. Kelly, EcoMat, 2020, 2, e12025 CrossRef CAS.
- X. Zhao, T. Liu, Q. C. Burlingame, T. Liu, R. Holley, G. Cheng, N. Yao, F. Gao and Y.-L. Loo, Science, 2022, 377, 307 CrossRef CAS PubMed.
- J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381 CrossRef CAS PubMed.
- J. Park, J. Kim, H.-S. Yun, M. J. Paik, E. Noh, H. J. Mun, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2023, 616, 724 CrossRef CAS PubMed.
- Z. Liang, Y. Zhang, H. Xu, W. Chen, B. Liu, J. Zhang, H. Zhang, Z. Wang, D.-H. Kang, J. Zeng, X. Gao, Q. Wang, H. Hu, H. Zhou, X. Cai, X. Tian, P. Reiss, B. Xu, T. Kirchartz, Z. Xiao, S. Dai, N.-G. Park, J. Ye and X. Pan, Nature, 2023, 624, 557 CrossRef CAS PubMed.
- F. Ma, Y. Zhao, Z. Qu and J. You, Acc. Mater. Res., 2023, 4, 716 CrossRef CAS.
- S. Liu, V. P. Biju, Y. Qi, W. Chen and Z. Liu, NPG Asia Mater., 2023, 15, 1 CrossRef.
- F. Ünlü, E. Jung, J. Haddad, A. Kulkarni, S. Öz, H. Choi, T. Fischer, S. Chakraborty, T. Kirchartz and S. Mathur, APL Mater., 2020, 8, 070901 CrossRef.
- F. Ünlü, E. Jung, S. Öz, H. Choi, T. Fischer and S. Mathur, in Perovskite Solar Cells, ed. M. Grätzel, S. Ahmad and S. Kazim, Wiley, 2021, pp. 1–31 Search PubMed.
- S. Wang, A. Wang and F. Hao, iScience, 2022, 25, 103599 CrossRef CAS PubMed.
- I. L. Ivanov, A. S. Steparuk, M. S. Bolyachkina, D. S. Tsvetkov, A. P. Safronov and A. Y. Zuev, J. Chem. Thermodyn., 2018, 116, 253 CrossRef CAS.
- F. B. Minussi, E. M. Bertoletti, J. A. Eiras and E. B. Araújo, Sustainable Energy Fuels, 2022, 6, 4925 RSC.
- C. L. C. Ellis, H. Javaid, E. C. Smith and D. Venkataraman, Inorg. Chem., 2020, 59, 12176 CrossRef CAS PubMed.
- F. B. Minussi, R. M. Da Silva and E. B. Araújo, J. Phys. Chem. C, 2023, 127, 8814 CrossRef CAS.
- F. B. Minussi, R. M. da Silva and E. B. Araújo, Inorg. Chem. Front., 2023, 10, 6129 RSC.
- S. Sun, A. Tiihonen, F. Oviedo, Z. Liu, J. Thapa, Y. Zhao, N. T. P. Hartono, A. Goyal, T. Heumueller, C. Batali, A. Encinas, J. J. Yoo, R. Li, Z. Ren, I. M. Peters, C. J. Brabec, M. G. Bawendi, V. Stevanovic, J. Fisher and T. Buonassisi, Matter, 2021, 4, 1305 CrossRef CAS.
- L. Liu, J. Lu, H. Wang, Z. Cui, G. Giorgi, Y. Bai and Q. Chen, Mater. Rep.: Energy, 2021, 1, 100064 CAS.
- A. Dualeh, P. Gao, S. I. Seok, M. K. Nazeeruddin and M. Grätzel, Chem. Mater., 2014, 26, 6160 CrossRef CAS.
- D. P. Nenon, J. A. Christians, L. M. Wheeler, J. L. Blackburn, E. M. Sanehira, B. Dou, M. L. Olsen, K. Zhu, J. J. Berry and J. M. Luther, Energy Environ. Sci., 2016, 9, 2072 RSC.
- B. Brunetti, C. Cavallo, A. Ciccioli, G. Gigli and A. Latini, Sci. Rep., 2016, 6, 31896 CrossRef CAS PubMed.
- E. J. Juarez-Perez, Z. Hawash, S. R. Raga, L. K. Ono and Y. Qi, Energy Environ. Sci., 2016, 9, 3406 RSC.
- J. A. McLeod and L. Liu, J. Phys. Chem. Lett., 2018, 9, 2411 CrossRef CAS PubMed.
- A. Latini, G. Gigli and A. Ciccioli, Sustainable Energy Fuels, 2017, 1, 1351 RSC.
- L. Ma, D. Guo, M. Li, C. Wang, Z. Zhou, X. Zhao, F. Zhang, Z. Ao and Z. Nie, Chem. Mater., 2019, 31, 8515 CrossRef CAS.
- A. Ciccioli and A. Latini, J. Phys. Chem. Lett., 2018, 9, 3756 CrossRef CAS PubMed.
- W. Kaiser, D. Ricciarelli, E. Mosconi, A. A. Alothman, F. Ambrosio and F. De Angelis, J. Phys. Chem. Lett., 2022, 13, 2321 CrossRef CAS PubMed.
- W. Kaiser, M. Carignano, A. A. Alothman, E. Mosconi, A. Kachmar, W. A. Goddard and F. De Angelis, J. Phys. Chem. Lett., 2021, 12, 11886 CrossRef CAS PubMed.
- D. W. Boukhvalov, I. S. Zhidkov, A. F. Akbulatov, A. I. Kukharenko, S. O. Cholakh, K. J. Stevenson, P. A. Troshin and E. Z. Kurmaev, J. Phys. Chem. A, 2020, 124, 135 CrossRef CAS PubMed.
- S. Biswas and B. M. Wong, Environ. Sci. Technol., 2023, 57, 6695 CrossRef CAS PubMed.
- E. J. Juarez-Perez, L. K. Ono and Y. Qi, J. Mater. Chem. A, 2019, 7, 16912 RSC.
- A. Ciccioli, R. Panetta, A. Luongo, B. Brunetti, S. V. Ciprioti, M. L. Mele and A. Latini, Phys. Chem. Chem. Phys., 2019, 21, 24768 RSC.
- A. Luongo, B. Brunetti, S. Vecchio Ciprioti, A. Ciccioli and A. Latini, J. Phys. Chem. C, 2021, 125, 21851 CrossRef CAS PubMed.
- T. Burwig, K. Heinze and P. Pistor, Phys. Rev. Mater., 2022, 6, 065404 CrossRef CAS.
- B. Charles, J. Dillon, O. J. Weber, M. S. Islam and M. T. Weller, J. Mater. Chem. A, 2017, 5, 22495 RSC.
- J. A. Schwenzer, T. Hellmann, B. A. Nejand, H. Hu, T. Abzieher, F. Schackmar, I. M. Hossain, P. Fassl, T. Mayer, W. Jaegermann, U. Lemmer and U. W. Paetzold, ACS Appl. Mater. Interfaces, 2021, 13, 15292 CrossRef CAS.
- W. Tan, A. R. Bowring, A. C. Meng, M. D. McGehee and P. C. McIntyre, ACS Appl. Mater. Interfaces, 2018, 10, 5485 CrossRef CAS PubMed.
- Y. Zhao, J. Zhang, Z. Xu, S. Sun, S. Langner, N. T. P. Hartono, T. Heumueller, Y. Hou, J. Elia, N. Li, G. J. Matt, X. Du, W. Meng, A. Osvet, K. Zhang, T. Stubhan, Y. Feng, J. Hauch, E. H. Sargent, T. Buonassisi and C. J. Brabec, Nat. Commun., 2021, 12, 2191 CrossRef CAS PubMed.
- Y. Zou, J. Eichhorn, J. Zhang, F. A. C. Apfelbeck, S. Yin, L. Wolz, C.-C. Chen, I. D. Sharp and P. Müller-Buschbaum, ACS Energy Lett., 2024, 9, 388 CrossRef CAS PubMed.
- Z. Chen, Z. Yang, S. Du, D. Lin, F. Zhang, Y. Zeng, G. Liu, Z. Nie and L. Ma, Phys. Chem. Chem. Phys., 2023, 25, 32966 RSC.
- X. Zang, S. Xiong, S. Jiang, D. Li, H. Wu, H. Ren, A. Cao, B. Li, Z. Ma, J. Chen, L. Ding, J. Tang, Z. Sun, J. Chu and Q. Bao, Adv. Mater., 2023, 2309991 CrossRef PubMed.
- F. Li, D. Wu, L. Shang, R. Xia, H. Zhang, Z. Huang, J. Gong, L. Mao, H. Zhang, Y. Sun, T. Yang, X. Sun, Z. Feng and M. Liu, Adv. Mater., 2024, 2311595 CrossRef PubMed.
- X. Yu, Y. Qin and Q. Peng, J. Phys. Chem. A, 2017, 121, 1169 CrossRef CAS PubMed.
- T. Burwig and P. Pistor, Phys. Rev. Mater., 2021, 5, 065405 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- H. Park, A. Ali, R. Mall, H. Bensmail, S. Sanvito and F. El-Mellouhi, Mach. Learn.: Sci. Technol., 2021, 2, 025030 Search PubMed.
- A. K. Galwey, J. Therm. Anal. Calorim., 2006, 86, 267 CrossRef CAS.
- F. B. Minussi, E. M. Bertoletti, S. P. Reis, J. F. Carvalho and E. B. Araújo, Chem. Commun., 2022, 58, 2212 RSC.
- I. Deretzis, E. Smecca, G. Mannino, A. La Magna, T. Miyasaka and A. Alberti, J. Phys. Chem. Lett., 2018, 9, 3000 CrossRef CAS PubMed.
- A. Senocrate, G. Y. Kim, M. Grätzel and J. Maier, ACS Energy Lett., 2019, 4, 2859 CrossRef CAS.
- F. B. Minussi, R. M. Silva and E. B. Araújo, Small, 2023, 2305054 Search PubMed.
- F. B. Minussi, R. M. Silva and E. B. Araújo, Interplay between cation composition and charge transport characteristics in GAxFAyMA1−x−yPbI3 halide perovskites, submitted, 2024.
Footnote |
| † Electronic supplementary information (ESI) available: It contains XRD data of thermally treated samples, determination of rate constants, differences between exposed and non-exposed surfaces, mass spectra at different thermal treatment times, thermal degradation data of GAxFAyMA1−x−yPbI3 perovskites, and degradation rate constants at 200 °C. See DOI: https://doi.org/10.1039/d4tc00395k |
| This journal is © The Royal Society of Chemistry 2024 |