Laser-induced breakdown spectroscopy to obtain quantitative three-dimensional hydrogen mapping in a nickel–metal-hydride battery cathode for interpreting its reaction distribution†
Susumu
Imashuku
 *,
Takumi
Kamimura
,
Tetsu
Ichitsubo
and
Kazuaki
Wagatsuma
*,
Takumi
Kamimura
,
Tetsu
Ichitsubo
and
Kazuaki
Wagatsuma
Institute for Materials Research, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai 980-8577, Japan. E-mail: susumu.imashuku.e8@tohoku.ac.jp
First published on 14th October 2022
Abstract
We present a method for obtaining a three-dimensional quantitative hydrogen distribution in a Ni–MH battery cathode using laser-induced breakdown spectroscopy (LIBS) and demonstrate that the reaction distribution in the cathode can be interpreted based on a state-of-charge (SOC) distribution converted from the hydrogen distribution. In this method, we measured the hydrogen emission-line intensities at 656.28 nm for a model cathode cycled five times at 2.3 mA cm−2 and a commercial Ni–MH battery cathode cycled 1000 times at 1C under a 3000 Pa helium atmosphere. Our results show that the average SOC in the SOC distributions of the cathodes agreed with those evaluated from X-ray diffraction and charge–discharge curves and that the overcharged areas exhibited SOC values above 100%. The present LIBS method will allow us to understand the deterioration mechanism of a Ni–MH battery and improve its cycle life and capacity.
Introduction
Nickel–metal hydride (Ni–MH) batteries have attracted attention for stationary battery applications where weight is not as critical, such as satellite, aircraft, and large-scale energy-storage systems.1,2 This attraction toward Ni–MH batteries is owing to their long cycle life at a deep depth of discharge, high durability, long-term stability, high recyclability, and low production cost1–3 compared with lithium-ion batteries that are used worldwide in portable devices and transportation vehicles. In stationary battery applications, Ni–MH batteries are operated at a high-power output, with a rapid charge–discharge cycle. This operational condition results in the deterioration of the cycle life and capacity of Ni–MH batteries because a nonuniform reaction distribution occurs on the electrodes. In particular, the cathode, which comprises Ni(OH)2 as an active material, readily exhibits a nonuniform reaction distribution because the cathode area is ∼0.7 times smaller than the anode area in commercial Ni–MH batteries.3 Thus, determining the state-of-charge (SOC) distribution in the cathode—which is closely linked to the reaction distribution—is a key to minimizing the inhomogeneous reaction distribution and improving the cycle life and capacity at a high-power output with a rapid charge–discharge cycle. For this purpose, it is necessary to establish an analytical method to quantitatively visualize the hydrogen distribution in the cathode because the charge–discharge cycle of the cathode involves the following proton-transfer reactions: | (1) |
Analytical techniques for visualizing hydrogen distributions have been actively applied to materials like steel.4 Currently, the hydrogen mapping in steel with the field of view ranging from mm2 to cm2 has been achieved using silver reduction and decoration,5 hydrogen microprint technique (HMT),6 scanning Kelvin probe (SKP),7 scanning Kelvin probe force microscopy (SKPEM),7 secondary ion mass spectroscopy (SIMS),8 neutron radiography,9–11etc. Some of these techniques are limited to surface analysis (silver reduction and decoration, HMT, SKP, and SKPEM) or to qualitative analysis (silver reduction and decoration, HMT, and SKPEM). Although SIMS and neutron radiography can provide three-dimensional hydrogen mappings, SIMS is conventionally applied for microanalysis (at a level below ∼0.1 mass%, which is more than two orders of magnitude lower than the hydrogen concentrations in the cathodes), and neutron radiography is not a convenient method because it requires a large-scale facility. Therefore, the development of an analytical technique suitable for determining the three-dimensional hydrogen distribution in the cathode of a Ni–MH battery is desirable.
Laser-induced breakdown spectroscopy (LIBS), which is an analytical technique for acquiring the optical spectrum emitted by atoms evaporated from a sample due to irradiation with a high-power-density pulsed laser, is one of the most promising methods for satisfying the above-mentioned requirements. This is because LIBS can display quantitative three-dimensional elemental distributions, including lithium mapping of electrodes in lithium-ion batteries.12–21 Additionally, LIBS can be performed in a laboratory (i.e., it does not require large-scale facilities). Several studies have employed LIBS to acquire quantitative hydrogen distributions; however, most studies have been limited to acquiring the hydrogen distributions in fuel gases.22–26 A few studies have obtained hydrogen distributions in solid materials using LIBS; however, the hydrogen distributions were qualitative or semiquantitative27–29 because only the intensities of the hydrogen emission line were displayed and the reference samples with known hydrogen concentrations were not measured. For the analysis of the hydrogen content of bulk materials without investigating the hydrogen distributions, some studies have succeeded in quantitatively obtaining hydrogen concentrations for zircaloy,30–32 titanium,33,34 minerals on Mars,35 and proteins36 using LIBS. In these studies, an internal-standard emission line—such as Zr I 655.0 nm, He I 667.8 nm, Ti I 498.2 nm, Ti I 656.5 nm, D I 656.1 nm, C I 247.9 nm, and O I 777.2 nm—was required for determining the hydrogen concentrations. By contrast, we have recently presented a method for estimating hydrogen concentrations ranging from 0.2 to 7.6 mass% in the bulk samples of MgH2 using LIBS, where only the hydrogen emission line (H I 656.28 nm) and reference samples with known hydrogen concentration were used to establish the calibration line.37 Thus, our LIBS method can measure hydrogen concentrations in any materials, including the cathodes of Ni–MH batteries. Then, we obtained a semi-quantitative two-dimensional hydrogen mapping of a model cathode of a Ni–MH battery using our LIBS method.38
The present study aims to develop a method using LIBS to quantitatively acquire the three-dimensional hydrogen distribution in the cathode of a Ni–MH battery. Subsequently, we examine the availability of the hydrogen distribution to interpret the reaction (SOC) distribution of the cathode. To the best of our knowledge, this is the first study to prove that LIBS can provide a quantitative three-dimensional hydrogen distribution in the cathode of a Ni–MH battery by measuring the hydrogen content quantitatively. In the present study, we first used a model Ni–MH battery cathode with a largely inhomogeneous reaction distribution to establish the method to quantitatively acquire the three-dimensional hydrogen distribution and SOC using LIBS. After that, the established LIBS method was applied to a commercial Ni–MH battery cathode for practical applications. Moreover, we show that the distribution of the charge–discharge reactions in the cathode can be interpreted based on the SOC distribution converted from the hydrogen distribution.
Experimental
A model cathode was prepared by mixing β-Ni(OH)2 powder (purity: 99.9%, Kojundo Chemical Laboratory Co., Ltd, Saitama, Japan), acetylene black, and polytetrafluoroethylene in a weight ratio of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. At this ratio, the hydrogen concentration of the pristine model cathode corresponded to 1.83 mass%. We stretched this mixture into a sheet using an agate mortar, cut the stretched model cathode into square shapes with a size of 10 mm × 10 mm, and pressed them into a nickel mesh (200 mesh, Nilaco Corporation, Tokyo, Japan) with a mesh size of 3 cm × 1.5 cm to obtain good electric contact between the nickel mesh and the model cathode. The thickness of the model cathode was ∼300 μm after it was pressed into the mesh. Except for an area that connected the nickel mesh with an electrode holder, the model cathode and the nickel mesh were sealed using Teflon adhesive tape and an epoxy adhesive to prevent the nickel mesh from being exposed to an electrolyte, as shown in Fig. 1(a). A charge–discharge test was performed in a three-compartment electrolysis cell at 25 °C (Fig. 1(b)). We used a 30 mm × 30 mm platinum plate as the anode and an Ag/AgCl electrode (2060A-10T, Horiba, Ltd, Kyoto, Japan) immersed in 3.33 M KCl (0.22 V vs. standard hydrogen electrode (SHE)) as the reference electrode. The electrolyte comprised a solution of 6 M KOH and 15 g L−1 LiOH,39 which was agitated using a magnetic stirring unit. The distance between the model cathode and the anode was 30 mm. The reference electrode was connected to the electrolyte via a 3.3 M KCl–agar salt bridge. We performed the first charge–discharge cycle and the second charge was conducted at 2.3 mA cm−2 using a potentiostat/galvanostat (HA-151B, Hokuto Denko Corporation, Tokyo, Japan), confirming that the fully charged potential was 0.60 V vs. SHE and the time required for complete discharge was 33 min. Subsequently, we repeated the cell discharge–charge cycle three times in 30 min at 2.3 mA cm−2 using a battery charge–discharge system (HJ1001SD8, Hokuto Denko Corporation, Tokyo, Japan). The cutoff voltages for the discharge and charge were fixed at 0.2 and 0.6 V (vs. SHE), respectively. After the charge–discharge test, the model cathode was gently washed using deionized water and stored in a desiccator containing silica gel for more than 3 days. Furthermore, we performed a charge–discharge test for a commercial Ni–MH battery with a capacity of 650 mA h using the same battery charge–discharge system. The thickness of the commercial Ni–MH battery cathode was 800 μm. The particle size of the active material (Ni(OH)2) in the cathode was ∼15 μm, and the chemical compositions of the cathode that were determined using X-ray fluorescence spectrometry (ZSX Primus II, Rigaku Corporation, Tokyo, Japan) are shown in Table 1. The battery was cycled 1000 times at 650 mA for 1 h (1C) with the cutoff voltages for the charging and discharging fixed at 1.95 and 0 V, respectively. The charge–discharge test was complete after the final charging. Subsequently, the cathode was removed from the battery in an argon-filled glove box where the concentrations of water and oxygen were controlled at less than 10 ppm. After the cathode was moved into ambient air, it was gently washed using deionized water and stored in a desiccator containing a silica gel for more than 3 days.
2. At this ratio, the hydrogen concentration of the pristine model cathode corresponded to 1.83 mass%. We stretched this mixture into a sheet using an agate mortar, cut the stretched model cathode into square shapes with a size of 10 mm × 10 mm, and pressed them into a nickel mesh (200 mesh, Nilaco Corporation, Tokyo, Japan) with a mesh size of 3 cm × 1.5 cm to obtain good electric contact between the nickel mesh and the model cathode. The thickness of the model cathode was ∼300 μm after it was pressed into the mesh. Except for an area that connected the nickel mesh with an electrode holder, the model cathode and the nickel mesh were sealed using Teflon adhesive tape and an epoxy adhesive to prevent the nickel mesh from being exposed to an electrolyte, as shown in Fig. 1(a). A charge–discharge test was performed in a three-compartment electrolysis cell at 25 °C (Fig. 1(b)). We used a 30 mm × 30 mm platinum plate as the anode and an Ag/AgCl electrode (2060A-10T, Horiba, Ltd, Kyoto, Japan) immersed in 3.33 M KCl (0.22 V vs. standard hydrogen electrode (SHE)) as the reference electrode. The electrolyte comprised a solution of 6 M KOH and 15 g L−1 LiOH,39 which was agitated using a magnetic stirring unit. The distance between the model cathode and the anode was 30 mm. The reference electrode was connected to the electrolyte via a 3.3 M KCl–agar salt bridge. We performed the first charge–discharge cycle and the second charge was conducted at 2.3 mA cm−2 using a potentiostat/galvanostat (HA-151B, Hokuto Denko Corporation, Tokyo, Japan), confirming that the fully charged potential was 0.60 V vs. SHE and the time required for complete discharge was 33 min. Subsequently, we repeated the cell discharge–charge cycle three times in 30 min at 2.3 mA cm−2 using a battery charge–discharge system (HJ1001SD8, Hokuto Denko Corporation, Tokyo, Japan). The cutoff voltages for the discharge and charge were fixed at 0.2 and 0.6 V (vs. SHE), respectively. After the charge–discharge test, the model cathode was gently washed using deionized water and stored in a desiccator containing silica gel for more than 3 days. Furthermore, we performed a charge–discharge test for a commercial Ni–MH battery with a capacity of 650 mA h using the same battery charge–discharge system. The thickness of the commercial Ni–MH battery cathode was 800 μm. The particle size of the active material (Ni(OH)2) in the cathode was ∼15 μm, and the chemical compositions of the cathode that were determined using X-ray fluorescence spectrometry (ZSX Primus II, Rigaku Corporation, Tokyo, Japan) are shown in Table 1. The battery was cycled 1000 times at 650 mA for 1 h (1C) with the cutoff voltages for the charging and discharging fixed at 1.95 and 0 V, respectively. The charge–discharge test was complete after the final charging. Subsequently, the cathode was removed from the battery in an argon-filled glove box where the concentrations of water and oxygen were controlled at less than 10 ppm. After the cathode was moved into ambient air, it was gently washed using deionized water and stored in a desiccator containing a silica gel for more than 3 days.
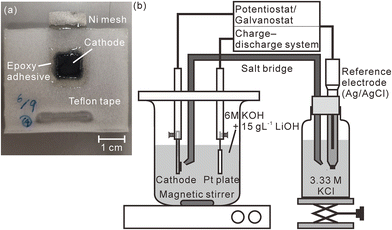 | ||
| Fig. 1 (a) Photograph of the model cathode and (b) schematic illustration of the charge–discharge test apparatus. The measured area is enclosed within the dotted line in Fig. 1(a). | ||
| F | Al | Mn | Co | Ni | Zn |
|---|---|---|---|---|---|
| 0.6 | 0.1 | 0.1 | 5.6 | 87.8 | 5.8 |
We performed LIBS measurements of the cathodes using a custom LIBS system described previously.37 In brief, the laser used in the present study was a Q-switched Nd:YAG laser (LS-2137, LOTIS TII Ltd, Minsk, Belarus) with a wavelength of 532 nm. The energy and duration of the pulsed laser used to irradiate the cathodes were 30 mJ per pulse and 16–18 ns, respectively. A single pulse from the laser was focused on the cathode surface using a plano-convex lens with a focal length of 150 mm and it was shot onto the cathodes for each measurement point. We defocused the laser to acquire sufficient emission intensities of a H I 656.28 nm line to determine the hydrogen contents of the cathodes. The focusing plane was under the ablation plane. The depth (from the surface to the deepest point in the dimple) and diameter of the dimples produced by each irradiation with the pulsed laser were ∼15 ± 5 μm and 250 ± 20 μm, respectively, which were measured by observing the sample surface after laser irradiation using a digital microscope (VHX-1000, KEYENCE Corp., Osaka, Japan).15,16 The light emitted from the plasma was collected using a plano-convex lens with a focal length of 100 mm and was transmitted through an optical fiber to a spectrometer system consisting of a Czerny–Turner spectrograph (MS 7504i, SOL instruments Ltd, Minsk, Belarus) with a resolution of 0.01 nm and an intensified charge-coupled device (ICCD) detector (DH334T-18F-03, Andor Technology Ltd, Belfast, UK). The gate of the ICCD detector was triggered via the laser, and the relative delay was controlled using a digital delay generator integrated into the ICCD detector. The gate width and relative delay were set to be 500 μs and 100 ns, respectively, because they provided the highest H I 656.28 nm emission intensities from the pristine model cathode. Each cathode was placed inside a chamber, thus enabling the atmosphere to be controlled by introducing gas and the connection of the chamber to a rotary pump. We attached a moisture trap (GL Sciences Inc., Tokyo, Japan) to the gas line between the chamber and the gas cylinder to remove water molecules from the introduced gas. The LIBS measurements were conducted under a helium atmosphere at 3000 Pa. The positions to be analyzed on the cathodes were controlled using linear-transition automatic stages that were placed under the chamber. We acquired the LIBS spectra of the cathodes by irradiating the same position on the cathodes 10 times each for the model cathode and 5 times each for the commercial Ni–MH battery cathode using a single shot pulsed laser, keeping the ablation plane and subsequently moving to the next position to be measured. The pitch of the measured points on the model cathode was 400 μm.
The phases of the cathodes were analyzed using X-ray diffractometry (XRD; Ultima IV/SG, Rigaku Corporation, Tokyo, Japan) using a Cu Kα line. The contents of the phases in the cathodes were calculated using XRD analysis software (PDXL, Rigaku Corporation, Tokyo, Japan). We also conducted elemental analyses of the slag samples using a SEM (TM3030 Plus, Hitachi High-Technologies Co., Tokyo, Japan) equipped with a silicon drift energy-dispersive X-ray (EDX) detector (Quantax70, Bruker Corp., Billerica, Massachusetts, USA).
Results & discussion
Hydrogen mapping of the model cathode
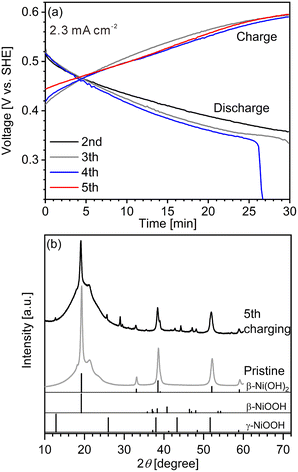
We first conducted LIBS measurement for a cathode with a largely inhomogeneous reaction distribution to easily confirm the validity of our hydrogen mapping method. However, obtaining cathodes of commercial Ni–MH batteries with an inhomogeneous reaction distribution is difficult because of their good cycle durability. The major reason for the good cycle durability is the formation of cobalt oxyhydroxide (β-CoOOH) surrounding β-Ni(OH)2 particles to maintain the electronic conductive network in the commercial Ni–MH battery cathodes.1,3,40 Thus, a cathode with an inhomogeneous reaction distribution is expected to be obtained easily using β-Ni(OH)2 which has a larger particle size than that of β-Ni(OH)2 in commercial Ni–MH battery cathodes (∼15 μm) without β-CoOOH. Consequently, we first prepared a model cathode comprising β-Ni(OH)2 (active material) with a relatively large particle size of ∼50 μm, acetylene black (conductive additive), and polytetrafluoroethylene (binder). The charge–discharge curves of the model cathode were in good agreement with the typical charge–discharge curves of a β-Ni(OH)2 cathode for a Ni–MH battery41–44 (Fig. 2(a)), demonstrating that the prepared model cathode functioned in the same way as the cathode of a Ni–MH battery. At the end point of the fourth discharging, the specific capacity of the model cathode was 19.3 mA h g−1, which is one-fifteenth of the theoretical capacity of β-Ni(OH)2 (289 mA h g−1),41,45–47 indicating that only a small part of the model cathode (∼7%) was involved in the charge–discharge reaction. The evolution of hydrogen and oxygen from the model cathode was also responsible for its lower specific capacity because the evolution of bubbles from the model cathode was observed during the charge–discharge cycle.Peaks of γ-NiOOH, that is produced by overcharging β-Ni(OH)2, was identified at 12.70° in the model cathode after the fifth charging by XRD (Fig. 2(b)), indicating the presence of preferentially charged areas in the model cathode. By contrast, peaks of β-NiOOH—which is the primary compound produced from β-Ni(OH)2 during the charging reaction—were not clearly detected by XRD because the primary peak of β-NiOOH (2θ = 19.19°) overlapped with that of β-Ni(OH)2 (2θ = 19.25°) and the second most intense peak of β-NiOOH was not detected at 40.75°. Instead, the intensity ratio of the peak at 19.24° to the peak at 33.12° in the model cathode after the fifth charging (I19.24°/I33.12° = 21) was higher than that in the pristine cathode (I19.24°/I33.12° = 12), suggesting that the presence of β-NiOOH because the peak at 19.24° originated from β-NiOOH and β-Ni(OH)2, whereas the peak at 33.12° only originated from β-Ni(OH)2. The contents of β-Ni(OH)2, β-NiOOH, and γ-NiOOH phases were roughly estimated as 70 mass%, 30 mass%, and ≤1 mass%, respectively, by the reference intensity ratio method using the XRD pattern of the model cathode after the fifth charging. Thus, XRD analysis also revealed that a large part of the model cathode (∼70%) was not involved in the charge–discharge reaction, which is roughly consistent with our findings from the charge–discharge curves.
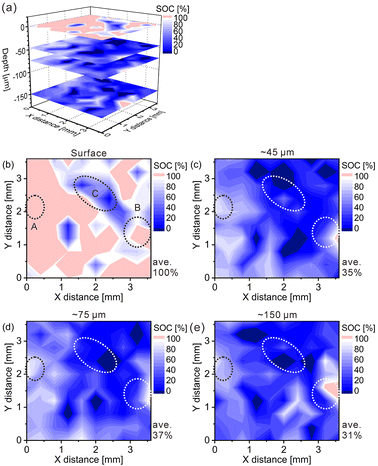
The charge–discharge curves and XRD patterns of the model cathode after the fifth charging suggest inhomogeneous charge–discharge reactions in the model cathode. We then conducted three-dimensional hydrogen mapping for the model cathode. The hydrogen mappings for 3D illustration and 2D illustrations of the first, third, fifth, and tenth layers from the surface are shown in Fig. 3(a–e). The tenth layer corresponds to ∼150 μm depth from the surface (the 1st layer). In these LIBS mapping measurements, we measured the emission intensities of the lower right quarter area of the model cathode shown in Fig. 1(a). To determine the hydrogen concentrations (CH2) in the model cathode, we assumed that the emission intensity of the H I 656.28 nm line for a pristine cathode corresponds to 1.83 mass% of hydrogen (Fig. 3(f)) and the emission intensity was zero at 0 mass% of hydrogen. Additionally, we considered that the emission intensity of the H I 656.28 nm line increased linearly with an increase in hydrogen concentration in the model cathode because our previous study demonstrated that the emission intensities of the H I 656.28 nm line increased linearly with an increase in hydrogen concentration of up to 7.6 mass%,37 as shown in Fig. S1.† The H I 656.28 nm line did not overlap with other emission lines, as shown in Fig. 3(f–h). We also confirmed that the effect of hydrogen originating from water molecules on the sample surfaces and in the measurement atmosphere on intensities of the H I 656.28 nm line can be minimized by storing the samples in a desiccator for over 3 days and attaching the moisture trap to the helium gas line.37 Additionally, we used a pristine cathode, whose structure was almost the same as the model cathode after the fifth charging, as a reference sample to establish a calibration line for determining the hydrogen contents. Ni(OH)2 is only involved in the charge reaction of the cathodes, and the molecular weight changes from 92.7 (Ni(OH)2) to 91.7 (NiOOH) by the charge reaction. This indicates that the chemical compositions of the cathodes are nearly unchanged during the charge–discharge cycle. The thicknesses and weights of both the pristine and the charged cathode were set to 0.15 g and 0.3 mm, respectively. Thus, the impact of the matrix effect is almost the same for the reference sample and the analyte. Table 2 shows the emission intensities of the H I 656.28 nm line for the pristine cathode and the standard deviations of the calibration lines are shown in Table 3. The emission intensity of the H I 656.28 nm line for the 1st layer was higher than those for the 3rd, 5th, and 10th layers because dimples formed on the model cathode surface by laser irradiation caused the absorption of a part of the light emitted from the model cathode (shielding effect), whereas this absorption does not occur for the first layer, which did not have the dimples. Below the 1st layer, a part of the emitted light is absorbed by the dimple wall, but this shielding effect was not a big difference among the 3rd, 5th, and 10th layers because the emission intensities of the H I 656.28 nm were close for each layer. To reduce influences on quantitative analysis caused by the shape of the dimple, such as shielding effect and heating effect, we established a calibration line for each layer. The relative standard deviation of the emission intensities for the 1st layer was relatively higher than those for the 3rd, 5th, and 10th layers, which showed similar values. This might be because the residual water molecules were not completely removed. Nevertheless, the relative standard deviations for all the layers were comparable to those of the reference samples that we used to acquire the calibration curve for determining the hydrogen concentrations in MgH2 samples.37 This indicates that the present LIBS measurements exhibit sufficient precision to determine the hydrogen concentrations of the model cathode. For example, using the present calibration line, the hydrogen concentration of NiOOH corresponded to 0.93 ± 0.08 mass% for the third layer of the model cathode. As shown in Fig. 3, we observe inhomogeneous hydrogen distributions in the model cathode after the fifth charging.
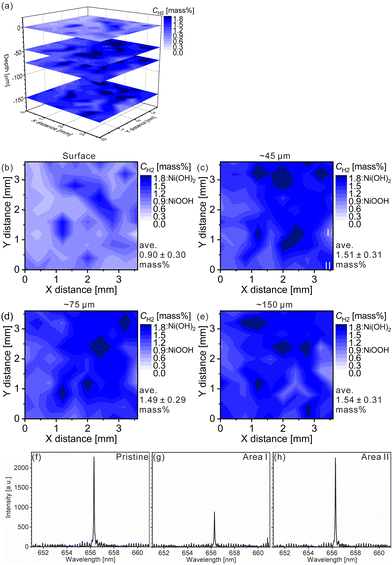 | ||
| Fig. 3 LIBS maps of the hydrogen concentrations (mass%) in the model cathode after the fifth charging for (a) 3D illustration and 2D illustrations of the (b) first layer, (c) third layer (∼45 μm in depth), (d) fifth layer (∼75 μm in depth), and (e) tenth layer (∼150 μm in depth). LIBS spectra of (f) the pristine cathode of the third layer and the model cathode after the fifth charging for areas (g) I and (h) II in Fig. 3(c). | ||
| Sample | State-of-charge [%] | Intensity [a.u.] | SD [a.u.] | RSD [%] | |
|---|---|---|---|---|---|
| a These values are assumed. | |||||
| Commercial Ni–MH battery cathode discharged at 0.1C | 1st layer | 0a | 3438 | 280 | 8.1 |
| 3rd layer | 0a | 1978 | 131 | 6.6 | |
| 5th layer | 0a | 1935 | 194 | 10.0 | |
| Commercial Ni–MH battery cathode charged at 0.1C | 1st layer | 100a | 5248 | 368 | 7.0 |
| 3rd layer | 100a | 2756 | 247 | 9.0 | |
| 5th layer | 100a | 2758 | 193 | 7.0 | |
| Standard deviation | |||
|---|---|---|---|
| Hydrogen content [mass%] | State of charge [%] | ||
| a “—” means not determined. | |||
| Model cathode | 1st layer | 0.21 (0.90 ± 0.30) | 23 (100) |
| 3rd layer | 0.15 (1.51 ± 0.31) | 16 (35) | |
| 5th layer | 0.16 (1.49 ± 0.29) | 17 (37) | |
| 10th layer | 0.15 (1.54 ± 0.31) | 16 (31) | |
| Commercial Ni–MH battery cathode | 1st layer | —a | 16 (0) |
| 3rd layer | — | 22 (15) | |
| 5th layer | — | 21 (21) | |
Furthermore, we converted the hydrogen distributions to SOC distributions by considering that the hydrogen concentrations of 1.83 and 0.93 mass% corresponded to the SOCs of 0% and 100%, respectively, as shown in Fig. 4. Table 4 lists the SOC reference values used for the conversion from the hydrogen concentrations, which were calculated from the reaction formula (1) and the weight ratio of β-Ni(OH)2 powder in the model cathode (85 mass%). As shown in Table 4, the SOC changed linearly with the hydrogen content. The charge–discharge reactions occurred in most areas of the first layer because ∼100% of the SOCs of the most measured points were distributed in the first layer. By contrast, ∼34% of the SOCs of the most measured points were distributed below the first layer, indicating that only a few areas in these layers were involved in the charge–discharge reactions. These SOCs were roughly consistent with the content of NiOOH phases (∼30%) estimated from the XRD patterns. Overcharged areas, which correspond to SOCs above100% (the pale red areas in Fig. 4), were detected in nearly half of the measured points in the first layer and a few measured points in the other layers of the model cathode, and the SOCs beneath the overcharged areas were also higher (e.g., areas A and B in Fig. 4(b)). Meanwhile, apparently ≤0% SOCs were observed beneath areas corresponding to ∼0% SOC in the first layer (e.g., area C in Fig. 4(b)). These results suggest that H+ diffused into a direction perpendicular to the model cathode during the charge–discharge reaction. The areas with apparently ≤0% SOCs under the third layer (the dark blue areas in Fig. 4), correspond to areas with hydrogen concentrations above 1.83 mass% (the dark blue areas in Fig. 3), which implies the presence of other compounds containing more hydrogen than β-Ni(OH)2. We observed areas with a high intensity of the characteristic X-rays of K on the model cathode subjected to LIBS measurement (Fig. 5), indicating that KOH, which is the residue of the electrolyte, was precipitated on the areas. Thus, the areas with apparently ≤0% SOCs on the model cathode indicate the presence of the residue of the electrolyte, such as KOH and LiOH.
 | ||
| Fig. 5 (a) SEM image and EDX elemental mappings of (b) O, (c) K, and (d) Ni for the model cathode after the fifth charging. | ||
| Hydrogen content [mass%] | 0.93 | 1.00 | 1.20 | 1.40 | 1.60 | 1.83 |
| State of charge [%] | 100 | 92 | 70 | 48 | 26 | 0 |
Information about the charge–discharge reactions of the model cathode, which we obtained from the SOC maps converted from the hydrogen maps obtained by LIBS, was consistent with that obtained from the charge–discharge curves and the XRD measurements; e.g., the inhomogeneous distribution of reactions, presence of overcharged areas, and large amounts of unreacted Ni(OH)2. This indicates that LIBS measurements can provide quantitative hydrogen mapping of the cathode of a Ni–MH battery and that we can evaluate the reaction distribution from the SOC distribution obtained from the hydrogen mapping.
SOC mapping of a commercial Ni–MH battery cathode
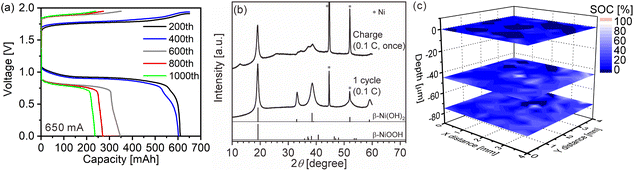
We quantitatively acquired hydrogen and SOC distributions for a model cathode of a Ni–MH battery using LIBS. Then, we next applied this method to the cathode in a used commercial Ni–MH battery for practical use. The Ni–MH battery was cycled 1000 times at 650 mA for 1 h (1C), and the charge–discharge curves of the Ni–MH battery are shown in Fig. 6(a). The capacity of the Ni–MH battery after the 1000th charging was 240 mA h, which is equivalent to 37% of its nominal capacity (650 mA h). Determining the hydrogen content in the cycled commercial Ni–MH battery cathode was difficult because the weight ratio of the active material in the cathode was unknown. Consequently, we displayed here only the SOC map according to the calibration line obtained under the assumption that the H I 656.28 nm line emission intensity corresponded to an SOC of 0% for the commercial Ni–MH battery cathode that was charged and discharged once at 65 mA for 10 h (0.1C) and the H I 656.28 nm line emission intensity corresponded to an SOC of 100% for the cathode after the commercial Ni–MH battery had been charged once at 0.1C, and the standard deviations of the calibration lines are shown in Table 3. The validity of this assumption was confirmed by XRD because peaks of β-NiOOH were detected and the peak only originating from β-Ni(OH)2 was not detected at 33.12° for the commercial Ni–MH battery cathode once charged at 0.1C, whereas the peak only originating from β-Ni(OH)2 was clearly detected at 33.12° for the commercial Ni–MH battery cathode that once experienced a charge–discharge cycle at 0.1C (Fig. 6(b)). Because we used the same brand of commercial Ni–MH battery cathodes with different charge–discharge conditions as the reference samples for degerming the SOC, we consider that the impact of the matrix effect is almost the same for the reference sample and the analyte. Furthermore, the relative standard deviations of the emission intensities in the two Ni–MH battery cathodes that once experienced a charge–discharge cycle and once charged at 0.1C showed similar values to those in the pristine cathode for the 3rd and 5th layers and were comparable to those of the reference samples that we used to determine the hydrogen concentrations in MgH2 samples37 (Table 2), indicating that the present LIBS measurements can quantitatively provide SOCs for the cycled commercial Ni–MH battery cathode. When we acquired the SOC maps from the surface to 80 μm depth in the cathode (Fig. 6(c)), the maps exhibited relatively uniform SOC distributions, compared with the model cathode. This demonstrates that the degradation of the commercial Ni–MH battery occurred uniformly in the planar and depth directions of the cathode. A few measured points exhibited apparently ≤0% SOCs (dark blue point in Fig. 6(c)). The points with apparently ≤0% SOCs were mostly detected near the surface, which had been contacted with the electrolyte. Unlike the model cathode, we did not observe areas with a high intensity of characteristic X-rays of K on the cathode subjected to LIBS measurement (Fig. 7), but the characteristic X-rays of K were detected in the EDX spectrum of the cathode (Fig. 7(b)). Thus, the areas with apparently ≤0% SOCs on the cathode indicate the presence of the residue of the electrolyte (e.g., KOH and LiOH), which supports that areas with apparently ≤0% SOCs were preliminary observed near the surface that had come into contact with the electrolyte. This suggests that the SOC mapping of the 5th layer was less affected by the residue of the electrolyte among the SOC mappings in Fig. 6(c). The average SOC of the 5th layer shown in Fig. 6(c) exhibited 21%, which is nearly consistent with the SOC evaluated from the charge–discharge curves (37%). We can obtain more precise SOC values and hydrogen concentrations of the cathode by thoroughly washing the cathode prior to the LIBS measurements. Nevertheless, to our knowledge, the present study is the first to demonstrate that three-dimensional quantitative SOC maps were obtained by measuring the hydrogen emission intensities using LIBS.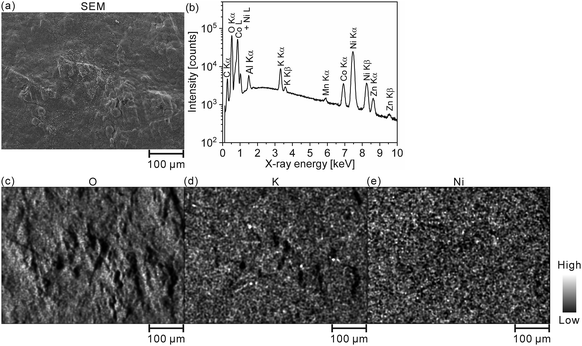 | ||
| Fig. 7 (a) SEM image and (b) EDX spectrum of the whole area in (a). EDX elemental mappings of (c) O, (d) K, and (e) Ni for the commercial Ni–MH battery cathode after the 1000th charging. | ||
The spatial resolution of the LIBS measurements in the present study was ∼250 μm in the plane and 15 μm in depth because the pulse duration of the laser in our LIBS system was 16–18 ns. This special resolution was insufficient for investigating the reaction distribution of a Ni–MH battery cathode. However, we can achieve a spatial resolution that is sufficient for such investigations (20 μm range in the plane and depth) by focusing the laser of the present set-up. In this case, however, the emission intensity of the H I 656.28 nm line will decrease, resulting in an increase of the error for determining the hydrogen contents. To overcome this issue, we will focus on improving the signal to noise ratio of the H I 656.28 nm line by reducing the residual water molecules on samples, and the measurement set-up (e.g., chamber and gas line) in future studies. Additionally, the LIBS system with a focused laser can contribute to the understanding of hydrogen embrittlement in metals and the improvement of performance in fuel cells and hydrogen-permeable films by acquiring their hydrogen distributions.
Conclusions
Herein, we presented a method to quantitatively acquire a three-dimensional hydrogen distribution for a cathode containing Ni(OH)2 as an active material in a Ni–MH battery using LIBS. Moreover, we demonstrated that the reaction distribution in the cathode can be interpreted from the SOC distribution converted from the hydrogen distribution. Quantitative hydrogen and SOC distributions for a model cathode cycled at 2.3 mA cm−2 and a commercial Ni–MH battery cathode cycled 1000 times at 1C were acquired by measuring the hydrogen emission intensity at 656.28 nm under a 3000 Pa helium atmosphere. We used a pristine model cathode and the commercial Ni–MH battery cathodes discharged or charged once at 0.1C as reference samples for determining the hydrogen and SOC distributions. The SOC distributions were obtained based on the assumption that the SOCs of the pristine cathode, the discharged Ni–MH battery cathode, and the charged Ni–MH battery cathode were 0%, 0%, and 100%, respectively, and the SOC decreased linearly with an increase in hydrogen emission intensity at 656.28 nm. By comparing the findings from the SOC distributions in the cathodes, the charge–discharge curves, and the XRD patterns together, we found—from the hydrogen distributions in the cycled cathodes—that SOC distributions of the cathodes can be quantitatively obtained using LIBS and the overcharged areas exhibited SOC values above 100%. Therefore, our results indicate that the present LIBS measurement system can provide information that will improve the understanding of the deterioration mechanism of a Ni–MH battery.Author contributions
The manuscript was written by S. I. The experiments were carried out by T. K. and T. I. and K. W provided advice.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Financial support for the present study was provided by JSPS KAKENHI Grant Number 19K22038. We are grateful to Professor Akichika Kumatani, Tohoku University, for letting us use the glove box.References
- B. Ash, V. S. Nalajala, A. K. Popuri, T. Subbaiah and M. Minakshi, Nanomaterials, 2020, 10, 1878 CrossRef CAS PubMed.
- W. Chen, Y. Jin, J. Zhao, N. Liu and Y. Cui, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 11694–11699 CrossRef CAS PubMed.
- B. Hariprakash, A. K. Shukla and S. Venugoplan, Encyclopedia of Electrochemical Power Sources, 2009, pp. 494–501 Search PubMed.
- M. Koyama, M. Rohwerder, C. C. Tasan, A. Bashir, E. Akiyama, K. Takai, D. Raabe and K. Tsuzaki, Mater. Sci. Technol., 2017, 33, 1481–1496 CrossRef CAS.
- T. Schober and C. Dieker, Metall. Trans. A, 1983, 14, 2440–2442 CrossRef.
- J. Ovejero-Garca, J. Mater. Sci., 1985, 20, 2623–2629 CrossRef.
- M. Rohwerder and F. Turcu, Electrochim. Acta, 2007, 53, 290–299 CrossRef CAS.
- K. Takai, J. Seki and Y. Homma, Mater. Trans., JIM, 1995, 36, 1134–1139 CrossRef CAS.
- K. Beyer, T. Kannengiesser, A. Griesche and B. Schillinger, J. Mater. Sci., 2011, 46, 5171–5175 CrossRef CAS.
- I. Manke, H. Markötter, C. Tötzke, N. Kardjilov, R. Grothausmann, M. Dawson, C. Hartnig, S. Haas, D. Thomas, A. Hoell, C. Genzel and J. Banhart, Adv. Eng. Mater., 2011, 13, 712–729 CrossRef CAS.
- N. Kardjilov, I. Manke, A. Hilger, M. Strobl and J. Banhart, Mater. Today, 2011, 14, 248–256 CrossRef.
- P. Gotcu, W. Pfleging, P. Smyrek and H. J. Seifert, Phys. Chem. Chem. Phys., 2017, 19, 11920–11930 RSC.
- D. Rettenwander, R. Wagner, A. Reyer, M. Bonta, L. Cheng, M. M. Doeff, A. Limbeck, M. Wilkening and G. Amthauer, J. Phys. Chem. C, 2018, 122, 3780–3785 CrossRef CAS PubMed.
- W. Pfleging, Nanophotonics, 2018, 7, 549–573 CAS.
- S. Imashuku, H. Taguchi, T. Kawamata, S. Fujieda, S. Kashiwakura, S. Suzuki and K. Wagatsuma, J. Power Sources, 2018, 399, 186–191 CrossRef CAS.
- S. Imashuku, H. Taguchi, S. Fujieda, S. Suzuki and K. Wagatsuma, Electrochim. Acta, 2019, 293, 78–83 CrossRef CAS.
- P. Smyrek, T. Bergfeldt, H. J. Seifert and W. Pfleging, J. Mater. Chem. A, 2019, 7, 5656–5665 RSC.
- S. Imashuku, H. Taguchi, T. Kawamata, H. Yorifuji, S. Fujieda, S. Kashiwakura, K. Shinoda, S. Suzuki and K. Wagatsuma, J. Electrochem. Soc., 2019, 166, A1972–A1976 CrossRef CAS.
- Y. Zheng, L. Pfäffl, H. J. Seifert and W. Pfleging, Appl. Sci., 2019, 9, 4218 CrossRef CAS.
- W. Pfleging, Int. J. Extreme Manuf., 2021, 3, 012002 CrossRef CAS.
- J. Park, H. Song, I. Jang, J. Lee, J. Um, S.-g. Bae, J. Kim, S. Jeong and H.-J. Kim, J. Energy Chem., 2022, 64, 93–102 CrossRef CAS.
- M. Hori, R. S. Hayano, M. Fukuta, T. Koyama, H. Nobusue and J. Tanaka, Rev. Sci. Instrum., 2009, 80, 103104 CrossRef CAS PubMed.
- T. Shudo and S. Oba, Int. J. Hydrogen Energy, 2009, 34, 2488–2493 CrossRef CAS.
- S. H. Lee, H. T. Hahn and J. J. Yoh, Spectrochim. Acta, Part B, 2013, 88, 63–68 CrossRef CAS.
- M. Kotzagianni, E. Kakkava and S. Couris, Appl. Spectrosc., 2016, 70, 627–634 CrossRef CAS PubMed.
- H. M. Jun, J. H. Kim, S. H. Lee and J. J. Yoh, Energy, 2018, 160, 225–232 CrossRef CAS.
- C. Li, X. Wu, C. Zhang, H. Ding, J. Hu and G.-N. Luo, J. Nucl. Mater., 2014, 452, 10–15 CrossRef CAS.
- J. Oelmann, E. Wüst, S. Brezinsek, C. Li, D. Zhao, M. Rasinski, C. P. Dhard, M. Mayer, D. Naujoks and Y. Gao, Nucl. Mater. Energy, 2021, 26, 100943 CrossRef CAS.
- C. Li, J. Oelmann, S. Brezinsek, M. Rasinski, C. P. Dhard, R. König, Y. Liang, H. Ding and C. Linsmeier, Spectrochim. Acta, Part B, 2019, 160, 105689 CrossRef CAS.
- K. H. Kurniawan, M. Pardede, R. Hedwig, Z. S. Lie, T. J. Lie, D. P. Kurniawan, M. Ramli, K. Fukumoto, H. Niki, S. N. Abdulmadjid, N. Idris, T. Maruyama, K. Kagawa and M. O. Tjia, Anal. Chem., 2007, 79, 2703–2707 CrossRef CAS PubMed.
- R. Hedwig, Z. S. Lie, K. H. Kurniawan, A. N. Chumakov, K. Kagawa and M. O. Tjia, J. Appl. Phys., 2010, 107, 023301 CrossRef.
- Z. S. Lie, A. Khumaeni, T. Maruyama, K.-i. Fukumoto, H. Niki and K. Kagawa, Appl. Phys. A, 2010, 101, 555–558 CrossRef CAS.
- S. N. Abdulmadjid, Z. S. Lie, H. Niki, M. Pardede, R. Hedwig, T. J. Lie, E. Jobiliong, K. H. Kurniawan, K. Fukumoto, K. Kagawa and M. O. Tjia, Appl. Spectrosc., 2010, 64, 365–369 CrossRef CAS PubMed.
- C. Feng, R. Yang, Q. Li, X. Ye, J. Wu, C. Chen, X. Wang and X. Chen, Appl. Opt., 2020, 59, 2866–2873 CrossRef CAS PubMed.
- W. Rapin, P. Y. Meslin, S. Maurice, R. C. Wiens, D. Laporte, B. Chauviré, O. Gasnault, S. Schröder, P. Beck, S. Bender, O. Beyssac, A. Cousin, E. Dehouck, C. Drouet, O. Forni, M. Nachon, N. Melikechi, B. Rondeau, N. Mangold and N. H. Thomas, Spectrochim. Acta, Part B, 2017, 130, 82–100 CrossRef CAS.
- Y. Markushin, A. Marcano, S. Rock and N. Melikechi, J. Anal. At. Spectrom., 2010, 25, 148–149 RSC.
- S. Imashuku, T. Kamimura, S. Kashiwakura and K. Wagatsuma, Anal. Chem., 2020, 92, 11171–11176 CrossRef CAS PubMed.
- S. Imashuku, T. Kamimura, T. Kawaguchi and T. Ichitsubo, e-J. Surf. Sci. Nanotechnol., 2022, 20, 7–12 CrossRef CAS.
- E. Shangguan, Z. Chang, H. Tang, X.-Z. Yuan and H. Wang, Int. J. Hydrogen Energy, 2010, 35, 9716–9724 CrossRef CAS.
- M. Oshitani, H. Yufu, K. Takashima, S. Tsuji and Y. Matsumaru, J. Electrochem. Soc., 1989, 136, 1590–1593 CrossRef CAS.
- J. Huang, D. Cao, T. Lei, S. Yang, X. Zhou, P. Xu and G. Wang, Electrochim. Acta, 2013, 111, 713–719 CrossRef CAS.
- K. Liu, W. Zhou, D. Zhu, J. He, J. Li, Z. Tang, L. Huang, B. He and Y. Chen, J. Alloys Compd., 2018, 768, 269–276 CrossRef CAS.
- Y. Nie, W. Li, J. Pan, R. A. Senthil, C. Fernandez, A. Khan, Y. Sun and J. Liu, Electrochim. Acta, 2018, 289, 333–341 CrossRef CAS.
- T. Iwai, S. Takai, T. Yabutsuka and T. Yao, J. Alloys Compd., 2019, 772, 256–262 CrossRef CAS.
- M. A. Kiani, M. F. Mousavi and S. Ghasemi, J. Power Sources, 2010, 195, 5794–5800 CrossRef CAS.
- W.-K. Hu, X.-P. Gao, D. Noréus, T. Burchardt and N. K. Nakstad, J. Power Sources, 2006, 160, 704–710 CrossRef CAS.
- L. J. Yang, X. P. Gao, Q. D. Wu, H. Y. Zhu and G. L. Pan, J. Phys. Chem. C, 2007, 111, 4614–4619 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an01147f |
| This journal is © The Royal Society of Chemistry 2022 |