A high-throughput study of oxynitride, oxyfluoride and nitrofluoride perovskites†
Hai-Chen
Wang
 a,
Jonathan
Schmidt
a,
Silvana
Botti
a,
Jonathan
Schmidt
a,
Silvana
Botti
 b and
Miguel A. L.
Marques
b and
Miguel A. L.
Marques
 *a
*a
aInstitut für Physik, Martin-Luther-Universität Halle-Wittenberg, 06120 Halle (Saale), Germany. E-mail: miguel.marques@physik.uni-halle.de
bInstitut für Festkörpertheorie und -Optik, Friedrich-Schiller-Universität Jena, European Theoretical Spectroscopy Facility, Max-Wien-Platz 1, 07743 Jena, Germany
First published on 18th February 2021
Abstract
Perovskite solar devices are nowadays the fastest advancing photovoltaic technology. Their large-scale application is however restrained by instability and toxicity issues. Alloying is a promising way to stabilize perovskites, optimizing at the same time their absorption and charge-transport properties. We perform an extensive computational study of the thermodynamic stability and electronic properties of oxynitride, oxyfluoride and nitrofluoride perovskites. We consider quaternary stoichiometries of the type ABX2Y, where A and B are any elements of the periodic table and X and Y are nitrogen, oxygen, or fluorine. As a starting point we explore the composition space using a simple five-atom perovskite unit cell. We then filter the candidate compositions according to their distance to the convex hull of thermodynamic stability. For the most stable systems, we then investigate other prototype structures, including more complex perovskite phases that allow for octahedral distortions, and a few non-perovskite geometries. Furthermore, for some paradigmatic cases, we study the effect of disorder by exhaustive enumeration of all possible disordered stoichiometric phases with up to 20 atoms in the unit cell. Our calculations are in very good agreement with data for experimentally known mixed anionic compounds, and predict a series of novel stable (perovskite and non-perovskite) oxynitride and oxyfluoride phases, including some with unexpected chemical composition, and one single nitrofluoride compound. Finally, we calculate and discuss the electronic properties of these compounds and their potential for application as photovoltaic absorbers.
Introduction
Perovskites are one of the best known and more extensively studied families of compounds. They possess the general formula ABX3, where X is a halide, a chalcogen, or even nitrogen, and A and B are two cations. Despite numerous applications of perovskites in the most diverse fields of physics and materials science,1–4 only a restricted number of experimentally accessible ternary systems5 exist. There are several possibilities to go beyond this limitation, and open the way to new materials with improved properties. For example, one can fill the A sites with organic molecules, leading to organic–inorganic hybrid perovskites such as CH3NH3PbI3. Hybrid perovskites have attracted enormous interest in the past few years, in particular due to their application as absorbers in high-efficiency photovoltaic devices.6–8 This is due to their unique properties, such as their high tolerance to defects,9 the origin of which is still under debate among sp antibonding coupling,8 polarons,10 and lattice softness.11 Alternatively, one can fill the B site with two different cations, leading to the so-called double perovskites.12–14 These have, for instance, been proposed as absorbing layers for photovoltaics or as p-type transparent conductive oxides.15–18 Another possibility to obtain quaternary perovskites, that we address in this article, is to mix more than one anion in the X position, leading to compositions of the type ABX2Y.19Mixed anion inorganic compounds are a versatile family of materials that contain more than one anionic species in a single phase.20 The different radii and oxidation states of the two anions offer extra degrees of freedom with respect to the single-anion phase, enabling further control and tuning of electronic properties. In the context of perovskites, the most interesting and also the most studied systems are oxynitride and oxyfluoride compounds.
Several quaternary oxynitrides and oxyfluorides have already been synthesized and characterized in the literature. The most common methods for synthesis are solid-state reactions, low-temperature fluorination or high-pressure synthesis.21,22 In solid-state reaction methods a mixture of metal oxides and nitrides or fluorides is simply heated in a furnace. One expects that high pressure stabilizes quaternary perovskites, as it suppresses the decomposition to oxides and nitrogen gas, and allows the reactions to be carried out at higher temperature.21 Experimentally synthesized compounds are presented in bold in Tables 1–5.
| Material | t | τ | E (5)hull | Str. | E hull | E gap | Mag. | Ref. |
|---|---|---|---|---|---|---|---|---|
| BaReN2O | 0.99 | 3.49 | 125 | c | −11 | 0 | 0 | |
| CaReN2O | 0.87 | 4.47 | 146 | a | −5 | 0 | 0 | |
| KReN2O | 1.01 | 3.71 | 248 | f | 7 | 1.94 | 0 | |
| LaNbN 2 O | 0.84 | 3.74 | 127 | a | −32 | 1.12 | 0 | 44 |
| LaReN2O | 0.87 | 2.83 | 128 | a | 22 | 0 | 0 | |
| LaTaN 2 O | 0.84 | 3.74 | 80 | a | −45 | 1.29 (1.9, 2.1) | 0 | 44–49 |
| LaTcN2O | 0.86 | 3.09 | 170 | a | 47 | 0 | 0 | |
| NaReN2O | 0.88 | 4.09 | 213 | f | 46 | 1.89 | 0 | |
| SrReN2O | 0.93 | 3.78 | 81 | c | −53 | 0 | 0 |
| Material | t | τ | E (5)hull | Str. | E hull | E gap | Mag. | Ref. |
|---|---|---|---|---|---|---|---|---|
| BaNbO 2 N | 0.95 | 3.54 | 65 | a | −22 | 1.25 (1.8) | 0 | 46 and 47 |
| BaReO2N | 0.98 | 3.47 | 94 | c | −41 | 0 | 0 | |
| BaTaO 2 N | 0.95 | 3.54 | 33 | b | −44 | 1.43 (1.8) | 0 | 46 and 47 |
| BaTcO2N | 0.97 | 3.48 | 82 | c | −54 | 0 | 0 | |
| CaNbO 2 N | 0.83 | 5.34 | 193 | a | 22 | 1.81 (2.1) | 0 | 46 and 47 |
| CaReO2N | 0.86 | 4.67 | 164 | b | −5 | 0.41 | 0 | |
| CaTaO 2 N | 0.83 | 5.34 | 146 | a | 13 | 1.67 (2.4) | 0 | 46–48 and 50 |
| CaTcO2N | 0.85 | 4.86 | 176 | b | −7 | 0.44 | 0 | |
| KReO2N | 1.01 | 3.64 | 124 | b | 25 | 0 | 0 | |
| LaHfO2N | 0.81 | 5.38 | 177 | a | 20 | 2.53 | 0 | |
| LaTaO2N | 0.83 | 4.57 | 220 | b | 140 | 0 | 0 | |
| LaTiO 2 N | 0.86 | 3.13 | 121 | a | 30 | 1.64 (1.9) | 0 | 44, 49 and 51 |
| LaZrO 2 N | 0.81 | 5.70 | 260 | a | 45 | 2.53 | 0 | 51 |
| LiReO2N | 0.78 | 5.76 | 223 | a | 40 | 0 | 0 | |
| NaReO2N | 0.88 | 4.09 | 92 | b | −7 | 0 | 0 | |
| PbReO2N | 0.92 | 3.80 | 171 | c | 34 | 0 | 0 | |
| SrNbO 2 N | 0.89 | 4.07 | 72 | a | −21 | 1.37 (1.9) | 0 | 46 and 47 |
| SrReO2N | 0.92 | 3.83 | 87 | c | −47 | 0 | 0 | |
| SrTaO 2 N | 0.89 | 4.07 | 65 | b | −14 | 1.68 (2.1) | 0 | 46–48 |
| SrTcO2N | 0.91 | 3.89 | 95 | c | −47 | 0 | 0 |
The interest in oxynitride perovskites comes from the numerous possible applications of these compounds. The smaller electronegativity of nitrogen with respect to oxygen leads to band gaps in the visible range, opening the way to a wealth of opto-electronic applications.23 In fact, and in contrast to oxide perovskites that are usually colourless, these quaternary systems display bright coloring in a diverse color spectrum, enabling their use as, for example, pigments or phosphors24–26 and photocatalysts.22,23
Initially, investigation into oxyfluoride perovskites was motivated by the discovery of superconductivity at 46 K in the cuprate Sr2CuO2F2+x.27–29 Oxifluoride systems can also possess interesting magnetic properties. For example, due to the interaction between the Fe3+ ions, BaFeO2F, SrFeO2F, and PbFeO2F exhibit magnetic (antiferromagnetic) ordering until a temperature of around 645 K,30 685 K,31 and >500 K,32 respectively. Iron-based oxyfluoride perovskites were also shown to exhibit multiferroic behavior.33
In this article, we provide a comprehensive computational study of oxynitride, oxyfluoride, and nitrofluoride perovskites. Our objective is threefold: (i) to provide a list of novel compositions that could be likely experimentally synthesized in the perovskite phase; (ii) to provide physical insight into the problem of disorder in these systems; and (iii) to study their electronic properties. We follow a systematic approach to unveil interesting materials that are not simple, evident substitutions of well-studied systems. This is particularly important for nitrofluorides, as no such perovskites are experimentally known at the moment. Our computational tool of choice is density-functional theory (DFT), a quantum approach to calculate the structural and electronic properties of materials which has demonstrated over the years unparalleled accuracy combined with reasonable computational costs.
Clearly, performing a study of the complete chemical space for oxynitride, oxyfluoride, and nitrofluoride perovskites including the effects of distortion, disorder, pressure, temperature, etc. is way beyond current computational possibilities. Therefore, we will follow a stepwise procedure conceived to be at the same time predictive and affordable. We start by looking at the simple, five-atom perovskite unit cell. The most interesting systems, from the point of view of thermodynamic stability, are then selected by comparison with the experimental data. We then take into account possible distortions by using more complex prototype structures. Disorder is studied by using exhaustive enumeration methods. Finally, we calculate and discuss the physical properties of some selected compounds.
Methods
We performed DFT calculations using the VASP code,34,35 where all parameters were set to guarantee compatibility with the data available in the materials project database.36 We used the PAW37 datasets of version 5.2 with a cutoff of 520 eV. The Brillouin zone was sampled by Γ-centered k-point grids with a uniform density calculated to yield 1000 k-points per atom (except where explicitly stated). All forces were converged to better than 0.005 eV Å−1. All calculations were performed with spin-polarization using the Perdew–Burke–Ernzerhof38 (PBE) exchange–correlation functional, with the exception of oxides and fluorides containing Co, Cr, Fe, Mn, Mo, Ni, V, and W, where an on-site Coulomb repulsive interaction U with a value of 3.32, 3.7, 5.3, 3.9, 4,38, 6.2, 3.25, and 6.2 eV, respectively, was added to correct the d-states. Band structures were also calculated with the HSE06 functional.39We prepared all possible compositions of type ABX2Y, where A and B run over the periodic table up to bismuth (with the exception of the noble gases, including La but removing the other lanthanides), and X and Y are N, O, and F. We used in a first instance the simple five-atom unit cell shown in Fig. 1. Considering the 6 possible combinations of X and Y, this leads to 6 × 3906 different stoichiometries. We optimized the geometry of each one of these structures and calculated their formation energy and used them to build the convex hull of thermodynamic stability using PYMATGEN.41 This robust open-source Python library for materials analysis is widely used in computational studies for a variety of tasks, including the visualization of calculations and the generation of standardized input files. In our case, we use PYMATGEN to query the materials project database and to calculate the energy distance to the convex hull. The construction of the convex hull considers all possible decomposition channels (in elementary, binary, ternary, and quaternary phases) present in the materials project database,36 complemented with the compounds found in ref. 42. Specifically, this means that the formation energy of each ABX2Y perovskite is compared to the formation energy of all stable crystalline phases of the A–B–X–Y phase diagram.
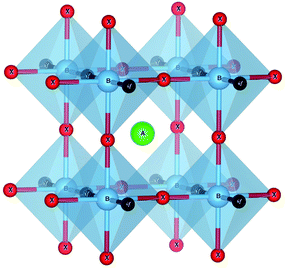 | ||
| Fig. 1 The crystal structure of the ABX2Y perovskite used for the high-throughput search. The orange ball denotes the A atom, while cyan balls are B atoms, green balls X atoms and pink balls Y atoms. The unit cell is tetragonal with space group P4/m2/m2/m (#123). Image produced with VESTA.40 | ||
To study the effect of disorder, we systematically constructed supercells using the software included in ATAT.43 We restricted the unit cells to a maximum of 20 atoms (4 formula units), and explored all possible ways to fill the Wyckoff 3d position with the X and Y atoms that respected the X2Y stoichiometry. Equivalent unit cells that were mapped by a symmetry operation were automatically discarded by ATAT.
Exploration of the chemical space
It is instructive to analyze the distance to the convex hull of stability (Ehull) for all chemical compositions when we use the five-atom perovskite unit cell. A histogram with this information can be found in Fig. 2. Although this plot does not give us information on specific materials, it does give us invaluable insights into the chemistry of inorganic perovskites. Interestingly, the curves for the different anion compositions exhibit different behaviors. For ABO2N and ABN2O the histograms are less asymmetric and are centered at around 1.5 eV. There is also a clear difference between ABO2N and ABN2O, with the former yielding more stable compounds than the latter. The histograms for the oxyfluorides rise very steeply until around 1 eV and then decay slowly until ∼4 eV. No noticeable difference in stability can be seen for ABO2F and ABF2O. The nitrofluorides display very few systems with a small distance to the hull, and show a large difference between ABN2F and ABF2N, with the latter yielding considerably more stable structures. The reduced stability of the ABN2Y crystal phases can be understood by noticing that the −3 standard oxidation state of nitrogen implies that cations A and B together have to compensate for at least a −7 valence. While this is certainly possible, the number of such combinations of A and B is considerably smaller than in the case of anions with lower charge states. Furthermore, the larger difference of ionic radii between N and F (with respect to the N–O and O–F pairs) can also lead to geometrical instabilities, thereby increasing the formation energy of nitrofluoride systems.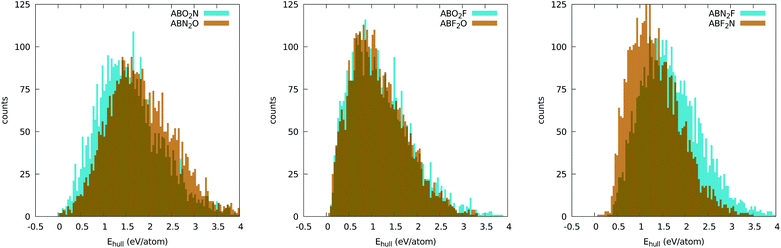 | ||
| Fig. 2 Distribution of the distances to the convex hull of all oxynitride (left), oxyfluoride (center), and nitrofluoride (right) perovskites. The bins have a size of 40 meV per atom. | ||
The most important information that we can obtain from the distance of the formation energy to the convex hull is which materials are predicted by theory to be stable. It is true that experimentally one can synthesize crystal phases that are not thermodynamically stable (i.e., not on the convex hull of stability), but the difficulty in realizing such phases increases considerably with their energy distance to the hull. We will therefore turn our attention to the materials contained in the left extreme of the distributions in Fig. 2. The selected compounds are listed, together with information on the experimentally realized phases, in Tables 1–5 and in the ESI.†
Lowest-energy compositions
Before we start discussing our results, we have to define the criteria for filtering in low-energy compositions for further analysis. Typically, this is done by setting a reasonable threshold in the distance to the convex hull. However, several considerations have to be taken into account in our case. First, the five-atom structure we used in the high-throughput search can be further stabilized by distortion (tilting or rotation of the octahedra as common in many perovskites, for example) or by rearranging the atomic positions of the X and Y atoms. As we will see in the following, this can sometimes lead to a decrease of the formation energy of about hundred meV per atom. Then, we can expect a reasonable degree of disorder in the occupation of the X and Y sites, leading to a further decrease of the free energy due to configurational entropy. This term is typically of the order of tens of meV per atom at room temperature.64 Note that there are still other (de)stabilization mechanisms, such as defects, temperature, pressure, etc., that also lead to corrections to the free-energy. Finally, we should consider the error of the PBE approximation in the estimation of formation energies,65–68 and hence in the determination of distances to the convex hull. This means that materials with a small positive distance to the hull might still be stable in the experiment.In order to alleviate these issues, we decided to use a pragmatic approach. We considered our calculations for the few oxynitride and oxyfluoride phases that were synthesized experimentally and observed that all these systems have formation energies close to the convex hull of thermodynamic stability. This fact validates on the one hand our approach to find new materials, and on the other hand it provides us a valid way to set a stability threshold. The experimentally known stable composition with the highest distance to the hull in our five-atom unit cell is LaZrO2N at 260 meV per atom above the convex hull (although most other experimental compounds lie well below 150 meV per atom). This number is considerably higher than the usual criterion for metastability,69,70 but one should keep in mind that we are filtering out compounds before having included stabilizing energy contributions coming from octahedral distortions and entropic effects. We will therefore take 260 meV per atom as the maximum distance to the convex hull of stability and pass on for further analysis only compounds that satisfy this condition.
In Tables 1–5 we summarize the most relevant results. The remainder of the data can be found in the ESI.† All structures and a summary of the calculations can be downloaded from our website.‡ At a first glance we find a variety of compositions below the 260 meV per atom stability threshold. The stability of perovskites is often discussed based on the Goldschmidt tolerance factor71
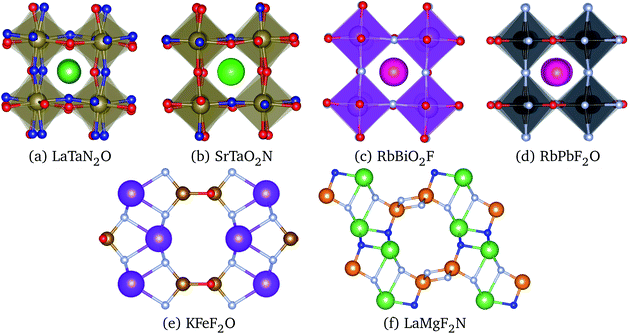
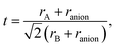 | (1) |
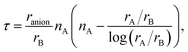 | (2) |
To use any of these formulae for mixed anions, we must decide on which value of ranion to use. In line with the suggestion of ref. 72 we decided to use the arithmetic average ranion = (2rX + rY)/3. Note that, however, it has been pointed out that the Goldschmidt factor using ranion can fail to capture the stability trends in mixed anionic perovskites53,73 and pyrochlores.74 The geometric mean has also been used to approximate the radius of a site with two ions,75 and more complicated factors that involve, e.g., octahedral factors and atomic packing fractions, have also been proposed.75,76 For simplicity, however, we decided to build our analysis in the traditional t and on τ.
All the considered materials have values of Goldschmidt tolerance factor between 1.09 (for CsCoF2O) and 0.78 (for LiReO2N and NaInF2O). All in all, this range of [0.78, 1.09] is perfectly consistent with the usual range reported for perovskites.72 Concerning τ we find that 79% of our low-energy phases have τ < 4.18 and should therefore be stable perovskites according to ref. 72. This percentage of true positives is reasonable, but considerably smaller than the stated accuracy of 92%. In view of this analysis, and considering that it is nowadays possible to perform efficient high-throughput DFT calculations and apply sophisticated machine learning models,77 it is unclear what is the benefit of using oversimplified empirical models for the prediction of novel stable materials.78
One last note concerning materials containing lanthanide atoms: as we removed these elements from our high-throughput search they do not appear in our results. However, one can reasonably expect that materials predicted to be low energy with La are also close to the hull after substitution of La by other lanthanides due to their chemical similarity.79,80
Oxynitrides
In what concerns oxynitride compounds of the ABN2O type, we find 16 systems that satisfy our filtering conditions. Interestingly, they exhibit combinations of cations with diverse oxidation states. For example, I–VII as in KReN2O, II–VI as in CaReN2O, or III–V as in LaReN2O. The lowest of this (at 69 meV per atom above the hull) is LaTaN2O, that has already been experimentally synthesized.44–49 At the B site, we find mostly a group V (Sr or Ba) or a group VII (Tc or Re) element. Perhaps surprisingly, the chemical element that yields more stable compounds is Re, which can combine with Na, K, Ca, Sr, Ba, La, and Pb. In view of the fact that there are, at the moment, no known Re-based oxynitrides, this finding can open the door to a completely new family of materials. We note that many of these compounds, although having low energy, require cations in less common oxidation states. Therefore, we can probably expect that, if synthesized, they will be off-stoichiometric, either due to the variation in the O–N ratio, or due to the creation of vacancies.The other stoichiometric oxynitride family, ABNO2, has considerably lower formation energies, so we find many more systems (35) within our energy threshold. In this list, we find cations in the oxidation states I–VI (as in KReO2N), II–V (as in BaTaO2N), and III–IV (as in LaTiO2N). The most likely element that we find at the B-site is again Re, that can be combined with (in ascending order of formation energy) Sr, Na, Ba, K, Ca, Pb, Li, and Rb. Interestingly, this list includes almost all alkali metals, although Li and Rb show clearly decreased stability, but not La, as LaReNO2 appears at 324 meV per atom above the hull. We find a similar situation with Tc at the B-site, yielding stable systems for A = Sr, Ba, Na, Ca, Pb, K, and La. Also many systems with Nb (A = Ba, Sr, Ca, La) and Ta (A = Sr, Ba, Ca, La, Pb, Sn) have small distances to the convex hull. When La is at the B-site, we find stable systems with the A-site being a group IV element (Ti, Zr, or Hf). Finally, we also find systems such as {Sr, Ba}{Mo, Ru}O2N and {Sr, Ba, Na}OsO2N.
Oxyfluorides
We now turn our attention to candidate oxyfluoride perovskites. At a glance these systems appear to be considerably more stable than oxynitrides, with 124 compositions of ABFO2 and 134 compositions of ABF2O below our stability threshold.For ABFO2 the most common oxidation state of the cations is I–III, although a few rare compounds with II–II (such as BaMgF2O) or III–I (such as LaLiF2O) do appear. The most likely elements occupying the A-site are Sr, Ba or an alkali-metal (in particular K and Rb, and to a lesser extent Na and Cs). The alkali-earths form low-energy oxyfluoride perovskites with a set of mostly first-row metals at the B-site. Particularly interesting are compounds with Mn, Fe, Co, Ni, etc. that should lead to materials with magnetic order. When Cs, Rb, and K are found at the A-site, one encounters at the B-site a transition metal. The ones leading to more stable compositions are the heavy elements Bi and Pb or group IV elements (Ti, Zr, or Hf). For Na, on the other hand, the B-site should contain lighter elements such as Ti, V, or Al. We find furthermore several compositions with Pb, Tl, and Ag at the A-site.
The materials that have already been synthesized (see Tables 3 and 4) are consistent with our predictions. We should note, however, that ref. 53 attempted the high pressure synthesis of NaTiO2F, which has essentially the same distance to the hull as KTiO2F, without success (it resulted in a mixture of NaF and TiO2). This emphasizes that the synthesis of an oxyfluoride material is a complex dynamical process whose success cannot be determined by the simple distance to the convex hull.
| Material | t | τ | E (5)hull | Str. | E hull | E gap | Mag. | Ref. |
|---|---|---|---|---|---|---|---|---|
| AgCuF 2 O | 0.93 | 3.75 | 176 | f | 33 | 0 | 0 | |
| AgFeF2O | 0.89 | 3.85 | 152 | e | 64 | 1.18 | 1.00 | 52 |
| AgGaF2O | 0.90 | 3.80 | 161 | f | 42 | 1.16 | 0 | |
| BaLiF2O | 247 | d | 34 | 3.38 | 0 | |||
| CsBiF2O | 0.90 | 3.58 | 120 | b | 3 | 2.60 | 0 | |
| CsCaF2O | 218 | e | 40 | 3.01 | 0 | |||
| CsHgF2O | 176 | e | −20 | 0.55 | 0.20 | |||
| CsPbF2O | 64 | d | 50 | 1.12 | 0 | |||
| CsSbF2O | 1.01 | 3.23 | 230 | b | 30 | 3.83 | 0 | |
| CsSrF2O | 242 | d | 44 | 2.83 | 0 | |||
| KAgF2O | 0.92 | 3.55 | 198 | e | 13 | 0.75 | 0.20 | |
| KAlF2O | 1.02 | 3.57 | 218 | f | 43 | 4.51 | 0 | |
| KAsF2O | 1.00 | 3.51 | 255 | e | 24 | 4.32 | 0 | |
| KBiF2O | 0.81 | 5.00 | 181 | f | −2 | 3.18 | 0 | |
| KSbF2O | 0.91 | 3.57 | 245 | b | 21 | 4.19 | 0 | |
| NaAlF2O | 0.89 | 3.97 | 190 | f | 26 | 4.84 | 0 | |
| NaFeF2O | 0.84 | 4.33 | 165 | f | 44 | 2.31 | 1.00 | |
| NaGaF2O | 0.85 | 4.21 | 202 | f | 25 | 3.65 | 0 | |
| NaMnF2O | 0.84 | 4.33 | 162 | e | 44 | 0.24 | 0.80 | |
| RbAgF2O | 0.97 | 3.36 | 189 | e | 1 | 0.46 | 0.20 | |
| RbAsF2O | 1.05 | 3.45 | 256 | a | 22 | 3.55 | 0 | |
| RbBiF2O | 0.85 | 4.09 | 133 | f | −17 | 3.24 | 0 | |
| RbCuF2O | 1.07 | 3.52 | 170 | e | 46 | 0.99 | 0 | |
| RbHgF2O | 167 | e | −31 | 0.89 | 0.20 | |||
| RbSbF2O | 0.96 | 3.36 | 209 | b | 17 | 3.73 | 0 | |
| RbTcF2O | 201 | e | −24 | 0.03 | 0 | |||
| TlBiF2O | 0.85 | 4.19 | 165 | f | 21 | 2.87 | 0 | |
| TlGaF2O | 1.02 | 3.40 | 214 | f | 40 | 3.24 | 0 | |
| TlSbF2O | 0.95 | 3.38 | 222 | e | 18 | 3.08 | 0 | |
| TlYF2O | 0.90 | 3.63 | 137 | f | 50 | 2.39 | 0 |
| Material | t | τ | E (5)hull | Str. | E hull | E gap | Mag. | Ref. |
|---|---|---|---|---|---|---|---|---|
| AgFeO2F | 0.81 | 6.20 | 269 | e | 117 | 0 | 0.82 | |
| AgTiO 2 F | 0.90 | 3.81 | 141 | f | 26 | 2.17 (2.8) | 0 | 53 |
| AgZrO2F | 0.85 | 4.14 | 204 | a | 69 | 1.97 | 0 | |
| BaAgO2F | 0.91 | 3.89 | 233 | f | 140 | 0 | 0.03 | |
| BaFeO 2 F | 0.95 | 3.50 | 130 | b | 56 | 1.52 | 1.00 | 30 and 54 |
| BaGaO2F | 0.97 | 3.45 | 248 | e | 110 | 3.52 | 0 | |
| BaInO 2 F | 0.89 | 4.20 | 146 | b | 82 | 2.05 | 0 | 21 |
| BaMnO2F | 0.95 | 3.50 | 92 | b | 64 | 0 | 0.80 | |
| BaScO 2 F | 0.91 | 3.86 | 90 | b | 13 | 4.11 | 0 | 55 |
| BaTlO2F | 0.85 | 4.98 | 222 | f | 75 | 1.98 | 0 | |
| CsTeO2F | 0.92 | 3.45 | 254 | a | 40 | 2.41 | 0 | |
| KGaO2F | 255 | a | 14 | 1.06 | 0.10 | |||
| KHfO2F | 0.93 | 3.53 | 141 | b | 36 | 4.40 | 0 | |
| KNbO 2 F | 0.95 | 3.51 | 124 | c | 28 | 0 | 0 | 56 |
| KTeO2F | 0.83 | 4.47 | 216 | e | 42 | 3.01 | 0 | |
| KTiO 2 F | 0.98 | 3.52 | 148 | f | 11 | 3.61 (3.2) | 0 | 57 and 58 |
| KZrO2F | 0.93 | 3.54 | 140 | b | 38 | 3.78 | 0 | |
| NaNbO 2 F | 0.82 | 4.59 | 207 | a | 108 | 0 | 0 | 56 |
| NaTiO 2 F | 0.86 | 4.18 | 158 | f | 31 | 3.52 | 0 | 59 |
| NaVO2F | 0.87 | 4.10 | 149 | f | −2 | 2.40 | 0.20 | |
| PbFeO 2 F | 0.90 | 4.00 | 195 | f | 81 | 2.04 | 1.00 | 32 and 60 |
| PbMnO 2 F | 0.90 | 4.00 | 155 | f | 70 | 0.52 | 0.80 | 61 |
| PbScO 2 F | 0.86 | 4.78 | 173 | f | 54 | 2.82 | 0.00 | 62 |
| RbBiO2F | 83 | c | 50 | 0 | 0 | |||
| RbIO2F | 231 | a | 15 | 2.07 | 0 | |||
| RbNbO2F | 1.00 | 3.38 | 144 | c | 44 | 0 | 0 | |
| RbTeO2F | 0.87 | 3.83 | 182 | a | 10 | 2.38 | 0 | |
| RbTiO2F | 1.03 | 3.44 | 205 | f | 2 | 3.59 | 0 | |
| RbVO2F | 1.05 | 3.48 | 229 | f | 16 | 2.40 | 0.20 | |
| SrCuO2F | 0.94 | 3.67 | 178 | e | 42 | 0.84 | 0 | |
| SrFeO 2 F | 0.89 | 4.05 | 171 | b | 90 | 1.57 | 1.00 | 63 |
| TlIO2F | 241 | a | 15 | 2.00 | 0 | |||
| TlTeO2F | 0.87 | 3.90 | 222 | a | 44 | 2.64 | 0 | |
| TlTiO2F | 1.03 | 3.45 | 228 | f | 12 | 3.09 | 0 |
Concerning ABF2O compositions, we could find information on the synthesis of AgFeF2O52 and of the ternary charge-disproportionate TlITlIIIOF2 compound.81 However, our calculations indicate that this family should be at least as common as ABO2F. For this composition we observe either the I–IV or II–III combination of cations. In particular, we find that the alkalis Cs, Rb, and K can form low-energy compounds with a variety of metals (such as Pb, Bi, Co, Ti, Sc, etc.). We also report several materials with Na, but only combined with lighter, first-row cations (Co, Ti, Fe, Al, etc.). Finally, there are a series of systems with Ta at the A-site, and with In, Sc, Y, Fe, Co, etc. at the B site, and with Ag at the A-site and Fe, Ga, Co, Cu, etc. at the B-site.
Nitrofluorides
We also looked into the possibility of obtaining nitrofluoride perovskites. To our knowledge, no such system has been synthesized experimentally. From our results, we can conclude that only one system, specifically LaMgF2N, has chances of being synthesized. The five-atom unit cell is 155 meV per atom above the hull, which is a sizeable but not insurmountable energy distance. All other compositions have an energy distance of more than 300 meV per atom from the hull.Effects of disorder
Having selected the compositions that possess the smallest formation energies in the perovskite structure, we now investigate how the energy depends on the specific arrangement of the anions. To that end, we pick a few interesting systems (namely SrTaO2N, LaTaN2O, RbPbF2O, RbBiO2F, KFeF2O, BaVO2F, and LaMgF2N) and construct all possible unit-cells with up to 20 atoms by considering the different configurations that we obtain by filling the 3d Wyckoff anionic site with the two different elements. We found 285 non-equivalent structures, for which we performed a further geometry optimization (using 2000 k-points per atom for increased precision). We note that many of these supercells are consistent with the typical deformations present in perovskites, such as tilting or rotation of the octahedra. Therefore, the resulting variations in the formation energy account for contributions coming from the different anion arrangements and the structural deformation upon relaxation.We found that the different ordering of the anions leads to a spread of energy of 100–150 meV per atom, and to a stabilization that can be as low as 15 meV per atom (for RbPbF2O) to 128 meV per atom (for LaMgF2N) with respect to the five-atom unit cell. We would like to note that these numbers are for the internal energy at T = 0 and not for the free energy. Therefore, they do not account for the term that stems from the configurational entropy that further stabilizes disordered phases.
Three examples are shown in Fig. 3, namely LaTaN2O, SrTaO2N, and RbBiO2F. We can see three different behaviors.
 | ||
| Fig. 3 Distribution of the energy of the disordered cell with respect to the energy of the five-atom unit cell. The width of the bins is 5 meV per atom. | ||
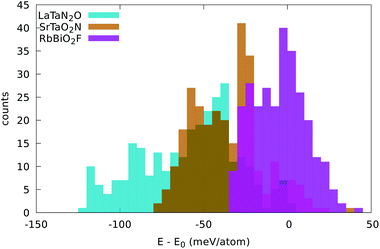
In LaTaN2O the relaxation of the anions leads to a large stabilization (of 124 meV per atom) with respect to the total energy of the simple five-atom unit cell. The lowest-energy structure we found (shown in Fig. 4) is a low-symmetry 20-atom cell, but we found 13 different anionic arrangements within 10 meV per atom from this phase. In this case the five-atom cell yields the highest energy structure. From the figure we can see the large alternating tilting of the octahedra and the distortions caused by the local mixed-anionic environment. The large distortion can also be assessed from the distributions of the atomic distances that read 3.39–3.69 for La–Ta (the half diagonal of the cube), 2.11–2.30 Å for Ta–O, and 1.92–2.20 Å for the Ta–N distance.
 | ||
| Fig. 4 Crystal structures of the lowest energy phases of (a) LaTaN2O (space group P1, #1), (b) SrTaO2N (space group P3221, #154), (c) RbBiO2F (space group I4/mmm #139), (d) RbPbF2O (space group Pmma, #51), (e) KFeF2O (space group Cmcm #63), and (f) LaMgF2N (space group P21/m, #11). K and Bi atoms are in purple, Rb in dark pink, La and Sr in green, Ta in brown, Fe in yellow, Mg in orange, Pb in black, O in red, and F in gray and N in blue. Images produced with VESTA.40 | ||
The compound SrTaO2N is an intermediate case. The relaxation of the anion positions in a larger supercell rearrangement leads to an energy decrease of 79 meV per atom, but we can also find supercells with energy higher by 25 meV per atom than the energy of the five-atom unit-cell. The minimum energy configuration that we found, shown in Fig. 4, has 15 atoms in the unit cell and belongs to the space group P3221 (#154). Interestingly, also the lowest-energy structures of BaVO2F and KFeF2O show the same anionic arrangement. In the figure we can observe the tilting of the octahedra, which is however less pronounced than for LaTaN2O. The smaller distortion is also evident from the inspection of the interatomic distances: the Sr–Ta distance is now in the range between 3.47 and 3.59 Å, the Ta–O distance is 2.00–2.15 Å, and the Ta–N distance is 1.98 Å.
Finally, the total energy of RbBiO2F assumes values essentially centered around the energy of the five-atom cell, with the lowest-energy structure 33 meV per atom below this energy. The most stable phase turns out to be a tetragonal cell with 20 atoms (space group I4/mmm #139). From the small stabilization energy we can expect a small deformation of the lattice, as can be confirmed by visually inspecting Fig. 4. The Rb–Bi bond length ranges between 3.80 and 3.98 Å, the Bi–O distance is in the range 2.14–2.16 Å, and the Bi–F distance is 2.45 Å. In fact, in this structure the F atoms form perfect square motifs.
We observe that in all considered systems except RbPbF2O the minority anion is never present in opposite vertices of the octahedra, i.e. preferring adjacent positions.
Effects of lattice distortion: prototype search
In the previous section we considered nonequivalent configurations due to different occupation of sublattice sites and distortion of the ideal perovskite structure. However, it is certainly possible that some of the considered systems choose to crystallize in other crystallographic arrangements. Ideally, one could use global structural prediction techniques82 that are capable of predicting the ground-state structure based solely on the chemical composition of the unit cell. Such techniques have already been used, for example, to investigate Cu, Ag, and Au ternary oxides83 or half-Heusler compounds,84 or nitride perovskites.85 However, the large number of systems and the large size of the unit cells required make this approach unaffordable. Therefore, we decided for an alternative procedure that consists in trying out experimental prototype ABX2Y crystal structures.To this effect, we searched for stoichiometric compounds (without partial occupancy of the Wyckoff positions) within the Inorganic Crystal Structure Database (ICSD)86 with compatible chemical compositions. We restricted the search to entries where X and Y are non-metals, but we imposed no further rules to match oxidation states, ionic radii, etc. The few systems found are listed in Table 6, and for many of them both X and Y are chalcogens. This again confirms that not so much is experimentally known about mixed anionic systems.
We performed geometry optimization runs for each one of these 20 prototypes, including the two cases ABX2Y and BAX2Y, considering again the 7 compositions included earlier in Sec. 4. We observed that several of these prototypes relaxed towards structures already studied in Sec. 4, while others resulted in very high energy phases. A couple of structures, however, turned out to be the ground state for some compositions, namely the crystal structures with ICSD references #68098 and #84635. The structure optimization of the former for KFeF2O leads to a very different geometry, depicted in Fig. 4, with space group Cmcm #63. This structure does not exhibit the traditional octahedral coordination of perovskites, and is 44 meV per atom lower in energy than the P3221 perovskite structure. For LaMgF2N the ICSD structure #84635 led to the geometry represented in Fig. 4. This phase has the space group P121/m1 (#11) and is also not a perovskite-like structure. It is only 21 meV per atom more stable than the lowest-energy perovskite phase. Interestingly, this structure has clear similarities to the geometry of KFeF2O, as can be seen in the figure.
Having identified the five structures of Fig. 4 as relevant for the low-energy phases of ABX2Y compounds, we used them for all other compositions within the imposed energy threshold. A plot of the stabilization energy, that we define as the energy of the most stable prototype minus the energy of the five-atom cell, is depicted in Fig. 1. As for the cases discussed above, this energy can vary considerably from essentially zero to 250 meV per atom. We expected to see a correlation between the deviation of the Goldschmidt tolerance factor t from 1 and the stabilization energy. In fact, for values of t < 0.9 we expected the perovskite to distort from its cubic form, leading to a considerable decrease of the energy. However, we could only find a very weak correlation in the data, i.e. only compounds with very small values of t lowered considerably their energy by distortion. In any case, we should recall that (i) we only used 5 prototypes that clearly do not allow for all possible orthorhombic and rhombohedral distortions that may be favorable for some systems, and (ii) our energies contain two distinct contributions that unfortunately are difficult to disentangle, namely geometrical distortions and effects of disorder.
The most stable structures found for each composition can be found in Tables 1–5. We also present the distance to the convex hull of the lowest energy phase, and its electronic band gap and magnetization (per atom). We should recall that the PBE approximation tends to underestimate the band gaps by nearly a factor of two,87,88 so real samples will have a gap larger than the one indicated in the table. Comparing with the experimental band gaps indicated in parentheses in the tables, we can see that the error is quite systematic.
Oxynitrides
We want to analyze more in detail the data in Tables 1–5. Most of the experimentally known compounds are on the convex hull of thermodynamic stability, or very close to it. This in our opinion validates the use of the distance to the convex hull as a direct measure of the probability that a certain mixed anionic perovskite can be experimentally realized.We can also see that most systems seem to indeed crystallize in a perovskite structure, with the exception of NaReN2O, KReN2O, SrTaN2O, KTcO2N, and SnTaO2N. From these non-perovskite systems, the most likely one to be realized in experiments is KReN2O which appears merely 7 meV per atom above the hull. This is a non-magnetic semiconductor, with a PBE gap of almost 2 eV.
There are a number of systems that appear listed with an ABO2N composition, but not with an ABN2O composition (or vice versa). These are, for example, the cases of CaNbO2N, CaTaO2N, CaTcO2N, LaHfO2N, LaReN2O, etc. Sometimes both compositions appear in Tables 1–5, but one of the variants has a considerably larger distance to the hull compared to the other. Examples are BaNbO2N, BaTaO2N, LaNbN2O, LaTaN2O, etc. We see these results as indicating that such systems can be synthesized in the specified stoichiometries, but there is only a limited flexibility for the anion composition range. On the other hand, systems that appear with both compositions should be stable with respect to larger variations of the O/N ratio. These are particularly interesting, as they present the largest potential for the engineering of electronic (or other) properties by adjusting the anionic ratio. The best examples are CaReO2N, SrReO2N, BaReO2N, and KReO2N, although some systems with Tc in the B position or SrTaO2N are also promising. Note that this last compound is experimentally known46–48 but not the others in this list.
Finally we notice in the list a few materials with a finite magnetic moment (BaMoO2N, KTcO2N, SrMoO2N, BaNbN2O, BaTaN2O, and SrNbN2O). However, none of these latter is particularly close to the hull, so we will not discuss them in more detail.
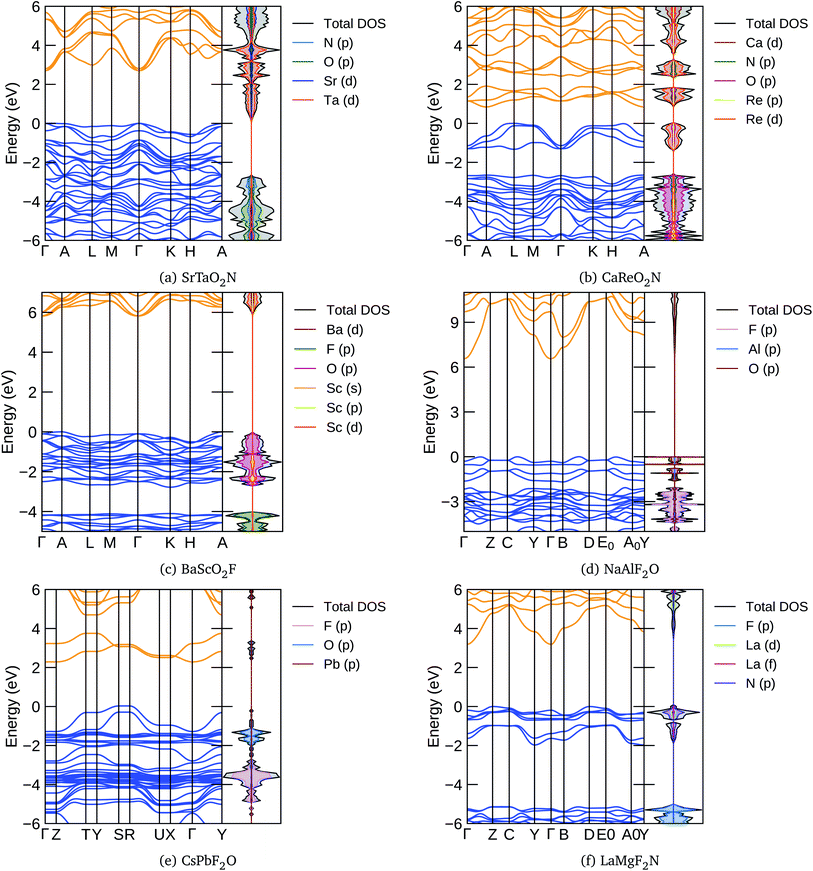
In Fig. 5 we present, as an example, the electronic band structure and density of states for SrTaO2N and CaReO2N. The first crystallizes in the perovskite structure shown in Fig. 4b and presents a rather isotropic band structure with a direct band gap at Γ of 2.70 eV in the HSE06 functional. The lowest conduction bands are highly dispersive, with an effective mass of 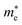 ∼ 0.8 m0. The upper valence bands are much less dispersive, which is reflected in the heavier hole mass of
∼ 0.8 m0. The upper valence bands are much less dispersive, which is reflected in the heavier hole mass of 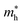 ∼ 5 m0. This significant difference between electron and hole masses is present in many of our systems, and has already been discussed in ref. 89. The valence states are mostly composed by p states of N and O with a small contribution coming from Ta d states, while the conduction bands have mainly Ta d character with a small O p character. The reduced hybridization between the anionic p-states and the B-metal states is probably the cause of the heavy holes. Finally, we see very few states associated with Sr in the [−6, 6] eV energy windows, which is compatible with the interpretation that the A atom is fully ionized in the perovskite structure (Fig. 6).
∼ 5 m0. This significant difference between electron and hole masses is present in many of our systems, and has already been discussed in ref. 89. The valence states are mostly composed by p states of N and O with a small contribution coming from Ta d states, while the conduction bands have mainly Ta d character with a small O p character. The reduced hybridization between the anionic p-states and the B-metal states is probably the cause of the heavy holes. Finally, we see very few states associated with Sr in the [−6, 6] eV energy windows, which is compatible with the interpretation that the A atom is fully ionized in the perovskite structure (Fig. 6).
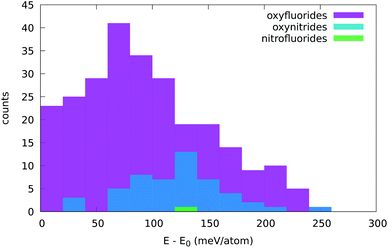 | ||
| Fig. 6 Distribution of the stabilization energy, defined as the lowest energy of all prototypes used minus the energy of the five-atom cell depicted in Fig. 1. The width of the bins is 20 meV per atom. | ||
The band structure of CaReO2N is rather different from that of SrTaO2N, even if they share the same crystal structure. The band gap of 0.87 eV is indirect, with the bottom of the conduction band at A and the top of the valence band along the line connecting H and A. Both electron and hole bands are mainly composed of Re d states hybridized with p states of O (valence band) or O and N (conduction band). The valence states are split into two manifolds, with the lowest group (starting at around 2.5 eV below the Fermi surface) mostly composed of the anionic p states with a small contribution from Re. The Ca states are found only in the conduction band above 5 eV, again indicating that this atom is ionized in this structure.
Oxyfluorides
From Tables 3 and 4 we can see that there are considerably more oxyfluoride systems, within our formation-energy cutoff, than oxynitrates. However, the lowest energy phases of many of these systems turn out to be a non-perovskite, i.e. one of the structures depicted in Fig. 4e and f. Furthermore, some of the experimentally known systems have slightly large distances to the convex hull (>50 meV per atom). Unfortunately, with the available data it is difficult to discern if this is due to the difficulty of describing fluorinated materials with the PBE approximation, or if disorder, defects or alloying have a greater stabilization role in these systems. Furthermore, we note that several of the experimentally known materials are magnetic. It is well known that the vast majority of magnetic semiconductors are indeed anti-ferromagnetic; however, all our calculations are performed for the ferromagnetic phase. This can also lead to an overestimation of the theoretical formation energy of typically a few tens of meV per atom.With Ag in the A position, we find stable compositions for B = Cu, Fe, Ga, Ti, and Zr. The most stable seems to be AgTiO2F, while AgZrO2F is the only one that the PBE predicts to crystallize in a perovskite structure. Filling the A site with Ba leads to the stabilization of a series of ABO2F compositions. Most of these systems have considerable band gaps, with the largest gap of 4.11 eV found for BaScO2F. One band structure of this kind is depicted in Fig. 5c. We can see that the HSE band gap of 5.82 eV between A and Γ is indirect, with the curvature of the conduction bands considerably larger than that of the valence bands. The top of the valence is mainly composed of O p-states with a smaller contribution of Sc states, while the bottom conduction has Sc d-character with a smaller component coming from Ba d and O p levels. The valence bands are split, with the top composed mainly of O p states and the bottom bands exhibiting mainly F p-character. Between the two manifolds there is a gap. These characteristics are shared by many of the oxynitride and nitrofluoride systems, ultimately due to the larger electronegativity of F and of the stronger ionic character of the cation–F bond when compared to the cation–O bond.
Some of the Ba containing materials are magnetic when the B site is occupied by a 3d metal such as Cr, Mn, Fe, or Ni. On the other hand, the only system with a perovskite structure that appears in our list is BaLiF2O, with a rather large PBE band gap of 3.38 eV. As such, we do not expect that the F/O ratio can be considerably increased for Ba-based systems.
Most of the systems in Tables 3 and 4 have an alkali metal in the A position (Na, K, Rb, or Cs). At the B site we find a rather diverse set of metals, ranging from the alkali earths Ca and Sr, passing through the magnetic metals Mn and Fe, a series of transition metals, and even the semi-metal atoms As, Te, and I. Many of these materials retain the perovskite structure, but some relax into the structures of Fig. 4e and f. They are mostly insulators with considerably large band gaps that can reach 4.51 eV for KAlF2O and 4.84 eV for NaAlF2O. In Fig. 5d we plot the band structure calculated with the HSE06 functional of this latter compound. We can see that the band gap is indirect, and the band structure is anisotropic, as can be expected from the crystal structure depicted in Fig. 4f. We again see a splitting of the valence bands with states with considerable F character in the lower valence band. The effective mass of the electrons is also clearly smaller than that of the holes. Note that the only AB combinations of cations that we can find in both short lists are CsSb and RbBi, so we expect that these systems are particularly resistant to variations of the F/O ratio.
Finally, interestingly, we find in the list the system CsPbF2O with a perovskite structure at 50 meV per atom above the hull. The counterpart composition, CsPbO2F, appears at 103 meV per atom above the hull, but with the structure of Fig. 4f. The interest in this structure comes from the fact that the perovskite CsPbI3 is the parent inorganic compound90 for the famous halide perovskites used for photovoltaic applications.6 Furthermore, the PBE electronic band gap of these systems is quite stable in what regards the composition, going from 1.12 eV for CsPbF2O to 1.18 eV for CsPbO2F, a value perfectly suitable for absorbers in photovoltaic modules.91 We should in fact consider that the PBE calculation underestimates the band gap, but we are also neglecting spin–orbit corrections that are sizable for heavy-element compounds and reduce the size of the gap. The HSE band structure of CsPbF2O is depicted in Fig. 5e. The band gap is indirect, with the top of the valence and bottom of the conduction bands composed of hybridized F p, O p, and Pb states. In this case the separation of the valence into two manifolds is not complete, leading to some overlap between the two sets of bands. The bottom of the conduction band, on the other hand, is separated by more than 1 eV from the rest of the conduction band.
Nitrofluorides
The calculated properties for LaMgF2N are shown in Table 5. We can see that this system is considerably stabilized by relaxing into the structure of Fig. 4f, which lies just 19 meV per atom above the hull. This is a large band gap semiconductor, with a PBE band gap of 2.26 eV. The HSE band structure of this material is presented in Fig. 5f. The highly dispersive lowest conduction band is mainly constructed from La d states, while the top valence has mostly N p character with smaller La d character. In the case of this nitrofluoride system we also see a clear splitting of the valence bands. However, due to the strongest electronegativity difference of N and F, the gap between the two manifolds is considerably larger than for the oxyfluoride systems.| Material | t | τ | E (5)hull | Str. | E hull | E gap | Mag. | Ref. |
|---|---|---|---|---|---|---|---|---|
| LaMgF2N | 0.81 | 5.64 | 155 | f | 19 | 2.26 | 0 |
| ICSD # | Composition | Spg. | N atoms |
|---|---|---|---|
| 80 | CeBiOS2 | P4/nmm (#129) | 10 |
| 2238 | LaGaOS2 | Pmca (#57) | 20 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 191 |
CeCrOS2 | B112/m (#12) | 10 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 192 |
LaCrOS2 | Pbnm (#62) | 20 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 636 636 |
NaNbO2F | Pbnm (# 62) | 20 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024 024 |
GaLaOSe2 | P21ab (#29) | 20 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
CeCrOSe2 | B112/m (#12) | 10 |
66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
AsPbO2Cl | P212121 (#19) | 40 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
PtCOI2 | C12/c1 (#15) | 20 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 869 869 |
CaFeO2Cl | A1m1 (#8) | 10 |
84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 635 635 |
CaBiO2Cl | P121/m1 (#11) | 10 |
86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229 229 |
PbSbO2Cl | Cmcm (#63) | 10 |
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
CdSbS2Cl | Pnma (#62) | 20 |
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723 723 |
CdSbS2Br | C12/m1 (#12) | 10 |
244![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028 028 |
LaVSe2O | C12/m1 (#12) | 10 |
411![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 137 |
TaSrNO2 | I4/mcm (#140) | 10 |
411![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 138 |
TaLaN2O | C12/m1 (#12) | 10 |
413![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
CuBiSCl2 | Cmcm (#63) | 10 |
419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 916 |
LaFCN2 | Cmcm (#63) | 10 |
424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
NaBOF2 | C12/c1 (#15) | 30 |
Although LaMgF2N is the only nitrofluoride system that we predict to have possibilities to be realized experimentally, we recall that La is often easily substituted by other lanthanides (or actinides),80 giving us hope that such nitrofluoride systems can be discovered in the future.
Conclusions
From our extensive computational study of quaternary oxynitride, oxyfluoride, and nitrofluoride perovskites it is clear that there are many more compounds that are experimentally accessible than the few systems that have been discovered to date. Some of them can be obtained by simple chemical substitutions of known compounds, such as LaHfO2N or AgTiO2F that can be obtained by substituting Zr in LaZrO2N or in AgZrO2F. However, many of the predicted materials do not have an experimentally known counterpart, such as the many Re-based oxynitride systems that we found. We note that although many of the low-energy compositions seem to crystallize in a perovskite phase, some systems prefer other atomic arrangements that do not exhibit the famous octahedra. Furthermore, we show that changing the arrangement of the anions and allowing for geometrical distortions can stabilize the structure of the perovskites by up to 150 meV per atom, although this number is highly dependent on the composition. This stabilization is in many cases fundamental, as it makes the composition thermodynamically stable, even without the need to resort to entropic arguments.Many of our systems turn out to be semiconducting or insulating, with electronic band gaps going from a fraction of an eV to several eV. Often the electron bands are highly dispersive, leading to rather small electron effective masses, while the hole bands are considerably flatter. This can be understood from the reduced hybridization between the cationic states and the anionic p levels. Furthermore, for the fluorine compounds we find that the valence states are often split, with the top of the valence characterized by a strong p-character from O or N atoms, and the lower manifold of states stemming from the F states. The splitting is considerably larger for the nitrofluoride systems than for the oxifluorides indicating that this is due to the larger electronegativity of F leading to a cation–F bond with a stronger ionic character. However, and in spite of these common features, we find a multitude of behaviors that illustrate the diversity and importance of these mixed ionic systems.
Our results confirm that alloying on the anion sublattice is a promising strategy to improve the stability and engineer the band gap of perovskite absorbers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. B. and M. A. L. M. acknowledge financial support from the DFG through Projects MA 6787/1-1 and BO 4280/8.Notes and references
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398 CrossRef CAS PubMed.
- S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402 CrossRef CAS PubMed.
- G. Schileo and G. Grancini, JPhys Energy, 2020, 2, 021005 CrossRef CAS.
- D. W. deQuilettes, K. Frohna, D. Emin, T. Kirchartz, V. Bulovic, D. S. Ginger and S. D. Stranks, Chem. Rev., 2019, 119, 11007–11019 CrossRef CAS PubMed.
- J. Schmidt, J. Shi, P. Borlido, L. Chen, S. Botti and M. A. L. Marques, Chem. Mater., 2017, 29, 5090–5103 CrossRef CAS.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS PubMed.
- W.-J. Yin, J.-H. Yang, J. Kang, Y. Yan and S.-H. Wei, J. Mater. Chem. A, 2015, 3, 8926–8942 RSC.
- W.-J. Yin, T. Shi and Y. Yan, Appl. Phys. Lett., 2014, 104, 063903 CrossRef.
- K. Miyata, T. L. Atallah and X.-Y. Zhu, Sci. Adv., 2017, 3, e1701469 CrossRef PubMed.
- W. Chu, Q. Zheng, O. V. Prezhdo, J. Zhao and W. A. Saidi, Sci. Adv., 2020, 6, eaaw7453 CrossRef CAS PubMed.
- M. Anderson, K. Greenwood, G. Taylor and k. Poepellmeier, Prog. Solid State Chem., 1993, 22, 197–233 CrossRef CAS.
- A. Hossain, P. Bandyopadhyay and S. Roy, J. Alloys Compd., 2018, 740, 414–427 CrossRef CAS.
- E. Meyer, D. Mutukwa, N. Zingwe and R. Taziwa, Metals, 2018, 8, 667 CrossRef.
- E. Greul, M. L. Petrus, A. Binek, P. Docampo and T. Bein, J. Mater. Chem. A, 2017, 5, 19972–19981 RSC.
- J. Kangsabanik, V. Sugathan, A. Yadav, A. Yella and A. Alam, Phys. Rev. Mater., 2018, 2, 055401 CrossRef CAS.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- H.-C. Wang, P. Pistor, M. A. Marques and S. Botti, J. Mater. Chem. A, 2019, 7, 14705–14711 RSC.
- Y. Kobayashi, Y. Tsujimoto and H. Kageyama, Annu. Rev. Mater. Res., 2018, 48, 303–326 CrossRef CAS.
- H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772 CrossRef PubMed.
- T. Katsumata, R. Suzuki, N. Satoh, S. Suzuki, M. Nakashima, Y. Inaguma, D. Mori, A. Aimi and Y. Yoneda, J. Solid State Chem., 2019, 279, 120919 CrossRef CAS.
- M. Ahmed and G. Xinxin, Inorg. Chem. Front., 2016, 3, 578–590 RSC.
- M. Sakar, R. M. Prakash, K. Shinde and G. R. Balakrishna, Inorg. Chem. Front., 2020, 45, 7691–7705 CAS.
- R.-J. Xie and H. T. B. Hintzen, J. Am. Ceram. Soc., 2013, 96, 665–687 CrossRef CAS.
- R. Aguiar, D. Logvinovich, A. Weidenkaff, A. Rachel, A. Reller and S. G. Ebbinghaus, Dyes Pigm., 2008, 76, 70–75 CrossRef.
- R.-J. Xie and N. Hirosaki, J. Adv. Mater., 2007, 8, 588–600 CAS.
- M. G. Francesconi and C. Greaves, Supercond. Sci. Technol., 1997, 10, A29–A37 CrossRef CAS.
- C. Greaves and M. G. Francesconi, Curr. Opin. Solid State Mater. Sci., 1998, 3, 132–136 CrossRef CAS.
- E. E. McCabe and C. Greaves, J. Fluorine Chem., 2007, 128, 448–458 CrossRef CAS.
- R. Heap, P. R. Slater, F. J. Berry, O. Helgason and A. J. Wright, Solid State Commun., 2007, 141, 467–470 CrossRef CAS.
- F. J. Berry, R. Heap, O. Helgason, E. A. Moore, S. Shim, P. R. Slater and M. F. Thomas, J. Condens. Matter Phys., 2008, 20, 215207 CrossRef.
- Y. Inaguma, J.-M. Greneche, M.-P. Crosnier-Lopez, T. Katsumata, Y. Calage and J.-L. Fourquet, Chem. Mater., 2005, 17, 1386–1390 CrossRef CAS.
- S. T. Hartman, S. B. Cho and R. Mishra, Inorg. Chem., 2018, 57, 10616–10624 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- H.-C. Wang, S. Botti and M. Marques, npj Comput. Mater., 2020 Search PubMed.
- A. van de Walle, Calphad, 2009, 33, 266–278 CrossRef CAS.
- R. Marchand, F. Pors and Y. Laurent, Ann. Chim., 1991, 553–560 CAS.
- M. Liu, W. You, Z. Lei, T. Takata, K. Domen and C. Li, Chin. J. Catal., 2006, 27, 556–558 CrossRef CAS.
- Y.-I. Kim, P. M. Woodward, K. Z. Baba-Kishi and C. W. Tai, Chem. Mater., 2004, 16, 1267–1276 CrossRef CAS.
- F. Oehler and S. G. Ebbinghaus, Solid State Sci., 2016, 54, 43–48 CrossRef CAS.
- E. Günther, R. Hagenmayer and M. Jansen, Z. Anorg. Allg. Chem., 2000, 626, 1519–1525 CrossRef.
- Y.-I. Kim, PhD thesis, The Ohio State University, 2005.
- R. Marchand, F. Pors and Y. Laurant, Rev. Int. Hautes Temp. Refract., 1986, 23, 11–15 CAS.
- S. J. Clarke, B. P. Guinot, C. W. Michie, M. J. C. Calmont and M. J. Rosseinsky, Chem. Mater., 2002, 14, 288–294 CrossRef CAS.
- F. Takeiri, T. Yamamoto, N. Hayashi, S. Hosokawa, K. Arai, J. Kikkawa, K. Ikeda, T. Honda, T. Otomo, C. Tassel, K. Kimoto and H. Kageyama, Inorg. Chem., 2018, 57, 6686–6691 CrossRef CAS PubMed.
- Y. Inaguma, K. Sugimoto and K. Ueda, Dalton Trans., 2020, 49, 6957–6963 RSC.
- F. J. Berry, F. C. Coomer, C. Hancock, Ö. Helgason, E. A. Moore, P. R. Slater, A. J. Wright and M. F. Thomas, J. Solid State Chem., 2011, 184, 1361–1366 CrossRef CAS.
- R. Needs and M. Weller, J. Solid State Chem., 1998, 139, 422–423 CrossRef CAS.
- W. Rüdorff and D. Krug, Z. Anorg. Allg. Chem., 1964, 329, 211–217 CrossRef.
- B. Chamberland, Mater. Res. Bull., 1971, 6, 311–315 CrossRef CAS.
- T. Katsumata, H. Umemoto, Y. Inaguma, D. Fu and M. Itoh, J. Appl. Phys., 2008, 104, 044101 CrossRef.
- V. Zaitsev and V. Senin, Vestn. Otd. nauk Zemle, 2012, 4, 8 Search PubMed.
- T. Katsumata, A. Takase, M. Yoshida, Y. Inaguma, J. E. Greedan, J. Barbier, L. M. D. Cranswick and M. Bieringer, MRS Online Proc. Libr., 2006, 988, 0988-QQ06-03 CrossRef.
- T. Katsumata, M. Nakashima, Y. Inaguma and T. Tsurui, Bull. Chem. Soc. Jpn., 2012, 85, 397–399 CrossRef CAS.
- T. Katsumata, M. Nakashima, H. Umemoto and Y. Inaguma, J. Solid State Chem., 2008, 181, 2737–2740 CrossRef CAS.
- F. J. Berry, X. Ren, R. Heap, P. Slater and M. F. Thomas, Solid State Commun., 2005, 134, 621–624 CrossRef CAS.
- F. Brivio, C. Caetano and A. Walsh, J. Phys. Chem. Lett., 2016, 7, 1083–1087 CrossRef CAS PubMed.
- R. Sarmiento-Pérez, S. Botti and M. A. L. Marques, J. Chem., 2015, 11, 3844–3850 Search PubMed.
- F. Tran, J. Stelzl and P. Blaha, J. Chem. Phys., 2016, 144, 204120 CrossRef PubMed.
- V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104 CrossRef.
- Y. Zhang, D. A. Kitchaev, J. Yang, T. Chen, S. T. Dacek, R. A. Sarmiento-Pérez, M. A. L. Marques, H. Peng, G. Ceder, J. P. Perdew and J. Sun, npj Comput. Mater., 2018, 4, 9 CrossRef.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- A. A. Emery and C. Wolverton, Sci. Data, 2017, 4, 170153 CrossRef CAS PubMed.
- V. M. Goldschmidt, Sci. Nat., 1926, 14, 477–485 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- G. Pilania, A. Ghosh, S. T. Hartman, R. Mishra, C. R. Stanek and B. P. Uberuaga, npj Comput. Mater., 2020, 6, 71 CrossRef CAS.
- R. Mouta, R. X. Silva and C. W. A. Paschoal, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 439–445 CrossRef CAS PubMed.
- W. Li, E. Ionescu, R. Riedel and A. Gurlo, J. Mater. Chem. A, 2013, 1, 12239 RSC.
- Q. Sun and W.-J. Yin, J. Am. Chem. Soc., 2017, 139, 14905–14908 CrossRef CAS PubMed.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83 CrossRef.
- J. George, D. Waroquiers, D. Di Stefano, G. Petretto, G.-M. Rignanese and G. Hautier, Angew. Chem., Int. Ed., 2020, 59, 7569–7575 CrossRef CAS PubMed.
- H. Glawe, A. Sanna, E. K. U. Gross and M. A. L. Marques, New J. Phys., 2016, 18, 093011 CrossRef.
- J. A. Flores-Livas, R. Sarmiento-Pérez, S. Botti, S. Goedecker and M. A. Marques, J. Phys. Mater., 2019, 2, 025003 CrossRef CAS.
- G. Demazeau, I. Grannec, A. Marbeuf, J. Portier and P. Hagenmuller, C. R. Acad. Sci., 1969, 269, 987–988 CAS.
- A. R. Oganov, Modern Methods of Crystal Structure Prediction, John Wiley & Sons, 2011 Search PubMed.
- T. F. T. Cerqueira, S. Lin, M. Amsler, S. Goedecker, S. Botti and M. A. L. Marques, Chem. Mater., 2015, 27, 4562–4573 CrossRef CAS.
- F. Yan, X. Zhang, Y. G. Yu, L. Yu, A. Nagaraja, T. O. Mason and A. Zunger, Nat. Commun., 2015, 6, 7308 CrossRef CAS.
- R. Sarmiento-Perez, T. F. Cerqueira, S. Körbel, S. Botti and M. A. Marques, Chem. Mater., 2015, 27, 5957–5963 CrossRef CAS.
- Crystallographic Databases, ed. G. G. F. H. Allen and R. Sievers, International Union of Crystallography, Chester, 1987 Search PubMed.
- P. Borlido, T. Aull, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, J. Chem., 2019, 15, 5069–5079 CAS.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- I. E. Castelli, D. D. Landis, K. S. Thygesen, S. Dahl, I. Chorkendorff, T. F. Jaramillo and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 9034–9043 RSC.
- W. Xiang and W. Tress, J. Adv. Mater., 2019, 31, 1902851 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10781f |
| ‡ https://tddft.org/bmg/data.php |
| This journal is © The Royal Society of Chemistry 2021 |