Entropy-driven stabilization of the cubic phase of MaPbI3 at room temperature†
A.
Bonadio
a,
C. A.
Escanhoela
Jr
a,
F. P.
Sabino
a,
G.
Sombrio
a,
V. G.
de Paula
a,
F. F.
Ferreira
 a,
A.
Janotti
b,
G. M.
Dalpian
a and
J. A.
Souza
a,
A.
Janotti
b,
G. M.
Dalpian
a and
J. A.
Souza
 *a
*a
aUniversidade Federal do ABC, Santo André, SP, Brazil. E-mail: joseantonio.souza@ufabc.edu.br
bDepartment of Materials Science and Engineering, University of Delaware, DE, USA
First published on 8th December 2020
Abstract
Methylammonium lead iodide (MAPbI3) is an important light-harvesting semiconducting material for solar-cell devices. We investigate the effect of long thermal annealing in an inert atmosphere of compacted MAPbI3 perovskite powders. The microstructure morphology of the MAPbI3 annealed samples reveals a well-defined grain boundary morphology. The voids and neck-connecting grains are observed throughout the samples, indicating a well-sintered process due to mass diffusion transfer through the grain boundary. The long 40 h thermal annealing at T = 522 K (kBT = 45 meV) causes a significant shift in the structural phase transition, stabilizing the low-electrical conductivity and high-efficiency cubic structure at room temperature. The complete disordered orientation of MA cations maximizes the entropy of the system, which, in turn, increases the Pb–I–Pb angle close to 180°. The MA rotation barrier and entropy analysis determined through DFT calculations suggest that the configurational entropy is a function of the annealing time. The disordered organic molecules are quenched and become kinetically trapped in the cubic phase down to room temperature. We propose a new phase diagram for this important system combining different structural phases as a function of temperature with annealing time for MAPbI3. The absence of the coexistence of different structural phases, leading to thermal hysteresis, can significantly improve the electrical properties of the solar cell devices. Through an entropy-driven stabilization phenomenon, we offer an alternative path for improving the maintenance, toughness, and efficiency of the optoelectronic devices by removing the microstructural stress brought by the structural phase transformation within the solar cell working temperature range.
1. Introduction
Light-harvesting organic–inorganic hybrid halide perovskites have been attracting considerable attention due to their excellent photovoltaic performance. Methylammonium (MA) lead iodide (CH3NH3PbI3) has been widely applied as an absorber layer of perovskite-based solar cells (PSCs) due to its excellent optoelectronic properties such as broad absorption spectrum (ranging from the visible light to the near-infrared spectrum),1 low charge recombination rates,2 and high charge carrier mobility.3 These properties can be useful for a wide range of technological applications, including photodetectors,4,5 light-emitting diodes,6 transistors,7 and photovoltaic devices.8,9 These beneficial effects, combined with low-cost and ease of fabrication, make the organic–inorganic MAPbI3 as promising candidate materials for the next generation of optoelectronic devices.10,11 Indeed, MAPbI3-based solar cells display high efficiency to convert solar energy into electricity, with a power conversion efficiency (PCE) exceeding 23%,12 with the cubic crystal phase being the most efficient structure for this perovskite family.13,14Despite the significant progress on the efficiency of perovskite solar cells (PSCs), one of the main drawbacks is the material structural stability.15,16 MAPbI3 undergoes two structural phase transitions, from orthorhombic (Pnma space group) to tetragonal (I4/mcm space group) at T = 160 K (−113 °C), and to the cubic crystal structure, with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry, at T = 330 K (57 °C).17 It is worth noting that the later tetragonal-to-cubic phase transition falls within the typical working temperature range of several devices. For instance, in the test protocols for solar-cell applications, the device temperature is higher than 350 K in order to simulate the real operation conditions; thus, the material switches back and forth several times between tetragonal and cubic structures during device operation.18 The induced thermal hysteresis caused by this first-order phase transition in this temperature range – the organic molecule, lead, and iodide atoms undergo a complex combination of ionic movements resulting in breaking and formation of Pb–I bonds – is also a major drawback for the useful applications of their optical and electrical properties.19,20 In this regard, several studies have investigated the impact of this structural transformation on the electrical, optical, thermal, and dielectric properties and even its influence on the MAPbI3 device performance.21,22 Since these devices are exposed to significant temperature changes day-and-night, it is important to devise a way to minimize the mismatch between different crystal structures and their interface with the surrounding component materials in the device to obtain higher efficiency and longer lifetimes.18,23 In this regard, suppression, shifting the phase transition, and stabilizing the cubic phase at room temperature will improve maintenance, durability, and efficiency of the device.13 Herein, we investigate the effect of long thermal annealing on compacted MAPbI3 perovskites, finding that the long thermal treatment causes a significant shift in the structural phase transition, and stabilizes the low electrical conductivity and high-efficiency cubic phase at room temperature. This cubic structure stabilization is attributed to an entropy-driven mechanism, where the complete disordered orientation of MA+ cations maximizes the configurational entropy of the system, minimizing its free energy. We then propose a new phase diagram combining different structural phases as a function of temperature with annealing time for MAPbI3. The entropy-driven stabilization phenomenon offers an extra alternative by improving the optical and electrical properties along with maintenance, toughness, and efficiency of the optoelectronic devices by removing the microstructural stress brought about by the structural phase transformation close to the working temperature range.
m space group symmetry, at T = 330 K (57 °C).17 It is worth noting that the later tetragonal-to-cubic phase transition falls within the typical working temperature range of several devices. For instance, in the test protocols for solar-cell applications, the device temperature is higher than 350 K in order to simulate the real operation conditions; thus, the material switches back and forth several times between tetragonal and cubic structures during device operation.18 The induced thermal hysteresis caused by this first-order phase transition in this temperature range – the organic molecule, lead, and iodide atoms undergo a complex combination of ionic movements resulting in breaking and formation of Pb–I bonds – is also a major drawback for the useful applications of their optical and electrical properties.19,20 In this regard, several studies have investigated the impact of this structural transformation on the electrical, optical, thermal, and dielectric properties and even its influence on the MAPbI3 device performance.21,22 Since these devices are exposed to significant temperature changes day-and-night, it is important to devise a way to minimize the mismatch between different crystal structures and their interface with the surrounding component materials in the device to obtain higher efficiency and longer lifetimes.18,23 In this regard, suppression, shifting the phase transition, and stabilizing the cubic phase at room temperature will improve maintenance, durability, and efficiency of the device.13 Herein, we investigate the effect of long thermal annealing on compacted MAPbI3 perovskites, finding that the long thermal treatment causes a significant shift in the structural phase transition, and stabilizes the low electrical conductivity and high-efficiency cubic phase at room temperature. This cubic structure stabilization is attributed to an entropy-driven mechanism, where the complete disordered orientation of MA+ cations maximizes the configurational entropy of the system, minimizing its free energy. We then propose a new phase diagram combining different structural phases as a function of temperature with annealing time for MAPbI3. The entropy-driven stabilization phenomenon offers an extra alternative by improving the optical and electrical properties along with maintenance, toughness, and efficiency of the optoelectronic devices by removing the microstructural stress brought about by the structural phase transformation close to the working temperature range.
2. Experimental details and theoretical approach
We have used the solvothermal method to synthesize the hybrid MAPbI3 perovskite. In this process, 50 mg of lead iodide were completely dissolved in 1 mL of hydriodic acid (45 wt% in water), and then 30 mL of isopropyl alcohol (IPA, 99.9%) were added under stirring at T = 80 °C. Subsequently, 0.3 mL of methylamine (40% in water) was added dropwise, and the final solution was stirred for 1 minute. The black precipitate was collected and washed twice, by centrifugation at room temperature – with isopropanol and then dried overnight in a desiccator. Compacted perovskite samples (pellets) were prepared by pressing the powder at room temperature under a pressure of P = 13 Pa m−2 for t = 10 min. Then, the pellets were submitted to thermal annealing by varying the temperature and time in a vacuum-sealed ampoule (T = 250 °C and t = 10, 20, and 40 hours). The structural properties were studied by using X-ray powder diffraction (XRPD) in transmission geometry on a STADI-P diffractometer (Stoe®, Darmstadt, Germany) with CuKα1 radiation (λ = 1.5406 Å) selected by a curved Ge(111) crystal, operating at a tube voltage of 40 kV and a current of 40 mA. A silicon microstrip detector – Mythen 1K (Dectris®, Baden, Switzerland) – collected the diffracted intensities, in the range from 2° to 100° (2θ), with step sizes of 1.05° and 300 s of integration time at each 1.05° room temperature. The Rietveld method,24 implemented in the TOPAS-Academic V.6 (ref. 25) software, was used to refine the structural parameters and peak shapes from the XRPD patterns. Morphological studies of the samples were carried out by scanning electron microscopy (SEM) (JEOL JSM-6010LA). To examine the phase transition in MAPbI3 microcrystals, differential scanning calorimetry (DSC) was carried out on a Q2000 calorimeter (TA Instruments). The experiment was conducted at a heating rate of 5 °C min−1 over a temperature range of 30 °C to 80 °C under a nitrogen atmosphere using around 5 mg of sample for each run. The impact of thermal annealing on the low-temperature phase transition was studied by heat capacity measurements in a commercial Physical Properties Measurement System (PPMS) from Quantum Design.First-principles calculations based on the density functional theory were carried out for the different phases of the MAPbI3 crystal. For the exchange and correlation functional, we used the Perdew–Burke–Ernzerhof revised for bulk solids systems (PBESol),26 as implemented in the Vienna ab initio simulation package (VASP).27,28 The interaction between the ionic cores and valence electrons was treated using the projected augmented waves (PAW) method.29,30 In this method we considered the following valence electrons: H (1s1), N (2s2 2p3), O (2s2 2p4), I (5s2 5p5), Pb (6s2 6p2). We used 600 eV for the plane waves cutoff to optimize the cell shape and volume, minimizing the stress tensor, within a force convergence criterion of 10 meV Å−1 in each atom. For the Brillouin zone integration, we employ a mesh of 4 × 4 × 4 for the cubic primitive cell of halide perovskites and the same density for the tetragonal and the supercell configurations. The barrier for the MA+ rotation was calculated based on a cubic 2 × 2 × 2 supercell, containing eight MA+ molecules. This system was relaxed to obtain the most stable configuration and the atomic position of each atom. Using this atomic setup as a reference, we applied the rotation matrix in only one MA+ molecule, assuming the geometric center as the rotation point. All I and Pb atoms were allowed to relax, while only H atoms of the rotated molecule were free to move. All the non-rotated molecules were kept frozen, as well as the distance between C–N of the rotated molecule. Under this approach, we assume that the molecule rotations are completely decorrelated, which is different from many reports in the literature.31,32 In those previous reports, only the primitive cell was considered, and therefore all the movements of the MA molecules were considered completely correlated.
3. Results and discussion
The MAPbI3 perovskite black powder was synthesized by using the solvothermal method. The powder was dried and then the crystal structure was identified by room temperature XRD measurements, as shown in Fig. S1 in the ESI.† The Bragg reflections were indexed as the tetragonal phase I4/mcm space group of MAPbI3 (COD ID 4124388).33 The refined unit-cell parameters, a = b = 8.850(1) Å and c = 12.637(2) Å – are in good agreement with data reported in the literature.34 The perovskite particles self-assembled into a cuboid-like morphology, which strongly depends on the reacting temperature.35 The particles have a high size dispersity, and the average size of the cube edges is around 7.2(2) μm, as shown in the inset of Fig. S1.† Subsequently, the cuboid-like shape powders were compacted by using hydrostatic pressure, which resulted in a high-density pellet with well-defined grain boundary morphology. The pressure brings about a process that deforms and compresses the polyhedral particles, resulting in a reduction of the particle size. The fractured surface image reveals a grain size of ∼5 μm and a very-low porosity degree, as shown in the Fig. S2–S6.†Interestingly, the perovskite particles have high viscosity, which results in the plastic deformation of the cuboids. In other words, the plasticity property of hybrid materials is observed when cuboid-shape MAPbI3 undergoes non-reversible deformation into a well-defined irregular grain morphology. As we shall see, the methylammonium molecules of the formed complexes might be contributing not only to this high viscosity characteristics but also to the formation of voids. After that, the pelletized samples were submitted to a long-time sintering process by performing a thermal treatment at TA = 250 °C (523 K). These sintering and densification processes have been performed during different annealing times tA = 0, 10, 20, and 40 h in vacuum ampoules. After these long annealing times, one can see small segregation of a yellow powder, suggesting the presence of the well-known PbI2 phase, which can be easily removed from the outer surface of the pellets. Fig. S2–S6† show the scanning electron micrographs of the fractured surface of these sintered samples at tA = 0, 10, 20, and 40 h that have been named as S0 h, S10 h, S20 h, and S40 h, respectively. The microstructure morphology of the MAPbI3 annealed samples reveals an interesting evolution. All samples have a well-defined grain boundary morphology, but the porosity and formation of voids have increased as the annealing time increases. The growth of voids indicates the microstructure has been modified due to mass diffusion transfer through the grain boundary. The average grain size has also increased with time, reaching a maximum value of ∼12 μm. Indeed, voids and neck-connecting grains are observed throughout the samples S10 h, S20 h, and S40 h, indicating a well-sintered process. The creation of voids and mass diffusion entities have been observed during the formation and evaporation of sub-products due to the extended annealing process. Regarding these chemical species, as we shall see in Rietveld refinements, we have observed the presence of not only the yellow PbI2 phase in the as-compacted sample but also traces of NH4PbI3 as a solid decomposition product after annealing. On the basis of our results and observations reported in the literature,36,37 small segregation of PbI2 and the appearance of voids is due to the thermal decomposition processes of the pelletized MAPbI3 perovskite involving CH3NH2, CH3I, and NH3 vapor.
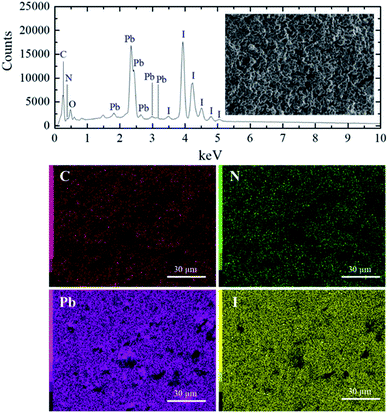
The energy dispersive spectroscopy (EDS) analysis of the S40 h annealed sample displayed in Fig. 1 (S0 h is shown in SM) shows the presence of carbon, nitrogen, oxygen, lead and iodide. The EDS map analysis indicates that all the elements (C, N, Pb and I) are well distributed in the samples. From these results, we can also determine the ratio of Pb and I atoms in the molecular formula to be 1Pb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3I for both S0 h and S40 h annealed samples indicating that the stoichiometry has not changed. A possible crystal structure change of the powdered MAPbI3 pellets after prolonged annealing was also investigated by ex situ X-ray powder diffraction. Fig. 2 shows the Bragg reflections for different annealing times. It is observed a reduction of the splitting between three different pairs of planes of the tetragonal structure into a single one, which indicates ionic movement and symmetry increasing. Indeed, atomic displacements are manifested by the shift of the (002) and (110) planes, which merge into the (100) plane, suggesting the appearance of the cubic phase. The splitting of the (004) and (220) Bragg reflections in the tetragonal phase is also derived from the cubic (200) reflection. It is worth mentioning that MAPbI3 undergoes a well-known structural phase transition around T = 333 K (60 °C), but, here, due to prolonged thermal annealing, we observe the cubic phase at room temperature. Indeed, the influence of distinct thermal annealing processes on the physical properties of MAPbI3 halide perovskite under several conditions has been recently reported in the literature.35,38 These processes can influence the microstructure, morphology, and also the performance of MAPbI3-based solar cells. For instance, the annealing process for temperatures around T = 100 °C for 5 min has shown that it is possible to increase the energy efficiency of the compound due to excitons longer lifetime. Another interesting result regarding the thermal annealing process of MAPbI3 consists of its impact on morphology and final composition under vacuum conditions.39 More recently,38 the impact of the annealing process on crystallinity and surface roughness was investigated under different conditions, and an optimized result was obtained at 90 °C annealing temperature. Before performing a careful analysis of the crystal structure, we looked for possible shifting or suppression of the structural phase transition due to prolonged thermal annealing effects.
3I for both S0 h and S40 h annealed samples indicating that the stoichiometry has not changed. A possible crystal structure change of the powdered MAPbI3 pellets after prolonged annealing was also investigated by ex situ X-ray powder diffraction. Fig. 2 shows the Bragg reflections for different annealing times. It is observed a reduction of the splitting between three different pairs of planes of the tetragonal structure into a single one, which indicates ionic movement and symmetry increasing. Indeed, atomic displacements are manifested by the shift of the (002) and (110) planes, which merge into the (100) plane, suggesting the appearance of the cubic phase. The splitting of the (004) and (220) Bragg reflections in the tetragonal phase is also derived from the cubic (200) reflection. It is worth mentioning that MAPbI3 undergoes a well-known structural phase transition around T = 333 K (60 °C), but, here, due to prolonged thermal annealing, we observe the cubic phase at room temperature. Indeed, the influence of distinct thermal annealing processes on the physical properties of MAPbI3 halide perovskite under several conditions has been recently reported in the literature.35,38 These processes can influence the microstructure, morphology, and also the performance of MAPbI3-based solar cells. For instance, the annealing process for temperatures around T = 100 °C for 5 min has shown that it is possible to increase the energy efficiency of the compound due to excitons longer lifetime. Another interesting result regarding the thermal annealing process of MAPbI3 consists of its impact on morphology and final composition under vacuum conditions.39 More recently,38 the impact of the annealing process on crystallinity and surface roughness was investigated under different conditions, and an optimized result was obtained at 90 °C annealing temperature. Before performing a careful analysis of the crystal structure, we looked for possible shifting or suppression of the structural phase transition due to prolonged thermal annealing effects.
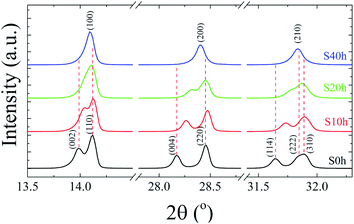 | ||
| Fig. 2 Room-temperature X-ray diffraction patterns of the pelletized MAPbI3 sample after being submitted to a heat treatment at T = 250 °C for different annealing times, t = 0, 10, 20, and 40 h. | ||
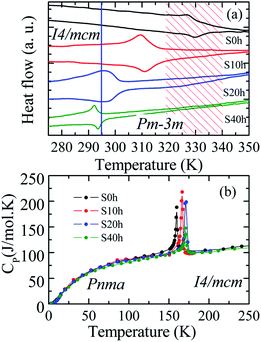
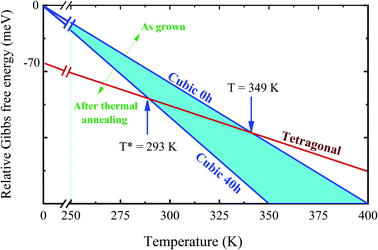
DSC analysis was carried out to confirm the presence of the well-known structural phase transition in the thermal annealed MAPbI3 pelletized samples. Fig. 3(a) reveals an endothermic (exothermic) peak at T = 329 K (T = 327 K), which indicates the presence of the reversible tetragonal-to-cubic phase transition.40,41 Most important here is that Fig. 3 reveals a systematic change of this structural phase transition towards room temperature. The tetragonal-to-cubic phase transition temperature is shifted to lower temperatures as the annealing time increases until it reaches a minimum value of T* = 293 K for t = 40 h annealed sample. The annealing process leads to a phase transition temperature reduction of about ΔT = 36 K leading to the stabilization of the cubic phase to slightly below room temperature. The nature of this structural phase transition, whether it is continuous or discontinuous, has been discussed in the literature. According to Landau's theory, it was suggested a second-order transition.42 On the other hand, other studies reached different conclusions based on different experimental results and suggested the first-order transition.43,44 The thermal hysteresis found in our data indicates phase coexistence leading to a first-order discontinuous nature of the structural transition.
For completeness, we have also performed heat capacity measurements of these MAPbI3 annealed samples to reveal the influence on the low-temperature orthorhombic-to-tetragonal phase transition. Fig. 3(b) shows the impact of the thermal annealing process on the temperature of the orthorhombic-to-tetragonal structural phase transition, which takes place around T = 160 K.45 The molar heat capacity peak involving latent heat due to the structural phase transition is shifted to higher temperatures as the annealing time increases. For instance, the structural phase transition temperature for the S40 h sample occurs at T = 172 K, which represents an increment toward room temperature of ΔT = 12 K in comparison to the as-compacted sample. In contrast to the larger variation of the cubic to tetragonal transition, here, the MA cations are strongly coupled to the Pb–I framework through hydrogen bonds, leading to the orthorhombic distortion of the tetragonal lattice. Therefore, prolonged thermal annealing shifts both orthorhombic-to-tetragonal and tetragonal-to-cubic structural phase transitions toward room temperature, i.e., in the opposite direction. Before sketching a new structural phase diagram for this important compound, we shed light on the nature of the stabilization of the cubic structure at room temperature by doing a careful analysis of the modified crystal parameters.
Detailed analysis of the crystal structure evolution of the powdered MAPbI3 annealed pellets was performed by Rietveld refinement using X-ray powder diffraction data obtained at room temperature for the samples with different annealing times. Fig. 4 displays high-intensity reflections indicating good counting statistics for the selected S0 h and S40 h samples (all analyzed samples are in the SM). The refinement for the S0 h and S10 h samples was carried out by using the I4/mcm tetragonal space group symmetry. However, the Rietveld refinements of the S20 h and S40 h samples using the tetragonal or the high-temperature cubic phase (or even a coexistence of them) resulted in a poor quality of Rietveld fit and statistical parameters. To overcome this problem and obtain a better description of the crystal structure, we examined more closely the rotation of the PbI6 octahedra of the distorted phase. To this end, a symmetry-mode decomposition was carried out in ISODISTORT46,47 for the S20 h and S40 h samples. With this approach, we could explore the structural distortion modes of the samples induced by irreducible representations (irreps) of the parent space-group symmetry (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Although, in our case, there are six irreps for the special R-point (R4+), with the k-point in the reciprocal space k = [1/2, 1/2, 1/2], the cubic-to-tetragonal transition can be represented by the R4+ rotational distortion mode amplitude. The R4+ is active in the Pm
m). Although, in our case, there are six irreps for the special R-point (R4+), with the k-point in the reciprocal space k = [1/2, 1/2, 1/2], the cubic-to-tetragonal transition can be represented by the R4+ rotational distortion mode amplitude. The R4+ is active in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → I4/mcm transition and involves a rotation of the octahedra along the c-axis, represented by an order-parameter direction (OPD) R4+ (a, 0, 0).48–50 The order parameter can also be the rotation angle around a particular axis of the PbI6 octahedra, which is equivalent to the R4+ distortion mode amplitude. The refinement illustrated in Fig. 4 shows 1.3 wt% of the extra PbI2 impurity phase for the S0 h sample while we observed 4.4 wt% of NH4PbI3(H2O)2 phase for the S40 h sample. All obtained parameters from Rietveld refinement analyses are shown in Table 1.
m → I4/mcm transition and involves a rotation of the octahedra along the c-axis, represented by an order-parameter direction (OPD) R4+ (a, 0, 0).48–50 The order parameter can also be the rotation angle around a particular axis of the PbI6 octahedra, which is equivalent to the R4+ distortion mode amplitude. The refinement illustrated in Fig. 4 shows 1.3 wt% of the extra PbI2 impurity phase for the S0 h sample while we observed 4.4 wt% of NH4PbI3(H2O)2 phase for the S40 h sample. All obtained parameters from Rietveld refinement analyses are shown in Table 1.
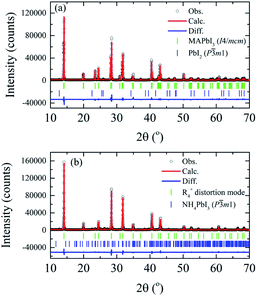 | ||
| Fig. 4 X-ray powder diffraction data and Rietveld refinements at room temperature of the (a) MAPbI3 as-compacted sample and (b) submitted to thermal annealing at 250 °C for 40 hours. | ||
| Annealing time | ||||
|---|---|---|---|---|
| 0 | 10 h | 20 h | 40 h | |
| Space group | I4/mcm | I4/mcm | I4/mcm | I4/mcm |
| DMA | — | — | R 4+ (a, 0, 0) | R 4 + (a, 0, 0) |
| a 1 | 0.572(5) | −0.192(6) | ||
| a = b (Å) | 8.8652(1) | 8.8613(1) | 8.8663(4) | 8.8836(8) |
| c (Å) | 12.6585(2) | 12.6195(2) | 12.5961(6) | 12.5639(5) |
| I1 (x) | 0 | 0 | 0 | 0 |
| I1 (y) | 0 | 0 | 0 | 0 |
| I1 (z) | 0.25 | 0.25 | 0.25 | 0.25 |
| I2 (x) | 0.2844(1) | 0.2791(1) | 0.2728(2) | 0.2423(3) |
| I2 (y) | 0.2156(1) | 0.2210(1) | 0.7728(2) | 0.7423(3) |
| I2 (z) | 0.5 | 0.5 | 0 | 0 |
| Pb (x, y) | 0 | 0 | 0 | 0 |
| Pb (z) | 0.5 | 0.5 | 0 | 0 |
| B C (Å2) | 8(2) | 15(2) | 16(2) | 17(2) |
| B N (Å2) | 8(2) | 15(2) | 16(2) | 17(2) |
| θ I2(Pb–I2–Pb) | 164.33(5) | 166.78(5) | 169.34(7) | 176.5(1) |
| Crystallite size (nm) | 215(3) | 204(3) | 280(19) | 219(5) |
| [PbI2] (%) | 1.3(6) | — | — | — |
| [NH4PbI3] (%) | — | 1.0(5) | 0.3 | 4.4(2) |
| R Bragg | 4.2 | 4.3 | 6.8 | 3.1 |
| R wp | 8.4 | 8.8 | 9.1 | 7.4 |
| G of | 3.4 | 1.9 | 3.3 | 3.2 |
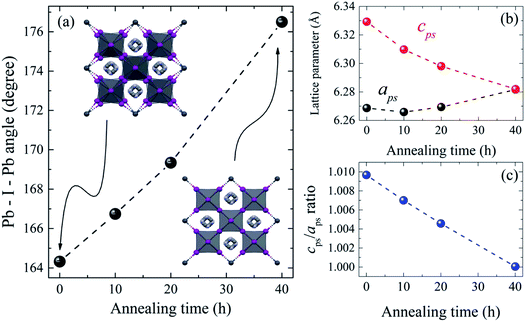
The refined lattice parameters and their evolution with annealing times are illustrated in Fig. 5. The lattice parameters of the tetragonal phase can be treated as a pseudocubic phase with 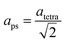 and
and  representations (Fig. 5(b)). To evidence the structural evolution of the compacted MAPbI3 sample to an almost cubic phase, the values of the parameters aps and cps became closer. Also, the decreasing of cps/aps (Fig. 5(c)) indicates that the crystalline structure changes to the high symmetry with the increasing of time annealing. The long annealing time promotes the octahedral tilting for a high symmetry perovskite structure since the temperature is kept constant for all samples (see Fig. 5(a)), allowing the increase of the Pb–I–Pb angle from 164.3° to 176.5°, leading the structure to the cubic phase. This change in the Pb–I–Pb angle is consistent with previous reports found in the literature.48,49 Thus, as the annealing time increases, the NH–I interaction becomes weaker, resulting in an increasingly free motion of the MA+ cation, which is rotationally disordered in the ab plane, as reported in the literature.51 Also, this free motion of the MA+ cation can be directly related to the atomic displacement parameter (B), which increases significantly as the annealing time increases, as shown in Table 1. The high B values indicate a high disorder of the MA+ cations. Consequently, the annealing time can tune the MAPbI3 structure between the tetragonal and the cubic phase, an important parameter to improve the photovoltaic performance of this material. The tetragonal to the cubic phase transition of MAPbI3 crystals occurs due to the relative rotations of neighboring layers of PbI6 octahedra along the c-axis. The low symmetry and order–disorder of the organic cation tilt the PbI6 octahedron, stimulating the structural phase transition. On the other hand, it is interesting that the tetragonal and cubic phases were observed to coexist at room temperature as a spontaneous phenomenon.52 The superlattices composed of a mixture of tetragonal and cubic phases are self-organized without a compositional change.
representations (Fig. 5(b)). To evidence the structural evolution of the compacted MAPbI3 sample to an almost cubic phase, the values of the parameters aps and cps became closer. Also, the decreasing of cps/aps (Fig. 5(c)) indicates that the crystalline structure changes to the high symmetry with the increasing of time annealing. The long annealing time promotes the octahedral tilting for a high symmetry perovskite structure since the temperature is kept constant for all samples (see Fig. 5(a)), allowing the increase of the Pb–I–Pb angle from 164.3° to 176.5°, leading the structure to the cubic phase. This change in the Pb–I–Pb angle is consistent with previous reports found in the literature.48,49 Thus, as the annealing time increases, the NH–I interaction becomes weaker, resulting in an increasingly free motion of the MA+ cation, which is rotationally disordered in the ab plane, as reported in the literature.51 Also, this free motion of the MA+ cation can be directly related to the atomic displacement parameter (B), which increases significantly as the annealing time increases, as shown in Table 1. The high B values indicate a high disorder of the MA+ cations. Consequently, the annealing time can tune the MAPbI3 structure between the tetragonal and the cubic phase, an important parameter to improve the photovoltaic performance of this material. The tetragonal to the cubic phase transition of MAPbI3 crystals occurs due to the relative rotations of neighboring layers of PbI6 octahedra along the c-axis. The low symmetry and order–disorder of the organic cation tilt the PbI6 octahedron, stimulating the structural phase transition. On the other hand, it is interesting that the tetragonal and cubic phases were observed to coexist at room temperature as a spontaneous phenomenon.52 The superlattices composed of a mixture of tetragonal and cubic phases are self-organized without a compositional change.
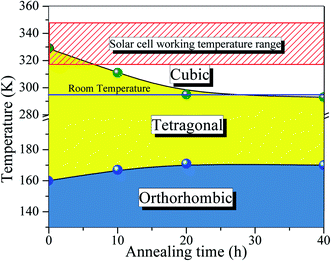
Turning back to the stabilization of the high symmetry cubic phase at room temperature, we propose a new phase diagram of MAPbI3 combining different structural phases and thermal annealing. It is important to emphasize that the crystal structure strongly influences the density of states, leading to different electrical conductivity mechanisms. The electrical resistivity in the tetragonal phase has a strong influence on the charge carrier scattering due to the misalignment of the crystal lattice between neighboring grains. The mismatch at the grain boundaries is reduced significantly in the cubic phase, which is assigned to the isotropic nature of the crystalline structure.53 Consequently, the electrical resistivity decreases drastically in the cubic phase which improves the transport of charge carriers. To confirm this, we have measured the electric resistivity of all synthesized samples. The values are ρ = 0.4, 0.1, 0.07, and 0.04 MΩ cm for S0, S10, S20, and S40, respectively. Also, the long thermal treatment also leads to large perovskite grains and, thus, low recombination rates.54Fig. 6 shows a new phase diagram, based on the experimental results of this work, indicating the evolution of the structural phase transitions as a function of annealing time. We also illustrate the room temperature position and the working temperature range for solar cells. It is straightforward that the temperature range for the stability of the tetragonal phase decreases as the annealing time increases. These surprising results suggest the use of the annealing process as a tool to control the MAPbI3 perovskite phase diagram. The shift of the tetragonal-to-cubic phase transition to room temperature due to thermal annealing is desirable to practical applications of solar cells. The suppression of the structural phase transition down to below room temperature is very important for power conversion efficiency and thermal stability – large carrier trap densities were observed through the transition at high operating temperatures which are detrimental to long-term stability.55 Our prolonged thermal annealing could effectively avoid the formation of phase-transition-induced carrier traps because of the suppression of the phase transition. The passivation of deep defect and suppression of trap densities either using ideal carrier transport layers or optimizing the fabrication route, is also vital to improving the device parameters approaching the theoretical limit. In this case, our thermal annealing can play the same role.56
The effects of thermal annealing on the temperature of the orthorhombic-to-tetragonal structural phase transition, which typically takes place around T = 160 K, shifts to T = 172 K (for the S40 h sample) as the annealing time increases, representing an increase of ΔT = 12 K. This is in the opposite direction and much smaller than the shift from the tetragonal-to-cubic transition, which is ΔT = −40 K. This might be indicative of the different nature of these shifts. It is important to mention that at lower temperatures, the MA cations are ordered strongly coupled to the Pb–I framework through hydrogen bonds leading to the orthorhombic distortion of the tetragonal lattice. In this case, the effect of the thermal annealing is expected to be reduced. There are two possible explanations for the different nature of both shifts: (i) the entropy of the tetragonal phase decreases with annealing time; (ii) the internal energy of tetragonal phase increases with annealing time. The first option is not possible, since the annealing time is supposed to increase the random distribution of MA molecules, and therefore, the entropy. The second option could be the main source of the transition (orthorhombic-to-tetragonal) shift towards higher energy with annealing. The heating during the annealing process increases the random distribution of MA molecules in cubic phase. However, when the temperature is cooled down and the transition from cubic-to-tetragonal phase occurs, the configuration of MA molecules could be different and leads to a different internal energy of tetragonal phase as we shall see. This behavior would increase the relatively stability of tetragonal phase when compared to the orthorhombic, and the tetragonal-to-orthorhombic transition is shifted toward higher energy. The internal energy also changes in the cubic system when the temperature increases, however, the variation in the entropy is larger and suppress this variation. When the system changes from tetragonal-to-cubic, the entropy increase due to two sources, the configurational and the vibrational entropy. On the other hand, the vibrational entropy in tetragonal and orthorhombic are very similar,57,58 which could not give the energy enough to suppress the enhancement in the internal energy.
The orientation of the MA+ cations plays an essential role in the MAPbI3 structure as a function of temperature, involving interaction between the NH3 groups and the framework iodide/lead atoms. At high temperatures, the thermal motion of the cation increases, and the NH–I interactions weaken. At the cubic phase boundary, the MA cations become rotationally disordered in the ab plane, contributing to the decrease in the c/a ratio, and an increase of the Pb–I–Pb angle takes place as shown in Fig. 5. In this case, the organic cations and their order–disorder transitions are coupled with tilts of the PbI6 octahedra. As a consequence, this isotropic rotation acts as a driving force for the deformation of the PbI3 frameworks.
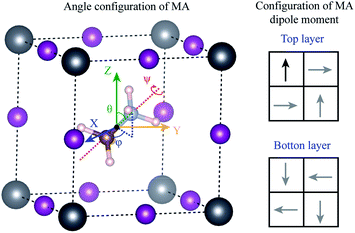
Using density functional theory, we calculated the energy barrier for the rotation of MA+ molecule. Different from the previous results in the literature,31,32,57–59 the movements of the molecules were considered to be completely decorrelated, i.e., the molecules were assumed to move independently of each other. To construct this system, we minimize the stress tensor and the forces in the primitive cubic perovskite cell, obtain a lattice parameter of 6.28 Å, which is in good agreement with our experimental results. Using the lattice parameter of this primitive cell, we construct a 2 × 2 × 2 supercell (containing 8 MA+ molecules), and rearrange the MA+ molecules according to the most stable dipole orientation obtained previously by J. Li et al.60 and shown in the right panel of Fig. 7. The he 2 × 2 × 2 supercell forces were minimized resulting in the configuration where only one molecule was allowed to rotate. In this molecule, the original C–N bond length was kept fixed, and the geometrical center of the MA molecule was used as the invariant rotational point as shown in Fig. 7. All the Pb and I atoms in the 2 × 2 × 2 supercell were allowed to relax, while only the H atoms in the rotated molecule were allowed to relax. The angles θ(φ) varies between 0° and 360° (0° and 180°) with an interval of 45°, while the ψ angle varies between 0° and 120° with an interval of 30°, resulting in a total of 128 different calculations.
The maximum energy barrier that we found is 276 meV to rotate the molecule by θ = 180° from the original position θ = 28°, φ = 91° and ψ = 0°, which correspond to a complete inversion of the dipole moment. This energy is higher than those found in the literature, which vary between 20 to 100 meV.31,32,54–56 This large difference can be attributed to the correlated movement of the MA+ molecules in previous works. The calculations in the literature use only the cubic primitive perovskite cell to calculate the energy barrier, i.e., all the neighboring MA+ molecules rotate together, in a perfectly correlated motion. This does not represent real systems at high temperatures, as obtained by our annealing experiments. When the movements are completely correlated, the PbI6 octahedra deform according to the MA+ dipole moment. The bond length between NH–I is shorter than the CH–I, resulting in ferroelectric distortion in the octahedra, which leads to large energy gain. In our assumption of completely decorrelated motion, the ferroelectric deformation is also observed, but with a small intensity because of the constrain that freezes all the remaining molecules in the system. Therefore, from the experimental perspective, we expect that the actual rotation barrier, considering the results shown in the literature and our results, is between 20–276 meV. The correlated motion of the molecules should have a lower barrier, while the uncorrelated motion should have a higher barrier.
Based on the results for the MA+ rotation energy barrier and the associated entropy, we are able to explain the change in the phase diagram of Fig. 6. The second law of thermodynamics implies that the transition between two different phases can be understood by the variation of the Gibbs free energy ΔG = ΔU − TS, which comprises the changes in the internal energy (ΔU) and entropy (S) of the system.61 The internal energy at T = 0 K for the tetragonal and cubic phase can be obtained from DFT calculations and it is shown in the schematic Fig. 8. As expected, the tetragonal phase is more stable than the cubic by 70 meV per f.u. However, as the temperature increases, the contribution of the TS term to the Gibbs free energy increases. Note that the entropy has two different sources: the vibrational and the configuration entropy.54–56 The vibrational entropy is determined basically by the phonons density of states. However, the similarity between the phonon modes in the tetragonal, and cubic phases in several hybrid perovskites gives only a small variation of Gibbs free energy, and it is not enough to explain the phase transition between these two phases.56–58 In this case, to correct this issue, we have also to consider the configuration entropy in the system.
From the Boltzmann's expression for the entropy, we can determine the configurational entropy by the expression: S = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ω), where kB is the Boltzmann constant, and Ω is the total number of states that are accessible to the system. The number of accessible states is a measure for the “disorder”, i.e., the higher the disorder, the higher the entropy. This interpretation of entropy suggests that a phase transition from a disordered to a more ordered phase can only take place if the loss in entropy is compensated by the decrease in internal energy. According to the calculated rotational energy barrier and the values reported in the literature, the annealing in high temperature results in kBT = 45 meV at 523 K, and can be associated with the generation of different numbers of accessible states (Ω) with respect to the time. The long period of sample exposition to high temperatures in the annealing process can randomly distribute the MA+ molecules and break the more “ordered” configuration of MA+ molecules of tetragonal phase.45 As the temperature decreases, the crystal becomes kinetically trapped entirely in the cubic phase, keeping a high configuration entropy. In this case, the completely disordered orientation of the MA+ cations maximizes the entropy of the system, stabilizing the cubic phase. In other words, we are assuming that the configuration entropy is not a constant as function of the annealing time, as assumed in previous reports in the literature.54–56,62 This model can successfully explain why the transition temperature changes with annealing time and the stabilization of the cubic structure of MAPbI3 at lower temperatures.
ln(Ω), where kB is the Boltzmann constant, and Ω is the total number of states that are accessible to the system. The number of accessible states is a measure for the “disorder”, i.e., the higher the disorder, the higher the entropy. This interpretation of entropy suggests that a phase transition from a disordered to a more ordered phase can only take place if the loss in entropy is compensated by the decrease in internal energy. According to the calculated rotational energy barrier and the values reported in the literature, the annealing in high temperature results in kBT = 45 meV at 523 K, and can be associated with the generation of different numbers of accessible states (Ω) with respect to the time. The long period of sample exposition to high temperatures in the annealing process can randomly distribute the MA+ molecules and break the more “ordered” configuration of MA+ molecules of tetragonal phase.45 As the temperature decreases, the crystal becomes kinetically trapped entirely in the cubic phase, keeping a high configuration entropy. In this case, the completely disordered orientation of the MA+ cations maximizes the entropy of the system, stabilizing the cubic phase. In other words, we are assuming that the configuration entropy is not a constant as function of the annealing time, as assumed in previous reports in the literature.54–56,62 This model can successfully explain why the transition temperature changes with annealing time and the stabilization of the cubic structure of MAPbI3 at lower temperatures.
4. Conclusions
We have investigated the effect of long thermal annealing in vacuum-ampoule on the compacted MAPbI3 perovskite powder. The microstructure morphology of the MAPbI3 annealed samples reveals exciting evolution. All the samples have a well-defined grain boundary morphology. The voids and neck-connecting grains are observed throughout the samples indicating a well-sintered process due to mass diffusion transfer through the grain boundary, probably caused by the evaporation of sub-products due to the extended annealing process. X-ray powder diffraction data reveal that the high-temperature cubic phase is established at room temperature. The refined lattice parameters indicate a symmetry increase as the thermal annealing increases brought about by simultaneously increase in both the c/a ratio and the Pb–I–Pb bond angle from ∼164° close to 180°. The organic cations and their order–disorder transitions are coupled with tilts of the PbI6 octahedra. We propose a new phase diagram of MAPbI3 combining different structural phases and thermal annealing. Most importantly, the low electrical conductivity and high-efficiency cubic phase have been stabilized at room temperature instead of taking place above T = 60 °C. It is important to emphasize that the crystal structure strongly influences the electrical conductivity, leading to a different charge transport mechanism. Through DFT calculation of the MA rotation barrier and entropy analysis, we suggest that the configuration entropy is a function of the annealing time. The high configurational entropy disordered organic molecules of the system are quenched due to thermal annealing at high temperatures; then, the system becomes kinetically trapped completely in the cubic phase down to room temperature. Therefore, the complete disordered orientation of the MA cations maximizes the entropy of the system, stabilizing the cubic phase – an entropy-driven stabilization phenomenon. The vanishing of the structural phase transition (and its coexistence of different phases), which leads to thermal hysteresis close to the working temperature range, can significantly improve the optical and electrical properties of the solar cell devices. Therefore, the absence of the microstructural stress brought about by the phase transformation may give an extra alternative for improving the maintenance, toughness, and efficiency of the optoelectronic devices.Author contributions
Student authors are in alphabetic order. All authors contributed equally to the work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Brazilian agency CNPq under grants no. 307950/2017-4 and 305601/2019-9, and FAPESP under grants no. 2018/14181-0, 2019/01785-8, 2019/21656-8, 2017/02317-2, and 2018/15682-3. The authors are grateful for the Multiuser Experimental Center of UFABC. A. J. was supported by the NSF Faculty Early Career Development Program DMR1652994. Ab initio calculations were performed at the LNCC supercomputer center (Santos Dumont) in Brazil.References
- A. Husainat, W. Ali, P. Cofie, J. Attia and J. Fuller, Simulation and Analysis of Methylammonium Lead Iodide (CH3NH3PbI3) Perovskite Solar Cell with Au Contact Using SCAPS 1D Simulator, Am. J. Optic. Photon., 2019, 7(2), 33, DOI:10.11648/j.ajop.20190702.12.
- N. K. Tailo, M. Abdi-Jalebi, V. Gupta, H. Hu, M. I. Dar, G. Li and S. Satapathi, Recent progress in morphology optimization in perovskite solar cell, J. Mater. Chem. A, 2020, 8, 21356–21386, 10.1039/d0ta00143k.
- T. S. Sherkar, C. Momblona, L. Gil-Escrig, J. Ávila, M. Sessolo, H. J. Bolink and L. J. A. Koster, Recombination in Perovskite Solar Cells: Significance of Grain Boundaries, Interface Traps, and Defect Ions, ACS Energy Lett., 2017, 2(5), 1214–1222, DOI:10.1021/acsenergylett.7b00236.
- F. Ye, H. Lin, H. Wu, L. Zhu, Z. Huang, D. Ouyang, G. Niu and W. C. H. Choy, High-Quality Cuboid CH3NH3PbI3 Single Crystals for High Performance X-Ray and Photon Detectors, Adv. Funct. Mater., 2019, 29(6), 1806984, DOI:10.1002/adfm.201806984.
- L. Chen, J. Cai, J. Li, S.-P. Feng, G. Wei and W.-D. Li, Nanostructured Texturing of CH3NH3PbI3 Perovskite Thin Film on Flexible Substrate for Photodetector Application, Org. Electron., 2019, 71, 284–289, DOI:10.1016/j.orgel.2019.05.036.
- Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Bright Light-Emitting Diodes Based on Organometal Halide Perovskite, Nat. Nanotechnol., 2014, 9(9), 687–692, DOI:10.1038/nnano.2014.149.
- M. U. Chaudhry, N. Wang, K. Tetzner, A. Seitkhan, Y. Miao, Y. Sun, M. C. Petty, T. D. Anthopoulos, J. Wang and D. D. C. Bradley, Light-Emitting Transistors Based on Solution-Processed Heterostructures of Self-Organized Multiple-Quantum-Well Perovskite and Metal-Oxide Semiconductors, Adv. Electron. Mater., 2019, 5(7), 1800985, DOI:10.1002/aelm.201800985.
- Z. Zhao, W. Sun, Y. Li, S. Ye, H. Rao, F. Gu, Z. Liu, Z. Bian and C. Huang, Simplification of device structures for low-cost, high-efficiency perovskite solar cells, J. Mater. Chem. A, 2017, 5, 4756–4773, 10.1039/c6ta10305g.
- X. Wu, H. Li, K. Wang, X. Sun and L. Wang, CH3NH3Pb1−xEuxI3 Mixed Halide Perovskite for Hybrid Solar Cells: The Impact of Divalent Europium Doping on Efficiency and Stability, RSC Adv., 2018, 8(20), 11095–11101, 10.1039/c7ra12754e.
- M. Cao, Y. Zhang, Y. Yu, L. Jin, Y. Li, Z. Chen, Y. Che, H. Dai, G. Zhang and J. Yao, Enhanced Perovskite Phototransistor by Multi-Step Slow Annealing Strategy, Opt. Mater., 2018, 84, 498–503, DOI:10.1016/j.optmat.2018.07.027.
- H. Jiang, H. Xue, L. Wang, F. Tang and F. Si, Effect of Pressure-Induced Structural Phase Transition on Electronic and Optical Properties of Perovskite CH3NH3PbI3, Mater. Sci. Semicond. Process., 2019, 96, 59–65, DOI:10.1016/j.mssp.2019.01.038.
- Z. Zolfaghari, E. Hassanabadi, D. Pitarch-Tena, S. J. Yoon, Z. Shariatinia, J. van de Lagemaat, J. M. Luther and I. Mora-Seró, Operation Mechanism of Perovskite Quantum Dot Solar Cells Probed by Impedance Spectroscopy, ACS Energy Lett., 2019, 4(1), 251–258, DOI:10.1021/acsenergylett.8b02157.
- B. Salhi, Y. S. Wudil, M. K. Hossain, A. Al-Ahmed and F. A. Al-Sulaiman, Review of Recent Developments and Persistent Challenges in Stability of Perovskite Solar Cells, Renewable Sustainable Energy Rev., 2018, 90, 210–222, DOI:10.1016/j.rser.2018.03.058.
- G. Niu, X. Guo and L. Wang, Review of recent progress in chemical stability of perovskite solar cells, J. Mater. Chem. A, 2015, 3, 8970–8980, 10.1039/c4ta04994b.
- X. Qian, X. Gu and R. Yang, Lattice Thermal Conductivity of Organic-Inorganic Hybrid Perovskite CH3NH3PbI3, Appl. Phys. Lett., 2016, 108(6), 063902, DOI:10.1063/1.4941921.
- A. Bonadio, L. S. de Oliveira, A. S. Polo and J. A. Souza, Liquid Water-Induced Growth of the 1D Morphology of CH3NH3PbI3 Hybrid Perovskites, CrystEngComm, 2019, 21(48), 7365–7372, 10.1039/c9ce01275c.
- F. Lehmann, A. Franz, D. M. Többens, S. Levcenco, T. Unold, A. Taubert and S. Schorr, The Phase Diagram of a Mixed Halide (Br, I) Hybrid Perovskite Obtained by Synchrotron X-Ray Diffraction, RSC Adv., 2019, 9(20), 11151–11159, 10.1039/c8ra09398a.
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubale and B.-J. Hwang, Organometal Halide Perovskite Solar Cells: Degradation and Stability, Energy Environ. Sci., 2016, 9(2), 323–356, 10.1039/c5ee02733k.
- T. Yin, Y. Fang, X. Fan, B. Zhang, J.-L. Kuo, T. J. White, G. M. Chow, J. Yan and Z. X. Shen, Hydrogen-Bonding Evolution during the Polymorphic Transformations in CH3NH3PbBr3: Experiment and Theory, Chem. Mater., 2017, 29(14), 5974–5981, DOI:10.1021/acs.chemmater.7b01630.
- B. Kang and K. Biswas, Preferential CH3NH3 + Alignment and Octahedral Tilting Affect Charge Localization in Cubic Phase CH3NH3PbI3, J. Phys. Chem. C, 2017, 121(15), 8319–8326, DOI:10.1021/acs.jpcc.7b01184.
- C. Quarti, E. Mosconi, J. M. Ball, V. D'Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Structural and Optical Properties of Methylammonium Lead Iodide across the Tetragonal to Cubic Phase Transition: Implications for Perovskite Solar Cells, Energy Environ. Sci., 2016, 9(1), 155–163, 10.1039/c5ee02925b.
- C. Caddeo, C. Melis, M. I. Saba, A. Filippetti, L. Colombo and A. Mattoni, Tuning the Thermal Conductivity of Methylammonium Lead Halide by the Molecular Substructure, Phys. Chem. Chem. Phys., 2016, 18(35), 24318–24324, 10.1039/c6cp04246e.
- L.-C. Chen, C.-C. Chen, J.-C. Chen and C.-G. Wu, Annealing Effects on High-Performance CH3NH3PbI3 Perovskite Solar Cells Prepared by Solution-Process, Sol. Energy, 2015, 122, 1047–1051, DOI:10.1016/j.solener.2015.10.019.
- H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2(2), 65–71, DOI:10.1107/s0021889869006558.
- A. A. Coelho, TOPAS and TOPAS-Academic: An Optimization Program Integrating Computer Algebra and Crystallographic Objects Written in C++, J. Appl. Crystallogr., 2018, 51(1), 210–218, DOI:10.1107/s1600576718000183.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100(13), 136406, DOI:10.1103/physrevlett.100.136406.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(17), 13115–13118, DOI:10.1103/physrevb.48.13115.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/physrevb.54.11169.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/physrevb.50.17953.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/physrevb.59.1758.
- S. Kanno, Y. Imamura, A. Saeki and M. Hada, Rotational Energy Barriers and Relaxation Times of the Organic Cation in Cubic Methylammonium Lead/Tin Halide Perovskites from First Principles, J. Phys. Chem. C, 2017, 121, 14051, DOI:10.1021/acs.jpcc.7b04589.
- J. S. Bechtel, R. Seshadri and A. Van der Ven, Energy Landscape of Molecular Motion in Cubic Methylammonium Lead Iodide from First-Principles, J. Phys. Chem. C, 2016, 120, 12403, DOI:10.1021/acs.jpcc.6b03570.
- Y. Yamada, T. Yamada, L. Q. Phuong, N. Maruyama, H. Nishimura, A. Wakamiya, Y. Murata and Y. Kanemitsu, Dynamic Optical Properties of CH3NH3PbI3 Single Crystals As Revealed by One- and Two-Photon Excited Photoluminescence Measurements, J. Am. Chem. Soc., 2015, 137(33), 10456–10459, DOI:10.1021/jacs.5b04503.
- Y. Dang, Y. Liu, Y. Sun, D. Yuan, X. Liu, W. Lu, G. Liu, H. Xia and X. Tao, Bulk Crystal Growth of Hybrid Perovskite Material CH3NH3PbI3, CrystEngComm, 2015, 17(3), 665–670, 10.1039/c4ce02106a.
- Y. Chen, S. Yang, X. Chen, Y. C. Zheng, Y. Hou, Y. H. Li, H. D. Zeng and H. G. Yang, Direct Insight into Crystallization and Stability of Hybrid Perovskite CH3NH3PbI3 via Solvothermal Synthesis, J. Mater. Chem. A, 2015, 3(31), 15854–15857, 10.1039/c5ta03616j.
- I. Deretzis, A. Alberti, G. Pellegrino, E. Smecca, F. Giannazzo, N. Sakai, T. Miyasaka and A. La Magna, Atomistic Origins of CH3NH3PbI3 Degradation to PbI2 in Vacuum, Appl. Phys. Lett., 2015, 106(13), 131904, DOI:10.1063/1.4916821.
- E. J. Juarez-Perez, Z. Hawash, S. R. Raga, L. K. Ono and Y. Qi, Thermal Degradation of CH3NH3PbI3 Perovskite into NH3 and CH3I Gases Observed by Coupled Thermogravimetry–Mass Spectrometry Analysis, Energy Environ. Sci., 2016, 9(11), 3406–3410, 10.1039/c6ee02016j.
- J.-C. Ke, Y.-H. Wang, K.-L. Chen and C.-J. Huang, Effect of Temperature Annealing Treatments and Acceptors in CH3NH3PbI3 Perovskite Solar Cell Fabrication, J. Alloys Compd., 2017, 695, 2453–2457, DOI:10.1016/j.jallcom.2016.11.143.
- F. X. Xie, D. Zhang, H. Su, X. Ren, K. S. Wong, M. Grätzel and W. C. H. Choy, Vacuum-Assisted Thermal Annealing of CH3NH3PbI3 for Highly Stable and Efficient Perovskite Solar Cells, ACS Nano, 2015, 9(1), 639–646, DOI:10.1021/nn505978r.
- R. Betancur, D. Ramirez, J. F. Montoya and F. Jaramillo, A Calorimetric Approach to Reach High Performance Perovskite Solar Cells, Sol. Energy Mater. Sol. Cells, 2016, 146, 44–50, DOI:10.1016/j.solmat.2015.10.024.
- X. Jia, Z. Hu, Y. Zhu, T. Weng, J. Wang, J. Zhang and Y. Zhu, Facile Synthesis of Organic–Inorganic Hybrid Perovskite CH3NH3PbI3 Microcrystals, J. Alloys Compd., 2017, 725, 270–274, DOI:10.1016/j.jallcom.2017.07.154.
- International Tables for Crystallography. Vol. A: Space-Group Symmetry, ed. T. Hahn, Internationale Union für Kristallographie, Springer, Dordrecht, 5 edn, 2005, reprinted with corrections Search PubMed.
- Y. Kawamura, H. Mashiyama and K. Hasebe, Structural Study on Cubic–Tetragonal Transition of CH3NH3PbI3, J. Phys. Soc. Jpn., 2002, 71(7), 1694–1697, DOI:10.1143/jpsj.71.1694.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, Calorimetric and IR Spectroscopic Studies of Phase Transitions in Methylammonium Trihalogenoplumbates (II), J. Phys. Chem. Solids, 1990, 51(12), 1383–1395, DOI:10.1016/0022-3697(90)90021-7.
- I. Deretzis and A. La Magna, Exploring the Orthorhombic–Tetragonal Phase Transition in CH3NH3PbI3: The Role of Atom Kinetics, Nanoscale, 2017, 9(18), 5896–5903, 10.1039/c7nr01818e.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, ISODISPLACE: A Web-Based Tool for Exploring Structural Distortions, J. Appl. Crystallogr., 2006, 39(4), 607–614, DOI:10.1107/s0021889806014075.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite Search PubMed.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Complete Structure and Cation Orientation in the Perovskite Photovoltaic Methylammonium Lead Iodide between 100 and 352 K, Chem. Commun., 2015, 51(20), 4180–4183, 10.1039/c4cc09944c.
- P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide, Sci. Rep., 2016, 6(1), 35685, DOI:10.1038/srep35685.
- J. Xie, Y. Liu, J. Liu, L. Lei, Q. Gao, J. Li and S. Yang, Study on the Correlations between the Structure and Photoelectric Properties of CH3NH3PbI3 Perovskite Light-Harvesting Material, J. Power Sources, 2015, 285, 349–353, DOI:10.1016/j.jpowsour.2015.03.114.
- K. P. Ong, T. W. Goh, Q. Xu and A. Huan, Structural Evolution in Methylammonium Lead Iodide CH3 NH3PbI3, J. Phys. Chem. A, 2015, 119(44), 11033–11038, DOI:10.1021/acs.jpca.5b09884.
- T. W. Kim, S. Uchida, T. Matsushita, L. Cojocaru, R. Jono, K. Kimura, D. Matsubara, M. Shirai, K. Ito, H. Matsumoto, T. Kondo and H. Segawa, Self-Organized Superlattice and Phase Coexistence inside Thin Film Organometal Halide Perovskite, Adv. Mater., 2018, 30, 1705230, DOI:10.1002/adma.201705230.
- G. Sombrio, Z. Zhang, A. Bonadio, L. S. de Oliveira, T. B. de Queiroz, F. F. Ferreira, A. Janotti and J. A. Souza, Charge Transport in MAPbI3 Pellets Across the Tetragonal-to-Cubic Phase Transition: The Role of Grain Boundaries From Structural, Electrical, and Optical Characterizations, J. Phys. Chem. C, 2020, 124(20), 10793–10803, DOI:10.1021/acs.jpcc.0c00887.
- X. Cao, L. Zhi, Y. Jia, Y. Li, X. Cui, K. Zhao, L. Ci, K. Ding and J. Wei, High Annealing Temperature Induced Rapid Grain Coarsening for Efficient Perovskite Solar Cells, J. Colloid Interface Sci., 2018, 524, 483–489, DOI:10.1016/j.jcis.2018.04.019.
- C. Qin, T. Matsushima, D. Klotz, T. Fujihara and C. Adachi, The Relation of Phase-Transition Effects and Thermal Stability of Planar Perovskite Solar Cells, Adv. Sci., 2018, 1801079, DOI:10.1002/advs.201801079.
- D. B. Khadka, Y. Shirai, M. Yanagida and K. Miyano, Unraveling the Impacts Induced by Organic and Inorganic Hole Transport Layers in Inverted Halide Perovskite Solar Cells, ACS Appl. Mater. Interfaces, 2019, 11, 7055–7065, DOI:10.1021/acsami.8b20924.
- K. T. Butler, K. Svane, G. Kieslich, A. K. Cheetham and A. Walsh, Microscopic origin of entropy-driven polymorphism in hybrid organic-inorganic perovskite materials, Phys. Rev. B, 2016, 94, 180103, DOI:10.1103/physrevb.94.180103.
- G. Kieslich, J. M. Skelton, J. Armstrong, Y. Wu, F. Wei, K. L. Svane, A. Walsh and K. T. Butler, Hydrogen Bonding versus Entropy: Revealing the Underlying Thermodynamics of the Hybrid Organic–Inorganic Perovskite CH3NH3PbBr3, Chem. Mater., 2018, 30, 8782, DOI:10.1021/acs.chemmater.8b03164.
- W. Wei, W. Li, K. T. Butler, G. Feng, C. J. Howard, M. A. Carpenter, P. Lu, A. Walsh and A. K. Cheetham, An Unusual Phase Transition Driven by Vibrational Entropy Changes in a Hybrid Organic–Inorganic Perovskite, Angew. Chem., Int. Ed., 2018, 57, 8932, DOI:10.1002/anie.201803176.
- J. Li, J. Järvi and P. Rinke, Multiscale model for disordered hybrid perovskites: The concepts of organic cation pair modes, Phys. Rev. B, 2018, 98, 045201, DOI:10.1103/physrevb.98.045201.
- K. Huang, Statistical Mechanics, in Statistical Mechanics, John Wiley & Sons, Inc, New York, 1987, pp. 22–25 Search PubMed.
- X.-G. Zhao, G. M. Dalpian, Z. Wang and A. Zunger, Polymorphous nature of cubic halide perovskites, Phys. Rev. B, 2020, 101, 155137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10492b |
| This journal is © The Royal Society of Chemistry 2021 |