Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Antimony-ligated dysprosium single-molecule magnets as catalysts for stibine dehydrocoupling†
Thomas
Pugh
 ,
Nicholas F.
Chilton
,
Nicholas F.
Chilton
 * and
Richard A.
Layfield
*
* and
Richard A.
Layfield
*
School of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: Richard.Layfield@manchester.ac.uk; Nicholas.Chilton@manchester.ac.uk
First published on 21st November 2016
Abstract
Single-molecule magnets (SMMs) are coordination compounds that exhibit magnetic bistability below a characteristic blocking temperature. Research in this field continues to evolve from its fundamental foundations towards applications of SMMs in information storage and spintronic devices. Synthetic chemistry plays a crucial role in targeting the properties that could ultimately produce SMMs with technological potential. The ligands in SMMs are invariably based on non-metals; we now report a series of dysprosium SMMs (in addition to their magnetically dilute analogues embedded in yttrium matrices) that contain ligands with the metalloid element antimony as the donor atom, i.e. [(η5-Cp′2Dy){μ-Sb(H)Mes}]3 (1-Dy) and [(η5-Cp′2Dy)3{μ-(SbMes)3Sb}] (2-Dy), which contain the stibinide ligand [Mes(H)Sb]− and the unusual Zintl-like ligand [Sb4Mes3]3−, respectively (Cp′ = methylcyclopentadienyl; Mes = mesityl). The zero-field anisotropy barriers in 1-Dy and 2-Dy are Ueff = 345 cm−1 and 270 cm−1, respectively. Stabilization of the antimony-ligated SMMs is contingent upon careful control of reaction time and temperature. With longer reaction times and higher temperatures, the stibine pro-ligands are catalytically dehydrocoupled by the rare-earth precursor complexes. NMR spectroscopic studies of the yttrium-catalysed dehydrocoupling reactions reveal that 1-Y and 2-Y are formed during the catalytic cycle. By implication, 1-Dy and 2-Dy should also be catalytic intermediates, hence the nature of these complexes as SMMs in the solid-state and as catalysts in solution introduces a strategy whereby new molecular magnets can be identified by intercepting species formed during catalytic reactions.
Introduction
The synthesis of complex magnetic materials from simple chemical building blocks encapsulates the intrinsic fascination of molecular magnetism. Molecular magnets are typically designed using bottom-up approaches that provide access to experimental testbeds for theoretical models of magnetism, and that enable modular approaches to applications based on the properties of well-defined magnetic units. For example, carefully constructed transition metal complexes display characteristics that could lead to their implementation as molecular qubits for quantum computing.1 The magnetocaloric effect, in which the entropy of a magnetic system is modulated by a magnetic field, introduces the possibility of using molecular magnets as refrigerants that function more efficiently than conventional cryogens.2 Spin-crossover materials, which have been intensively studied for many years,3 have been proposed for applications in displays, sensors and information storage devices.4 Lanthanide complexes continue to play important roles in enhancing our understanding of ligand field theory,5 and many such species find applications in NMR spectroscopy as shift reagents6 and in magnetic resonance imaging.7Single-molecule magnets (SMMs) are coordination compounds that can be defined by an effective energy barrier (Ueff) to reversal of their magnetization.8 The pioneering work on SMMs focused on exchange-coupled transition metal cage compounds,9,10 and monometallic 3d complexes have recently emerged as another important class of SMM.11–13 Many of the most exciting developments in single-molecule magnetism have been accounted for by the lanthanides terbium, dysprosium and erbium,14–19 and lanthanide SMMs have been described with very high Ueff values and magnetic blocking temperatures.20–22 Studies of the interactions between electrical currents and SMMs on surfaces has also led to the development of prototype molecular spintronic devices.23,24
Despite the remarkable progress with SMMs, challenges remain, including overcoming the need for liquid-helium temperatures to observe slow relaxation of the magnetization, and the need to organise and stabilise molecules on surfaces for devices to become viable. To address these challenges, novel synthetic coordination chemistry strategies are of prime importance. Ligand environments in SMMs, especially those containing lanthanides, are dominated by hard, oxygen- and nitrogen-donor atoms.8–22 Targeting lanthanide SMMs with ligands in which the donor atoms have metallic character would introduce new ways of influencing the metal–ligand bonding and hence the electronic structure of the metal ion, potentially providing a way of enhancing the magnetic relaxation properties. Furthermore, using metalloid donor ligands as building blocks in SMMs could unearth new reactivity, which could itself be manipulated further for the synthesis of new molecular magnets.
Results and discussion
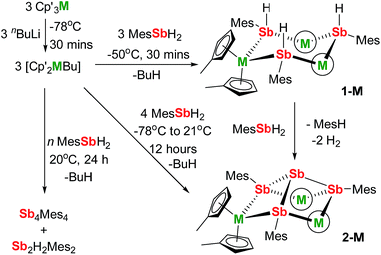
We now describe two dysprosium-containing SMMs based on the metallocene building block {Cp2Dy(E)2}, where E denotes a ligand with the 5p metalloid element antimony as the donor atom. We focus on the trimetallic complexes [(η5-Cp′2Dy){μ-Sb(H)Mes}]3 (1-Dy) and [(η5-Cp′2Dy)3{μ-(SbMes)3Sb}] (2-Dy), which contain the stibinide ligand [Mes(H)Sb]− and the Zintl-like ligand [Sb4Mes3]3−, respectively (Cp′ = methylcyclopentadienyl; Mes = mesityl). Compound 1-Dy and the yttrium analogue 1-Y were synthesized by adding three equivalents of MesSbH2 to a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of Cp′3M and nBuLi over 30 minutes at −50 °C (Scheme 1). Compounds 2-M were synthesized in a similar fashion with four equivalents of MesSbH2, with the reaction being warmed from −78 °C to room temperature overnight. Without careful control of reaction time and temperature, stibine dehydrocoupling occurs to give the 1,2-distibane Sb2H2Mes2 (Fig. S1†), the tetrastibetane Sb4Mes4,25,26 and H2. This unanticipated reactivity introduced the possibility of converting 1-M into 2-Mvia cross-dehydrocoupling of the former with MesSbH2: in the case of 2-Y, the reaction is quantitative by 1H NMR spectroscopy (Fig. S5†), and for 2-Dy the isolated yield was 45%. The dehydrocoupling reactivity is considered further after discussion of the structural and magnetic properties of 1-Dy and 2-Dy.
3 mixture of Cp′3M and nBuLi over 30 minutes at −50 °C (Scheme 1). Compounds 2-M were synthesized in a similar fashion with four equivalents of MesSbH2, with the reaction being warmed from −78 °C to room temperature overnight. Without careful control of reaction time and temperature, stibine dehydrocoupling occurs to give the 1,2-distibane Sb2H2Mes2 (Fig. S1†), the tetrastibetane Sb4Mes4,25,26 and H2. This unanticipated reactivity introduced the possibility of converting 1-M into 2-Mvia cross-dehydrocoupling of the former with MesSbH2: in the case of 2-Y, the reaction is quantitative by 1H NMR spectroscopy (Fig. S5†), and for 2-Dy the isolated yield was 45%. The dehydrocoupling reactivity is considered further after discussion of the structural and magnetic properties of 1-Dy and 2-Dy.
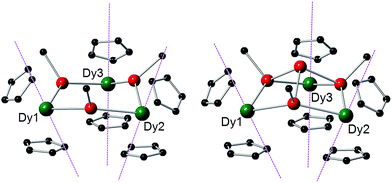
The structures of 1-M and 2-M were determined by X-ray diffraction (Fig. 1, Tables S1 and S2†). Each compound contains a chair-like M3Sb3 ring in which the metal atoms bond to two μ-[Mes(H)Sb]− ligands in 1-M or to two antimony atoms of the [Sb4Mes3]3− ligand in 2-M. The metal atoms also bond to two η5-Cp′ ligands, such that they adopt pseudo-tetrahedral geometries. The central antimony atom in 2-M connects the three μ-{MesSb} groups, with Sb–Sb distances of 2.8583(11)–2.8687(11) Å in 2-Dy. The Dy3Sb3 rings in both dysprosium compounds are similar in size, with the Dy–Sb bond lengths in 1-Dy being 3.092(6)–3.212(3) Å, and those in 2-Dy 3.119(1)–3.138(1) Å. The Dy⋯Dy separations are 5.7174(7)–5.8535(5) Å and 5.7175(8)–5.8293(8) Å in 1-Dy and 2-Dy, respectively. The Sb–Dy–Sb angles are 87.53(8)–103.85(12)° in 1-Dy and 85.32(3)–89.15(3)° in 2-Dy; the Dy–Sb–Dy angles are 128.26(3)–136.73(14)° and 132.03(3)–136.96(3)°, respectively. The Dy–C distances in 1-Dy and 2-Dy are 2.59(1)–2.651(9) Å and 2.58(1)–2.66(1) Å, and the Cpcent–Dy–Cpcent angles are 129.30(17)–130.92(19)° and 129.9(2)–130.3(2)°. The geometric parameters for 1-Y and 2-Y are similar to those of their dysprosium analogues (Fig. S2 and Table S2†). The C1 symmetry of 1-Y and 2-Y in the solid state is reflected in their 1H NMR spectra, which show multiple resonances for the inequivalent CH and CH3 groups in both molecules (Fig. S3 and S4†). Characteristic Sb–H stretches were observed in the IR spectra of 1-M at 1860–1875 cm−1 (Fig. S6†).
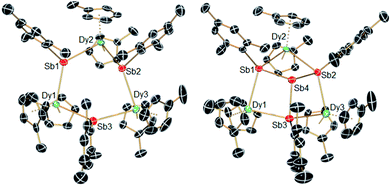 | ||
| Fig. 1 Molecular structures of 1-Dy (left) and 2-Dy (right). Thermal ellipsoids at the 50% probability level. Hydrogen atoms not shown. | ||
Molecular rare-earth complexes of antimony ligands are extremely rare. The sole prior example of a Zintl-ligated rare-earth complex is 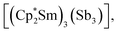 which contains the chain-like [Sb3]3− ligand.27 The [Sb4R3]3− ligand motif is itself extremely rare, with the only previous example being found in [(Cp2Ti)3{(SbR)3Sb}], which forms in the reaction of [Cp2Ti{C2(SiMe3)2}] with Sb2R4 (R = 2-(Me2NCH2)C6H4).28
which contains the chain-like [Sb3]3− ligand.27 The [Sb4R3]3− ligand motif is itself extremely rare, with the only previous example being found in [(Cp2Ti)3{(SbR)3Sb}], which forms in the reaction of [Cp2Ti{C2(SiMe3)2}] with Sb2R4 (R = 2-(Me2NCH2)C6H4).28
Magnetic properties
The magnetic susceptibilities of 1-Dy and 2-Dy were measured in a d.c. field of 1 kOe. The plots of χMT(T) in the range 2–300 K for both compounds are similar (Fig. S7†) and consistent with the presence of three Dy3+ ions with 6H15/2 ground terms and gJ = 4/3 (theoretical χMT = 42.5 cm3 K mol−1 at 300 K). For 1-Dy, χMT is 40.57 cm3 K mol−1 at 300 K before gradually decreasing upon cooling to 50 K; at lower temperatures the decrease in χMT is more rapid, reaching 10.01 cm3 K mol−1 at 2 K. The values of χMT for 2-Dy at 300 K and 2 K are 42.69 cm3 K mol−1 and 10.10 cm3 K mol−1, respectively. The field (H) dependence of the magnetization (M) at 1.8 K is also similar for 1-Dy and 2-Dy, with both showing a steep increase in M as the field increases to 20 kOe, and then a slower increase, before reaching 15.17 μB and 15.82 μB, respectively, at 70 kOe (Fig. S8†).Comparing the experimental and calculated magnetic properties for 1-Dy and 2-Dy in the absence of intramolecular exchange interactions, it is clear that the experimental decrease in χMT at low temperatures cannot be due to ligand field effects alone. Similarly, the increase in magnetization at low fields is slower than calculated. These observations imply non-negligible antiferromagnetic exchange interactions between the dysprosium centres, which were simulated by implementing the Lines model29,30 and the Hamiltonian shown in eqn (1) using PHI.31
 | (1) |
The SMM properties of 1-Dy and 2-Dy were investigated using a.c. magnetic susceptibility measurements, employing a weak a.c. field of 1.55 Oe and zero d.c. field. In order to explore the impact of exchange interactions on the SMM properties, we also studied the magnetically dilute analogues [(Cp′2Dy)(Cp′2Y)2{Sb(H)Mes}]3 (Dy@1-Y) and [(Cp′2Dy)(Cp′2Y)2{(SbMes)3Sb] (Dy@2-Y). Dilution levels of 5% were achieved by combining Cp′3Y and Cp′3Dy in 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and performing the syntheses according to Scheme 1, which produced Dy@1-Y and Dy@2-Y in matrices of 1-Y and 2-Y, respectively. The frequency (ν) dependence of the in-phase (χ′) (Fig. S9 and S10†) and the out-of-phase (χ′′) (Fig. 2) magnetic susceptibilities reveal prominent SMM behaviour for 1-Dy and 2-Dy. The χ′′(ν) plots for both systems show well-defined maxima in the temperature range 5–36 K and 4–33 K, respectively, using a.c. frequencies up to 1400 Hz. The plots of χ′′ vs. χ′ for the undiluted SMMs are semi-circular in nature, and were fitted using a modified Debye model with α parameters of 0.20–0.52 and 0.19–0.40 for 1-Dy and 2-Dy, respectively, indicating broad distributions of relaxation times (Fig. S11†). The diluted systems Dy@1-Y and Dy@2-Y also show pronounced SMM behaviour, with maxima in χ′′(ν) being observed up to slightly higher temperatures relative to the undiluted SMMs (Fig. 2, S12 and S13†). The α parameters for the dilute SMMs are 0.25–0.44 and 0.03–0.43 for Dy@1-Y and Dy@2-Y, respectively (Fig. S14†).
1 ratio and performing the syntheses according to Scheme 1, which produced Dy@1-Y and Dy@2-Y in matrices of 1-Y and 2-Y, respectively. The frequency (ν) dependence of the in-phase (χ′) (Fig. S9 and S10†) and the out-of-phase (χ′′) (Fig. 2) magnetic susceptibilities reveal prominent SMM behaviour for 1-Dy and 2-Dy. The χ′′(ν) plots for both systems show well-defined maxima in the temperature range 5–36 K and 4–33 K, respectively, using a.c. frequencies up to 1400 Hz. The plots of χ′′ vs. χ′ for the undiluted SMMs are semi-circular in nature, and were fitted using a modified Debye model with α parameters of 0.20–0.52 and 0.19–0.40 for 1-Dy and 2-Dy, respectively, indicating broad distributions of relaxation times (Fig. S11†). The diluted systems Dy@1-Y and Dy@2-Y also show pronounced SMM behaviour, with maxima in χ′′(ν) being observed up to slightly higher temperatures relative to the undiluted SMMs (Fig. 2, S12 and S13†). The α parameters for the dilute SMMs are 0.25–0.44 and 0.03–0.43 for Dy@1-Y and Dy@2-Y, respectively (Fig. S14†).
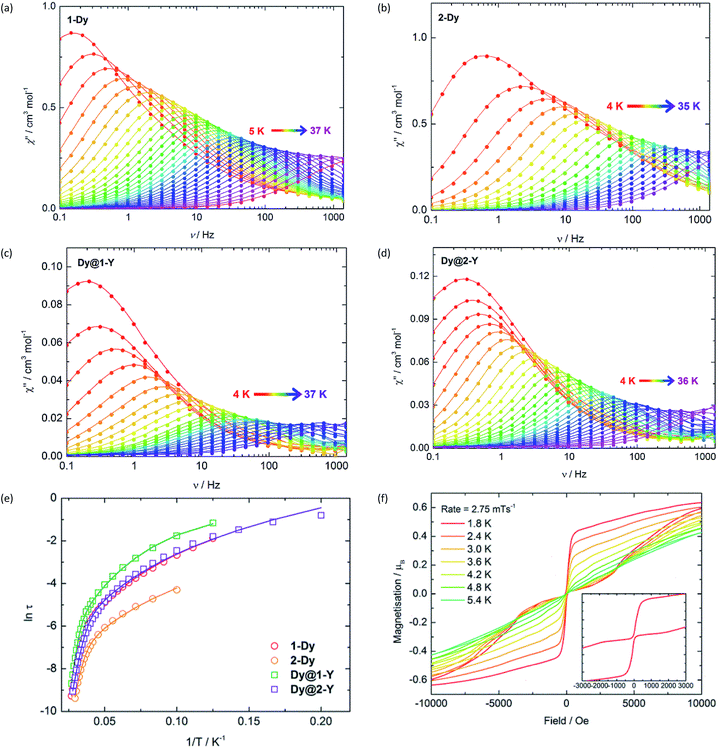 | ||
| Fig. 2 Frequency dependence of the out-of-phase (χ′′) magnetic susceptibility for: (a) 1-Dy; (b) 2-Dy; (c) Dy@1-Y; (d) Dy@2-Y. (e) Temperature dependence of the magnetization relaxation times (τ) plotted as ln(τ/s) vs. T−1, with the solid lines representing theoretical fits using the parameters in Table 1. (f) Magnetization (M) vs. field (H) hysteresis loops for Dy@1-Y with a scan rate of 2.8 mT s−1. | ||
Insight into the relaxation dynamics of the SMMs was obtained by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus T−1 (Fig. 2), where τ is the relaxation time. The four SMMs display similar properties, where the high-temperature regimes show a linear dependence of ln
τ versus T−1 (Fig. 2), where τ is the relaxation time. The four SMMs display similar properties, where the high-temperature regimes show a linear dependence of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ on T−1, indicating relaxation via Orbach and/or thermally assisted quantum tunnelling of the magnetization (TA-QTM) mechanisms. At lower temperatures, the relaxation shows a weaker temperature dependence, suggesting relaxation via a Raman process; as the experiment was conducted in zero field, relaxation via the direct process is expected to be negligible. Notably, the relaxation dynamics do not enter a temperature-independent regime (usually assigned to ground-state QTM) at the lowest temperatures attainable by our SQUID magnetometer. The data was modelled for each SMM using the equation τ−1 = τ0−1e−Ueff/kBT + CTn, where τ0 and Ueff are the Orbach parameters, and C and n are the Raman parameters (Table 1). The Ueff value of 345 cm−1 for 1-Dy is one of the largest yet determined for a polymetallic SMM in zero applied field. The highest anisotropy barriers in SMMs based on lanthanide ions with oblate electron density in the most magnetic mJ states – such as Dy3+ – typically occur when strong crystal fields are applied on high-order symmetry axes.8 Thus, the current record anisotropy barrier is 1261 cm−1, which was determined for a D5h-symmetric dysprosium complex with a pentagonal bipyramidal arrangement of donor atoms.21 In light of this, a remarkable observation on 1-Dy is that a very large barrier can still be obtained when the Dy3+ occupies a much lower symmetry environment of approximately C2v (assuming ring whizzing of the Cp′ ligands). The Raman exponents n are similar to those in other metallocene-based SMMs.32
τ on T−1, indicating relaxation via Orbach and/or thermally assisted quantum tunnelling of the magnetization (TA-QTM) mechanisms. At lower temperatures, the relaxation shows a weaker temperature dependence, suggesting relaxation via a Raman process; as the experiment was conducted in zero field, relaxation via the direct process is expected to be negligible. Notably, the relaxation dynamics do not enter a temperature-independent regime (usually assigned to ground-state QTM) at the lowest temperatures attainable by our SQUID magnetometer. The data was modelled for each SMM using the equation τ−1 = τ0−1e−Ueff/kBT + CTn, where τ0 and Ueff are the Orbach parameters, and C and n are the Raman parameters (Table 1). The Ueff value of 345 cm−1 for 1-Dy is one of the largest yet determined for a polymetallic SMM in zero applied field. The highest anisotropy barriers in SMMs based on lanthanide ions with oblate electron density in the most magnetic mJ states – such as Dy3+ – typically occur when strong crystal fields are applied on high-order symmetry axes.8 Thus, the current record anisotropy barrier is 1261 cm−1, which was determined for a D5h-symmetric dysprosium complex with a pentagonal bipyramidal arrangement of donor atoms.21 In light of this, a remarkable observation on 1-Dy is that a very large barrier can still be obtained when the Dy3+ occupies a much lower symmetry environment of approximately C2v (assuming ring whizzing of the Cp′ ligands). The Raman exponents n are similar to those in other metallocene-based SMMs.32
| 1-Dy | Dy@1-Y | 2-Dy | Dy@2-Y | |
|---|---|---|---|---|
| U eff/cm−1 | 345 | 345 | 272 | 270 |
| τ 0/s | 1.57 × 10−10 | 2.96 × 10−10 | 1.10 × 10−9 | 2.87 × 10−9 |
| C/s−1 K−n | 6.15 × 10−3 | 2.57 × 10−3 | 0.128 | 6.36 × 10−3 |
| n | 3.35 | 3.39 | 2.72 | 3.30 |
Variable-field magnetization measurements on the SMMs revealed marked differences between the non-dilute and dilute systems. For 1-Dy, a sweep rate of 2 mT s−1 produced a narrow S-shaped hysteresis loop at 1.8 K (Fig. S15†), whereas butterfly-shaped loops were observed for Dy@1-Y at 1.8–5.4 K (Fig. 2). The hysteresis properties of 2-Dy and Dy@2-Y (Fig. 2 and S15†) mirror those of the stibine-ligated compounds, albeit with the M(H) loops for the diluted system remaining open up to 4.0 K. The likeliest explanation for the closed hysteresis loops in the non-dilute SMMs is that exchange interactions between the Dy3+ ions provide tunnelling pathways that close upon replacement with diamagnetic Y3+. The precipitous drop in magnetization for the diluted SMMs around zero field is characteristic of the vast majority of SMMs and can be attributed to single-ion effects such as hyperfine coupling to spin-active isotopes of dysprosium.33
Theoretical characterization
Deeper insight into the magnetic properties of 1-Dy and 2-Dy was obtained by performing complete active space self-consistent field (CASSCF) calculations.34 For both complexes, the electronic structure of the individual Dy3+ ions is dominated by the [Cp′]− ligands, which creates a strong axial potential and leads to the ground Kramers doublet at each Dy3+ ion being well described as mJ = ±15/2. The main magnetic anisotropy axis of each Dy3+ ion is therefore oriented along the local [Cp′]⋯[Cp′] direction, where all three form a teepee-like arrangement (Fig. 3). The dominant axial potential generated by the [Cp′]− ligands also results in the first- and second-excited states being highly axial in nature and collinear with the ground-state axis for all sites in 1-Dy and 2-Dy (Tables 2 and S3–S8†).| Doublet | Energy/cm−1 | g x | g y | g z | Angle/° |
|---|---|---|---|---|---|
| 1-Dy | |||||
| 1 | 0 | 0.00 | 0.00 | 19.57(5) | |
| 2 | 167(3) | 0.00 | 0.00 | 17.04(7) | 2.6(7) |
| 3 | 329(5) | 0.04(3) | 0.05(3) | 14.74(3) | 3.5(9) |
| 4 | 416(3) | 2(1) | 4(3) | 11(1) | 24(33) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| 2-Dy | |||||
| 1 | 0 | 0.00 | 0.00 | 19.66(1) | |
| 2 | 166(1) | 0.00 | 0.00 | 17.12(3) | 3.0(5) |
| 3 | 324(9) | 0.03(2) | 0.04(3) | 14.69(5) | 1.6(5) |
| 4 | 417(13) | 0.6(3) | 0.7(3) | 11.6(2) | 3.9(7) |
The C2v symmetry of the dysprosium environments renders a rhombic third excited state in both complexes; this is likely to be the origin of the most efficient thermal relaxation pathway in 1-Dy since the rhombic state is calculated to lie at 416(3) cm−1, which is comparable to the experimental Ueff value of 345 cm−1. For 2-Dy, the rhombic third excited state lies at 413(17) cm−1, which is much larger than the experimental barrier of 270 cm−1. Although relaxation via higher-lying Kramers' doublets is known,35–37 it remains a relatively uncommon phenomenon, with thermally activated relaxation thought to proceed via the first-excited doublet in most SMMs.38 In both cases, magnetic dilution does not significantly alter the a.c. susceptibility properties, hence the discrepancy between theory and experiment for 2-Dy cannot arise from intramolecular interactions. Despite the differing ligand environments in 1-Dy and 2-Dy, the properties of the low-lying Kramers doublets in both complexes are remarkably similar, as are the orientations of the ground-state anisotropy axes. The LoProp charges on the antimony atoms bonded to the Dy3+ centres range from −0.17 to −0.23 for 1-Dy and from −0.28 to −0.29 for 2-Dy, respectively.39 Although the accumulation of charge on the donor atoms is not large in either case, the negligible difference in the average Dy–Sb bond lengths of 0.036 Å between the two systems combined with the slightly greater charge density on the antimony atoms in the equatorial plane in 2-Dy relative to 1-Dy can account for the lower Ueff value in the former, which is consistent with observations on related SMMs containing [MesE(H)]− and [MesE]2− ligands (E = P, As).40,41 The Ueff value determined for 1-Dy of 345 cm−1 is markedly larger than those determined for the isostructural phosphide- and arsenide-bridged analogues [(η5-Cp′2Dy){μ-E(H)Mes}]3 (E = P, As), of 210 cm−1 and 256 cm−1, respectively. The only significant differences in the molecular structures of 1-Dy and the two lighter congeners are the dysprosium–pnictogen bond lengths, which increase significantly with the radius of pnictogen (those in 1-Dy are, on average, 0.168 Å longer than those in the As-bridged analogue). Since the main magnetic axes in the phosphide-, arsenide- and stibinide-bridged SMMs all adopt similar orientations along the [Cp′]⋯[Cp′] directions, the pnictogens occupy equatorial sites; as the Dy–E bond lengths increase, the influence of the pnictogen on the splitting of the Dy3+ crystal field levels diminishes, leading to a more dominant axial crystal field and hence larger Ueff values.
Being intrigued by the unusual [Sb4Mes4]3− ligand, we endeavoured to determine the electronic structure of this species. The Dy3+ ions in 2-Dy were replaced with Lu3+ to ensure a well-defined active space for the antimony-containing ligand, and the restricted active space (RAS) probing approach was employed with 2-Lu to identify an appropriate orbital manifold near the Fermi level to describe the Sb4 unit. The resulting CAS, which consisted of 12 electrons in 9 orbitals for the lowest lying ten S = 0 and ten S = 1 states delocalized over the Sb4 unit, is dominated by the antimony 5p orbitals (Fig. S16†). The ground state of [Sb4Mes4]3− is a well-isolated S = 0, as expected, however after the first excitation to the S = 1 state at ca. 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, there is a continuum of states up to at least 45
000 cm−1, there is a continuum of states up to at least 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Table S9 and Fig. S17†). This delocalized set of continuum states is reminiscent of a semi-conductor, and it is possible that this feature also contributes to diminishing Ueff in 2-Dy. Unfortunately, however, all efforts to calculate the properties of the individual Dy3+ ions while allowing excitation into the Sb4 continuum failed owing to the extremely large active space required for the calculation.
000 cm−1 (Table S9 and Fig. S17†). This delocalized set of continuum states is reminiscent of a semi-conductor, and it is possible that this feature also contributes to diminishing Ueff in 2-Dy. Unfortunately, however, all efforts to calculate the properties of the individual Dy3+ ions while allowing excitation into the Sb4 continuum failed owing to the extremely large active space required for the calculation.
Stibine dehydrocoupling reactivity
In optimizing the synthesis of 1-M and 2-M, it was apparent from 1H NMR spectroscopic studies of the yttrium derivatives that 1-Y, 2-Y, Sb2H2Mes2, Sb4Mes4 and H2 all form during the same reaction. Furthermore, the relative amounts of each component depend on reaction time and temperature, with longer times and higher temperatures producing greater amounts of Sb4Mes4. These observations implied that yttrium mediates – or even catalyses – the dehydrocoupling of MesSbH2. To investigate this possibility, 1H NMR spectroscopy was used to study the reactions of MesSbH2 with 10 mol% of Cp′3Y at 40, 50, 60 and 70 °C (Fig. S18–S21†). The initial 1H NMR spectrum of the 40 °C reaction shows the resonances of the two starting materials (Fig. S18†), whereas after 20 hours MesSbH2, Sb2H2Mes2 (both diastereomers) and Sb4Mes4, account for 40%, 43% and 17% of the antimony-containing species (Fig. 4). The 1H NMR spectrum also shows H2 at 4.47 ppm. The amount of Sb2H2Mes2 then gradually decreases, accounting for 20% after 170 h, whereas the amount of Sb4Mes4 increases to reach 71%, with 7% MesSbH2 remaining. Also noteworthy in the 1H NMR spectrum is the rapid emergence of a series of broad resonances in the region δ ≈ 6.1–6.6 ppm, which correspond to the methine CH resonances of 1-Y. After 170 h, all the signals due to 1-Y have been replaced by those of 2-Y. At 50 °C, the conversion of MesSbH2 to Mes4Sb4 increases to 80% at a faster rate, but at higher temperatures the conversion level decreases and, at 70 °C, an appreciable amount of mesitylene was observed due to decomposition of MesSbH2 (Fig. S22†). Thus, Cp′3Y does catalyse the dehydrocoupling of MesSbH2 to give Sb2H2Mes2 and then Sb4Mes4.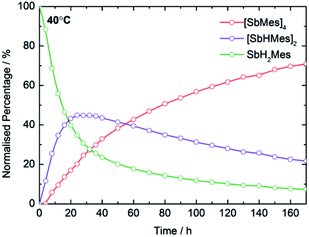 | ||
| Fig. 4 Product distribution as a function of time at 40 °C for the dehydrocoupling of MesSbH2 initiated by 10 mol% Cp′3Y. | ||
The initial yttrium-containing product of the dehydrocoupling is 1-Y, which is subsequently converted into 2-Y. Since our stoichiometric (Scheme 1) and catalytic reaction studies have established that 1-Y reacts quantitatively with MesSbH2 to give 2-Y (Fig. S5†), the fate of 2-Y once formed is of interest. This was probed by adding 3.33 mol% of 2-Y (i.e. 10 mol% yttrium) to MesSbH2 and following the reaction by 1H NMR spectroscopy at 40 °C (Fig. S23†). The resulting spectra acquired over 345 h reveal that, although the reaction is slower than with Cp′3Y as the catalyst, 2-Y does dehydrocouple MesSbH2 to give Sb2H2Mes2 and H2, and then Sb4Mes4.
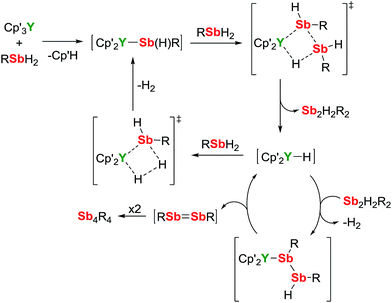
A mechanism for the catalytic dehydrocoupling of MesSbH2 by Cp′3Y is proposed in Scheme 2. The variation in the relative amounts of MesSbH2, Sb2H2Mes2 and Sb4Mes4 as a function of time, in addition to the formation of H2, suggests: (i) that the distibine is formed from dehydrocoupling of MesSbH2, and; (ii) that the tetrastibetane is formed subsequently from further reactivity of the distibine. The formation of Sb2H2Mes2 also implies that the dehydrocoupling does not occur via stibinidene (i.e. RSb) elimination, which would only produce cyclic oligomers of the type [MesSb]n. Thus, we envisage deprotonation of MesSbH2 by Cp′3Y, which acts as a pre-catalyst, leading to the putative stibinide complex [Cp′2YSb(H)Mes], i.e. the monomeric unit of the trimer 1-Y. Addition of a second equivalent of MesSbH2 can lead to the formation of a cyclic, four-membered transition state in which the distibine Sb2H2Mes2 forms, thus generating a hydride-ligated intermediate [Cp′2YH]. A second four-membered transition state can then be proposed from which [Cp′2YSb(H)Mes] is re-formed along with elimination of dihydrogen. The proposed σ-bond metathesis transition states in Scheme 2 are consistent with those thought to occur in several different types of dehydrocoupling reactions catalysed by main group and transition metal complexes.42 To account for the formation of Sb4Mes4 from Sb2H2Mes2, we propose a mechanism in which the distibine is deprotonated by [Cp′2YH] to give an intermediate distibinide complex [Cp′2Y{RSb–Sb(H)R}], which subsequently undergoes a β-hydride elimination to regenerate the yttrium hydride and form the distibene MesSb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SbMes. Since heavy p-block analogues of alkenes tend to cyclo-oligomerize owing to the weak nature of the multiple bonds,43 the formation of Sb4Mes4 can be accounted for by dimerization of the distibene.
SbMes. Since heavy p-block analogues of alkenes tend to cyclo-oligomerize owing to the weak nature of the multiple bonds,43 the formation of Sb4Mes4 can be accounted for by dimerization of the distibene.
Dehydrocoupling catalysis has emerged as one of the most important methods for the synthesis of homo- or hetero-nuclear bonds between p-block elements.44 Considerable attention has focused on the synthesis of inorganic polymers, especially poly(ammonia-borane) and poly(amine-boranes), owing to their proposed applications as hydrogen storage and delivery materials.45 Notably, only one example of metal-catalysed stibine dehydrocoupling has previously been reported, which employed the group 4 metallocenes [(Cp*)(Cp)M(H)Cl] (M = Zr, Hf) as catalysts at 5 mol% loading for the formation of Sb4Mes4 from MesSbH2.46 This reaction is thought to proceed via a mechanism that involves α-elimination of highly reactive stibinidene (SbR) fragments, which subsequently cyclo-oligomerize to SbnRn. Many catalysts based on main group metals and transition metals are well established for the dehydrocoupling of a range of element–element bonds,42,44 however surprisingly few examples employ rare earth elements. A recent study has shown that divalent rare earth alkyl complexes are effective catalysts for the cross-dehydrocoupling of silanes and amines to give silazanes.47
The cross-dehydrocoupling of 1-Dy with mesitylstibine to give 2-Dy is the first example of such reactivity being used to synthesize an SMM. Our observations therefore represent a new catalytic transformation in rare-earth chemistry and a new synthetic strategy in molecular magnetism. The observation of SMM behaviour for 1-Dy, 2-Dy and their magnetically dilute analogues in light of the role of 1-Y and 2-Y in stibine dehydrocoupling is also significant. Although the paramagnetism of the dysprosium systems precludes detailed study by NMR spectroscopy, crystalline Sb2H2Mes2, Sb4Mes4 can be isolated from the dehydrocoupling of MesSbH2 catalysed by 10 mol% Cp′3Dy. In light of the similar chemistry of Y3+ and Dy3+, 1-Dy and 2-Dy should therefore also be intermediates in the catalytic stibine dehydrocoupling. Thus, the dysprosium–antimony compounds display two functions that can be accessed by varying the temperature, since cooling 1-Dy and 2-Dy below 40 K leads to SMM behaviour, and heating them in solution above 313 K results in catalytic stibine dehydrocoupling.
Conclusions
In summary we have synthesized the first antimony-ligated SMMs. The anisotropy barriers of 1-Dy, 2-Dy in zero applied field, and of their diluted analogues, are Ueff = 345 cm−1 and 270 cm−1, respectively, placing them amongst the highest yet reported. The conversion of 1-Dy into 2-Dyvia cross dehydrocoupling with mesitylstibine represents a novel synthetic strategy in molecular magnetism. Indeed, our initial aim of targeting SMMs with lanthanide–metalloid bonds has resulted in the identification new catalytic reactivity for the rare earth elements. Given the broad scope of dehydrocoupling chemistry, the synthetic strategy has considerable potential to be extended to incorporate many new and unconventional chemical environments into molecular magnets. The next challenge is to extend the reactivity to synthesize SMMs that can be regarded as molecular alloys, i.e. systems in which the magnetic centres are bonded to the heaviest stable metallic elements. Based on the periodic trend in the anisotropy barrier unearthed during this study, i.e. that Ueff tends to increase with increasing radius of the pnictogen, substantial increases in Ueff can be expected for SMMs ligated by the 6p elements thallium, lead and bismuth, provided the chemical environments can be stabilized. On-going work in our laboratory will pursue these targets.Acknowledgements
R.A.L. thanks the European Research Council for the Consolidator Grant ‘RadMag’ (646740), and also the EPSRC for an Early Career Fellowship (grant EP/M022064/1). N.F.C. thanks the Ramsay Memorial Trust for a Research Fellowship. The authors acknowledge the EPSRC UK National Electron Paramagnetic Resonance Facility and Service at The University of Manchester for access to the SQUID magnetometer.Notes and references
- M. S. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344 CrossRef CAS PubMed.
- Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462 RSC.
- S. Brooker, Chem. Soc. Rev., 2015, 44, 2880 RSC.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC.
- O. A. Blackburn, A. M. Kenwright, A. R. Jupp, J. M. Goicoechea, P. D. Beer and S. Faulkner, Chem.–Eur. J., 2016, 22, 8929 CrossRef CAS PubMed.
- W.-M. Liu, P. H. J. Keizers, M. A. S. Hass, A. Blok, M. Timmer, A. J. C. Sarris, M. Overhand and M. Ubbink, J. Am. Chem. Soc., 2012, 134, 17306 CrossRef CAS PubMed.
- C. Shen and E. J. New, Curr. Opin. Chem. Biol., 2013, 17, 158 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- C. Papatriantafyllopoulou, E. E. Moushi, G. Christou and A. J. Tasiopoulos, Chem. Soc. Rev., 2016, 45, 1597 RSC.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470 RSC.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577 CrossRef CAS PubMed.
- R. A. Layfield, Organometallics, 2014, 33, 1084 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed.
- (a) M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874 CrossRef CAS PubMed; (b) U. J. Williams, B. D. Mahoney, P. T. DeGregorio, P. J. Carroll, E. Nakamura-Ogiso, J. M. Kikkawa and E. J. Schelter, Chem. Commun., 2012, 48, 5593 RSC.
- P. Zhang, L. Zhang, C. Wang, S. F. Xue, S. Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- R. A. Layfield, J. J. W. McDouall, S. A. Sulway, D. Collison, F. Tuna and R. E. P. Winpenny, Chem.–Eur. J., 2010, 16, 4442 CrossRef CAS PubMed.
- P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923 RSC.
- (a) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829 CrossRef CAS PubMed; (b) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016 DOI:10.1002/anie.201609685.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181 RSC.
- C. Cervetti, A. Rettori, M. G. Pini, A. Cornia, A. Repollé, F. Luis, M. Dressel, S. Rauschenbach, K. Kern, M. Burghard and L. Bogani, Nat. Mater., 2016, 15, 164 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135 CrossRef CAS PubMed.
- M. Ateş, H. J. Breunig, S. Güleç, W. Offermann, K. Häberle and M. Dräger, Chem. Ber., 1989, 122, 473 CrossRef.
- G. Balázs, H. J. Breunig, E. Lork and W. Offerman, Organometallics, 2001, 20, 2666 CrossRef.
- W. J. Evans, S. L. Gonzales and J. W. Ziller, J. Chem. Soc., Chem. Commun., 1992, 1138 RSC.
- H. J. Breunig, E. Lork, O. Moldovan, C. I. Rat, U. Rosenthal and C. Silvestru, Dalton Trans., 2009, 5065 RSC.
- N. Iwahara and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438 CrossRef.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed.
- T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082 CrossRef CAS PubMed.
- F. Pointillart, K. Bernot, S. Gohlen, B. Le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Angew. Chem., Int. Ed., 2015, 54, 1504 CrossRef CAS PubMed.
- F. Aquilante, et al. , J. Comput. Chem., 2016, 37, 506 CrossRef CAS PubMed.
- (a) R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673 CrossRef CAS PubMed; (b) Y. N. Guo, L. Ungur, G. E. Granroth, A. K. Powell, C. J. Wu, S. E. Nagler, J. Tang, L. F. Chibotaru and D. M. Cui, Sci. Rep., 2014, 4, 5471 CAS.
- J. Wu, J. Jung, P. Zhang, H. Zhang, J. Tang and B. Le Guennic, Chem. Sci., 2016, 7, 3632 RSC.
- I. Oyarzabal, J. Ruiz, E. Ruiz, D. Aravena, J. M. Seco and E. Colacio, Chem. Commun., 2015, 51, 12353 RSC.
- J. P. Costes, C. Duhayon, S. Titos-Padilla, E. Colacio, I. Oyarzabal, T. Gupta and G. Rajaraman, Inorg. Chem., 2016, 55, 4428 CrossRef CAS PubMed.
- L. Gagliardi, R. Lindh and G. Karlström, J. Chem. Phys., 2004, 121, 4494 CrossRef CAS PubMed.
- T. Pugh, F. Tuna, L. Ungur, D. Collison, E. J. L. McInnes, L. F. Chibotaru and R. A. Layfield, Nat. Commun., 2015, 6, 7492 CrossRef PubMed.
- T. Pugh, V. Vieru, L. F. Chibotaru and R. A. Layfield, Chem. Sci., 2016, 7, 2128 RSC.
- E. M. Leitao, T. Jurca and I. Manners, Nat. Chem., 2013, 5, 817 CrossRef CAS PubMed.
- P. P. Power, J. Chem. Soc., Dalton Trans., 1998, 2939 RSC.
- R. Waterman, Chem. Soc. Rev., 2013, 42, 5629 RSC.
- S. Bhunya, T. Malakar, G. Ganguly and A. Paul, ACS Catal., 2016, 6, 7907 CrossRef CAS.
- R. Waterman and T. D. Tilley, Angew. Chem., Int. Ed., 2006, 45, 2926 CrossRef CAS PubMed.
- A. Pindwal, A. Ellern and A. D. Sadow, Organometallics, 2016, 35, 1674 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic details, spectroscopic characterization for all compounds, X-ray crystallography details and crystallographic information files, computational details. CCDC 1484570–1484573 and 1485316. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc04465d |
| This journal is © The Royal Society of Chemistry 2017 |