Self-assembly of hard helices: a rich and unconventional polymorphism

Abstract

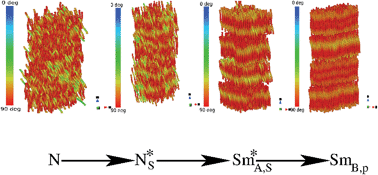
Hard helices can be regarded as a paradigmatic elementary model for a number of natural and synthetic soft matter systems, all featuring the helix as their basic structural unit, from natural polynucleotides and polypeptides to synthetic helical polymers, and from bacterial flagella to colloidal helices. Here we present an extensive investigation of the phase diagram of hard helices using a variety of methods. Isobaric Monte Carlo numerical simulations are used to trace the phase diagram; on going from the low-density isotropic to the high-density compact phases a rich polymorphism is observed, exhibiting a special chiral screw-like nematic phase and a number of chiral and/or polar smectic phases. We present full characterization of the latter, showing that they have unconventional features, ascribable to the helical shape of the constituent particles. Equal area construction is used to locate the isotropic-to-nematic phase transition, and the results are compared with those stemming from an Onsager-like theory. Density functional theory is also used to study the nematic-to-screw-nematic phase transition; within the simplifying assumption of perfectly parallel helices, we compare different levels of approximation, that is second- and third-virial expansions and a Parsons–Lee correction.