Nonuniform growth and topological defects in the shaping of elastic sheets†
Abstract
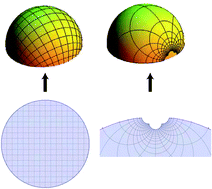
We demonstrate that shapes with zero Gaussian curvature, except at singularities, produced by the growth-induced buckling of a thin elastic sheet are the same as those produced by the Volterra construction of topological defects in which edges of an intrinsically flat surface are identified. With this connection, we study the problem of choosing an optimal pattern of growth for a prescribed developable surface, finding a fundamental trade-off between optimal design and the accuracy of the resulting shape which can be quantified by the length along which an edge should be identified.

 Please wait while we load your content...
Please wait while we load your content...