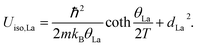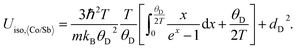Low thermal conductivity in La-filled cobalt antimonide skutterudites with an inhomogeneous filling factor prepared under high-pressure conditions

Abstract

La-filled skutterudites La_xCo₄Sb₁₂ (x = 0.25 and 0.5) have been synthesized and sintered in one step under high-pressure conditions at 3.5 GPa in a piston-cylinder hydrostatic press. The structural properties of the reaction products were characterized by synchrotron X-ray powder diffraction, clearly showing an uneven filling factor of the skutterudite phases, confirmed by transmission electron microscopy. The non-homogeneous distribution of La filling atoms is adequate to produce a significant decrease in lattice thermal conductivity, mainly due to strain field scattering of high-energy phonons. Furthermore, the lanthanum filler primarily acts as an Einstein-like vibrational mode having a strong impact on the phonon scattering. Extra-low thermal conductivity values of 2.39 W m⁻¹ K⁻¹ and 1.30 W m⁻¹ K⁻¹ are measured for La_0.25Co₄Sb₁₂ and La_0.5Co₄Sb₁₂ nominal compositions at 780 K, respectively. Besides this, lanthanum atoms have contributed to increase the charge carrier concentration in the samples. In the case of La_0.25Co₄Sb₁₂, there is an enhancement of the power factor and an improvement of the thermoelectric properties.

---

Introduction

In the modern era, a significant amount of waste heat is lost in energy generation, transport and information processing. Recovery and transformation of this heat into usable electrical energy offers the possibility to improve production efficiencies. Therefore, thermoelectric (TE) materials, which can directly and reversibly convert heat into electrical energy, have been attractive constituents in the research field of sustainable energy. Despite the numerous advantages of thermoelectric generators or cooling devices, such as reliability, stability, endurance or the absence of mobile parts, they are not cost-effective so far because of their low conversion efficiency and are used merely for specific applications.^1–6

The efficiency in thermoelectric materials is assessed by the figure of merit ZT = (S²σ)T/κ, where S stands for the Seebeck coefficient and σ stands for the electrical conductivity, κ is the thermal conductivity, which contains the sum of the electronic and the lattice contributions and T is the absolute temperature.³

In order to attain higher thermoelectric performance, many different approaches have emerged during the last few decades, such as band engineering, nanostructuring, hierarchical architectures, etc. Among them, the phonon-glass electron-crystal (PGEC) proposed by Slack,⁷ consisting in the introduction of “rattling” atoms in structural cages, has had a strong impact on thermoelectric research and is the main motivation driving the investigation of complex materials such as clathrates, Zintl phases and skutterudites.⁸

Nowadays, the research on new thermoelectric materials is focused on lead and telluride-free, environmentally friendly materials that comprise earth-abundant elements and are suitable for industrial applications.⁹ Skutterudites are lead free materials with promising features for thermoelectric applications.¹⁰ These compounds present an intricate CoAs₃-like structure defined in the cubic space group Im3̄, with the general formula MPn₃, where Pn is a pnictogen (P, As, or Sb) and M is a transition metal. There are two main covalent interactions in the structure: between the pnictogen atoms, which form rectangular Pn₄ rings, and between the pnictogen and transition metal atoms, forming MPn₆ octahedra. Each unit-cell is formed by eight formula units and presents two large voids in 2a positions enclosed by MPn₆ octahedra, which can be partially filled with guest atoms. Accordingly, as the atomic volume of the elements constituting the crystal structure increases, the void size increases.

Most efforts have been dedicated to the study and improvement of the thermoelectric properties of cobalt antimonide skutterudite (CoSb₃). This compound displays high carrier mobility, high electrical conductivity and a notably good Seebeck coefficient. Nevertheless, its high thermal conductivity hinders the optimization of the thermoelectric figure of merit. In order to improve its thermoelectric efficiency, three different strategies are commonly employed: (i) modification of the crystal structure by doping (at antimony or cobalt positions),^11–13 (ii) filling in 2a structural voids^14–17 and (iii) nanostructuring or tuning of the grain morphology through different synthesis methods so that the phonon scattering and power factor are enhanced.^10,18–22

As possible candidates for the PGEC, filled CoSb₃ has been thoroughly investigated.^23–30 Guest atoms located at 2a voids are supposed to act as Einstein oscillators, which interact with phonon dispersion processes, thus reducing the lattice thermal conductivity.^10,14 Moreover, filler atoms favorably affect the electrical properties of the material as they act as electropositive donors and their effect on the band structure near the Fermi level is minimal.^31,32 Partially filled skutterudites with no substitution in the Co or Sb site always give rise to n-type thermoelectrics, as the filler donor effect is not compensated. However, the material can be doped in the Co or Sb site for charge compensation. These are p-type materials and the filling limit reaches full occupancy of the 2a position. Most common filler atoms are alkali-metals, alkaline-earth metals and rare-earth elements. Jeitschko and Braun carried out the first synthesis and structural study of La filled Fe₄P₁₂ and isotypic polyphosphides.³³ Afterwards, many attempts of filling different skutterudites have been carried out. G. S. Nolas et al. found that fractionally filled lanthanum skutterudites show lower thermal conductivity than fully filled ones due to disorder effects.³¹ In the same vein, the simultaneous inclusion of diverse kinds of elements as fillers, the so-called multiple-filled skutterudites, has achieved improved phonon scattering affected by the different resonance frequencies of the rattlers, thus involving a wider range of phonon wavelengths.^18,34–36

Very recently, a novel approach has been described to efficiently reduce κ, consisting in the uneven filling-fraction distribution in filled skutterudites.³⁷ The effect of strain-field scattering of high-energy phonons is observed, revealing that an uneven distribution of filling atoms is efficient to further reduce the lattice thermal conductivity of caged crystals: this was realized in filled La_0.8Ti_0.1Ga_0.1Fe₄Sb₁₂, synthesized by melt spinning, which showed an ultralow thermal conductivity as a consequence of the segregation of La rich nanodots, randomly distributed in the bulk, and thus, a wider spectrum of phonons is scattered in this system.³⁷

Along these lines, in the present work, we describe the direct synthesis of La_xCo₄Sb₁₂ (x = 0.25, 0.5) skutterudites under high-pressure (HP) conditions followed by quenching: we discovered that these conditions favor fluctuations in the filling fraction, leading to a “glass-like” ultralow thermal conductivity. By synchrotron X-ray diffraction we have observed the segregation into La-rich and La-poor coexisting skutterudite phases, confirmed by transmission electron microscopy (TEM); the heterogeneous distribution of the rattler element (La) in the sample produces an impressive reduction of the lattice thermal conductivity, mainly due to the strain field scattering of high-energy phonons for x = 0.5, along with an enhancement of the power factor for x = 0.25. As a result, a figure of merit ZT = 0.51 was obtained for this composition at 657 K.

Experimental

La_xCo₄Sb₁₂ (x = 0, 0.25 and 0.5) pellets were prepared by a solid-state reaction at moderate temperature and under high pressure conditions. About 1.3 g of a stoichiometric mixture of starting elements La, Co (99%, ROC/RIC) and Sb (99.5%, Alfa Aesar) were carefully ground and placed in a niobium capsule (5.5 mm diameter), sealed and introduced inside a cylindrical graphite heater. To prevent oxidation, the capsule was properly manipulated inside an argon-filled glovebox. Reactions were carried out in a piston-cylinder press (Rockland Research Co.), at a pressure of 3.5 GPa, at 800 °C for 1 h. Afterwards, the products were quenched to room temperature and the pressure was released. The samples were obtained as hard pellets, which were partially ground to powder for structural characterization, or cut with a diamond saw in a bar shape for transport measurements.

Phase characterization was carried out using X-ray diffraction (XRD) on a Bruker-AXS D8 diffractometer (40 kV, 30 mA), run using DIFFRACTPLUS software, in the Bragg–Brentano reflection geometry with Cu Kα radiation (λ = 1.5418 Å). The data were collected in 0.04 steps over a 2θ range from 10° to 64°. A synchrotron X-ray powder diffraction (SXRPD) study was essential to investigate the structural details of La_xCo₄Sb₁₂ (x = 0, 0.25 and 0.5) and possible phase segregation, which is not evident with conventional X-ray diffraction techniques. SXRPD patterns were collected in high angular resolution mode (so-called MAD set-up) on the MSPD-diffractometer at ALBA synchrotron in Barcelona, Spain, selecting an incident beam with 29 keV energy (λ = 0.4267 Å). The powdered samples were kept in 0.5 mm diameter quartz capillaries. Temperature dependent SXRPD patterns were collected at 295 (RT), 473, 673, 873 and 1073 K. The structural analysis determined that the samples are mixtures of segregated regions of two phases with different La filling fractions. Throughout the manuscript, the samples will, nonetheless, be referred to as their nominal compositions.

The FullProf program³⁸ was used to study the synchrotron data by Rietveld refinement. The line shape of the diffraction peaks was defined by a pseudo-Voigt function. No regions were excluded in the refinement. Complete analysis was carried out refining the following parameters: the scale factor, background coefficients, zero-point error, pseudo-Voigt corrected for asymmetry parameters, occupancy of La, Co and Sb, atomic positions and anisotropic displacements for all the atoms.

The analysis of the microstructure and the surface of the pellets at low spatial resolutions was performed by scanning electron microscopy (SEM) on a Hitachi table-top HT-100 microscope. The density of the consolidated pellets was measured using an Archimedes balance ADAM PW184. It was found to be ca. 97% of the crystallographic value for the La_0.25Co₄Sb₁₂ sample and ca. 96% for La_0.5Co₄Sb₁₂. Transmission electron microscopy (TEM) observations have been carried out on a JEOL 3000F microscope operated at 300 kV, equipped with both an Oxford Instruments electron dispersive X-ray (EDX) analyzer (“Inca”) and a Gatan Enfina electron energy-loss spectroscopy (EELS) analyzer. The latter system, used in the scanning TEM (STEM) modes, enables chemical analyses in the nanometric range.

The Seebeck coefficient was measured using a commercial MMR-technologies system. Measurements were performed under vacuum (10⁻³ mbar) in the temperature range of 300–800 K. A constantan wire was used as a reference for comparison of bar-shaped samples cut with a diamond saw perpendicular to the pressing direction. Reproducibility was checked with different contacts and constantan wire.

A Linseis LFA 1000 instrument was used to measure the thermal diffusivity (α) of the samples over a temperature range of 300 K ≤ T ≤ 800 K by using the laser-flash technique. A thin graphite coating was applied to the surface of the pellet to maximize heat absorption and emissivity. The thermal conductivity (κ) is determined using κ = αC_pd, where C_p is the specific heat and d is the sample density. Specific heat was calculated using the Dulong–Petit equation.

Results and discussion

Structural characterization

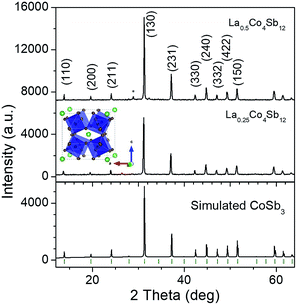
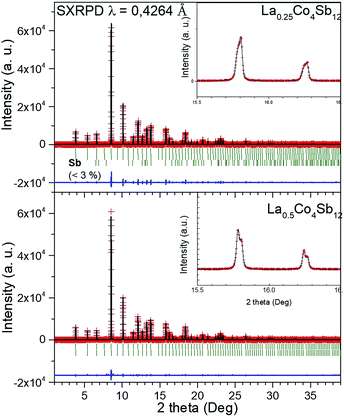
The reaction products were first characterized by XRD with CuK_α radiation; the patterns of La_0.5Co₄Sb₁₂ and La_0.25Co₄Sb₁₂ prepared under high pressure conditions are shown in Fig. 1 and compared with a simulated CoSb₃ skutterudite pattern.

Fig. 1 XRD pattern of La_xCo₄Sb₁₂ (x = 0.25 and 0.5) and simulated CoSb₃ indexed to a cubic body centered unit cell with a ≈ 9 Å. The star indicates the most intense reflection of Sb impurity. Inset: View of the crystal structure: La (green), Co (blue) and Sb (brown).

A synchrotron X-ray powder diffraction (SXRPD) study was essential to investigate the structural details of La_xCo₄Sb₁₂. The crystal structure was defined in the Im3̄ (no. 204) space group. Co atoms occupy 8c Wyckoff positions (1/4, 1/4, 1/4) while Sb atoms occupy the 24g position (0, y, z), and the filler La atoms are located at 2a sites (0, 0, 0). The high-resolution SXRPD patterns exhibit the splitting of all the diffraction peaks at high scattering angles (see the full patterns and insets in Fig. 2). The patterns could be modelled as a mixture of two skutterudite phases with very close unit-cell parameters and different filling factors. The occupancy factors of the segregated phases were independently refined. Table 1 shows the unit-cell parameters, La occupancy and proportion of each phase in the mixture. The lanthanum content of the La-rich phase is close to x = 0.14 for the nominal La_0.25Co₄Sb₁₂ composition and x = 0.17 for La_0.5Co₄Sb₁₂. For the La-poor phase, x was refined to 0 and 0.052 for nominal La_0.25Co₄Sb₁₂ and La_0.5Co₄Sb₁₂ compositions, respectively (Table 1). The global refined La content is always lower than the nominal stoichiometry, with x = 0.11–0.13. The reproducibility of the synthesis was checked for several specimens. Similar average filling levels have been described elsewhere for La-filled skutterudites.¹⁸ A minor impurity of the Sb metal was detected and included as a tertiary phase in the refinement of La_0.25Co₄Sb₁₂; from the scale factors, this phase corresponds to a fraction of <3%. A structural representation of La_xCo₄Sb₁₂ is shown as an inset in Fig. 1, highlighting the tilting of the CoSb₃ octahedra. The quality of the Rietveld fit from synchrotron powder diffraction data at 295 K is shown in Fig. 2 for both nominal compositions. Lattice parameters, atomic positions, thermal parameters, bond distances and refinement agreement factors at 295 K are summarized in Table 1. A temperature dependent SXRD study was carried out for La_0.5Co₄Sb₁₂. The structural parameters in the 473–1073 K temperature range are listed in Table ESI.1,† including the atomic displacement parameters (ADPs), whereas Fig. ESI.1† shows the Rietveld plots above room temperature.

Fig. 2 Observed (red crosses), calculated (black full line) and difference (blue line) SXRPD profiles of La_xCo₄Sb₁₂ (x = 0.25, 0.5) at 295 K. Insets: close up of the high-angle region showing the splitting of all reflections corresponding to two phases with different filling fractions.

Table 1 Refined structural parameters of La_xCo₄Sb₁₂ (x = 0, 0.25 and 0.5) at room temperature. Space group: Im3̄^a

a Sb at 24g, (0, y, z); Co at 8c (1/4, 1/4, 1/4); La at 2a (0, 0, 0), anisotropic U × 10^4, Co: *U11 = U22 = U33; **U12 = U23 = U13; Sb: ***U12 = U13 = 0; La: ****U11 = U22 = U33.
Nominal composition	CoSb3	La0.25Co4Sb12		La0.5Co4Sb12
Refined composition	Co4Sb11.49	La0.14Co4Sb11.68	Co4Sb11.67	La0.17Co4Sb11.64	La0.052Co4Sb11.68
Phase abundance	97% (Sb 3%)	80.5% (Sb 1%)	18.5%	63.3%	36.7%
Lattice parameter (Å)	9.0360(9)	9.0499(8)	9.0393(9)	9.0545(8)	9.0405(8)
Volume (Å^3)	737.80(4)	741.2(4)	738.6(2)	742.3(2)	738.9(1)
U11 (Co)/Å^2*	0.0068(7)	0.0072(7)		0.0063(6)
U12 (Co)/Å^2**	0.0006(6)	0.0009(9)		0.0003(7)
Y (Sb)	0.3349(1)	0.3352(3)		0.3351(3)
z (Sb)	0.1578(1)	0.1581(6)		0.1581(4)
Occ. Sb (<1)	0.966(1)	0.973(10)	0.972(4)	0.971(6)	0.974(8)
U11 (Sb)/Å^2***	0.0078(2)	0.0063(6)		0.0075(5)
U22 (Sb)/Å^2	0.0108(4)	0.0115(8)		0.0106(7)
U33 (Sb)/Å^2	0.0079(1)	0.0080(7)		0.0077(6)
U23 (Sb)/Å^2	0.0012(4)	0.0019(5)		0.0011(4)
Occ. La (<1)	—	0.141(13)	—	0.176(7)	0.052(13)
U11 (La)/Å^2****	—	0.019(6)	—	0.008(5)
d Co–Sb (Å)	2.527(1)	2.532(5)	2.528(6)	2.531(9)	2.528(1)
d 1 Sb–Sb (Å)	2.851(0)	2.864(7)	2.860(3)	2.863(9)	2.859(5)
d 2 Sb–Sb (Å)	2.983(0)	2.984(4)	2.979(8)	2.985(8)	2.981(2)
R p (%)	7.53	8.67		6.02
R wp (%)	11.9	10.40		7.67
R exp (%)	4.85	5.71		5.89
R Bragg (%)	6.04	3.11	2.50	1.69	1.78
χ ^2 (%)	1.21	7.26		4.39

---

J. L. Mi et al. conducted a thorough analysis of the ADPs based on the Einstein model for different partially filled M_0.1Co₄Sb₁₂ (M = La, Ce, Nd, Eu, Yb, Sm) and described a direct relationship between the ADPs of the guest atom and the magnitude of the lattice thermal conductivity.³⁹

The Einstein-oscillator energy corresponding to the rattling motion of the La filler (θ_La) and possible static displacement (d_La², found to be negligible) were determined by fitting the temperature (T) dependent atomic displacement parameter (ADP or U_iso of the La atom) to:

The Debye temperature was estimated from the ADPs of the framework atoms (Co and Sb) averaged by site-occupancy (again, static displacement was found to be negligible):

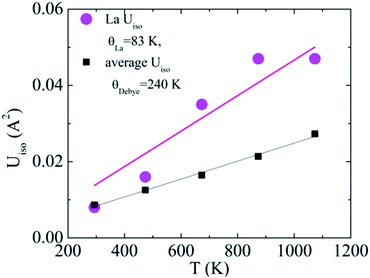
Here, this type of analysis of the averaged U_iso of the atoms of the host structure, Co and Sb, shows that the Debye temperature is reduced upon La incorporation into the structure, from a value typical for CoSb₃ of 262 K to 240 K for La_0.5Co₄Sb₁₂ and La_0.25Co₄Sb₁₂, indicative of overall softening of the phonon bands and strong hybridization between the modes of the host and “rattler” (Fig. 3). The disorder parameters are modest in both cases, around 0.03 Å. The temperature dependent U_iso of the La rattler can be analyzed as an Einstein oscillator^39,40 and yields an oscillator temperature of around 83 K with no static disorder for La_0.5Co₄Sb₁₂. An important conclusion of ref. 39 based on a study of various M_xCo₄Sb₁₂ samples was that what really reduces the thermal conductivity is simply a large U_iso of the “rattler”, independent of the Einstein oscillator energies. The room temperature value of U_iso of La around 0.008 Ų is comparable to that found in other studies.³⁹ We can take this as another indication that, in our samples, κ is driven by the fluctuating filling fraction of the rattler in a nanostructured sample, rather than by changes in the intrinsic phonon modes.

Fig. 3 Temperature dependent isotropic/averaged atomic displacement parameters of the majority phase of the La_0.5Co₄Sb₁₂ sample. The ADP of La, analysed as an Einstein oscillator, gives θ_La = 83 K. The average ADP, analysed in the Debye model, yields θ_Debye = 240 K.

The surface texture is evaluated via SEM images (Fig. 4). The nonporous nature of the samples yielded by high-pressure synthesis is assessed in this picture. A compact bulk of apparently single-crystalline grains is observed, which are densely packed and sintered to adjacent ones.

Fig. 4 SEM image of La_0.5Co₄Sb₁₂ showing a compact, well-sintered morphology.

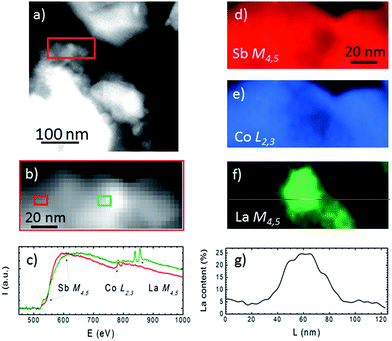
The TEM study of the La_0.25Co₄Sb₁₂ compound is displayed in Fig. 5 and 6. Fig. 5a exhibits a high resolution image of a typical grain. Although the sample is polycrystalline, a dominant orientation close to the [100] zone axis is observed, as shown by the Fourier transform in Fig. 5b. Panel 5c shows a few typical crystals of La_0.25Co₄Sb₁₂, being the grain from Fig. 5a highlighted with a red square. The chemical analysis of eight grains shown in Fig. 5c was assessed by EDX, revealing that they contain 1–4% of La, in accordance with the nominal composition. In order to see if this concentration is homogeneously distributed in the grains, we have performed spatially resolved chemical analyses by means of EELS in STEM mode, which allows obtaining compositional information in the 1–10 nm range. EELS data show that the La concentration within the grains is not homogeneous. In contrast, it varies within the grains, as deduced from the data depicted in Fig. 6. Fig. 6a shows a low magnification annular dark field (ADF) image of the sample, measured in STEM mode. The region marked with a red rectangle was used to obtain an EEL spectrum image. During the EELS acquisition, the ADF signal was acquired simultaneously to disregard the presence of any major spatial drift (Fig. 6b). The Sb M_4,5, the Co L_2,3, and the La M_4,5 edges were measured simultaneously, and variations in the relative Sb/Co/La local intensities were detected. Spectra from two different areas in our EEL spectrum image (depicted with red and green rectangles on panel (b)) are shown in corresponding colors in Fig. 6c. Variations in the relative edge intensities can be clearly observed. For example, the intense La M_4,5 edge signal detected in the central area (green rectangle) is almost completely absent in the left (red rectangle) area of the grains. Elemental maps, obtained by integrating the signal under the Sb M_4,5, Co L_2,3 and La M_4,5 edges (after background subtraction using a power law fit) are shown in panels (d–f) in a false color scale (red = Sb, blue = Co, and green = La). While Sb and Co maps are relatively even within the area analyzed (only minor fluctuations are observed), the La map in Fig. 6f exhibits a pronounced tendency to segregation, detecting as much as 25 at% of La in the middle of the grain (see the line profile shown in panel 6g obtained along the red line in Fig. 6f). A minor decrease of the Co signal is observed in the area where the La species segregate, pointing towards the nucleation of a slightly different phase. However, from these data, we cannot fully identify its local composition. The absolute values of the compositional quantification obtained from the EELS analysis have to be taken with a grain of salt due to the significant overlap of the Co L_2,3 and La M_4,5 absorption edges used here. In this respect, the EDX analysis is more reliable since it is based on the analysis of high energy Sb L, La L and Co K edges. In any case, we can conclude that significant La segregation within lateral length scales of approximately 10–30 nm is present. In spite of this local segregation, the average concentration of La in the material remains within the nominal composition range (1.5%).

Fig. 5 (a) High resolution image of a polycrystalline La_0.25Co₄Sb₁₂ grain. (b) Fourier transform of image (a) showing a predominant [100] crystal orientation in this grain. (c) Overview of grains used for EDX analysis with the grain from panel (a) highlighted with a red square.

Fig. 6 (a) Low magnification STEM annular dark field (ADF) image of a few grains, with the region used for EELS analysis highlighted with a red rectangle. (b) ADF signal acquired simultaneously with the EELS data. (c) Two EEL spectra, taken from the regions depicted with the green and red rectangles marked on panel (b). For presentation purposes, the background was subtracted from the Sb M_4,5 edge using a power law fit. (d–f) Elemental maps extracted from the Sb M_4,5, Co L_2,3 and La M_4,5 edges (red, blue and green, respectively). (g) Intensity profile of the La concentration (atomic%), measured along the direction marked with a red line on the La map in (f).

Thermoelectric properties

The electrical transport properties of the La_xCo₄Sb₁₂ (nominal x = 0.25 and 0.50) samples are displayed in Fig. 7 along with those of pure CoSb_3−δ, for the sake of comparison, prepared under identical HP conditions.⁴¹ The reproducibility of the transport results was checked in several samples as shown in Fig. ESI.3 and ESI.4.† La-filled samples display an almost constant value of the electrical resistivity with temperature.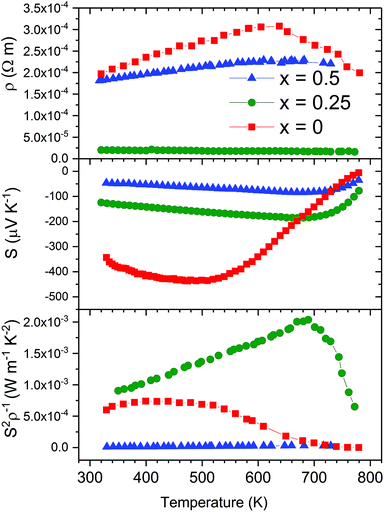

Fig. 7 Temperature dependence of the electrical resistivity (ρ), Seebeck coefficient (S) and power factor (S²ρ⁻¹) of La_xCo₄Sb₁₂ (x = 0, 0.25, and 0.5).

There is partial charge transfer from La to the CoSb₃ host, which increases the carrier concentration and thus decreases the resistivity. The resistivity of La_0.25Co₄Sb₁₂ slowly decreases with temperature, implying the thermal excitation of carriers. However, La_0.5Co₄Sb₁₂ shows metallic behavior: the resistivity slowly increases in this temperature range. This change from semiconductor to metallic behavior was previously described by G. S. Nolas et al., who found a similar decrease of resistivity when La fractions of 0.05 and 0.23 were introduced into the structure.³¹

The Seebeck coefficient is plotted in the middle panel of Fig. 7. Two significant changes take place as a consequence of La filling: The absolute value of the Seebeck coefficient is reduced for the whole temperature range and the maximum is moved towards higher temperatures. The increase in charge carrier concentration, due to lanthanum filling, decreases the Seebeck coefficient, while the effect of minority carriers' excitation at higher temperatures diminishes. The higher the content of La incorporated into the structure, the higher the carrier concentration achieved. Therefore, La_0.5Co₄Sb₁₂ shows further reduction and a shift in the maximum absolute Seebeck coefficient. A similar trend was found in the literature for partially lanthanum-filled CoSb₃.³¹

The power factor of La_0.25Co₄Sb₁₂ is enhanced as a consequence of its low electrical resistivity with a maximum measured value of 2000 μW m⁻¹ K⁻² at 657 K. The reduction of the resistivity is large enough to overcome the fact that the power factor of unfilled CoSb₃ is dominated by the Seebeck coefficient, which is diminished in La filled skutterudites.

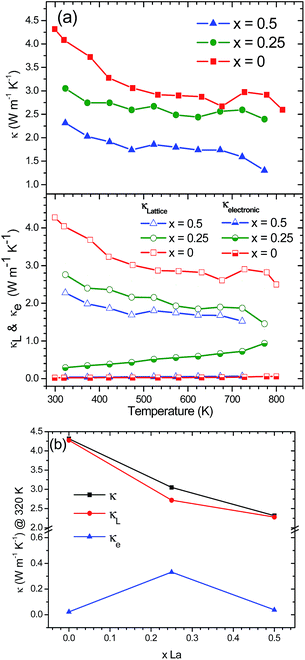
Temperature dependence of the thermal conductivity is shown in Fig. 8. Filled and unfilled compounds show a similar tendency, as the total thermal conductivity decreases with temperature. This is a typical behavior as the lattice thermal conductivity decreases at higher temperatures. The electrical thermal conductivity contribution was calculated using the Wiedemann–Franz law which states κ_e = LσT, where L is the Lorentz number, σ is the electrical conductivity (σ = ρ⁻¹) and T corresponds to the absolute temperature. The value of the temperature-dependent Lorentz number was calculated using the approximation L = 1.5 + exp(−|S|/116) × (10)⁻⁸.⁴²

Fig. 8 (a) Temperature dependence of the total thermal conductivity (upper panel) and electronic (κ_e) and lattice (κ_L) contributions (bottom panel) of La_xCo₄Sb₁₂ (x = 0, 0.25, and 0.5) and (b) total, lattice and electronic thermal conductivity at 320 K vs. the degree of La filling.

CoSb₃ synthesized by conventional methods exhibits a high thermal conductivity of around 8–10 W m⁻¹ K⁻¹ at room temperature.^19,43 An exceptionally low thermal conductivity was achieved for a CoSb_3−δ specimen obtained under HP conditions. The total thermal conductivity slightly decreased from 4.3 W m⁻¹ K⁻¹ at room temperature to 2.6 W m⁻¹ K⁻¹ at 800 K.⁴¹ Remarkably, the inclusion of La rattling atoms into the skutterudite cavity further reduces the lattice thermal conductivity. Filled La_0.25Co₄Sb₁₂ skutterudite displays a reduction in lattice thermal conductivity by approx. 29% at room temperature, whereas for La_0.5Co₄Sb₁₂, the reduction is approx. 46% compared to pure CoSb_3−δ at the same temperature (Fig. 8a). This drastic change in filled skutterudites is brought about by the rattling of filler atoms in the 2a position, which comes from the strong resonant scattering dependent on the frequency of the rattler. Besides, room-temperature thermal conductivities of 3.0 and 2.3 W m⁻¹ K⁻¹ for La_0.25Co₄Sb₁₂ and La_0.5Co₄Sb₁₂ samples, respectively, are really low values even compared to other filled skutterudites.^18,20,37 Nolas et al.³¹ measured a lattice thermal conductivity of 4 W m⁻¹ K⁻¹ in La_0.23Co₄Sb₁₂ and 7 W m⁻¹ K⁻¹ at 400 K in La_0.05Co₄Sb₁₂ prepared by a solid state reaction in sealed quartz ampoules at 1073 K and densified by hot pressing at 179 MPa and 873 K. Liu et al.⁴⁴ reported values between 3.0 and 8 W m⁻¹ K⁻¹ for a series of La_xCo₄Sb₁₂ (x = 0.0–1.0) at 373 K prepared by mechanical alloying and SPS. Park et al.⁴⁵ found thermal conductivity values in the range of 4.0–5.0 W m⁻¹ K⁻¹ at 300 K in La_xCo₄Sb₁₂ (x = 0.0, 0.1, 0.2, 0.3, and 0.4) synthesized by encapsulated melting and hot pressing. The electronic and lattice dependence of the thermal conductivity is represented in the bottom panel of Fig. 8a. Lattice thermal conductivity is the main contribution of the total thermal conductivity, which indicates that the process is mainly due to phonon conduction with only an insignificant electronic contribution. The low lattice thermal conductivity values suggest that a filling-fraction fluctuation produced by the phase segregation in the samples has a significant influence on the thermal transport properties. Fig. 8b shows the influence of the La filling degree to the total thermal conductivity together with the lattice and electronic contributions at 320 K. It can be observed that the decrease of κ and κ_L is not completely linear.^31,46 Nevertheless, there is a reduction of approx. 17% in κ and approx. 15% in κ_L from La_0.25Co₄Sb₁₂ to La_0.5Co₄Sb₁₂.

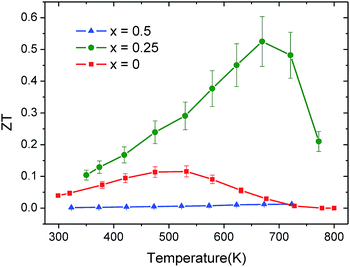
The increase of the power factor together with the impressive reduction in thermal conductivity in La_0.25Co₄Sb₁₂ results in an increase in the figure of merit ZT, compared to HP synthesized CoSb_3−δ. In the case of the sample La_0.5Co₄Sb₁₂, although the reduction in κ is more substantial, the worsening of the electronic transport properties produces a less-competitive ZT (Fig. 9). An optimization of the electron counts in La_xCo₄Sb₁₂, while maintaining the reduced lattice thermal conductivity, is expected to produce an enhancement of the TE properties in the future.

Fig. 9 Temperature dependence of the figure of merit, ZT, of La_xCo₄Sb₁₂ (x = 0, 0.25, and 0.5). ±15% error bars are included in the graph, based on the accumulation of 5% error for the Seebeck coefficient, 5% for the kappa error and 1.5% for the electrical resistivity error (obtained after 3 repetitions of the measurements).

Conclusion

The synthesis and sintering of La_xCo₄Sb₁₂ (x = 0.25 and 0.5) were performed in one step under high pressure conditions, followed by quenching. This procedure drives a segregation of La-filled skutterudite phases, as observed by using synchrotron X-ray diffraction experiments and visualized by TEM. The heterogeneous distribution of La rattler elements in the sample produces an impressive reduction of the thermal conductivity, mainly due to strain field scattering of high energy phonons. Additionally, a decrease of the electrical resistivity was observed for La_0.25Co₄Sb₁₂, causing the enhancement of its power factor. This result, along with the improvement in thermal conductivity, produces an increase of the figure of merit, ZT, reaching a value of 0.51 at 657 K. These findings may open a new approach to radically decrease the thermal conductivity by promoting the formation of unevenly filled skutterudites.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Spanish Ministry of Economy and Competitivity through grants MAT2013-41099-R, MAT2014-52405-C2-2-R and MAT2015-66888-C3-3-R. JPG would also like to acknowledge this Ministry for granting a Juan de la Cierva fellowship. Financial support from the ERC grant PoC2015-MAGTOOLS is also acknowledged. The authors wish to express their gratitude to ALBA technical staff for making the facilities available for the synchrotron X-ray diffraction experiment. Transmission electron microscopy studies were performed in the Centro Nacional de Microscopia Electronica (CNME) at the Universidad Complutense de Madrid (UCM).

Notes and references

1. D. M. Rowe, Thermoelectrics and Its Energy Harvesting, CRC press, Boca Raton, 2012.
2. L. E. Bell, Science, 2008, 321, 1457–1461.
3. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
4. T. C. G. Chen, M. S. Dresselhaus, G. Dresselhaus and J.-P. Fleurial, Int. Mater. Rev., 2003, 48, 45.
5. C. Uher, Thermoelectric Materials Research I, Elsevier, 2001.
6. G. S. Nolas, J. Poon and M. Kanatzidis, MRS Bull., 2006, 31, 199–205.
7. G. A. Slack, in CRC Handbook of hermoelectrics, ed. D. M. Rowe, CRC press, Boca Raton, Florida, 1995, pp. 407–440.
8. B. C. Sales, in Handbook on the Physics and Chemistry of Rare Earths, 2003, pp. 1–34.
9. European Union, Off. J. Eur. Union, 2002, 54, 88–110.
10. M. Rull-Bravo, A. Moure, J. F. Fernández and M. Martín-González, RSC Adv., 2015, 5, 41653–41667.
11. Z. Zhou, C. Uher, A. Jewell and T. Caillat, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 235209.
12. J. Yang, D. T. Morelli, G. P. Meisner, W. Chen, J. S. Dyck and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165207.
13. J. Yang, G. P. Meisner, D. T. Morelli and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 14410.
14. V. Keppens, D. Mandrus, B. C. Sales, B. C. Chakoumakos, P. Dai, R. Coldea, M. B. Maple, D. a. Gajewski, E. J. Freeman and S. Bennington, Nature, 1998, 395, 876–878.
15. M. M. Koza, M. R. Johnson, R. Viennois, H. Mutka, L. Girard and D. Ravot, Nat. Mater., 2008, 7, 805–810.
16. J. L. Feldman, P. Dai, T. Enck, B. C. Sales, D. Mandrus and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 14306.
17. J. Prado-Gonjal, P. Vaqueiro, C. Nuttall, R. Potter and A. V. Powell, J. Alloys Compd., 2017, 695, 3598–3604.
18. X. Shi, S. Bai, L. Xi, J. Yang, W. Zhang, L. Chen and J. Yang, J. Mater. Res., 2011, 26, 1745–1754.
19. J. W. Sharp, E. C. Jones, R. K. Williams, P. M. Martin and B. C. Sales, J. Appl. Phys., 1995, 78, 1013.
20. L. Fu, J. Yang, J. Peng, Q. Jiang, Y. Xiao, Y. Luo, D. Zhang, Z. Zhou, M. Zhang, Y. Cheng and F. Cheng, J. Mater. Chem. A, 2015, 3, 1010–1016.
21. Y. Tang, Z. M. Gibbs, L. A. Agapito, G. Li, H. Kim, M. B. Nardelli, S. Curtarolo and G. J. Snyder, Nat. Mater., 2015, 14, 1223.
22. S. Katsuyama, F. Maezawa and T. Tanaka, J. Phys.: Conf. Ser., 2012, 379, 12004.
23. P. N. Alboni, X. Ji, J. He, N. Gothard and T. M. Tritt, J. Appl. Phys., 2008, 103, 113707.
24. Y. Li, P. Qiu, Z. Xiong, J. Chen, R. Nunna, X. Shi, L. Chen, Y. Li, P. Qiu, Z. Xiong and J. Chen, AIP Adv., 2015, 5, 117239.
25. J. W. Graff, X. Zeng, a. M. Dehkordi, J. He and T. M. Tritt, J. Mater. Chem. A, 2014, 2, 8933.
26. G. A. Lamberton, S. Bhattacharya, R. T. Littleton, M. A. Kaeser, R. H. Tedstrom, T. M. Tritt, J. Yang and G. S. Nolas, Appl. Phys. Lett., 2002, 80, 598–600.
27. P. F. Qiu, J. Yang, R. H. Liu, X. Shi, X. Y. Huang, G. J. Snyder, W. Zhang and L. D. Chen, J. Appl. Phys., 2011, 109, 63713.
28. Y. Z. Pei, J. Yang, L. D. Chen, W. Zhang, J. R. Salvador and J. Yang, Appl. Phys. Lett., 2009, 95, 3–6.
29. Y. Tang, R. Hanus, S. Chen and G. J. Snyder, Nat. Commun., 2015, 6, 7584.
30. X. Zhou, G. Wang, L. Guo, H. Chi, G. Wang, Q. Zhang, C. Chen, T. Thompson, J. Sakamoto, V. Dravid, G. Cao and C. Uher, J. Mater. Chem. A, 2014, 2, 20629–20635.
31. G. S. Nolas, J. L. Cohn and G. A. Slack, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 164–170.
32. W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 184304.
33. W. Jeitschko and D. Braun, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3401–3406.
34. S. Q. Bai, X. Y. Huang, L. D. Chen, W. Zhang, X. Y. Zhao and Y. F. Zhou, Appl. Phys. A, 2010, 100, 1109–1114.
35. X. Shi, J. Yang, J. R. Salvador, M. Chi, J. Y. Cho, H. Wang, S. Bai, J. Yang, W. Zhang and L. Chen, J. Am. Chem. Soc., 2011, 133, 7837–7846.
36. L. Zhang, A. Gritsiv, P. Rogl, E. Bauer and M. Zehetbauer, J. Phys. D: Appl. Phys., 2009, 42, 225405.
37. R. Wei, G. Huiyuan, Z. Zihao and Z. Lixia, Phys. Rev. Lett., 2017, 118, 245901.
38. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
39. J. Mi, M. Christensen, E. Nishibori and B. B. Iversen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 64114.
40. W. Paschinger, G. Rogl, A. Grytsiv, H. Michor, P. R. Heinrich, H. Müller, S. Puchegger, B. Klobes, R. P. Hermann, M. Reinecker, C. Eisenmenger-Sitter, P. Broz, E. Bauer, G. Giester, M. Zehetbauer and P. F. Rogl, Dalton Trans., 2016, 45, 11071–11100.
41. J. Prado-Gonjal, F. Serrano-Sánchez, N. M. Nemes, O. J. Dura, J. L. Martínez, M. T. Fernández-Díaz, F. Fauth and J. A. Alonso, Appl. Phys. Lett., 2017, 111, 83902.
42. H. S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 41506.
43. Y. Kawaharada, K. Kurosaki, M. Uno and S. Yamanaka, J. Alloys Compd., 2001, 315, 193–197.
44. K. Liu, X. Dong and Z. Jiuxing, Mater. Chem. Phys., 2006, 96, 371–375.
45. K.-H. Park, S. Lee, W.-S. Seo, S. Baek, D.-K. Shin and I.-H. Kim, J. Korean Phys. Soc., 2014, 64, 1004–1008.
46. B. C. Sales, D. G. Mandrus and B. C. Chakoumakos, Semicond. Semimetals, 2001, 70, 1–36.

---

Footnote

† Electronic supplementary information (ESI) available: SXRD and XRD Rietveld refinement data and thermoelectric properties of different sample batches. See DOI: 10.1039/c7ta08545a

---