Crystal structure and anti-site boundary defect characterisation of Cu2ZnSnSe4
B. G.
Mendis
 *a,
K. P.
McKenna
*a,
K. P.
McKenna
 b,
G.
Gurieva
c,
M. S.
Rumsey
d and
S.
Schorr
ce
b,
G.
Gurieva
c,
M. S.
Rumsey
d and
S.
Schorr
ce
aDept. of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: b.g.mendis@durham.ac.uk
bDept. of Physics, University of York, Heslington, York, YO10 5DD, UK
cDept. Structure and Dynamics of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109 Berlin, Germany
dMineral and Planetary Sciences Division, Earth Sciences Department, Natural History Museum, Cromwell Road, London, SW7 5BD, UK
eInstitute of Geological Sciences, Freie Universität Berlin, Malteserstraße 64-100, 12249 Berlin, Germany
First published on 7th December 2017
Abstract
The crystal structure identification of the photovoltaic material Cu2ZnSnSe4 (CZTSe) is challenging due to the distinguishing feature between the two polymorphs, kesterite and stannite, being the arrangement of Cu and Zn ions. Here an energy dispersive X-ray (EDX) technique, based on electron beam channeling along specific crystallographic planes in a transmission electron microscope (TEM), is used to identify the structure. Regions a few 100 nm in size can be analysed using this method, unlike neutron or anomalous X-ray scattering. The parent crystal structure of CZTSe, annealed on either side of the order–disorder transition temperature, was correctly identified as being kesterite. The presence of 1/2[110] (001) and 1/4[201] (101) anti-site boundaries (ASBs) has also been investigated. The density of ASBs is higher above the transition temperature, due to a smaller energy penalty for disordering on the 2c and 2d Wyckoff sites. A nearest neighbour cation analysis predicted the 1/2[110] (001) ASB to have the lowest formation energy. From density functional theory (DFT) simulations the 1/2[110] (001) ASB energy is only 43 mJ m−2 and furthermore it is not a recombination site or current blocking layer, so that photovoltaic device performance is not significantly degraded.
Introduction
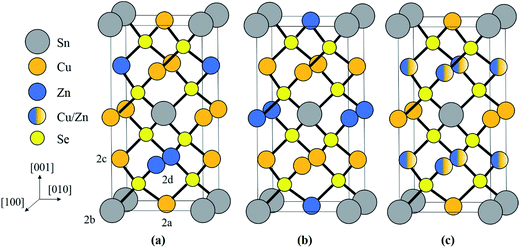
The adamantine compound Cu2ZnSn(S,Se)4, commonly abbreviated as CZTSSe or CZTS(e) depending on the composition, is a promising material for tera-watt scale photovoltaic energy generation, since it is strongly light absorbing and consists entirely of earth abundant, cheap and non-toxic elements.1 The record cell efficiency is however only 12.6% and defects within the material are thought to be a limiting factor.2,3 In particular disorder of the Cu and Zn cations can lead to electrostatic and band gap fluctuations which limit the device efficiency.4–11 The two most common crystal structures are kesterite (space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ) and stannite (I
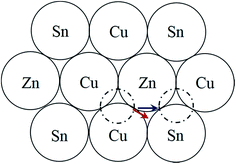
) and stannite (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m), which are both tetragonal and are shown in Fig. 1a and b respectively. Kesterite is the lower energy structure, although the difference between the two is theoretically estimated to be only 0.3 eV per atom.12 Using neutron diffraction and anomalous X-ray scattering on bulk materials Schorr and co-workers have confirmed that CZTS(e) is formed as kesterite, but above a critical temperature of 203 °C the Cu and Zn atoms in the 2c and 2d sites, corresponding to the z = 1/4 and 3/4 planes (see Fig. 1a), become fully disordered to give a structure with the same space group as stannite (Fig. 1c).13,14 The Cu atoms on the 2a sites (i.e. z = 0 and 1/2 planes; Fig. 1a) however remain ordered. The order–disorder transition is a second order phase transformation, so that in practice some disorder persists even below the critical temperature.6
2m), which are both tetragonal and are shown in Fig. 1a and b respectively. Kesterite is the lower energy structure, although the difference between the two is theoretically estimated to be only 0.3 eV per atom.12 Using neutron diffraction and anomalous X-ray scattering on bulk materials Schorr and co-workers have confirmed that CZTS(e) is formed as kesterite, but above a critical temperature of 203 °C the Cu and Zn atoms in the 2c and 2d sites, corresponding to the z = 1/4 and 3/4 planes (see Fig. 1a), become fully disordered to give a structure with the same space group as stannite (Fig. 1c).13,14 The Cu atoms on the 2a sites (i.e. z = 0 and 1/2 planes; Fig. 1a) however remain ordered. The order–disorder transition is a second order phase transformation, so that in practice some disorder persists even below the critical temperature.6
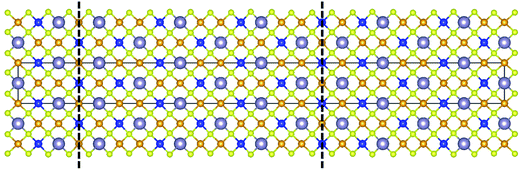
Kattan et al. recently reported two new types of anti-site boundaries (ASBs) in CZTS kesterite nanoparticles grown using a hot injection method.15 They are due to a 1/2[110] shear on a (001) plane and 1/4[201] shear on a (101) plane respectively. A schematic of the two boundaries, as viewed along the [100] crystal projection, is shown in Fig. 2a and b respectively. The 1/2[110] (001) boundary gives rise to ZnCu and CuZn point defects on the 2c and 2d sites of the bottom half of the crystal, while the 1/4[201] (101) boundary produces SnCu anti-site atoms on 2c sites with respect to the top half of the crystal (for the latter SnZn point defects are also possible if the perfect crystal is rotated 180° about [100] prior to shear15). Both the 1/2[110] and 1/4[201] vectors are consistent with 1/2〈110〉 shear in the diamond cubic crystal structure, from which kesterite can be derived16 (the c/2a lattice parameter ratio for tetragonal kesterite and stannite is approximately unity). However, the ASB plane does not correspond to the {112} close packed plane. In fact for the 1/4[201] (101) ASB there is a shear component normal to the boundary plane, meaning that material must be removed during its formation (in this case Cu atoms from the bottom crystal).15
 | ||
| Fig. 2 Supercell of the (a) 1/2[110] (001) and (b) 1/4[201] (101) ASBs in kesterite viewed along [100] (the vertical axis is [001], while the horizontal axis is [010]). Cu, Zn, Sn and Se atoms are depicted by orange, blue, silver and yellow circles, respectively. The dashed line represents the ASB plane and the arrow the ASB shear vector projected onto the [100] viewing plane. In both figures the bottom half of the crystal is displaced with respect to the top half. Figures adapted from ref. 15. | ||
Kesterite and stannite differ in the arrangement of Cu+ and Zn2+ cations, so that it is not possible to identify the crystal structure using conventional X-ray and electron diffraction, since the number of electrons in the two ions is identical. Neutron diffraction and anomalous X-ray scattering are however not limited by this constraint, but have other drawbacks such as the requirement for large volumes of material and/or access to expensive beamlines. Identifying the crystal structure is important, since it governs the point defect structure in the material, which in the case of kesterite gives rise to an order–disorder transition that directly impacts the efficiency of photovoltaic devices.17 It is also not understood how the order–disorder transition influences the ASB defects in the material.
The aims of this paper are two-fold. First we employ a method for identifying the crystal structure of CZTSe that eliminates the above mentioned disadvantages of neutron and anomalous X-ray scattering. The method is an energy dispersive X-ray (EDX) analysis technique, known as ALCHEMI or atom location by channeling enhanced microanalysis.18,19 It requires only a standard transmission electron microscope (TEM) and the crystal structure can be determined from regions only a few 100 nm in size (e.g. individual grains in a thin-film device). Second, having used ALCHEMI to confirm the crystal structure of our samples as kesterite, we examine the role of order–disorder on ASB defects. TEM observations are supplemented with density functional theory (DFT) simulations to assess the impact of ASBs on device performance.
Experimental
Materials
In this paper bulk CZTSe powder samples are analysed. Unlike thin films these samples are highly uniform in composition and have undergone extensive annealing to achieve thermodynamic equilibrium. This makes it ideal for investigating crystal structure and order–disorder effects. The samples were prepared by annealing the constituent elements (5 N purity) in an evacuated quartz ampoule at 700 °C for 240 hours, followed by grinding in an agate mortar to homogenise the material and subsequently annealing at 700 °C for a further 240 hours. Small amounts of the material were then sealed in evacuated quartz ampoules, placed together in a furnace and subjected to heat treatments at different temperatures, starting from high to low temperature, in order to induce varying degrees of disorder. Once a given annealing process was complete one of the ampoules was rapidly removed from the furnace and quenched in ice water. In this paper samples annealed at 250 °C for 24 hours and 100 °C for 100 hours were analysed. Due to the nature of preparation the 100 °C annealed sample had also undergone the 250 °C/24 hour high temperature heat treatment. Wavelength dispersive X-ray (WDX) analysis using a scanning electron microscope showed the material to be Cu-poor (Cu/(Zn + Sn) = 0.96) and Zn-rich (Zn/Sn = 1.08) with no secondary phases. Further details can be found in ref. 14.In order to demonstrate the validity of the ALCHEMI method naturally occurring ferrokesterite and ferrostannite minerals, of composition Cu2(Fe,Zn)SnS4, were obtained on loan from the Natural History Museum in London, UK. These minerals contain Fe in Zn atom positions,20 so that the Fe X-ray signal can be used to determine the sub-lattice through which the electron beam is being channelled (see the Results and discussion for further details). In practice the two minerals were found to be a mixture containing both kesterite and stannite phases, and therefore all results presented in this paper were from the sample labelled ‘ferrokesterite’ (Museum number BM 2016, 25). The source of the mineral was the San Jose mine in Bolivia.
Electron microscopy
CZTSe powder samples were ultrasonicated in isopropanol prior to being deposited on Mo grids with a carbon support film. The ‘ferrokesterite’ mineral was finely crushed in an agate mortar, dispersed in isopropanol, and subsequently deposited on Mo grids with a carbon film. A JEOL 2100F field emission gun TEM operating at 200 kV with an Oxford INCA X-sight Si(Li) EDX detector was used for electron microscopy analysis, i.e. ALCHEMI experiments and ASB defect characterisation. The Mo grid did not affect the ALCHEMI measurements, since the Mo L background X-ray signal does not overlap with any of the Cu, Zn, and Sn cation X-ray peaks. A 240 nm diameter area of the specimen was illuminated with a parallel electron beam during the ALCHEMI measurements. The sample thickness was measured using the convergent beam electron diffraction (CBED) technique,21 and was typically ∼150 nm after tilting to the desired orientation.Density functional theory simulations
To predict the structure, stability and electronic properties of the 1/2[110] (001) anti-site boundary (ASB) defect in CZTS and CZTSe we perform first principles calculations using density functional theory. We employ the projector augmented wave method as implemented in the Vienna ab initio simulation package22,23 together with the Heyd, Scuseria, and Ernzerhof (HSE) hybrid exchange–correlation (XC) functional,24 which gives much improved predictions with respect to band gaps compared to standard local or semi-local XC functionals. The 3p, 3d and 4s electrons of Cu, 3d and 4s electrons of Zn, 4d, 5s and 5p electrons of Sn, 3s and 3p electrons of S, and 4s and 4p electrons of Se are treated as valence electrons and expanded in a plane wave basis with energies up to 500 eV. For the calculation of bulk kesterite properties we use a 16-atom conventional unit cell with a gamma point centred 8 × 8 × 4 Monkhorst–Pack (MP) grid to sample the Brillouin zone. The Fock exchange potential is sampled using a coarser 4 × 4 × 2 MP grid. The total energy is optimised with respect to the position of atoms and the unit cell dimensions using a conjugate gradient algorithm until all forces are less than 0.01 eV Å−1. Using this approach we predict the properties of bulk Cu2ZnSnS4 (a = 5.435 Å, c = 10.856 Å, and Eg = 1.47 eV) and Cu2ZnSnSe4 (a = 5.715 Å, c = 11.412 Å, and Eg = 0.91 eV) in good agreement with previous calculations and experiments.25,26To model the ASB defects we expand the conventional unit cell into a 1 × 1 × 6 supercell (96 atoms in total) and displace half of the atoms in the supercell by 1/2[110] creating two equally spaced ASBs. The separation between the periodically repeating ASBs is >30 Å, ensuring that artificial interactions are minimised. The structure of the supercell is optimised using the same methods described for the bulk but with the MP grid reduced to 3 × 3 × 1. A similar approach was employed recently to model anti-phase boundary defects in Fe3O4.27 The total energy is also calculated for a 1 × 1 × 6 supercell without the ASB displacement (corresponding to a bulk crystal) in order to calculate the ASB formation energy.
Results and discussion
ALCHEMI results
When a crystal is tilted close to two-beam conditions, such that only a single Bragg beam is excited along with the unscattered beam, the incident electrons in the TEM will channel either along or between the Bragg diffracting planes, with the nature of the channeling depending on the precise specimen orientation.18,19 If the incident angle of the TEM electrons is smaller than the Bragg angle, i.e. the so-called negative deviation parameter,28 then channeling largely takes place along the diffracting crystal plane, while for incident angles larger than the Bragg angle (i.e. positive deviation parameter) channeling is largely between the crystal planes. EDX spectra acquired under negative deviation parameter conditions therefore show an increased X-ray signal from those elements that make up the crystal plane of interest. This is the origin of the ALCHEMI effect. It can be used to distinguish between the kesterite and stannite phases. For example, assume that Bragg diffraction is due to the (002) planes. For negative deviation parameter channeling is therefore along the z = 0 and 1/2 planes containing Sn atoms (Fig. 1). The other cation within these planes is Cu for kesterite, and Zn for stannite. On the other hand for positive deviation parameter channeling is along the z = 1/4 and 3/4 planes, which consist of equal amounts of Cu and Zn for kesterite and pure Cu for stannite. Thus for kesterite the (Zn/Cu) ratio is smaller for the EDX spectrum acquired under negative deviation parameter conditions compared to positive deviation parameter conditions, while the opposite is true for stannite. Examination of the crystal structures in Fig. 1 shows that the same effect must be observed if the diffracting plane is (110) rather than (002).Although channeling can distinguish between kesterite and stannite phases it cannot however distinguish between the ordered and disordered states of kesterite, since disorder occurs amongst the 2c (Cu) and 2d (Zn) sites within the z = 1/4 and 3/4 crystal planes, while the 2a (Cu) sites remain ordered.14 Hence what is determined is the parent crystal structure, i.e. for a fully disordered kesterite, with the same I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m space group as stannite, the ALCHEMI method would identify the crystal structure as being kesterite, but provide no information on the degree of disorder. Bosson et al. have reported that for Sn-poor, Zn-rich CZTS (i.e. Cu/(Zn + Sn) = 0.97, Zn/Sn = 1.62) approximately one third of the Cu 2a kesterite sites are occupied by Zn;29 although this does not preclude crystal structure identification it does mean that there would be less variation between EDX spectra acquired under different channeling conditions, thus placing greater demands on the signal to noise ratio of the ALCHEMI measurement.
2m space group as stannite, the ALCHEMI method would identify the crystal structure as being kesterite, but provide no information on the degree of disorder. Bosson et al. have reported that for Sn-poor, Zn-rich CZTS (i.e. Cu/(Zn + Sn) = 0.97, Zn/Sn = 1.62) approximately one third of the Cu 2a kesterite sites are occupied by Zn;29 although this does not preclude crystal structure identification it does mean that there would be less variation between EDX spectra acquired under different channeling conditions, thus placing greater demands on the signal to noise ratio of the ALCHEMI measurement.
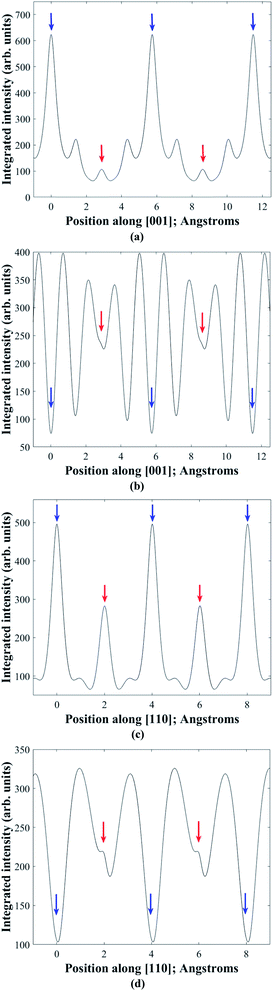
In practice it is difficult to satisfy two-beam conditions due to the large unit cell, and what is observed is many-beam excitation along a systematic row. Meaningful results are nevertheless obtained for EDX spectra acquired in the symmetry orientation (i.e. incident electron beam parallel to the diffracting planes) and with a slightly positive deviation parameter of ∼0.005 nm−1 from 008 or 220 higher order Bragg conditions. Bloch wave calculations28 of the electron wavefunction within the crystal confirm these observations. Fig. 3a and b show the depth integrated electron intensity along the [001] crystal direction for a 150 nm thick kesterite specimen tilted to the symmetry orientation and near (i.e. 0.005 nm−1 deviation parameter) 008 Bragg condition respectively. Note that what is plotted here is the elastic electron intensity integrated through the specimen thickness. The spatial distribution of thermal diffuse scattered (TDS) electrons cannot be calculated using a Bloch wave simulation, although the TDS contribution to the channeling signal is expected to be comparatively smaller due to its more delocalised nature. Comparing integrated electron intensities along the z = 0 and 1/2 planes containing 2a and 2b atom sites with the z = 1/4 and 3/4 planes containing 2c and 2d sites, the former is found to be relatively higher for the symmetry orientation (Fig. 3a), while the latter is relatively higher near the 008 Bragg condition (Fig. 3b). Although the integrated electron intensities for the many-beam scenario, particularly near the 008 Bragg condition, do not strictly follow the predictions of two-beam theory discussed earlier, the channeling is nevertheless sufficiently similar to the ideal two-beam case for the purpose of distinguishing the crystal structure. Furthermore, the integrated electron intensity along the [110] crystal direction for a 150 nm thick kesterite specimen tilted to the symmetry orientation and near (i.e. 0.005 nm−1 deviation parameter) 220 Bragg condition is shown in Fig. 3c and d respectively. The channeling is similar to that in Fig. 3a and b, confirming the suitability of these diffraction conditions for ALCHEMI measurements. Although results for only a 150 nm thick kesterite specimen are presented here, calculations for other specimen thicknesses (i.e. 50, 100 and 200 nm) showed similar trends. The conclusions were also found to be valid for the stannite phase.
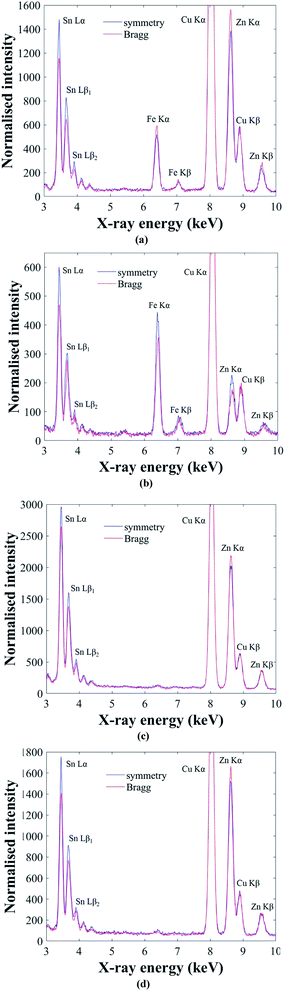
The ALCHEMI method is first demonstrated on the Cu2(Fe,Zn)SnS4 ‘ferrokesterite’ mineral, since the Fe X-ray signal can be used to confirm the sub-lattice through which the electron beam is channeling. Fig. 4a and b show the results for kesterite and stannite phases in the ‘ferrokesterite’ mineral. In each figure the EDX spectrum acquired at symmetry orientation is superimposed with that acquired close to the 008/220 higher order Bragg conditions. The Cu Kα X-ray intensity is normalised for direct comparison and the intensity scale has been expanded so that the full Cu Kα peak is not visible. For both kesterite and stannite phases the Sn L X-ray signal is higher in the symmetry orientation, due to the electron beam preferentially channeling along the planes containing 2b (Sn) sites. The EDX spectrum obtained near the higher order Bragg condition shows a relative increase in the Fe Kα and the Zn Kα X-ray signal for the kesterite phase (Fig. 4a) and a relative decrease for stannite (Fig. 4b). These observations are consistent with the fact that for these specimen orientations there is a larger EDX signal from planes containing 2c (Cu) and 2d (Zn) sites in kesterite, and 4d (Cu) sites in stannite. Fe occupies the Zn sub-lattice and therefore the X-ray signal for the two elements shows similar intensity variations with respect to channeling.
The successful demonstration of the ALCHEMI method on a Cu2(Fe,Zn)SnS4 test sample means that it can now be applied to the CZTSe bulk powder samples. Fig. 4c and d show representative ALCHEMI results for CZTSe annealed at 250 °C and 100 °C respectively (the figures have been plotted in a similar manner to Fig. 4a and b). Previous anomalous X-ray scattering results for these same samples have shown that at 250 °C the Cu and Zn cations on the 2c and 2d crystallographic sites in the parent kesterite structure are completely disordered (0.5 site occupation factor), while at 100 °C partial ordering is restored, such that the site occupation factor increases to ∼0.8.14 The Cu atoms on the 2a sites remain almost fully ordered, even at high temperature. In both Fig. 4c and d the Zn Kα X-ray signal has higher intensity when acquired near the higher order Bragg conditions, which is consistent with a parent kesterite crystal structure (recall that the ALCHEMI technique is not sensitive to the ordering of the 2c and 2d sites). Measurements were carried out on at least three grains for each heat treatment temperature, and in all cases the results indicated a kesterite phase, in agreement with anomalous X-ray scattering.14 The advantage of ALCHEMI however is that the measurements were carried over regions a few 100 nm in size. This opens up new possibilities, such as analysing the crystal structure of individual grains in a thin-film device.
Anti-site boundary imaging
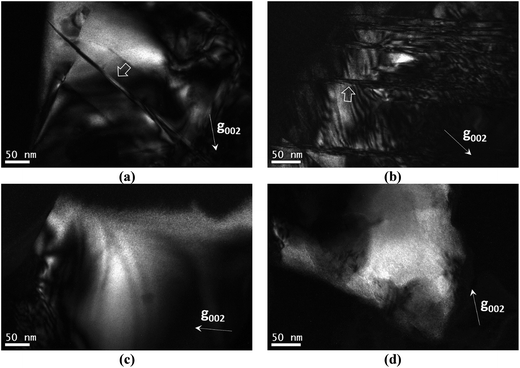
In this section the presence of 1/4[201] (101) and 1/2[110] (001) anti-site boundaries in the CZTSe bulk powder samples, annealed at 250 °C and 100 °C, is reported. As described in ref. 15 the 1/4[201] (101) boundaries are visible using g = 002 TEM dark-field imaging (any 1/2[110] (001) boundaries are however invisible). Alternating black and white interference fringes are observed along the projection of the inclined ASB plane, due to the 1/4[201] shear causing a phase shift of the g = 002 diffracted beam relative to the unscattered beam.28Fig. 5a and b show 1/4[201] (101) ASBs in two different particles of the 250 °C annealed sample. The dark-field images were acquired close to the [110] zone-axis; the measured angle between the g = 002 diffracting vector and trace of the ASB is consistent with a (101) habit plane. Note that the angle is also consistent with a (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2) close packed plane, although this habit plane can be ruled out since the ASBs would be approximately end-on and should not therefore exhibit significant black–white interference fringes. g = 002 dark-field images for the 100 °C annealed sample are shown in Fig. 5c and d and did not reveal any 1/4[201] (101) ASBs. Recall that the 100 °C sample had also undergone the same high temperature heat treatment at 250 °C (see the Experimental section), and therefore had the same starting ASB defect population as the 250 °C sample. All three particles analysed in the 250 °C sample showed 1/4[201] (101) ASBs, while for the 100 °C sample ASBs were not detected in five particles analysed. They are small numbers, and are due to the laborious process of finding particles that can be tilted to the desired orientation. Nevertheless the apparent scarcity of ASBs at low temperature suggests that they become unstable with respect to the ordering of the bulk crystal.
2) close packed plane, although this habit plane can be ruled out since the ASBs would be approximately end-on and should not therefore exhibit significant black–white interference fringes. g = 002 dark-field images for the 100 °C annealed sample are shown in Fig. 5c and d and did not reveal any 1/4[201] (101) ASBs. Recall that the 100 °C sample had also undergone the same high temperature heat treatment at 250 °C (see the Experimental section), and therefore had the same starting ASB defect population as the 250 °C sample. All three particles analysed in the 250 °C sample showed 1/4[201] (101) ASBs, while for the 100 °C sample ASBs were not detected in five particles analysed. They are small numbers, and are due to the laborious process of finding particles that can be tilted to the desired orientation. Nevertheless the apparent scarcity of ASBs at low temperature suggests that they become unstable with respect to the ordering of the bulk crystal.
1/2[110] (001) ASBs can be revealed using g = 101 dark field imaging. Of the major zone axes in CZTSe however the 101 reciprocal vector is found only along the [010] direction. In this specimen orientation the ASBs are end-on, so that lattice imaging, using high resolution electron microscopy (HREM), is more appropriate for characterising the defects. Fig. 6a is an HREM image of the 250 °C annealed CZTSe sample along [010], and shows a high density of 1/2[110] (001) ASBs. The HREM image has a limited field of view, but the selected area electron diffraction pattern of the same particle, as shown in Fig. 6b, exhibits streaking along the 002 reciprocal direction. The streaking is due to the shape transform of the two-dimensional ASB in reciprocal space (i.e. relrod28) and indicates a high density of such defects over a larger area than that observed in the HREM image. Fig. 6c is the corresponding [010] HREM image of the 100 °C annealed CZTSe sample. No ASBs are visible and the selected area diffraction pattern in Fig. 6d does not show any streaking, which suggests that the 1/2[110] (001) ASBs become less abundant with ordering of the bulk crystal. The statistics however are poor, i.e. only one and two particles were analysed for the 250 °C and 100 °C samples respectively.
The scarcity of 1/4[201] (101) and 1/2[110] (001) ASBs at the lower annealing temperature suggests that the boundary energy increases for the ordered crystal. This can be explained by examining the structure of the two ASBs, as shown in Fig. 2a and b. In both cases the anti-site atoms and vacancies are at the 2c and 2d Wyckoff positions. For the 1/2[110] (001) ASB there are ZnCu and CuZn anti-site atoms with respect to the bottom half of the crystal (Fig. 2a). For the 1/4[201] (101) boundary the defects are SnCu on 2c sites in the top half of the crystal and furthermore Cu atoms are removed from the 2c sites of the bottom crystal, due to the shear component normal to the boundary plane (Fig. 2b). As the annealing temperature is lowered below the critical ordering temperature, the Gibbs energy of such 2c and 2d anti-site atoms and vacancies increases, thereby increasing the ASB energy.
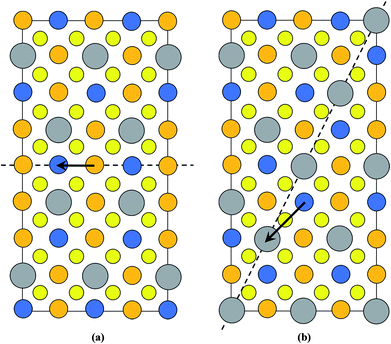
It is interesting that the habit plane of the ASBs does not correspond to {112}, i.e. the close packed plane in the parent diamond cubic crystal structure on which shear occurs comparatively easily.30 HREM images were also acquired along the [201] zone-axis, since in this orientation two out of the four unique {112} planes are end-on, i.e. (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) and (
) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 12). Three particles in the 250 °C sample and two particles in the 100 °C sample were analysed, and only one isolated defect with the {112} habit plane was detected in the latter. For a 1/2[110] or 1/4[201] shear the preferred habit plane is therefore not {112}. This can be easily explained for the 1/2[110] (001) ASB. Table 1 lists the nearest neighbour cations for Cu, Zn and Sn in bulk kesterite. The twelve nearest neighbours are along the 1/2〈110〉 directions in the parent diamond cubic crystal. Examination of Fig. 2a reveals that the same nearest neighbour cations are preserved for the 1/2[110] (001) ASB, and consequently its formation energy should be low, a fact confirmed by DFT simulations (see the next section). Compare this with a 1/2〈110〉 shear along the {112} plane, where the nearest neighbour cations are not preserved. This is evident from Fig. 7 which shows the structure of the {112} cation plane in kesterite. A 1/2[110] shear, the same as the 1/2[110] (001) ASB, shifts a cation on the close packed layer above (dashed circle) along the blue arrow indicated in the figure. In this particular case Sn is substituted for Cu as one of the nearest neighbours for the displaced cation. It may be argued that a 1/12[241] shear, equivalent to a 1/6[121] shear in the diamond cubic crystal, is more likely along the {112} plane. The shear is indicated by the red arrow in Fig. 7 and it is clear that the resulting nearest neighbours are the same as for a 1/2[110] shear. Examination of the 1/4[201] (101) ASB in Fig. 2b shows that the nearest neighbour cations are also not preserved. Thus this defect as well as ASBs on {112} habit planes are expected to have relatively higher formation energies. Nevertheless the importance of {112} ASBs must not be entirely ruled out. Our preliminary investigations on a CZTS thin-film device revealed a high density of {112} twins in certain grains (see also ref. 31). This could be caused by strain build up in the CZTS layer during film growth; the strain is most readily relieved by shearing the {112} close packed planes, where the Peierls–Nabarro stress for dislocation glide is minimal.30 The CZTSe powder in this study and CZTS nanoparticles in ref. 15 are however free standing, so that strain considerations do not apply.
12). Three particles in the 250 °C sample and two particles in the 100 °C sample were analysed, and only one isolated defect with the {112} habit plane was detected in the latter. For a 1/2[110] or 1/4[201] shear the preferred habit plane is therefore not {112}. This can be easily explained for the 1/2[110] (001) ASB. Table 1 lists the nearest neighbour cations for Cu, Zn and Sn in bulk kesterite. The twelve nearest neighbours are along the 1/2〈110〉 directions in the parent diamond cubic crystal. Examination of Fig. 2a reveals that the same nearest neighbour cations are preserved for the 1/2[110] (001) ASB, and consequently its formation energy should be low, a fact confirmed by DFT simulations (see the next section). Compare this with a 1/2〈110〉 shear along the {112} plane, where the nearest neighbour cations are not preserved. This is evident from Fig. 7 which shows the structure of the {112} cation plane in kesterite. A 1/2[110] shear, the same as the 1/2[110] (001) ASB, shifts a cation on the close packed layer above (dashed circle) along the blue arrow indicated in the figure. In this particular case Sn is substituted for Cu as one of the nearest neighbours for the displaced cation. It may be argued that a 1/12[241] shear, equivalent to a 1/6[121] shear in the diamond cubic crystal, is more likely along the {112} plane. The shear is indicated by the red arrow in Fig. 7 and it is clear that the resulting nearest neighbours are the same as for a 1/2[110] shear. Examination of the 1/4[201] (101) ASB in Fig. 2b shows that the nearest neighbour cations are also not preserved. Thus this defect as well as ASBs on {112} habit planes are expected to have relatively higher formation energies. Nevertheless the importance of {112} ASBs must not be entirely ruled out. Our preliminary investigations on a CZTS thin-film device revealed a high density of {112} twins in certain grains (see also ref. 31). This could be caused by strain build up in the CZTS layer during film growth; the strain is most readily relieved by shearing the {112} close packed planes, where the Peierls–Nabarro stress for dislocation glide is minimal.30 The CZTSe powder in this study and CZTS nanoparticles in ref. 15 are however free standing, so that strain considerations do not apply.
| Ion | Nearest neighbour cations |
|---|---|
| Cu (2a, 2c sites) | 4 Cu, 4 Zn, 4 Sn |
| Zn (2d) | 8 Cu, 4 Sn |
| Sn (2b) | 8 Cu, 4 Zn |
Density functional theory calculations
DFT calculations are performed for the 1/2[110] (001) ASB, since this is predicted to have the lowest formation energy. The optimised structure of the CZTSe ASB supercell (see the Experimental section) is shown in Fig. 8. The ASB causes very little perturbation in the atomic structure, with atoms at the interface retaining the same coordination and very similar bond lengths to the perfect crystal. The formation energy (Ef) of the ASB is calculated using,| Ef = (EASB − Ebulk)/2A | (1) |
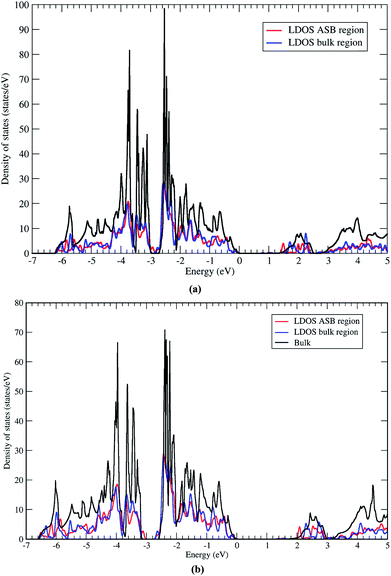
Next we address the electronic properties of the CZTSe ASB defect. We characterise the electronic structure of the ASB by calculating the local density of states (LDOS) in a region of width 4 Å centered on one of the ASBs and in the centre of the bulk region. The two LDOS values are shown in Fig. 9a along with a reference density of states calculated for the bulk crystal supercell. The ASBs are found to introduce no new states into the gap near the valence band maximum or conduction band minimum. Therefore the ASB would appear to be relatively benign for carrier transport as it does not represent a Shockley–Read–Hall (SRH) recombination site for electrons or holes. In fact the LDOS values in the bulk and ASB regions are remarkably similar across a wide range of energies. The only significant difference appears above the conduction band minimum, at around 1.5 and 2.1 eV, where electronic states at the ASB appear to be slightly deeper than the corresponding states in the bulk region. These resonant states may play some role in the transport of hot electrons, but given the relatively fast relaxation of hot electrons it should not impact significantly the device performance. Furthermore, the absence of a band offset between the ASB and bulk crystal for both valence and conduction bands means that the defects do not act as electron/hole current blocking layers, cf. ZnSe in CZTSe32 or grain boundary hole barriers in CuInSe2 (CIS).33
The LDOS for the CZTS ASB defect is almost identical, albeit with a larger band gap (Fig. 9b). Again there are no localised states associated with the ASB inside the band gap. The resonant states in the conduction band occur at higher energies of 2.0 and 2.6 eV. As for CZTSe the conclusion is that the 1/2[110] (001) ASB in CZTS does not represent a SRH recombination centre and has no band discontinuities and should therefore be favourable for device performance.
Summary
In the ALCHEMI technique TEM-EDX spectra are acquired under diffraction conditions that induce channeling of the electron beam along certain crystallographic planes. It can be used to identify the parent crystal structure of CZTS(e) within regions a few 100 nm in size, which is otherwise not possible using standard techniques such as neutron diffraction and anomalous X-ray scattering. As a proof of principle ALCHEMI has been applied to identify the kesterite and stannite phases in a Cu2(Fe,Zn)SnS4 mineral, where the Fe X-ray signal can be used to monitor channeling or non-channeling of the electron beam along the Zn sub-lattice. The technique was also used to characterise CZTSe powder samples annealed on either side of the order–disorder temperature, and confirmed the parent crystal structure to be kesterite, consistent with previous anomalous X-ray scattering results.1/2[110] (001) and 1/4[201] (101) ASBs, previously reported for CZTS nanoparticles, have also been observed in the CZTSe powder samples. The ASB density is however lower for the ordered sample, suggesting that the Gibbs energy of the defects increases as the material is cooled below the order–disorder transition temperature. This can be related to the ASB shear induced, anti-site atoms and/or vacancies at the 2c and 2d Wyckoff positions. An analysis of the nearest neighbour cations predicts that the 1/2[110] (001) ASB has the lowest formation energy. From DFT calculations the formation energy of the 1/2[110] (001) ASB in CZTSe is only 43 mJ m−2 (35 mJ m−2 for CZTS). Although there is a low energy barrier for creating 1/2[110] (001) defects the coordination environment is similar to the perfect crystal, at least for the nearest neighbour cations, so that there are no localised electronic states within the band gap and no valence/conduction band discontinuities. The 1/2[110] (001) ASBs are therefore not Shockley–Read–Hall recombination sites or current blocking layers, and will not have any significant influence on photovoltaic device performance.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
KPM acknowledges support from the EPSRC (EP/K003151/1 and EP/P023843/1). This work made use of the facilities of Archer, the UK's national high-performance computing service, via our membership in the UK HPC Materials Chemistry Consortium, which is funded by the EPSRC (EP/L000202). All data relating to the density functional theory calculations created during this research are available on request from the University of York Research database (https://doi.org/10.15124/c0cd73d0-ec8e-4eda-abeb-4e9dd5cd3b3f).References
- K. Ito, Copper Zinc Tin Sulfide-Based Thin Film Solar Cells, Wiley, United Kingdom, 2015 Search PubMed.
- M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovolt: Res. Appl., 2017, 25, 668 CrossRef.
- X. Liu, Y. Feng, H. Cui, F. Liu, X. Hao, G. Conibeer, D. B. Mitzi and M. Green, Prog. Photovolt: Res. Appl., 2016, 24, 879 CrossRef.
- J. H. Werner, J. Mattheis and U. Rau, Thin Solid Films, 2005, 480, 399 CrossRef.
- T. Gokmen, O. Gunawan, T. K. Todorov and D. B. Mitzi, Appl. Phys. Lett., 2013, 103, 103506 CrossRef.
- J. J. S. Scragg, L. Choubrac, A. Lafond, T. Ericson and C. Platzer-Björkman, Appl. Phys. Lett., 2014, 104, 041911 CrossRef.
- G. Rey, A. Redinger, J. Sendler, T. P. Weiss, M. Thevenin, M. Guennou, B. E. Adib and S. Siebentritt, Appl. Phys. Lett., 2014, 105, 112106 CrossRef.
- D. P. Halliday, R. Claridge, M. C. J. Goodman, B. G. Mendis, K. Durose and J. D. Major, J. Appl. Phys., 2013, 113, 223503 CrossRef.
- B. G. Mendis, M. D. Shannon, M. C. J. Goodman, J. D. Major, R. Claridge, D. P. Halliday and K. Durose, Prog. Photovolt: Res. Appl., 2014, 22, 24 CrossRef CAS.
- J. A. Aguiar, M. E. Erkan, D. S. Pruzan, A. Nagaoka, K. Yoshino, H. Moutinho, M. Al-Jassim and M. A. Scarpulla, Phys. Status Solidi A, 2016, 213, 2392 CrossRef CAS.
- B. G. Mendis, A. A. Taylor, M. Guennou, D. M. Berg, M. Arasimowicz, S. Ahmed, H. Deligianni and P. J. Dale, Sol. Energy Mater. Sol. Cells, 2018, 174, 65 CrossRef CAS.
- S. Chen, X. G. Gong, A. Walsh and S. Huai Wei, Appl. Phys. Lett., 2009, 94, 041903 CrossRef.
- S. Schorr, H.-J. Hoebler and M. Tovar, Eur. J. Mineral., 2007, 19, 65 CrossRef CAS.
- D. M. Többens, G. Gurieva, S. Levcenko, T. Unold and S. Schorr, Phys. Status Solidi B, 2016, 253, 1890 CrossRef.
- N. A. Kattan, I. J. Griffiths, D. Cherns and D. J. Fermin, Nanoscale, 2016, 8, 14369 RSC.
- S. Schorr, Thin Solid Films, 2007, 515, 5985 CrossRef CAS.
- G. Rey, T. P. Weiss, J. Sendler, A. Finger, C. Spindler, F. Werner, M. Melchiorre, M. Hála, M. Guennou and S. Siebentritt, Sol. Energy Mater. Sol. Cells, 2016, 151, 131 CrossRef CAS.
- J. C. H. Spence and J. Taftø, J. Microsc., 1983, 130, 147 CrossRef CAS.
- I. P. Jones, Adv. Imaging Electron Phys., 2002, 125, 63 CAS.
- P. Bonazzi, L. Bindi, G. P. Bernardini and S. Menchetti, Can. Mineral., 2003, 41, 639 CrossRef CAS.
- I. P. Jones, Chemical Microanalysis Using Electron Beams, The Institute of Materials, London, 1992 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- J. Paier, R. Asahi, A. Nagoya and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115126 CrossRef.
- Y. S. Yee, B. Magyari-Köpe, Y. Nishi, S. F. Bent and B. M. Clemens, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195201 CrossRef.
- K. P. McKenna, F. Hofer, D. Gilks, V. K. Lazarov, C. Chen, Z. Wang and Y. Ikuhara, Nat. Commun., 2014, 5, 5740 CrossRef CAS PubMed.
- P. B. Hirsch, A. Howie, R. B. Nicholson, D. W. Pashley and M. J. Whelan, Electron Microscopy of Thin Crystals, Butterworths, Great Britain, 1965 Search PubMed.
- C. J. Bosson, M. T. Birch, D. P. Halliday, K. S. Knight, A. S. Gibbs and P. D. Hatton, J. Mater. Chem. A, 2017, 5, 16672 CAS.
- D. Hull and D. J. Bacon, Introduction to Dislocations, Butterworth-Heinemann, Oxford, 2001 Search PubMed.
- J. Ge, J. Jiang, P. Yang, C. Peng, Z. Huang, S. Zuo, L. Yang and J. Chu, Sol. Energy Mater. Sol. Cells, 2014, 125, 20 CrossRef CAS.
- J. T. Wätjen, J. Engman, M. Edoff and C. P. Björkman, Appl. Phys. Lett., 2012, 100, 173510 CrossRef.
- C. Persson and A. Zunger, Phys. Rev. Lett., 2003, 91, 266401 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |