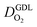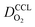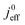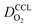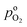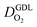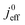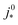Tipping water balance and the Pt loading effect in polymer electrolyte fuel cells: a model-based analysis†
Tasleem
Muzaffar
 a,
Thomas
Kadyk
a,
Thomas
Kadyk
 b and
Michael
Eikerling
*a
b and
Michael
Eikerling
*a
aDepartment of Chemistry, Simon Fraser University, Burnaby, British Columbia, Canada. E-mail: meikerl@sfu.ca
bInstitute of Energy and Process Systems Engineering, Technische Universität Braunschweig, Braunschweig, Germany
First published on 24th March 2018
Abstract
The commercial deployment of polymer electrolyte fuel cells (PEFCs) hinges on breakthroughs in design and integration of highly performing and durable catalyst layers with markedly reduced platinum loading. Experimental studies have shown an unexpected increase in voltage losses upon a drastic reduction in the Pt content. In an effort to unravel this peculiar behavior, an existing physical model of catalyst layers in PEFCs is employed to analyze a wide range of fuel cell performance data from the literature. The analysis reveals correlated trends in key fuel cell parameters. These findings can be explained in view of the tipping water balance that affects the interplay of transport and reaction in catalyst layer and gas diffusion media. This represents a compelling alternative to the widespread ionomer-film hypothesis that links observed power losses at low Pt loading to a mesoscopic oxygen transport resistance. The presented theoretical analysis warrants the definition of a correlation exponent that should find use in assessing the merit of different approaches in catalyst layer fabrication.
Following the footprints in numerous reports of the Department of Energy1 and in peer-reviewed articles,2–4 the highly original and once coveted design of membrane-electrode assemblies (MEAs) developed by the company 3M should have levered a breakthrough in polymer electrolyte fuel cell (PEFC) technology. 3M MEAs with nanostructured thin film electrodes showed impressive gains in performance and durability combined with excellent prospects for production scale-up.5 What's more, the platinum loading at the cathode catalyst layer (CCL) that performs the notoriously sluggish oxygen reduction reaction (ORR) undercut the loading of conventional layers by about a factor 10.2 The 3M approach to MEA fabrication has been the most impressive demonstration to date that a drastic reduction of Pt loading, mpt, is achievable without sacrificing performance, as these MEAs indeed exhibited the highest power performance reported to date.2 However liquid water removal clearly transpired as the Achilles heel of catalyst layer design.6 Moreover, the 3M design demonstrated an important principle of catalyst layer operation: liquid water is sufficient as the medium for proton transport in the catalyst layer.7–9
In the conventional cell layout, the Pt-based catalyst contributes about 40–50% to the cost of a PEFC stack manufactured at high volume.1 Moreover, the ORR at the cathode incurs about 30–40% of the voltage losses during operation, as can be gleaned from a polarization curve analysis.10 The pioneering 3M technology triggered an avalanche of activities in catalyst layer research11–16 with a common mission: bringing down the demand of Pt to a level that renders its cost and limited abundance insignificant, while improving, or at least preserving, power performance and durability.
At this point, none of these strategies in materials modification and catalyst layer fabrication constitutes a resounding success. Promising results in laboratory tests were not reproduced in tests under typical fuel cell operating conditions or the improvements failed to transpire at the level of fuel cell stack operation – where it matters. A presumed culprit for the unexplained, additional losses was found: a thin ionomer film covering the Pt particles, causing a strong local transport resistance.17–24 This unverified hypothesis spread and solidified rapidly in the community with large research efforts dedicated to follow-up work.
However, this article exposes an alternative and more general explanation of the mpt effect: a tipping water balance in catalyst layers with ultra-low mpt, i.e., mpt < 0.1 mg cm−2. This hypothesis emerges from the presented modeling-based analysis that assesses the impact of a reduction in mpt on electrochemical performance for a wide range of approaches in CCL design and fabrication. The analysis unravels the concerted impact of the core set of parameters that control catalyst layer operation. The revealed trends in parameter variation are the key to a much-needed mechanistic interpretation of the mpt effect.
Strategies to achieve a Pt loading reduction
A drastic reduction of mpt can be achieved via two principal modification strategies:(1) Reduction of catalyst layer thickness, LCCL, at constant composition, i.e., fixed volume fractions of catalyst, support, ionomer, and pores;25–36
(2) Dilution of catalyst at constant LCCL, i.e., reduction of the catalyst volume fraction.31–33
In practice, a significant mpt reduction is usually achieved by a blend of these strategies.
Evidently, LCCL should be considered as a key parameter to monitor in this context. Usually, drastic changes in mpt will come along with other structural modifications of the CCL, as is obvious for thin-film substrates like the 3M nanowhisker morphology2–4 or nanoporous metal structures.37–39
Thick and thin electrodes: basic concepts
From a modeling perspective, it is instructive to categorize catalyst layers into two classes: gas diffusion electrodes (GDEs) and flooded porous electrodes (FPEs). GDEs consist of three interpenetrating and percolating phases (solid, electrolyte and gas phase). GDE-type CCLs are impregnated with ionomer and they have typical thickness of 5–10 μm. A GDE-type CCL will operate well only if reactant supply via gas diffusion is warranted; it will fail if liquid water blocks percolating pathways of gaseous diffusion.FPE on the other hand do not contain a separate percolating gas-phase and the reactant gas dissolves in water-filled pores at the interface with the gas diffusion layer (GDL). An FPE-type CCL is usually ionomer-free and has much reduced thickness, LCCL ∼50–300 nm. This small thickness decisively lowers the requirement on oxygen diffusivity, rendering oxygen transport through the liquid water phase sufficient. A CCL of this type will exhibit its best electrochemical performance if it is fully flooded with liquid water, thus utilizing all of the available catalyst surface area. Ionomer impregnation of FPEs is not needed, as the proton demand of the reaction can be satisfied by proton transport in water-filled pores.7,8,40 The distinction of GDEs and FPEs alludes to the important role of water as the pore filling liquid and it underlines the importance of the liquid saturation, Sr, as a crucial composition variable to determine effective properties of the layer. Sr needed for optimal performance of a catalyst layer is intimately tied to its thickness. Here, we will briefly discuss, in a qualitative fashion, the impact of Sr on catalyst layer performance, following more detailed treatments of water phenomena in PEFC electrodes in ref. 41–46. A detailed quantitative treatment of the impact of Sr is beyond the scope of this article.
An FPE-type CCL, in which Sr = 1,46 must be ultrathin for the liquid water phase to warrant a sufficiently high diffusion flux of dissolved oxygen. Moreover, efficient operation of an FPE-based MEA demands an adjacent gas diffusion medium with high vaporization capability. If Sr approaches 1 in a GDE-type CCL, oxygen flux will be severely impaired.41,43,44 Therefore, the porous electrode layers will be more prone to flooding with negative consequences for oxygen supply and overall ORR activity. The catalyst layers analyzed in this article are all of GDE-type.
A vital concept to rationalize the aforementioned interdependence of Sr and LCCL is the reaction penetration depth due to oxygen diffusion, defined as42
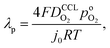 | (1) |
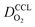 the effective oxygen diffusion coefficient of the CCL,
the effective oxygen diffusion coefficient of the CCL, 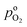 the oxygen partial pressure at the interface between CCL and GDL, and j0 the operating current density. A GDE-type CCL at T = 350 K, j0 = 1 A cm−2,
the oxygen partial pressure at the interface between CCL and GDL, and j0 the operating current density. A GDE-type CCL at T = 350 K, j0 = 1 A cm−2, 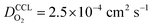 and
and 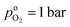 has λp ∼ 33 μm, whereas an FPE-type CL under the same conditions but at
has λp ∼ 33 μm, whereas an FPE-type CL under the same conditions but at 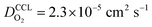 , and
, and 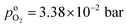 , exhibits λp ∼ 100 nm. The value of
, exhibits λp ∼ 100 nm. The value of 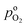 used for FPE-type CCL accounts for dissolution of O2 in water with a Henry law constant, HO2 = 1.3 × 10−3 L−1 bar−1 mol. When λp ≪ LCCL, the reaction is limited to a portion of the CCL near the GDL interface and the rest of the CCL is not utilized. For λp ≥ LCCL, the reaction rate is distributed uniformly throughout the CCL. Optimal Pt utilization will be achieved with λp ≥ LCCL.
used for FPE-type CCL accounts for dissolution of O2 in water with a Henry law constant, HO2 = 1.3 × 10−3 L−1 bar−1 mol. When λp ≪ LCCL, the reaction is limited to a portion of the CCL near the GDL interface and the rest of the CCL is not utilized. For λp ≥ LCCL, the reaction rate is distributed uniformly throughout the CCL. Optimal Pt utilization will be achieved with λp ≥ LCCL.
What is the impact of the type and thickness of the CCL on cell operation?
At given j0, a thick GDE has a low volumetric current density and a high vaporization capability owed to a highly developed liquid–gas interface in the partially flooded pore space.43,44 Upon reduction of LCCL, the volumetric current density grows (LCCL)−1. At the same time, the vaporization capability of the layer decreases proportionally to LCCL at first. This results from the decrease of the liquid–vapor interfacial area under constant Sr, as indicated in Fig. 1(a). Upon further reduction of LCCL, as Sr increases, the vaporization capability decreases over-proportionally until it reaches zero under fully flooded conditions.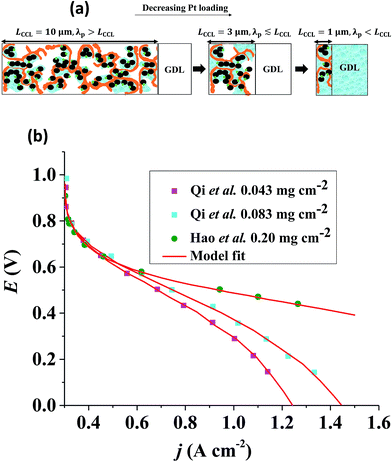 | ||
Fig. 1 (a) Schematic of CCL|GDL configuration in different regimes of CCL thickness and water accumulation. The picture on the left corresponds to ideal operation of a relatively thick CCL (LCCL = 10 μm). As the vaporization capability wanes with the LCCL reduction, more liquid water will accumulate first in the CCL (a-2) and then in the adjacent diffusion medium (a-3). (b) Fits of fuel cell polarization curves extracted from ref. 25–36 with the physical models developed in ref. 10, 41–45 and 47–49 and implemented as an executable routine in ref. 48. Only a subset of experimental studies that were analyzed are shown; fits for all sets of experimental data analyzed are provided as ESI.† These fits were used to extract the parameters that change in response to the variation in mptviz. 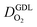 , , 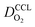 , , 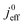 , and σel. , and σel. | ||
To clarify the last point, let us consider a ten-fold reduction of LCCL; then the ratio of the rate of water production to the rate of vaporization will increase by at least one order of magnitude. Inevitably, more water has to leave the catalyst layer in liquid form aggravating problems with flooding in the GDL as seen in Fig. 1(a). In order to understand the impact of CCL modification and especially of a reduction in LCCL on PEFC operation, it is thus crucial to closely monitor changes in water distribution, not only in the CCL, but in the whole cell, especially the GDL and flow channels on the cathode side.
Modeling capabilities
The genealogy of physical models of CCL operation traces back to the beginnings of porous electrode theory, as reviewed in ref. 10 Over time, CCL models have been developed and refined to incorporate structure vs. property relations based on percolation theory,41,42,47 treat water phenomena,43,44 and account for the self-consistent coupling of transport phenomena and reaction conditions at different scales.45 A range of analytical solutions of CCL models have been obtained10,42,47–49 and model-based tools to analyze fuel cell polarization curves have been demonstrated.48If sufficient information on thickness, composition, and pore space morphology is available, CCL models are capable of closely reproducing fuel cell polarization curves, as demonstrated in ref. 10, 45 and 48. Based on high-quality fits of the physical model to experimental polarization curves, the basic parameters of the CCL including proton conductivity, oxygen diffusivity and exchange current density were determined in those works. Further model-based analyses could then be applied to generate a voltage loss breakdown, calculate the effectiveness factor of Pt utilization, and plot the spatial map of catalyst activity in the layer. However, in spite of analytical capabilities of existing models they have never been employed to perform comprehensive analyses of large experimental data sets. The exploration of the mpt effect for a wide range of experimental studies is an excellent case to demonstrate model capabilities. To this end, we have evaluated data sets from recent literature.25–36
We have athe dopted the physical model developed through various generations in ref. 10, 41–45 and 47–49 and implemented by Kulikovsky in ref. 48 to analyze performance data of PEFCs with varying mpt. We have considered four parameters as variable and used them for fitting of experimental data. They are the exchange current density, 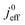 , proton conductivity in the CCL, σel, as well as the oxygen diffusion coefficient in the CCL,
, proton conductivity in the CCL, σel, as well as the oxygen diffusion coefficient in the CCL, 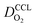 , and the GDL,
, and the GDL, 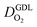 .
.
Comparison with experiment
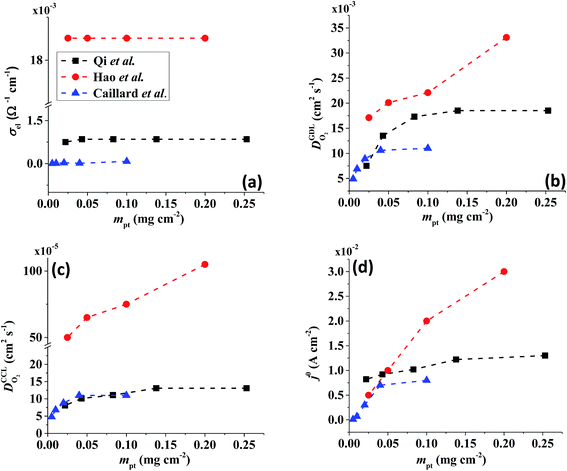
All layers that were analyzed are GDE type electrodes. Model fits of experimental polarization curves are shown in Fig. 1(b) for a subset of experimental studies. The complete set of fits and parameters for all experimental studies25–36 are provided in the ESI.†Fig. 2 depicts the variation of physical properties extracted from the fitting. The following trends can be discerned:(1) The proton conductivity, σel, remains relatively constant with the reduction in mpt. Since water is the medium for proton conduction, increased water accumulation is not expected to exert a detrimental effect on proton conductivity.
(2) In studies with strong correlation between mpt and LCCL, the oxygen diffusion coefficient in the GDL, 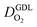 , exhibits a marked decrease when mpt is reduced to below 0.1 mg cm−2.25,26,30,32,33,35
, exhibits a marked decrease when mpt is reduced to below 0.1 mg cm−2.25,26,30,32,33,35
In this scenario, more liquid water flows out of the CCL because of its diminished vaporization capability. As a consequence, more liquid water will accumulate in the GDL resulting in its flooding, hence blocking pathways for the gaseous supply of oxygen. The large scatter in values of 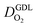 for different studies can be explained by different MEA fabrication methods and different types of GDL used; details for each system can be found in ESI.† We also applied the model-based analysis to MEAs fabricated by the direct membrane deposition method of Klingele et al.50 and Breitwieser et al.51 In this case,
for different studies can be explained by different MEA fabrication methods and different types of GDL used; details for each system can be found in ESI.† We also applied the model-based analysis to MEAs fabricated by the direct membrane deposition method of Klingele et al.50 and Breitwieser et al.51 In this case, 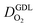 remains constant with the reduction in mpt as can be seen in ESI.† This can be explained by enhanced water removal from the CCL via transport of water towards the anode side that is enabled by the extremely thin and highly permeable PEM that they employed.
remains constant with the reduction in mpt as can be seen in ESI.† This can be explained by enhanced water removal from the CCL via transport of water towards the anode side that is enabled by the extremely thin and highly permeable PEM that they employed.
(3) Similarly, 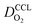 exhibits a decrease with decreasing mpt in studies with strong correlation between mpt and LCCL. This effect can be explained with the diminished vaporization capability and the correspondingly increased Sr in the CCL that inhibits gaseous transport of oxygen. Based on eqn (1), flooding of the CCL results in λp ≪ LCCL. This situation is described well with modeling approaches presented in ref. 10, 42 and 47 that predict a doubling of the Tafel-slope in this thickness regime.
exhibits a decrease with decreasing mpt in studies with strong correlation between mpt and LCCL. This effect can be explained with the diminished vaporization capability and the correspondingly increased Sr in the CCL that inhibits gaseous transport of oxygen. Based on eqn (1), flooding of the CCL results in λp ≪ LCCL. This situation is described well with modeling approaches presented in ref. 10, 42 and 47 that predict a doubling of the Tafel-slope in this thickness regime.
(4) Interestingly, the trend observed in the effective exchange current density, 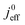 follows the trend in
follows the trend in 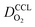 . It has been long-observed albeit remained unexplained that kinetic voltage losses upon reduction of LCCL increase by an amount that exceeds the extent expected based on the pure geometric effect of the reduction in electrochemically active surface area. Where do the additional “kinetic” losses upon LCCL reduction come from? To resolve this issue, we must consider the interplay of electrochemical kinetics and oxygen diffusion in the CCL.
. It has been long-observed albeit remained unexplained that kinetic voltage losses upon reduction of LCCL increase by an amount that exceeds the extent expected based on the pure geometric effect of the reduction in electrochemically active surface area. Where do the additional “kinetic” losses upon LCCL reduction come from? To resolve this issue, we must consider the interplay of electrochemical kinetics and oxygen diffusion in the CCL.
The generic exchange current density of a CCL is given by10
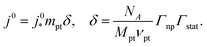 | (2) |
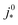 is the intrinsic exchange current density, NA the Avogadro constant, Mpt the atomic mass of Pt, Γnp the surface-to-volume atom ratio of Pt nanoparticles, Γstat the statistical utilization of Pt particles, and νpt the number of Pt atoms per units surface area of the catalyst.
is the intrinsic exchange current density, NA the Avogadro constant, Mpt the atomic mass of Pt, Γnp the surface-to-volume atom ratio of Pt nanoparticles, Γstat the statistical utilization of Pt particles, and νpt the number of Pt atoms per units surface area of the catalyst.
Severe starvation of the oxygen flow on its path through the catalyst layer brings about a doubling of the Tafel-slope in the polarization curve, as explained in ref. 10 and 47. Furthermore, the doubling of the Tafel-slope entails a modification of the effective exchange current density that results in10
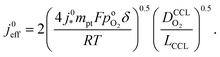 | (3) |
Moreover, a reduction of mpt increases the propensity of the CCL for flooding. The corresponding decrease of 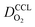 , discussed in the previous paragraph, will lead to a situation with λp ≪ LCCL. This effect introduces another factor
, discussed in the previous paragraph, will lead to a situation with λp ≪ LCCL. This effect introduces another factor 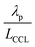 in the effective exchange current density,
in the effective exchange current density,
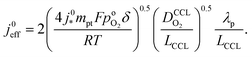 | (4) |
Using λp as defined in eqn (1) and re-arranging results in
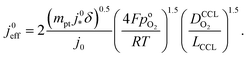 | (5) |
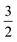 . For convenience, we introduce a correlation exponent, γ, with an expectation range
. For convenience, we introduce a correlation exponent, γ, with an expectation range 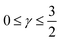 , to write the foregoing equation in generalized form,
, to write the foregoing equation in generalized form,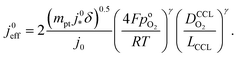 | (6) |
Based on the preceding analysis, the value of γ allows for three cases to be distinguished:
(1) CCL operation in the purely kinetic regime (excellent oxygen transport, λp > LCCL) results in γ ≃ 0.
(2) CCL operation in the intermediate regime, with nonlinear interplay of reaction and diffusion indicated by double Tafel slope behavior (λp ≲ LCCL) caused by the first effect being present, results in  .
.
(3) CCL operation in the oxygen starvation regime with λp ≪ LCCL, where the total effect will be a superposition of both (or mathematically a multiplicative effect), results in 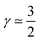 .
.
By assessing the value of γ, we can see where we are on the scale from 0 to 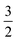 and determine which effects of oxygen depletion and starvation occur in a particular type of electrode. A prerequisite for the use of eqn (6) is that the comparison of different electrodes using this relation is done at the same operating current density j0.
and determine which effects of oxygen depletion and starvation occur in a particular type of electrode. A prerequisite for the use of eqn (6) is that the comparison of different electrodes using this relation is done at the same operating current density j0.
The first case with γ ≃ 0 represents excellent catalyst utilization, whereas the second case with 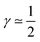 corresponds to a CCL that exhibits high power performance.47 The third case with
corresponds to a CCL that exhibits high power performance.47 The third case with 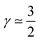 , obviously, signifies poor catalyst effectiveness as well as poor performance.
, obviously, signifies poor catalyst effectiveness as well as poor performance.
The correlation described by eqn (6) is tested in Fig. 3. The slopes determined from the log–log plot of 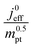 vs.
vs.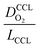 corresponds to the values of γ shown at the plots. However, in the experimental studies the values of LCCL are not known. Therefore, we proceeded in two steps. In the first step, the correlations were tested for two limiting scenarios, assuming either
corresponds to the values of γ shown at the plots. However, in the experimental studies the values of LCCL are not known. Therefore, we proceeded in two steps. In the first step, the correlations were tested for two limiting scenarios, assuming either
(1) Constant composition, i.e., assuming mpt ∝ LCCL, using mpt = 0.2 mg cm−2 and LCCL = 10 μm as reference, or
(2) Pt dilution at constant LCCL = 10 μm.
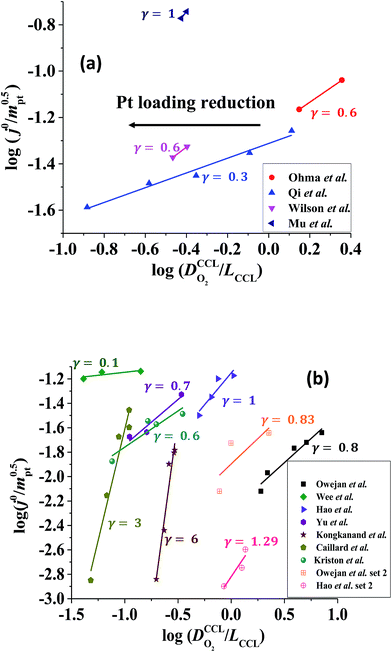 | ||
Fig. 3 log–log plot of 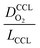 vs. vs.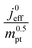 for experimental studies with (a) LCCL ∝ mpt, where LCCL = 10 μm was used as a reference at mpt = 0.2 mg cm−2 and (b) fixed LCCL = 10 μm. for experimental studies with (a) LCCL ∝ mpt, where LCCL = 10 μm was used as a reference at mpt = 0.2 mg cm−2 and (b) fixed LCCL = 10 μm. | ||
To evaluate the values of γ for the studies analysed in this work, knowledge of relevant scenario in terms of thickness reduction and dilution effects would be required. However, for most studies, we did not know a priori which scenario would be valid. So an approach by exclusion was employed. We tested each data set for both scenarios. One of the two scenarios resulted in a positive-defined and thus meaningful value of γ, whereas the other scenario yielded an unphysical (negative) value of γ. Only the solution with physically meaningful γ value (positive) is included in Fig. 3.
The log–log plot in Fig. 3 reveals the concerted impact of ECSA loss and reduction in λp upon mpt reduction. The phenomenological exponent γ represents the correlation between transport properties and effective exchange current density. Small γ implies weak correlation, whereas large γ implies that a reduction in mpt incurs apparent activity losses that are caused by reduced oxygen transport properties under electrode flooding, embodied in λp. Based on the presented analyses, a benign catalyst layer design would be achieved with 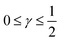 , as this implies that the mpt reduction could be achieved without prompting dramatic changes to the transport properties of the layer. The correlation exponent, γ can thus be used to assess the design of catalyst layers with ultra-low Pt loading. Systematic experimental studies, in which the impact of mpt on LCCL and composition is precisely controlled and monitored, and model based analyses, as presented above, should be highly insightful in this regard.
, as this implies that the mpt reduction could be achieved without prompting dramatic changes to the transport properties of the layer. The correlation exponent, γ can thus be used to assess the design of catalyst layers with ultra-low Pt loading. Systematic experimental studies, in which the impact of mpt on LCCL and composition is precisely controlled and monitored, and model based analyses, as presented above, should be highly insightful in this regard.
For most of the experimental studies in Fig. 3, γ lies in the predicted range from 0.5–1.5. The study by Wee et al.29 exhibits a lower value of γ. The studies of Kongkanand et al.34 and Caillard et al.35,36 show significantly larger values of γ that lie out of the expected range. This observation could be indicative of severe structural changes associated with mpt reduction, e.g., catalyst compaction due to particle aggregation, which may affect the value of 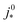 in eqn (2), or encapsulation of Pt particles by carbon or by a dense layer of ionomer. More detailed structural data will be needed to further scrutinize this aspect.
in eqn (2), or encapsulation of Pt particles by carbon or by a dense layer of ionomer. More detailed structural data will be needed to further scrutinize this aspect.
The present model-based analysis yields a well-founded hypothesis: reduction in mpt strongly affects water fluxes and distribution in GDE-type CCL and adjacent media. The shifted water balance, which is expected as a logical consequence of the shifting ratio of volumetric rate of water production to rate of vaporization, affects effective properties and local reaction conditions in a way that leads to trends seen in Fig. 3. Especially, the GDL water balance will be strongly impaired by flooding for low mpt systems.
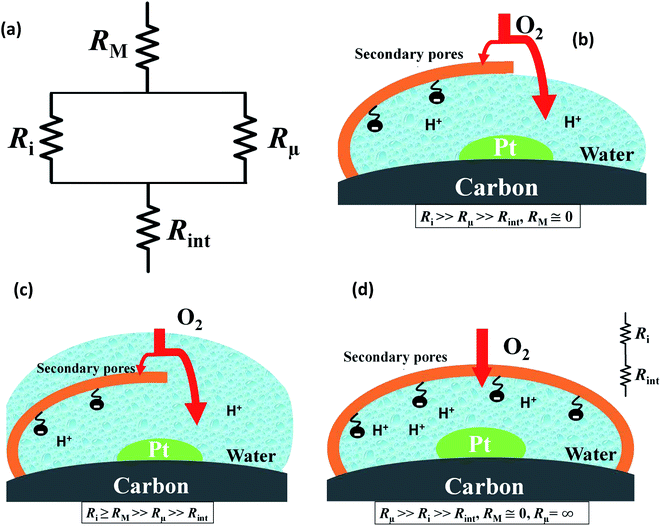
Fig. 4 presents a graphical illustration of this hypothesis, comparing various states of flooding at the mesoscale. Fig. 4(a) depicts a resistor network analogue for the oxygen fluxes towards the catalyst. In order to reach the Pt surface, oxygen molecules have to pass a resistance in the macropore space, RM. Then, in order to enter the micropore space surrounding the catalyst particle, oxygen molecules have to pass the resistance of the ionomer film, Ri, or bypass this film through the water-filled primary pore space via Rμ. Finally, oxygen molecules diffuse through a resistance posed by the interfacial water layer surrounding the Pt nanoparticle, Rint. Even though slightly different network configurations might be drawn, the essential point to maintain is the parallel configuration of Ri and Rμ which allows oxygen molecules to bypass the ionomer film in cases with Ri ≫ Rμ. Fig. 4(b) represents the expected typical configuration encountered in a well-functioning GDE with gas diffusion in secondary pores. Fig. 4(c) illustrates the change that occurs upon flooding of a GDE as a consequence of a mpt reduction.
Finally, Fig. 4(d) depicts an unlikely special case of scenarios in Fig. 4(b) and (c). It misrepresents the significance of the ionomer-film resistance Ri. The idea behind Fig. 4(d) is that a strong local transport resistance could be caused by oxygen diffusion through a thin ionomer film, Ri that encapsulates Pt completely. In comparison to Fig. 4(b) and (c), it represents the most restrictive and unlikely scenario of local transport resistances encountered by oxygen molecules on their path towards the Pt surface. This idea surfaced in ref. 17. Thereafter it triggered an avalanche of follow-up work and adoption.18–24 Groups from Toyota, and GM have reported similar speculative ideas.19–21,23,24,34 Ultimately, the ionomer-film hypothesis underlying this case is based on two critical assumptions: (1) the ionomer film poses a severe resistance to oxygen diffusion, meaning that Ri ≫ RM, Rint; (2) the ionomer film completely encapsulates the catalyst, thereby blocking any alternative diffusion pathway for oxygen, implying Rμ → ∞. As for the first assumption, the thickness of the ionomer film is still under debate;22 however, for realistic film thicknesses, it is highly unlikely to generate a sufficiently inhibiting effect on oxygen diffusion.19–21,23,24,34 The second assumption corresponds to an idealized structure of the ionomer film that is neither observed in experiment nor in MD studies of Malek et al.52,53 In fact, these MD simulations and other works54–56 suggest that the skin-type ionomer film only partially covers the microporous agglomerates of Pt/C leaving a pathway for O2 with finite Rμ. Moreover, a perfectly encapsulating, dense ionomer film would not only shield oxygen supply but also inhibit proton transport. We thus believe that the ionomer-film hypothesis is misconstrued and unnecessarily reduces the more general scenario represented by Fig. 4(b) and (c).
As discussed in ref. 10, to render the catalyst active, it must be surrounded by liquid water, which functions as a proton shuttle. The liquid phase must be continuously connected to guarantee a sufficient rate of proton supply. The water phase that sustains the continuous proton flux functions equally well as a medium for the transport of oxygen via diffusion as demonstrated by 3M in their thin-film CCL design. Oxygen concentration in water will remain sufficiently high if the length of the diffusion path is ≲200 nm. Asphyxiation will occur in CCL with thicknesses above this range and pores flooded. Any alternative explanation for the poor performance of CCL with low mpt must refute or disprove at least one of the basic statements in this paragraph.
The model-based analysis of polarization data thus prompts a logical alternate explanation to the widespread ionomer resistance hypothesis. It is not exclusive and certainly other hypotheses must be scrutinized as well. It should be left to the reader to decide if the hypothesis presented in this work is worth pursuing or other approached should be tried.
Follow-up work to understand the mechanistic principles that underlie our observations and interpretation demand a model that connects the reduction in mpt with associated changes in composition, structure, water fluxes, effective properties, and local reaction conditions.43,44 The work on a such a model is underway in our group.
Summary
This article proposes a conducive strategy for the analysis and interpretation of performance data of CCL with low Pt loading. Physical models were employed to analyze and explain the drastic decline in performance of cathode catalyst layers with small amounts of Pt loaded into them. The study has revealed vital trends and correlations in crucial parameters. Oxygen diffusion coefficients in cathode catalyst layer and gas diffusion layer as well as the exchange current density exhibit strong declines with reduction in Pt loading. These trends can be explained with the loss of vaporization capability in the cathode catalyst layer that leads to a higher liquid saturation in the active layer and more liquid water entering the diffusion medium. Both cathode catalyst layer and gas diffusion layer will thus be flooded, which explains the increase in voltage losses as consequences of inhibited oxygen diffusion and diminished effective activity. These results warrant a paradigm-shift in explaining the voltage losses in ultra-low Pt loading electrodes. The presented hypothesis should initiate a large-scale discussion in the fuel cell community and shape future research directions in the field.Ideally, for a certain approach pursued in CCL design and fabrication, a series of CCL with systematically mass-reduced loading of Pt should be made and characterized. Polarization curves obtained should be treated with state-of-the-art performance models to determine the physical parameters of CCL and GDL. The correlation between 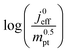 and
and 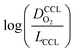 , should then be analyzed to extract the value of the correlation exponent γ. As a general rule, a small γ implies a CCL structure, in which the Pt loading reduction, is achieved without causing massive transport losses. With this logical strategy outlined, the article could help guide the community towards a new generation of systematically planned and analyzed experiments.
, should then be analyzed to extract the value of the correlation exponent γ. As a general rule, a small γ implies a CCL structure, in which the Pt loading reduction, is achieved without causing massive transport losses. With this logical strategy outlined, the article could help guide the community towards a new generation of systematically planned and analyzed experiments.
Author contributions
T. M. and M. E. conceived the research. T. M. applied the model to the experimental data and extracted the physical properties. T. M., T. K., and M. E. analyzed and interpreted results, and wrote and reviewed the manuscript. M. E. supervised the whole project.Nomenclature
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors gratefully acknowledge financial assistance by an Automotive Partnership Canada grant, file number APCPJ417858, that supports the Catalysis Research for Polymer Electrolyte Fuel Cells (CaRPE-FC) network. Simon Fraser University assisted in meeting the publication costs of this article.References
- DOE, Annual Merit Review Fuel Cell Program, Department of energy usa, hydrogen and fuel cell programs technical report, 2016 Search PubMed.
- M. Debe, Nature, 2012, 486, 43–51 CrossRef CAS PubMed.
- M. Debe, R. Atanasoski and A. Steinbach, ECS Trans., 2011, 41, 937–954 Search PubMed.
- M. Debe, J. Electrochem. Soc., 2013, 160, 522–534 CrossRef.
- M. Debe, A. Schmoeckel, G. Vernstrom and R. Atanasoski, J. Power Sources, 2006, 161, 1002–1011 CrossRef CAS.
- M. Debe and A. Steinbach, ECS Trans., 2007, 11, 659–673 CAS.
- J. Huang, A. Malek, J. Zhang and M. Eikerling, J. Phys. Chem. C, 2016, 120, 13587–13595 CAS.
- K. Chan and M. Eikerling, J. Electrochem. Soc., 2011, 1, B18–B28 CrossRef.
- T. Muzaffar, T. Kadyk and M. Eikerling, Electrochim. Acta, 2017, 245, 1048–1058 CrossRef CAS.
- M. Eikerling and A. Kulikovsky, Polymer Electrolyte Fuel Cells: Physical Principles of Materials Operation, CRC Press Taylor & Francis Group, 2014 Search PubMed.
- A. Orfanidi, P. Madkikar, H. El-Sayed, G. Harzer, T. Kratky and H. Gasteiger, J. Electrochem. Soc., 2017, 164, F418–F426 CrossRef CAS.
- H. Su, T. Jao, O. Barron, B. Pollet and S. Pasupathi, J. Power Sources, 2014, 267, 155–159 CrossRef CAS.
- S. Shukla, K. Domican, K. Karan, S. Bhattacharjee and M. Secanell, Electrochim. Acta, 2015, 156, 289–300 CrossRef CAS.
- T. Huang, H. Shen, T. Jao, F. Weng and A. Su, Int. J. Hydrogen Energy, 2012, 37, 13872–13879 CrossRef CAS.
- S. Jiang, B. Yi, L. Cao, W. Song, Q. Zhao, H. Yu and Z. Shao, J. Power Sources, 2016, 329, 347–354 CrossRef CAS.
- T. Shu, D. Dang, D. Xu, R. Chen, S. J. Liao, C. Hsieh, A. Su, H. Song and L. Du, Electrochim. Acta, 2015, 177, 168–173 CrossRef CAS.
- K. Sakai, K. Sato, T. Mashio, A. Ohma, K. Tamaguchi and K. Shinohara, ECS Trans., 2009, 25, 1193–1201 CAS.
- Y. Ono, A. Ohma, K. Shinohara and K. Fushinobu, J. Electrochem. Soc., 2013, 160, F779–F787 CrossRef CAS.
- K. Kudo and Y. Morimoto, ECS Trans., 2012, 50, 1487–1494 CrossRef.
- K. Kudo, R. Jinnouchi and Y. Morimoto, Electrochim. Acta, 2016, 209, 682–690 CrossRef CAS.
- R. Jinnouchi, K. Kudo, N. Kitano and Y. Morimoto, Electrochim. Acta, 2016, 188, 767–776 CrossRef CAS.
- H. Liu, W. Epting and S. Lister, Langmuir, 2015, 31, 9853–9858 CrossRef CAS PubMed.
- A. Kongkanand and M. Mathias, J. Phys. Chem. Lett., 2016, 7, 1127–1137 CrossRef CAS PubMed.
- A. Weber and A. Kusoglu, J. Mater. Chem. A, 2014, 2, 17207–17211 CAS.
- A. Ohma, T. Mashio, K. Sato, H. Iden, Y. Ono, K. Sakai, K. Akizuki, S. Takaichi and K. Shinohara, Electrochim. Acta, 2011, 56, 10832–10841 CrossRef CAS.
- M. Wilson, J. Electrochem. Soc., 1992, 139, L28–L30 CrossRef CAS.
- Z. Qi and A. Kaufman, J. Power Sources, 2003, 113, 37–43 CrossRef CAS.
- S. Mu and M. Tian, Electrochim. Acta, 2012, 60, 437–442 CrossRef CAS.
- J.-H. Wee, K.-Y. Lee and S. Kim, J. Power Sources, 2007, 165, 667–677 CrossRef CAS.
- H. Yu, J. Roller, W. Mustain and R. Maric, J. Power Sources, 2015, 283, 84–94 CrossRef CAS.
- L. Hao, K. Moriyama, W. Gu and C.-Y. Wang, J. Electrochem. Soc., 2015, 162, F854–F867 CrossRef CAS.
- A. Kriston, T. Xie and B. Popov, Electrochim. Acta, 2014, 121, 116–127 CrossRef CAS.
- J. Owejan, J. Owejan and W. Gu, J. Electrochem. Soc., 2013, 160, F824–F833 CrossRef CAS.
- A. Kongkanand, N. Subramanian, Y. Yu, Z. Liu, H. Igarashi and D. Muller, ACS Catal., 2016, 6, 1578–1583 CrossRef CAS.
- A. Caillard, C. Charles, R. Boswell and P. Brault, J. Phys. D Appl. Phys., 2008, 41, 185307–185316 CrossRef.
- A. Caillard, C. Charles, D. Ramdutt, R. Boswell and P. Brault, J. Phys. D Appl. Phys., 2009, 42, 045207–045215 CrossRef.
- J. Erlebacher and J. Snyder, ECS Trans., 2009, 25, 603–612 CAS.
- J. Erlebacher, M. Aziz, A. Karma, N. Dimitrov and S. Karl, Nature, 2001, 410, 5–8 CrossRef PubMed.
- A. Garsuch, D. Stevens, R. Sanderson, S. Wang, R. Atanasoski, S. Hendricks, M. Debe and J. Dahn, J. Electrochem. Soc., 2010, 157, B187–B194 CrossRef CAS.
- J. Huang, J. Zhang and M. Eikerling, Faraday Discuss., 2016, 193, 427–446 RSC.
- M. Eikerling, A. Iosselevich and A. Kornyshev, Fuel Cells, 2004, 4, 131–140 CrossRef CAS.
- M. Eikerling, A. Kornyshev and A. Kulikovsky, Encyclopeida of Electrochemistry, VCH-Wiley, 2007, pp. 447–453, Ch. 8.2 Search PubMed.
- M. Eikerling, J. Electrochem. Soc., 2006, 153, E58–E70 CrossRef CAS.
- J. Liu and M. Eikerling, Electrochim. Acta, 2008, 53, 4435–4446 CrossRef CAS.
- E. Sadeghi, A. Putz and M. Eikerling, J. Electrochem. Soc., 2013, 160, F1159–F1169 CrossRef CAS.
- K. Chan and M. Eikerling, Phys. Chem. Chem. Phys., 2014, 16, 2106–2117 RSC.
- M. Eikerling and A. Kornyshev, J. Electroanal. Chem., 1998, 453, 89–106 CrossRef CAS.
- A. Kulikovsky, J. Electrochem. Soc., 2013, 161, F263–F270 CrossRef.
- A. Kulikovsky, J. Electrochem. Soc., 2014, 161, E3171–E3179 CrossRef CAS.
- M. Klingele, M. Breitwieser, R. Zengerle and S. Thiele, J. Mater. Chem. A, 2015, 3, 11239–11245 CAS.
- M. Breitwieser, M. Klingele, S. Vierrath, C. Klose, R. Zengerle and S. Thiele, IMTEK Present, CaRPE, 2014 Search PubMed.
- K. Malek, M. Eikerling, Q. Wang, T. Navessin and Z. Liu, J. Phys. Chem. C, 2007, 111, 13627–13634 CAS.
- K. Malek, T. Mashio and M. Eikerling, Electrocatalysis, 2011, 2, 141–157 CrossRef CAS.
- S. Holdcroft, J. Mater. Chem., 2014, 26, 381–393 CrossRef CAS.
- T. Soboleva, K. Malek, Z. Xie, T. Navessin and S. Holdcroft, ACS Appl. Mater. Interfaces, 2011, 3, 1827–1837 CAS.
- M. Uchida, Y. Fukuoka, Y. Sugawara, N. Eda and A. Ohta, J. Electrochem. Soc., 1996, 143, 2245–2252 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8se00026c |
| This journal is © The Royal Society of Chemistry 2018 |