Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Manganese pyrosilicates as novel positive electrode materials for Na-ion batteries†
Viktor
Renman
 a,
Mario
Valvo
a,
Cheuk-Wai
Tai
a,
Mario
Valvo
a,
Cheuk-Wai
Tai
 b,
Cesar Pay
Gómez
a,
Kristina
Edström
a and
Anti
Liivat
b,
Cesar Pay
Gómez
a,
Kristina
Edström
a and
Anti
Liivat
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Ångström Advanced Battery Centre, Uppsala University, Box 538, SE-751 21 Uppsala, Sweden. E-mail: anti.liivat@kemi.uu.se
bDepartment of Materials and Environmental Chemistry, Stockholm University, SE-106 91 Stockholm, Sweden
First published on 13th March 2018
Abstract
A carbon-coated pyrosilicate, Na2Mn2Si2O7/C, was synthesized and characterized for use as a new positive-electrode material for sodium ion batteries. The material consists of 20–80 nm primary particles embedded in a ≈10 nm-thick conductive carbon matrix. Reversible insertion of Na+ ions is clearly demonstrated with ≈25% of its theoretical capacity (165 mA h g−1) being accessible at room temperature at a low cycling rate. The material yields an average potential of 3.3 V vs. Na+/Na on charge and 2.2 V on discharge. DFT calculations predict an equilibrium potential for Na2Mn2Si2O7 in the range of 2.8–3.0 V vs. Na+/Na, with a possibility of a complete flip in the connectivity of neighboring Mn-polyhedra – from edge-sharing to disconnected and vice versa. This significant rearrangement in Mn coordination (≈2 Å) and large volume contraction (>10%) could explain our inability to fully desodiate the material, and illustrates well the need for a new electrode design strategy beyond the conventional “down-sizing/coating” procedure.
Once overlooked in favour of high energy density Li-ion batteries (LIBs), research in the field of non-aqueous Na-ion batteries (NIBs) is now undergoing a revival by virtue of its economic advantages and the relative abundance of Na compared to Li.1–3 Layered oxides (NaMO2, with M = Co, Fe, Mn, etc.) are by far the most extensively investigated candidates as positive electrode materials.4 A range of Fe and Mn compounds combined with PO43−, SO42−, P2O74−, etc. polyanions have recently been reported and characterized as positive electrodes in NIBs with the ambition of overcoming the performance, cost and safety limitations of the layered oxides.5
Generally, polyanion-based Mn compounds exhibit a higher cell potential (>0.5 V) than their Fe-counterparts, yet pose greater challenges in terms of electrochemical performance, typically resulting from the Jahn–Teller (J–T) distortion of Mn3+ (3d4 valence electron configuration), leading to poor electronic conductivity and sluggish structural conversion between their (de)lithiated/(de)sodiated phases.6 Though nano-sizing of the active particles and the use of electronically conducting coatings7 can often resolve the first challenge, the structural issues still remain. If the crystal structure framework is not able to withstand the strain caused by the J–T distortion of Mn3+, this might even result in significant atomic rearrangement, making it energetically favourable for Mn to migrate into alkali ion sites and/or dissolve in the electrolyte.8 Although these possibilities are certainly discouraging, the potential rewards for taming Mn in these electrochemical applications remain huge – thereby justifying continued effort within the battery materials research community.
The structural stress on Na-ion (de)insertion could be greatly alleviated through the use of some polyhedral linkage in the structures. Recent studies have highlighted that the performance of pyrophosphates containing larger P2O74− moieties can benefit from the introduction of this type of structural flexibility. For instance, corner-sharing [Mn–O] polyhedra in Na2MnP2O7 are believed to give better performance than the corresponding edge-sharing connectivity in Li2MnP2O7.9,10 The Na2MnP2O7 structure can, in this way, better accommodate the strain introduced by the J–T distortion of Mn3+, resulting in only minor atomic rearrangement under charge/discharge.11
We report herein the synthesis of a novel carbon-coated, nanosized pyrosilicate Na2Mn2Si2O7 and a preliminary study of its electrochemical properties in Na half-cells. Na2Mn2Si2O7 has a theoretical capacity of 165 mA h g−1, equal to that of other state-of-the-art Li-based compounds in this family of materials; typically, LiFePO4.12 To the best of our knowledge, pyrosilicates have remained unexplored in terms of electrochemical properties until very recently,13 unlike their orthosilicate counterparts (A2MSiO4, where M = Mn, Fe, Co; A = Li,14–17 Na18–20). A few relevant pyrosilicates, such as Na2Mn2Si2O7 and Na2Zn2Si2O7 were reported more than five decades ago; they were synthesized hydrothermally under alkaline conditions at both high pressures and high temperatures.21 We speculate here that this family of compounds could provide new opportunities in terms of cost-effective and environmentally sustainable materials for both Li- and Na-ion secondary batteries through careful control of composition, particle size and conductive coating.
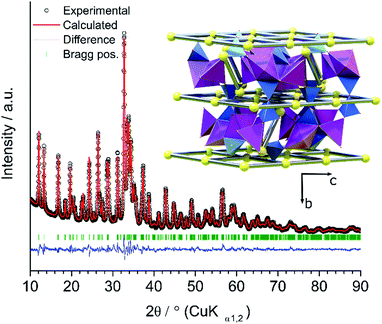
The target phase, carbon-coated Na2Mn2Si2O7 (“Na2Mn2Si2O7/C”) was synthesized through a solvothermally assisted sol–gel technique based on the well-known mechanism of acid-catalyzed hydrolysis and condensation of tetraethyl orthosilicate (TEOS); see the ESI.† The structure was refined successfully (Rp = 3.87%, Rwp = 5.00%, χ2 = 3.73) from powder XRD data (Fig. 1), using a monoclinic structural model derived earlier from single-crystal XRD data.22 A model involving mixed site occupation of Mn- and Na-sites23 did not result in a significant improvement in the fit. The atomic parameters of the refined structural model are reported separately in Table S2 in the ESI.†
Impurity-free manganese silicates are known to be difficult to synthesize, especially in the presence of carbon.24 Indeed, the phase purity of Na2Mn2Si2O7/C is here ≈94 wt%, with ≈6 wt% of Na2MnSiO4 impurity. The uncoated sample was free from impurity phases (Fig. S1 in the ESI†). An Electron Paramagnetic Resonance (EPR) spectrum of Na2Mn2Si2O7/C (Fig. S6 in the ESI†) displays a single Lorentzian absorption line (width of 21 mT and a g-factor of 2.01) indicating the presence of Mn2+ species – in good agreement with an earlier report.25
The structure of Na2Mn2Si2O7 is made up of layers of Mn ions separated by [SiO3–Ob–SiO3]6− silicate dimers (illustrated as conjoined blue tetrahedra in Fig. 1 inset). These dimers serve as spacers, effectively opening up the structure and accommodating the Na ions. The conjoined silicate tetrahedra have a close to staggered configuration relative to one another, and have a non-straight Si–Ob–Si bond angle of 120.9°. The Si–O bond lengths are distributed over the range 1.46–1.74 Å with the longest bond to the bridging Ob as found in earlier studies of other pyrosilicates.26 The Mn ions assume two distinct crystallographic positions within each Mn layer: tetrahedral in a corner-sharing configuration, and square-pyramidal (Mn–O < 2.5 Å) with both corner and edge-sharing connectivity to their neighbouring coordination polyhedra (Fig. 1 inset).
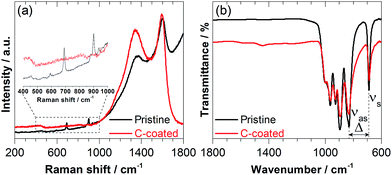
The carbon content of the Na2Mn2Si2O7/C compound was estimated by thermogravimetric analysis (TGA) to be ∼13 wt% (Fig. S3 in the ESI†). Raman spectroscopy confirmed the presence of typical pyrolytic carbon on the surface of Na2Mn2Si2O7/C with maxima centred at 1594 cm−1 and 1345 cm−1, attributed to the so-called G (“Graphitic”) and D (“Disorder”) bands27,28 (Fig. 2a).
The spectrum of pristine Na2Mn2Si2O7 shows only weak G and D bands, apparently due to minimal amounts of pyrolysis by-products from the acetate precursor. The additional peaks and bands below 1000 cm−1 are assigned to the pyrosilicate phase.29 The fact that these characteristic peaks and bands are not visible in the Na2Mn2Si2O7/C sample demonstrates complete coverage of Na2Mn2Si2O7 surface with highly Raman active carbon. The main peak at 691 cm−1 is ascribed to a symmetric stretching vibration νs (Si–Ob–Si) of the pyrosilicate phase and serves as a fingerprint for the presence of the Si2O7 groups.30,31
The presence of the pyrosilicate bands is also confirmed by IR spectroscopy, where the bands related to the various symmetric stretching modes within the Si2O7 groups appear at 689, 895, 927, 964 and 997 cm−1 for both C-coated and pristine specimens (Fig. 2b). An additional IR peak centred at 830 cm−1 can be assigned to an antisymmetric stretching vibration νas (Si–Ob–Si) of the Si2O7 groups, which is typical of non-straight Si–Ob–Si bridges (Si–Ob–Si angle < 180°) and appears to be inactive in Raman.32 The characteristic separation (Δ) between the symmetric (νs) and antisymmetric (νas) Si–Ob–Si bridge stretching modes in Fig. 2b is then 141 cm−1. As suggested by Lazarev,33 this separation typically increases as the Si–Ob–Si angle increases. Finally, the purity (within the detection limit) of both products is confirmed by the absence of IR absorption bands at higher wavenumbers, which might have arisen from residues of their xerogel precursors and/or water in the final powders.
Scanning electron microscopy (SEM) shows that Na2Mn2Si2O7/C is made up of micron-sized agglomerates (>1 μm) of primary particles with typical dimensions ∼100 nm (Fig. S4†). More accurate determination of the size of the primary particles is hindered by the presence of the surrounding carbon.
Using volume-weighted integral breadth (LVol-IB) in the XRD data, a crude evaluation of the average crystallite size gives ∼46 nm.
High resolution transmission electron microscopy (HRTEM) of the Na2Mn2Si2O7/C sample confirms that the secondary particles comprise agglomerated crystallites with typical size 20–80 nm (Fig. 3b and c). Characteristic d-spacings for Na2Mn2Si2O7 are d110 ≈ 7.3 Å, d111 ≈ 4.5 Å and d230 ≈ 3.2 Å (Fig. 3b and c). It is also evident that the crystallites are effectively embedded in a matrix of conductive carbon, which apparently inhibits the growth of the crystallites beyond nano-size under these synthesis conditions. The carbon is mainly amorphous (dominant sp3 hybridization), although turbostratic ordering (sp2 hybridized) is also observed in parts of the Na2Mn2Si2O7/C composite, in line with our Raman observations. A Selected Area Electron Diffraction (SAED) pattern originating from a larger area of the composite material shows that both the main phase and the minor impurity product are monoclinic. As such, they contain a large number of observable (and partly overlapping) diffraction lines, as evidenced by the numerous reciprocal lattice points in Fig. 3d. Totally correct indexing of the diffraction pattern is inhibited by instrument resolution, though the largest d-spacings (those closest to the primary beam) are uniquely attributed to the primary phase, Na2Mn2Si2O7, by virtue of its significantly larger unit cell (see dashed semicircles in Fig. 3d).
The typical size of the primary particles – spanning tens of nanometers – along with the limited thickness (≈10 nm) of the conductive carbon coating should ensure short diffusion pathways for the mobile Na+ ions and thereby enhance the overall electronic conductivity of the entire composite electrode. Both factors are deemed necessary in order to mitigate the adverse effects of low conductivity in such polyanionic materials. Note that Na-ion conductivity in Na2Mn2Si2O7 is not expected to be a performance limiting factor considering the similarity of the Bond Valence Sum (BVS) based Na-ion migration pathways to those in Na2Fe2Si2O7,13 see Fig. S9.†
Na half-cells with Na2Mn2Si2O7/C and Na2Mn2Si2O7 cathodes both exhibit an open circuit voltage (OCV) of about 2.5–2.6 V vs. Na+/Na.
However, Na2Mn2Si2O7 shows poor charging performance, as expected in the absence of a proper conductive coating. It was therefore excluded from our further studies.
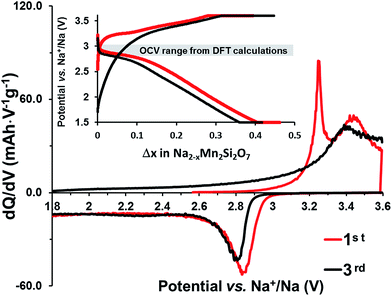
The cells with Na2Mn2Si2O7/C clearly cycled better providing approximately 25% of the theoretical capacity at a low cycling rate (C/100); see the inset in Fig. 4.
The differential capacity plot in Fig. 4 reveals two oxidation maxima at ≈3.2 and ≈3.4 V in the first charge and a broadened peak around 3.4 V in subsequent cycles. Only one maximum near 2.8 V is observed during discharge, together with a sloping voltage profile below 2.8 V (see the inset). Increasing the upper voltage cut-off beyond 4.0 V makes it possible to access ≈50% of the theoretical capacity (Fig. S2 inset in the ESI†). However, this was detrimental in terms of higher polarization and could well cause the onset of electrolyte oxidation. Such sluggish cycling behaviour cannot be ascribed to poor electronic contact in the active material or to long diffusion times for the Na+ ions, since our HRTEM data show the opposite. Alternatively, structural rearrangement, occurring in the desodiation-induced amorphization of Na2MnSiO4,16 could lead to such electrochemical behavior.
Density Functional Theory (DFT) calculations were used to probe in more depth the possible structural origins of such a slow reaction kinetics and the local structural rearrangement occurring under sodium removal from Na2Mn2Si2O7. In a fully sodiated structure (Fig. 5a), the tetrahedrally coordinated Mn1 sites are ≈4 Å apart, while the five-fold coordinated Mn2 sites form an edge-sharing dimer. However, a completely desodiated structure (Fig. 5d) shows an inversion of the Mn1–Mn1 and Mn2–Mn2 connectivity: the Mn1 sites switch to five-coordination and edge-sharing, whereas the Mn2 sites break up their edge-sharing configuration through a rearrangement of the coordinating oxygen positions. This is highlighted by the change in the Mn2–O3 distance from ≈4.3 Å in the fully sodiated (Fig. 5a) to ≈2 Å in the fully desodiated structure (Fig. 5d). Note that large changes in the metal–oxygen distance (up to 1.2 Å) were reported on the extraction of guest ions for structurally related Li2MnP2O7. This was argued to be the main cause of the sluggish cycling performance in this system.11 Here, we observe even larger changes in the bonding environment of the Mn ions; displacements over a range of ≈2 Å occur on full extraction of Na (Fig. S8 in the ESI†). Accordingly, it is not surprising that large overpotentials occur to overcome the excessive stress built-up in the structure, especially considering the substantial volume contraction (Δvol = −12%) and monoclinic distortion (Δβ = +15°) accompanying this conversion (Fig. S7 in the ESI†).
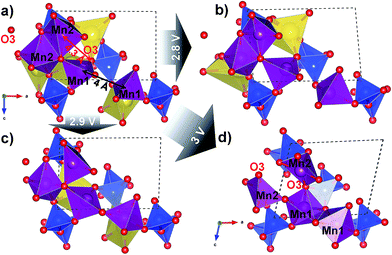 | ||
| Fig. 5 Series of DFT-optimised Na2Mn2Si2O7 structures shown along their b-direction in the vicinity of two neighbouring Mn1 and Mn2 sites (purple) in sodiated (a), half-desodiated with only Na2 (b) or Na1 (c) sites (yellow) occupied, and fully desodiated (d) states. The marked distances undergo large contraction upon desodiation with the connectivity of Mn polyhedra flipping from edge-sharing to disconnected and vice versa for Mn2 and Mn1, respectively. The arrows departing from the initial structure show the calculated desodiation voltages for the states (b)–(d). Si (blue) and O (red) of the Si2O7 dimers in the vicinity are also shown. The structure pictures are prepared in VESTA.34 | ||
Structural features of this kind could also account for similarly modest electrochemical behaviour in the isostructural Na2Fe2Si2O7 system.13
Simulated XRD patterns from the DFT models for x = 2, 1(Na2), 1(Na1) and x = 0 suggest a gradual increase of the (020) reflection intensity relative to the other peaks (Fig. S2c†). This is consistent with ex situ XRD data collected for a cycled electrode recovered after charging to 4.2 V using constant current followed by holding the voltage at this constant cut-off value (Fig. S2b†). Such an increase in the intensity of (020) reflection originates from the increase in the ordering of the layer structure of Na2Mn2Si2O7 under desodiation (Fig. 6).
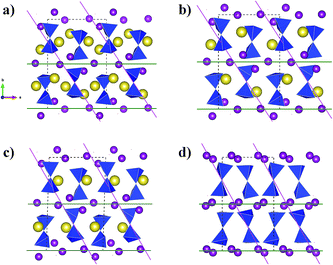 | ||
| Fig. 6 A layer arrangement of Mn ions (purple) and the Si2O7-dimers (blue) together with Na (yellow) is shown for a series of DFT-optimised Na2Mn2Si2O7 structures in sodiated (a), half-desodiated (b and c) and completely desodiated (d) states as in Fig. 5. The lattice planes corresponding to the reflections (020) (green) and (110) (pink) are shown. | ||
The calculated OCV values shown for the extraction of Na1 (with the Na2 site occupied, Fig. 5b) and Na2 (with the Na1 site occupied, Fig. 5c) are 2.8 V and 2.9 V vs. Na+/Na, respectively. We see here that the configuration in which the Na2 site is still occupied (Fig. 5b) corresponds to a smaller structural rearrangement (judging from the changes in the Mn–Mn and Mn–O distances) compared to the initial structure and is therefore the more probable de-sodiation path in the first charge half-cycle (see S2.7 in the ESI† for further details).
Nevertheless, it is likely that Na1 site occupation (Fig. 5c) can occur at higher overpotentials, and this can also lead to structural perturbation, as reflected in experimental differential capacity data (Fig. 4) which shows a smearing out of the two distinct oxidation processes during subsequent cycling. We speculate, however, that this fully desodiated structure (Fig. 5d) cannot be formed under the test conditions because the available capacity is <50% of the theoretical value, despite the calculated OCV value of ≈3 V vs. Na+/Na (Fig. 5a–d). In practice, only one sodium per formula unit is extracted from Na2Mn2Si2O7.
To conclude, manganese pyrosilicate was successfully prepared for the use as a new positive electrode material for sodium ion batteries. Despite its very attractive working voltage of ∼2.8 V and high theoretical capacity of 165 mA h g−1, the electrochemical activity of this compound, as exhibited in Na half-cells, appears rather moderate. DFT calculations reveal the possibility for complete flip in the connectivity of neighbouring Mn-polyhedra – from edge-sharing to disconnected and vice versa. Such a large rearrangement of the Mn coordination (≈2 Å) accompanied by a substantial volume contraction (>10%) could well explain our difficulties in completely desodiating the material. Clearly, some alternative to a conventional “down-sizing/coating” strategy is needed in these and also other polyanion structures exhibiting similar structural freedom. Further studies of the pyrosilicate family using, for example, structure stabilizing dopants, could open new opportunities for cost-effective and environmentally friendly materials for Li- and Na-ion batteries.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible through the financial support from the Swedish Research Council (Grants 2011-6512, 2010-4824), the Röntgen-Ångström Cluster, StandUp for Energy and Swedish Electromobility Centre. The authors would like to thank Henrik Eriksson for his valuable technical support. Mario Valvo gratefully acknowledges the contribution from the Swedish Research Council (FORMAS) through a personal grant no. 245-2014-668. The Knut and Alice Wallenberg (KAW) Foundation is acknowledged for its financial support of the electron microscopy facilities at Stockholm University. The computations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at Linköping University. Fikret Mamedov is also gratefully acknowledged for preliminary EPR measurements.References
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- H. Kim, H. Kim, Z. Ding, M. H. Lee, K. Lim, G. Yoon and K. Kang, Adv. Energy Mater., 2016, 6, 1600943 CrossRef.
- M. Valvo, F. Lindgren, U. Lafont, F. Björefors and K. Edström, J. Power Sources, 2014, 245, 967–978 CrossRef CAS.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef CAS PubMed.
- Q. Ni, Y. Bai, F. Wu and C. Wu, Adv. Sci., 2017, 4, 1600275 CrossRef PubMed.
- G. Chen, A. K. Shukla, X. Song and T. J. Richardson, J. Mater. Chem., 2011, 21, 10126 RSC.
- N. Ravet, J. B. Goodenough, S. Besner, M. Simoneau, P. Hovington and M. Armand, in Abstract no. 127, 196th Meeting of the Electrochemical Society, HI, 1999 Search PubMed.
- T. Nordh, R. Younesi, M. Hahlin, R. F. Duarte, C. Tengstedt, D. Brandell and K. Edström, J. Phys. Chem. C, 2016, 120, 3206–3213 CAS.
- M. Tamaru, P. Barpanda, Y. Yamada, S. Nishimura and A. Yamada, J. Mater. Chem., 2012, 22, 24526 RSC.
- P. Barpanda, T. Ye, M. Avdeev, S.-C. Chung and A. Yamada, J. Mater. Chem. A, 2013, 1, 4194 CAS.
- C. S. Park, H. Kim, R. A. Shakoor, E. Yang, S. Y. Lim, R. Kahraman, Y. Jung and J. W. Choi, J. Am. Chem. Soc., 2013, 135, 2787–2792 CrossRef CAS PubMed.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188 CrossRef CAS.
- A. Panigrahi, S. Nishimura, T. Shimada, E. Watanabe, W. Zhao, G. Oyama and A. Yamada, Chem. Mater., 2017, 29, 4361–4366 CrossRef CAS.
- A. Nytén, A. Abouimrane, M. Armand, T. Gustafsson and J. O. Thomas, Electrochem. Commun., 2005, 7, 156–160 CrossRef.
- R. Dominko, M. Bele, M. Gaberšček, A. Meden, M. Remškar and J. Jamnik, Electrochem. Commun., 2006, 8, 217–222 CrossRef CAS.
- M. S. Islam, R. Dominko, C. Masquelier, C. Sirisopanaporn, A. R. Armstrong and P. G. Bruce, J. Mater. Chem., 2011, 21, 9811 RSC.
- A. Boulineau, C. Sirisopanaporn, R. Dominko, A. R. Armstrong, P. G. Bruce and C. Masquelier, Dalton Trans., 2010, 39, 6310 RSC.
- C.-Y. Chen, K. Matsumoto, T. Nohira and R. Hagiwara, Electrochem. Commun., 2014, 45, 63–66 CrossRef CAS.
- Y. Kee, N. Dimov, A. Staykov and S. Okada, Mater. Chem. Phys., 2016, 171, 45–49 CrossRef CAS.
- J. C. Treacher, S. M. Wood, M. S. Islam and E. Kendrick, Phys. Chem. Chem. Phys., 2016, 18, 32744–32752 RSC.
- B. N. Litvin, I. M. Dianova and L. A. Kogan, Kristallografiya, 1964, 9, 571–574 CAS.
- L. P. Otroshchenko, V. I. Simonov and N. V. Belov, Dokl. Akad. Nauk SSSR, 1982, 265, 76–79 CAS.
- R. Tripathi, S. M. Wood, M. S. Islam and L. F. Nazar, Energy Environ. Sci., 2013, 6, 2257 CAS.
- R. J. Gummow and Y. He, J. Power Sources, 2014, 253, 315–331 CrossRef CAS.
- O. V. Kachalov and N. M. Kreines, J. Exp. Theor. Phys., 1968, 26, 522–525 Search PubMed.
- V. Kahlenberg, E. Brunello, C. Hejny, H. Krüger, D. Schmidmair, M. Tribus and D. M. Többens, J. Solid State Chem., 2015, 225, 155–167 CrossRef CAS.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef CAS.
- A. Cuesta, P. Dhamelincourt, J. Laureyns, A. Martínez-Alonso and J. M. D. Tascón, Carbon, 1994, 32, 1523–1532 CrossRef CAS.
- M. Wierzbicka-Wieczorek, U. Kolitsch and E. Tillmanns, Can. Mineral., 2010, 48, 51–68 CrossRef CAS.
- G. Clowry, Z. Molnár and P. Rakic, J. Anat., 2010, 217, 276–288 CrossRef PubMed.
- M. E. Fleet and G. S. Henderson, Phys. Chem. Miner., 1997, 24, 345–355 CrossRef CAS.
- A. N. Lazarev, T. F. Tenisheva, I. A. Bondar’ and L. N. Koroleva, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1962, 11, 514–516 CrossRef.
- A. N. Lazarev and T. F. Tenisheva, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1961, 10, 894–901 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Materials, methods, and supplementary results (PDF). See DOI: 10.1039/c7se00587c |
| This journal is © The Royal Society of Chemistry 2018 |