Examining the chemical and structural properties that influence the sensitivity of energetic nitrate esters

Abstract

The sensitivity of explosives is controlled by factors that span from intrinsic chemical reactivity and chemical intramolecular effects to mesoscale structure and defects, and has been a topic of extensive study for over 50 years. Due to these complex competing chemical and physical elements, a unifying relationship between molecular framework, crystal structure, and sensitivity has yet to be developed. In order to move towards this goal, ideally experimental studies should be performed on systems with small, systematic structural modifications, with modeling utilized to interpret experimental results. Pentaerythritol tetranitrate (PETN) is a common nitrate ester explosive that has been widely studied due to its use in military and commercial explosives. We have synthesized PETN derivatives with modified sensitivity characteristics by substituting one –CCH₂ONO₂ moiety with other substituents, including –CH, –CNH₂, –CNH₃X, –CCH₃, and –PO. We relate the handling sensitivity properties of each PETN derivative to its structural properties, and discuss the potential roles of thermodynamic properties such as heat capacity and heat of formation, thermal stability, crystal structure, compressibility, and inter- and intramolecular hydrogen bonding on impact sensitivity. Reactive molecular dynamics (MD) simulations of the C/H/N/O-based PETN-derivatives have been performed under cook-off conditions that mimic those accessed in impact tests. These simulations infer how changes in chemistry affect the subsequent decomposition pathways.

---

Introduction

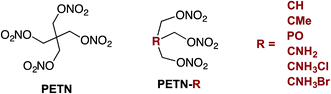
Although explosives have been developed for improved performance and sensitivity since the 1800's, the ability to predictably manipulate explosive sensitivity remains an elusive goal. The handling sensitivity of explosives is controlled by factors that span from intrinsic chemical reactivity to intramolecular effects to mesoscale structure and defects. For example, recent studies have focused on bond dissociation energy¹ and the electrostatic potential of reactive functional groups,² to larger scale effects, such as crystal packing³ and hot spot formation.⁴ Numerous recent articles have focused on understanding how hydrogen bonding might influence the insensitivity of materials like TATB (2,4,6-triamino-1,3,5-trinitrobenzene),⁵ and DAAF (3,3′-diamino-4,4′-azoxyfurazan).^6–10 In addition to these in-depth analyses on well-characterized explosives, there have been many recent reviews examining the influence of various physical characteristics of large classes of explosives on overall handling sensitivity.¹¹ Though this is an extensively studied topic, it is clear that a unifying relationship between molecular framework, crystal structure, and sensitivity has yet to be developed. In 1979, Kamlet and coworkers wrote that a more detailed knowledge of crystal structure properties and thermal decomposition, among other fundamental chemical and physical properties, would hopefully lead to “a unified theory of structure, sensitivity, and thermal stability of organic high explosives”.¹² However, almost 40 years later, Zeman and coworkers recently stated that “a single universal relationship between molecular structure and initiation reactivity does not yet exist”.¹³ In order to move towards this goal, we believe that experimental studies should be performed with small, systematic structural modifications, and modeling should ideally be used to interpret experimental work more frequently. The purpose of the present work was to design a series of nitrate ester explosives and evaluate – both experimentally and theoretically – how changes to the molecular structure affect thermodynamic properties and crystal packing, and correlate with mechanical sensitivity and thermal activation barriers. This is one of the first studies to combine experimental results with theory and simulation to explore explosive sensitivity and reactivity on a fundamental level.

Pentaerythritol tetranitrate (PETN), a common explosive containing the nitrate ester functionality, has been widely studied in large part because of its importance as a military and commercial explosive. Although modeling efforts have focused on the mechanism of decomposition of PETN,^1,14,15 experimental studies that give insight into sensitivity and decomposition are rare.^16–18 In order to better understand and manipulate the structure and sensitivity of this initiating explosive, we prepared derivatives of PETN by replacing one of the –CH₂ONO₂ substituents with either a hydrogen atom, amino group, or methyl group (Fig. 1). A PETN-derivative was also prepared by replacing the central carbon atom and one of the nitrate ester groups with a phosphorous oxide group (Fig. 1).¹⁹ It is generally accepted that the initial reactions for nitrate ester decompositions arise from that moiety and that they are the origin of the sensitivity of this class of compounds. By methodically varying only the non-energetic substituents within the PETN-R framework (Fig. 1), we have been able to observe and isolate the effect of molecular and crystalline structure on the reactivity of the nitrate ester functional group. Reactive molecular dynamics (MD) simulations were performed to evaluate the decomposition reactivity, and correlated to impact sensitivity and thermal decomposition studies. Additionally, basic properties such as heat capacity, heat of formation, oxygen balance, and crystal packing were evaluated experimentally and computationally. This is a rare example of a system where systematic changes have been made to an explosive molecule and evaluated with both experimental techniques as well as modeling in order to understand the effects on handling sensitivity.

Fig. 1 Structure of PETN and a list of the PETN-R derivatives examined in this study.

Results

Synthesis

Six derivatives of PETN were prepared for this study (Fig. 1). The preparation and crystallographic characterization of the amino derivatives, PETN–CNH₂ and PETN–CNH₃X (X = Cl, Br), have been outlined in a recent report.²⁰ The derivative PETN–CMe is a liquid explosive commonly referred to as metriol trinitrate, or trimethylolethane trinitrate (TMETN). PETN–CH is analogous to nitroglycerin, with an extra methylene group at the 2-position. Both PETN–CH and PETN–CMe are liquid explosives that are readily prepared by nitration of the parent alcohol in mixed acid using a modification of literature procedures.²¹ The solid explosive PETN–PO, trihydroxymethyloxyphosphine trinitrate (TNMPO), was prepared by nitrating tetrakis(hydroxymethyl)phosphonium chloride with nitric acid in acetic acid and acetic anhydride.²²

Sensitivity testing

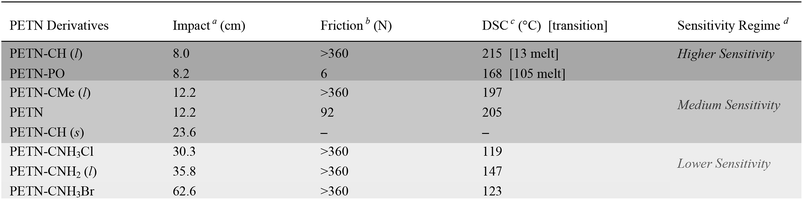
Small-scale sensitivity testing was performed on all of the materials to determine their response to impact and friction stimuli as well as thermal stability, relative to a PETN standard (Table 1). Half of the PETN derivatives exist as room temperature liquids, which are denoted in Table 1. The liquid compounds all have lower friction sensitivities, which is apparent in the observed data (no liquids were initiated by friction, which is a common result for liquids²³). At room temperature, PETN–PO and PETN–CH have measurably higher sensitivity to impact than the other materials, with drop heights of ∼8 ± 2 cm, using a 2.5 kg drop weight (PETN has an impact sensitivity of 12 ± 2 cm; larger numbers indicate less sensitive materials). Thermal stability (differential scanning calorimetry; DSC) peak exotherm values are also summarized in Table 1. Some of the materials also exhibited an endotherm, corresponding to melting prior to decomposition. PETN–PO exhibited a clear melt endotherm at 105 °C, and PETN–CH exhibited a melt at 13 °C. When water was present in PETN–CH, an extra peak was present at ∼25 °C as well.

Table 1 Sensitivity characteristics of PETN derivatives

^a Impact drop height values using a 2.5 kg drop weight; ±25% (H50). ^b Friction values ±25% (F50). ^c Differential scanning calorimetry peak exotherms ±10 °C [endotherms ±2 °C]. ^d Relative description of sensitivity based on impact sensitivity values for this series.

---

Because PETN–CH melts at 13 °C, we were able to collect impact data for the material as a solid as well as the liquid. Impact tests were conducted for crystals of PETN–CH at ∼7–8 °C while monitoring the temperature of the anvil, giving an impact value of 23.6 ± 1.8 cm. This is significantly higher than the value for the liquid (8.0 ± 2 cm). The reduction of handling sensitivity that occurs upon freezing the liquid is consistent with the behavior of nitroglycerin (a property that was commonly exploited in nitroglycerin for transport safety).²⁴ It is unlikely that the reduction in temperature (from 22 °C to 8 °C) influences the impact sensitivity significantly, as literature reports have shown impact sensitivities of materials such as PETN and TNT fall within error under similar temperature variations.²⁵

Differential scanning calorimetry (DSC) measurements

Heat capacity measurements with modulated DSC. Measurements of the heat capacity at constant pressure, C_P, were performed using modulated DSC on each material at ∼4–7 mg quantities (excluding PETN–CNH₂, which is not stable for long periods of time) and are summarized in Table 2. The values are assessed from the reversing heat flow signal. The average heating rate was 3 °C min⁻¹ with a modulation period of 120 seconds and an amplitude of 1.0 °C. Samples were held in aluminum hermetic pans with pinhole lids. The measured values for PETN (0.99 ± 0.16 J g⁻¹ °C⁻¹) and RDX correspond well with literature values (some of which are C_v, which should be comparable for solids).^26,27 All samples were placed in the instrument and ramped up and down in temperature three times, to ensure that decomposition or evaporation was not occurring during the test. Additionally, samples were prepared with different quantities and inserted and run in the instrument multiple times to ensure that sample mass and pan placement were accounted for in the error analysis. Though data was collected at a range of values, Table 2 summarizes the heat capacity at 30 °C, a temperature where none of the materials exhibited a melt or decomposition behavior.

Table 2 Thermal decomposition and heat capacity measurements with predicted values

^a kJ mol⁻¹ (±4%). ^b 1 min⁻¹ (±4%). ^c Specific heat capacity (C_P) J g⁻¹ °C⁻¹ at 30 °C [molar heat capacity (C_P,m) J mol⁻¹ °C⁻¹ at 30 °C]. ^d Calculated specific heat capacity (C_Vⁱ) using 3Rn/MW (J g⁻¹ °C⁻¹) at classical limit [calculated molar heat capacity (C_V,mⁱ) using 3Rn (J mol⁻¹ °C⁻¹)].

---

Thermal DSC kinetics measurements. Most of the parameters measured in this system have focused on the thermodynamic properties of the PETN materials, mainly because of their ease of accessibility. However, the sensitivity of materials should be more directly influenced by activation barriers rather than thermodynamic properties. Additionally, impact test results are complicated by the fact that the initiation events are a combination of factors, involving friction, variation in sample size and form, along with statistical variations in stresses. In order to address some of these concerns, we determined the activation energy experimentally. Variable ramp rate DSC measurements on the materials from 0.5 °C–20 °C per minute were performed. We then plotted log₁₀ β (heating rate, K min⁻¹) versus (1/T), where T is the peak maximum temperature of the first decomposition peak in Kelvin. The slope of a least squares “best fit” line through these points is taken as the value for 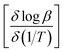, and the activation energy is then taken as 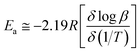where R = 8.314 J mol⁻¹ K⁻¹.²⁸

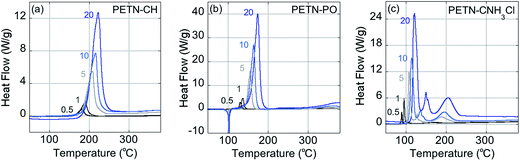
Fig. 2 shows typical DSC overlay plots for PETN–CNH₃Cl, PETN–CH, and PETN–PO. For all samples, the first peak value was used in the calculations, but that was often not representative of complete reactivity. For example, PETN–CH has a higher baseline after the first decomposition peak (Fig. 2a) and PETN–PO has a small broad peak at ∼350–400 °C (Fig. 2b), suggesting that further reactivity is occurring. In contrast to these subtle observations, all three amines have significant second and third peaks. Fig. 2c shows that after the initial decomposition peak for PETN–CNH₃Cl, there is a second peak at ∼125–175 °C and a third peak at ∼175–225 °C, indicating that reactions occur after the initial decomposition. The activation energy and pre-exponential factors based on the first decomposition peaks are shown in Table 2. No apparent trend is observed in this system between activation parameters and impact sensitivity, which is likely because DSC kinetics are only looking at the initial reactions on a slow timescale. The second and third decomposition peaks observed with the amine samples are likely important in the more complete reactivity that occurs during an impact test.

Fig. 2 DSC kinetics plots, showing ramp rates at 0.5 °C, 1 °C, 5 °C, 10 °C, and 20 °C per minute, for (a) PETN–CH, (b) PETN–PO, and (c) PETN–CNH₃Cl.

Crystal structures. Crystallographic characterization was obtained for PETN–CH and PETN–PO (Fig. 3). PETN–CH crystals were grown by dissolving the liquid material in diethyl ether and allowing the solvent to slowly evaporate in a freezer. Due to the low melting point of PETN–CH the crystals were mounted under a constant stream of cold nitrogen gas from evaporating liquid nitrogen. Crystals of PETN–PO were grown from slow diffusion in THF/hexanes.

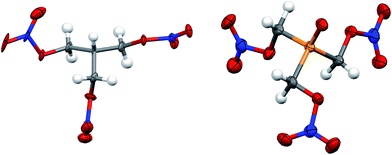Fig. 3 Solid state structure of PETN–CH (left) and PETN–PO (right). Orange, red, blue, grey and white ellipsoids represent P, O, N, C and H atoms respectively. Ellipsoids at 50% probability.

Both PETN–CH and PETN–PO have bond lengths and angles that are largely consistent with other PETN derivatives. Replacement of the central carbon atom with phosphorous in PETN–PO results in P–C bond lengths (1.824(5) Å) that are significantly longer than the corresponding C–C bond lengths (∼1.53 Å) in the other derivatives (Table 3). The P=O bond lengths are similar to other systems, and the P–C bond lengths are only slightly longer than those observed in similar, non-energetic molecules (∼1.80 Å).²⁹

Table 3 Average bond lengths and angles for PETN–CH, PETN–PO compared with PETN–CNH₃Cl, PETN–CNH₃Br, and PETN²⁰

Average bond lengths (Å)
Bond type	PETN–CH	PETN–PO	PETN–CNH3Cl	PETN–CNH3Br	PETN
C–C	1.526(4)	N/A	1.529(2)	1.529(2)	1.532
P–C	N/A	1.824(5)	N/A	N/A	N/A
P–O	N/A	1.495(4)	N/A	N/A	N/A
C–Namine	N/A	N/A	1.487(2)	1.567(2)	N/A
C–O	1.451(4)	1.437(6)	1.431(2)	1.451(2)	1.446
Nnitro–Obridge	1.392(4)	1.426(6)	1.396(2)	1.386(2)	1.401
Nnitro–Oterminal	1.192(4)	1.193(6)	1.195(2)	1.210(2)	1.199

---

Average angle (°)
Angle type	PETN–CH	PETN–PO	PETN–CNH3Cl	PETN–CNH3Br	PETN
C–C–Namine	N/A	N/A	109.4(3)	107.7(2)	N/A
C–P–O	N/A	114.4(2)	N/A	N/A	N/A
C–C–Obridge	106.6(2)	N/A	108.8(3)	108.0(2)	106.8
P–C–Obridge	N/A	104.5(3)	N/A	N/A	N/A
C–Obridge–Nnitro	114.6(2)	113.0(3)	112.8(3)	113.6(2)	113.0
Obridge–N–Oterminal	115.6(3)	114.8(4)	114.9(3)	115.1(2)	115.2

---

The crystal structures for PETN–CNH₃Cl and PETN–CNH₃Br have recently been published,²⁰ and the Cl and Br derivatives exhibit typical lengths observed for hydrogen bonds between the halide ion and the N–H hydrogens.³⁰ For example, H–Br lengths in PETN–CNH₃Br are generally ∼2.5 Å (with a range of 2.37–2.54 Å). In PETN–CNH₃Cl, the H–Cl distances are generally ∼2.3 Å (with a range of 2.24–2.87 Å). Additionally, (N)O–H(N) contacts in these crystal structures are in a similar range, at generally ∼2.5–2.6 Å.

Modeling

Calculations of heat of formation, oxygen balance, piezoelectric effects, packing index, and compressibility. The gas phase heat of formation was obtained for all of the PETN derivatives except PETN–CNH₃Br and PETN–CNH₃Cl using the atom-equivalent models of Byrd and Rice,³¹ and Guthrie.³² Dispersion corrected solid state density functional theory (DFT)³³ was used to estimate the intermolecular cohesion of the crystalline derivatives to derive ΔH_f(s) for PETN, PETN–CH (solid), and PETN–PO (Table 4). For the liquid samples, PETN–CMe and PETN–CNH₂, the value was estimated in the vapor phase (ΔH_f(v); Table 4). These values were used along with density measurements (for the solids with known crystal structures) or estimates (for the liquids) in Cheetah Thermochemical Code version 8.0 (ref. 34) to calculate the total energy of detonation for each material (Table 4). Oxygen balance was calculated assuming each derivative formed standard gaseous products (Table 4).³⁵ Erythritol tetranitrate (ETN), a similar sensitive nitrate ester we have studied previously,²¹ is included in this table as a reference material.

Table 4 Calculated thermodynamic parameters and piezoelectricity properties for PETN derivatives in this study (along with ETN as a comparison)

^a Cheetah thermochemical code, version 8.0, using the densities obtained from the crystal structures for the solids, and assuming a density of 1.6 g cm⁻¹ (from rough measurement of PETN–CH) for all liquids. ^b Calculated oxygen balance to CO₂: 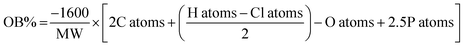, where MW = molecular weight of the molecule, and X atoms is the number of atoms of X in the molecule.⁴³

---

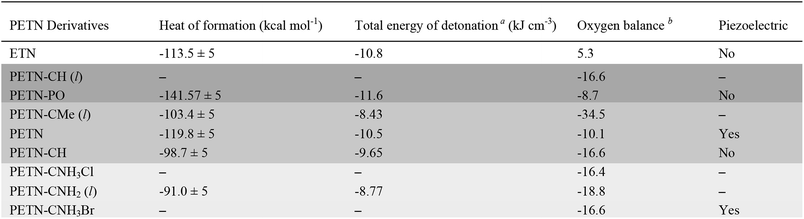
The space group of PETN belongs to a piezoelectric class. It was suggested that the piezoelectric effect might account for the relatively high impact sensitivity of PETN with respect to other non-piezoelectric energetic materials.³⁶ Of all the PETN derivatives considered here only PETN–CNH₃Br is piezoelectric. Since this has the lowest impact sensitivity of those tested, and other derivatives that are not piezoelectric have higher impact sensitivities than PETN, it appears that there are no obvious correlations between impact sensitivity and piezoelectric responses in these materials.

Compressibilities were extracted from zero temperature isothermal compression curves, or cold curves, computed using dispersion-corrected plane wave DFT with the VASP code. The calculations used the exchange correlation functional of Perdew, Burke, and Ernzerhof,³⁷ the D3(BJ) empirical dispersion correction of Grimme and coworkers,³⁸ a 500 eV plane wave cut off energy, and projector augmented wave pseudopotentials.³⁹ With the exception of PETN–CNH₃Br, all of our calculations used multiple k-points within the Brillouin zone in order to improve the accuracy of the total energies. The lattice parameters and internal coordinates of the PETN, PETN-CH, PETN-PO, PETN–CNH₃Br, and ETN unit cells were first optimized at constant volume. The cells were then compressed in uniform increments up to V/V₀ = 0.73 followed by the reoptimization of the lattice parameters and internal coordinates at constant volume. The bulk moduli were obtained by a least squares fit of the Vinet equation of state to the cold curves.^27,40 The compressibilities are taken as the inverse of the bulk moduli.

The Kitaigorodskii packing index (%), which is the volume of the molecules in the unit cell divided by the unit cell volume in a crystal, was calculated from each crystal structure using the PLATON program.^41,42

Calculations of first reactions

The effects of the chemical modifications on the underlying decomposition chemistry of the derivatives were studied using condensed-phase reactive MD simulations. The interatomic bonding in the PETN derivatives was represented using semi-empirical density functional tight binding (DFTB) theory.⁴⁴ DFTB is a fast, approximate electronic structure method that naturally captures the formation of covalent bonds and charge transfer between species of different electronegativities. It has been applied extensively in simulations of organic materials, including explosives.⁴⁵ The simulations employed the DFTB parameterizations for C/H/N/O-containing molecules developed using the numerical optimization framework that was advanced recently by Krishnapriyan et al.⁴⁶

Gas phase bond dissociation energies (BDEs) and isomerization energies for first reactions have been emphasized as important for interpreting PETN reactivity.^1,15 Since our DFTB theory is an approximate, semi-empirical method, we have tested the accuracy of its predictions against more exact ab initio calculations.⁴⁷ Our analysis of bond dissociation and isomerization energies of PETN using the DFTB-lanl1 parameter set⁴⁶versus density functional theory calculations by Tsyshevsky et al.¹⁵ showed very good quantitative agreement, which allows us to apply DFTB theory to nitrate ester chemistry with good confidence. The reactive MD simulations presented here were performed with a new parameterization, DFTB-lanl22, which improves the description of the relative energies of the HONO and HNO₂ isomers with respect to DFTB-lanl1. The DFTB-lanl22 parameterization for C/H/N/O-containing molecules is provided as ESI.†

The thermal decomposition chemistry of PETN–CH, PETN–CMe, and PETN–CNH₂ were simulated under ‘cook-off’ conditions, i.e., at elevated temperatures but ambient density. Since impact tests cannot generate the highly compressed states that are accessible in shock experiments, cook-off is a physically reasonable initial condition for this work. Cubic, periodic simulation cells containing 10 PETN–CH, PETN–CMe, and PETN–CNH₂ molecules (>200 atoms) were generated by adding molecules randomly while avoiding overlaps and close-approaches between adjacent molecules. The atomic positions within the cells were first optimized using molecular statics relaxation and were subsequently thermalized at 1400 K using a Langevin thermostat⁴⁸ to generate liquid-like distributions of the molecules. The PETN–CH and PETN–CMe systems were generated at their measured room temperature densities, 1.56 and 1.51 g cm⁻³, respectively. We lacked experimental data on density of PETN–CNH₂ at room temperature and used a value of 1.52 g cm⁻³ based on its similarity to liquid PETN–CH and PETN–CMe. Since our simulations use initial temperatures that lead to chemical decomposition on picosecond time scales, it is unlikely small errors in the initial densities of the simulations will have a meaningful effect on the subsequent reaction pathways.

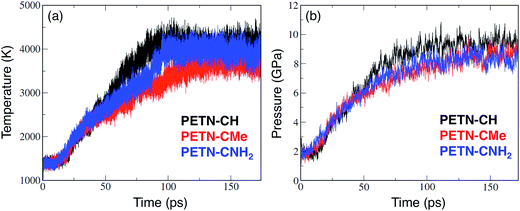
A time step of 0.1 fs was used to integrate the equations of motion for the nuclear degrees of freedom. An electronic temperature corresponding to k_BT_e = 0.3 eV was used in the evaluation of the density matrix to smear the occupancies of the eigenstates in the vicinity of the chemical potential, where k_B is the Boltzmann constant. The use of a finite electronic temperature is crucial to ensure energy conservation during the making and breaking of covalent bonds. Following the thermalization of the three derivatives to set the initial temperature, we switched to microcanonical dynamics in order to allow the temperature to evolve with onset of endo- and exothermic chemistry.⁴⁹ Precise, long-term conservation of the total energy during microcanonical dynamics was obtained using the extended Lagrangian Born-Oppenheimer MD formalism of Niklasson et al.⁵⁰ Each simulation was run for ∼200 ps until they had decomposed into product species. The evolution of the interatomic bonding was computed by post-processing the stored trajectories. Under these conditions, all the molecules studied reacted extensively, and at similar rates. Fig. 4 shows the evolution of temperature and pressure for PETN–CH, PETN–CMe, and PETN–CNH₂ (the pressure data was smoothed using a 50 pt running average).

Fig. 4 Evolution of the (a) temperature and (b) pressure in liquid PETN–CH, PETN–CMe, and PETN–CNH₂ initialized at a temperature of 1400 K. The pressure data were smoothed using a 50 point running average.

From the temperature and pressure profiles in Fig. 4, it is clear that all three derivatives react at similar timescales. The temperature profiles are all flat for the first 15–20 ps, and then begin a sharp rise indicating the onset of exothermic reactions. At ∼50 ps, there is a slight divergence in behavior. Both the PETN–CH and PETN–CNH₂ derivatives reach a steady-state T at ∼100 ps, though with somewhat different profiles and ultimate values. PETN–CMe is more lethargic and does not reach a steady-state until ∼130 ps. In the pressure profiles, the differences are less marked. Again, there is a quiescent period for the first ∼20 ps, though PETN–CNH₂ shows a slight rise, but all three species appear to reach steady-state at 130–150 ps.

For the analysis of the chemistry of these simulations, we focused on the coordination geometries (the numbers and types of atoms bonded to particular central atoms), because this is easier to numerically analyze than counting up all possible molecular species.⁴⁷ The presence of a bond was defined by two atoms being separated by less than a specified cutoff distance for 10 ps (∼1/4 of a vibrational period for the heavy atoms). The cutoff distances were defined from the well-marked minimum observed in the radial distribution functions for the atom pairs throughout these simulations, clearly demarking bonded from non-bonded atoms.⁴⁷

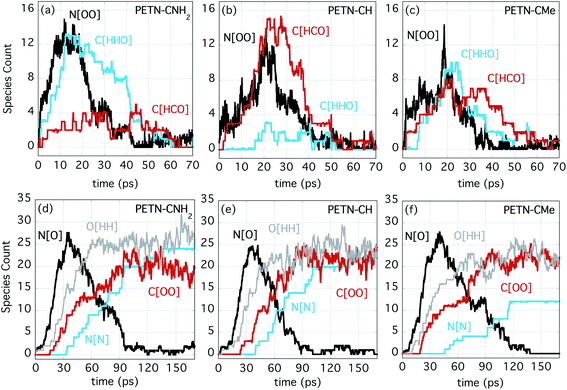
Fig. 5a–c shows the number evolution for some important early intermediate species for each PETN derivative. The species N[OO] represents NO₂ as well as HONO, and this product is forming on similar timescales for each derivative, though a bit more rapidly for PETN–CNH₂. When N[OO] forms in the presence of C[HHO] rather than C[HCO], this indicates that the molecule is likely eliminating NO₂ along with formaldehyde. This is very clearly the case for PETN–CNH₂ (Fig. 5a). The presence of formaldehyde is therefore more diagnostic of NO₂ evolution in this particular system, which is why the evolution of both species are shown in Fig. 5. However, N[OO] elimination in the presence of C[HCO] indicates the formation of HONO, leaving behind a somewhat stable formyl group intermediate, which can be seen with PETN–CH in Fig. 5b. Finally, Fig. 5c shows that PETN–CMe has two competing pathways for NO₂versus HONO elimination, with similar values of C[HHO] and C[HCO] in the early products. Given the negligible temperature change over the first 20 ps, these reactions are apparently close to thermoneutral.

Fig. 5 Species count for the three PETN derivatives, showing N[OO], C[HCO], and C[HHO] for (a) PETN–CNH₂, (b) PETN–CH, (c) PETN–CMe, and N[O], O[HH], C[OO], and N[N] for (d) PETN–CNH₂, (e) PETN–CH, and (f) PETN–CMe.

At later times, the evolution of the important intermediate NO (N[O]) and the products H₂O (O[HH]), CO₂ (C[OO]), and N₂ (N[N]) are shown in Fig. 5d–f. Despite the differences in the initial NO₂/HONO branching, the formation of NO occurs on very similar timescales. This indicates that the transfer of O/OH from NO₂/HONO to either form water or to oxidize C occur at similar rates. These reactions also correlate with the strong temperature rise that begins at ∼20 ps. The formation of the final products (H₂O, CO₂, and N₂) also proceed at similar rates for the three species. It is also noteworthy that they occur in the same order; first H₂O, then CO₂ and finally N₂. The most noticeable difference is that the production of N₂ from PETN–CMe is somewhat suppressed. Because of the increased number of H atoms in this system, the production of amines is enhanced, which diminishes the amount of N₂ produced.

The decomposition pathways observed in the reactive MD simulations of PETN–CH, PETN–CNH₂, and PETN–CMe correlate well with trends in the bond dissociation energies of the C–ONO₂ and O–NO₂ bonds. The BDEs calculated in the gas phase for these materials with the DFTB-lanl22 parameter set are presented in Table 5. Clearly, O–N cleavage should be favored over C–O cleavage, as has been noted previously,^1,14,15 and which is demonstrated here in our dynamic simulations. PETN–CNH₂ has the overall weakest O–N bond, though the differences are small, and it does react most rapidly. It is also interesting that its initial decomposition step favors the formation of NO₂. PETN has a similarly low bond dissociation energy, and so might follow the same path, though direct comparison is more complicated due to the extra energetic nitrate ester functional group. While all the initial reactions of the derivatives start at the nitrate ester moiety with similar values for reaction energies and similar temperature and pressure profiles, the character of the substituent group appears to affect the mechanism of the decomposition (NO₂ elimination versus HONO elimination).

Table 5 Bond dissociation energies in kcal mol⁻¹ for the O–NO₂ and C–ONO₂ bonds in PETN–CH, PETN–CMe, and PETN–CNH₂, with PETN for comparison, computed in the gas phase using the DFTB-lanl22 model and, for PETN, density functional theory with the wB97XD functional¹⁵

Molecule	O–NO2	C–ONO2
PETN (wB97XD)	41.2	86.0
PETN	48.5	93.7
PETN–CH	49.2	92.8
PETN–CMe	49.5	95.0
PETN–CNH2	48.2	95.5

---

Discussion

Sensitivity testing

Within this series of nitrate ester explosives, we sought to determine the relative importance of the factors that influence handling sensitivity. Measuring and interpreting handling sensitivity using impact test data is not a straightforward task, even when data are collected using consistent methods on the same instrument.⁵¹ The standard impact test results will vary with background temperature, amount of material, humidity, operator, and sometimes particle morphology (though we have found examples where particle morphology, i.e., large crystals versus fine powder, is not important²¹). In some cases the rebound impact causes reaction, and liquids likely initiate with a different mechanism than solids.^52,53 It was interesting to note the difference between liquid and solid PETN–CH where, like nitroglycerin, the difference in impact sensitivity is likely due to bubble collapse in the liquid.⁵⁴ Therefore, it is particularly important to take care when directly comparing liquid to solid materials. Additionally, the mechanisms of reaction for solid materials are still debated. The impact test likely does not generate a stable detonation, but rather thermal activation through internal shear or interfacial friction⁵⁵ at varying temperatures.⁵⁶ These varying conditions could result in different types of initiation with different functional groups, so it has been suggested that comparisons should generally be made within similar families of explosives,^12,57 which is the approach we have taken in this study.

Though liquids and solids are not directly comparable, probing the sensitivity characteristics of closely-related solids and liquids offers several advantages. Experimentally, solids are necessary for crystallographic structural analysis and relatively straightforward comparisons with sensitivity tests (since liquids often introduce less predictable physical phenomena such as hot spot initiation). However, the liquids are extremely useful for molecular dynamics simulations, in order to obtain a basic understanding of chemical reactivity mechanisms when crystal packing and other solid interactions do not come into play. Together, the information from both liquids and solids adds breadth of understanding to this study that we could not access by studying one phase of material. To avoid confusion, we have emphasized clearly which materials are liquids in Table 1 so they can be compared directly. Additionally, our MD simulations only address the liquid PETN derivatives, while the crystal packing analysis focuses only on the solids.

Though impact tests are difficult to interpret since physical phenomena spanning multiple length and time scales are involved, they have proven to be an important screening tool for practical handling safety when performed consistently. Different classes of energetic materials typically fall within predictable sensitivity regimes when subjected to insults in consistent conditions – peroxide primaries such as triacetone triperoxide (TATP) are consistently more sensitive than RDX, which is consistently more sensitive than TNT and TATB. Furthermore, in our labs using consistent measurement techniques, multiple samples of PETN–CNH₂, PETN–CNH₃Cl, and ETN¹⁹ prepared under different conditions and tested for impact on different days by different operators resulted in consistent values that varied by less than 5 cm (Table 1). These tests are a somewhat direct measure of handling sensitivity. In contrast, shock compression tests – which measure explosive initiation at known input pressures – do not necessarily correlate directly with handling safety.^58,59 Though we do not know the exact mechanism of reaction in impact tests, we and others^21,52,60 use these data as a general guideline for correlating handling sensitivity with the structure of materials. To emphasize this, we have separated the materials into three general sensitivity regimes (described in Table 1), with shading that is consistent throughout the remainder of the tables in this paper.

Thermodynamic measurements

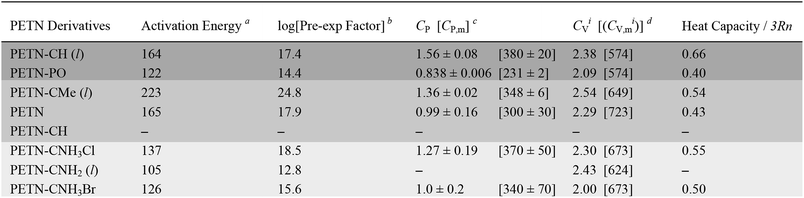
Heat capacity was measured in order to investigate whether the presence of heavier atoms (Cl and Br) in the amine derivatives would affect the system enough to influence how these materials might dissipate energy during an impact test. We also wanted to see if factors such as hydrogen bonding and thermal expansion properties would impact heat capacity in a way that could not be captured in a simple calculation that only took the number of atoms in the molecule into account. In Table 2, we compare the measured C_P value to the ideal heat capacity at the classical limit (C_Vⁱ), using the molecular weight of the molecule, with three degrees of freedom per atom of the molecule. C_Vⁱ = 3Rn/MW, where n is the number of atoms in the molecule, R, the gas constant (8.3143 J mol⁻¹ K⁻¹), and MW, the molecular weight of the formula unit. Table 2 also shows the ratio of the measured specific heat to the calculated classical limit. This ratio is typically ∼0.5 for organic molecules, given the presence of higher frequency vibrational modes, particularly from the presence of hydrogen atoms (e.g. C–H stretching modes).²⁷ A higher value would correspond to a more classical system (lower average frequencies) and a lower value should indicate a less classical system. The system with the lower relative heat capacities should then have a larger temperature rise for the same amount of added heat per molecule, and might then be expected to be more sensitive.

In this system, PETN and PETN–PO are lower than expected, whereas PETN–CH is significantly higher. Because this comparison is rigorously between C_V and C_P values, we assume these deviations arise from differences in the thermal expansion coefficient, density, and isothermal compressibility of the materials.⁶¹ The solid amines (PETN–CNH₃Cl and PETN–CNH₃Br) are within the expected values, indicating that hydrogen bonding does not cause the heat capacity values to deviate significantly from classical predictions.⁶² Additionally, the presence of heavier halide elements does not appear to affect heat capacity values significantly within the system. Heat capacity is typically expressed as a per gram value, which may correlate better with the impact test setup presented in this study (samples are measured per mass, rather than per mole). However, in Table 2 we also present measured and calculated molar heat capacity values. No apparent correlations between the impact sensitivity and the heat capacity (on a per gram or per molecule basis) were observed in this comparison.

In order to examine whether general thermodynamic explosive properties correlate with impact sensitivity, we calculated heat of formation and total energy of detonation for each PETN derivative (Table 4). We were unable to calculate heats of formation for the two energetic salt materials PETN–CNH₃Cl and PETN–CNH₃Br using atom equivalents and thus were unable to determine their energies of detonation. Although we observe generally higher heats of formation and energies of detonation for some of the more impact sensitive materials (PETN–PO has the highest value compared with PETN–CNH₂, which has the lowest value), there are notable outliers. For example, the exceptionally high heat of detonation of PETN–PO does not render it more sensitive than PETN–CH. Since the high heat of detonation of PETN–PO is driven by the assumed formation of P₂O₅ as a detonation product, which probably happens at later times, it is unclear whether there is truly a significant difference between the activation energies of PETN–CH and PETN–PO. Comparing the two liquid non-amine materials, PETN–CH and PETN–CMe, the lower heat of detonation of PETN–CMe correlates with a lower sensitivity towards impact. Overall, we observe a weak, but inconsistent trend between the thermodynamic properties of the materials with their impact sensitivity, which is similar to other larger-scale studies.^53,59,63 However, we did not see a correlation between impact sensitivity and oxygen balance in this system (Table 4), in contrast to some of the larger-scale early studies focusing on this topic.^12,57

MD simulations

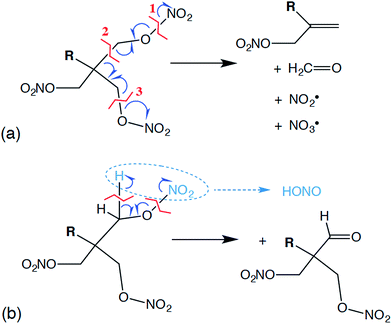
Reactive molecular dynamics simulations were performed to further understand and predict basic chemistry properties of the liquid PETN-based molecules. Modeling under cook-off conditions assumes ambient density, and these conditions are somewhat similar to the low-pressure initiation conditions in an impact sensitivity test. For example, in our impact tests using a 2.5 kg weight and assuming an elastic collision with a rebound of ∼10 ms, we estimate that a sample that initiates at ∼15 cm is exposed to a pressure of ∼0.05 GPa.⁶⁴

Following the product evolution described in Fig. 5, all three molecules undergo some degree of the same set of two competing initial reactions. One of these is a coordinated “unzippering” of two of the nitrate ester arms of the molecules (∼100% of PETN–CNH₂ and ∼50% of PETN–CMe follow this pathway). The overall reaction can be thought of as the following: first appears to be the cleavage of one of the O–N bonds, liberating an NO₂˙ radical and leaving behind a C–O˙ radical. This is rapidly followed by the release of a H₂C=O molecule by cleaving the C–C bond, transferring the radical to the central C atom. This is again rapidly followed by the cleavage of a C–O bond on one of the remaining nitrate ester arms, releasing an NO₃˙ radical but then forming a C=C double bond in the process, leaving R(CH₂ONO₂)C=CH₂ (Fig. 6a). In most of our simulations, these reactions appear to occur near simultaneously, within the resolution of our sampling of the data (10 fs). Occasionally, this can be observed as a two-step process, where the two NO_x˙ radicals appear ∼10 fs apart. From this, we conclude that the reactions are not required to occur simultaneously, but the activation energies for the second and third reactions must be rather low. Overall, this reaction is only mildly exothermic, causing the temperature in the microcanonical (NVE) simulations to rise ∼100 K.

Fig. 6 Proposed mechanisms for some of the likely first reactions for PETN derivatives including initial intermediate products, where R = NH₂ [PETN–CNH₂; mechanism (a)], H [PETN–CH; mechanism (b)], or CH₃ [PETN–CMe; mechanisms (a) and (b)].

Competing with this rather extraordinary reaction was a more mundane HONO elimination reaction that leaves a formyl group coordinated to the central carbon (Fig. 6b; ∼100% of PETN–CH and ∼50% of PETN–CMe follow this pathway). This reaction itself appears to be thermoneutral, but it is followed by more strongly exothermic processes. What is interesting is the difference in rates for both reactions between the three molecules. Though all molecules react at very similar times (Fig. 4), the unzippering reaction for the PETN–CNH₂ derivative appears slightly faster than the others (Fig. 5a; N[OO] peaks at ∼10 ps). This is perhaps not surprising, since nitrate esters β to amine groups are known to be thermally unstable.⁶⁵ These slightly faster calculated reaction rates do parallel the activation energies (and thermal instability) of the amines determined from the experimental DSC measurements, which give us confidence in the results. In contrast, for the PETN–CMe and PETN–CH derivatives, N[OO] formation peaks at ∼20 ps. Both the HONO and NO₂ species then fairly rapidly form NO, and then N₂.

The reason for the different mechanisms of reactivity for the three liquid PETN derivatives is not immediately obvious. The charge on the central carbon atom was calculated for each derivative, and the values were not influenced by the electronegativity of the R group. It is important to note that the MD simulations do not take hydrogen bonding interactions into account. These simulations, along with others at different temperatures, are currently being analyzed in greater detail and will be discussed in a separate publication.⁴⁷ Overall, we observe that all three derivatives have very similar temperature and pressure profiles and reaction times (Fig. 4), which means that the differences in impact sensitivity among the PETN derivatives are likely due to larger scale effects such as crystal packing.

Crystal packing studies

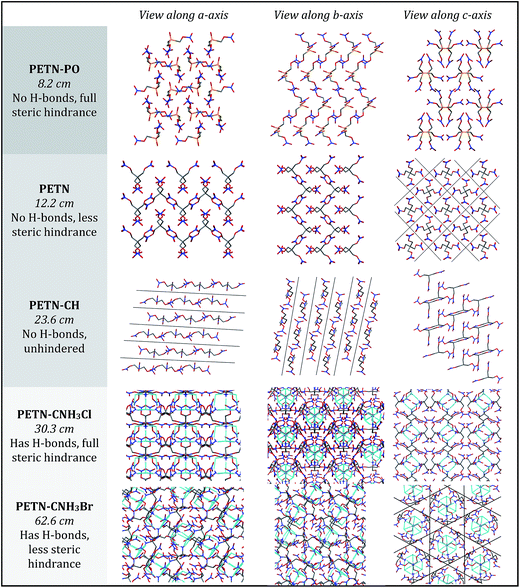
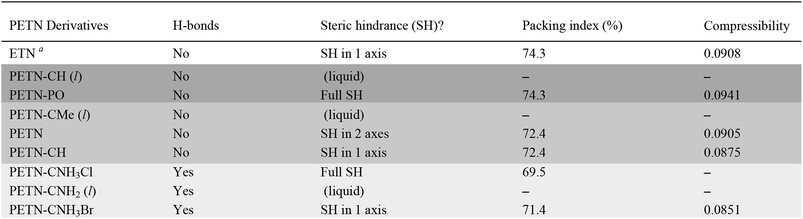
To fully explore the sensitivity characteristics of this nitrate ester system, we looked beyond the intrinsic chemistry within single molecules. Recent studies have focused on both the presence of hydrogen bonding and sterically unhindered ‘slip’ planes as important in reducing sensitivity for molecules like TATB.⁶⁶ For example, recent reviews of crystal structures have shown that crystal sheets (in at least two directions) correlate with insensitivity.⁶⁷ At the same time, equally plausible chemical, rather than structural, explanations of the low impact sensitivity of TATB have been proposed.⁶⁸ Furthermore, DATB has comparable impact sensitivity⁶⁹ to TATB but it lacks the layered crystal structure of the latter.⁷⁰ The anisotropic shock sensitivity of PETN single crystals has been studied in detail.⁷¹ Based on the relative values of the Hugoniot elastic limit as a function of crystal orientation, Jerry Dick et al. proposed a connection between dislocation-mediated plasticity and shock sensitivity. In essence, crystals that are oriented such that dislocation-mediated plastic flow can relax shear stresses (such as those induced by shock compression) are insensitive, whereas those orientations for which plastic flow (slip) is difficult are relatively sensitive, presumably because fracture or shear band-like features arise instead. This work suggests that dislocations cannot glide on planes where molecules are sterically hindered because such features lead to high-energy barriers to dislocation motion. PETN is perhaps the only material for which anisotropic impact sensitivity has been measured. The body centered tetragonal crystal structure of PETN also makes it relativity straightforward to understand its slip systems. Recent work on understanding dislocation-mediated plasticity in orthorhombic RDX led to 13 slip systems, whose connections with anisotropic impact and shock sensitivities are currently unknown.⁷² In this work, we use TATB and PETN as prototypical energetic materials in order to understand whether the molecular packing of the PETN derivatives might promote sensitivity (high steric hindrance) or insensitivity (low steric hindrance).

Table 6 summarizes some important qualitative observations of intermolecular interactions for the PETN derivatives in this study, along with ETN for comparison. From the data collected, it is clear that the nitrate esters with the lowest sensitivity towards impact (PETN–CNH₂, PETN–CNH₃Cl, and PETN–CNH₃Br) all have intermolecular hydrogen bonding networks. It is thought that the presence of hydrogen bonding allows for materials to dissipate energy more rapidly through heightened thermal conductivity.¹¹ This is consistent with presence of hydrogen bonding in some of the least sensitive known explosives such as TATB,⁷³ FOX-7 (1,1-diamino-2,2-dinitroethene),⁷⁴ LLM-105 (2,6-diamino-3,5-dinitropyrazine-1-oxide),⁷⁵ and DAAF.⁷⁶ In the absence of hydrogen bonding, the presence of sterically unhindered planes appears to correlate with decreased sensitivity. The crystal packing arrangements of nitrate esters PETN–PO, PETN–CH, PETN–CNH₃Cl, and PETN–CNH₃Br are shown in Fig. 7. PETN–PO packs in a sterically hindered crossing interlocking pattern, while PETN–CH molecules pack with distinct sheets that are not sterically hindered. Furthermore, the orientation of the nitrate esters in PETN–CH are also unhindered. Further comparisons can be made with our recent previous work on PETN–CNH₃Cl and PETN–CNH₃Br,²⁰ along with the standard nitrate ester explosive PETN.^7,77 As we have previously noted, both PETN–CNH₃Cl and PETN–CNH₃Br have hydrogen bonding and similar packing structures, but alternating orientations of nitrate esters in PETN–CNH₃Cl lead to sterically hindered planes, while repeating orientations of nitrate esters in PETN–CNH₃Br avoids steric hindrance. Notably, in Fig. 7, impact sensitivity decreases from top (high steric hindrance and no hydrogen bonding) to bottom (has both hydrogen bonding and no steric hindrance in at least one direction).

Table 6 Summary of crystallographic properties of PETN derivatives in this system

^a ETN has an impact value of 6.1 cm; crystal structure information from ref. 21.

---

Fig. 7 Solid state packing in PETN–PO, PETN, PETN–CH, PETN–CNH₃Cl, and PETN–CNH₃Br, viewed along the a, b, and c crystallographic axes. Each material has the impact sensitivity listed below it (in cm; decreases from top to bottom), with a summary of whether hydrogen bonding and planes exist.

Though many studies have identified the importance of hydrogen bonding^6–10 as well as crystal packing³ in influencing explosive sensitivity, it is often difficult to separate the effects of each of these, as hydrogen bonding will almost always influence crystal packing. Analysis of this system suggests for the first time that hydrogen bonding has a more important effect on sensitivity than crystal packing, however, further study is warranted to rank the general importance of hydrogen bonding versus crystal packing in other explosive systems.

To find a more quantitative method for describing crystal packing effects in this system, we investigated the Kitaigorodskii Packing Index, which is the volume of the molecules in the unit cell divided by the unit cell volume in a crystal.⁴¹ A weak link has been observed by Politzer and coworkers⁶⁰ with impact sensitivity and a similar metric, free space per molecule (with much larger sample sizes than in this report). We have observed in our recent report that the packing index value is lower as expected for PETN–CNH₃Cl than PETN–CNH₃Br.²⁰ However, within this system, the overall trend between packing index and impact sensitivity is the opposite of what is expected: higher values of void space in the crystal structures (lower packing index %) have relatively low sensitivity (Table 6). However, assigning certain sizes to individual atoms in a molecule is a somewhat empirical process, which may give misleading results in this case.

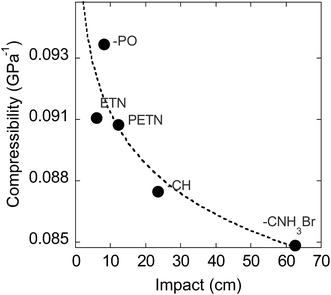
We also examined whether there is any correlation between the elastic compressibility of the derivatives and their impact sensitivities since materials with greater compressibility might be expected to give rise to more adiabatic heating under impacts. In this system of nitrate esters, we observe a correlation between compressibility and impact sensitivity (Fig. 8; Table 6). In summary, qualitative observations (steric hindrance and hydrogen bonding in crystal structures) as well as calculated parameters (compressibility) support the fact that crystal packing and intermolecular interactions have an important role in handling sensitivity when the energetic functional group is held constant. This is the first example of a study that has investigated the relationship between compressibility and impact sensitivity within a nitrate ester system, and gives us a somewhat quantitative method to connect crystal structure properties to handling sensitivity.

Fig. 8 Calculated compressibility vs. impact height (cm).

Conclusions

We have investigated chemical structural modifications on a PETN-based nitrate ester system of explosives, both experimentally and with reactive MD simulations. Modeling results suggest that within this nitrate ester system, reactivity occurs at very similar timescales, though via competing NO₂vs. HONO elimination. Notably, the amines are more reactive by thermal measurements, and are slightly faster to eliminate NO₂ in the simulations, but are least reactive by impact sensitivity measurements. Thermal DSC measurements (over longer timescales – 100 s of minutes) show that later time reactions occur with the amines, after the initial decomposition is over. The results point to the significance of later time reactions in explosive decomposition, and highlight the importance of looking beyond simple treatments to predict explosive sensitivity in a system. A weak trend can be observed in this system between the energy of detonation and handling sensitivity. However, we observe that hydrogen bonding and reduced steric hindrance in the crystal structure correlate most with reduced handling sensitivity of a material, when the energetic functional group stays constant. More quantitatively, the calculated compressibility of each PETN derivative decreases with impact drop height values, supporting the fact that intermolecular interactions and crystal lattice effects are important players in handling sensitivity.

In conclusion, this is the first study to systematically modify the non-energetic substituents in a series of nitrate ester explosives for the purpose of investigating the relationships between basic chemistry, crystal structure properties, and handling sensitivity. This allowed for several important advances in understanding sensitivity: (1) the MD modeling shows that these secondary structural modifications result in only subtle changes to the characteristic reactivity of the nitrate ester group – a topic that has never been directly probed before, and (2) experimental work shows that the resulting changes in hydrogen bonding and crystal packing are the important drivers in ranking the reactivity of the nitrate esters. In a more general view, investigating how chemical structural modifications influence crystal packing is a high impact area for molecular design in the field of chemistry. We have discovered that very small modifications of chemical structure can influence crystal packing significantly and unpredictably, and further work involving more subtle changes to molecular structure is underway.

Experimental

Reagents were purchased from Aldrich and solvents from Fisher Scientific. Infrared spectroscopy measurements were taken using a Thermo Nicolet NEXUS 670 FT-IR, and NMR (nuclear magnetic resonance) experiments were performed on a 400 MHz Bruker Avance system. PETN–CNH₃Cl (MW = 292.59 g mol⁻¹), PETN–CNH₃Br (MW = 337.04 g mol⁻¹), and PETN–CNH₂ (MW = 256.13 g mol⁻¹) were prepared following literature procedures.^19,20

Sensitivity testing

Small-scale sensitivity testing and differential scanning calorimetry (DSC) were performed by the High Explosives Science & Technology Group at Los Alamos National Laboratory. The setup and determination of sensitivity consist of the ERL Type 12 drop hammer (2.5 kg drop weight on a 40 mg sample with a base of 150 grit paper for solid materials, and no grit paper for liquids) and BAM friction sensitivity test machine (fixed porcelain pin and a movable porcelain plate that executes a reciprocating motion at a rate of 141 rpm with a stroke length of 10 mm with applied force varying from 5–360 N). Both the drop weight and friction sensitivity are expressed as the applied load at which initiation will occur 50% of the time, H₅₀ and F₅₀, respectively, and were calculated using the Neyer D-Optimal method. Onset DSC exotherms and endotherms were measured at a 10 °C min⁻¹ ramp rate.

Room temperature impact tests for liquid PETN–CH were performed at ∼70–75 °F (∼21–24 °C). In order to directly compare the solid to the liquid, all tests were performed without the presence of grit paper. For the impact tests of solid PETN–CH at reduced temperature, Table 7, ice packs were placed around the anvil to cool it for approximately 2 hours before data was collected. A thermocouple was placed on top of the anvil, and the temperature was measured before and after each drop test. The temperature was stable at ∼46 °F (7.8 °C) for 15 minutes before tests were collected. The striker was cooled in a refrigerator and removed just prior to the tests. It appears that the striker cooling ability and the sample reaction heating ability competed with each other: once the striker warmed (by drop 4), the heating from sample reaction produced ∼2 °F (−1 °C) increase in temperature (see table below). A total of 12 drops were performed with the results shown below using the microphone readings for Go and No-Go determinations. Drop 9 was slightly ambiguous but was interpreted as a Go based on noise heard by the operators.

Table 7 Impact tests of solid PETN–CH at reduced temperature

Drop/striker	Temp. (°F)	Operator determination	Post observation
1/1	46.8	No	Cooled 1 degree
2/1	46.4	Go	Warmed 2 degrees
3/1	47.9	Snap	None
4/1	47.7	Go	Warmed 2.2 degrees
5/2	47.3	Weak Go, double snap	Cooled 1 degree
6/2	47.5	No Go	Cooled 0.3 degrees
7/2	47.3	Medium Go	Warmed 0.2 degrees
8/3	47.0	Snap	Cooled 1 degree
9/3	46.5	Hard snap, maybe Go	Warmed 0.2 degrees
10/3	47.6	Snap	Cooled 1.3 degrees
11/3	47.3	Weak snap	Cooled 0.8 degrees
12/4	47.4	Go	Warmed 0.4 degrees

---

Synthesis

CAUTION! PETN and the PETN derivatives prepared in this study are very sensitive explosives that should only be handled in an explosives facility by knowledgeable workers.

PETN–CH

Following a related procedure,²¹ 1.67 g of 2-hydroxymethyl-1,3-propanediol was dissolved in a solution of approx. 3 mL concentrated sulfuric acid (H₂SO₄). This solution was added to a freshly prepared solution of 4.9 g 70% nitric acid (HNO₃) + 12.9 g H₂SO₄ in an ice/water bath, and allowed to stir at room temperature for 1.5 h. The solution was poured into approx. 150 mL water and a cloudy, oily precipitate formed. The solution was extracted 3× with diethyl ether (Et₂O), and the Et₂O layer was washed 3× with a concentrated solution of sodium bicarbonate (NaHCO₃). Magnesium sulfate (MgSO₄) was added to the Et₂O layer, then removed, and the Et₂O was evaporated to collect 1.4 g of an oily product (PETN–CH, MW = 241.11 g mol⁻¹). ¹H NMR (acetonitrile) δ: 2.78 (m, 1H), 4.63 (d, 6H). IR spectroscopy showed nitrate ester peaks at 1641 cm⁻¹, 1277 cm⁻¹, and 852 cm⁻¹.

PETN–CMe

Following the above procedure, 1.8 g of 1,1,1-tris(hydroxymethyl)ethane was dissolved in a solution of approx. 1 mL concentrated sulfuric acid (H₂SO₄). This solution was added to a freshly prepared solution of 4.9 g 70% nitric acid (HNO₃) + 12.8 g H₂SO₄ in an ice/water bath, and allowed to stir at room temperature for 1 h. The solution was poured into approx. 150 mL water and a cloudy, oily precipitate formed. The solution was extracted 3× with Et₂O, and the Et₂O layer was washed 3× with a concentrated solution of NaHCO₃. MgSO₄ was added to the Et₂O layer, then removed, and the Et₂O was evaporated to collect approx. 1.5 g of an oily product (PETN–CMe, MW = 255.14 g mol⁻¹). ¹H NMR (acetonitrile) δ: 1.19 (s, 3H), 4.52 (s, 6H). IR spectroscopy showed nitrate ester peaks at 1641 cm⁻¹, 1277 cm⁻¹, and 858 cm⁻¹.

PETN–PO

Following a literature procedure,²² a solution was prepared containing 100% fuming nitric acid (9.96 g), acetic acid (AcOH; 9.48 g), and acetic anhydride (16.14 g). The solution was cooled to 5 °C, and 2.64 g of a solution of 80% tetrakis(hydroxymethyl)phosphonium chloride in water was slowly added dropwise, while keeping the temperature of the solution below 15 °C. The solution was stirred for 45 min, and poured into approx. 110 mL water to precipitate a white solid, which was filtered and washed with water and NaHCO₃ solution. The solid was collected and dissolved in 5–10 mL acetone, any solid remaining was removed, and the solution was poured into approx. 100 mL water to precipitate 1.3 g white powder (PETN–PO, MW = 275.07 g mol⁻¹). ¹H NMR (acetonitrile) δ: 5.09 (d, 6H). IR spectroscopy showed nitrate ester peaks at 1645 cm⁻¹, 1269 cm⁻¹, and 833 cm⁻¹.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Campaign 2 at Los Alamos National Laboratory for funding of this work. This manuscript has been authored by Los Alamos National Security under contract no. DE-AC52-06NA25396 with the U.S Department of Energy. Approved for public release: LA-UR-17-29886. We thank A. M. Giambra and M. Sandstrom for assistance with elemental, thermal, and mechanical sensitivity analysis in the High Explosives Science & Technology Group. In addition, we thank K. Ramos and G. K. Windler for assistance with explosive single crystal XRD.

References

1. A. C. Landerville, I. I. Oleynik and C. T. White, J. Phys. Chem. A, 2009, 113, 12094–12104.
2. B. M. Rice and J. J. Hare, J. Phys. Chem. A, 2002, 106, 1770–1783.
3. A. V. Kimmel, P. V. Sushko, A. L. Shluger and M. M. Kuklja, J. Phys. Chem. A, 2008, 112, 4496–4500.
4. (a) D. M. Dattelbaum, S. A. Sheffield, D. B. Stahl and A. M. Dattelbaum, Influence of Hot Spot Features on the Shock Initiation of Heterogeneous Nitromethane, in Shock Compression of Condensed Matter – 2009, ed. M. Elert, M. D. Furnish, W. W. Anderson, W. G. Proud and W. T. Butler, American Institute of Physics, New York, 2009, pp. 263–266, vol. 1195, AIP Conf. Proc; (b) G. D. Coley and J. E. Field, Combust. Flame, 1973, 21, 335–342.
5. (a) H. H. Cady and A. C. Larson, Acta Crystallogr., 1965, 18, 485–496; (b) J. R. Kolb and H. F. Rizzo, Propellants, Explos. Pyrotech., 1979, 4, 10–16.
6. (a) Y. Ma, A. Zhang, C. Zhang, D. Jiang, Y. Zhu and C. Zhang, Cryst. Growth Des., 2014, 14, 4703–4713; (b) J. C. Bennion, A. McBain, S. F. Son and A. J. Matzger, Cryst. Growth Des., 2015, 15, 2545–2549.
7. E. A. Zhurova, A. I. Stash, V. G. Tsirelson, V. V. Zhurov, E. V. Bartashevich, V. A. Potemkin and A. A. Pinkerton, J. Am. Chem. Soc., 2006, 128, 14728–14734.
8. (a) B. M. Rice, J. P. Larentzos, E. F. C. Byrd and N. S. Weingarten, J. Chem. Theory Comput., 2015, 11, 392–405; (b) A. D. Yau, E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2009, 113, 6166–6171.
9. (a) A. A. Dippold and T. M. Klapötke, J. Am. Chem. Soc., 2013, 135, 9931–9938; (b) J. Evers, M. Gobel, B. Krumm, F. Martin, S. Medvedyev, G. Oehlinger, F. X. Steemann, I. Troyan, T. M. Klapötke and M. I. Eremets, J. Am. Chem. Soc., 2011, 133, 12100–12105; (c) T. M. Klapötke and C. M. Sabate, Chem. Mater., 2008, 20, 3629–3637.
10. R. S. Chellappa, D. M. Dattelbaum, J. D. Coe, N. Velisavljevic, L. L. Stevens and Z. Liu, J. Phys. Chem. A, 2014, 118, 5969–5982.
11. (a) P. Pagoria, Propellants, Explos. Pyrotech., 2016, 41, 452–469; (b) P. Politzer and J. S. Murray, Propellants, Explos. Pyrotech., 2016, 41, 414–425.
12. M. J. Kamlet and H. G. Adolph, Propellants Explos., 1979, 4, 30–34.
13. S. Zeman and M. Jungova, Propellants, Explos. Pyrotech., 2016, 41, 426–451.
14. R. M. Eason and T. D. Sewell, J. Phys. Chem. C, 2012, 116, 2226–2239.
15. R. V. Tsyshevsky, O. Sharia and M. M. Kuklja, J. Phys. Chem. C, 2013, 117, 18144–18153.
16. S. Iyer, Propellants, Explos., Pyrotech., 1982, 7, 37–39.
17. (a) T. M. Klapötke, B. Krumm, R. Ilg, D. Troegel and R. Tacke, J. Am. Chem. Soc., 2007, 129, 6908–6915; (b) W.-G. Liu, S. V. Zybin, S. Dasgupta, T. M. Klapötke and W. A. Goddard III, J. Am. Chem. Soc., 2009, 131, 7490–7491.
18. J. M. Veauthier, D. E. Chavez, B. C. Tappan and D. A. Parrish, J. Energ. Mater., 2012, 28, 229–249.
19. V. W. Manner, D. N. Preston, C. J. Snyder, D. M. Dattelbaum and B. C. Tappan, Tailoring the Sensitivity of Initiating Explosives, in Shock Compression of Condensed Matter – 2015, ed. R. Chau, T. Germann, I. Oleynik, S. Peiris, R. Ravelo and T. Sewell, American Institute of Physics, New York, 2017, p. 040036, vol. 1793, AIP Conf. Proc.
20. T. W. Myers, C. J. Snyder and V. W. Manner, Cryst. Growth Des., 2017, 17, 3204–3209.
21. V. W. Manner, B. C. Tappan, B. L. Scott, D. N. Preston and G. W. Brown, Cryst. Growth Des., 2014, 14, 6154–6160.
22. J. Lutfalla, C. Amalric and J. P. Rafard, Ind. Chim. Belge, 1967, 32, 623–625.
23. M. M. Sandstrom, G. W. Brown, D. N. Preston, C. J. Pollard, K. F. Warner, D. N. Sorensen, D. L. Remmers, J. J. Phillips, T. J. Shelley, J. A. Reyes, P. C. Hsu and J. G. Reynolds, Propellants, Explos. Pyrotech., 2015, 40, 109–126.
24. T. Urbanski, Chemistry and Technology of Explosives, Pergamon Press, New York, NY, 1965, pp. 52–54, vol. 2.
25. (a) G. Zhang and B. L. Weeks, Propellants, Explos. Pyrotech., 2010, 35, 440–445; (b) J. E. Plum, The Effect of Low Temperatures on Impact Sensitivity of TNT, Thesis, Naval Postgraduate School, Department of the Navy, Monterey, CA, 1972.
26. (a) M. J. Cawkwell, D. S. Montgomery, K. J. Ramos and C. A. Bolme, J. Phys. Chem. A, 2017, 121, 238–243; (b) E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1996, 25, 1–523.
27. M. J. Cawkwell, D. J. Luscher, F. L. Addessio and K. J. Ramos, J. Appl. Phys., 2016, 119, 185106.
28. ASTM International E698-16, http://www.astm.org.
29. (a) K. A. Al-Farhan, J. Crystallogr. Spectrosc. Res., 1992, 22, 687–689; (b) A. C. Durrell, H. B. Gray, N. Hazari, C. D. Incarvito, J. Liu and E. C. Y. Yan, Cryst. Growth Des., 2010, 10, 1482–1485.
30. (a) L. Brammer, E. A. Bruton and P. Sherwood, Cryst. Growth Des., 2001, 1, 277–290; (b) N. K. Duggirala, G. P. F. Wood, A. Fischer, L. Wojitas, M. L. Perry and M. J. Zaworotko, Cryst. Growth Des., 2015, 15, 4341–4354.
31. E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005.
32. J. P. Guthrie, J. Phys. Chem. A, 2001, 105, 9196.
33. D. C. Sorescu and B. M. Rice, J. Phys. Chem. C, 2010, 114, 6734.
34. S. Bastea, L. E. Fried, W. M. Howard, I.-F. W. Kuo, P. C. Souer and P. Vitello, Cheetah 8.0, Lawrence Livermore National Laboratory, 2015.
35. P. Cooper, Explosives Engineering, Wiley-VCH, Inc., New York, NY, 1996.
36. K. Raha and J. S. Chhabra, J. Hazard. Mater., 1993, 34, 385–391.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
38. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
39. (a) G. Kresse and J. Joubert, Phys. Rev. B, 1999, 59, 1759; (b) G. Blochl, Phys. Rev. B, 1994, 50, 17953.
40. P. Vinet, J. Ferrante, J. R. Smith and J. H. Rose, J. Phys. C, 1986, 19, L467.
41. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, D65, 148.
42. PLATON Program, Multipurpose Crystallographic Tool©, ed. A. L. Spek, Utrecht University, Padualaan 8, 3584 CH Utrecht, The Netherlands, 1980–2016, URL, http://www.cryst.chem.uu.nl/spek/platon/.
43. Using assumption from Cheetah 8.0 that Cl is converted to HCl, Br is converted to Br₂, and P is converted to P₂O₅.
44. (a) T. Frauenheim, G. Seifert, M. Elstner, Z. Hajnal, G. Jungnickel, D. Porezag, S. Suhai and R. Scholz, Phys. Status Solidi B, 2000, 217, 41; (b) M. Elstner, D. Poresag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B, 1998, 58, 7260.
45. (a) E. J. Reed, M. R. Manaa, L. E. Fried, K. R. Glaesemann and J. D. Joannopoulos, Nat. Phys., 2008, 4, 72; (b) M. R. Manaa, E. J. Reed, L. E. Fried and N. Goldman, J. Am. Chem. Soc., 2009, 131, 5483–5487.
46. A. Krishnapriyan, P. Yang, A. M. N. Niklasson and M. J. Cawkwell, J. Chem. Theory Comput., 2017, 13, 6191.
47. (a) M. J. Cawkwell, E. M. Kober, R. Perriot, T. W. Myers and V. W. Manner, Molecular Dynamics Simulations of the First Reactions in Nitrate Ester-based Explosives, in Shock Compression of Condensed Matter-2017, AIP Conference Proceedings, ed. R. Chau, T. C. Germann and J. M. D. Lane, American Institute of Physics, Melville, NY, accepted, 2018; (b) M. J. Cawkwell and E. M. Kober, manuscript in preparation; (c) E. M. Kober, manuscript in preparation.
48. E. Martinez, M. J. Cawkwell, A. F. Voter and A. M. N. Niklasson, J. Chem. Phys., 2015, 142, 154120.
49. M. J. Cawkwell, A. M. N. Niklasson and D. M. Dattelbaum, J. Chem. Phys., 2015, 142, 064512.
50. A. M. N. Niklasson, Phys. Rev. Lett., 2008, 100, 123004.
51. See, for example, the variation in values for RDX when collected on different instruments at different labs, and the discussion therein: R. M. Doherty and D. S. Watt, Propellants, Explos. Pyrotech., 2008, 33, 4–13.
52. D. N. Preston, G. W. Brown, B. C. Tappan, D. Oschwald and M. Schoonover, J. Phys.: Conf. Ser., 2014, 500, 182033.
53. A. A. Denisaev, B. L. Korsunskii, V. I. Pepekin and Y. N. Matyushin, Combust. Explos. Shock Waves, 2010, 46, 74–80.
54. F. P. Bowden and A. D. Yoffe, Initiation and Growth of Explosion in Liquids and Solids, 1952, Cambridge at the University Press, ch. 3.
55. W. C. Davis, High Explosives: The Interaction of Chemistry and Mechanics, in Los Alamos Science, Los Alamos National Laboratory, 1981, vol. 2, number 1, p. 70.
56. J. Wenograd, Trans. Faraday Soc., 1961, 57, 1612.
57. M. J. Kamlet, The relationship of Impact Sensitivity with Structure of Organic High Explosives. I. Polynitroaliphatic Explosives, Proceedings of the 6^th Symposium on Detonation, ONR Report ACR 221, San Diego, CA, 1976, p. 312.
58. V. W. Manner, T. W. Myers, M. J. Cawkwell, E. M. Kober, G. W. Brown, H. Tian, C. J. Snyder and D. N. Preston, Understanding and manipulating the sensitivity of nitrate esters, in Shock Compression of Condensed Matter-2017, AIP Conference Proceedings, ed. R. Chau, T. C. Germann and J. M. D. Lane, American Institute of Physics, Melville, NY, accepted, 2018.
59. S. Zeman, Sensitivities of High Energy Compounds, in High Energy Density Compounds, Structure & Bonding, ed. T. M. Klapotke, Springer, Heidelberg, Germany, 2007, pp. 195–271, vol. 125.
60. P. Politzer and J. S. Murray, Adv. Quant. Chem., 2014, 69, 1–30.
61. C_V is related to C_P using the equation C_V = C_P + (α₂T)/(ρβ), where α = thermal expansion coefficient, T = temperature, ρ = density, and β = bulk modulus. We can assume T and β are similar for all derivatives, so the higher thermal expansion of the liquids likely contributes to their larger values. The higher density of PETN–PO would be expected to result in a lower value for C_P..
62. It is often presumed that hydrogen bonding represents a strong contribution to the heat capacity of a system based on the high specific heat of water and ammonia. It is important to note that although the heat capacity per mass values are very high, it is primarily because of the low molecular weight of the molecules and high number of hydrogen atoms. CH₄ has a similarly high specific heat. See for example, R. S. Berry, S. A. Rice and J. Ross, Physical Chemistry, John Wiley & Sons, New York, NY, 1980, Ch. 14, and D. A. McQuarrie, Statistical Mechanics, Harper & Row, New York NY, 1973, Ch. 11. Hydrogen bonding does contribute somewhat by lowering the vibrational frequencies, so that the system behaves more classically, but this is a secondary effect.
63. P. Politzer and J. S. Murray, J. Mol. Model., 2015, 21, 262.
64. Using the equations F = 2M_f/t, where M_f = 2.5 (velocity of the striker), and t = (time it takes the striker to compress the sample and rebound) and P = F/A, where A = (area of the sample ≈ 4 mm × 4 mm = 1.6 × 10⁻⁵ m₂). We do not know the value for t, but if we estimate it as 0.1 s, a drop height of 15 cm [v = gt for compression and rebound: (2 × 9.8 m s⁻² × 0.15 m)^1/2 = 1.71 m s⁻¹] gives F = 2 × 4.3 m s⁻¹/0.1 s = 85.7 N, and P = F/A = 0.0054 GPa. A time of 0.01 s gives P = 0.054 GPa.
65. M. A. Hiskey, M. J. Hatch and J. C. Oxley, Propellants, Explos. Pyrotech., 1991, 16, 40–42.
66. (a) C. Zhang, J. Phys. Chem. B, 2007, 111, 14295; (b) C. Zhang, X. Wang and H. Huang, J. Am. Chem. Soc., 2008, 130, 8359.
67. M. M. Kuklja and S. N. Rashkeev, Appl. Phys. Lett., 2007, 90, 151913.
68. M. R. Manaa, E. J. Reed, L. E. Fried and N. Goldman, J. Am. Chem. Soc., 2009, 131, 5483–5487.
69. T. R. Gibbs and A. Popolato, LASL Explosives Property Data, University of California Press, 1980.
70. J. R. Holden, Acta Crystallogr., 1967, 22, 545.
71. (a) J. J. Dick and J. P. Ritchie, J. Appl. Phys., 1994, 76, 2726; (b) J. J. Dick, J. Appl. Phys., 1997, 81, 601.
72. D. J. Luscher, F. L. Addessio, M. J. Cawkwell and K. J. Ramos, J. Mech. Phys. Solid., 2017, 98, 63–86.
73. (a) H. H. Cady and A. C. Larson, Acta Crystallogr., 1965, 18, 485–496; (b) J. R. Kolb and H. F. Rizzo, Propellants, Explos., Pyrotech., 1979, 4, 10–16.
74. N. V. Latypov and J. Bergman, Tetrahedron, 1998, 54, 11525–11536.
75. R. D. Gilardi and R. J. Butcher, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, o657–o658.
76. D. E. Chavez, L. Hill, M. Hiskey and S. Kinkead, J. Energ. Mater., 2000, 18, 219–236.
77. (a) J. Trotter, Acta Crystallogr., 1963, 16, 698–699; (b) H. H. Cady and A. C. Larson, Acta Crystallogr., 1975, B31, 1864–1869.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1582617 and 1582618. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc00903a

‡ Current address: Lawrence Livermore National Laboratory, USA.

---