Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Precise control of pore hydrophilicity enabled by post-synthetic cation exchange in metal–organic frameworks†
Ashley M.
Wright
 a,
Adam J.
Rieth
a,
Adam J.
Rieth
 a,
Sungwoo
Yang
b,
Evelyn N.
Wang
b and
Mircea
Dincă
a,
Sungwoo
Yang
b,
Evelyn N.
Wang
b and
Mircea
Dincă
 *a
*a
aDepartment of Chemistry, Massachusetts Institute of Technology, 77 Mass Ave., Cambridge, Massachusetts 02139, USA. E-mail: mdinca@mit.edu
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, 77 Mass Ave., Cambridge, Massachusetts 02139, USA
First published on 21st March 2018
Abstract
The ability to control the relative humidity at which water uptake occurs in a given adsorbent is advantageous, making that material applicable to a variety of different applications. Here, we show that cation exchange in a metal–organic framework allows precise control over the humidity onset of the water uptake step. Controlled incorporation of cobalt in place of zinc produces open metal sites into the cubic triazolate framework MFU-4l, and thereby provides access to materials with uptake steps over a 30% relative humidity range. Notably, the MFU-4l framework has an extremely high water adsorption capacity of 1.05 g g−1, amongst the highest known for porous materials. The total water capacity is independent of the cobalt loading, showing that cation exchange is a viable route to increase the hydrophilicity of metal–organic frameworks without sacrificing capacity.
Introduction
Mainstream deployment of devices such as adsorption heat pumps (AHPs) and atmospheric water generators (AWGs) require materials that adsorb water vapor below 100% relative humidity (RH).1–3 The salient properties of the adsorbent depend on the specific application but generally require water stability, water sorption with a steep uptake step at a desirable relative humidity, and a high total uptake capacity. Metal–organic frameworks (MOFs) have emerged as strong candidate materials for applications involving water vapor sorption due to their record maximal water uptakes, engendered by very high internal void volumes, and tunable material properties. Although many MOFs are unstable to water vapor, MOFs that use azolate linkers such as pyrazoles, imidazoles, and triazoles, exhibit enhanced stability towards polar molecules.4–7The functioning parameters of an AHP or an AWG system are determined largely by the position and the steepness of the uptake step, where most of the water is adsorbed. For instance, sorbents that are very hydrophilic may adsorb water at low RH, which is advantageous for applications such as water vapor capture in desert areas, or AHP systems requiring large temperature gradients. However, these advantageous properties come with the caveat that high adsorbent regeneration temperatures are required to remove the water once adsorbed. Control over the position (%RH) of the uptake step is therefore vital to achieve a desirable driving force for water uptake while minimizing the required regeneration temperature.
Due to their modular nature, MOFs are well positioned for precise tuning of the uptake step with regard to both position (i.e. RH), and steepness (which can be controlled by modulating the pore size). Control over the position of the uptake step has previously been demonstrated through functionalization of the normally hydrophobic organic linkers.8–11 However, installation of polar groups on aromatic rings normally results in a reduction of the pore volume, which negatively impacts the overall uptake. An alternative strategy to increase the hydrophilicity of a MOF is to incorporate open metal sites through cation exchange. Cation exchange can be used to functionalize the secondary building units in a variety of MOFs.12 By substituting coordinatively saturated metals with cations that can favorably achieve higher coordination numbers, the density of open metal sites where water can bind will increase, consequently increasing hydrophilicity with negligible effect on the pore volume. Herein, we report the first example of water uptake step tuning via post-synthetic cation exchange. Increasing substitution of five coordinate-accommodating Co(II) ions for tetrahedral Zn(II) in the cubic triazolate framework MFU-4l results in precise control of the water uptake step over a range of ∼30% RH.2,6,7
Results and discussion
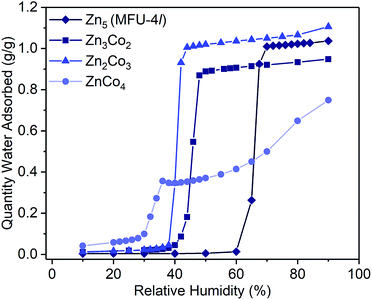
Examination of the water sorption properties of MFU-4l, Zn5Cl4(BTDD)3 (1, BTDD2− = bis(1,2,3-triazolo[4,5-b],[4′,5′-i])dibenzo[1,4]dioxin), at 25 °C revealed a type IV isotherm. Very little water is adsorbed between 0–65% RH, but once pore filling is initiated at 65% RH, the uptake step is large and steep with 1.01 gH2O gMOF−1, adsorbed by 70% RH (Fig. 1). The saturation uptake capacity at 95% RH is 1.05 gH2O gMOF−1 indicating most of the water is adsorbed during the sharp uptake step. Notably, the water uptake capacity is amongst the highest reported for any material, surpassed only by MIL-101(Cr) which saturates at 1.3 gH2O gMOF−1.2,8 Upon water desorption, a small hysteresis loop with a gap of ∼10% RH is observed. For comparison, the isoreticular material MFU-4, which displays a smaller pore adsorbs 0.42 gH2O gMOF−1 with an uptake step between 10% and 35% RH and also exhibits a small hysteresis loop.13 Material 1 is stable under water sorption conditions. It retains its crystallinity and porosity as evidenced by N2 sorption analysis, which revealed a Brunauer–Emmett–Teller (BET) surface area of 3423 m2 g−1 after water sorption measurements, in line with the BET surface area of 3525 m2 g−1 observed for the original MFU-4l (Fig. S2†).With this near-record water saturation capacity, we envisioned that MFU-4l could serve as a versatile water sorption material if its hydrophilicity could also be modulated in a systematic manner. To do so, we aimed to take advantage of the metal nodes, where four of the 5 Zn2+ ions comprising the secondary building unit (SBU) are peripheral and exposed to the pore surface in a trispyrazolylborate (Tp)-like environment.14 Because these Zn2+ are tetrahedral and are not known to bind additional solvent molecules, we surmised that replacing zinc ions with Co2+ ions, as previously reported, would enable up to four water molecules binding to each SBU (one for each peripheral cation) and potentially enhanced hydrophilicity (Scheme 1).15–20 Indeed, whereas the majority of reported TpZn compounds are predominately four-coordinate,21,22 TpCo complexes prefer higher coordination numbers (coordination numbers of 5 and 6 account for >72% of 200 reported structures) with many examples featuring monodentate ligands, such as TpCoCl(THF).23
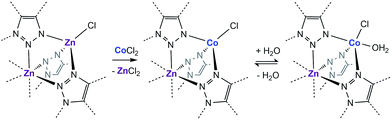 | ||
| Scheme 1 Cation exchange of the peripheral Zn with Co and the subsequent coordination of water in a fragment of the secondary building unit of MFU-4l. | ||
To systematically test the effect of Co2+ substitution on the water uptake properties of MFU-4l, we prepared materials where, on average, two, three, or all peripheral Zn ions were exchanged with Co2+ in each SBU to give Zn2.9Co2.1Cl4(BTDD)3 (Zn3Co2, 2), Zn1.8Co3.2Cl4(BTDD)3 (Zn2Co3, 3), and ZnCo4Cl4(BTDD)3 (ZnCo4, 4).16 Water adsorption experiments of activated 2 and 3 showed a type IV isotherm with a steep uptake step in a narrow RH range (Fig. 1). Notably, the pore filling step is shifted to lower RH with increasing cobalt loading (α values:24: 1, 0.65; 2, 0.45; 3, 0.40). Furthermore, the water uptake prior to the pore filling step increased with higher Co loadings, which we attribute to an equilibrium between tetrahedral Co2+ and water-bound 5-coordinate Co2+. Notably, the amount of water adsorbed prior to the uptake step is approximately one water molecule per cobalt for 2–4. Adsorption of water prior to the pore filling step enhances pore hydrophilicity, resulting in an onset of capillary condensation at lower RH. Importantly, the total uptake capacity is unaffected by the cobalt loading and ranges between 0.95–1.10 gH2O gMOF−1 for 1–3 (Table 1). Materials 1–3 are stable under the water adsorption conditions and retain crystallinity and porosity after exposure to 0.95 RH as revealed by PXRD (Fig. S1†) and surface area analysis (Fig. S2–4†). Fitting N2 adsorption isotherms at 77 K to the BET equation gave apparent surface areas of 2760 and 2799 m2 g−1 for 2 and 3, respectively, although lower than the initial values of 3349 and 3543 m2 g−1 (Fig. S3 and S4†).
| Compound | Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co ratio Co ratio |
Total uptake capacity (g g−1) | α-value (RH) |
|---|---|---|---|
| 1 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
1.04 | 0.65 |
| 2 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.95 | 0.44 |
| 3 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
1.11 | 0.40 |
| 4 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
0.75 | ∼0.30 |
When all four peripheral Zn atoms are exchanged with Co to give 4, the framework becomes unstable under measurement conditions. The water adsorption isotherm of 4 features a stepwise adsorption curve. An initial onset of pore filling occurs at 30% RH with a sharp increase until 36% RH when the water capacity reaches 0.35 gH2O gMOF−1 (Fig. 1). Subsequently, a second gradual adsorption occurs with increasing water uptake until saturation at 90% RH, giving a total water uptake of 0.75 gH2O gMOF−1. The isotherm behavior is characteristic of pore collapse at ∼35% RH followed by swelling or condensation of water. Notably, the desorption curve was hysteretic and did not follow the adsorption curve, confirming that a phase change has occurred (Fig. S11†). In agreement with decomposition of the MOF, the surface area after water adsorption was significantly diminished to 680 m2 g−1, corresponding to a loss of 80% compared to pristine, activated 4 prior to water vapor exposure (Fig. S5†). The phase change observed upon water exposure also occurs with loss of crystallinity, as evidenced by an amorphous PXRD pattern (Fig. S1†).
The water desorption profiles were hysteretic irrespective of the cobalt loading. This is unexpected because hysteresis is generally associated with capillary condensation and is a feature of porous materials with a critical diameter (Dc) greater than 20 Å.7 MFU-4l, however, is a 3D cubic network with a network of three-dimensionally connected void spaces with pore diameters ranging between 12.0 Å and 18.6 Å. It is particularly noteworthy that the smaller-pore MFU-4 framework also exhibits a slight hysteresis upon an adsorption/desorption cycle of water and its pore sizes are significantly below the Dc.25 Alternative reasons for hysteresis in water adsorption by MOFs have been put forward. Recently, the Do–Do model for water adsorption and desorption in activated carbons, has been invoked to explain hysteresis in a microporous MOF.26 In this model, water clusters form at sites where water can bind or hydrogen bond until they reach a critical size where they can be sustained within the pore.27,28 The smaller water clusters subsequently combine to yield larger superclusters, filling the pores in this process. Upon desorption, more energy is required to break up these superclusters back into small water clusters to pass through small pore windows, resulting in hysteresis loops. Therefore, the observed hysteresis may be partially attributed to the topology and pore connectivity of the MOF. In MFU-4l, pore windows of only 9.1 Å interconnect larger pore cages. The constricted pore aperture may impede the flow of larger water superclusters that require greater energy to be broken up.
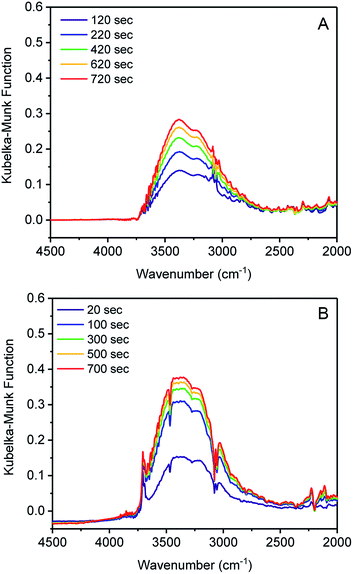
Initiation of water clustering can occur by water coordinating to an open metal site or by hydrogen bonding with a polar functional group.29 Evidence for water binding to cobalt was obtained by monitoring the adsorption of water in 1 and 3 using diffuse-reflectance IR spectroscopy (DRIFTS). Argon with controlled relative humidity of 80% or 60% was flowed over samples of 1 and 3, respectively, providing RH levels in slight excess of the position of the water uptake step for both samples. IR spectra were recorded periodically over 20 minutes. Inspection of the difference spectrum for 1 revealed an increase in intensity of two broad bands centered at 3375 and 3200 cm−1 assignable to water adsorbed in the pore (Fig. 2A).29–31 By contrast, when 3 was exposed to water, new bands at 3707 cm−1 and 3694 cm−1 were initially observed. These remained constant over 1200 seconds (20 min), while the stretching bands of pore-adsorbed water at 3360 and 3210 cm−1 continued to grow in intensity (Fig. 2B). An additional band at 1641 cm−1 also grows in intensity and is assigned to the bending mode of water (Fig. S12†).30,31 Bands above 3500 cm−1 are assignable to O–H stretches in water with minimal hydrogen bonding.32 The stretch at 3707 cm−1 is assigned to a cobalt-bound water (Co ← OH2) and the peak at 3694 cm−1 is assigned to the proximal water molecule hydrogen-bound to the Co ← OH2 group (Co ← OH2⋯H2O).32 Notably, these bands are absent in 1, which again supports the assertion that water is binding to tetrahedral Co2+, but not to tetrahedral Zn2+. O–H stretching energies lower than 3500 cm−1 are associated with water with many hydrogen bonds, as would be expected for bulk water adsorbed in the pores. Over time the sharp bands at 3707 and 3694 cm−1 disappear as the bulk water stretches become much more intense (Fig. S14†). The IR data therefore supports the water clustering mechanism for pore filling, wherein water initially clusters at the cobalt sites and subsequently adsorbs within the pore. When D2O was used, the broad feature was shifted to 2520 cm−1 and the Co-OD2 IR stretch was observed at 2720 cm−1. Overall, these results support our hypothesis that water coordination to the open metal center of cobalt is important for lowering the relative humidity/pressure of adsorption.
Conclusions
The above results illustrate how incorporation of open metal sites through cation exchange provides precise control over the relative pressure of water uptake. The position of the uptake step can be varied over a 30% RH range by controlling the number of sites where water can bind and initiate water clustering, a process which is proposed to play an important role in water adsorption.24,33 It is also notable that cation exchange does not affect the total water adsorption capacity of the material. The change from zinc to cobalt has a trivial effect on the pore volume and therefore the amount of water adsorbed is within a consistent range for all cobalt loadings. In comparison, alternative methods of increasing pore hydrophilicity such as functionalization with polar organic groups can result in severely reduced uptake capacities. This was the case, for instance, with NH2, NO2, and SO3H derivatives of MIL-101, which adsorb 30–50% less water than their parent material.8 These results therefore highlight post-synthetic cation exchange as an alternative method to systematically tune the relative pressure at which water adsorption occurs in MOFs, with cobalt-exchanged MFU-4l as an example with near-record, tunable water sorption capacities relevant to water sorption technologies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Ford Motor Company. AJR is supported by the Tata Center for Technology and Design. Fundamental studies of cation exchange in MOFs were supported through a CAREER grant from the National Science Foundation to M. D. (DMR-1452612).Notes and references
- M. F. De Lange, K. J. F. M. Verouden, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Chem. Rev., 2015, 115, 12205–12250 CrossRef CAS PubMed.
- H. Furukawa, F. Gándara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS PubMed.
- H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434 CrossRef CAS PubMed.
- V. Colombo, S. Galli, H. J. Choi, G. D. Han, A. Maspero, G. Palmisano, N. Masciocchi and J. R. Long, Chem. Sci., 2011, 2, 1311 RSC.
- H. J. Choi, M. Dincă, A. Dailly and J. R. Long, Energy Environ. Sci., 2010, 3, 117–123 CAS.
- A. J. Rieth, Y. Tulchinsky and M. Dincă, J. Am. Chem. Soc., 2016, 138, 9401–9404 CrossRef CAS PubMed.
- A. J. Rieth, S. Yang, E. N. Wang and M. Dincă, ACS Cent. Sci., 2017, 3, 668–672 CrossRef CAS PubMed.
- G. Akiyama, R. Matsuda, H. Sato, A. Hori, M. Takata and S. Kitagawa, Microporous Mesoporous Mater., 2012, 157, 89–93 CrossRef CAS.
- C. R. Wade, T. Corrales-Sanchez, T. C. Narayan and M. Dincă, Energy Environ. Sci., 2013, 6, 2172 CAS.
- B. P. Biswal, S. Kandambeth, S. Chandra, D. B. Shinde, S. Bera, S. Karak, B. Garai, U. K. Kharul and R. Banerjee, J. Mater. Chem. A, 2015, 3, 23664–23669 CAS.
- G. E. Cmarik, M. Kim, S. M. Cohen and K. S. Walton, Langmuir, 2012, 28, 15606–15613 CrossRef CAS PubMed.
- C. K. Brozek and M. Dincă, Chem. Soc. Rev., 2014, 43, 5456–5467 RSC.
- S. Biswas, M. Grzywa, H. P. Nayek, S. Dehnen, I. Senkovska, S. Kaskel and D. Volkmer, Dalton Trans., 2009, 9226, 6487–6495 RSC.
- D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832–5836 CrossRef CAS PubMed.
- D. Denysenko, J. Jelic, K. Reuter and D. Volkmer, Chem.–Eur. J., 2015, 21, 8188–8199 CrossRef CAS PubMed.
- D. Denysenko, T. Werner, M. Grzywa, A. Puls, V. Hagen, G. Eickerling, J. Jelic, K. Reuter and D. Volkmer, Chem. Commun., 2012, 48, 1236–1238 RSC.
- R. J. Comito, K. J. Fritzsching, B. J. Sundell, K. Schmidt-Rohr and M. Dincă, J. Am. Chem. Soc., 2016, 138, 10232–10237 CrossRef CAS PubMed.
- E. D. Metzger, C. K. Brozek, R. J. Comito and M. Dincă, ACS Cent. Sci., 2016, 2, 148–153 CrossRef CAS PubMed.
- S. Trofimenko, Chem. Rev., 1993, 93, 943–980 CrossRef CAS.
- C. K. Brozek and M. Dincă, Chem. Commun., 2015, 51, 11780–11782 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, 72, 171–179 CrossRef CAS.
- H. Vahrenkamp, Dalton Trans., 2007, 9226, 4751 RSC.
- K. Uehara, S. Hikichi and M. Akita, J. Chem. Soc., Dalton Trans., 2002, 3529 RSC.
- J. Canivet, J. Bonnefoy, C. Daniel, A. Legrand, B. Coasne and D. Farrusseng, New J. Chem., 2014, 38, 3102 RSC.
- S. Biswas, M. Grzywa, H. P. Nayek, S. Dehnen, I. Senkovska, S. Kaskel and D. Volkmer, Dalton Trans., 2009, 9226, 6487 RSC.
- R. G. AbdulHalim, P. M. Bhatt, Y. Belmabkhout, A. Shkurenko, K. Adil, L. J. Barbour and M. Eddaoudi, J. Am. Chem. Soc., 2017, 139, 10715–10722 CrossRef CAS PubMed.
- D. D. Do and H. D. Do, Carbon, 2000, 38, 767–773 CrossRef CAS.
- D. D. Do, S. Junpirom and H. D. Do, Carbon, 2009, 47, 1466–1473 CrossRef CAS.
- K. Tan, S. Zuluaga, Q. Gong, P. Canepa, H. Wang, J. Li, Y. J. Chabal and T. Thonhauser, Chem. Mater., 2014, 26, 6886–6895 CrossRef CAS.
- A. Vimont, J. M. Goupil, J. C. Lavalley, M. Daturi, S. Surblé, C. Serre, F. Millange, G. Férey and N. Audebrand, J. Am. Chem. Soc., 2006, 128, 3218–3227 CrossRef CAS PubMed.
- M. Falk, Spectrochim. Acta, Part A, 1984, 40, 43–48 CrossRef.
- K. Tan, S. Zuluaga, Q. Gong, P. Canepa, H. Wang, J. Li, Y. J. Chabal and T. Thonhauser, Chem. Mater., 2014, 26, 6886–6895 CrossRef CAS.
- N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575–10612 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00112j |
| This journal is © The Royal Society of Chemistry 2018 |