Using knowledge space theory to compare expected and real knowledge spaces in learning stoichiometry

Abstract

This paper proposes a novel application of knowledge space theory for identifying discrepancies between the knowledge structure that experts expect students to have and the real knowledge structure that students demonstrate on tests. The proposed approach combines two methods of constructing knowledge spaces. The expected knowledge space is constructed by analysing the problem-solving process, while the real knowledge space is identified by applying a data-analytic method. These two knowledge spaces are compared for graph difference and the discrepancies between the two are analysed. In this paper, the proposed approach is applied to the domain of stoichiometry. Although there was a decent agreement between expected and real knowledge spaces, a number of relations that were not present in the expected one appeared in the real knowledge space. The obtained results led to a general conclusion for teaching stoichiometry and pointed to some potential improvements in the existing methods for evaluating cognitive complexity.

---

Introduction

In developed societies, there is a significant decline in students’ interest in learning chemistry (Hofstein and Mamlok-Naaman, 2012; Stuckey and Eiliks, 2014). Numerous studies have shown that students perceive chemistry as a subject that is hard to comprehend (Gabel, 1999; Özmen, 2004; Sirhan, 2007). Some of the most important factors that make chemistry a difficult subject to learn are the abstract nature of its concepts, a large number of entities being studied, shifting among the levels of representations of chemical phenomena and the specific language used to describe them. As cited in Barak and Dori (2005) and Özmen (2004), difficulties in learning chemistry are often related to its abstract concepts and unobservable particles. Gabel (1999) recognised additional factors such as the need for constant shifting among the levels of chemistry representations, and frequent use of mathematical symbols, formulae and equations to express relations at the macroscopic and submicroscopic levels. Another specific difficulty is related to chemistry language. The use and meaning of some words in chemistry can be different from their use and meaning in everyday life (Gabel, 1999). Thus, there are a number of students who fail to adopt the basic chemical concepts during primary education, forming misconceptions, which will prevent them from mastering more complex chemical concepts in their future education. Therefore, the importance of proposing tools to identify and overcome such misconceptions has been emphasized by Voska and Heikkinen (2000), Milenković et al. (2016a), Milenković et al. (2016b), Yan and Subramaniam (2018), etc. In addition to the difficulties of the subject itself and inherent complexity of phenomena being studied, problems in studying chemistry sometimes result from inadequate instructions as teachers sometimes do not fully perceive students’ knowledge (Osman and Sukor, 2013). The gap between teachers' expectations and students' real learning in chemistry could be explained with pedagogical content knowledge (PCK). The concept of PCK observes the importance of transforming the content knowledge per se into content knowledge adequate for teaching (Park and Oliver, 2008). Numerous studies have indicated that chemistry teachers might have difficulties in transforming chemistry content knowledge into a comprehensive form for teaching, as well as for students' learning (Van Driel et al., 2002; Okanlawon, 2010). PCK indicates that, for teachers, it is not enough to be able to comprehend content knowledge for themselves (Park and Oliver, 2008), but also to consider their students' learning processes, conceptions and difficulties (Van Driel et al., 2002). Sometimes teachers occasionally plan their instruction without taking into consideration the real students’ knowledge structures, but rather expected, which should result from the process of education. However, there are often significant differences between such expected and real knowledge structures (Segedinac et al., 2011).

Our research introduces a novel approach to the evaluation of experts’ comprehension of the way in which students understand the domain. The approach is based on knowledge space theory (KST), and it allows the construction of the knowledge structure that experts expect students to have and the real knowledge structure that students demonstrate on tests and the comparison of the two. The proposed approach is applied to the domain of stoichiometry, and from the analysis of the differences between the expected and real knowledge structures, general implications for teaching stoichiometry are derived.

Theoretical background

Knowledge space theory

Most of the traditional educational settings use quantitative methods for evaluating students’ knowledge that reduce it to a single grade (Falmagne and Doignon, 2011). Real students’ knowledge structure, i.e. a particular set of skills that lead to the achievement represented by this single grade, is being ignored. Knowledge space theory (KST) introduces techniques of mathematical modelling and evaluation of the structure of students’ knowledge and offers new possibilities for keeping track of students’ achievement and guiding the learning process.

If students’ knowledge is to be modelled using KST, it has to be represented by a finite set of problems, such that each of them has exactly one correct answer. That means that KST is suitable for representing conceptual knowledge, but it is not adequate, for example, when representing tacit knowledge. The set of problems – called a domain – should be large enough to contain fine-grained, representative coverage of the field (Falmagne and Doignon, 2011). In fact, each task of the domain has to clearly represent the skill required to address that task. It means that a particular student's skill could be represented by several tasks of various complexities.

Skills that a student possesses are being represented by a set of problems which could be answered (solved) correctly under ideal conditions, namely the knowledge state (Falmagne and Doignon, 2011). Taking into consideration that assessment never occurs under ideal conditions, students’ answers are always afflicted by lucky guesses and accidental mistakes. Therefore, the knowledge state cannot be observed directly, but it has to be inferred from the student's answers and the characteristics of the domain itself.

For a test with n problems, there can be 2ⁿ knowledge states. This means that the set of knowledge states for a non-trivial domain is very large; for example, if a test contains 20 problems, there will be 1 048 576 potential knowledge states. Luckily, most of these knowledge states cannot be achieved by a student. For instance, if a student is not able to solve a task wherein the mass of a product is required, and the mass of a reactant and the chemical equation are given, he or she will not be able to solve an analogous task wherein the equation is not given.

This fact allows us to construct a knowledge structure that represents the set of all possible knowledge states for a given domain. For every domain it is assumed that there is an empty knowledge state, demonstrating that a student has mastered none of the skills required to solve the problems and that there is a knowledge state containing all the problems, representing that a student has mastered all of the assessed skills.

One particularly significant family of knowledge structures is that in which mastering new skills represented by the domain problems always leads to some knowledge states in the domain. In such knowledge structures, for any knowledge states the K₁ and K₂ union (K₁UK₂) is a knowledge state as well, meaning that the knowledge structure is U-closed. Such knowledge structures are identified as knowledge spaces (Falmagne, 1989; Albert and Kaluscha, 1997).

An important characteristic of knowledge spaces is that they can be represented by a surmise relation that assigns a set of preconditions to each problem. For a set of problems, it is said that they are preconditions of a problem p if a student has to be able to solve them in order to be able to solve the problem p. The problem p surmises the problems in the mentioned set. A student needs the prior knowledge and understanding assessed by the problems surmised by the problem p for solving the problem p.

A special family of knowledge spaces consists of those in which each problem has exactly one set of preconditions, meaning that they are not only U-closed but also ∩-closed. In such knowledge spaces a surmise relation is quasi-ordering, i.e. it is reflexive and transitive, and can be defined as follows: “problem a surmises problem b, if we know that a student is able to solve the problem a, we can infer that student is also able to solve the problem b” (Segedinac et al., 2011). In this paper, students’ knowledge is represented by such knowledge spaces.

KST can give significant contributions to the chemical education due to the fact that knowing knowledge structures can help in overcoming discrepancies among teachers, textbooks and syllabi concerning conceptual organization and adequate instructional strategies. This research proposes one such method which compares the expected knowledge space, constructed by experts, with the real knowledge space, constructed by analysing test results.

Methods for identifying knowledge spaces

There are a number of methods to identify knowledge spaces. According to Segedinac et al. (2010), these methods can be classified into:

(I) Those that construct a knowledge space by querying experts

(II) Those that are based on the analysis of the problem-solving process

(III) Data-analytic methods

When a knowledge space is to be identified by systematically querying experts, appropriate combinations of questions are selected using special purpose algorithms, and these combinations of questions are presented to the experts who assess if these combinations are feasible. From these data, the surmise relation is constructed on the set of problems. One such method uses the QUERY algorithm (Koppen, 1993). The main advantage of these methods lies in the fact that they allow construction of a knowledge space before evaluation of students’ achievement. The most serious flaw of these methods is the requirement to continuously involve the experts in the process of knowledge space construction (Segedinac et al., 2011).

Methods based on the analysis of the problem-solving process chunk the problems that are to be solved by students into sets of sub-problems. One such method that identifies a set of motives necessary to solve each problem is proposed by Schrepp et al. (1999). These methods, similarly to the previous family of methods, can be applied prior to the assessment of students’ knowledge. In addition to that, these methods can be formalized to some extent (provided that the experts just have to identify the set of motives for each problem) and, therefore, it is possible to reduce the experts’ involvement (Segedinac et al., 2011).

Data-analytic techniques identify surmise relations on the sets of items. These methods are based on the assumptions that there is a true surmise relation underlying the data and that the careless errors and lucky guesses make the data noisy. All of these methods basically share the same structure. Firstly, they construct a set of candidate surmise relations and, after that, the candidates are evaluated against the data using a specific fit measure. Finally, the best-fitting candidate is selected as the surmise relation (Ünlü et al., 2013). The main advantage of these methods is that they do not require the involvement of experts, at all. The most important drawback of these methods results from the fact that it requires students’ knowledge to be evaluated before the knowledge space can be identified (Segedinac et al., 2011).

The most well-known data-analytic method is the inductive item tree analysis (IITA) – a method that identifies a surmise relation on a set of items. An overview of algorithms based on IITA and their application for the organization of educational objectives is given by Segedinac et al. (2011).

Besides the construction of the quasi-orders (reflexive and transitive binary relation), it is very important that the quasi-order, obtained by the data-analytic method, optimally fits the data. In IITA, the idea is to estimate the number of counterexamples for each quasi-order, and to find the quasi-order where there is a minimal discrepancy between the observed and expected numbers of counterexamples covering the entire competing quasiorders.

The inductive construction of the quasi-orders is stated as one of the main advantages of this algorithm (Schrepp, 1999, 2003). However, the inductive construction can be criticized as it is possible that two implications together could cause intransitivity, added separately. This drawback is overcome by corrected and minimized IITA, the method which is utilized in this paper.

The applications of KST

Taking into account the fact that KST is a mathematical method for modelling students’ knowledge, it is not surprising that some of the first applications of this theory were exactly in mathematical education. Doignon and Falmagne (1985) illustrated the application of KST in a case of learning combinatorics. The applications of KST in mathematics education continued, so, for instance, Falmagne et al. (1990) used it to represent students’ arithmetic knowledge in a test that assessed fractions and decimal numbers, while Falmagne et al. (2007) used the same approach to represent students’ knowledge of algebra.

Regarding science education, one of the first applications of KST was related to the evaluation of an instructional strategy for teaching the concepts of pressure, density and the conservation of matter (Taagepera et al., 1997). In that paper, KST is used to identify the most probable learning pathways and to evaluate the efficiency of the applied instructional strategies.

Further research included various chemistry concepts such as organic chemistry concepts (Taagepera and Noori, 2000), bonding concepts (Taagepera et al., 2002), chemical and physical properties of matter (Tóth and Kiss, 2006), concepts of the plane of symmetry, chirality, isomerism (Taagepera et al., 2011), the concept of solutions (Segedinac et al., 2011), etc. It is worth mentioning that the KST framework has allowed researchers to identify the students’ critical learning pathways (e.g.Tóth and Kiss, 2006), as well as to compare them with experts’ critical learning pathways (Vaarik et al., 2008). Some novel applications of KST in science education include its combination with other methodologies, such as phenomenography (Tóth and Ludányi, 2007), with the aim of investigating students’ reasoning and changes in cognitive structures.

Literature review on KST in chemistry education indicated that stoichiometry has been one of the most extensively researched topics. Research has been conducted to determine learning pathways while solving stoichiometric problems (Arasasingham et al., 2004), to assess students’ understanding of stoichiometry (Arasasingham et al., 2005; Tóth, 2007), to compare knowledge spaces of the students who use different strategies for solving stoichiometric problems (Tóth and Sebestyén, 2009), and to determine the quality of students’ cognitive structure, i.e. to examine if it consists of interconnected or fragmented chemical concepts (Taagepera and Arasasingham, 2013).

In contrast to the examined papers, which mostly utilized KST either to evaluate instructional strategies or to track the development of scientific concepts, our research introduces a novel application of KST, namely, evaluation of experts’ comprehension of the way in which students understand the domain. The fact that experts observe the domain in light of their own knowledge influences their expectations of the students’ knowledge space. The approach proposed in this paper, therefore, includes the construction of the (i) expected knowledge space by experts and (ii) real knowledge space using a data-analytic method, comparing the obtained knowledge spaces, and analysing the differences between them.

Methodology

Research objective

In studies of Knaus et al. (2011) and Raker et al. (2013), the assessment of cognitive complexity was carried out by experts who independently categorised the solving steps of each task. To reduce the subjective component of the process, the aforementioned authors crafted a rubric. According to these authors, one same task can be solved in one step of medium difficulty or in 2 easy steps, and based on the rubric, the difference in the estimated number of steps is annulled by introducing the step difficulty level. So, by applying a rubric, the task will be evaluated by the same value of cognitive complexity, whether it is to be solved in one medium or in two easy steps. Yet such an assessment of cognitive complexity could imply a certain dose of subjectivity reflected in an expert assessment of the step difficulty level, as assessments are made independently. To make the assessment even more objective, and also to speed up the process of assessing cognitive complexity, Horvat et al. (2016) constructed a table of concepts for assessing the cognitive complexity of stoichiometry tasks. On the basis of the tasks presented in the test, 4 experts (one full professor in the field of chemistry didactics with 40 years of experience in university teaching, including 10 years of experience in teaching general chemistry to students of medicine, two teaching assistants in the field of chemistry didactics with five years of experience in introductory courses which include numerical problems in chemistry and one secondary school chemistry teacher with nearly 20 years of experience in teaching chemistry in secondary medical school) compiled a table in which all the concepts needed for solving stoichiometric test tasks were presented. In this table, concepts are divided into groups of basic and additional concepts. Through the panel discussion and collaboration, the experts compared concepts and then from the perspective of a student estimated the difficulty level for each individual concept presented in the table. Any disagreements were resolved through negotiations. An agreement was reached and consent was given to the final table proposal by all the experts involved in the process. Using the constructed table, the same task is assessed with the same value of cognitive complexity, regardless of the person who performs its assessment. This further reduces the amount of subjectivity. This procedure was validated by the statistically significant correlation between students' performances on the test and cognitive complexity estimated by experts, expressed as Pearson's correlation coefficient (r = −0.88; p = 0.00).

In this research, we aimed to compare the knowledge space constructed by experts with the one identified by the analysis of students’ responses (using corrected and minimized IITA). Due to the fact that both methods result in ∩-closed knowledge spaces, it is possible to compare the obtained knowledge spaces by applying graph differences. The obtained differences were utilized to analyse experts’ understanding of students’ knowledge about the domain.

Research context

Segedinac et al. (2011) have shown that there are certain discrepancies between the knowledge spaces that experts expect and the real students’ knowledge spaces. There are two possible reasons for that:

A surmise relation that determines a knowledge space can:

(I) be inherent to the logical structure of the domain itself, or

(II) can result from a pure contingency.

Sometimes experts overlook some of the surmise relations that occur in knowledge spaces constructed by analysing students’ responses. Such relations can be very valuable because they can help experts to refine their understanding of students’ learning.

Therefore, the main contribution of this paper is reflected in the fact that this application of KST allows the refinement of experts’ comprehension of students’ understanding of the domain.

Research steps

This research consists of the following steps:

(I) Constructing the test that is the domain for the knowledge spaces. In this particular research, the test has been taken from Horvat et al. (2016) with permission.

(II) Constructing the expected knowledge space for the given domain by analysing the problem-solving processes. This knowledge space is constructed by domain experts.

(III) Constructing the real knowledge space using a data-analytic method for the obtained students’ responses

(IV) Identifying the differences between the expected and real knowledge spaces

(V) Analysing the obtained differences

Sample and instrument

The education system in the Republic of Serbia includes compulsory primary education of eight years, after which students enrol in secondary school according to their own preferences and possibilities (based on their marks and qualification exam). Students can opt for grammar school (4 years) or some vocational school (3–4 years). Chemistry as a subject first appears in the 7th grade of primary school with 2 classes a week through 7th and 8th grades. The number of chemistry classes per week in secondary school depends on the type of school.

The testing was conducted on a sample of 82 students studying to be pharmaceutical technicians at secondary medical school “Dr Andra Jovanović” from Šabac, Republic of Serbia, 15–18 years old. In the chemistry curriculum of this educational profile, chemistry is realized through several obligatory subjects: chemistry, medical biochemistry, analytical chemistry and pharmaceutical chemistry. Stoichiometry is studied in the first year within the subject chemistry.

All the students were of a similar socio-economic status, predominantly the urban population. Testing was anonymous, and before testing, students were introduced to the goal and purpose of the research. All the participants, included in the study, accepted to willingly participate in the study without any constraint or expectation of reward. They were informed about the test two weeks in advance so that they could revise the topic on stoichiometry.

The test consisted of 20 stoichiometric problems covering the following chemistry concepts: writing and balancing chemical equations, stoichiometric calculations, and calculations with impure substances or solutions. Some of the problems required knowledge of additional concepts such as Archimedes' principle and the reactivity series of metals. The test with the cognitive complexity rating procedure is available in Appendix A (ESI†).

Results and discussion

Knowledge spaces considered in this paper are represented as directed unlabelled graphs, more precisely by their adjacency matrices, due to the fact that such a representation allows for simple graph manipulations that are necessary for this research (in particular graph comparison). Appendix B (ESI†) contains the adjacency matrices for both knowledge spaces. From these data and using the software tools developed as part of this research (https://github.com/milansegedinac/kst_tools), the results obtained in this paper can be reproduced.

The construction of the expected knowledge space

The construction of the expected knowledge space was carried out using a method based on the analysis of the problem-solving process (method II, vide supra). Similar to other studies (e.g.Falmagne et al., 1990) where the knowledge space is constructed by experts using the tasks’ difficulties, in this research, the expected knowledge space is constructed also by experts using a numerical rating (Table 1) for the cognitive complexity of problems (Appendix A, ESI†). The ability to solve less cognitively complex problems is taken as a precondition for solving more cognitively complex ones.

Table 1 Cognitive complexity rating

Cognitive complexity rating	Problems
1	1, 7, 14
2	2, 15
3	4, 16
4	3, 8, 9, 10, 18
5	11, 17
6	12, 19
7	5, 13
8	6, 20

---

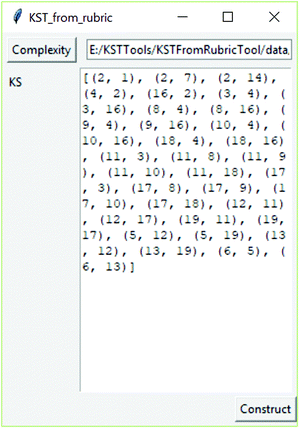
The software tool (available at https://github.com/milansegedinac/kst_tools/tree/master/KSTFromRubricTool/KSTFromRubricTool with an example of its use shown in Fig. 1) that implements this above-mentioned procedure is developed as part of this research. The software tool takes cognitive complexity ratings as an input (file in the CSV format) and produces the knowledge space. The obtained knowledge space is given by its edges.

Fig. 1 The software tool for constructing the knowledge space from experts’ estimation of cognitive complexity.

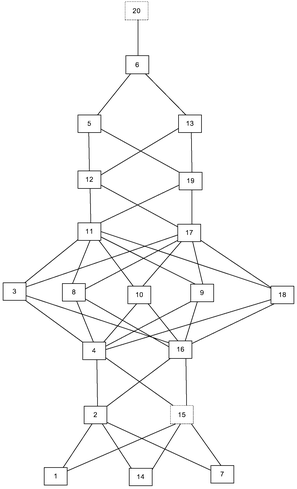
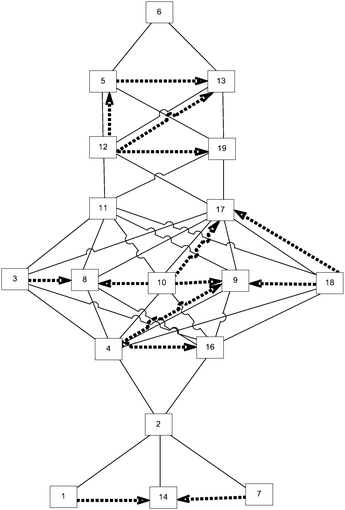
This cognitive complexity rating allowed us to construct the expected knowledge space, as shown in Fig. 2.

Fig. 2 The expected knowledge space.

The given Hasse diagram (Fig. 2), which represents the expected knowledge space, shows, for instance, that problem 2 surmises problem 7, and that it is surmised by problem 4. This means that a student who is able to solve problem 4 can also solve problems 1, 7, 14, and 2. The most complex is problem 20, and, according to the expected knowledge space, if a student can solve this problem, he or she can solve any other problem on the test.

This approach is suitable when there are no experimental test results. One of the key characteristics of such an approach is that it reflects experts’ premises about students’ learning. Therefore, the comparison of such knowledge space and the one obtained by analysing the test results can point to some of the surmise relations that experts overlook, and therefore, it can help experts to refine their comprehension of students’ learning.

The construction of the real knowledge space

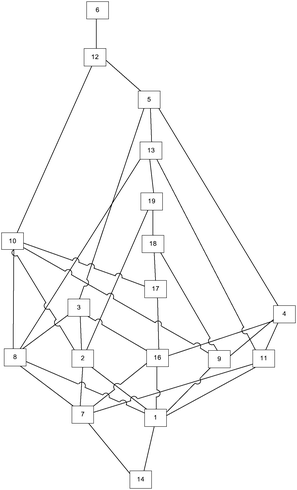
The real knowledge space was obtained by applying the corrected and minimized IITA algorithm on the provided test results. For that purpose, programming language R (https://www.r-project.org/) and its package DAKS: Data Analysis and Knowledge Spaces (https://cran.r-project.org/web/packages/DAKS/index.html) were utilised. The original IITA algorithm should be used specifically for data sets when the error rates are very low (Unlü and Anatol, 2010). In our case the error rate is 0.108, which makes corrected and minimized IITA applicable. The obtained knowledge space is given in Fig. 3.

Fig. 3 The real knowledge space.

The estimation of cognitive complexity from the real knowledge space

An estimation of cognitive complexity for problems from a knowledge space is an inverse to the construction of a knowledge space from an experts’ assigned problem complexity. This estimation allows experts’ complexity estimations to be explored on the basis of students’ achievements. Such estimation could indicate the problems whose complexities are possibly underestimated/overestimated by an expert.

An estimation of a problem's complexity from a real knowledge space in this paper is based on the concept of the outer fringe of a knowledge state (Falmagne and Doignon, 2011). Within the context of this research, the outer fringe represents a set of items that a student is ready to learn (Falmagne and Doignon, 2011). Relying on the outer fringe concept, a procedure for calculation of cognitive complexity is defined as follows:

All items without predecessors have a cognitive complexity value k = 1.

All items belonging to an outer fringe set containing items with cognitive complexity k receive a cognitive complexity value k + 1.

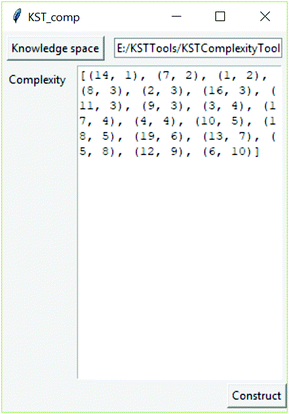
For determining cognitive complexity from a real knowledge space, the software tool was developed which calculates this cognitive complexity by implanting the above-described algorithm. The application, which is available on the link https://github.com/milansegedinac/kst_tools/tree/master/KSTComplexityTool/KSTComplexityTool, takes a knowledge space (adjacency matrix) as an input and returns a list of pairs (itemNo, CogCompl), where ItemNo is the problem ID and CogCompl is the corresponding cognitive complexity (Fig. 4).

Fig. 4 Software tool for determining cognitive complexity from the real knowledge space.

Table 2 depicts cognitive complexities calculated for the obtained real knowledge space.

Table 2 Cognitive complexity obtained from the real knowledge space

Cognitive complexity rating	Problem
1	14
2	1, 7
3	2, 8, 9, 11, 16
4	3, 4, 17
5	10, 18
6	19
7	13
8	5
9	12
10	6

---

Identifying differences between the expected and real knowledge spaces

Since both expected and real knowledge spaces can be observed as directed unlabelled graphs, and they are defined on the same set of vertices, they were compared for graph difference. The graph difference between any two graphs H and G is a graph with an adjacency matrix given by the difference of the adjacency matrices of graphs H and G.

The knowledge space obtained from test results has a greater number of complexity levels than the one constructed by experts. Therefore, the scales that represent the cognitive complexity have a different number of ratings (in the expected knowledge space ratings range from 1 to 8, while in the real one they range from 1 to 10). This does not mean that a task that has a cognitive complexity rating of 6 in the real knowledge space has to be more complex than the one rated as 5 in the expected one. Thus, instead of comparing the numerical rates of cognitive complexity between the real and expected knowledge spaces, we propose to analyse the relative position of the problems in the two knowledge spaces and the relationships among the problems.

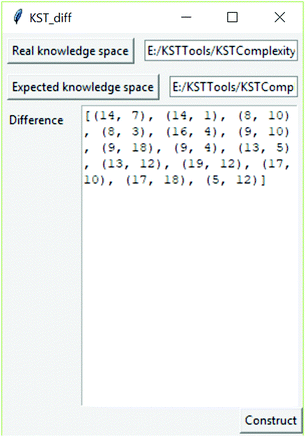
As part of this research, a software tool was developed to determine the difference between knowledge spaces. This software tool is available at link https://github.com/milansegedinac/kst_tools/tree/master/KSTComplexityTool/KSTComplexityTool, and an example of its usage is shown in Fig. 5. The tool takes two knowledge spaces represented as graphs (in this research these spaces were expected and real knowledge spaces) and produces a graph representing their difference as a set of edges (set of pairs of connected nodes).

Fig. 5 Software tool for identifying the difference between two knowledge spaces.

There is a 71.32% match between the expected and real knowledge space graphs, where 71.32% of the expected knowledge space is represented in the real knowledge space. It should be noted that the real knowledge space contained a number of relations that were not present in the expected one. Those relations are shown as dashed arrows in Fig. 6. It should be noted that during the construction of the real knowledge space, problems 15 and 20 were identified as outliers, and, therefore, removed from any further observations. To facilitate the observation of differences, the annotated graph is available in Appendix A (ESI†).

Fig. 6 The expected knowledge space extended with the relations from the real knowledge space.

The relations identified in the real knowledge space that were not present in the expected knowledge space are (14, 1), (14, 7), (16, 4), (8, 3), (8, 10), (9, 10), (9, 18), (19, 12), (13, 5).

The relations that are inversed in the real and expected knowledge spaces are (5, 12), (9, 4), (17, 10), (17, 18), (13, 12).

Comparison of the real and expected knowledge spaces

Considering the expected knowledge space, it can be easily noted that problems 1, 7, and 14 have the same complexity rating of 1 (Table 1) because in all three tasks the given and required substances are expressed as the same physical quantities. However, in the real knowledge space, problem 14 was identified as a precondition for problems 1 and 7. These relations indicate that there is a difference in the cognitive complexity of such problems. Re-examining these tasks, we were able to notice that in problem 14, coefficients can be directly observed from the equation, while in problem 1 reaction participants’ masses are compared, so students are required to calculate molar masses which additionally complicates the task. There are reports in the literature that indicate a lack of understanding of the concept of molar mass. BouJaoude and Barakat (2003) found that a significant percentage of students enrolled in their study calculated the molar mass of a substance by adding the atomic masses followed by multiplying or dividing the sum by its coefficient in the chemical equation. The same authors also found that it was easier for students to use a mole approach than to perform calculations with masses as some students did not understand the meaning of the coefficients in the chemical equation. As a result, they used the following formula in their calculations: mass₁/mass₂ = coeff₁/coeff₂. The latter case appeared in our study and represents a situation difficult to predict by experts. Concerning task 7, it also contains an easy concept since the required and given substances are the same physical quantities (V:V), but unlike the two previously described tasks, task 7 contains an additional concept (one substance is liquid). Although experts estimated that this additional concept did not increase interactivity, and therefore the overall cognitive complexity, some published literature does not support this. BouJaoude and Barakat (2003) found that more than half of the students involved in their study used 22.4 dm³ mol⁻¹ for water and solutions. A significant percentage of students used the formula coeff₁/coeff₂ = V₁/V₂ for liquid water and solids. Ayyıldıza and Tarhan (2013) also found that students believe that one mole of water occupies a volume of 22.4 dm³ in all three physical phases. Since the cognitive scheme of experts differs greatly from the cognitive scheme of students, the experts will likely overlook some concepts that can affect the overall complexity of the task. Therefore, the proposed method for applying knowledge space theory can help in achieving finer structuring of concepts that experts overlook or estimate as easy.

Furthermore, experts have rated problems 16 and 4 with a cognitive complexity value of 3 (Table 1), since both problems 16 and 4 include one easy and one medium concept. Both tasks include the chemical equation concept, and also calculating molar mass. However, what distinguishes them is the complexity of equations. Namely, the oxidation–reduction reaction equation has only 3 participants while a non-oxidation–reduction reaction equation has 5 participants. Constructing the table, the experts defined the determination of coefficients in the non-oxidation–reduction reaction equation as an easy concept, while the determination of the coefficients in the oxidation–reduction reaction equation was defined as the concept of medium difficulty. In doing so, they overlooked the fact that students can effectively determine coefficients in the simple oxidation-reducing equation using an inspection method, while they may have difficulty in using the same method to equate a complex equation that is a non-oxidation–reduction reaction. Further, if the inspection method is used, the procedure for equalizing chemical equations becomes more complicated if there are more sources of an element in equation (Staver and Jacks, 1988). If we compare the equations of the two above-mentioned tasks, it can be noted that in task 16 there is one source of K, one source of Cl and one source of O on both the left and right sides of the equation, while there are two sources of O on the right side of the equation of task 4, which makes it more complex. This example also showed that knowledge space theory recognizes nuances in complexity that experts failed to observe.

For problems 8, 3, 9 and 10, which are all rated with a cognitive complexity rating of 4, there are three newly established relations (8, 3), (8, 10) and (9, 10) in the real knowledge space. Problem 8 includes one difficult concept, while problem 3 includes two medium concepts and one additional concept according to the experts’ evaluation. This insensitivity of the rubric, which is reflected in the fact that different numbers and types of concepts are rated with the same cognitive complexity, led to the formation of a novel relation (8, 3) in the real knowledge space. If we add the fact that the equation in task 3 is quite complex, since on the right side of the equation we have two sources of N and two sources of O (as previously described), and the partial reduction of the nitrate ion, the cause of the inversion becomes clear. On the other hand, tasks 8, 9 and 10 include one difficult concept, and the newly established relation (8, 10) and (9, 10) could be explained by a different molar ratio between the given and required substances. In tasks 8 and 9, it is 1 : 1, while in task 10, it is 1 : 5. This is in accordance with the research of Anamuah-Mensah (1986), who found that problems involving 2 : 1 ratios caused various conceptual problems to students, which did not exist in problems involving 1 : 1 ratios.

A similar situation was observed in tasks 4 and 9. While the expected knowledge space placed problem 4 as a precondition for problem 9, in the real knowledge space it is the opposite way around, i.e. problem 9 is a precondition for problem 4. In both tasks, the given and required substances are different physical quantities; however, task 9 involves a 2 : 2 (i.e. 1 : 1) ratio, while task 4 involves a 2 : 1 ratio.

Problems 18 and 9 represent a typical example of two completely different tasks, which experts assessed with the same value of cognitive complexity, relying on the table. Task 9 contains one difficult concept while task 18 contains 3 easy concepts. However, although the concepts in task 18 are easy, working memory load should be considered. To successfully solve this task, the student has to recognize one of the two equations necessary to perform the calculation, then to know how to calculate the molar masses of the reactant and product, to deal with a complex chemical equation containing a large number of participants (which puts additional load on working memory).

Further, in the expected knowledge space, problem 10 is identified as a precondition for the problem 17, while in the real knowledge space, problem 17 is surmised by problem 10. This inversion results from the specificity of problem 17. If a student can write the stoichiometric equation in problem 17, he or she can read the amounts of a required substance directly, while problem 10 requires him or her to compare the number of molecules of the required substance with the mass of the given substance. A similar reason can explain the inversion of the surmise relation between problems 18 and 17. Instead of problem 18 being a precondition for problem 17, as expected by the knowledge space constructed by experts’ evaluation, it turns out that in the real knowledge space problem 18 surmises problem 17. This is probably because in problem 18 students have to compare the masses of the required and given substances, which requires a calculation of the relevant molecular masses, as previously explained.

There is also the new relation between problems 13 (2 easy and 1 difficult concepts) and 5 (1 easy and 2 difficult concepts), with a complexity rating of 7. This is an example of two completely different tasks of the same estimated cognitive complexity. A particularly important difference, which should be noted, is the fact that in task 5 it is necessary to know how to write a requested chemical equation. A similar situation is observed in tasks 12 and 13, as well as tasks 19 and 12. In the expected knowledge space, task 12 (2 difficult and 1 additional concept) precedes task 13 (2 easy and 1 difficult concept), while in the real knowledge space task 13 precedes task 12. Furthermore, problem 19 precedes problem 12 in the real knowledge space, which also requires writing a chemical equation. Numerous studies have shown that students often have no problem in equating chemical equations, commonly using the inspection method. However, it has been shown that students very often do not understand the essence of the underlying chemical change (Talanquer, 2011). Therefore, if a student does not understand the essence of a chemical change, he or she will not be able to present it with an equation and therefore will not be able to solve the task even if the request is simple.

Finally, the expected knowledge space assumes that problem 5 requires students to be able to solve problem 12, whilst in the real knowledge space it is the opposite. It could be explained by the fact that students have not mastered the reactivity series of metals. Namely, many of the students made a mistake, believing that the gas produced in the reaction of zinc and sulfuric acid is SO₂ instead of H₂.

Conclusion

This paper proposes an application of knowledge space theory in identifying discrepancies between the knowledge space that experts expect students to have (the expected knowledge space) and the knowledge space that is obtained by applying a data-analytic method (the real knowledge space). The proposed approach was applied to the domain of stoichiometry.

The results of this study have shown that the real knowledge space is richer in levels of complexity than the expected one. This fact led us to compare the knowledge spaces themselves, and the comparison has shown that there is a finer structuring in the real one.

The proposed approach can help experts identify the fine structure of easy concepts. This structure is often neglected by experts, who tend to rate certain concepts as easy, finding them trivial, although those are not trivial to students who have not fully mastered them, potentially causing cognitive overload.

Some of the methods for sequencing learning experiences, e.g. cognitive complexity rating rubrics, place all the difficult concepts in the same category. The approach proposed in this paper can improve on this and help experts to identify a fine structure in the set of difficult concepts.

In addition to that, it can also point to some flaws in the existing methods for evaluating cognitive complexity. For instance, the method utilized in the paper by Horvat et al. (2016) rated the cognitive complexity same value to problems which include two difficult and one easy concepts, and those with one difficult and two easy concepts. The approach proposed in this paper suggests that there are cases in which this does not hold.

This approach is also important for the development of problem-solving strategies in stoichiometry and can help teachers in task design as it could point to some overlooked facts. In this regard, this research provides the following implications for teaching stoichiometry:

(I) Cognitive complexity is conditioned by the complexity of the reaction manifested in two ways. Firstly, students encountered more difficulties in equating chemical equations with a larger number of reaction participants. Secondly, the existence of more than one source of an element on the left or right side of the equation further increased the complexity of tasks.

(II) Students know how to equate the chemical equation using the method of inspection, without proper reasoning for underlying concepts.

(III) Tasks which include 1 : 1 ratios of given and required substances, or those that could be reduced to 1 : 1 ratios, are easier than those tasks which include ratios different from 1 : 1.

(IV) Incorrectly adopted concepts, which experts are sometimes not aware of, can cause an increase in cognitive complexity.

(V) Students preferably choose to compare amounts as direct stoichiometric coefficients rather than as masses where they have to calculate molar masses. It is important to note that this implication is strictly related to the students involved in this research, and could be a consequence of an applied instructional method used by teachers during regular classes or a wrongly acquired conception of molar mass.

Some of the recommendations for teachers would be to dedicate more teaching time to complex equations, especially those involving multiple sources of one element. It is especially important to reflect on the submicroscopic reality represented by a chemical equation in order to encourage meaningful understanding of chemical equation concepts. In addition, more examples of tasks with ratios different from 1 : 1 should be given. Finally, it is especially important to determine whether students already have some misconceptions.

The most important constraint of the proposed application of knowledge space theory is the fact that it requires experts to give a detailed analysis of the difference between the expected and real knowledge spaces. Each relation given by the graph deference has to be appraised by a domain expert. Our further research will, therefore, be focused on designing software tools that will assist and help experts in this task.

For the purpose of the construction of the expected knowledge space, a software tool was developed as a part of this research. The real knowledge space analyzed in this research was constructed using the DAKS library for programming language R. To identify the difference between the knowledge spaces, another software tool was developed. One of the paths of further research will be to develop a single software application that will put together the functionalities of constructing, comparing and analysing knowledge spaces that will simplify the use of knowledge space theory in educational research.

Finally, different instructional strategies will result in different knowledge spaces. This feature of the proposed approach can actually be utilized to compare different instructional strategies, which will be another path for our further research.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (#47003). The authors wish to thank Mirjana Segedinac for her support and helpful comments on the manuscript. The authors owe special gratitude to anonymous referees for their constructive feedback and suggestions.

References

1. Albert D. and Kaluscha R., (1997), Adapting knowledge structures in dynamic domains, Proceedings of the 8th Workshop of the GI SIG “Intelligent Tutoring Systems”, Duisburg, pp. 89–100.
2. Anamuah-Mensah J., (1986), Cognitive strategies used by chemistry students to solve volumetric analysis problems, J. Res. Sci. Teach., 23(9), 759–769.
3. Arasasingham R. D., Taagepera M., Potter F. and Lonjers S., (2004), Using knowledge space theory to assess student understanding of stoichiometry, J. Chem. Educ., 81(10), 1517–1523.
4. Arasasingham R. D., Taagepera M., Potter F., Martorell I. and Lonjers S., (2005), Assessing the effect of web-based learning tools on student understanding of stoichiometry using knowledge space theory, J. Chem. Educ., 82(8), 1251–1262.
5. Ayyıldıza Y. and Tarhan L. (2013), Case study applications in chemistry lesson: gases, liquids, and solids, Chem. Educ. Res. Pract., 14(4), 408–420.
6. Barak M. and Dori Y. J., (2005), Enhancing undergraduate students' chemistry understanding through project-based learning in an IT environment, Sci. Educ., 89(1), 117–139.
7. BouJaoude S. and Barakat H., (2003), Students' problem solving strategies in stoichiometry and their relationships to conceptual understanding and learning approaches, Sci. Educ., 7(3), available at: https://wolfweb.unr.edu/homepage/crowther/ejse/boujaoude.pdf, accessed 20 December 2017.
8. Doignon J. P. and Falmagne J. C., (1985), Spaces for the assessment of knowledge, Int. J. Man-Mach. Stud., 23(2), 175–196.
9. Falmagne J. C., (1989), A latent trait theory via a stochastic learning theory for a knowledge space, Psychometrika, 54(2), 283–303.
10. Falmagne J., Cosyn E., Doble C., Thiery N. and Uzan H., (2007), Assessing mathematical knowledge in a learning space: validity and/or reliability, in the proceedings of the Annual Meeting of the American Educational Research Association (AERA), available at: https://www.aleks.com/paper_psych/Validity_in_L_Spaces.pdf, accessed 25 June 2015.
11. Falmagne J. C. and Doignon J. P., (2011), Learning spaces: interdisciplinary applied mathematics, Berlin, Springer.
12. Falmagne J. C., Koppen M., Villano M., Doignon J. P. and Johannesen L., (1990), Introduction to knowledge spaces: how to build, test, and search them, Psychol. Rev., 97(2), 201–224.
13. Gabel D., (1999), Improving teaching and learning through chemistry education research: A look to the future, J. Chem. Educ., 76(4), 548–554.
14. Hofstein A. and Mamlok-Naaman R., (2012), High-school students’ attitudes toward and interest in learning chemistry, Educ. Quim., 22(2), 90–102.
15. Horvat S., Segedinac M., Milenković D. and Hrin T., (2016), Development of procedure for the assessment of cognitive complexity of stoichiometric tasks, Maced. J. Chem. Chem. Eng., 35(2), 275–284.
16. Knaus K., Murphy K., Blecking A. and Holme T., (2011), A valid and reliable instrument for cognitive complexity rating assignment of chemistry exam items, J. Chem. Educ., 88(5), 554–560.
17. Koppen M., (1993), Extracting human expertise for constructing knowledge spaces: an algorithm, J. Math. Psychol., 37(1), 1–20.
18. Milenković D., Hrin T., Segedinac M. and Horvat S., (2016a), Development of a three-tier test as a valid diagnostic tool for identification of misconceptions related to carbohydrates, J. Chem. Educ., 93(9), 1514–1520.
19. Milenković D., Segedinac M., Hrin T. and Horvat S., (2016b), The impact of instructional strategy based on the triplet model of content representation on elimination of students’ misconceptions regarding inorganic reactions, J. Serb. Chem. Soc., 81(6), 717–728.
20. Okanlawon A. E., (2010), Constructing a framework for teaching reaction stoichiometry using pedagogical content knowledge, Chemistry, 19(2), 27–44.
21. Osman K. and Sukor N. S., (2013), Conceptual understanding in secondary school chemistry: a discussion of the difficulties experienced by students, Am. J. Appl. Sci., 10(5), 433–441.
22. Özmen H. (2004), Some student misconceptions in Chemistry: A literature review of chemical bonding, J. Sci. Educ. Technol., 13(2), 147–159.
23. Park S. and Oliver J. S., (2008), Revisiting the conceptualisation of pedagogical content knowledge (PCK): PCK as a conceptual tool to understand teachers as professionals, Res. Sci. Educ., 38(3), 261–284.
24. Raker J. R., Trate J. M., Holme T. A. and Murphy K., (2013), Adaptation of an instrument for measuring the cognitive complexity of organic chemistry exam items, J. Chem. Educ., 90(10), 1290–1295.
25. Schrepp M., (1999), An empirical test of a process model for letter series completion problems, in Albert D. and Lukas J. (ed.), Knowledge Spaces: Theories, Empirical Research, and Applications, Mahwah: Lawrence Erlbaum Associates Publishers, pp. 133–154.
26. Schrepp M., (2003), A method for the analysis of hierarchical dependencies between items of a questionnaire, Meth. Psychol. Res. Online, 8(1), 43–79.
27. Schrepp M., Held T. and Albert D., (1999), Component-based construction of surmise relations for chess problems, in Albert D. and Lukas J. (ed.), Knowledge Spaces: Theories, Empirical Research, and Applications, Mahwah: Lawrence Erlbaum Associates Publishers, pp. 41–66.
28. Segedinac M., Savić G. and Konjović Z., (2010), Optimal counterexamples expectation based method for knowledge space construction, Proceedings of the 8th International Symposium on IEEE, Subotica, pp. 273–278.
29. Segedinac M., Segedinac M., Konjović Z. and Savić G., (2011), A formal approach to organization of educational objectives, Psihologija, 44(4), 307–323.
30. Sirhan G., (2007), Learning difficulties in chemistry: an overview, J. Turk. Sci. Educ., 4(2), 2–20.
31. Staver J. R. and Jacks T., (1988), The influence of cognitive reasoning level, cognitive restructuring ability, disembedding ability, working memory capacity, and prior knowledge on students’ performance on balancing equations by inspection, J. Res. Sci. Teach., 25(9), 763–775.
32. Stuckey M. and Eiliks I., (2014), Increasing students motivation and the perception of chemistry's relevance in the classroom by learning about tattooing from a chemical and societal view, Chem. Educ. Res. Pract., 15(2), 156–168.
33. Taagepera M. and Arasasingham R. D., (2013), Using knowledge space theory to assess student understanding of chemistry, in Falmagne J. C., Albert D., Doble C., Eppstein D. and Hu X. (ed.), Knowledge Spaces: Applications in Education, Berlin: Springer-Verlag Berlin Heidelberg, pp. 115–128.
34. Taagepera M. and Noori S., (2000), Mapping students’ thinking patterns in learning organic chemistry by the use of knowledge space theory, J. Chem. Educ., 77(9), 1224–1229.
35. Taagepera M., Arasasingham R. D., King S., Potter F., Martorell I., Ford D., Wu J. and Kearney A. M., (2011), Integrating symmetry in stereochemical analysis in introductory organic chemistry, Chem. Educ. Res. Pract., 12(3), 322–330.
36. Taagepera M., Arasasingham R., Potter F., Soroudi A. and Lam G. (2002), Following the development of the bonding concept using knowledge space theory, J. Chem. Educ., 79(6), 756–762.
37. Taagepera M., Potter F. Miller G. E. and Lakshminarayan K., (1997), Mapping students’ thinking patterns by the use of the knowledge space theory, Int. J. Sci. Educ., 19(3), 283–302.
38. Talanquer V., (2011), Macro, submicro, and symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33(2), 179–195.
39. Tóth Z. and Kiss E., (2006), Using particulate drawings to study 13–17 year olds’ understanding of physical and chemical composition of matter as well as the state of matter, Pract. Theory Syst. Educ., 1(1), 109–125.
40. Tóth Z. and Ludányi, L., (2007), Using phenomenography combined with knowledge space theory to study students’ thinking patterns in describing an ion, J. Balt. Sci. Educ., 6(3), 27–33.
41. Tóth Z. and Sebestyén A., (2009), Relationship between students’ knowledge structure and problem-solving strategy in stoichiometric problems based on the chemical equation, Eurasian J. Phys. Chem. Educ., 1(1), 8–20.
42. Tóth Z., (2007), Mapping students’ knowledge structure in understanding density, mass percent, molar mass, molar volume and their application in calculations by the use of the knowledge space theory, Chem. Educ. Res. Pract., 8(4), 376–389.
43. Unlü, A., and Anatol S., (2010), DAKS: an R package for data analysis methods in knowledge space theory. J. Stat. Softw.37(2), 1–31.
44. Ünlü A., Schrepp M., Heller J., Hockemeyer C., Wesiak G. and Albert D., (2013), Recent developments in performance-based knowledge space theory, in Falmagne J. C., Albert D., Doble C., Eppstein D. and Hu X. (ed.), Knowledge Spaces: Applications in Education, Berlin: Springer-Verlag Berlin Heidelberg, pp. 147–192.
45. Vaarik A., Taagepera M. and Tamm L., (2008), Following the logic of student thinking patterns about atomic orbital structures, J. Balt. Sci. Educ., 7(1), 27–36.
46. Van Driel J. H., de Jong O. and Verloop N., (2002), The development of preservice chemistry teachers' pedagogical content knowledge, Sci. Educ., 86(4), 572–590.
47. Voska K. W. and Heikkinen H. W., (2000), Identification and analysis of student conceptions used to solve chemical equilibrium problems, J. Res. Sci. Teach., 37(2), 160–176.
48. Yan Y. K. and Subramaniam R., (2018), Using a multi-tier diagnostic test to explore the nature of students’ alternative conceptions on reaction kinetics, Chem. Educ. Res. Pract., 19(1), 213–226.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8rp00052b

---