Crystal structure and physical properties of radical cation salt based on 4,5-ethylenedioxy-4′-iodotetrathiafulvalene (EDO-TTF-I) with iodine bonding ability†
Yoshiaki
Nakano
 *ab,
Yusuke
Takahashi
a,
Kohdai
Ishida
*ab,
Yusuke
Takahashi
a,
Kohdai
Ishida
 a,
Manabu
Ishikawa
a,
Manabu
Ishikawa
 b,
Hideki
Yamochi
ab and
Mikio
Uruichi
c
b,
Hideki
Yamochi
ab and
Mikio
Uruichi
c
aDepartment of Chemistry, Graduate School of Science, Kyoto University, Kitashirakawa Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan. E-mail: nakano.yoshiaki.5x@kyoto-u.ac.jp
bResearch Center for Low Temperature and Materials Sciences, Kyoto University, Yoshida Honmachi, Sakyo-ku, Kyoto 606-8501, Japan
cInstitute for Molecular Science, Myodaiji, Okazaki, Aichi 444-8585, Japan
First published on 29th January 2018
Abstract
Single crystals of 4,5-ethylenedioxy-4′-iodotetrathiafulvalene (EDO-TTF-I) with iodine bonding ability were obtained by recrystallization from acetonitrile and crystallized in the orthorhombic system with the space group Pbca. Bent EDO-TTF-I molecules formed the dimer structure, and a short I⋯O contact was observed between dimers. Electrocrystallization of EDO-TTF-I in absolute ethanol containing tetrabutylammonium hexafluorophosphate, (TBA)PF6, afforded single crystals of (EDO-TTF-I)2PF6. An X-ray structural analysis revealed that EDO-TTF-I molecules form dimerized stacking columns in a head-to-tail manner, which is referred to as a β′-type arrangement. Iodine bonds between EDO-TTF-I and PF6 anions and short I⋯S contacts between EDO-TTF-I molecules were observed. Tight-binding band calculations indicated that the strong molecular dimerization splits the energy band into upper and lower bands with a small energy gap, where the upper band is effectively half-filled. It was found that (EDO-TTF-I)2PF6 is semiconducting (σRT = 5.3 S cm−1 and Ea = 0.17 eV) and exhibits magnetic properties reminiscent of a low-dimensional localized spin system. The magnetic data were analyzed by the Bonner–Fisher model incorporating interchain interactions: |J|/kB = 67.1 K and zJ′/kB = −61.1 K. No splitting of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes was observed in the range of 5–300 K by Raman spectroscopy, indicating a homogeneous charge distribution of EDO-TTF-I0.5+. Therefore, (EDO-TTF-I)2PF6 is considered as a dimerized Mott insulator.
C stretching modes was observed in the range of 5–300 K by Raman spectroscopy, indicating a homogeneous charge distribution of EDO-TTF-I0.5+. Therefore, (EDO-TTF-I)2PF6 is considered as a dimerized Mott insulator.
Introduction
The concept of crystal engineering is attractive for controlling molecular arrangements. Supramolecular noncovalent interactions such as hydrogen and halogen bonds have been effectively utilized in order to develop molecular conductors since the bulk physical properties are dominated by the crystal structure.1 A halogen bond is formed in the manner of C–Hal⋯B (Hal = F, Cl, Br, or I; B = Lewis base) when a Lewis base comes close to a halogen. This originates from the anisotropy of the electron density around the atomic nucleus of a halogen, around which electron-rich and -poor regions exist in the directions across and along bonding axis, respectively. As a result, the electron-poor region (a so-called σ-hole) of a halogen electrostatically interacts with the electron-rich region of a Lewis base. Therefore, the halogen bond is highly directional, and iodine, which is the most polarizable, forms the most directional and strongest halogen bond.2 In addition to these characteristics, the electronegativity of iodine is smaller than that of carbon, unlike the other halogens according to the Allred–Rochow scale: I (2.21) < C (2.50) < Br (2.74) < Cl (2.83) < F (4.10).3 The low electronegativity does not cause a noticeable decrease in the electron donation properties, even if iodine is introduced into some donor molecule. On the basis of such characteristics, iodine-containing molecular conductors have been developed to construct unique structures and physical properties.4–6Previously, we reported that 4,5-ethylenedioxytetrathiafulvalene (EDO-TTF, Chart 1) affords a radical cation salt that undergoes a thermal metal–insulator transition accompanied with distinct molecular deformation, which is driven cooperatively by the Peierls, charge-ordering, and anion-ordering mechanisms.7a,d Furthermore, an ultrafast and highly efficient photoinduced phase transition in this salt was discovered,7b and a detailed picture of the dynamic process in a nonequilibrium state,7j which is different from the thermal equilibrium state, is being clarified by time-resolved spectroscopies7c,e,g,h and electron diffraction.7f,i In order to develop another functional system based on an EDO-TTF derivative, we focused on 4,5-ethylenedioxy-4′-iodotetrathiafulvalene (EDO-TTF-I) with the iodine bonding ability mentioned above. EDO-TTF-I is a known donor molecule, as is the diiodonated derivative EDO-TTF-I2. Although various complexes with EDO-TTF-I2 have been investigated,5a–d,6a–d,8 those with EDO-TTF-I have not been well-studied. Only semiconducting (EDO-TTF-I)2(TCNQ) has been reported to the best of our knowledge, where TCNQ stands for 7,7,8,8-tetracyanoquinodimethane.6a,8 Here, we report the crystal structure and physical properties of a radical cation salt based on EDO-TTF-I.
Results and discussion
Crystal and band structures
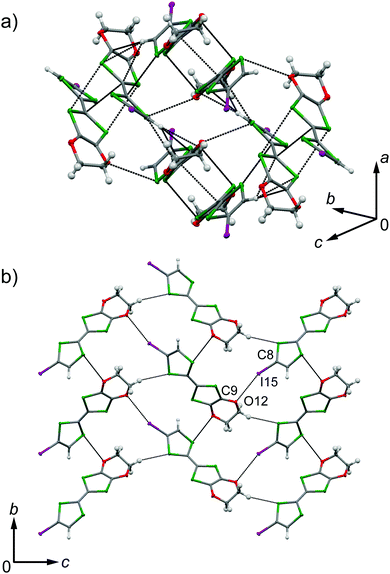
EDO-TTF-I was prepared through the iodination of EDO-TTF according to a slightly modified method in the literature.8 EDO-TTF was lithiated with a slight excess of lithium diisopropylamide (LDA) in tetrahydrofuran (THF), followed by reaction with perfluorohexyl iodide to afford EDO-TTF-I. Single crystals of EDO-TTF-I suitable for X-ray structural analysis were obtained by recrystallization from acetonitrile. EDO-TTF-I crystallizes in the orthorhombic system with the space group Pbca (Table 1). One EDO-TTF-I molecule is crystallographically unique, and bent EDO-TTF-I molecules form a dimer structure (Fig. 1a and Fig. S1, ESI†). Regarding the short atomic contact of an iodine atom, short I15⋯O12 contacts of 3.324(2) Å [3.429(4) Å] with a C8–I15⋯O12 angle of 160.36(8)° [160.1(1)°] and a I15⋯O12–C9 angle of 115.0(1)° [112.1(3)°] were observed at 100 K [300 K] between the dimers (Fig. 1b).| EDO-TTF-I | (EDO-TTF-I)2PF6 | |||
|---|---|---|---|---|
| a R = ∑||Fo| − |Fc||/∑|Fo|. b R w = [∑w(|Fo| − |Fc|)2/∑w|Fo|2]1/2. c S = [∑w(|Fo| − |Fc|)2/(No − Np)]1/2, No: number of reflections observed, Np: number of parameters. | ||||
| Empirical formula | C8H5IO2S4 | C16H10F6I2O4PS8 | ||
| Formula weight | 388.26 | 921.49 | ||
| Crystal color | Deep orange | Black | ||
| Crystal dimensions | 0.24 × 0.20 × 0.04 | 0.12 × 0.11 × 0.03 | ||
| Temperature (K) | 100 | 300 | 100 | 300 |
| Crystal system | Orthorhombic | Orthorhombic | Triclinic | Triclinic |
| Space group | Pbca (#61) | Pbca (#61) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (#2) (#2) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (#2) (#2) |
| Lattice parameter | ||||
| a (Å) | 8.1944(5) | 8.3903(6) | 6.4961(6) | 6.5423(9) |
| b (Å) | 14.4974(8) | 14.7805(11) | 7.4115(7) | 7.5209(11) |
| c (Å) | 19.7587(11) | 19.6241(15) | 14.3958(13) | 14.593(2) |
| α (°) | 90 | 90 | 92.1840(10) | 91.270(2) |
| β (°) | 90 | 90 | 76.2630(10) | 76.695(2) |
| γ (°) | 90 | 90 | 110.4120(10) | 110.167(2) |
| V (Å3) | 2347.3(2) | 2433.6(3) | 630.24(10) | 654.65(16) |
| Z value | 8 | 8 | 1 | 1 |
| D calc (g cm−3) | 2.197 | 2.119 | 2.428 | 2.337 |
| F 000 | 1488 | 1488 | 441 | 441 |
| μ(Mo Kα) (mm−1) | 3.414 | 3.293 | 3.293 | 3.170 |
| Radiation (Å) | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| 2θmax (°) | 58.706 | 58.468 | 58.22 | 54.04 |
| No. independent reflections | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 141 141 |
2999 | 3116 |
| No. reflections observed | 3036 | 3161 | 3925 | 4072 |
| No. parameters | 127 | 136 | 169 | 169 |
| R int | 0.0344 | 0.0496 | 0.0131 | 0.0161 |
| R (I > 2.0σ) | 0.0246 | 0.0419 | 0.0239 | 0.0341 |
| R w (all data) | 0.0542 | 0.1043 | 0.0570 | 0.0724 |
| Goodness-of-fit indicator, Sc | 1.038 | 0.991 | 1.019 | 1.014 |
| Max. shift/error in final cycle | 0.000 | 0.000 | 0.000 | 0.000 |
| Max. and min. peaks in final diff. map (e Å−3) | 0.83, −0.68 | 1.10, −0.71 | 1.02, −0.48 | 0.70, −0.54 |
| CCDC | 1590291 | 1590292 | 1590293 | 1590294 |
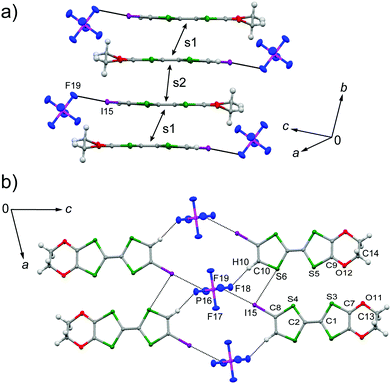
The galvanostatic electrocrystallization of EDO-TTF-I in absolute ethanol containing tetrabutylammonium hexafluorophosphate, (TBA)PF6, afforded black crystals of (EDO-TTF-I)2PF6. (EDO-TTF-I)2PF6 crystallizes in the triclinic system with the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table 1). The PF6 anion is located at the center of inversion, and one EDO-TTF-I molecule and one half of a PF6 anion are crystallographically unique (Fig. S2, ESI†). The arrangement of EDO-TTF-I molecules and the notation of the intermolecular overlap integrals between the highest occupied molecular orbitals (HOMOs) are shown in Fig. 2. EDO-TTF-I molecules form a dimerized stacking column along the b axis in a head-to-tail manner (Fig. 3a and Fig. S3, ESI†). In the face-to-face stack, ring-over-bond (s1) and ring-over-atom (s2) overlapping modes alternate (Fig. 3a and Fig. S4, ESI†); this molecular arrangement is known as β′ type in BEDT-TTF conductors.9 Focusing on the iodine-mediated intermolecular interaction, short I15⋯F19 contacts of 3.102(2) Å [3.202(5) Å] with a C8–I15⋯F19 angle of 172.25(9) [172.0(1)°] and a I15⋯F19–P16 angle of 114.56° [114.9°] were observed, and I15⋯S6 contacts of 3.6617(8) Å [3.712(1) Å] with a C8–I15⋯S6 angle of 91.52(8) [91.9(1)°], a I15⋯S6–C2 angle of 165.2(1) [164.1(1)°], and a I15⋯S6–C10 angle of 85.3(1) [85.6(2)°] were observed at 100 K [300 K] (Fig. 3b). A similar manner of short atomic contacts has been reported for (EDT-TTF-I)2Ag(CN)2 and (EDT-TTF-I)2Br.10 Therefore, the monoiodinated tetrathiafulvalene skeleton seems to induce the C–I⋯anion and C–I⋯S interactions and the dimerized stack with a ring-over-bond stacked dimer as a structural unit, although it is absolutely necessary to intensively research the crystal structures of monoiodinated tetrathiafulvalene radical cation salts.
(Table 1). The PF6 anion is located at the center of inversion, and one EDO-TTF-I molecule and one half of a PF6 anion are crystallographically unique (Fig. S2, ESI†). The arrangement of EDO-TTF-I molecules and the notation of the intermolecular overlap integrals between the highest occupied molecular orbitals (HOMOs) are shown in Fig. 2. EDO-TTF-I molecules form a dimerized stacking column along the b axis in a head-to-tail manner (Fig. 3a and Fig. S3, ESI†). In the face-to-face stack, ring-over-bond (s1) and ring-over-atom (s2) overlapping modes alternate (Fig. 3a and Fig. S4, ESI†); this molecular arrangement is known as β′ type in BEDT-TTF conductors.9 Focusing on the iodine-mediated intermolecular interaction, short I15⋯F19 contacts of 3.102(2) Å [3.202(5) Å] with a C8–I15⋯F19 angle of 172.25(9) [172.0(1)°] and a I15⋯F19–P16 angle of 114.56° [114.9°] were observed, and I15⋯S6 contacts of 3.6617(8) Å [3.712(1) Å] with a C8–I15⋯S6 angle of 91.52(8) [91.9(1)°], a I15⋯S6–C2 angle of 165.2(1) [164.1(1)°], and a I15⋯S6–C10 angle of 85.3(1) [85.6(2)°] were observed at 100 K [300 K] (Fig. 3b). A similar manner of short atomic contacts has been reported for (EDT-TTF-I)2Ag(CN)2 and (EDT-TTF-I)2Br.10 Therefore, the monoiodinated tetrathiafulvalene skeleton seems to induce the C–I⋯anion and C–I⋯S interactions and the dimerized stack with a ring-over-bond stacked dimer as a structural unit, although it is absolutely necessary to intensively research the crystal structures of monoiodinated tetrathiafulvalene radical cation salts.
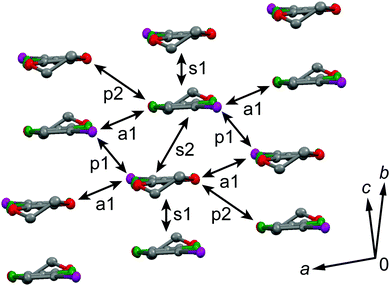 | ||
| Fig. 2 Molecular arrangement in (EDO-TTF-I)2PF6 at 300 K and the notation for the intermolecular overlap integrals between HOMOs. | ||
From the intradimer and interdimer overlap integrals s1 and s2 (s1 > s2), the degree of molecular dimerization along the stacking direction (Δs/〈s〉) is defined as11
| Δs/〈s〉 = 2(s1 − s2)/(s1 + s2) | (1) |
The degree of molecular dimerization in (EDO-TTF-I)2PF6 is summarized in Table S1 (ESI†). Judging from the values of Δs/〈s〉 without the sulfur 3d orbitals, the molecular dimerization is comparable to those in (TMTTF)2PF6 and (TMTTF)2AsF6, which are in the dimerized Mott state.12 In the case of (TMTTF)2PF6 and (TMTTF)2AsF6, the degree of molecular dimerization decreases as the temperature decreases, whereas that in (EDO-TTF-I)2PF6 increases. The energy band structure and Fermi surface are shown in Fig. 4 and Fig. S5 (ESI†). The strong molecular dimerization splits the energy band into upper and lower bands, although the energy gap (Eg) is very small (Table S1, ESI†). Considering only the upper band, an effective half-filled band is realized. The Fermi surface calculated without the sulfur 3d orbitals is slightly open along the ka direction, indicating a quasi-one-dimensional nature. However, the direction of opening in the Fermi surface is quite different from that calculated with the sulfur 3d orbitals (Fig. S5, ESI†). The anisotropic nature will be examined in the future.
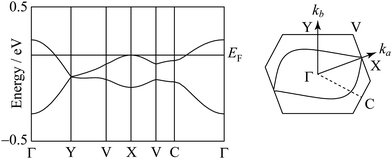 | ||
| Fig. 4 Energy band structure and Fermi surface at 300 K. The contribution of the sulfur 3d orbitals is not included in the calculation. | ||
Electrical and magnetic properties
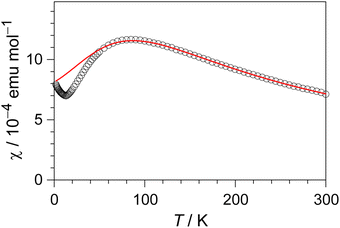
The electrical resistivity of (EDO-TTF-I)2PF6 was measured along the b axis corresponding to the stacking direction. The temperature dependence of the electrical resistivity is shown in Fig. S6 (ESI†). (EDO-TTF-I)2PF6 exhibits semiconducting behavior with an electrical conductivity of 5.3 S cm−1 at room temperature with an activation energy Ea = 0.17 eV.The temperature dependence of the magnetic susceptibility (χ) of (EDO-TTF-I)2PF6 is shown in Fig. 5 and Fig. S7 (ESI†). The value of χ is 7.1 × 10−4 emu mol−1 at 300 K, increases as the temperature decreases, and decreases through the maximum at 85 K. The magnetic behavior is reminiscent of some type of low-dimensional localized spin system. Below 13 K, the value of χ increases again, probably owing to a paramagnetic impurity. Assuming that the paramagnetic impurity obeys Curie's law, the amount of paramagnetic impurity was estimated as 0.76%. The magnetic data were analyzed by the Bonner–Fisher model (eqn (2)),13 which describes an antiferromagnetic uniform chain with S = 1/2 spins, and by a modified model incorporating interchain interactions (eqn (3)):14
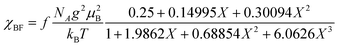 | (2) |
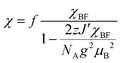 | (3) |
Normal-mode analysis and vibrational spectroscopy
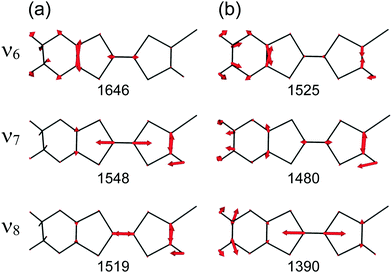
At the B3LYP/Aug-cc-pVTZ(-PP) level of theory, a full geometry optimization and normal-mode analysis for neutral EDO-TTF-I0 and monocationic EDO-TTF-I˙+ were conducted, and the calculated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes (ν6, ν7, and ν8 modes) are illustrated in Fig. 6. In EDO-TTF-I0, the ν6 mode is considered to be the C
C stretching modes (ν6, ν7, and ν8 modes) are illustrated in Fig. 6. In EDO-TTF-I0, the ν6 mode is considered to be the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching of a 1,3-dithiole ring with an ethylenedioxy group, while the ν7 and ν8 modes are the out-of-phase and in-phase C
C stretching of a 1,3-dithiole ring with an ethylenedioxy group, while the ν7 and ν8 modes are the out-of-phase and in-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching of a 1,3-dithiole ring and bridge, respectively. According to Fig. 6, the manner of mode mixing slightly changes upon one-electron oxidation, and the C
C stretching of a 1,3-dithiole ring and bridge, respectively. According to Fig. 6, the manner of mode mixing slightly changes upon one-electron oxidation, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes of the 1,3-dithiole rings with and without the ethylenedioxy group are mixed in the ν6 mode. Moreover, the frequency shifts upon oxidation are not the same among the ν6, ν7, and ν8 modes. However, the outstanding frequency shifts upon oxidation can be utilized to estimate the molecular charge as well as the other molecular conductors.15
C stretching modes of the 1,3-dithiole rings with and without the ethylenedioxy group are mixed in the ν6 mode. Moreover, the frequency shifts upon oxidation are not the same among the ν6, ν7, and ν8 modes. However, the outstanding frequency shifts upon oxidation can be utilized to estimate the molecular charge as well as the other molecular conductors.15
The infrared and Raman spectra of EDO-TTF-I along with the theoretical spectra are shown in Fig. S8 (ESI†). The present theoretical calculation reproduces the observed spectra well when a frequency scaling factor of 0.969 is applied. The assignments of the experimentally observed bands are summarized in Table S2 (ESI†). In both the infrared and Raman spectra of EDO-TTF-I, the CH2 scissoring and wagging modes are observed in addition to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes of ν6, ν7, and ν8 in the spectral region. However, these modes are observed at much weaker intensities than the C
C stretching modes of ν6, ν7, and ν8 in the spectral region. However, these modes are observed at much weaker intensities than the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes. Therefore, we can confidently distinguish the C
C stretching modes. Therefore, we can confidently distinguish the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes from the other modes.
C stretching modes from the other modes.
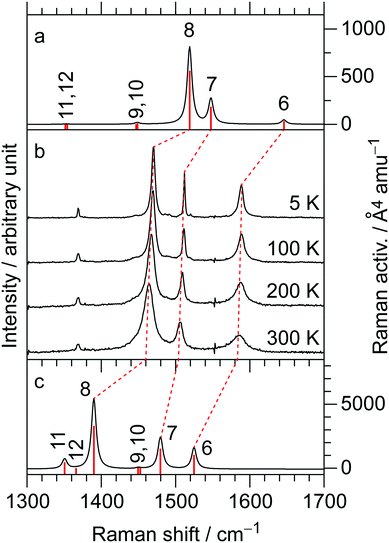
The temperature-variable Raman spectra of (EDO-TTF-I)2PF6 are shown in Fig. 7. Three intense bands are observed at 1587, 1507, and 1465 cm−1 at 300 K. Compared with the theoretical spectra of EDO-TTF-I0 and EDO-TTF-I˙+, these bands are assignable to the ν6, ν7, and ν8 modes, respectively. No spectral splitting of the ν6, ν7, and ν8 modes indicates that all EDO-TTF-I molecules have a homogeneous charge of +0.5 based on the chemical composition, or the molecular charge difference is so small that Raman spectroscopy cannot detect it. Therefore, we rule out charge disproportionation in (EDO-TTF-I)2PF6. This is also consistent with the result that one EDO-TTF-I molecule is crystallographically unique. As the temperature decreases, the ν6, ν7, and ν8 modes exhibit slight shifts that are less than 5 cm−1 to 1589, 1512, and 1470 cm−1, respectively, at 5 K, accompanied by spectral narrowing. These results suggest that the molecular charge remains unchanged down to 5 K without charge disproportionation. The strong molecular dimerization is regarded to be the origin of the suppression of charge disproportionation by analogy with the abovementioned results for (TMTTF)2PF6 and (TMTTF)2AsF6.12 Taking into account the results of the calculated band structure, electrical conductivity, magnetic properties, and Raman spectroscopy, (EDO-TTF-I)2PF6 is considered to be a dimerized Mott insulator.
Conclusions
An X-ray structural analysis and tight-binding band calculations revealed a strongly dimerized columnar structure with a β′-type molecular arrangement in (EDO-TTF-I)2PF6, where the iodine atom showed effective short I⋯F and I⋯S contacts between an EDO-TTF-I molecule and a PF6 anion and between EDO-TTF-I molecules. The band consisting of the HOMOs split into two bands owing to this strong molecular dimerization, and the upper band is effectively half-filled. The salt showed semiconducting behavior and magnetic properties characteristic of a low-dimensional localized spin system, which was analyzed by the modified Bonner–Fisher model with interchain interaction. Along with the results obtained by temperature-variable Raman spectroscopy, (EDO-TTF-I)2PF6 is considered to be a dimerized Mott insulator in the range of 5–300 K.Experimental and computational
General
Dry THF was obtained from Kanto Chemical. Perfluorohexyl iodide and 2.0 M LDA in THF/heptane/ethylbenzene were purchased from Aldrich. EDO-TTF was prepared according to the literature.8 For electrocrystallization, ethanol was distilled from Mg/I2 in an argon atmosphere, and (TBA)PF6 was purified by recrystallization from ethanol. 1H and 13C NMR spectra were measured using a JEOL JNM-ECA600 spectrometer. The chemical shift was recorded relative to an internal TMS standard. X-ray diffraction images were acquired by the use of a Bruker SMART ApexII CCD diffractometer with graphite monochromated Mo Kα radiation at 300 and 100 K. Data reduction was performed by the Bruker SAINT program, and the multiscan absorption correlation was applied. The space group was determined by the Xprep program. The structural solution was obtained utilizing the Yadokari-XG interface.16 The structures were solved by SIR-201417 and refined by SHELXL-2014.18 Hydrogen atoms were introduced at the calculated positions (riding model). The electrical resistivities of (EDO-TTF-I)2PF6 single crystals were measured by the four-probe method. The gold wires were bonded to the sample surface by using carbon paste (DOTITE XC-12). The magnetic susceptibilities of the polycrystalline samples were measured in a 5000 Oe field by a Quantum Design MPMS-XL system. The raw data were corrected for both the magnetization of the sample holder alone and the diamagnetic contribution of sample itself. The diamagnetic contribution was estimated by using Pascal's constants: χdia = −378.74 × 10−6 emu mol−1. Infrared spectra of KBr pellets were acquired with a Perkin-Elmer Spectrum 400 spectrophotometer. Raman spectra were measured using a Renishaw inVia Reflex system in the 180° backreflecting geometry. The sample was irradiated by a 633 nm laser. The intensity of the excitation light was reduced below 100 µW to avoid sample heating and radiation damage.Synthesis of 4,5-ethylenedioxy-4′-iodotetrathiafulvalene (EDO-TTF-I)
To a solution of EDO-TTF (1.00 g, 3.81 mmol) in dry THF (100 mL), 2.0 M LDA in THF/heptane/ethylbenzene (2 mL, 4.0 mmol) was added for 4 min in an argon atmosphere at −78 °C. After stirring at −78 °C for 1 h, perfluorohexyl iodide (3.0 mL, 13 mmol) was added for 17 min. The resulting mixture was stirred at −78 °C for 1.5 h and then allowed to room temperature. Saturated NH4Claq (150 mL) was added to the resulting mixture, which was extracted with CS2 and washed with saturated NaClaq. The organic layer was dried over MgSO4, and the solvent was evaporated. The residue was chromatographed on silica gel with CS2 as eluent, where purification by chromatography was performed twice, to afford a brown oil. Acetonitrile was added to the oil and cooled in a refrigerator. A black powdery solid was removed by filtration, and the filtrate was evaporated to afford EDO-TTF-I as a red solid (1.07 g, 72%). EDO-TTF-I was further purified by recrystallization from acetonitrile and used for the following experiments. mp 81–82 °C (decomp.) (lit.,8 78–79 °C (decomp.)); 1H NMR (600 MHz, CDCl3) δ 4.37 (4H, s), 6.46 (1H, s); 13C NMR (150 MHz, CDCl3) δ 63.7, 66.2, 100.7, 116.8, 123.1, 123.2, 124.0 (only seven signals were observed, probably owing to the overlap of two signals assigned to C–I and CH2 at 66.2 ppm. This is supported by the fact that the signal at 66.2 ppm is stronger than that at 63.7 ppm and by the literature,8 which indicates that diiodonated EDO-TTF-I2 shows two signals assigned to CH2 and C–I at 66.1 and 77.2 ppm.); calc. for C8H5IO2S4: C, 24.75; H, 1.30; I, 32.68; O, 8.24; S, 33.03. Found: C, 24.81; H, 1.29; I, 32.49; O, 8.28; S, 33.15%.Electrocrystallization of (EDO-TTF-I)2PF6
(EDO-TTF-I)2PF6 was prepared by the electrocrystallization of EDO-TTF-I in an H-shaped electrochemical cell with a glass frit separating the anode and cathode arms. Typically, EDO-TTF-I (ca. 16 mg) was placed in the anode arm of the cell and (TBA)PF6 (ca. 32 mg) in each arm, which was then filled with absolute ethanol (18 mL). The mixture was stirred to give a homogeneous solution. Using Pt electrodes (2 and 1 mm in diameter for the anode and cathode, respectively), galvanostatic electrolysis (0.5 µA) for less than two weeks at room temperature afforded black platelets on the anode electrode. The most developed crystal face was the (001) surface elongated along the b axis.Computational
The HOMO of the EDO-TTF-I molecule and the intermolecular overlap integrals between HOMOs were estimated on the basis of the extended Hückel method. The transfer integral (t) was assumed to be proportional to the overlap integral (s) between HOMOs and estimated as t = Es (E = −10 eV). Using these transfer integrals, the band structure was calculated within the tight-binding approximation. The parameters of the atomic orbitals were taken from the literature.19,20 The calculations were carried out without and with the sulfur 3d orbitals in order to investigate the parameter dependence. The program developed by Mori et al.19 was used.Density functional theory calculations based on the B3LYP functional21 were performed using the Aug-cc-pVTZ (C, H, O, and S atoms)22 and Aug-cc-pVTZ-PP (I atom)23 basis sets. For the full geometry optimizations and frequency calculations for EDO-TTF-I0 and EDO-TTF-I˙+, both “Opt = Tight” and “Int = UltraFine” were specified. All density functional theory calculations were performed using the Gaussian 09 program package.24
Note added after first publication
This article replaces the version published on 5 February 2018, which contained errors in eqn (2).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by a Grant-in-Aid for Scientific Research on Innovative Areas, “π-System Figuration: Control of Electron and Structural Dynamism for Innovative Functions,” from the Japan Society for the Promotion of Science (JSPS) JP17H05153 and by JSPS KAKENHI, grant numbers JP15K17901 and JP26288035. Elemental analyses were performed at the Organic Elemental Microanalysis Laboratory, Kyoto University. Raman spectroscopy was conducted at the Institute for Molecular Science, supported by the Nanotechnology Platform Program (Molecule and Material Synthesis) of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. The computations were performed using the Research Center for Computational Science, Okazaki, Japan.Notes and references
- M. Fourmigué and P. Batail, Chem. Rev., 2004, 104, 5379 CrossRef PubMed.
- (a) A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514 CrossRef CAS PubMed; (b) G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Cryst. Growth Des., 2014, 14, 2697 CrossRef CAS; (c) P. Politzer, J. S. Murray, G. V. Janjić and S. D. Zarić, Crystals, 2014, 4, 12 CrossRef.
- A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264 CrossRef CAS.
- (a) K. S. Shin, O. Jeannin, M. Brezgunova, S. Dahaoui, E. Aubert, E. Espinosa, P. Auban-Senzier, R. Świetlik, A. Frąckowiakd and M. Fourmigué, Dalton Trans., 2014, 43, 5280 RSC; (b) J. Lieffrig, R. L. Pennec, O. Jeannin, P. Auban-Senzier and M. Fourmigué, CrystEngComm, 2013, 15, 4408 RSC; (c) M. Brezgunova, K. S. Shin, P. Auban-Senzier, O. Jeannin and M. Fourmigué, Chem. Commun., 2010, 46, 3926 RSC; (d) J. Lieffrig, O. Jeannin, A. Frąckowiak, I. Olejniczak, R. Świetlik, S. Dahaoui, E. Aubert, E. Espinosa, P. Auban-Senzier and M. Fourmigué, Chem. – Eur. J., 2013, 19, 14804 CrossRef CAS PubMed; (e) K. S. Shin, M. Brezgunova, O. Jeannin, T. Roisnel, F. Camerel, P. Auban-Senzier and M. Fourmigué, Cryst. Growth Des., 2011, 11, 5337 CrossRef CAS; (f) T. Devic, B. Domercq, P. Auban-Senzier, P. Molinié and M. Fourmigué, Eur. J. Inorg. Chem., 2002, 2844 CrossRef CAS; (g) M. Fourmigué and P. Auban-Senzier, Inorg. Chem., 2008, 47, 9979 CrossRef PubMed; (h) B. Domercq, T. Devic, M. Fourmigué, P. Auban-Senzier and E. Canadell, J. Mater. Chem., 2001, 11, 1570 RSC; (i) A. Alberola, M. Fourmigué, C. J. Gómez-García, R. Llusar and S. Triguero, New J. Chem., 2008, 32, 1103 RSC.
- (a) A. Łapiński, R. Świetlik, M. Polomska, L. Ouahab and T. Imakubo, J. Low Temp. Phys., 2006, 142, 597 CrossRef; (b) L. Ouahab, F. Setifi, S. Golhen, T. Imakubo, R. Lescouëzec, F. Lloret, M. Julve and R. Świetlik, C. R. Chim., 2005, 8, 1286 CrossRef CAS; (c) M. Tamura, K. Yamanaka, Y. Mori, Y. Nishio, K. Kajita, H. Mori, S. Tanaka, J.-I. Yamaura, T. Imakubo, R. Kato, Y. Misaki and K. Tanaka, Synth. Met., 2001, 120, 1041 CrossRef CAS; (d) T. Imakubo, T. Shirahata, K. Hervé and L. Ouahab, J. Mater. Chem., 2006, 16, 162 RSC; (e) T. Imakubo, N. Tajima, M. Tamura, R. Kato, Y. Nishio and K. Kajita, J. Mater. Chem., 2002, 12, 159 RSC; (f) T. Imakubo, T. Shirahata, M. Kibune and H. Yoshino, Eur. J. Inorg. Chem., 2007, 4727 CrossRef CAS; (g) T. Imakubo and M. Kobayashi, Eur. J. Inorg. Chem., 2014, 3973 CrossRef CAS; (h) T. Shirahata, M. Kibune, M. Maesato, T. Kawashima, G. Saito and T. Imakubo, J. Mater. Chem., 2006, 16, 3381 RSC; (i) T. Imakubo and R. Murayama, CrystEngComm, 2013, 15, 3072 RSC; (j) T. Imakubo, M. Kibune, H. Yoshino, T. Shirahata and K. Yoza, J. Mater. Chem., 2006, 16, 4110 RSC.
- (a) Y. Kuwatani, E. Ogura, H. Nishikawa, I. Ikemoto and M. Iyoda, Chem. Lett., 1997, 817 CrossRef CAS; (b) J. Nishijo, E. Ogura, J. Yamaura, A. Miyazaki, T. Enoki, T. Takano, Y. Kuwatani and M. Iyoda, Solid State Commun., 2000, 116, 661 CrossRef CAS; (c) J. Nishijo, E. Ogura, J. Yamaura, A. Miyazaki, T. Enoki, T. Takano, Y. Kuwatani and M. Iyoda, Synth. Met., 2003, 133–134, 539 CrossRef CAS; (d) A. Miyazaki, K. Enomoto, K. Okabe, H. Yamazaki, J. Nishijo, T. Enoki, E. Ogura, K. Ugawa, Y. Kuwatani and M. Iyoda, J. Solid State Chem., 2002, 168, 547 CrossRef CAS; (e) U. Kux, H. Suzuki, S. Sasaki and M. Iyoda, Chem. Lett., 1995, 183 CrossRef CAS.
- (a) A. Ota, H. Yamochi and G. Saito, J. Mater. Chem., 2002, 12, 2600 RSC; (b) M. Chollet, L. Guerin, N. Uchida, S. Fukaya, H. Shimoda, T. Ishikawa, K. Matsuda, T. Hasegawa, A. Ota, H. Yamochi, G. Saito, R. Tazaki, S. Adachi and S. Koshihara, Science, 2005, 307, 86 CrossRef CAS PubMed; (c) K. Onda, S. Ogihara, K. Yonemitsu, N. Maeshima, T. Ishikawa, Y. Okimoto, X. F. Shao, Y. Nakano, H. Yamochi, G. Saito and S. Koshihara, Phys. Rev. Lett., 2008, 101, 067403 CrossRef PubMed; (d) Y. Nakano, H. Yamochi, G. Saito, M. Uruichi and K. Yakushi, J. Phys.: Conf. Ser., 2009, 148, 012007 CrossRef; (e) N. Fukazawa, M. Shimizu, T. Ishikawa, Y. Okimoto, S. Koshihara, T. Hiramatsu, Y. Nakano, H. Yamochi, G. Saito and K. Onda, J. Phys. Chem. C, 2012, 116, 5892 CrossRef CAS; (f) M. Gao, C. Lu, H. Jean-Ruel, L. C. Liu, A. Marx, K. Onda, S. Koshihara, Y. Nakano, X. F. Shao, T. Hiramatsu, G. Saito, H. Yamochi, R. R. Cooney, G. Moriena, G. Sciaini and R. J. D. Miller, Nature, 2013, 496, 343 CrossRef CAS PubMed; (g) Y. Matsubara, S. Ogihara, J. Itatani, N. Maeshima, K. Yonemitsu, T. Ishikawa, Y. Okimoto, S. Koshihara, T. Hiramatsu, Y. Nakano, H. Yamochi, G. Saito and K. Onda, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 161102(R) CrossRef; (h) M. Servol, N. Moisan, E. Collet, H. Cailleau, W. Kaszub, L. Toupet, D. Boschetto, T. Ishikawa, A. Moréac, S. Koshihara, M. Maesato, M. Uruichi, X. F. Shao, Y. Nakano, H. Yamochi, G. Saito and M. Lorenc, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 024304 CrossRef; (i) L. Chung Liu, Y. Jiang, H. M. Mueller-Werkmeister, C. Lu, G. Moriena, M. Ishikawa, Y. Nakano, H. Yamochi and R. J. D. Miller, Chem. Phys. Lett., 2017, 683, 160 CrossRef; (j) K. Onda, H. Yamochi and S. Koshihara, Acc. Chem. Res., 2014, 47, 3494 CrossRef CAS PubMed.
- M. Iyoda, Y. Kuwatani, E. Ogura, K. Hara, H. Suzuki, T. Takano, K. Takeda, J. Takano, K. Ugawa, M. Yoshida, H. Matsuyama, H. Nishikawa, I. Ikemoto, T. Kato, N. Yoneyama, J. Nishijo, A. Miyazaki and T. Enoki, Heterocycles, 2001, 54, 833 CrossRef CAS.
- T. Mori, Bull. Chem. Soc. Jpn., 1998, 71, 2509 CrossRef CAS.
- T. Imakubo, H. Sawa and R. Kato, Synth. Met., 1995, 73, 117 CrossRef CAS.
- J. P. Pouget and S. Ravy, J. Phys. I, 1996, 6, 1501 CrossRef CAS; Y. Nakano, T. Nishi, M. Uruichi, K. Yakushi and H. Yamochi, Phys. B, 2010, 405, S49 CrossRef.
- Y. Nogami, T. Ito, K. Yamamoto, N. Irie, S. Horita, T. Kambe, N. Nagao, K. Oshima, N. Ikeda and T. Nakamura, J. Phys. IV, 2005, 131, 39 CAS.
- J. C. Bonner and M. E. Fisher, Phys. Rev. A: At., Mol., Opt. Phys., 1964, 135, 640 Search PubMed; W. E. Hatfield, R. R. Weller and J. W. Hall, Inorg. Chem., 1980, 19, 3825 CrossRef CAS.
- W. E. Estes, D. P. Gavel, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1978, 17, 1415 CrossRef CAS.
- (a) S. Matsuzaki, R. Kuwata and K. Toyoda, Solid State Commun., 1980, 33, 403 CrossRef CAS; (b) S. Matsuzaki, T. Moriyama and K. Toyoda, Solid State Commun., 1980, 34, 857 CrossRef CAS; (c) S. Matsuzaki, T. Moriyama, M. Onomichi and K. Toyoda, Bull. Chem. Soc. Jpn., 1983, 56, 369 CrossRef CAS; (d) H. H. Wang, J. R. Ferraro, J. M. Williams, U. Geiser and J. A. Schlueter, J. Chem. Soc., Chem. Commun., 1994, 1893 RSC; (e) O. Drozdova, H. Yamochi, K. Yakushi, M. Uruichi, S. Horiuchi and G. Saito, J. Am. Chem. Soc., 2000, 122, 4436 CrossRef CAS; (f) T. Yamamoto, M. Uruichi, K. Yamamoto, K. Yakushi, A. Kawamoto and H. Taniguchi, J. Phys. Chem. B, 2005, 109, 15226 CrossRef CAS PubMed; (g) X. F. Shao, Y. Nakano, M. Sakata, H. Yamochi, Y. Yoshida, M. Maesato, M. Uruichi, K. Yakushi, T. Murata, A. Otsuka, G. Saito, S. Koshihara and K. Tanaka, Chem. Mater., 2008, 20, 7551 CrossRef CAS; (h) Y. Nakano, T. Nishi, M. Uruichi, K. Yakushi and H. Yamochi, Physica B, 2010, 405, S49 CrossRef CAS.
- K. Wakita (2001). Yadokari-XG. Software for Crystal Structure Analyses. Release of Software (Yadokari-XG 2009) for Crystal Structure Analyses, C. Kabuto, S. Akine, T. Nemoto and E. Kwon, J. Crystallogr. Soc. Jpn., 2009, 51, 218 CrossRef.
- M. C. Burla, R. Caliandro, B. Carrozzini, G. L. Cascarano, C. Cuocci, C. Giacovazzo, M. Mallamo, A. Mazzone and G. Polidori, J. Appl. Crystallogr., 2015, 48, 306 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- T. Mori, A. Kobayashi, Y. Sasaki, H. Kobayashi, G. Saito and H. Inokuchi, Bull. Chem. Soc. Jpn., 1984, 57, 627 CrossRef CAS.
- R. S. Summervile and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 7240 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef CAS; D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358 CrossRef.
- (a) K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877 CrossRef CAS PubMed; (b) D. Feller, J. Comput. Chem., 1996, 17, 1571 CrossRef CAS; (c) K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal structures, overlap integrals, energy band structures, Fermi surfaces, sample dependence on the electrical resistivity, temperature dependence of the magnetic susceptibility fitted by Bonner–Fisher model, and infrared/Raman spectra and frequencies of EDO-TTF-I. CCDC 1590291–1590294. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7qm00575j |
| This journal is © the Partner Organisations 2018 |