Functional liquid structures by emulsification of graphene and other two-dimensional nanomaterials†
Abstract
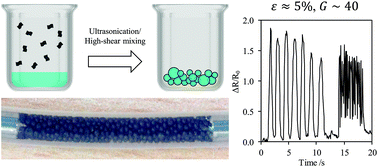
Pickering emulsions stabilised with nanomaterials provide routes to a range of functional macroscopic assemblies. We demonstrate the formation and properties of water-in-oil emulsions prepared through liquid-phase exfoliation of graphene. Due to the functional nature of the stabiliser, the emulsions exhibit conductivity due to inter-particle tunnelling. We demonstrate a strain sensing application with a large gauge factor of ∼40; the highest reported in a liquid. Our methodology can be applied to other two-dimensional layered materials opening up applications such as energy storage materials, and flexible and printable electronics.
- This article is part of the themed collection: Nanoscale Most Popular Articles


 Please wait while we load your content...
Please wait while we load your content...