Temporal multi-sensor system for voltammetric recognition of L- and D-tryptophan enantiomers based on generalized principal component analysis
R. R.
Nigmatullin
 a,
H. C.
Budnikov
a,
H. C.
Budnikov
 b,
A. A.
Khamzin
c,
A. V.
Sidelnikov
b,
A. A.
Khamzin
c,
A. V.
Sidelnikov
 d and
E. I.
Maksyutova
d and
E. I.
Maksyutova
 *d
*d
aRadioelectronic and Informative-Measurements Techniques Department, Kazan National Research Technical University (KNRTU-KAI), 10, K. Marx Str., 420111, Kazan, Russian Federation
bInstitute of Chemistry, Kazan Federal University (KFU), 18, Kremlyovskaya Str., 420008, Kazan, Russian Federation
cInstitute of Physics, Kazan Federal University (KFU), 16a, Kremlyovskaya Str., 420111, Kazan, Russian Federation
dChemistry Department, Bashkir State University (BSU), 32, Validy Str., 450076, Ufa, Russian Federation. E-mail: elzesha@gmail.com
First published on 24th November 2017
Abstract
The results of a quantitative reading of the cyclic voltammetry behavior of the tryptophan (Trp) enantiomers deposited on an electrochemically activated glassy carbon electrode (GCE) are presented. A combined method for “reading” the analytical signals based on the modified Fourier transform and GPCA was applied. It allows a quantitative description of a derivative (dJ/dU) of the measured VAG. This combined method essentially increases the limits of conventional PCA and can be applied to a wide set of electrochemical data. This combined method allows the differentiation and quantitative description of signals governed by the different structures of L- and D-Trp(s) in aqueous solutions.
1. Introduction and formulation of the problem
Modern methods of analytical chemistry have wide possibilities in the quantitative and qualitative analysis of a broad set of various compounds.With the active development of mathematical methods for processing different signal data over the last few decades, one can observe the development of multi-sensor methods associated with the simultaneous treatment of a massive amount of data. So, multisensor systems such as the “electronic tongue” (“electronic nose”) were created. They allow the identification of a few components simultaneously present in the analyzed solution and in complex solutions without detailed quantitative analysis (for example, in problems of definite qualitative identification, such as evaluation of taste or smell1).
Voltammetric and potentiometric multisensor systems have been widely propagated. Now, there are well-known commercial variants of these systems: “α-Astree electronic tongue” (France) and “Insent taste sensing system TS-5000Z” (Japan).2 To increase the sensitivity and selectivity of such electrochemical sensor systems, one creates hybrid variants that incorporate sensors of various types. Depending on the analytical problem, a researcher uses various types of mathematical methods that can be applied to the treatment of the experimental data.
For qualitative detection of various solutions, PCA and SIMCA are used;3,4 while for quantitative analysis, PLS, artificial intellectual nets (AIN) and other systems are applied.5,6 Alongside these methods, there are alternative mathematical methods that are applied for the preliminary data treatment: wavelet-analysis, Fourier transform and others.7,8 The main difficulties are associated with the problems of recognition and quantitative detection of substances which have a similar structure. Therefore, there are many papers in electroanalytical chemistry devoted to modifications of sensor surfaces to increase the selectivity to and detection of these similar substances. Isomers can be included in this class of substances because they can be reduced and oxidized at near potentials. They are used as drug substances and have different biological activities depending on their molecular structure. Their pharmacological activity is presumably associated with the action of one stereoisomer,9,10 only. This peculiarity stimulates the development of enantioselective sensors and multisensor systems that can be used for the identification of biologically active enantiomers.11–14 In this class of sensors, one can include tryptophan, cysteine (in the class of amino acids), propranolol, and atenolol (used as an anti-arrhythmia remedy). They exhibit electroactivity in the anode potential range that allows the use of voltammetric methods as detectors in pharmacology.
The most popular peculiarity in the voltammetric analysis of enantiomers takes place when the various supramolecular structures, nanoparticles and polymers modify the chemical sensors. These additional structures give the electrodes used an additional selectivity and counterbracing sensitivity. As an example, for detection of Trps-enantiomers the polymer chitosan is used or the structural analogs of uracil: cyanuric acid and melamine.15,16 The various self-assembled structures and mechanisms of the functioning of enantio-selective sensor layers have been studied in.13,17–19 In the field of enantio-selective recognition using these chiral platforms, the distinctive difference lies in the types and bond energies between functional groups of the self-organized structures and the corresponding enantiomers. Besides the detection problem, there is a significant problem with the quantitative determination of the given enantiomers in their combined presence. With the help of nanoparticles and composite materials, methods of detection of the presence of L- and D-Trps in medical preparations, bio-liquids and food products were considered in papers.20–24
The numerous papers devoted to the creation of enantio-selective sensors9,14,25–31 show that one of the approaches in the creation of an enantio-selective layer is the electrochemical oxidation/reduction polarization of an electrode surface in the presence of one enantiomer. For example, in papers28,29,31 one of the variants of such a realization was considered.
There are a variety of voltammetric sensors based on inclusion complexes,32,33 molecularly imprinted polymers,34–36 elements of living systems37–39 and sensors including various organic and nonorganic structures.40,41 The practical application of these sensors for multicomponent analysis is limited by their low selectivity with respect to the given enantiomer and sensitivity to random/obstructive components and the short life of the enantioselective layer during the electrolysis response time. In the results of applications of conventional treatment methods (the analysis of a value of the peak current, potential peak of oxidation/reduction), the evolution of the signal drift and its dispersion exceed the limiting values of the sensor resolution. One of the ways to solve this problem could consist in the creation of new methods of registration of voltammetric data, including the activation of the sensor surface under conditions of continuous sensor functioning. As was shown in paper,42 there is a possibility of receiving a new type of analytical signal purified from random noise even in cases when the electroactive component is absent.
The problem that is considered in this paper can be formulated as follows:
Is it possible to modify conventional PCA in order to produce a general and reliable method for the quantitative reading of any component of the score matrix?
More specifically, the problem posed above should give an answer to the question: is it possible to differentiate the registered signals of sensors activated in solutions of different enantiomers based on the proposed approach?
In this paper, we suggest a combined method based on the modified Fourier transform and generalized principal component analysis (GPCA) that allows us to receive additional quantitative information under the conditions of the continuous functioning of multi-sensor systems based on using a multi-stage electrochemical setup with multistage electrical modification of the working electrode in time processing.
2. Experimental
The proposed multi-sensor system consists of a sensor block with two GCEs and an electrochemical cell, a potentiostat/galvanostat Elins-P30S (Chernogolovka, Russia) and a mathematical treatment block (see Fig. 1, for details).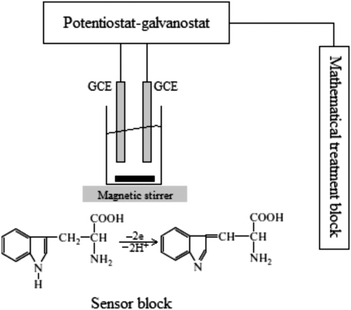 | ||
| Fig. 1 The schematic block of the experiment and chemical reaction of tryptophan oxidation.43 | ||
As a background electrolyte, standard phosphate buffer solution (pH 6.86, mixture of Na2HPO4 and KH2PO4) was used. The analyzed tryptophan solutions at a concentration of 10−3 M (SIGMA-ALDRICH, assay ≥98.0% (HPLC)) were prepared by dissolving an accurately weighed portion in the background electrolyte. The linear range of the tryptophan enantiomer was 10−3–10−1 M (R2 = 0.982).
Electrochemical activation of the sensor layer takes place under the condition of continuous registration of 100 cycles of polarizations. This process includes two stages:
(1) Electrochemical regeneration – five successive cyclings with a potential scan rate of 2.5 V s−1 in the presence of one (L- or D-) enantiomer solution.
(2) Registration of the VAG oxidation/reduction curve in the solution at the given potential scan rate of 0.5 V s−1 in the range of potentials 0–1.9 V. The scheme of the activation cycle is presented in Fig. 2.
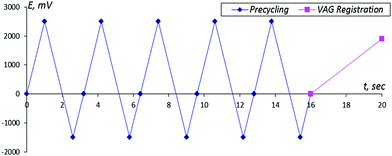 | ||
| Fig. 2 The scheme of the activation cycle. The time interval between measurements is 16 s. The period of the VAG registration is 4 s. | ||
For testing the possibilities of the sensor system, a set of experiments was performed in which, after activation of the sensor system in a conventional solution of one of the enantiomers, the electrodes were placed in another enantiomer solution with subsequent registration of the given VAGs. As one can see from Fig. 2, each VAG was registered during 16 s with cycling equaling 4 s. and the duration between successive VAGs was (16 + 4) = 20 s. Therefore, the total duration of the whole experiment was 100 × 20 = 2000 s.
3. Results and discussions
3.1. Preliminary data analysis
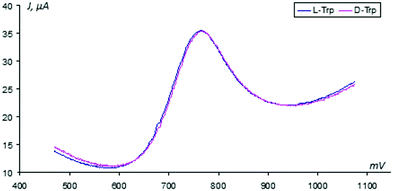
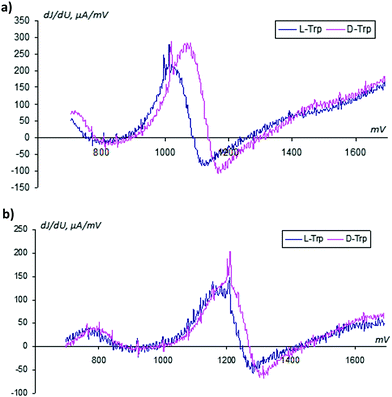
For treatment of the given data, the Faraday range of the voltammograms was used, where the desired oxidation peak of tryptophan (+600…+1700 mV) is observed. In Fig. 3, for example, a couple of the registered VAGs obtained in the absence of sensor activation are shown. One can notice that integral voltammograms obtained under these conditions on the unmodified GCEs are practically merged with each other.This observation directly indicates the correct preparation of the isomer solutions and the equality of their molar concentrations. After the sensor activation procedure, the VAGs of L- and D-tryptophans are differentiated easily with respect to their oxidation peak positions (see Fig. 4, for details).
(a) In this plot one can see that after sensor activation in the L-Trp solution the VAGs of L- and D-Trps differ from each other by the values of the peak oxidation potentials: the peak of D-Trp is shifted in the anode region.
(b) This plot illustrates the activation of the sensor in the D-Trp solution that leads to the shifting of the oxidation D-peak toward the anode region. Therefore, this observed shifting is not related to the background changes in electrode potentials over time; this shift evokes the electrochemical activation of the sensor used due to the nature of the enantiomer used.
The experimental results show that the order of the replacement of the L- and D-solutions does not influence the location of the corresponding peaks. The peak shifting is the result of the directed (controlled) changing of the sensor surface. The surface modification is shown in the resulting electrode activation in the enantiomer solution. For qualitative confirmation of the sensor surface modification as a result of its modification, another experiment was conducted, where the impedance spectra are registered after each activation cycle.
Now, for a better understanding of the originality of the proposed algorithm, we should say a few words about impedance spectroscopy. Impedance spectroscopy is a highly-sensitive method applicable for studying the boundary phase division near the electrode surface. It is also known44 that impedance spectra are registered for different processes in an electrochemical cell (charge transfer, semi-infinite and quasi-spherical diffusions, diffusion in some limited region, non-Faradaic processes in substance sorption/desorption on the electrode surface, etc.) and, therefore, they have different forms. Depending on the formulated problem, various mathematical methods and algorithms for decoding the impedance spectra have been proposed. It follows from45–48 in a study of electrochemical systems “electrode/solution”, all problems are divided into one or other of two sub-problems: (a) determination of the physicochemical parameters (the chemical reaction velocities, diffusion coefficients, etc.) with subsequent identification of the nature of these dynamical processes; (b) identification of the kinetic reaction (nature) of the identified process.
Earlier in papers49,50 based on PCA, we proposed a combined impedance-kinetic method that allows us to determine the quantity and intervals of the time associated with various stages of physical and chemical processes related to interaction with the electrode surface. Now we want to generalize conventional PCA and, for the first time, we have applied this combined approach to confirm electrode activation under continuous sensor system functioning conditions.
Impedance spectra were recorded on an impedance spectrometer “Elins” Z500R (Chernogolovka, Russia) in the frequency range of alternating current from 500 kHz to 10 Hz with an amplitude of 5 mV with constant mixing on a magnetic stirrer.
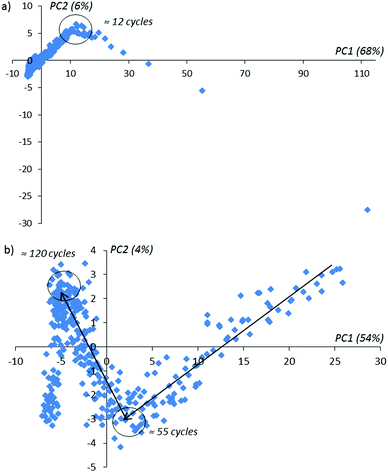
Using conventional PCA, we plot the lowest score matrix components corresponding to the imaginary impedance components obtained during 160 sensor cycles with and without an activation procedure in a solution of D-Trp (Fig. 5).
In Fig. 5 one can notice that in the activation procedure, the typical bends on achieving the 12-th, 55-th and 120-th activation cycles are observed. These bends contain information about the changing of the sensor layer during the activation procedure inside the enantiomer solution. In the absence of the applied potential on the sensor (without activation) for the same experimental duration time as realized with activation, only one bend in the 12-th cycle is observed (see Fig. 6 for comparison). With the further continuation of this experiment, these extreme peculiarities in the behavior of the compared PCA-components are not observed. We explain this behavior as the absence of the changes in the sensor surface placed in the given enantiomer solution.
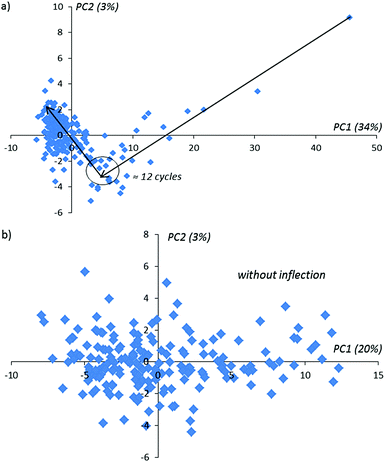 | ||
| Fig. 6 PCA-kinetic impedance curves obtained without activation: (a) 1–160 cycles, (b) 12–160 cycles. Black arrows in the figure above show the direction of the number of activation cycles in time. | ||
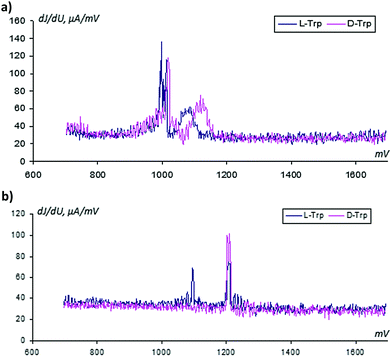
From classical metrological analysis, the large share of the uncontrolled random component in the registered VAGs does not allow us to identify two enantiomers when their oxidation potentials have a small difference. In Fig. 7 we show the standard current deviations with respect to the applied potential.
(a) The standard deviations related to instantaneous current values depend on the applied potential; they are increased in the Faraday region. This peculiarity informs us about the additional information in the mass of data associated with modifications of the sensor surface over time and requires the application of special methods for reading these specific types of data.
(b) The narrow peaks inform us about more uniform changes in the sensor surface at activation in the D-trp solution.
From analysis of Fig. 4 and 7, it follows that the relative deviation of the analytical signal in the region of the tryptophan oxidation can exceed a value of 50%. A review of the admissible literature51 related to analysis of noise in electrochemical systems shows that there is a possibility of applying background signals for analytical purposes: i.e. for detection of unknown substances, their structures, etc. See, for example, the papers.52–55
For initial analysis of the VAGs and their derivatives, one can use PCA,13,56,57 allowing the discovery of the internal data structure and seeing some new relationships in the massive dataset analyzed. In this paper, we use GPCA in combination with Fourier analysis that allows us to read quantitatively the large amount of data at any stage of their possible evolution.
3.2. Mathematical section: PCA and the modified F-transform
In this section, we remind a potential reader of the basic expressions and definitions of PCA for a better understanding of the original part of this research. We consider a rectangular matrix Mi,j (i = 1, 2,…,Nr, j = 1, 2, …, Nc), where indexes i, j define all rows (Nr) and columns (Nc ≤ Nr), respectively. In accordance with the general algorithm accepted in PCA, the initial matrix should be presented in the form: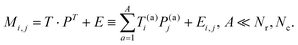 | (1) |
| M = USPT, S(σ1 ≥ σ2 ≥…σNr), | (2) |
| TTT = USS × UT = S2, | (3) |
In this paper we show how to consider a large set of T(a) (a > 3) and prove that the further components being plotted with respect to each other and looking initially like a random distribution of the data points actually have a certain deterministic nature. Therefore, one can restore more information from an analysis of these plots if they are presented in another way. This new modification of the conventional PCA actually solves the problem formulated above and allows an increase in the limits of the application of PCA. Below, as an illustration of the new presentation associated with analysis of VAGs, it is convenient to use the dimensionless potential (we simply normalize the applied potential U to 1 V, i.e. u = U(V)/1 V) and use a uniform scale:
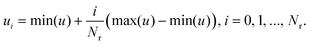 | (4) |
Then we use the normalized matrix G determined below from expression (5) (associated with measurements of the background by means of the cycling potential U) for a glassy carbon electrode (GCE) and covering the Faraday region that is determined as the current region associated with oxidation of different organic compounds (in the case of their presence in the given solution). The basic problem is to find a general platform for a quantitative description of the basic components of the score matrix T(a). A plot of these experiments for the normalized matrix
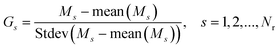 | (5) |
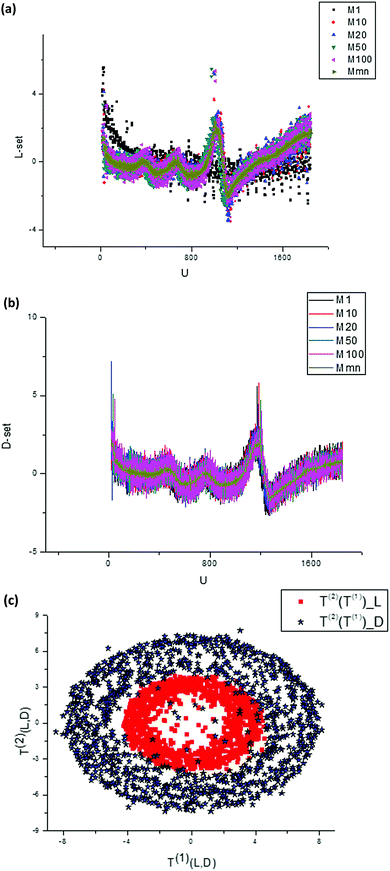 | ||
| Fig. 8 (a) A randomly selected set of measured curves dJ/du obtained for L-Trps. These initial curves are changed essentially with respect to a number (m = 1, 10, 20, 50, 100) of experiments. The time interval between measurements is 16 s. (b) A randomly selected set of measured curves dJ/du obtained for D-Trps. These initial curves are changed essentially with respect to a number (m = 1, 10, 20, 50, 100) of experiments. If we compare this set with the set depicted in the previous figure then one can notice that they are similar, but the peaks are shifted and the amplitudes for D-Trps slightly exceed the values calculated for L-Trps. We should notice that all curves given in Fig. 8(a and b) are normalized in accordance with expression (5). (c) If we plot the T(2)(u) component of the score matrix with respect to the T(1)(u) component for L-,D-(Trps) respectively, then one can notice that these figures form two “fat” ellipses with the same center. This peculiarity is explained in the main text and in Fig. 9 below. | ||
We should stress here that in Fig. 8(a) we use the derivatives dJ/du as sensitive components in comparison with integral curves that are ineffective in this case. Differentiation of these curves with respect to u allows elimination of the undesirable envelopes and allows the desired shift to be expressed more clearly. Then after application of the SVD procedure we present the second component of the score matrix T(2) as a function of the vector T(1). This plot is shown in Fig. 8(c).
Taking the Fourier transform of the vectors T(1) belonging to L- and D-Trps, we obtain the key picture shown in Fig. 9. This observation follows from the fact that the Fourier transform of these vectors contains a couple of the leading frequencies. From analysis of this figure, one can notice two dominant frequencies with amplitudes approximately satisfying the condition ω(1)0 + ω(1)0 ≅ 2π and other frequencies with unnoticeable amplitudes that can be omitted in the first stage. Mathematically, the dependence of the vector T(1)(u) can be approximately expressed as:
T(1)(u) = A(1)0 + Ac(1)m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ω(1)0u − φ(1)0) cos(ω(1)0u − φ(1)0) | (6) |
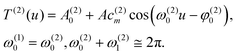 | (7) |
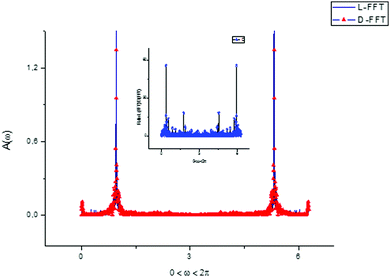 | ||
| Fig. 9 For an explanation of the previous figures we calculated the fast Fourier transform (FFT) of the components of the score matrix T(1)(u) for two types of tryptophans. One can notice that the F-spectrum for L- and D-(Trps) are very close to each other and have two leading frequencies. This peculiarity prompts the decomposition of the score matrix components to a segment of the Fourier series. Other details are explained by expressions (6)–(8) and are given in the main text. The ratio FFT(L)/FFT(D) between the two spectra is shown in the small inset figure above. | ||
Therefore, the plots T(2) = F(T(1)) depicted in Fig. 8(c) express the different Lissajous figures that are accepted in the conventional theory of mechanical vibrations. In particular, for the case φ(1)0 = φ(2)0 we obtain the straight line that is usually considered in PCA to be an indication of a strong correlation between compared random sequences; for 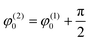 we obtain a classical ellipse; for φ(2)0 = φ(1)0 + α we obtain an ellipse rotated counterclockwise on the angle α. For ω(1)0 ≠ ω(2)0, φ(2)0 − φ(2)0 = α we obtain the different Lissajous figures that can be observed in the case of clusterization of different data points forming the initial vectors T(1,2). As proved in Fig. 8(c) we show the dependence T(2) = F(T(1)) for the real data described above that forms “fat” ellipses.
we obtain a classical ellipse; for φ(2)0 = φ(1)0 + α we obtain an ellipse rotated counterclockwise on the angle α. For ω(1)0 ≠ ω(2)0, φ(2)0 − φ(2)0 = α we obtain the different Lissajous figures that can be observed in the case of clusterization of different data points forming the initial vectors T(1,2). As proved in Fig. 8(c) we show the dependence T(2) = F(T(1)) for the real data described above that forms “fat” ellipses.
The envelope of the ellipse is slightly destroyed by the influence of other small frequencies present in the decomposition of both Fourier series forming the vectors T(1,2). This simple observation prompts us to use for quantitative characterization and parameterization the fragments of the Fourier series belonging to the vectors of the score matrix.
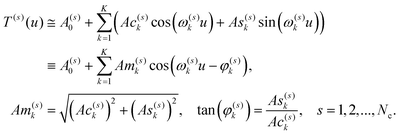 | (8) |
We should stress here the following fact. If ω(s)k+1 − ω(s)k = a(s), 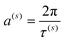 and τ(s) coincides with the period of vibration of vector T(s) then the fragment (8) coincides completely with the Fourier decomposition. Otherwise, when ω(s)k+1 − ω(s)k ≠ a(s) this decomposition recovers the NAFASS (Non-orthogonal Amplitude–Frequency Analysis of the Smoothed Signals) approach considered in papers,58,59 where the set of frequencies follows another dispersion law. Concluding this section, one can say that the behavior T(s)(u) can be characterized naturally by its AFR (amplitude–frequency response) (ω(s)k, Am(s)k) and, therefore, the dependencies T(s+1)(u) = F(T(s)(u)) which look initially like random dependencies can receive their natural (and we want to stress deterministic) explanation. Actually, we found the parameterization of the score vectors, using for this purpose the dimensionless potential u. Therefore, as a criterion of neglecting by a possible functional dependence T(s)(u) for relatively large s one can use the range of this vector, defined as max(T(s)(u)) − min(T(s)(u)). This follows from the definition of T(s)(u) (US ≡ T): when this vector is multiplied by the eigenvalue σs it decreases its range with a growth in the order of s. The main problem of this behavior lies in finding an adequate chemical interpretation of the AFR, especially for the spectrum {ω(s)k} belonging to each component of the score matrix T(s). However, the problem formulated above for finding an adequate parameterization of the components T(s)(u) has been solved.
and τ(s) coincides with the period of vibration of vector T(s) then the fragment (8) coincides completely with the Fourier decomposition. Otherwise, when ω(s)k+1 − ω(s)k ≠ a(s) this decomposition recovers the NAFASS (Non-orthogonal Amplitude–Frequency Analysis of the Smoothed Signals) approach considered in papers,58,59 where the set of frequencies follows another dispersion law. Concluding this section, one can say that the behavior T(s)(u) can be characterized naturally by its AFR (amplitude–frequency response) (ω(s)k, Am(s)k) and, therefore, the dependencies T(s+1)(u) = F(T(s)(u)) which look initially like random dependencies can receive their natural (and we want to stress deterministic) explanation. Actually, we found the parameterization of the score vectors, using for this purpose the dimensionless potential u. Therefore, as a criterion of neglecting by a possible functional dependence T(s)(u) for relatively large s one can use the range of this vector, defined as max(T(s)(u)) − min(T(s)(u)). This follows from the definition of T(s)(u) (US ≡ T): when this vector is multiplied by the eigenvalue σs it decreases its range with a growth in the order of s. The main problem of this behavior lies in finding an adequate chemical interpretation of the AFR, especially for the spectrum {ω(s)k} belonging to each component of the score matrix T(s). However, the problem formulated above for finding an adequate parameterization of the components T(s)(u) has been solved.
3.3. Application of the modified platform to real data
In this section, we want to show how to apply this modified method for detection of the differences between L- and D-tryptophans.We use the following algorithm:
(1) Normalization of the initial rectangular matrix in accordance with expression (5).
(2) Application of the SVD procedure for calculation of the score components of the vector T(s)(u).
(3) Analysis of the neighboring plots T(s+p)(u) (s, p = 0, 1, 2, 3,…) with respect to T(s)(u). This preliminary observation helps to differentiate the most distinguishing vectors. In our case it is sufficient to choose the initial vectors satisfying the condition s + p = 1, 3.
(4) After the selection of the desired vectors, it is necessary to decompose them to the segment of the Fourier series in accordance with relationship (8). The dispersion law ω(s)k and the dependence of the modulus Am(s)kω(s)k form the desired quantitative identifications. These markers serve as necessary functions for the description of any score vector T(s)(u), especially in the case of the absence of a microscopic model.
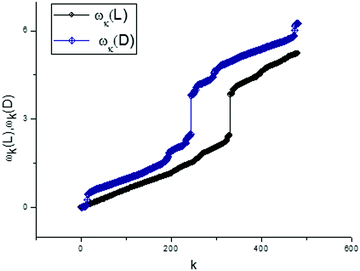
A part of this applied algorithm was explained by Fig. 8 and 9. Actually, we have a new possibility for presenting any vector of the score matrix in the form of expression (8). In order to finish the analysis of the first components for two types of tryptophan, we present the dispersion laws for L- and D-types. They are shown in Fig. 10. These frequency spectra are obtained as a part of the total set of frequencies and located in the interval [mean(ωk)/2 < ωk < max(ωk)]. This selected set of frequencies is sufficient for providing an acceptable fit with the value of the relative error:
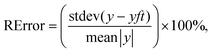 | (9) |
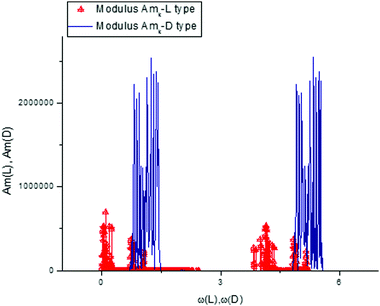
The calculated fit of the components T(1)(u) for L- and D-Trps are shown in Fig. 11(a and b), respectively. As one can notice from these figures, the fitting function (8) provides an acceptable fit with a relative error [0–10%] for the components T(1)(u), which initially look like “random” sequences. However, expression (8) gives a possibility for the usage of another data presentation that is widely used in radioelectronics. We use the modified F-transform based on a limited number of frequencies. This presentation helps us to find easily the desired discrepancies expressed in the form of AFRs. These AFRs are shown in Fig. 12.
 | ||
| Fig. 11 (a) This plot demonstrates the fit of the T(1)(u) associated with L-Trp. The accuracy of this fit reaches 7.5% and the initially spurious random component can be described with the spectral language associated with expression (8). (b) In a similar manner one can obtain the fit of the component T(1)(u) associated with D-Trp. The accuracy of this fit reaches 5.7% and again the initially spurious random component can be described in terms of the AFR associated with expression (8). | ||
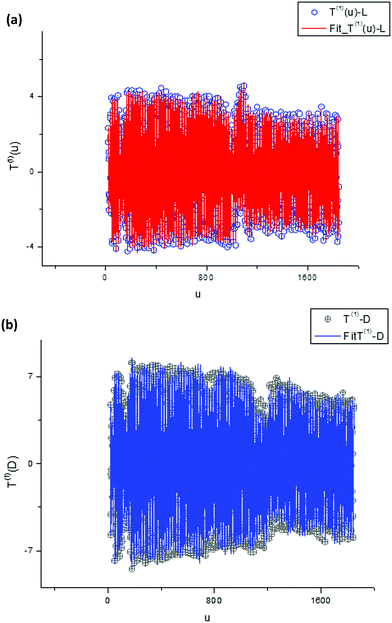
From this simple analysis, one can notice the significant set of frequencies that allows differentiation of the L- and D-Trps expressed in the “frequency” language. We want to stress here two interesting points. We realize the desired fit with acceptable accuracy for the large set of data points (N = 1190) using only 480 frequencies. However, the set of selected frequencies from the interval [mean(ωk)/2 < ω < ωmax] are sufficient for differentiation of two types of tryptophans with the fitting error defined by expression (9) and located in the interval [0–10%]. Another point is associated with the values of the calculated AFRs. If we compare the values of the amplitudes illustrated in Fig. 11 with the values of the fitting vectors T(1)(u), then one can notice that the values of the amplitudes exceed the initial values by 106 or more times. This AFR presentation also serves as a specific zoom lens for the differentiation of small differences. In the same manner one can consider other components of the score matrix such as T(0)(u) and T(3)(u). Consideration of the T(2)(u) component is omitted because its behavior is similar to T(1)(u). In order to save a limited space for consideration of these components, we show only their conventional presentation.
We omit the comparison of the components T(3)(T(0)) for two L- and D-tryptophans that do not form ellipses; however, the F-transform can be applied for this case, as well.
We again use a limited number of frequencies (K = 500) in order to provide an acceptable fit in the given interval [0–10%]. We demonstrate the desired fit of the components T(0,3)(u) (Fig. 13 and 15) and their AFRs (Fig. 14 and 16).
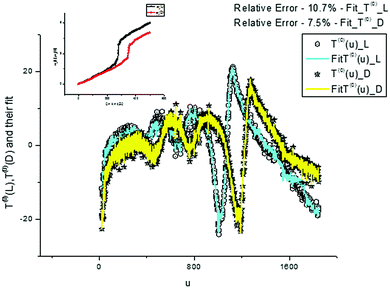 | ||
| Fig. 13 These plots demonstrate the fit obtained with the help of expression (8) for T(0)(u). The dispersion laws containing 450 frequencies are shown in the small inset figure above together with the value of the fitting error. | ||
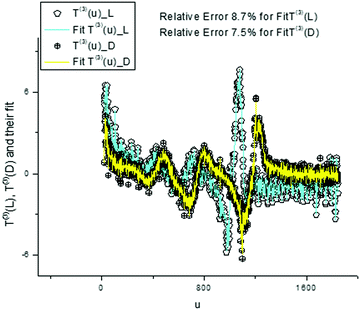 | ||
| Fig. 15 These plots demonstrate the fit obtained with the help of expression (8) for T(3)(u). The values of the fitting errors are shown above. In order to obtain this acceptable fit, we should increase the number of frequencies to 500 values. The calculated dispersion laws are depicted in the next figure. | ||
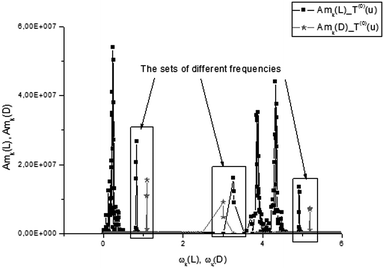
From analysis of these figures, one can conclude that the differences between the two types of tryptophans are observed for all components; however, they are expressed to different degrees. The most significant differences are observed for the components T(1)(u), while the other components also demonstrate the desired differences however, they are expressed to a lesser degree (see caption to Fig. 17).
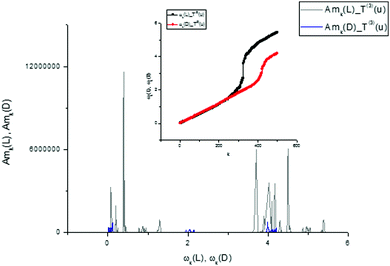 | ||
| Fig. 17 The comparison of the AFRs for the score vector components T(3)(L,D). Here, as in Fig. 11, one can easily notice the spectroscopic differences for two types of tryptophan, analyzing the third components T(3)(L,D) in the frequency domain. If we compare the AFRs for three vectors T(0,1,3)(u) (Fig. 11, 14 and this figure), then one can notice that the most significant differences are observed for the T(1)(L,D) component. The corresponding spectra are shown in the small inset figure above. | ||
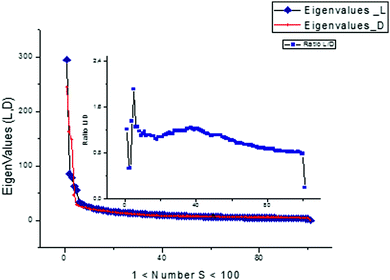
Besides this new “frequency” platform associated with analysis of the functions Amk(ωk), one can add information obtained from the distribution of the eigenvalues of the initial matrix S. The distributions of the eigenvalues expressed in descending order for both cases are presented in Fig. 16. They are different for L- and D-Trps and can also be used as specific fingerprints differentiating the two types of tryptophans from each other.
One can give a qualitative explanation for this L- and D-detection on the surface of the electrode from the chemical point of view.
It is known60 that the electrochemical electrode response arises as the result of interaction of an analyte with a chiral reagent (or selector), with one of the enantiomer forms immobilized on the electrode surface. The control of its interaction can be detected by kinetic or thermodynamic methods. With thermodynamic control, the time for establishing the desired equilibrium between the analyte and the selector plays an important role. If this successive signal registration is repeated many times, then the preferable thermodynamic conditions are created and, therefore, the electrode gives the desired response for one of the enantiomers. One can see an analogy with the method of liquid chromatography, when the interaction of the selector with the analyte (which is in the moveable phase) takes place in heterogeneous conditions, i.e. on the boundary between the solid and liquid phases. The accumulation of a sufficient quantity of the reagent-selector, which can be associated with the tryptophan oxidation product, depends on the total electrolysis time, in our case from the successive numbers of the VAGs. During this time, we have two important processes: (a) the sorption of the chiral reagent (i.e. immobilization of the selector on the electrode surface) and (b) subsequent formation of its thin film during the total electrolysis time. The selector presumably provides an accumulation of one isomer on the electrode surface; after that, the created electrode reaction causes its quantitative transformation and generates the expected response. The temporal factor is evaluated mathematically from the given experimental conditions.
4. Conclusions
In the final section, we would like to stress the most significant results obtained in this paper.(1) The results presented in this paper essentially increase the possibilities for multi-sensor systems in studying compounds with a similar nature. The accumulation of chemical information about the analyte nature, formation and quantitative identification of a massive amount of analytical signals specifically related to a small amount of a substance located in a given solution becomes possible, and not only in the presence of a massive number of sensors as is conventionally accepted in the practice of multi-sensor analysis. In this paper, we propose another way: the accumulation of a large amount of chemical information under the condition of the continuous functioning of even one (initially non-selective) working electrode.
The conventional multisensory method lying in the background of the formation of most electronic “tongues” and “noses” implies a wide spectrum of “tuned” electrodes for detection of the presence of a specific substance in a given solution.
In this paper, we suggest another method of multisensory formation using only one electrode during the whole duration of the electrochemical experiment. Each activation cycle changes the sensibility of the given sensor (and, hence, its response) and the large number of similar measurements can significantly change the surface of an electrode. The large number of activation cycles in turn generates large amounts of different states of the working electrode. Therefore, we create a number of fictitious “pseudo-sensors” shifted in time and in the resulting repetition of similar measurements, we obtain a large amount of information about the evolution of the given solution and its components. The combination of PCA with the Fourier transform allows us to receive a new informative block related to the measured analytical signals in the frequency domain expressed in the form of the Fourier spectrum.
(2) We essentially modified conventional PCA by adding the possibility for a quantitative reading of the basic components T(s) (s = 0, 1, 2,…) of the score matrix. This possibility is based on expression (8) that helps to give a potential researcher a new spectroscopic “space” associated with the set of frequencies (ωk) and their amplitudes (Ack, Ask, Amk) for the measured electrochemical data.
3. This combined platform is relatively flexible and universal. It can be applied to the analysis of different types of curves registered in an electrochemical cell, especially in cases when the microscopic model is absent.
List of basic abbreviations
| AFR | Amplitude-frequency response |
| CFFT | Complex fast Fourier transform |
| GCE | Glassy carbon electrode |
| (G)PCA | (Generalized) principal component analysis |
| SVD | Singular values decomposition |
| Trps | Tryptophans |
| VAGs | Voltammogram(s) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Foundation for Basic Research, project No. 17-43-020232 r-Povolzh'ye-a. The co-author of this paper, Dr A. Khamzin, expresses also his acknowledgements to the Ministry of Education and Science of Russia for supporting the research in the framework of the state assignment (# 3.2166.2017/4.6) and is thankful for a partial support of the Russian Government Program of Competitive Growth of Kazan Federal University.Notes and references
- F. Winquist, Microchim. Acta, 2008, 163(1–2), 3–10 CrossRef CAS.
- K. Woertz, C. Tissen, P. Kleinebudde and J. Breitkreutz, Int. J. Pharm., 2011, 417(1–2), 256–271 CrossRef CAS PubMed.
- A. Kutyła-Olesiuk, U. E. Wawrzyniak, M. Jańczyk and W. Wróblewski, Procedia Eng., 2014, 87, 580–583 CrossRef.
- H. Xiao and J. Wang, J. Food, Agric. Environ., 2012, 10, 227–230 CAS.
- X. Cetó, J. Capdevil, S. Mínguez and M. del Valle, Food Res. Int., 2014, 55, 455–461 CrossRef.
- R. H. Labrador, J. Olsson, F. Winquist, R. Martínez-Máñez and J. Soto, Electroanalysis, 2009, 21(3–5), 612–617 CrossRef CAS.
- X. Cetó, J. M. Gutiérrez, M. Gutiérrez, F. Céspedes, J. Capdevila, S. Mínguez, C. Jiménez-Jorquera and M. del Vall, Anal. Chim. Acta, 2012, 732, 172–179 CrossRef PubMed.
- X. Cetó, C. Apetrei, M. Del Valle and M. L. Rodríguez-Méndez, Electrochim. Acta, 2014, 120, 180–186 CrossRef.
- E. L. Izake, J. Pharm. Sci., 2007, 96(7), 1659–1676 CrossRef CAS PubMed.
- A. L. Lehninger, D. L. Nelson and M. M. Cox, Principles of Biochemistry, Worth Publishers, NY, 1993 Search PubMed.
- W. Feng, C. Liu, S. Lu, C. Zhang, X. Zhu, Y. Liang and J. Nan, Microchim. Acta, 2014, 181(5–6), 501–509 CrossRef CAS.
- L. Yu, Q. Liu, X. Wu, X. Jiang, J. Yu and X. Chen, RSC Adv., 2015, 119(5), 98020–98025 RSC.
- A. V. Sidel’nikov, V. N. Maistrenko, R. A. Zil’berg, Yu. A. Yarkaeva and E. M. Khamitov, J. Anal. Chem., 2017, 75(5), 575–581 CrossRef.
- Q. Chen, J. Zhou, Q. Han, Y. Wang and Y. Fu, J. Solid State Electrochem., 2012, 16(7), 2481–2485 CrossRef CAS.
- X. Gu, Y. Tao, Y. Pan, L. Deng, L. Bao and Y. Kong, Anal. Chem., 2015, 87(18), 9481–9486 CrossRef CAS PubMed.
- R. A. Zilberg, A. V. Sidelnikov, V. N. Maistrenko, Yu. A. Yarkaeva, E. M. Khamitov, V. M. Kornilov and E. I. Maksutova, Electroanalysis, 2017, 29 DOI:10.1002/elan.201700404.
- L. Bao, Y. Tao, X. Gu, B. Yang, L. Deng and Y. Kong, Electrochem. Commun., 2016, 64, 21–25 CrossRef CAS.
- Y. Tao, J. Dai, Y. Kong and Y. Sha, Anal. Chem., 2014, 86(5), 2633–2639 CrossRef CAS PubMed.
- Y. Tao, X. Gu, B. Yang, L. Deng, L. Bao, Y. Kong, F. Chu and Y. Qin, Anal. Chem., 2017, 89(3), 1900–1906 CrossRef CAS PubMed.
- F. Khaleghi, A. E. Irai, V. K. Gupta, S. Agarwal, M. Bijad and M. Abbasghorbani, J. Mol. Liq., 2016, 223, 431–435 CrossRef CAS.
- Y. Haldorai, S.-H. Yeon, Y. S. Huh and Y.-K. Han, Sens. Actuators, B, 2017, 239, 1221–1230 CrossRef CAS.
- J. V. Kumar, R. Karthik, S.-M. Chen, S. Marikkani, A. Elangovan and V. Muthuraj, J. Colloid Interface Sci., 2017, 496, 78–86 CrossRef CAS PubMed.
- M. Shabani-Nooshabadi, M. Roostaee and H. Karimi-Maleh, J. Iran. Chem. Soc., 2017, 14(5), 955–961 CrossRef CAS.
- C. Wang, T. Li, Z. Liu, Y. Guo, C. Li, C. Dong and S. Shuang, J. Electroanal. Chem., 2016, 781, 363–370 CrossRef CAS.
- M. Trojanowicz, Electrochem. Commun., 2014, 38, 47–52 CrossRef CAS.
- H. Y. Aboul-Enein and R.-I. Stefan, Crit. Rev. Anal. Chem., 1998, 28(3), 259–266 CrossRef CAS.
- S. Arnaboldi, T. Benincori, R. Cirilli, W. Kutner, M. Magni, P. R. Mussini, K. Noworyta and F. Sannicolo, Chem. Sci., 2015, 6, 1706–1711 RSC.
- T. Yutthalekha, C. Warakulwit, J. Limtrakul and A. Kuhn, Electroanalysis, 2015, 27(9), 2209–2213 CrossRef CAS.
- T. Yutthalekha, C. Wattanakit, V. Lapeyre, S. Nokbin, C. Warakulwit, J. Limtrakul and A. Kuhn, Nat. Commun., 2016, 7(12678), 1–8 Search PubMed.
- P. Qu, J. Lei, R. Ouyang and H. Ju, Anal. Chem., 2009, 81(23), 9651–9656 CrossRef CAS PubMed.
- C. Wattanakit, Y. B. S. Côme, V. Lapeyre, P. A. Bopp, M. Heim, S. Yadnum, S. Nokbin, C. Warakulwit, J. Limtrakul and A. Kuhn, Nat. Commun., 2014, 5(3325), 1–8 Search PubMed.
- P. Shahgaldian and U. Pieles, Sensors, 2006, 6(6), 593–615 CrossRef CAS.
- G. Zhu, Y. Yi and J. Chen, TrAC, Trends Anal. Chem., 2016, 80, 232–241 CrossRef CAS.
- Y. Kong, W. Zhao, S. Yao, J. Xu, W. Wang and Z. Chen, J. Appl. Polym. Sci., 2010, 115(4), 1952–1957 CrossRef CAS.
- W. J. Cheong, F. Ali, J. H. Choi, J. O. Lee and K. Y. Sung, Talanta, 2013, 106, 45–59 CrossRef CAS PubMed.
- M. P. Tiwari and A. Prasad, Anal. Chim. Acta, 2015, 853, 1–18 CrossRef CAS PubMed.
- L. Feng, B. Xu, J. Ren, C. Zhao and X. Qu, Chem. Commun., 2012, 48(72), 9068–9070 RSC.
- Y. Fu, Q. Chen, J. Zhou, Q. Han and Y. Wang, Anal. Biochem., 2012, 421, 103–107 CrossRef CAS PubMed.
- Y. Wang, Q. Han, Q. Zhang, Y. Huang, L. Guo and Y. Fu, J. Solid State Electrochem., 2013, 17(3), 627–633 CrossRef CAS.
- R.-I. Stefan-van-Staden, S.-C. Balasoiu, G. Bazylak, J. F. van Staden, H. Y. Aboul-Enein and G. L. Radu, J. Electrochem. Soc., 2013, 160(10), B192–B195 CrossRef CAS.
- A. B. F. Vitoreti, O. Abrahao, R. da Silva Gomes, G. R. Salazar-Banda and R. T. S. Oliveira, Int. J. Electrochem. Sci., 2014, 9, 1044–1054 Search PubMed.
- R. R. Nigmatullin, H. K. Budnikov, A. V. Sidelnikov and E. I. Maksyutova, CCC, 2017, 5(3), 12–32 Search PubMed.
- C. G. Nan, Z. Z. Feng, W. X. Li, D. J. Ping and C. H. Qin, Anal. Chim. Acta, 2002, 452(2), 245–254 CrossRef CAS.
- Electroanalytical Methods, Guide to Experiments and Applications, ed. F. Scholz, Springer-Verlag, Berlin Heidelberg, 2002 Search PubMed.
- K. J. Vetter, Z. Phys. Chem., 1952, 199, 300 CAS.
- Impedance spectroscopy – Emphasizing solid materials and systems, ed. J. R. Macdonald, Wiley-Interscience, NY, 1987 Search PubMed.
- M. Sluyters-Rehbach and J. H. Sluyters, in Comprehensive Treatise of Electrochemistry, ed. E. Yeager, J. M. Bockris, B. E. Conway and S. Sarangapani, Plenum Press, NY, 1984, vol. 9, p. 177 Search PubMed.
- W. P. Gomes and D. Vanmaekelbergh, Electrochim. Acta, 1996, 41(7–8), 967–973 CrossRef CAS.
- A. V. Sidelnikov, D. M. Bikmeev, D. I. Dubrovskii, F. K. Kudasheva and V. N. Maistrenko, J. Anal. Chem., 2015, 70(7), 837–842 CrossRef CAS.
- V. Y. Gus'kov, A. V. Sidel'nikov, D. A. Suhareva, Y. Y. Gainullina, F. H. Kudasheva and V. N. Maistrenko, Sorbtsionnye Khromatogr. Protsessy, 2016, 16(6), 797–802 Search PubMed , http://www.sorpchrom.vsu.ru/articles/20160604.pdf.
- S. F. Timashev and Yu. S. Polyakov, Fluct. Noise Lett., 2007, 07(02), 1–59 Search PubMed.
- H. A. A. Al-Mazeedi and R. A. Cottis, Electrochim. Acta, 2004, 49, 2787–2793 CrossRef CAS.
- R. A. Cottis, Corrosion, 2001, 57(3), 265–285 CrossRef CAS.
- J. R. Kearns, J. R. Scully, P. R. Roberge, D. L. Reichert and J. L. Dawson, Proceedings of the First International Symposium on Electrochemical Noise Measurement for Corrosion Applications, held in Montreal, Quebec, 1994.
- A. Hassibi, R. Navid, R. W. Dutton and Th.H. Lee, J. Appl. Phys., 2004, 96, 1074–1082 CrossRef CAS.
- A. V. Sidel'nikov, R. A. Zil'berg, Yu. A. Yarkaeva, V. N. Maistrenko and V. A. Kraikin, J. Anal. Chem., 2015, 70(10), 1261–1266 CrossRef.
- D. M. Bikmeev, A. V. Sidel’nikov, F. K. Kudasheva and V. N. Maistrenko, J. Anal. Chem., 2015, 70(6), 718–724 CrossRef CAS.
- R. R. Nigmatullin, S. I. Osokin and V. A. Toboev, Chaos, Solitons Fractals, 2011, 44, 226–240 CrossRef.
- R. R. Nigmatullin and W. Zhang, Commun. Nonlinear Sci. Numer. Simul., 2013, 18, 547–558 CrossRef.
- G. K. Budnikov, G. A. Evtyugin, Y. G. Budnikova and V. A. Al’fonsov, J. Anal. Chem., 2008, 63(1), 2–12 CrossRef CAS.
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2018 |