Origin of low electron–hole recombination rate in metal halide perovskites†
Francesco
Ambrosio
 *a,
Julia
Wiktor
*a,
Julia
Wiktor
 a,
Filippo
De Angelis
a,
Filippo
De Angelis
 bc and
Alfredo
Pasquarello
bc and
Alfredo
Pasquarello
 a
a
aChaire de Simulation à l'Echelle Atomique (CSEA), Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: Francesco.Ambrosio@epfl.ch
bComputational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), CNR-ISTM, Via Elce di Sotto 8, I-06123 Perugia, Italy
cD3-Computation, Istituto Italiano di Tencologia, Via Morego 30, Genova, Italy
First published on 21st December 2017
Abstract
To address the slow recombination of photogenerated charges in tetragonal CH3NH3PbI3, the evolution of extra electrons and holes is simulated through advanced ab initio molecular dynamics. We show that the localization of the charge carriers and their hopping from one polaronic state to another occur on a subpicosecond time scale. The localization, attended by weak bond contractions and elongations in the inorganic sublattice, is induced by thermal vibrations and only moderately perturbed by the disordered field generated by the organic cations. The simultaneous simulation of extra electrons and holes shows that they preferentially localize in spatially distinct regions. As determined by the overlap between the electron and hole wave functions, the probability of radiative bimolecular recombination is lowered by two orders of magnitude compared with that of optical generation. The separate polaronic localization of electrons and holes emerges as the key feature for achieving exceptional photovoltaic properties.
Broader contextSolar cells based on metal halide perovskites show promising photovoltaic properties with efficiencies exceeding 20% in only a few years. The identification of materials with even better properties is contingent on the understanding of the physics behind their exceptional photovoltaic performance, such as that leading to low electron–hole recombination rates and long charge carrier lifetimes. In this Communication, we perform advanced ab initio molecular dynamics in the presence of extra electrons and holes in CH3NH3PbI3 and highlight the occurrence of polaronic states. The thermal vibrations of the inorganic sublattice lead to spatial separation between polaronic holes and electrons, which is only moderately affected by the disorder in the orientation of the organic cations. This behavior is found to be the key feature for suppressing the recombination of photogenerated carriers. |
Metal halide perovskites have recently emerged as a promising alternative to silicon-based solar cells.1–3 Among their peculiar electronic and optical properties,4–9 the most intriguing feature is the slow recombination of photogenerated carriers.10–13 Most of the materials currently studied (e.g. CH3NH3PbI3) lack long-term thermodynamic stability and possess a complex phase-diagram,14 in which not all of the phases are suitable for photovoltaics. For example, while a low electron–hole recombination rate has been measured for tetragonal CH3NH3PbI3, the orthorhombic phase carries less desirable electronic properties.12 In this framework, unveiling the origin of the low recombination rate in CH3NH3PbI3 would aid the rational design of new materials with both long-term stability and desirable electronic properties.
Large efforts have been devoted to understand the underlying reasons for the slow recombination between electrons and holes in CH3NH3PbI3 with rates lower by four to five orders of magnitude than those derived from the classical electrostatic Langevin model.15,16 Early studies have shown that metal halide perovskites are defect-tolerant17–19 and it is commonly accepted that the measured recombination rate is an intrinsic property of the material, defined by its structure (phase) and its constituent atoms (metal, halide, and organic cation) and dominated by the bimolecular recombination process.3,20,21 The charge separation efficiency has been associated to the disordered orientation of the organic cations and shown to lead to different nanoscale localization of the valence and the conduction band-edge states.22,23 In an alternative interpretation, an exciton screening mechanism based on the collective motion of the organic cations has been proposed.24 However, this picture has been questioned on the basis that the optically active modes are too slow to efficiently screen the exciton, and it has instead been suggested that electron and hole polarons are formed upon photoexcitation.20,21,25–29 However, the nature of polarons in metal halide perovskites has also been largely debated.20,21,26–29 In fact, early results suggested that the polarons in these materials consist of a dipolar screening field associated with the caged organic cation.20,30 In contrast, recent time-resolved Kerr-effect spectroscopy experiments indicate that polaron formation occurs on the subpicosecond timescale, thus being much faster than the rotation of the organic cation.29,31 In line with this observation, bimolecular recombination coefficients for CsPbI3 have recently found to be very close to those of hybrid perovskites.32 These results suggest a possible overestimation of the role of the organic cation in determining the outstanding optoelectronic properties of metal halide perovskites.32–35 The interplay between direct and indirect band-gap transitions in tetragonal CH3NH3PbI3 has also been proposed to explain the low recombination rate of this material,12,36,37 but the invoked effect would possibly be operative only close to the surface.36–38
It is well established that organic metal halide perovskites possess second-order bimolecular recombination coefficients k2 that are comparable with the best crystalline inorganic semiconductors, such as GaAs.10–12,39 Furthermore, monomolecular and Auger recombination processes are negligible for this class of materials even at low carrier densities where trap-assisted monomolecular recombination should dominate.3,20,21 Therefore, bimolecular recombination is recognized as being dominant in metal halide perovskites and the low value of k2 is directly responsible for the low recombination rates.3,20,21 This feature distinguishes these materials from high-purity inorganic semiconductors, in which other recombination processes contribute significantly.40 Going beyond the merely electrostatic description of the Langevin model, theoretical models based on band-to-band transitions give calculated k2 values in good agreement with experiment for both GaAs and CH3NH3PbI3.41 However, the polaronic nature of the charge carriers in CH3NH3PbI3 would profoundly modify this picture.20,29,31 Indeed, the formation of polarons entails higher effective masses and non-parabolic band dispersions, which lead to an increase of k2 by over one order of magnitude due to the enhanced density of states.20 Hence, the account of the polaronic effect through the sole density of states would deteriorate the previously found agreement between theory and experiment for k2.41 The current understanding of the physics of this class of materials is unable to reconcile such contrasting results.
In this work, we address the behavior of charge carriers in tetragonal CH3NH3PbI3 for representative thermal configurations through molecular dynamics (MD) simulations, based on an advanced ab initio electronic-structure scheme.42 Our simulations reveal charge localization in specific regions of the inorganic sublattice on a subpicosecond timescale and hopping between differently localized states on the same time scale. In the excitonic state, when the electron and the hole occur simultaneously and are subject to the attractive Coulomb interaction, the localization persists and occurs in spatially distinct regions. The separate localization of electrons and holes leads to a drop-off of the oscillator strength for electron–hole recombination by two orders of magnitude with respect to that for optical generation, suggesting a peculiar behavior not captured by Langevin's model of recombination. This result reconciles the low bimolecular recombination coefficient k2 with the polaronic nature of the charge carriers in the material. The present description applied to the orthorhombic phase can explain its significantly higher recombination rate, in accord with the experimental characterization.12 Furthermore, we demonstrate that polaron formation is induced by the structural disorder resulting mainly from thermal distortions of the inorganic sublattice, being only moderately affected by the dipolar field associated with the organic cations. These conclusions agree with the timescale of polaron formation inferred from time-resolved Kerr-effect spectroscopic data31 and with the similar values for k2 measured in organic and completely inorganic metal halide perovskites.32
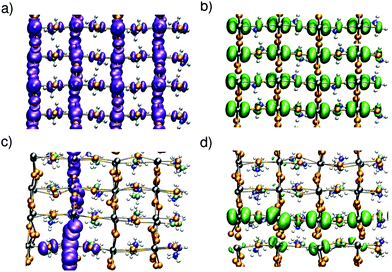
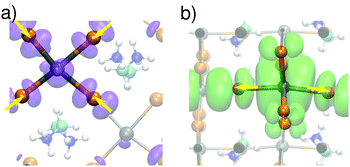
Upon the MD simulations of CH3NH3PbI3 with a separately added electron or hole,42 we notice localization of the charges in both cases. A representation of the charge density for instantaneous configurations is given in Fig. 1. In panels (a) and (b), we show the charge densities of the hole and the electron, respectively, corresponding to a nonpolar initial configuration of the neutral ground state. The charge distributions in both systems are delocalized and represent a hole in the valence band and an electron in the conduction band, respectively. Evolving the system through MD, we observe charge localization on a subpicosecond timescale for both the hole and the electron [cf.Fig. 1(c) and (d)]. We note that such a subpicosecond timescale for polaron formation agrees with recent experimental estimates.31 The localization is induced by local structural distortions in the inorganic sublattice. The extra hole localizes in a xy plane [cf.Fig. 1(c)], and frequently hops from one plane to the other during the dynamics (Fig. S1 in ref. 42). The highest hole density is found on the PbI4 units, in which the Pb–I bonds have undergone contractions of about 0.1 Å [cf.Fig. 2(a)]. The contraction of the Pb–I bonds results from the anti-bonding hybridization of Pb 6s and I 5p orbitals, which form the highest valence band state43 and lead to a reduced repulsion between Pb and I upon electron removal. In the case of the extra electron, the charge density is found to localize in one-dimensional chains of Pb–I bonds, which can instantaneously be oriented along any of the three Cartesian directions [cf.Fig. 1(d)] with frequent jumps from one chain to the other (cf. Fig. S1 in ref. 42). The localization is associated with bond elongations of about ∼0.2 Å in the chain [cf.Fig. 2(b)], which is consistent with the weak anti-bonding hybridization between Pb 6p and I 5p in the conduction band.43 We verify that the localization properties observed here persist when the strong spin–orbit coupling effects observed for this material6,9 are accounted for.42
To further sustain the picture of polaronic states observed above, we evaluate the corresponding binding energies. Since the methylammonium cations are allowed to rotate within the Pb–I cage, it is necessary to resort to the thermodynamic integration method, which is suitable for determining free-energy differences.42 Our calculations indicate the occurrence of shallow states, with binding energies of 0.09 and 0.06 eV for the localized hole and electron, respectively. The latter value is consistent with the experimental estimate of 0.03 eV for CH3NH3PbBr344 and with previous theoretical estimates.31
Next, we aim at describing the excitonic state, in which the electron and the hole evolve simultaneously. To achieve such a description, we carry out a MD simulation in the triplet spin state. We start the simulation from an initial state in which the charge densities are delocalized in band-edge states [cf.Fig. 3(a)], as expected from a vertical excitation from the neutral ground state. Upon time evolution, the electron and the hole show the same behavior as when they evolve independently [cf.Fig. 1]. More interestingly, the combined evolution of the hole and the electron reveals that their instantaneous localization occurs in distinct spatial regions. The two charge densities are often found to be localized on perpendicular planes [cf.Fig. 3(b)], but configurations in which the hole and the electron are localized on two parallel planes are also observed [cf.Fig. 3(c)]. The nature of the evolution with frequent hopping from plane to plane (cf. Fig. S1, ESI† and Fig. 3) demonstrates that steady state conditions are attained on the timescale of the simulations. This guarantees that the structural configurations visited during our dynamics are representative of those occurring during the timescale pertaining to bimolecular recombination. Therefore, these configurations can be used for evaluating the probability of the radiative transition, which is responsible for the long recombination timescale. In this way, our study bridges the different timescales between polaron formation and bimolecular recombination.
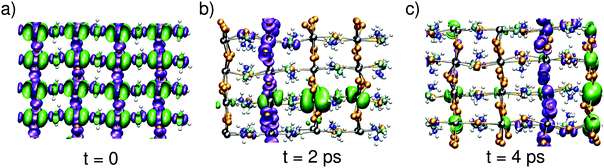 | ||
| Fig. 3 Isodensity representations of the hole and the electron at different times in the evolution of the exciton. The tetragonal axis lies horizontally. | ||
To examine how the relative localization of the hole and the electron influences the recombination rate, we focus on the square modulus of the overlap between their wave functions, Ψh and Ψe, respectively:
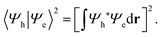 | (1) |
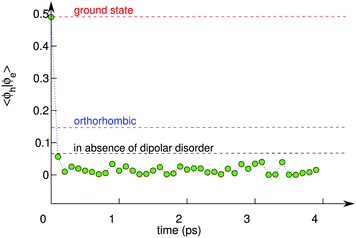
To further support the picture arising from our simulations, we take under consideration the orthorhombic phase of CH3NH3PbI3, for which a higher recombination rate has been measured than for the tetragonal phase.12 The orthorhombic phase is stable at low temperature (T ≤ 165 K) and does not allow the methylammonium cations to rotate freely within the inorganic framework.12 We thus set up a MD simulation at 150 K for the excitonic state in this phase and calculate the corresponding square overlap 〈Ψh|Ψe〉2. We obtain values for 〈Ψh|Ψe〉2 which are higher by over one order of magnitude with respect to those calculated for the tetragonal phase [cf.Fig. 4]. This result can directly be related to the higher degree of delocalization associated with the wave functions of the hole and the electron (cf. Fig. S2 in ref. 42). Hence, the present picture also provides a consistent interpretation for the different recombination rates measured for the tetragonal and the orthorhombic phases of CH3NH3PbI3.12
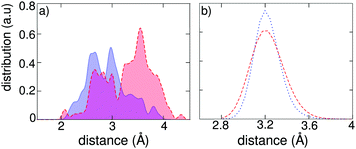
It is of interest to investigate more deeply the origin of the localization of charge carriers during the molecular dynamics of the exciton in the tetragonal phase of CH3NH3PbI3. Two sources for the presence of a disordered field can be identified, namely the dipolar field associated to the orientation of the organic cations and the thermal vibrations associated to the inorganic Pb–I sublattice. We first search for a correlation between the charge localization and the orientation of the dipolar cations. We focus on the hole density in the exciton state and determine the distances between the positively charged plane and the C and N atoms belonging to the adjacent inorganic cations. The distribution of these distances in Fig. 5(a) clearly shows that the C atoms, i.e. the negative poles of the dipolar cations, locate on average more closely to the positively charged plane than the N atoms (negative poles). An analogous correlation holds for the electron localization (cf. Fig. S3 in ref. 42). As a further demonstration of the role of the molecular dipoles, we focus on a single structural configuration taken from the molecular dynamics simulation of the neutral ground state. Addition of an extra hole or an extra electron followed by structural relaxation leads to different charge localizations in the two cases (cf. Fig. S4 in ref. 42). We then repeated the same analysis after exchanging the C and N atoms within the organic cations, effectively reversing the associated dipolar field. We observe that the charge densities before and after inversion are different, confirming once more the connection with the orientation of the organic cations.
To distinguish the effect associated to the thermal vibrations, we carried out a molecular dynamics of the excitonic state in an artificial tetragonal phase, in which the organic cations have been replaced by immobile Cs+ ions at the cage centers. By construction, this system is devoid from any dipolar field, but remains sensitive to the thermally induced disorder in the inorganic sublattice. Fig. 5(b) shows that the width of the distribution of Pb–I bond lengths is only slightly reduced in the absence of a dipolar field. To evaluate the importance of this effect, we calculate the square overlap for the evolution of the exciton in our artificial system. We find that the square overlap is almost as low as for the system with organic cations (cf.Fig. 4 and Fig. S2 in ref. 42). Hence, this analysis assigns the dominant origin for the polaronic charge localization to the thermal disorder in the inorganic sublattice, with the dipolar field of the organic cations acting as an adjuvant, which blandly enhances the overall degree of disorder. We remark that this result is consistent with the recently measured sub-picosecond timescale for polaron formation, which is indeed shorter than the timescale associated to the rotation of the organic cations.29,31 Furthermore, the ancillary role of organic dipoles is supported by experiments that reveal similar values of k2 for organic and completely inorganic metal halide perovskites.32
To sum up, we have identified and analyzed the origin for the slow electron–hole recombination in metal halide perovskites. Our work emphasizes the spatially separate localization of the electron and the hole as induced by the structural disorder resulting mainly from the thermal distortions of the inorganic sublattice with a limited contribution of the dipolar field associated with the organic cations. This emerges as a key feature for achieving exceptional photovoltaic properties for this class of materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been performed in the context of the National Center of Competence in Research (NCCR): Materials' Revolution: Computational Design and Discovery of Novel Materials (MARVEL) of the Swiss National Science Foundation. We used computational resources of the Swiss National Supercomputing Center (CSCS).References
- L. Etgar, P. Gao, Z. Xue, Q. Peng, A. K. Chandiran, B. Liu, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2012, 134, 17396–17399 CrossRef CAS PubMed.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007 CrossRef CAS.
- F. Chiarella, A. Zappettini, F. Licci, I. Borriello, G. Cantele, D. Ninno, A. Cassinese and R. Vaglio, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045129 CrossRef.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- Y. Ogomi, A. Morita, S. Tsukamoto, T. Saitho, N. Fujikawa, Q. Shen, T. Toyoda, K. Yoshino, S. S. Pandey, T. Ma and S. Hayase, J. Phys. Chem. Lett., 2014, 5, 1004–1011 CrossRef CAS PubMed.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 CAS.
- P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467 CrossRef PubMed.
- C. S. Ponseca, T. J. Savenije, M. Abdellah, K. Zheng, A. Yartsev, T. Pascher, T. Harlang, P. Chabera, T. Pullerits, A. Stepanov, J.-P. Wolf and V. Sundström, J. Am. Chem. Soc., 2014, 136, 5189–5192 CrossRef CAS PubMed.
- E. Edri, S. Kirmayer, S. Mukhopadhyay, K. Gartsman, G. Hodes and D. Cahen, Nat. Commun., 2014, 5, 3461 Search PubMed.
- E. M. Hutter, M. C. Gélvez-Rueda, A. Osherov, V. Bulović, F. C. Grozema, S. D. Stranks and T. J. Savenije, Nat. Mater., 2017, 16, 115–120 CrossRef CAS PubMed.
- T. W. Crothers, R. L. Milot, J. B. Patel, E. S. Parrott, J. Schlipf, P. Müller-Buschbaum, M. B. Johnston and L. M. Herz, Nano Lett., 2017, 17, 5782–5789 CrossRef CAS PubMed.
- D. Li, P. Liao, X. Shai, W. Huang, S. Liu, H. Li, Y. Shen and M. Wang, RSC Adv., 2016, 6, 89356–89366 RSC.
- C. Wehrenfennig, M. Liu, H. J. Snaith, M. B. Johnston and L. M. Herz, Energy Environ. Sci., 2014, 7, 2269–2275 CAS.
- H. Oga, A. Saeki, Y. Ogomi, S. Hayase and S. Seki, J. Am. Chem. Soc., 2014, 136, 13818–13825 CrossRef CAS PubMed.
- J. Kim, S.-H. Lee, J. H. Lee and K.-H. Hong, J. Phys. Chem. Lett., 2014, 5, 1312–1317 CrossRef CAS PubMed.
- Y. Yamada, M. Endo, A. Wakamiya and Y. Kanemitsu, J. Phys. Chem. Lett., 2015, 6, 482–486 CrossRef CAS PubMed.
- A. Buin, P. Pietsch, J. Xu, O. Voznyy, A. H. Ip, R. Comin and E. H. Sargent, Nano Lett., 2014, 14, 6281–6286 CrossRef CAS PubMed.
- Y. Chen, H. Yi, X. Wu, R. Haroldson, Y. Gartstein, Y. Rodionov, K. Tikhonov, A. Zakhidov, X.-Y. Zhu and V. Podzorov, Nat. Commun., 2016, 7, 12253 CrossRef CAS PubMed.
- M. B. Johnston and L. M. Herz, Acc. Chem. Res., 2016, 49, 146–154 CrossRef CAS PubMed.
- J. Ma and L.-W. Wang, Nano Lett., 2015, 15, 248–253 CrossRef CAS PubMed.
- C. Quarti, E. Mosconi and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 9394–9409 RSC.
- J. Even, L. Pedesseau and C. Katan, J. Phys. Chem. C, 2014, 118, 11566–11572 CAS.
- M. Bokdam, T. Sander, A. Stroppa, S. Picozzi, D. Sarma, C. Franchini and G. Kresse, Sci. Rep., 2016, 6, 28618 CrossRef CAS PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- T. M. Brenner, D. A. Egger, A. M. Rappe, L. Kronik, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 4754–4757 CrossRef CAS PubMed.
- X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- A. Walsh, J. Phys. Chem. C, 2015, 119, 5755–5760 CAS.
- K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. De Angelis and X.-Y. Zhu, Sci. Adv., 2017, 3, 1701217 CrossRef PubMed.
- S. Dastidar, S. Li, S. Y. Smolin, J. B. Baxter and A. T. Fafarman, ACS Energy Lett., 2017, 2, 2239–2244 CrossRef CAS.
- M. Kulbak, D. Cahen and G. Hodes, J. Phys. Chem. Lett., 2015, 6, 2452–2456 CrossRef CAS PubMed.
- G. R. Berdiyorov, A. Kachmar, F. El-Mellouhi, M. A. Carignano and M. El-Amine Madjet, J. Phys. Chem. C, 2016, 120, 16259–16270 CAS.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 136001 CrossRef PubMed.
- T. Wang, B. Daiber, J. M. Frost, S. A. Mann, E. C. Garnett, A. Walsh and B. Ehrler, Energy Environ. Sci., 2017, 10, 509–515 CAS.
- E. Mosconi, T. Etienne and F. De Angelis, J. Phys. Chem. Lett., 2017, 8, 2247–2252 CrossRef CAS PubMed.
- D. Niesner, M. Wilhelm, I. Levchuk, A. Osvet, S. Shrestha, M. Batentschuk, C. Brabec and T. Fauster, Phys. Rev. Lett., 2016, 117, 126401 CrossRef PubMed.
- D. D. Sell and H. C. Casey, J. Appl. Phys., 1974, 45, 800 CrossRef CAS.
- J. Piprek, Semiconductor optoelectronic devices: introduction to physics and simulation, Academic Press, 2013 Search PubMed.
- A. Filippetti, P. Delugas and A. Mattoni, J. Phys. Chem. C, 2014, 118, 24843–24853 CAS.
- For a detailed description of the computational details, the polaron binding energy, the hopping of the charge density, the degree of localization, and the role of the dipolar field, see ESI†.
- T. Umebayashi, K. Asai, T. Kondo and A. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155405 CrossRef.
- K. Zheng, M. Abdellah, Q. Zhu, Q. Kong, G. Jennings, C. A. Kurtz, M. E. Messing, Y. Niu, D. J. Gosztola, M. J. Al-Marri, X. Zhang, T. Pullerits and S. E. Canton, J. Phys. Chem. Lett., 2016, 7, 4535–4539 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee01981e |
| This journal is © The Royal Society of Chemistry 2018 |