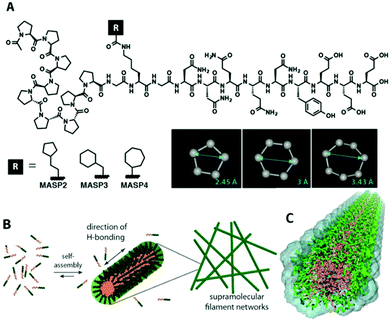
Isomeric control of the mechanical properties of supramolecular filament hydrogels†
Yi-An
Lin‡
ab,
Myungshim
Kang‡
 c,
Wei-Chiang
Chen
abd,
Yu-Chuan
Ou
a,
Andrew G.
Cheetham
ab,
Pei-Hsun
Wu
abe,
Denis
Wirtz
abeg,
Sharon M.
Loverde
c,
Wei-Chiang
Chen
abd,
Yu-Chuan
Ou
a,
Andrew G.
Cheetham
ab,
Pei-Hsun
Wu
abe,
Denis
Wirtz
abeg,
Sharon M.
Loverde
 *cd and
Honggang
Cui
*cd and
Honggang
Cui
 *abfg
*abfg
aDepartment of Chemical & Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: hcui6@jhu.edu
bInstitute for NanoBiotechnology, Johns Hopkins University, Baltimore, MD 21218, USA
cDepartment of Chemistry and Biochemistry, The City University of New York, College of Staten Island, Staten Island, NY 10314, USA. E-mail: sharon.loverde@csi.cuny.edu
dPh.D. Programs in Chemistry, Biochemistry, and Physics, The Graduate Center of the City University of New York, New York, NY 10016, USA
ePhysical Sciences-Oncology Center, Johns Hopkins University, Baltimore, MD 21218, USA
fDepartment of Materials Science and Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
gDepartment of Oncology and Sidney Kimmel Comprehensive Cancer Center, Johns Hopkins School of Medicine, Baltimore, MD 21205, USA
First published on 24th November 2017
Abstract
Supramolecular filament hydrogels are an emerging class of biomaterials that hold great promise for regenerative medicine, tissue engineering, and drug delivery. However, fine-tuning of their bulk mechanical properties at the molecular level without altering their network structures remains a significant challenge. Here we report an isomeric strategy to construct amphiphilic peptides through the conjugation of isomeric hydrocarbons to influence the local viscoelastic properties of their resulting supramolecular hydrogels. In this case, the packing requirements of the chosen isomeric hydrocarbons within the supramolecular filaments are dictated by their atomic arrangements at the molecular and intermolecular levels. Atomistic molecular dynamics simulations suggest that this design strategy can subtly alter the molecular packing at the interface between the peptide domain and the hydrophobic core of the supramolecular assemblies, without changing both the filament width and morphology. Our results from wide-angle X-ray scattering and molecular simulations further confirm that alterations to the intermolecular packing at the interface impact the strength and degree of hydrogen bonding within the peptide domains. This subtle difference in the isomeric hydrocarbon design and their consequent packing difference led to variations in the persistence length of the individual supramolecular filaments. Microrheological analysis reveals that this difference in filament stiffness enables the fine-tuning of the mechanical properties of the hydrogel at the macroscopic scale. We believe that this isomeric platform provides an innovative method to tune the local viscoelastic properties of supramolecular polymeric hydrogels without necessarily altering their network structures.
Introduction
The mechanical properties of materials are known as the key features that affect their functionality. The rigidity of scaffolding materials, for instance, is a known physical cue that can impact cellular behaviour at various levels.1–7 Such synthetic matrices can be constructed by employing molecular self-assembly as the fundamental principle, in which the building blocks associate spontaneously into filamentous assemblies through non-covalent interactions.8–14 This strategy highlights the connections between the molecular design of the underlying building blocks and the resulting properties of their supramolecular assemblies, thus providing a possibility of controlling the mechanical properties from the very bottom-up.15–19 In general, the mechanical properties of these supramolecular matrices are the combinative consequence of several factors, including the stiffness and entanglement/alignment of the filaments, mesh size (largely determined by the concentration of the building units), as well as the presence of other additives such as multivalent ions or other types of molecules.20–23 Oftentimes, it is difficult to decouple the individual effects of each factor from the overall combinative effect, and this in turn causes complications in interpreting the results of interfacing these supramolecular hydrogels with the cells of interest. In this study, we report a strategy to tune the local viscoelastic properties of supramolecular filament networks without inducing any variations in the mesh size and salt concentration.Supramolecular one-dimensional (1D) nanostructures can be formed by the self-assembly of amphiphilic molecules that intrinsically adopt strong, directional intermolecular interactions, such as hydrogen bonding or π–π interactions.24 These 1D supramolecular structures are regarded as semi-flexible filaments that can further entangle to form a 3D network.25–29 MacKintosh et al. showed that for solutions of entangled semi-flexible filaments (such as F-actins), the storage modulus G′ scales as G′ ∼ κ2/kBTξ−2Le−3.20 Here, κ is the semi-flexible chain bending modulus, ξ is the mesh size of the network related to the monomer concentration, Le is the chain entanglement length, kB is the Boltzmann constant, and T is the temperature. The overall stiffness of such supramolecular networks is often controlled by varying the bulk concentration of the monomers.30 While this approach usually enhances the mechanical strength of the matrix, it is complicated by simultaneous changes in the mesh size because both ξ and Le are dependent on the concentration.31 In particular, when Le ≥ ξ and the persistence length lp ∼ κ/kBT ≥ ξ, it is found that Le ∼ (κ/kBT)1/5(acA)−2/5, where cA is the concentration of the monomers of size a, and that 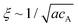 .32,33 Thus, for semi-flexible networks with Le ≥ ξ and the persistence length lp ≥ ξ, the storage modulus G′ scales with the concentration as G′ ∼ κ(κ/kBT)2/5(ac)11/5.20 For example, the persistence length lp of biological filaments (such as F-actin) can be related to the linear mass density λp of the filament such that lp ∼ (Y/4πkBTρm2)λp2, where Y is the Young's modulus of the filament and ρm is the mass per unit volume.34 These studies suggest that it is theoretically possible to use the bending modulus, κ, to tune the mechanical properties of semi-flexible filament networks without affecting other network parameters such as mesh size and monomer concentration.
.32,33 Thus, for semi-flexible networks with Le ≥ ξ and the persistence length lp ≥ ξ, the storage modulus G′ scales with the concentration as G′ ∼ κ(κ/kBT)2/5(ac)11/5.20 For example, the persistence length lp of biological filaments (such as F-actin) can be related to the linear mass density λp of the filament such that lp ∼ (Y/4πkBTρm2)λp2, where Y is the Young's modulus of the filament and ρm is the mass per unit volume.34 These studies suggest that it is theoretically possible to use the bending modulus, κ, to tune the mechanical properties of semi-flexible filament networks without affecting other network parameters such as mesh size and monomer concentration.
Inspired by these pioneering studies, herein we present a peptide-based supramolecular platform that utilizes isomeric hydrocarbons to dictate the mechanical properties of supramolecular filament networks through the modulation of the bending modulus of individual filaments. This strategy highlights the control of the persistence length of individual filaments—not through the variation of the linear mass density of the filament, a common mechanism for biological filaments found in nature—but through the modulation of the strength of the filament interface due to differences originating from intermolecular packing and hydrogen bonding. This strategy offers an effective means to tune the mechanical properties of semi-flexible networks at the molecular level. Given the rapidly growing interest in peptide-based supramolecular hydrogels,17,35–45 we believe that our findings have broad implications for their biomedical applications in regenerative medicine and drug delivery.
Results and discussion
Molecular design and assembly
We conjugated a series of isomeric alicyclic groups to an identical peptide segment to imbue the necessary overall amphiphilicity for self-assembly under aqueous conditions (Fig. 1A). The differences in atomic arrangements offer different molecular packing requirements within the hydrophobic/hydrophilic interfacial area, further affecting the mechanical properties of the respective supramolecular networks while ensuring identical surface functionality and similar pore/mesh size at a fixed monomer concentration (the mesh size is a function of the monomer size and concentration in such networks).20 This miktoarm star peptide platform includes a β-sheet adopting the peptidic domain GNNQQNY (originated from the yeast prion Sup35),46 an oligoproline segment, and a cyclic hydrocarbon segment.47 The designed peptides MASP2, MASP3, and MASP4 carried a cyclopentylpropionyl, a cyclohexylacetyl or a cycloheptanecarboxyl group, respectively (Fig. 1A). The details of molecular synthesis, purification and characterization can be found in ESI, S1–S2 and Fig. S1–S3.† MASP1, an analogue of the MASP series, which bears a linear but not cyclic hydrocarbon, has been reported previously in an effort devoted to developing enzymatically degradable supramolecular filaments.47 Since MASP1 contains two more hydrogen atoms than MASP2–4 and thus cannot be considered as an isomer, its assembly behaviour is not discussed in detail. Specifically, the three chosen isomeric building units possess different ring sizes—five, six and seven carbons—with the remaining methylenes acting as spacer groups between the ring and carboxyl—two, one and zero carbons, respectively. These differences are expected to alter the packing within the hydrophilic/hydrophobic interfacial environment of the assemblies (Fig. 1B). We utilized atomistic molecular dynamics simulations of the pre-assembled filaments (Fig. 1C) to reveal that while the core dimensions of the filament remain unchanged, the increasing ring size of the isomer ultimately alters the molecular packing at the interface. This difference in packing leads to a variation in hydrogen bonding within the filament corona and also a calculated variation in interfacial tension while maintaining the same diameter of the three assemblies, ultimately causing a variation in the persistence length of single filaments on the order of 250–4000 nm.Nanostructure characterization
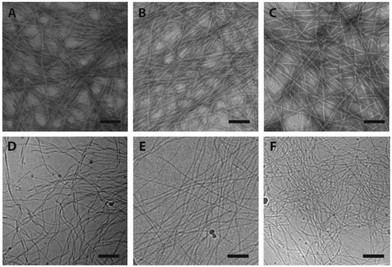
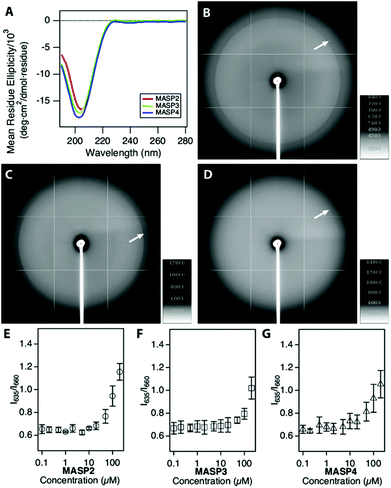
The supramolecular nanostructures formed by the self-assembly of each isomeric peptide were characterized by transmission electron microscopy (TEM) and cryogenic-TEM (cryo-TEM) (Fig. 2). When dissolved in water (pH 4.5), all the three designed molecules were found to associate into filamentous assemblies of ∼10 nm in width, while the length could reach several microns after one day of incubation at a concentration of 1% (w/v, 2.1 mM). Circular dichroism (CD) spectroscopy reveals that all the designed peptides showed characteristic absorption of polyproline type II-like (PPII) secondary structures (strong negative peak at 205 nm, very weak positive peak at 235 nm) (Fig. 3A). The expected characteristics of β-sheet conformation of the Sup35 segments were not explicitly revealed in the CD spectra, potentially due to their weaker absorption intensity relative to the PPII-like conformation stemming from the oligoproline segment.47 It is noteworthy that MASP1 revealed a very similar assembly behaviour in water, forming filamentous assemblies with a PPII-like peptide conformation.47 Wide angle X-ray scattering (WAXS), however, could confirm the presence of β-sheets for all the designed peptides (Fig. 3B–D). The reflective peaks at ∼4.7 Å are indicative of the typical spacing of hydrogen bonds among the neighbouring peptides. Notably, MASP3 and MASP4 exhibited a more diffusive peak at 4.7 Å than that of MASP2, an observation that is very likely linked to the molecular packing of the isomeric hydrocarbons, which will be expounded in the later discussion. The β-sheet conformation is considered crucial for the formation and propagation of filamentous nanostructures.48,49The mesh/pore size is dependent only on the size and concentration of the monomer that forms the supramolecular filaments.20 In the case reported here, the isomeric peptides differ only in the hydrocarbons and are structurally identical in the dominant peptidic segment. Hence, the monomer sizes among MASP2–4 should be approximately the same, and thus at the same monomer concentration the mesh size of their resulting networks should be identical for all the three molecules. However, given that there exists a dynamic equilibrium between the monomers and the assembled filaments and only these assembled monomers actually contribute to the network mesh size, it is important to assess the critical aggregation concentration (CAC) of the building blocks. The CAC value of each molecule was thus measured by incubating the peptide solutions of various concentrations with a reporter dye Nile red.50 Nile red is a hydrophobic dye that exhibits a blue-shifted fluorescence emission with enhanced intensity when exposed to hydrophobic environments.51,52 Each isomeric peptide solution (in MES buffer, pH 4.5) at various concentrations was mixed with a fixed content of Nile red, and then the emergence of the blue-shifted emission upon encapsulation within the hydrophobic cores was carefully monitored as the peptide concentration surpasses the CAC value (ESI S3 and Fig. S4†). The transition concentration was determined by plotting the ratio of the emission maximum of Nile red in hydrophobic environments (λmax: 635 nm) to that under aqueous conditions (λmax: 660 nm) against the bulk peptide concentrations. Our results suggested that the CAC values of MASP2, MASP3, and MASP4 are very similar and are in the range of ∼50 μM at pH 4.5 (Fig. 3E–G). These results implied that MASP2, MASP3, and MASP4 would have the same proportion of building blocks remaining in the assembled state at a given bulk concentration. Since our results from TEM imaging (Fig. 2) have demonstrated that there were no distinguishable morphological differences between the filament length and width, we speculate that the mesh size of the resulting hydrogels would be essentially the same for all MASPs at the investigated concentrations (∼4.2 mM) in the limit of low filament bundling.
Molecular dynamics simulation
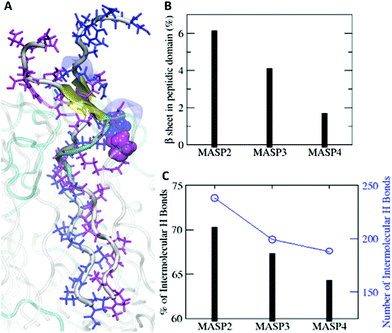
Simulations have become an indispensable tool to investigate the structure of peptide-amphiphile filamentous assemblies.53–55 We subsequently performed atomistic molecular dynamics (MD) simulations to provide molecular-level insight into the differences of atomic arrangements in the molecular packing and accordingly the mechanical properties of the supramolecular filaments (ESI S4†).56,57 Three pre-assembled MASP supramolecular filaments were simulated for 100 ns, allowing the interfacial density profile to relax and the peptides to form β-sheets along the filament axis. Each system was pre-assembled into an 8-layered fibril with 9 monomers per layer. The systems were neutralized by Cl− ions and solvated in a water box. The force field used in the MD simulations was AMBER ff99SB.58 The force field for the hydrocarbon segments of the MASPs was parameterized using the general AMBER force field (GAFF)59 with the atomic partial charges assigned by using VCharge v1.01 (VeraChem, LLC),60 and the TIP3P model61 was employed for water. Atomistic MD simulations were carried out using a parallel molecular dynamics code NAMD2.62 All systems were simulated in the NPT ensemble at 1 atm and 310 K for 100 ns with full periodic boundary conditions (see the ESI† for additional simulation methods).The radial density profile was calculated for each component of the simulated MASPs to examine the correlation between the ring size of the cycloalkyl chain and the molecular packing (Fig. 4), with their filamentous nanostructures shown in Fig. S5.† These results showed that the filament widths (∼12 nm) were nearly identical between MASP2, MASP3, and MASP4 filaments (Fig. 4D), consistent with our experimental observations from TEM imaging. We did notice a difference in the molecular packing among the peptides. However, this difference in packing did not propagate to the inner hydrophobic core of the oligoproline segments. The radial density profile showed that the density of the isomeric hydrocarbons of the MASP2 filaments exhibited a peak shifted towards the location of the peptide domain, compared with the density of the isomeric hydrocarbons of the MASP3 and MASP4 filaments. Furthermore, the peak density of the isomeric hydrocarbon of MASP2 (∼0.8 g cm−3) is lower when compared with the peak density of the isomeric hydrocarbons of the MASP3 and MASP4 filaments (∼1.05 g cm−3), indicating that the hydrocarbon density is distributed across a larger radius (Fig. 4E). In contrast, the onset of the hydrocarbon density of the MASP4 filaments in particular was shifted towards the inner hydrophobic core (∼15 Å), compared with that of its MASP2 counterpart (∼20 Å).
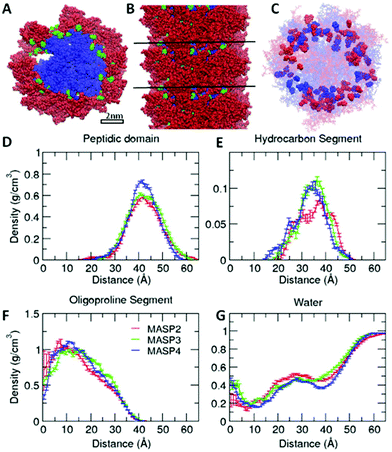 | ||
| Fig. 4 Molecular dynamics simulation of the density profile of each component in assembled filaments. Snapshots (A, B), positions of hydrocarbon segments (C) and the radial density profile (D–G) of each MASP component in preassembled filaments after molecular dynamics simulation for 100 ns. The peptide domain, hydrocarbon segment (denoted as R in Fig. 1A), and oligoproline segment are displayed in red, green and blue, respectively, in the top (A) and side (B) view of the preassembled MASP4 filament. Cycloalkyl rings of MASP2 and MASP4 in the filaments are highlighted in red and blue, respectively, in (C). The density profile is averaged over the last 50 ns. | ||
The difference could be rooted in the varied ring size, as well as the variations in the length and flexibility of the isomeric hydrocarbons. Since the cyclopentylpropionyl group of MASP2 possesses a smaller ring, it could possibly extend further due to its two alkyl carbons outside of the ring structure providing extra flexibility in comparison with the cyclohexylacetyl or cycloheptanecarboxyl groups on MASP3 or MASP4, respectively. Moreover, this increased flexibility could allow the hydrocarbon tails to adopt conformations that are more favourable toward efficient β-sheet formation compared with the MASP4 filaments. The two cyclopentyl rings of neighbouring MASP2 molecules would be more distant from the peptide backbones, causing less steric restrictions between the neighbouring MASP2 molecules and allowing them to be spatially close to form tighter intermolecular hydrogen bonds, as shown in Fig. 5A. The formation of β-sheets and intermolecular hydrogen bonds at the simulation timescale was also evaluated, finding that there was a corresponding reduction of β-sheet formation in the peptide domain as the ring size was increased (Fig. 5B). Likewise, both the total number of hydrogen bonds and the fraction of intermolecular hydrogen bonds to the total hydrogen bonds in the MASPs decreased in a similar fashion (Fig. 5C).
Microrheological measurements
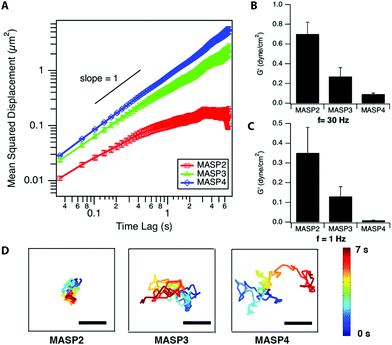
The local viscoelastic properties of the resulting supramolecular materials were determined using particle-tracking microrheology. Unlike the conventional macrorheology, the particle-tracking rheology provides the information of local stiffness in the materials at the submicron to micron scale.63–65 The viscoelastic properties are determined by tracking the movement of the probing particles trapped within the studied viscoelastic materials, in which the fluctuation of filaments governs the motion of embedded particles and reveals the stiffness/flexibility of the surrounding materials. The mean-squared displacement (MSD), the critical parameter in microrheology, of the embedded particles can be described by using the generalized Stokes–Einstein equation.65–67 For viscoelastic materials, the MSD of the embedded particles follows the relationship 〈Δr2〉 ∝ tα, where α is the logarithmic slope of MSD versus time lag.64–66 At a fixed molar concentration (4.2 mM; 1 wt% for MASP2–4), the ensemble-averaged MSD of the probing particles in the resulting scaffolds showed the trend, MSDMASP2 < MSDMASP3 < MSDMASP4, at all monitored timescales (Fig. 6A). The logarithmic slopes of MSD vs. time lag, α, of the probing particles ranged between zero and unity, suggesting the sub-diffusive behaviour of each hydrogel (Fig. S6†). The diffusion coefficient, D, is calculated from the MSD by using D = MSD/4t.de Gennes and co-workers have proposed that the motion of a particle of diameter d through a network of average mesh size ξ is an activated process dictated by the activation energy, which is determined by the elastic free energy associated with the expansion of a mesh formed by Gaussian chains.32,69 The estimation for the diffusion coefficient D can be derived as follows:
D = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−β(d/ξ)δ) exp(−β(d/ξ)δ) | (1) |
| D(cA,d) = D(0,d)exp(−β′d2cA) | (2) |
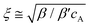 , which stated the same dependence of ξ on the concentration as we previously introduced
, which stated the same dependence of ξ on the concentration as we previously introduced 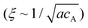 . Moreover, it is implied that more factors besides the monomer size can determine the mesh size ξ, which can be captured by fitting the diffusion data. Here, D0 is calculated directly from the Stokes–Einstein equation, D0 = kBT/6πηr, with the dynamics viscosity of water η = 8.90 × 10−3 dyn s cm−2 and the particle radius r = 0.5 μm. By plugging this D0 and the experimental diffusion coefficient D into the above equation, we estimated the constant β′. Assuming β ≈ 1, as Schmidt and co-workers suggested, the mesh size ξ was estimated: approximately 1219 nm, 793 nm, and 580 nm for MASP2, MASP3, and MASP4, respectively. The storage modulus (G′) could be calculated by using the generalized Stokes–Einstein equation, showing a trend of G′MASP2 > G′MASP3 > G′MASP4 at two frequencies (1 Hz and 30 Hz) (Fig. 6B and C).
. Moreover, it is implied that more factors besides the monomer size can determine the mesh size ξ, which can be captured by fitting the diffusion data. Here, D0 is calculated directly from the Stokes–Einstein equation, D0 = kBT/6πηr, with the dynamics viscosity of water η = 8.90 × 10−3 dyn s cm−2 and the particle radius r = 0.5 μm. By plugging this D0 and the experimental diffusion coefficient D into the above equation, we estimated the constant β′. Assuming β ≈ 1, as Schmidt and co-workers suggested, the mesh size ξ was estimated: approximately 1219 nm, 793 nm, and 580 nm for MASP2, MASP3, and MASP4, respectively. The storage modulus (G′) could be calculated by using the generalized Stokes–Einstein equation, showing a trend of G′MASP2 > G′MASP3 > G′MASP4 at two frequencies (1 Hz and 30 Hz) (Fig. 6B and C).
Discussion
According to the theory depicted by MacKintosh et al., the storage modulus G′ ∼ κ(κ/kBT)2/5(ac)11/5 for sterically entangled semi-flexible networks.20 The persistence length lp could be approximated by the MacKintosh scaling, when using the estimated values of mesh size derived previously and applying the relationship between the bending modulus κ and the persistence length lp (κ ∼ lpkBT). Using a = ∼4.7 Å, the corresponding spacing of the hydrogen bonds of β-strands in the neighbouring peptides observed in WAXS for all designed peptides, lp values were approximately 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112 nm, 1995 nm and 340.5 nm for MASP2, MASP3, and MASP4, respectively by calculation. While the mesh size exhibited a 52% reduction from MASP2 to MASP4, the persistence length plummeted for 98%. For MASP2 and MASP3, the estimated persistence lengths were much larger than their mesh sizes, and therefore they can be regarded as networks composed of semi-flexible chains. However, this expectation did not hold for MASP4 since its estimated persistence length lp was not longer than its mesh size ξ, which suggests that some of the assumptions for β and ξ can be further clarified in future studies.
112 nm, 1995 nm and 340.5 nm for MASP2, MASP3, and MASP4, respectively by calculation. While the mesh size exhibited a 52% reduction from MASP2 to MASP4, the persistence length plummeted for 98%. For MASP2 and MASP3, the estimated persistence lengths were much larger than their mesh sizes, and therefore they can be regarded as networks composed of semi-flexible chains. However, this expectation did not hold for MASP4 since its estimated persistence length lp was not longer than its mesh size ξ, which suggests that some of the assumptions for β and ξ can be further clarified in future studies.
Since the lp values for MASP2–4 were calculated, the interfacial tension could also be roughly calculated by using the following relationship for a D*-dimensional object when the rigidity is κ = Φγdc4−D* ∼ lpkBT, in which Φ is an interfacial coupling constant, γ is the interfacial tension, and dc is the diameter of the hydrophobic core.70 The interfacial coupling constant Φ ≈ 0.05 is found for cylindrical block copolymer filomicelles.70 Using D* = 1 and dc = 8 nm together with the previously mentioned Φ, we obtained the interfacial tension γ ≈ 2267 pN nm−1, 320 pN nm−1, and 55 pN nm−1 for MASP2, MASP3, and MASP4, respectively. The estimated γ values for MASP2/MASP3 were greater than the typical interfacial tension values, suggesting the necessity for characterization of the interfacial coupling constant Φ of the assemblies in our design platform, which could be obtained with further characterization of the mechanical properties through both experiment and simulation.71 One way to interpret this phenomenon is to use the Gibbs adsorption equation, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ/log
γ/log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = −2.303 ΓRT, where C is the concentration, R is the gas constant, T is the temperature, and Γ is the number of moles of the component adsorbed per unit area (mol m−2). The higher local density of the hydrocarbon segment of MASP3 and MASP4 compared to that of MASP2 at the peak radius (Fig. 4B) might partially contribute to their lower interfacial tension. Thus, we showed that the conjugation of isomeric hydrocarbons induced a variation in the expected interfacial tension, and that their packing in the interfacial region of the self-assembled structures subsequently leads to differences in the bending rigidity and the storage modulus. From the microrheological results, the larger the conjugated cycloalkyl group in the amphiphilic peptides, the larger the magnitude of the MSD. This was also evident from the representative trajectories of an embedded particle in MASP2, MASP3, and MASP4, in which the probing particles display a larger displacement over a 7-second period when trapped in the relatively weaker hydrogel formed by MASP4 (Fig. 6D).
C = −2.303 ΓRT, where C is the concentration, R is the gas constant, T is the temperature, and Γ is the number of moles of the component adsorbed per unit area (mol m−2). The higher local density of the hydrocarbon segment of MASP3 and MASP4 compared to that of MASP2 at the peak radius (Fig. 4B) might partially contribute to their lower interfacial tension. Thus, we showed that the conjugation of isomeric hydrocarbons induced a variation in the expected interfacial tension, and that their packing in the interfacial region of the self-assembled structures subsequently leads to differences in the bending rigidity and the storage modulus. From the microrheological results, the larger the conjugated cycloalkyl group in the amphiphilic peptides, the larger the magnitude of the MSD. This was also evident from the representative trajectories of an embedded particle in MASP2, MASP3, and MASP4, in which the probing particles display a larger displacement over a 7-second period when trapped in the relatively weaker hydrogel formed by MASP4 (Fig. 6D).
A number of previous reports have detailed the use of different peptide sequences to construct peptide-based hydrogels to control the mechanical properties, yet these reported instances are often accompanied by changes in surface chemistry or fundamental self-assembling behaviour due to the alteration of the peptide segments. For instance, Gooch and co-workers reported that the storage modulus of peptide hydrogels could decrease by a factor of ∼4.8 after incorporating a RGD segment into their peptidic building blocks.72 In another study, an enzymatic cleavable peptide was included within the building units to form hydrogels, leading to the reduction of storage moduli from >300 kPa to 43 Pa.73 Although using isomeric peptides as building blocks or incorporating different hydrophobic side chains have both shown to be possible strategies to control the morphology of the assembled structures,74,75 the use of this rationale to control the mechanical properties has been scarcely reported. Most recent work has focused on the biophysical consequences of the materials after modifying the amino acid order in the peptidic domains. For example, an interesting study reported by Pashuck et al. utilized a series of peptide amphiphiles with different combinations of valine/alanine to construct hydrogels with different mechanical properties, and further demonstrated that the intensity of β-sheet signals in the circular dichroism spectra was associated with the stiffness of the hydrogels.76 A recent study conducted by Schneider and co-workers has shown that a single amino acid change in a 20-amino acid peptide, APC1, could provide drastic differences in rheological behaviours (such as the sol–gel transition and shear-thin recovery).77 These examples stressed the control of mechanical properties from the peptidic domains, and the origin of stiffness change was due to the order of intermolecular interactions among the side chains of the amino acids. Recently, Tantakitti et al. showed that the mechanical properties (governed by hydrogen bonding along the filament at the amino acid level) can be modulated due to the strength of the local salt concentration.78
In our case, the reported design platform keeps the peptide segment unchanged among all the designed building blocks to guarantee the same surface functionality, without changing the local electrostatic environment and with a similar contour length per filament. From our microrheological results, we observed a trend of lower stiffness of hydrogels when conjugating large-ring bearing side chains to the peptide segments. As stated previously, the mesh/pore size of all peptides in this study was similar at a fixed bulk concentration. Therefore, it was unlikely that the stiffness variations of MASP2–4 hydrogels were due to the differences in the mesh/pore size. Interestingly, the results from microrheological studies were in good correlation with our results of peptide secondary conformation study and prediction of simulation. A reported study has suggested that the alignment of hydrogen bonds in peptide amphiphiles can dictate the mechanical stiffness of hydrogels, showing that increased stiffness could originate from the ordered β-sheet formation along the length of the fibre.76 Experimentally, we have observed a reduction of the ordered β-sheet structure in WAXS when a bulkier hydrocarbon was incorporated into the peptide. This is complemented by our data from molecular simulations that suggest that the observed shift in mechanical properties for these MASP filaments could arise from cooperative effects due to (1) the shift in hydrocarbon locations towards the inner hydrophobic core with the increase in ring size, and (2) decrease in the degree of hydrogen bond formation within the peptide domain and subsequent decrease in β-sheet formation (due to the increase in the hydrocarbon ring size). The experimental observations from WAXS and microrheology can be traced down to the molecular design, where the size of the ring of the isomeric hydrocarbons alters the packing in the hydrophilic/hydrophobic interfacial environments in the filaments without causing alterations in the surface chemistry.
Conclusions
In conclusion, we have developed an isomeric platform to construct 3D matrices that allows control over the local viscoelastic properties without affecting other material parameters, an ability that originates from the bottom-up design of synthetic peptides. Since such peptide-based hydrogels are relatively clean systems for further applications compared with many naturally occurring matrices, the fine-tuning of the local mechanical properties will be highly effective if these synthetic materials are applied in cell culture. We believe this design rationale could also be an effective means to construct synthetic materials with an aim to elucidate or differentiate the roles of local mechanical properties and geometric sensing in directing cell behaviors with controlled surface chemistry and mesh size.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. M. L. and H. C. would like to gratefully acknowledge the National Science Foundation (NSF) 1506937 for support. D. W. acknowledges the funding support from National Cancer Institute (U54CA143868 and R01CA174388). We also acknowledge the NSF for the purchase of the MALDI-ToF mass spectrometer used in this work. We also acknowledge NSF XSEDE resources under grant number TG-CHE130099 and a grant of computer time from the City University of New York High Performance Computing Center under NSF Grants CNS-0855217, CNS-0958379 and ACI-1126113. M. K. would also like to acknowledge partial support by the Rosemary O'Halleran scholarship.Notes and references
- D. E. Discher, P. Janmey and Y. L. Wang, Science, 2005, 310, 1139–1143 CrossRef CAS PubMed.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS PubMed.
- J. W. Shin and D. E. Discher, Nat. Mater., 2012, 11, 662–663 CrossRef CAS PubMed.
- A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468–473 CrossRef CAS PubMed.
- M. P. Lutolf and J. A. Hubbell, Nat. Biotechnol., 2005, 23, 47–55 CrossRef CAS PubMed.
- M. P. Lutolf, P. M. Gilbert and H. M. Blau, Nature, 2009, 462, 433–441 CrossRef CAS PubMed.
- B. Trappmann and C. S. Chen, Curr. Opin. Biotechnol., 2013, 24, 948–953 CrossRef CAS PubMed.
- J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319 CrossRef.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- T. F. A. De Greef, M. M. J. Smulders, M. Wolffs, A. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687–5754 CrossRef CAS PubMed.
- T. Aida, E. W. Meijer and S. I. Stupp, Science, 2012, 335, 813–817 CrossRef CAS PubMed.
- A. E. X. Brown, R. I. Litvinov, D. E. Discher, P. K. Purohit and J. W. Weisel, Science, 2009, 325, 741–744 CrossRef CAS PubMed.
- J. H. Ortony, C. J. Newcomb, J. B. Matson, L. C. Palmer, P. E. Doan, B. M. Hoffman and S. I. Stupp, Nat. Mater., 2014, 13, 812–816 CrossRef CAS PubMed.
- T. Shimada, N. Sakamoto, R. Motokawa, S. Koizumi and M. Tirrell, J. Phys. Chem. B, 2012, 116, 240–243 CrossRef CAS PubMed.
- H. Acar, S. Srivastava, E. J. Chung, M. R. Schnorenberg, J. C. Barrett, J. L. LaBelle and M. Tirrell, Adv. Drug Delivery Rev., 2017, 110, 65–79 CrossRef PubMed.
- J. D. Hartgerink, E. Beniash and S. I. Stupp, Science, 2001, 294, 1684–1688 CrossRef CAS PubMed.
- B. F. Lin, K. A. Megley, N. Viswanathan, D. V. Krogstad, L. B. Drews, M. J. Kade, Y. C. Qian and M. V. Tirrell, J. Mater. Chem., 2012, 22, 19447–19454 RSC.
- Y. C. Yu, P. Berndt, M. Tirrell and G. B. Fields, J. Am. Chem. Soc., 1996, 118, 12515–12520 CrossRef CAS.
- S. M. Zhang, M. A. Greenfield, A. Mata, L. C. Palmer, R. Bitton, J. R. Mantei, C. Aparicio, M. O. de la Cruz and S. I. Stupp, Nat. Mater., 2010, 9, 594–601 CrossRef CAS PubMed.
- F. C. MacKintosh, J. Käs and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428 CrossRef CAS PubMed.
- J. C. Stendahl, M. S. Rao, M. O. Guler and S. I. Stupp, Adv. Funct. Mater., 2006, 16, 499–508 CrossRef CAS.
- B. Ozbas, K. Rajagopal, L. Haines-Butterick, J. P. Schneider and D. J. Pochan, J. Phys. Chem. B, 2007, 111, 13901–13908 CrossRef CAS PubMed.
- Y. Li, Y. Sun, M. Qin, Y. Cao and W. Wang, Nanoscale, 2015, 7, 5638–5642 RSC.
- F. J. M. Hoeben, P. Jonkheijm, E. W. Meijer and A. Schenning, Chem. Rev., 2005, 105, 1491–1546 CrossRef CAS PubMed.
- A. Aggeli, M. Bell, N. Boden, J. N. Keen, P. F. Knowles, T. C. B. McLeish, M. Pitkeathly and S. E. Radford, Nature, 1997, 386, 259–262 CrossRef CAS PubMed.
- B. Ozbas, K. Rajagopal, J. P. Schneider and D. J. Pochan, Phys. Rev. Lett., 2004, 93, 4 CrossRef PubMed.
- J. Y. Huh and E. M. Furst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 031802 CrossRef PubMed.
- V. Castelletto, I. W. Hamley and P. J. F. Harris, Biophys. Chem., 2008, 138, 29–35 CrossRef CAS PubMed.
- M. C. Branco, F. Nettesheim, D. J. Pochan, J. P. Schneider and N. J. Wagner, Biomacromolecules, 2009, 10, 1374–1380 CrossRef CAS PubMed.
- R. A. Hule, R. P. Nagarkar, A. Altunbas, H. R. Ramay, M. C. Branco, J. P. Schneider and D. J. Pochan, Faraday Discuss., 2008, 139, 251–264 RSC.
- R. H. Colby, M. Rubinstein and J. L. Viovy, Macromolecules, 1992, 25, 996–998 CrossRef CAS.
- C. F. Schmidt, M. Baermann, G. Isenberg and E. Sackmann, Macromolecules, 1989, 22, 3638–3649 CrossRef CAS.
- P. G. Degennes, P. Pincus, R. M. Velasco and F. Brochard, J. Phys., 1976, 37, 1461–1473 CAS.
- D. H. Boal, Mechanics of the Cell, Cambridge University Press, 2012 Search PubMed.
- E. J. Chung, Y. Cheng, R. Morshed, K. Nord, Y. Han, M. L. Wegscheid, B. Auffinger, D. A. Wainwright, M. S. Lesniak and M. V. Tirrell, Biomaterials, 2014, 35, 1249–1256 CrossRef CAS PubMed.
- C. J. Newcomb, S. Sur, J. H. Ortony, O. S. Lee, J. B. Matson, J. Boekhoven, J. M. Yu, G. C. Schatz and S. I. Stupp, Nat. Commun., 2014, 5, 3321 Search PubMed.
- G. A. Silva, C. Czeisler, K. L. Niece, E. Beniash, D. A. Harrington, J. A. Kessler and S. I. Stupp, Science, 2004, 303, 1352–1355 CrossRef CAS PubMed.
- D. S. Chu, D. L. Sellers, M. J. Bocek, A. E. Fischedick, P. J. Horner and S. H. Pun, Biomater. Sci., 2015, 3, 41–45 RSC.
- Y. J. Chuah, Y. Peck, J. E. J. Lau, H. T. Heec and D. A. Wang, Biomater. Sci., 2017, 5, 613–631 RSC.
- G. Cinar, A. Ozdemir, S. Hamsici, G. Gunay, A. Dana, A. B. Tekinay and M. O. Guler, Biomater. Sci., 2017, 5, 67–76 RSC.
- D. Kalafatovic, M. Nobis, N. Javid, P. Frederix, K. I. Anderson, B. R. Saunders and R. V. Ulijn, Biomater. Sci., 2015, 3, 246–249 RSC.
- J. E. P. Sun, B. Stewart, A. Litan, S. J. Lee, J. P. Schneider, S. A. Langhans and D. J. Pochan, Biomater. Sci., 2016, 4, 839–848 RSC.
- P. D. Tatman, E. G. Muhonen, S. T. Wickers, A. O. Gee, E. S. Kim and D. H. Kim, Biomater. Sci., 2016, 4, 543–554 RSC.
- M. N. M. Walter, A. Dehsorkhi, I. W. Hamley and C. J. Connon, Biomater. Sci., 2016, 4, 346–354 RSC.
- Z. Q. Yu, Z. Cai, Q. L. Chen, M. H. Liu, L. Ye, J. Y. Ren, W. Z. Liao and S. W. Liu, Biomater. Sci., 2016, 4, 365–374 RSC.
- R. Nelson, M. R. Sawaya, M. Balbirnie, A. O. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778 CrossRef CAS PubMed.
- Y.-A. Lin, Y.-C. Ou, A. G. Cheetham and H. Cui, Biomacromolecules, 2014, 15, 1419–1427 CrossRef CAS PubMed.
- M. W. West, W. Wang, J. Patterson, J. D. Mancias, J. R. Beasley and M. H. Hecht, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11211–11216 CrossRef CAS.
- A. Aggeli, I. A. Nyrkova, M. Bell, R. Harding, L. Carrick, T. C. B. McLeish, A. N. Semenov and N. Boden, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11857–11862 CrossRef CAS PubMed.
- Y.-A. Lin, Y.-C. Ou, A. G. Cheetham and H. Cui, ACS Macro Lett., 2013, 2, 1088–1094 CrossRef CAS PubMed.
- P. Greenspan, E. P. Mayer and S. D. Fowler, J. Cell Biol., 1985, 100, 965–973 CrossRef CAS PubMed.
- E. R. Gillies, T. B. Jonsson and J. M. J. Frechet, J. Am. Chem. Soc., 2004, 126, 11936–11943 CrossRef CAS PubMed.
- Y. S. Velichko, S. I. Stupp and M. O. de la Cruz, J. Phys. Chem. B, 2008, 112, 2326–2334 CrossRef CAS PubMed.
- O. S. Lee, S. I. Stupp and G. C. Schatz, J. Am. Chem. Soc., 2011, 133, 3677–3683 CrossRef CAS PubMed.
- S. Tsonchev, A. Troisi, G. C. Schatz and M. A. Ratner, Nano Lett., 2004, 4, 427–431 CrossRef CAS.
- M. Kang, P. Zhang, H. Cui and S. M. Loverde, Macromolecules, 2016, 49, 994–1001 CrossRef CAS.
- M. Kang, H. Cui and S. M. Loverde, Soft Matter, 2017, 13, 7721–7730 RSC.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. K. Gilson, H. S. R. Gilson and M. J. Potter, J. Chem. Inf. Comput. Sci., 2003, 43, 1982–1997 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- F. C. MacKintosh and C. F. Schmidt, Curr. Opin. Colloid Interface Sci., 1999, 4, 300–307 CrossRef CAS.
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685–742 CrossRef.
- D. Wirtz, Ann. Rev. Biophys., 2009, 38, 301–326 CrossRef CAS PubMed.
- T. G. Mason, K. Ganesan, J. H. vanZanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282–3285 CrossRef CAS.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- D. Langevin and F. Rondelez, Polymer, 1978, 19, 875–882 CrossRef CAS.
- P. G. de Gennes, P. Pincus and R. M. Velasco, personal communication, quoted in D. Langevin, F. Rondelez, Polymer, 1978, 19, 875 edn.
- P. Dalhaimer, F. S. Bates and D. E. Discher, Macromolecules, 2003, 36, 6873–6877 CrossRef CAS.
- B. M. Discher, H. Bermudez, D. A. Hammer, D. E. Discher, Y.-Y. Won and F. S. Bates, J. Phys. Chem. B, 2002, 106, 2848–2854 CrossRef CAS.
- M. D. Stevenson, H. Piristine, N. J. Hogrebe, T. M. Nocera, M. W. Boehm, R. K. Reen, K. W. Koelling, G. Agarwal, A. L. Sarang-Sieminski and K. J. Gooch, Acta Biomater., 2013, 9, 7651–7661 CrossRef CAS PubMed.
- K. M. Galler, L. Aulisa, K. R. Regan, R. N. D'Souza and J. D. Hartgerink, J. Am. Chem. Soc., 2010, 132, 3217–3223 CrossRef CAS PubMed.
- H. G. Cui, A. G. Cheetham, E. T. Pashuck and S. I. Stupp, J. Am. Chem. Soc., 2014, 136, 12461–12468 CrossRef CAS PubMed.
- J. A. Lehrman, H. G. Cui, W. W. Tsai, T. J. Moyer and S. I. Stupp, Chem. Commun., 2012, 48, 9711–9713 RSC.
- E. T. Pashuck, H. Cui and S. I. Stupp, J. Am. Chem. Soc., 2010, 132, 6041–6046 CrossRef CAS PubMed.
- D. J. Smith, G. A. Brat, S. H. Medina, D. D. Tong, Y. Huang, J. Grahammer, G. J. Furtmuller, B. C. Oh, K. J. Nagy-Smith, P. Walczak, G. Brandacher and J. P. Schneider, Nat. Nanotechnol., 2016, 11, 95–102 CrossRef CAS PubMed.
- F. Tantakitti, J. Boekhoven, X. Wang, R. V. Kazantsev, T. Yu, J. Li, E. Zhuang, R. Zandi, J. H. Ortony, C. J. Newcomb, L. C. Palmer, G. S. Shekhawat, M. O. de la Cruz, G. C. Schatz and S. I. Stupp, Nat. Mater., 2016, 15, 469–476 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed experimental and simulation procedures of molecular synthesis, characterization, and computation. See DOI: 10.1039/c7bm00722a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2018 |