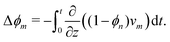DOI:
10.1039/C7SM01279A
(Paper)
Soft Matter, 2017,
13, 9199-9210
Monomer diffusion into static and evolving polymer networks during frontal photopolymerisation†
Received
29th June 2017
, Accepted 13th October 2017
First published on 29th November 2017
Abstract
Frontal photopolymerisation (FPP) is a directional solidification process that converts monomer-rich liquid into crosslinked polymer solid by light exposure and finds applications ranging from lithography to 3D printing. Inherent to this process is the creation of an evolving polymer network that is exposed to a monomer bath. A combined theoretical and experimental investigation is performed to determine the conditions under which monomer from this bath can diffuse into the propagating polymer network and cause it to swell. First, the growth and swelling processes are decoupled by immersing pre-made polymer networks into monomer baths held at various temperatures. The experimental measurements of the network thickness are found to be in good agreement with theoretical predictions obtained from a nonlinear poroelastic model. FPP propagation experiments are then carried out under conditions that lead to swelling. Unexpectedly, for a fixed exposure time, swelling is found to increase with incident light intensity. The experimental data is well described by a novel FPP model accounting for mass transport and the mechanical response of the polymer network, providing key insights into how monomer diffusion affects the conversion profile of the polymer solid and the stresses that are generated during its growth. The predictive capability of the model will enable the fabrication of gradient materials with tuned mechanical properties and controlled stress development.
1. Introduction
New developments in the field of polymeric additive manufacturing, including 3D printing, are leading to the next generation of rapid, cost-effective techniques for fabricating complex structures across a broad range of length scales. Reductions in manufacturing costs and fabrication time, along with increasing ability to create objects that cannot be made with traditional methods, have stimulated world-wide growth of 3D printing and the value of the industry is expected to reach 20 billion USD by 2020.1 The versatility and accessibility of 3D printing has led to its wide-spread use in fields such as tissue engineering and drug delivery,2–4 microfluidics,5 electronics,6,7 and battery design.8 Of the various approaches to 3D printing, which include fused deposition modelling9 and selective laser sintering,10 light-driven technologies based on, e.g. stereolithography, have shown exceptional promise due to their speed and resolution. More recently, UV-based 3D printing has been used to develop a continuous fabrication process,11 enabling further reductions in manufacturing time and surface roughness compared with stepwise methods.
The key process in light-driven 3D printing is the conversion of liquid monomer into crosslinked polymer solid upon exposure to UV light. Absorption of light by the photosensitive monomer-rich liquid initiates a sequence of chemical reactions that result in photopolymerisation and crosslinking.12 Generally, the rate of conversion is proportional to the intensity of radiation.13 As light passes through the mixture and is absorbed, the corresponding decay in intensity leads to a reduction in the rate of conversion. Thus, photopolymerisation naturally gives rise to a spatially varying monomer-to-polymer conversion profile. In the context of 3D printing, this non-uniform profile can be both advantageous and detrimental. For instance, it provides a means of fabricating gradient materials14–16 with tunable density, refractive index, elastic modulus, and permeability. By further modulation of the conversion profile via coupling photopolymerisation with the diffusion of an inhibitory species, wrinkled surfaces17,18 and three-dimensional microstuctures19 can be generated. However, non-uniform conversion can also lead to residual stresses within the solid and cause pattern failure and delamination. Precise control over the conversion profile is therefore needed in practical applications.
During photopolymerisation, the evolving polymer network is exposed to the monomer bath. It is well known that monomer can diffuse into polymer networks, leading to swelling20,21 and, under certain conditions, the onset of mechanical instability.22,23 In photopolymerising systems, the relative rate of monomer conversion with respect to monomer diffusion is expected to dictate the relevance of the latter to the evolution of the network. Evidently, under conditions of rapid conversion, the monomer is effectively immobile, while at slow conversion, diffusion may become significant. The intricate interplay between conversion and diffusion of monomer will, therefore, play a key role in setting the patterning window of operation and in controlling the surface and mechanical properties of the polymer solid.
This paper presents the results of a combined experimental and theoretical study of photopolymerisation that aims to (i) elucidate the conditions under which monomer diffusion and conversion occur simultaneously and (ii) determine how diffusion can influence the conversion profile and generate internal stresses within the polymer network.
A schematic diagram of the experimental configuration is shown in Fig. 1(a). A photosensitive monomer bath is covered with a transparent surface and exposed to collimated UV radiation with intensity I0. The strong absorption of light by the bath leads to the onset of frontal photopolymerisation (FPP), which is characterised by the development of a thin interfacial region separating monomer-rich liquid from polymer-rich solid, yielding a sharp solidification front that propagates from the illuminated surface into the bulk. FPP is therefore a directional solidification process, which finds applications in 3D printing24 and the fabrication of multi-level patterns used in microfluidic devices.25 The position of the sharp solidification front, zf, gives the instantaneous height of the polymer solid and can be defined as the point at which the volume fraction of polymer network reaches a critical value ϕc;16,26,27 see Fig. 1(b). Physically, ϕc corresponds to the gel point of the polymer: material below ϕc is insufficiently crosslinked and thus washes away upon selective dissolution and development of the solid. As the front propagates away from the illuminated surface, unreacted monomer from the bath can, in principle, diffuse into the polymer network and cause it to swell. Due to the adhesion between the polymer network and the illuminated surface, the volumetric expansion mainly occurs in the growth direction; this constrained swelling results in the generation of elastic stresses in the polymer network. Using this model FPP system, we investigate how changes in the bath temperature and the intensity of radiation, two key factors which control the kinetics of monomer diffusion and front propagation, influence the onset of swelling during FPP, as measured through the front position zf. Due to the creation of new crosslinks in the polymer network by FPP, we refer to these as ‘evolving’ networks.
 |
| | Fig. 1 Monomer diffusion into a growing polymer network during frontal photopolymerisation (FPP). (a) Exposing a photosensitive monomer-rich bath to radiation with incident intensity I0 leads to a planar polymerisation front that propagates from the illuminated surface into the bulk. At the same time, monomer from the bath can diffuse into the network and cause it to expand. (b) The composition of the mixture is described by the volume fractions of polymer network ϕn and monomer ϕm = 1 − ϕn. A sharp polymerisation front can be defined as the location where the network fraction reaches a critical solidification value ϕc. | |
Swelling during FPP is reminiscent of isothermal frontal polymerisation (IFP), which is also driven by diffusion of monomer into the growing polymer network. However, in IFP, the diffusion of monomer converts the network into a viscous gel that swells and propagates into the bulk.28,29 Due to the Tromsdorff–Norish (or ‘gel’) effect, the gel layer polymerises faster than the bulk, allowing the process to continue. IFP is therefore auto-catalytic, unlike FPP, which is driven by the absorption of radiation and can be terminated upon stopping the illumination.
To further investigate the role of monomer diffusion during FPP, a secondary set of experiments, which decouple the growth and swelling processes, is carried out using ‘pre-made’ polymer networks. That is, FPP is first used to create a set of polymer networks with varying material properties under conditions of negligible swelling. These pre-made polymer networks are then immersed in the monomer bath from which they were created and allowed to freely swell. The dimensions of the networks are measured as a function of time, enabling the determination of the kinetics of diffusion. These networks are referred to as ‘static’ networks, since no crosslinks are formed during the swelling process.
The results of both sets of experiments are interpreted with the aid of theoretical models. In the case of a static network, the model is based on the classical theories of nonlinear swelling of hydrogels20,30,31 and adapted to use Eulerian coordinates,32,33 which allow the equations to be written in physically intuitive forms. The governing equations are then extended to account for the growth of the polymer network by FPP.26,34–36
A wide range of models for photopolymerisation have been developed that account for detailed reaction steps,37–40 oxygen inhibition,41,42 polydisperse chain lengths,43,44 heat generation and transport,36,45 and the onset of convection.46 Models that capture monomer diffusion during photopolymerisation have been proposed,35,47 but these do not consider the mechanical response of the network. Although these detailed physico-chemical models can provide insight into the fundamental processes that occur during photopolymerisation, they can be impractical due, in part, to their large number of parameters. Thus, we incorporate mass transport and mechanics into a ‘minimal’ model of FPP that is capable of accurately describing experiments carried out using thiol–ene systems16,25–27 and based on key experimental observables and a limited number of parameters.
The experimental methods are described in Section 2. In Sections 3 and 4, theoretical models for the swelling of static and evolving polymer networks are presented and the experimental data is interpreted. The paper concludes in Section 5.
2. Experimental methods
2.1. Fabrication of static polymer networks
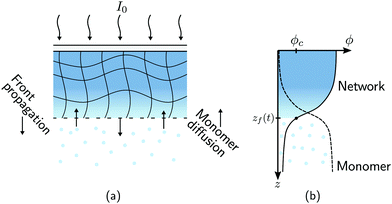
FPP was employed to create a set of static polymer networks with varying material properties, as shown in Fig. 2(a). A thermally cured polydimethylsiloxane (PDMS) mold with a vertical depth of 0.3 mm was filled with a photosensitive thiol–ene monomer bath (optical adhesive NOA81, Norland Products) and covered with a glass slide. A square 2 × 2 cm2 photomask was placed on the glass slide to allow for selective illumination of the bath away from the lateral container boundaries. The bath was held at room temperature and exposed to collimated UV light (Omnicure S1500 equipped with a 365 nm filter) with an incident intensity of I0 = 6.6 W m−2. The UV exposure time was selected to obtain a precise monomer-to-polymer conversion in each sample. The conversion fraction χ of each sample was measured by FT-IR spectroscopy using a Bruker 27 spectrometer coupled to a Hyperion microscope.16 The decrease in absorbance of reactive thiol groups (with absorption peak centred at 2572 cm−1) was monitored, taking the absorbance of carbonyl groups (with a peak centred at 1735 cm−1) as a reference. The conversion fraction χ is then defined in terms of the absorbance of thiol and carbonyl groups, A2572 and A1735, respectively, as χ = 1 − (A2572t/A1735t)/(A25720/A17350), where A0 is the initial absorbance (before UV exposure) and At is the absorbance at a given time t. The dimensions of the resulting crosslinked samples were 19.7 × 19.7 × 0.3 mm3 (x × y × z). Due to the limited thickness, the conversion fraction χ is assumed to be spatially uniform throughout all samples.
 |
| | Fig. 2 Swelling of static polymer networks. (a) FPP is used to create thin polymer networks with uniform monomer-to-polymer conversion fraction χ. (b) Each static network is immersed in a monomer bath held at temperature T and allowed to swell. Swelling occurs predominantly in the growth direction. The centerline and free surfaces of the polymer network are denoted by z = 0 and z = ±h(t), respectively, where h(0) = 0.15 mm. The half-height of the polymer network, h, is measured as a function of time for different bath temperatures T and conversion fractions χ. | |
To minimise swelling during fabrication of static networks, the samples were created at room temperature with high-intensity light. These conditions ensure the time scale of network fabrication is much shorter than that of monomer diffusion.35 The fabrication times for networks with χ = 0.12, 0.35, 0.42, and 0.85 are 1, 2, 5, and 30 min, respectively. In Section 3.2, we show that these networks expand by less than 1% when exposed to a monomer bath held at room temperature for the same amount of time. Moreover, in previous FPP experiments16 carried out under similar conditions, the spatiotemporal evolution of the conversion fraction was found to be in excellent agreement with predictions from a minimal model26 that does not account for mass diffusion, also suggesting that swelling is negligible.
2.2. Characterisation of the static networks
Each static network sample is characterised by its conversion fraction χ. The elastic modulus of the network, E, has been measured by atomic force microscopy with a Bruker Innova instrument16 and is plotted as a function of the conversion fraction χ and the temperature T in Fig. 3. There is a sharp increase in the elastic modulus near χ = χg ≃ 0.77, indicative of the glass transition. Although the elastic modulus varies slightly with temperature, we make the simplifying assumption that it is temperature independent within the range considered. The data is fit to a curve of the form E(χ) = Emax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(g(χ)), where g is a piecewise linear polynomial with a kink at χg, which approximates detailed physico-chemical models of E(χ) near the glass transition.48 The parameter Emax = 187 MPa corresponds to the elastic modulus at χmax = 0.85. We find that g(χ) = 4.16(χ − χg) − 1.67 for χ < χg and g(χ) = 24.2(χ − χmax) for χ > χg, where χg = 0.77. The fitted curve is shown as the black line in Fig. 3.
exp(g(χ)), where g is a piecewise linear polynomial with a kink at χg, which approximates detailed physico-chemical models of E(χ) near the glass transition.48 The parameter Emax = 187 MPa corresponds to the elastic modulus at χmax = 0.85. We find that g(χ) = 4.16(χ − χg) − 1.67 for χ < χg and g(χ) = 24.2(χ − χmax) for χ > χg, where χg = 0.77. The fitted curve is shown as the black line in Fig. 3.
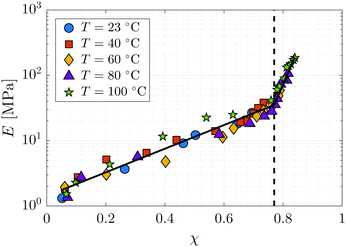 |
| | Fig. 3 The dependence of the elastic modulus E on the monomer-to-polymer conversion fraction χ at different temperatures. The dashed line denotes the glass transition. | |
2.3. Swelling of static networks
The static network samples were immersed in baths of monomer, held at various temperatures, and allowed to freely swell; see Fig. 2(b). The dimensions of the networks were measured at various times using a digital caliper (Mitutoyo, with ±0.001 mm resolution) and a reflection optical microscope (Olympus BX41M) for each bath temperature T and conversion fraction χ. In all cases, swelling occurred predominantly along the growth direction; relative changes in the lateral dimensions were negligible.
2.4. Swelling of evolving networks
Swelling during FPP was studied with the experimental setup described in Section 2.1 using a PDMS mold with a depth of 3.5 mm. A RayTemp8 infrared thermometer and hot plate were used to maintain a bath temperature of T = 65 °C, which led to significant swelling of static networks. Three experiments were performed using different light intensities of I0 = 0.1, 1, and 10 W m−2. Each bath was illuminated for different amounts of time t, the uncrosslinked material was removed with acetone and ethanol, and the height of the polymer network zf(t) was measured.
3. Swelling of static polymer networks
3.1. Model formulation
We first consider the diffusion of monomer into a static polymer network. Due to the relatively large lateral dimensions of the networks and the observation that swelling mainly occurs along the growth direction, it is sufficient to consider a one-dimensional model. Swelling is assumed to occur symmetrically about the centerline of the network, denoted by z = 0, so that the total thickness is given by 2h(t), where z = ±h(t) corresponds to the time-dependent free surfaces of the network; see Fig. 2(b).
Swelling is rationalised as the result of two competing mechanisms. Firstly, monomer diffuses into the network in order to reduce the free energy of mixing. Secondly, the polymer network must expand in order to accommodate the volume of absorbed monomer, which increases the elastic energy of the mixture. Equilibrium is reached when the decrease in energy of mixing due to additional uptake of monomer is exactly balanced by the increase in elastic energy due to further expansion. A theoretical model of swelling must therefore consider mass transport, the mechanical response of the polymer network, and the thermodynamics of the mixture.
3.1.1. Mass transport and volume conservation.
The composition of the mixture is described by the volume fractions of the monomer and polymer network, ϕm and ϕn, respectively. The deformation of the polymer network is characterised by the local stretch λ, describing the degree of expansion (λ > 1) or shrinkage (λ < 1) that a material element has undergone. It is assumed that the specific densities of the monomer and network are constant and equal, and that no density change occurs upon mixing, i.e., the mixture is ideal. These assumptions imply that the monomer and polymer network are incompressible at the microscopic level. However, the polymer network, which can be envisioned as a porous material, can still experience macroscopic compression through changes in the pore shape and volume. As the density of the mixture remains constant, the volume fractions of monomer and polymer must satisfyfor all time t. Additionally, due to the microscopic incompressibility of the liquid monomer and the elastic polymer network, volume must be conserved at a local level. That is, the volumetric expansion of a material element in the polymer network must be exactly equal to the volume of absorbed monomer; therefore,Global conservation of volume implies (see ESI† for details) that the net expansion of the polymer network is equal to the total volume of absorbed monomer:| | 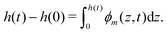 | (3) |
Applying the law of conservation of mass to both the monomer and polymer phases yields two transport equations of the form| | 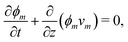 | (4a) |
| | 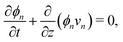 | (4b) |
where vm and vn correspond to the velocity of monomer and polymer, respectively, as measured from a fixed laboratory frame. By adding the two conservation equations in (4) and using (1), it follows that the mixture velocity, v ≡ ϕmvm + ϕnvn, is divergence-free,| | 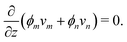 | (5) |
We assume that the static polymer network is initially dry and free of monomer, corresponding to initial conditions given by ϕn(z,0) = 1 and ϕm(0,t) = 0.
3.1.2. Mixture mechanics.
Governing equations for the monomer and network velocities, vm and vn, can be obtained by considering the mechanics of the two-phase mixture. Eulerian stress balances can be derived by volume averaging the single-phase equations32,49,50 or applying the maximum dissipation principle51,52 or various forms of the second law of thermodynamics.53 These approaches generally result in the same system of equations, representing the conservation of linear momentum in each phase. Under the assumptions of negligible inertia and viscous effects in the monomer,54,55 and the existence of a dissipative drag force between the two phases, the momentum balances can be written as| | 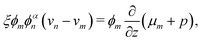 | (6a) |
| | 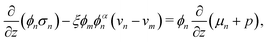 | (6b) |
where σn is the deviatoric stress of the network, ξ is the drag (friction) coefficient between monomer and the network, α characterises the change in network geometry (e.g., mesh size) during swelling,33μi is the chemical potential of phase i associated with changes in the Helmholtz free energy, and p is the pressure.
The drag coefficient can be interpreted as the inverse of the monomer mobility and written in terms of the conversion-dependent mutual diffusion coefficient D using the Einstein relation,
| | 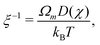 | (7) |
where
Ωm is the volume of a monomer unit and
kB is Boltzmann's constant. The momentum balance for the monomer
(6a) can then be written as
| | 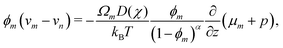 | (8) |
which shows that the relative volumetric flux of monomer is driven by gradients in the chemical potential (Fick's law) and pressure (Darcy's law). The
ϕm-dependent prefactor on the right-hand side of
(8) represents the permeability of the polymer network. We assume the permeability law is linear and set
α = 1. A detailed comparison of linear (
α = 1) and nonlinear (1.5 ≤
α ≤ 2)
33,56–58 permeability laws is given in the ESI.
† We find that the differences are negligible.
The deviatoric stress of the polymer network is expressed in terms of the Terzaghi effective stress, σen, which represents the contribution of the elastic stresses to the total stress:32,33
Summing the two equations in
(6) and invoking the Gibbs–Duhem relation
ϕmd
μm +
ϕnd
μn = 0 yields a momentum balance for the mixture given by
| | 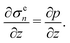 | (10) |
From
(10) it is seen that
Σ =
σen −
p corresponds to the Cauchy stress of the mixture. Given that the polymer network is assumed to undergo one-dimensional deformation, the Cauchy stress tensor of the mixture can be written as
where
ez is the unit vector pointing in the positive
z direction and
I is the identity tensor.
Eqn (11) shows that swelling will generate lateral compressive stresses given by −
p.
3.1.3. Free energy considerations.
The Flory–Rehner theory of ideal polymeric gels30 is used to decompose the Helmholtz free energy density, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , into elastic and mixing contributions,
, into elastic and mixing contributions, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e and
e and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix, depending only on the local stretch and composition, respectively:
mix, depending only on the local stretch and composition, respectively:| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (λ,ϕm,ϕn) = λ−1 (λ,ϕm,ϕn) = λ−1![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e(λ) + e(λ) + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix(ϕm,ϕn). mix(ϕm,ϕn). | (12) |
The pre-factor of λ−1 accounts for the fact that ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e is traditionally defined per unit reference (undeformed) volume rather than per current (deformed) volume.
e is traditionally defined per unit reference (undeformed) volume rather than per current (deformed) volume.
The elastic response of the polymer network is assumed to be neo-Hookean. The corresponding elastic energy density for the one-dimensional deformations considered here is given by
| | 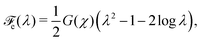 | (13) |
where
G is a conversion-dependent elastic constant that plays the role of the shear modulus at small strains. Thus, we set
G(
χ) =
E(
χ)/[2(1 +
ν)], where
ν ≃ 0.5 is the Poisson ratio, and
E is the elastic modulus shown in
Fig. 3. The volume fraction of monomer absorbed by the network is assumed to be sufficiently small that the modulus is unchanged by the swelling process. The effective stress can be derived from the elastic energy
via σen ≡ ∂
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e
e/∂
λ, yielding
The free energy density of mixing ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix is obtained from the Flory–Huggins theory of polymer solutions59 and written as
mix is obtained from the Flory–Huggins theory of polymer solutions59 and written as
| | 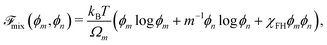 | (15) |
where
m is the number of monomer units per polymer chain, and
χFH is an interaction parameter. As the polymer networks under consideration consist of polymer chains that have been formed from the mobile (diffusing) monomer, enthalpic interactions between monomer and polymer are expected to be small,
i.e., the mixtures are close to being athermal. Therefore, we set
χFH = 0 for the remainder of the paper. The chemical potentials can be derived from the Helmholtz free energy
59via the relations
μm −
μ0m =
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix +
ϕnΔ
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix,
μn −
μ0n =
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix −
ϕmΔ
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix, and Δ
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix = ∂
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix/∂
ϕm − ∂
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix
mix/∂
ϕn, which give
| | 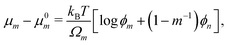 | (16a) |
| | 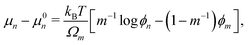 | (16b) |
where
μ0m and
μ0n are the chemical potentials of the pure monomer and polymer network, respectively.
3.1.4. Boundary conditions.
Symmetry at the centerline requires the monomer and polymer velocities to vanish: vm(0,t) = vn(0,t) = 0. The surface of the polymer network, z = h(t), is assumed to be stress-free and in chemical equilibrium with the monomer bath; therefore, σen(h(t),t) − p(h(t),t) = 0 and μm(h(t),t) + p(h(t),t) = μ0m. The two conditions at the surface play an important role because they set the equilibrium monomer fraction ϕeqm and thus the degree of swelling that the network experiences. Solving the model under equilibrium conditions (see ESI†) yields an equation for ϕeqm given by| | 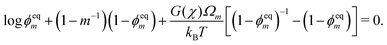 | (17) |
Eqn (17) shows that the equilibrium monomer fraction is controlled by a single dimensionless number β ≡ G(χ)Ωm/(kBT) characterising the relative contribution of the elastic energy to the total free energy.
3.1.5. Reduction of the governing equations.
The governing equations can be reduced to a single nonlinear diffusion equation given by| | 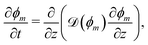 | (18a) |
where the effective diffusivity ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is
is| | ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (ϕm) = D(χ)(1 − (1 − m−1)ϕm + βϕm[1 + (1 − ϕm)−2]). (ϕm) = D(χ)(1 − (1 − m−1)ϕm + βϕm[1 + (1 − ϕm)−2]). | (18b) |
The associated boundary and initial conditions are| | 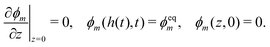 | (18c) |
By differentiation of (3) with respect to time, an evolution equation for the half thickness of the polymer network can be obtained,| | 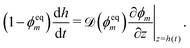 | (18d) |
This is supplemented with the initial condition h(0) = hi, where hi is the initial half thickness of the polymer network.
3.2. Experimental results and model validation
We next analyse swelling experiments using static polymer networks with varying conversion fraction χ and monomer baths held at different temperatures T. The thickness of each film 2h(t) was measured as a function of time and used to calculate the mean strain ε(t) = h(t)/h(0) − 1; the experimental results are plotted as symbols in Fig. 4. The data clearly shows that as the conversion fraction increases, or as the bath temperature decreases, the swelling that occurs in a given time decreases as well.
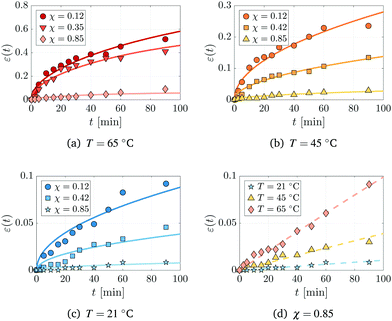 |
| | Fig. 4 Swelling of pre-made polymer networks of four representative conversions χ at (a) 65 °C, (b) 45 °C, (c) 21 °C and (d) at a single conversion χ = 0.85 and three temperatures. Each panel shows the evolution of the strain ε(t) = h(t)/h(0) − 1, where h(0) = 150 μm. Symbols and solid lines respectively correspond to experimental data and numerical fits of the reduced model (18). | |
The reduced swelling model (18) is numerically simulated and fit to each set of data. The polymer network is taken to be a polymer chain with infinite length and thus we set m = ∞, which is consistent with previous hydrogel models20,30,57,60 and validated against experimental data.61 Using finite values of m ≥ 100 resulted in small and insignificant quantitative changes to the results. Satisfactory agreement between theory and experiment is found if the molar volume of monomer, Vm = ΩmNA, where NA is Avodagro's number, is set to Vm = 525 × 10−6 m3 mol−1, which is roughly 30 times that of water (Vm ≃ 18 × 10−6 m3 mol−1). The only undetermined parameter is the diffusivity D(χ), which is treated as a fitting parameter. Numerical values for the diffusivity can be found in the ESI† and are found to increase strongly with temperature, as expected.
The solid lines in Fig. 4(a)–(c) depict numerical simulations of the model (18) using the fitted values of the diffusivity. The agreement between theory and experiment is especially good for polymer networks that have been created from FPP solids with small to moderate conversion fractions (χ ≤ 0.42), and when the bath is above room temperature (T = 45 °C or T = 65 °C). In particular, the t1/2 behaviour of the strain is clearly captured in these cases. When T = 21 °C and χ ≤ 0.42, the model overpredicts the initial expansion of the network, which is linear in time.
Physically, the t1/2 behaviour of the strain emerges due to (i) the overall diffusive nature of the swelling process and (ii) the assumption that the surface of the network is in chemical equilibrium with the monomer bath. More specifically, the conditions in (18c) imply that the monomer fraction at the surface instantaneously attains its equilibrium value, whereas the bulk volume fraction remains close to zero, leading to strong composition gradients near the surface of the network. These strong gradients induce the rapid initial expansion of the network, as seen from (18d). For warmer baths (T = 45 °C and 65 °C), the assumption of chemical equilibrium at the surface appears to be valid. For colder baths (T = 21 °C), however, the linear dependence of the strain on time suggests that chemical equilibrium is not immediately reached and an alternative boundary condition that captures the relaxation to equilibrium would be more suitable.62,63
The data obtained from highly converted networks (χ = 0.85) is presented in Fig. 4(d), which clearly shows a linear increase in the strain with time for all bath temperatures. A distinguishing feature of these polymer networks is that they are glassy;16 thus, the linear expansion of the polymer films is likely due to the onset of case-II diffusion,64,65 not captured by our model. Case-II diffusion occurs in glassy polymers when the polymer chains are not sufficiently mobile to allow monomer to penetrate the polymer network.66 Consequently, the rate of expansion becomes set by the time scale of polymer relaxation rather than diffusion.
4. Swelling of evolving networks during FPP
4.1. Model formulation
The theoretical models for swelling of static and evolving polymer networks are based on the same underlying principles. Consequently, many of the governing equations presented in Section 3.1 carry over, although modifications are required to account for the conversion of monomer and formation of the polymer network.
4.1.1. Problem geometry and preliminary assumptions.
A schematic diagram of the FPP experiment is shown in Fig. 1. The model is formulated in terms of a downwards-pointing Eulerian coordinate z, where z = 0 is chosen to coincide with the illuminated surface. The height of the polymer network at each point in time is denoted by zf(t) and is a key experimental observable. The precise definition of zf is given in Section 4.1.2.
While photopolymerisation processes can be strongly exothermic67 and result in volume shrinkage,68 the NOA81 formulation that is used here has been shown to release only a small amount of heat and undergo negligible volume changes upon exposure to light.16 Therefore, it is assumed that the mixture remains isothermal and that conversion does not lead to changes in the mixture volume.
4.1.2. Definition of the polymer network.
It is assumed that a polymer network is formed when the network fraction exceeds a critical value ϕc, which is required for the polymer chains to be sufficiently crosslinked. The polymer network can thus be implicitly defined as the points which satisfy ϕn(z,t) > ϕc. The precise point zf(t) where ϕn(zf(t),t) = ϕc represents the position of the propagating front and corresponds to the instantaneous height of the FPP solid. For this system, the value of ϕc is remarkably small, due to the presence of oligomeric species, and given by ϕc ≃ 0.05.16,27
4.1.3. A sequential growth-swelling approximation.
A primary difference between static and evolving polymer networks is the role of the conversion fraction χ and its link to the volume fraction of polymer network ϕn. In the former case, χ is treated as an experimental control variable, setting the degree of conversion in the polymer network, and is assumed to be independent of the network fraction. In the latter case, the conversion fraction is intrinsically linked to the network fraction and the evolution of these two quantities cannot be trivially decoupled.
On a conceptual level, the conversion and network fractions can be decoupled by decomposing the mixture evolution into a series of alternating growth and swelling steps, which allows the previous modelling framework to be applied with minimal changes. In particular, the Flory–Rehner decomposition of the free energy (12) still holds and, thus, the chemical potentials of the monomer and polymer network are given by (16). In fully coupled growth-swelling models, the dependence of elastic energy on the mixture composition can introduce stress-dependent contributions to the chemical potentials.69–71 In the interest of retaining model simplicity, such effects are not considered here.
4.1.4. Conservation of mass and momentum.
The starting points for mass and momentum conservation are (4), (5), (8), and (10). The mass balances (4) are modified to account for the conversion of monomer into polymer at a rate R, which will be specified in Section 4.1.5. The pressure p is eliminated from the problem via(10). The equations representing conservation of mass and momentum can be written as| | 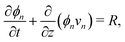 | (19a) |
| | 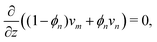 | (19b) |
| | 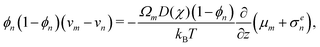 | (19c) |
where the monomer fraction has been eliminated via ϕm = 1 − ϕn.
The chemical potential of monomer μm, appearing in (19c), is given by (16a) and depends on the chain length m. By decomposing the mixture into the polymer network (ϕn > ϕc) and the monomer-rich bath (ϕn < ϕc), we see that m = ∞ for ϕn > ϕc and m < ∞ for ϕn < ϕc, implying the chain length should be a strongly increasing function of the network fraction. This is in stark contrast to the model for a static network, which only considers points within the polymer network where m = ∞. Explicitly capturing the growth of chains and the functional relationship between of m and ϕn is beyond the scope of our coarse-grained modelling approach, which does not distinguish polymerisation from crosslinking. Instead, we focus on capturing monomer diffusion in the weakly crosslinked region that lies slightly ahead of the polymerisation front, where diffusion is expected to be the most relevant, and take m to be a constant and finite value. Although taking m to be finite may lead to inaccuracies when describing monomer transport in the polymer network, any errors are expected to be mitigated by the sharp decrease in the diffusion coefficient with conversion fraction, which rapidly immobilises the monomer. To capture this immobilisation, the diffusion coefficient is written as D(χ) = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−aχ). This form of diffusivity leads to an exponential permeability law, the consequences of which are explained in the ESI.†
exp(−aχ). This form of diffusivity leads to an exponential permeability law, the consequences of which are explained in the ESI.†
4.1.5. Light-driven growth of a polymer network.
Keeping in line with previous ‘minimal’ models of FPP,25,34–36 the conversion rate R is assumed to be proportional to the local amount of monomer, ϕm = 1 − ϕn, and the intensity of radiation, I(z,t), leading to a rate of the formwhere K is an effective rate coefficient for the conversion process. A more precise description of K in terms of detailed chemical reactions can be found in Purnama et al.72 The intensity of light is modelled using a Beer–Lambert law| | I(z,t) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(− exp(−![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) z), z), | (21) |
where ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is the average attenuation coefficient of the mixture, assumed to be constant. Extending (21) to capture changes in
is the average attenuation coefficient of the mixture, assumed to be constant. Extending (21) to capture changes in ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) with composition is straightforward,26,34 but not needed here.
with composition is straightforward,26,34 but not needed here.
4.1.6. Kinematics and mechanics.
For static polymer networks, algebraic relationships exist between (i) the local stretch λ and the monomer fraction ϕm, i.e., λ = (1 − ϕm)−1, and (ii) the elastic stress and the local stretch, i.e., σen = G(χ)(λ − λ−1). These relationships are not adequate for describing the stretch and stress in a polymer network grown by FPP because the photoconversion of monomer should not modify (i) the existing local stretch nor (ii) the elastic stress through the corresponding increase in the elastic modulus. However, conversion can potentially reduce the elastic stress through the creation of new crosslinks. Rather than using algebraic relationships for the local stretch and the effective stress, it is more suitable to use evolution equations for these quantities.
In one dimension, the rate of volume change (stretch) that a material element experiences can be related to its velocity gradient via73
| | 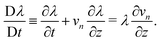 | (22) |
Similarly, we assume that the stress evolves according to
| | 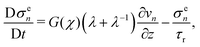 | (23) |
where
τr is the time scale associated with the reduction of stress due to the creation of new crosslinks. Accordingly, we take
τr = (
KI0χ)
−1 so that the reduction in stress occurs on the same time scale as monomer conversion at a rate that is proportional to the conversion fraction
χ.
Eqn (23) can be derived by taking the convective derivative of the elastic stress
(14) with a fixed conversion fraction
χ, using
(22), and then including stress-reduction effects. This type of approach has been used to model shrinkage-induced stresses during FPP.
68 The role of crosslink-induced stress reduction is discussed in the ESI.
†
4.1.7. Initial and boundary conditions.
As the mixture is initially pure in monomer, the initial conditions ϕn(z,0) = 0, λ(z,0) = 1, and σen(z,0) = 0 are prescribed. The illuminated glass surface is impermeable and rigid; thus, we set vn(0,t) = vm(0,t) = 0. This latter condition is equivalent to imposing a zero-displacement condition on the polymer network. It has also been assumed that no-slip conditions (zero tangential velocity and displacement) apply on the illuminated surface, which is consistent with a one-dimensional model. In contrast to the model for a static network, the model for an evolving network does not explicitly track the interface between the network and the monomer bath; therefore, there is no need to impose boundary conditions there. Instead, the bath is assumed to have infinite depth and the far-field boundary conditions are ∂vn/∂z → 0 and ∂vm/∂z → 0 as z → ∞.
4.2. Presentation and interpretation of experimental data
Three FPP experiments have been carried out using a monomer bath held at a temperature of T = 65 °C and different light intensities of I0 = 0.1, 1, and 10 W m−2. The height of the polymer network, zf, was measured as a function of time and is shown as symbols in Fig. 5. The data for I0 = 1 and 10 W m−2 is truncated at 300 s, after which the network surface becomes rough, making it difficult to obtain precise values of zf. To aid the interpretation of the data, we also plot the predicted heights of the polymer network in the absence of diffusion (dashed lines), which are obtained by fitting (25) to the first few data points of each experiment, using ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = 4.05 mm−1, ϕc = 0.05, and treating the effective rate constant K as a fitting parameter; we find K ≃ 0.015 m2 J−1.
= 4.05 mm−1, ϕc = 0.05, and treating the effective rate constant K as a fitting parameter; we find K ≃ 0.015 m2 J−1.
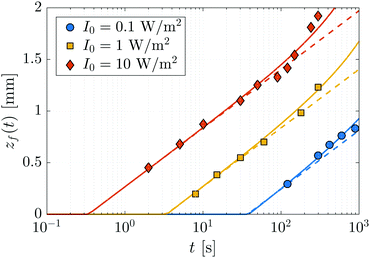 |
| | Fig. 5 Evolution of the height zf of a polymer network grown from a monomer bath by FPP as a function of the incident light intensity I0. The temperature of the bath is held at T = 65 °C. Symbols correspond to experimental data. In the absence of monomer diffusion, the height of the network grows logarithmically in time according to (25), shown as dashed lines. The departure of the data from the logarithmic curves is due to the onset of diffusion-induced swelling. The solid lines are numerical fits of the FPP-swelling model given by (19)–(23). | |
Fig. 5 shows that the extent of swelling for a fixed time t, as measured relative to the unswollen network height, increases with the incident radiation intensity, I0. For medium to high-intensity light, I0 = 1, 10 W m−2, the growth of the polymer network can be decomposed into two main regimes. First, there is a reaction-dominated regime, whereby the front position evolves according to the logarithmic kinetics associated with an absence of monomer diffusion. As the growth of the polymer network slows, a second, diffusion-dominated regime is entered. Here, monomer diffusion leads to substantial swelling and a marked departure from the logarithmic kinetics observed in the first regime. For low-intensity light, I0 = 0.1 W m−2, these two regimes are difficult to distinguish because swelling occurs early in the growth process due to the slow conversion of monomer.
A useful approximation for the network height zf can be derived by first noting that the two growth regimes shown in Fig. 5 indicate that monomer conversion and diffusion can initially occur on vastly different time scales,35 with diffusion being the slower process. By exploiting this separation of time scales in the FPP-swelling model (19)–(23), the height of the polymer network can be approximated as (see ESI† for details)
| | zf(t) ≃ ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −1 −1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(t/τi) + (1/2) log(t/τi) + (1/2)![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1(t − τi), D0m−1(t − τi), | (26) |
where
τi ≃
τ(0)i. Thus, the observed height
zf(
t) can be decomposed into the sum of the unswollen height,
z(0)f(
t) =
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log(
t/
τi), and a diffusive correction accounting for changes in the height due to swelling,
z(s)f(
t) = (1/2)
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1
D0m−1(
t −
τi). The latter contribution to
zf shows that, for a fixed time
t, an increase in the incident light intensity,
I0, will drive an increase in swelling due to the reduction in the induction time. In other words, the polymer network undergoes a greater expansion as
I0 is increased because it has existed for a longer period of time and the monomer has had more time to diffuse into it.
The onset of swelling can be estimated from the rates at which the network grows by monomer conversion and expands due to monomer uptake. The rate of network growth is given by dz(0)f/dt = (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) t)−1 and decreases with time. The rate of expansion can be calculated as dz(s)f/dt = (1/2)
t)−1 and decreases with time. The rate of expansion can be calculated as dz(s)f/dt = (1/2)![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1, which is constant in time. The onset of swelling will occur when these two rates become comparable, i.e., when ts ∼ 2m
D0m−1, which is constant in time. The onset of swelling will occur when these two rates become comparable, i.e., when ts ∼ 2m![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −2D0−1. Thus, the onset of swelling is independent of the incident light intensity, a feature which is experimentally confirmed in Fig. 5; substantial deviations from the unswollen height profile begin to occur at roughly the same time, ts ≃ 300 s.
−2D0−1. Thus, the onset of swelling is independent of the incident light intensity, a feature which is experimentally confirmed in Fig. 5; substantial deviations from the unswollen height profile begin to occur at roughly the same time, ts ≃ 300 s.
To obtain an estimate of the diffusion coefficient, the full FPP-swelling model (19)–(23) is fit to the experimental data. We set Vm = ΩmNA = 525 × 10−6 m3 mol−1 to be consistent with the value used in the swelling experiments with static networks. The effective reaction constant is obtained from earlier fits using the unswollen height (25) and set to K = 0.015 m2 J−1. Satisfactory agreement with the data is obtained using a chain length of m = 5 and a diffusivity exponent of a = 5. By treating D0 as a fitting parameter, we find that D0 ≃ 0.08 mm2 min−1, which is roughly four times smaller than the self-diffusion coefficient of water74 (D0 ≃ 0.34 mm2 min−1). The results from the fit are shown as solid lines in Fig. 5, in excellent agreement with experiment.
Numerical simulations (details in ESI†) are used to examine the composition of the network and the stresses that are generated during its growth. Fig. 6(a), (c) and (e) show, in the case of I0 = 1 W m−2, the spatial variation of the network fraction ϕn (solid line), the network fraction without diffusion ϕ(0)n (dashed line), the excess monomer fraction Δϕm (dashed-dotted line), and the local stretch λ (dotted line) at times t = 26, 150, and 680 s, corresponding to zf = 0.5, 1.0, and 1.5 mm, respectively. The excess monomer is defined as the net amount of monomer that has accumulated in a volume element due to diffusion and can be calculated via
| | 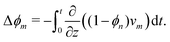 | (27) |
As the system transitions from a reaction-dominated (
Fig. 6(a)) to diffusion-dominated (
Fig. 6(e)) regime, the gradient of the network fraction undergoes a substantial decrease, resulting in a broader conversion profile compared to when diffusion is absent. Interestingly, both positive and negative monomer excesses can develop within the polymer network, as shown in
Fig. 6(e). The region near the illuminated surface (
z < 0.6 mm) experiences a net accumulation of monomer, which is exactly offset by a net depletion of monomer away from the illuminated surface (
z > 0.6 mm). Thus, substantial monomer transport occurs behind the polymerisation front,
zf, which is made possible by the low value of the critical conversion fraction
ϕc, and is driven by the stronger gradients in composition (chemical potential) in this region. Despite the depletion of monomer, the network still experiences an overall stretch (
λ > 1) due to the extensional flow that arises from the conservation of mass. As
Fig. 6(b), (d) and (f) show, the network velocity has a positive gradient, leading to stretching of material elements; see
(22). Thus, while monomer diffusion leads to an expansion of the network, this is not caused by swelling in the traditional sense.
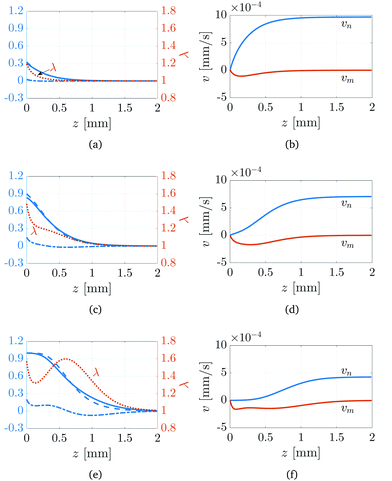 |
| | Fig. 6 Numerical simulation of the FPP-swelling model (19)–(23) when the incident light intensity is I0 = 1 W m−2. The solutions are shown at times t = 26 s (panels (a) and (b)), 150 s (panels (c) and (d)), and 680 s (panels (e) and (f)), corresponding to zf = 0.5, 1.0, and 1.5 mm, respectively. Panels (a), (c) and (e) show the network fraction ϕn (solid line), unswollen network fraction ϕ(0)n (dashed line), and the excess monomer fraction Δϕm (dashed-dotted line). Panels (b), (d) and (f) show the monomer and network velocity. | |
The non-monotonicity of the local stretch λ shown in Fig. 6(e) is directly related to the transition between reaction- and diffusion-dominated regimes. During the reaction-dominated regime (Fig. 6(a)), diffusion is negligible except in a thin boundary layer near the illuminated surface, leading to a localised expansion of the network. However, as the system transitions into and later evolves in the diffusion-dominated regime (Fig. 6(c) and (e)), significant expansion of the network occurs in regions away from the illuminated surface behind the polymerisation front zf, resulting in λ developing a second maximum.
Fig. 7 provides a detailed examination of the conversion profiles and the elastic stresses within the polymer network for the three incident light intensities I0. Panels (a)–(c) and (d)–(f) show the results at a fixed time of t = 300 s and a fixed solid height of zf = 1.5 mm, respectively. In each panel, the effective stress, normalised by its maximal value σmax, is superposed on the conversion profile. Recall from (11) that the effective stress σen also corresponds to the magnitude of in-plane lateral compressive stresses.
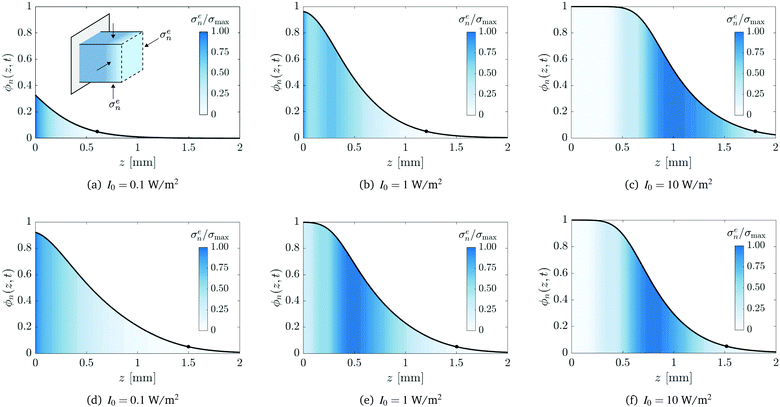 |
| | Fig. 7 Conversion profiles at a fixed time of t = 300 s (panels (a–c)) and at a fixed network height zf = 1.5 mm (panels (d–f)). Superposed is the effective stress σen normalised by its maximal value σmax. The effective stress also corresponds to the magnitude of in-plane lateral compressive stresses, shown in the inset of panel (a). The circle corresponds to the position of the polymerisation front zf(t). Values for the maximal effective stress, in units of MPa, are σmax = 1.7 (a), 2.0 (b), 0.16 (c), 9.4 (d) 1.2 (e), and 0.20 (f). | |
For a fixed exposure time (Fig. 7(a)–(c)), an increase in the light intensity leads to a corresponding increase in the overall extent of conversion, as expected. However, the distribution of the stress within the network is significantly altered as the intensity increases. For low-intensity light (I0 = 0.1 W m−2), the induction time and the time scale of diffusion are of the same order of magnitude and thus monomer can diffuse into the network as soon as it is created. Consequently, the stress is localised near the illuminated surface and we find that σmax = 1.7 MPa. For high-intensity light (I0 = 10 W m−2), substantial conversion can occur before monomer diffusion takes place, resulting in a fully developed conversion profile with a stress-free region near the illuminated surface. In this case, the stress is localised to the interfacial layer behind the solidification front that separates liquid-rich bath from fully converted solid. In this case, σmax = 0.16 MPa. FPP with medium-intensity light (I0 = 1 W m−2) gives rise to an intermediate case where stress accumulates near the illuminated surface and the interfacial layer. Furthermore, medium-intensity light is found to produce the highest stress of the three cases, σmax = 2.0 MPa; this is because conversion is slow enough for diffusion to take place immediately, yet fast enough to create a substantial polymer network with strong gradients in the chemical potential.
Similar trends are seen when the intensity of radiation is increased for fixed solid height zf (Fig. 7(d)–(f)). In particular, there is a corresponding increase in the overall conversion and the localisation of the stress shifts from the illuminated surface to the interfacial region just behind the solidification front. However, in this case, there is a monotonic decrease in the stress as the intensity increases; we find σmax = 9.4, 1.2, and 0.2 MPa for I0 = 0.1, 1, and 10 W m−2, respectively. The inverse proportionality between σmax and I0 is a consequence of the additional exposure time that is required to create a polymer network of a given height when the intensity is decreased, hence allowing more time for monomer to diffuse into and deform the network.
5. Conclusions
We examine the role of monomer diffusion in frontal photopolymerisation (FPP), combining patterning experiments and theory. We find that the swelling of (static) polymer networks is generally well described by a poroelastic model based on the classical theory of swelling hydrogels, enabling the quantification of monomer diffusion kinetics as a function of the network conversion and temperature.
The role of monomer diffusion during FPP was then investigated as a function of light intensity. By contrast with the logarithmic growth kinetics observed in the absence of monomer diffusion,26,35 for a fixed exposure time, network swelling was found to increase with the light intensity due to the earlier creation of the polymer network. However, for a fixed network height, swelling was found to decrease with increasing light intensity due to the increased velocity of the polymerisation front.
A novel model of FPP, incorporating mass transport and the mechanical response of the polymer network, was found to describe all experimental data obtained using a commercial thiol–ene formulation (NOA81). By accounting for heat generation and transport36 or multiple reaction steps,72 the applicability of the model can be extended to a range of non-commercial thiol–ene and acrylate systems, as previously demonstrated.27 Significantly, the model yields an estimate of the time at which swelling is relevant, and is found to agree with experiments. From a patterning perspective, this estimate provides a useful guideline for the maximum exposure time that will result in a stress-free solid, which can otherwise cause delamination or other undesirable effects. The model provides insight into how the monomer-to-polymer conversion fraction and distribution of elastic stresses within the network vary with experimental parameters. It can therefore serve as a useful predictive tool and facilitate the fabrication of gradient materials with highly tuned mechanical properties and well-controlled internal stresses.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was supported by the Engineering and Physical Sciences Research Council (EPSRC) Manufacturing with Light Grant EP/L022176/1. MH has been partially funded by the CERCA Programme of the Generalitat de Catalunya.
References
-
L. Columbus, 2015 Roundup of 3D Printing Market Forecasts and Estimates, 2015, Available online: http://www.forbes.com/sites/louiscolumbus/2015/03/31/2015-roundup-of-3d-printing-market-forecasts-and-estimates, accessed June 2017.
- D. B. Kolesky, R. L. Truby, A. Gladman, T. A. Busbee, K. A. Homan and J. A. Lewis, Adv. Mater., 2014, 26, 3124–3130 CrossRef CAS PubMed.
- S. V. Murphy and A. Atala, Nat. Biotechnol., 2014, 32, 773–785 CrossRef CAS PubMed.
- J.-F. Xing, M.-L. Zheng and X.-M. Duan, Chem. Soc. Rev., 2015, 44, 5031–5039 RSC.
- A. I. Shallan, P. Smejkal, M. Corban, R. M. Guijt and M. C. Breadmore, Anal. Chem., 2014, 86, 3124–3130 CrossRef CAS PubMed.
- J. A. Lewis and B. Y. Ahn, Nature, 2015, 518, 42–43 CrossRef CAS PubMed.
- M. Zarek, M. Layani, I. Cooperstein, E. Sachyani, D. Cohn and S. Magdassi, Adv. Mater., 2015, 28, 4449–4454 CrossRef PubMed.
- K. Sun, T.-S. Wei, B. Y. Ahn, J. Y. Seo, S. J. Dillon and J. A. Lewis, Adv. Mater., 2013, 25, 4539–4543 CrossRef CAS PubMed.
- F. Ning, W. Cong, J. Qiu, J. Wei and S. Wang, Composites, Part B, 2015, 80, 369–378 CrossRef CAS.
- R. Goodridge, C. Tuck and R. Hague, Prog. Mater. Sci., 2012, 57, 229–267 CrossRef CAS.
- J. R. Tumbleston, D. Shirvanyants, N. Ermoshkin, R. Janusziewicz, A. R. Johnson, D. Kelly, K. Chen, R. Pinschmidt, J. P. Rolland, A. Ermoshkin, E. T. Samulski and J. M. DeSimone, Science, 2015, 347, 1349–1352 CrossRef CAS PubMed.
- C. Decker, Prog. Polym. Sci., 1996, 21, 593–650 CrossRef CAS.
- E. Andrzejewska, Prog. Polym. Sci., 2001, 26, 605–665 CrossRef CAS.
- M. V. Turturro and G. Papavasiliou, J. Biomater. Sci., Polym. Ed., 2012, 23, 917–939 CrossRef CAS PubMed.
- M. V. Turturro, D. M. Rendón, F. Teymour and G. Papavasiliou, Macromol. React. Eng., 2013, 7, 107–115 CrossRef CAS.
- A. Vitale, M. G. Hennessy, O. K. Matar and J. T. Cabral, Macromolecules, 2015, 48, 198–205 CrossRef CAS.
- D. Chandra and A. J. Crosby, Adv. Mater., 2011, 23, 3441–3445 CrossRef CAS PubMed.
- J. Lacombe and C. Soulié-Ziakovic, Polym. Chem., 2017, 8, 1129–1137 RSC.
- J. H. Kim, K. Je, T. S. Shim and S.-H. Kim, Small, 2017, 13, 1603516 CrossRef PubMed.
- M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001 CrossRef.
- M. Quesada-Pérez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 10536–10547 RSC.
- T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798 CrossRef CAS.
- J. Dervaux and M. B. Amar, Annu. Rev. Condens. Matter Phys., 2012, 3, 311–332 CrossRef CAS.
- A. Vitale and J. T. Cabral, Materials, 2016, 9, 760 CrossRef PubMed.
- J. T. Cabral, S. D. Hudson, C. Harrison and J. F. Douglas, Langmuir, 2004, 20, 10020–10029 CrossRef CAS PubMed.
- J. T. Cabral and J. F. Douglas, Polymer, 2005, 46, 4230–4241 CrossRef CAS.
- A. Vitale, M. G. Hennessy, O. K. Matar and J. T. Cabral, Adv. Mater., 2015, 27, 6118–6124 CrossRef CAS PubMed.
- L. L. Lewis, C. S. Debisschop, J. A. Pojman and V. A. Volpert, J. Polym. Sci., Part A-1: Polym. Chem., 2005, 43, 5774–5786 CrossRef CAS.
- C. A. Spade and V. A. Volpert, Math. Comput. Modell., 1999, 30, 67–73 CrossRef.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS.
- S. A. Chester and L. Anand, J. Mech. Phys. Solids, 2010, 58, 1879–1906 CrossRef CAS.
- C. W. MacMinn, E. R. Dufresne and J. S. Wettlaufer, Phys. Rev. Appl., 2016, 5, 044020 CrossRef.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Phys. Rev. Appl., 2016, 6, 064010 CrossRef.
- J. A. Warren, J. T. Cabral and J. F. Douglas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 021801 CrossRef PubMed.
- M. G. Hennessy, A. Vitale, O. K. Matar and J. T. Cabral, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062402 CrossRef PubMed.
- M. G. Hennessy, A. Vitale, J. T. Cabral and O. K. Matar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022403 CrossRef PubMed.
- N. B. Cramer, T. Davies, A. K. O’Brien and C. N. Bowman, Macromolecules, 2003, 36, 4631–4636 CrossRef CAS.
- M. D. Goodner and C. N. Bowman, Chem. Eng. Sci., 2002, 57, 887–900 CrossRef CAS.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3673–3680 CrossRef CAS.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3681–3687 CrossRef CAS.
- A. K. O’Brien and C. N. Bowman, Macromol. Theory Simul., 2006, 15, 176–182 CrossRef.
- D. Dendukuri, P. Panda, R. Haghgooie, J. M. Kim, T. A. Hatton and P. S. Doyle, Macromolecules, 2008, 41, 8547–8556 CrossRef CAS.
- O. Okay and C. Bowman, Macromol. Theory Simul., 2005, 14, 267–277 CrossRef CAS.
- G. Terrones and A. J. Pearlstein, Macromolecules, 2003, 36, 6346–6358 CrossRef CAS.
- A. K. O’Brien and C. N. Bowman, Macromolecules, 2003, 36, 7777–7782 CrossRef.
- M. Belk, K. G. Kostarev, V. Volpert and T. M. Yudina, J. Phys. Chem. B, 2003, 107, 10292–10298 CrossRef CAS.
- G. Terrones and A. J. Pearlstein, Macromolecules, 2004, 37, 1565–1575 CrossRef CAS.
- S. L. Simon, G. B. Mckenna and O. Sindt, J. Appl. Polym. Sci., 2000, 76, 495–508 CrossRef CAS.
-
D. A. Drew and S. L. Passman, Theory of Multicomponent Fluids, Springer, 2006, vol. 135 Search PubMed.
- C. Liu and N. J. Walkington, Arch. Ration. Mech. Anal., 2001, 159, 229–252 CrossRef.
- Y. Hyon, D. Y. Kwak and C. Liu, Discret. Cont. Dyn. Syst., 2010, 26, 1291–1304 CrossRef.
- V. Camacho, A. Fogelson and J. Keener, SIAM J. Appl. Math., 2016, 76, 341–367 CrossRef.
- H. Zhang and M. C. Calderer, SIAM J. Appl. Math., 2008, 68, 1641–1664 CrossRef.
-
O. Coussy, Poromechanics, John Wiley & Sons, 2004 Search PubMed.
-
P. Howell, G. Kozyreff and J. Ockendon, Applied Solid Mechanics, Cambridge University Press, 2009, vol. 43 Search PubMed.
- M. Tokita and T. Tanaka, J. Chem. Phys., 1991, 95, 4613–4619 CrossRef CAS.
- M. Engelsberg and W. Barros Jr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062602 CrossRef CAS PubMed.
- C. A. Grattoni, H. H. Al-Sharji, C. Yang, A. H. Muggeridge and R. W. Zimmerman, J. Colloid Interface Sci., 2001, 240, 601–607 CrossRef CAS PubMed.
-
M. Doi, Introduction to Polymer Physics, Oxford University Press, 1996 Search PubMed.
- A. D. Drozdov and J. de C. Christiansen, Int. J. Solids Struct., 2013, 50, 1494–1504 CrossRef CAS.
- J. Li, Y. Hu, J. J. Vlassak and Z. Suo, Soft Matter, 2012, 8, 8121–8128 RSC.
- Y. Liu, H. Zhang, J. Zhang and Y. Zheng, Int. J. Solids Struct., 2016, 80, 246–260 CrossRef CAS.
- M. G. Hennessy, G. L. Ferretti, J. T. Cabral and O. K. Matar, J. Colloid Interface Sci., 2017, 488, 61–71 CrossRef CAS PubMed.
- N. L. Thomas and A. Windle, Polymer, 1982, 23, 529–542 CrossRef CAS.
- G. Rossi, P. Pincus and P.-G. De Gennes, Europhys. Lett., 1995, 32, 391 CrossRef CAS.
- L. Masaro and X. X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
-
J. A. Pojman, Polymer Science: A Comprehensive Reference, Elsevier, Amsterdam, 2012, pp. 957–980 Search PubMed.
- Z. Zhao, J. Wu, X. Mu, H. Chen, H. J. Qi and D. Fang, Sci. Adv., 2017, 3, e1602326 CrossRef PubMed.
- F. Larché and J. W. Cahn, Acta Metall., 1973, 21, 1051–1063 CrossRef.
- C. H. Wu, J. Mech. Phys. Solids, 2001, 49, 1771–1794 CrossRef.
- J. Chakraborty, C. P. Please, A. Goriely and S. J. Chapman, Int. J. Solids Struct., 2015, 54, 66–81 CrossRef CAS.
- A. R. Purnama, M. G. Hennessy, A. Vitale and J. T. Cabral, Polym. Int., 2017, 66, 752–760 CrossRef CAS.
-
O. Gonzalez and A. M. Stuart, A First Course in Continuum Mechanics, Cambridge University Press, 2008 Search PubMed.
-
O. Dietrich, Diffusion coefficients of water, 2015, http://dtrx.de/od/diff/, accessed June 2017.
Footnotes |
| † Electronic supplementary information (ESI) available: Complementary derivations and discussions. See DOI: 10.1039/c7sm01279a |
| ‡ Present address: Centre de Recerca Matemàtica, Campus de Bellaterra, Edifici C, 08193 Bellaterra (Barcelona), Spain. |
| § Present address: Department of Applied Science and Technology, Politecnico di Torino, 10129 Torino, Italy. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Alessandra
Vitale§
,
Alessandra
Vitale§
 ,
Omar K.
Matar
,
Omar K.
Matar
 and
João T.
Cabral
and
João T.
Cabral
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(g(χ)), where g is a piecewise linear polynomial with a kink at χg, which approximates detailed physico-chemical models of E(χ) near the glass transition.48 The parameter Emax = 187 MPa corresponds to the elastic modulus at χmax = 0.85. We find that g(χ) = 4.16(χ − χg) − 1.67 for χ < χg and g(χ) = 24.2(χ − χmax) for χ > χg, where χg = 0.77. The fitted curve is shown as the black line in Fig. 3.
exp(g(χ)), where g is a piecewise linear polynomial with a kink at χg, which approximates detailed physico-chemical models of E(χ) near the glass transition.48 The parameter Emax = 187 MPa corresponds to the elastic modulus at χmax = 0.85. We find that g(χ) = 4.16(χ − χg) − 1.67 for χ < χg and g(χ) = 24.2(χ − χmax) for χ > χg, where χg = 0.77. The fitted curve is shown as the black line in Fig. 3.

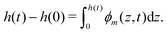
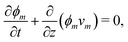
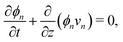
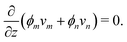
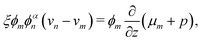
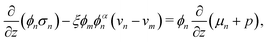
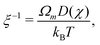
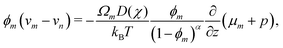
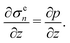
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , into elastic and mixing contributions,
, into elastic and mixing contributions, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e and
e and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix, depending only on the local stretch and composition, respectively:
mix, depending only on the local stretch and composition, respectively:![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (λ,ϕm,ϕn) = λ−1
(λ,ϕm,ϕn) = λ−1![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e(λ) +
e(λ) + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix(ϕm,ϕn).
mix(ϕm,ϕn).![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e is traditionally defined per unit reference (undeformed) volume rather than per current (deformed) volume.
e is traditionally defined per unit reference (undeformed) volume rather than per current (deformed) volume.
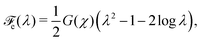
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) e/∂λ, yielding
e/∂λ, yielding![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix is obtained from the Flory–Huggins theory of polymer solutions59 and written as
mix is obtained from the Flory–Huggins theory of polymer solutions59 and written as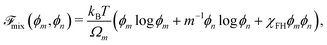
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix + ϕnΔ
mix + ϕnΔ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix, μn − μ0n =
mix, μn − μ0n = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix − ϕmΔ
mix − ϕmΔ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix, and Δ
mix, and Δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix = ∂
mix = ∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix/∂ϕm − ∂
mix/∂ϕm − ∂![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix/∂ϕn, which give
mix/∂ϕn, which give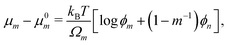
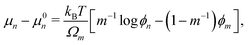
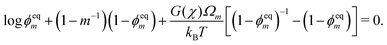
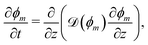
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is
is![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (ϕm) = D(χ)(1 − (1 − m−1)ϕm + βϕm[1 + (1 − ϕm)−2]).
(ϕm) = D(χ)(1 − (1 − m−1)ϕm + βϕm[1 + (1 − ϕm)−2]).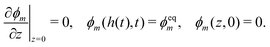
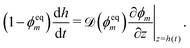

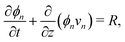
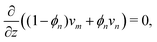
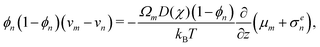
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−aχ). This form of diffusivity leads to an exponential permeability law, the consequences of which are explained in the ESI.†
exp(−aχ). This form of diffusivity leads to an exponential permeability law, the consequences of which are explained in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−
exp(−![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) z),
z),![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is the average attenuation coefficient of the mixture, assumed to be constant. Extending (21) to capture changes in
is the average attenuation coefficient of the mixture, assumed to be constant. Extending (21) to capture changes in ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) with composition is straightforward,26,34 but not needed here.
with composition is straightforward,26,34 but not needed here.
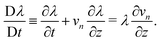
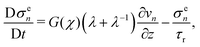
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−
exp(−![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) z)].
z)].![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(t/τ(0)i).
log(t/τ(0)i).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(1/(1 − ϕc)) is an induction time, corresponding to the finite amount of time that is required for the critical network fraction ϕc to first be exceeded. The logarithmic kinetics (25) imply that the propagation of polymerisation front and monomer conversion slow with time. This slowing is caused by the spatial decay of light intensity and it reflects the light-driven nature of the growth process. Eqn (24) and (25) have been shown to successfully capture FPP experiments carried out with this system near room temperature or up to 100 °C but sufficiently small times.16
log(1/(1 − ϕc)) is an induction time, corresponding to the finite amount of time that is required for the critical network fraction ϕc to first be exceeded. The logarithmic kinetics (25) imply that the propagation of polymerisation front and monomer conversion slow with time. This slowing is caused by the spatial decay of light intensity and it reflects the light-driven nature of the growth process. Eqn (24) and (25) have been shown to successfully capture FPP experiments carried out with this system near room temperature or up to 100 °C but sufficiently small times.16
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = 4.05 mm−1, ϕc = 0.05, and treating the effective rate constant K as a fitting parameter; we find K ≃ 0.015 m2 J−1.
= 4.05 mm−1, ϕc = 0.05, and treating the effective rate constant K as a fitting parameter; we find K ≃ 0.015 m2 J−1.

![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(t/τi) + (1/2)
log(t/τi) + (1/2)![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1(t − τi),
D0m−1(t − τi),![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(t/τi), and a diffusive correction accounting for changes in the height due to swelling, z(s)f(t) = (1/2)
log(t/τi), and a diffusive correction accounting for changes in the height due to swelling, z(s)f(t) = (1/2)![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1(t − τi). The latter contribution to zf shows that, for a fixed time t, an increase in the incident light intensity, I0, will drive an increase in swelling due to the reduction in the induction time. In other words, the polymer network undergoes a greater expansion as I0 is increased because it has existed for a longer period of time and the monomer has had more time to diffuse into it.
D0m−1(t − τi). The latter contribution to zf shows that, for a fixed time t, an increase in the incident light intensity, I0, will drive an increase in swelling due to the reduction in the induction time. In other words, the polymer network undergoes a greater expansion as I0 is increased because it has existed for a longer period of time and the monomer has had more time to diffuse into it.
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) t)−1 and decreases with time. The rate of expansion can be calculated as dz(s)f/dt = (1/2)
t)−1 and decreases with time. The rate of expansion can be calculated as dz(s)f/dt = (1/2)![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) D0m−1, which is constant in time. The onset of swelling will occur when these two rates become comparable, i.e., when ts ∼ 2m
D0m−1, which is constant in time. The onset of swelling will occur when these two rates become comparable, i.e., when ts ∼ 2m![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) −2D0−1. Thus, the onset of swelling is independent of the incident light intensity, a feature which is experimentally confirmed in Fig. 5; substantial deviations from the unswollen height profile begin to occur at roughly the same time, ts ≃ 300 s.
−2D0−1. Thus, the onset of swelling is independent of the incident light intensity, a feature which is experimentally confirmed in Fig. 5; substantial deviations from the unswollen height profile begin to occur at roughly the same time, ts ≃ 300 s.