The short device lifetimes of blue PhOLEDs: insights into the photostability of blue Ir(III) complexes

Abstract

Using Ir(III) complexes as dopants in phosphorescent organic light-emitting diodes (PhOLEDs) is the most successful strategy to attain long-lasting and highly-performant electroluminescent devices. Whilst highly efficient blue PhOLEDs are accessible, their limited operational lifetimes still restraint their practical use in lighting and displays. These short lifetimes are directly related to the low intrinsic photostability of blue Ir(III) complexes. This work uses first principles to unveil the mechanisms of degradation of blue phosphors arising from energetically hot excited states (≅6.0 eV), and to propose a strategy for improving the stability of blue phosphors.

---

Introduction

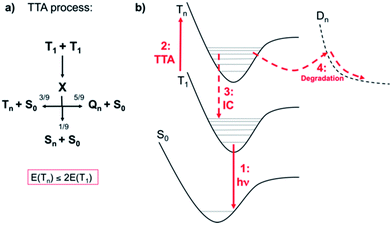
Phosphorescent-based OLEDs (PhOLEDs), the so-called second generation of OLEDs, are the most widespread electroluminescent devices since they can attain low power consumption and record external quantum efficiencies.¹ Electroluminescence in PhOLEDs takes place from the triplet excited states of the organometallic complexes, i.e., typically Ir(III) and Pt(II) complexes, which enables the conversion of nearly 100% of the excitons created into photons.² Besides high efficiencies, it is essential that the devices possess long-lived operational stability.³ In contrast to red or green PhOLEDs, the fabrication of a long-lasting blue PhOLED has not been achieved yet, which has consequently limited the large-scale commercialization of PhOLEDs. For both lighting and display applications, operational lifetimes of T₉₅ > 10000 h are mandatory³ (where T_X is the time under constant current operation in which the luminance decreases to X% of its initial value). To illustrate the size of the gap to be bridged, state-of-the-art blue^4,5 and greenish-blue^6,7 PhOLEDs are characterized by T₈₀ of <10 h and <160 h, respectively, values clearly insufficient for practical applications. Degradation in PhOLEDs manifests itself through the formation of dark spots, the occurrence of a catastrophic failure and/or the decrease of the overall luminance during continuous operation.⁸ Whilst the dark spots and the catastrophic failure can be minimized by an optimal device fabrication, the long-term decrease of the overall luminance during prolonged operation is the major obstacle for the commercial exploitation of PhOLEDs, especially for the blue ones. Intrinsic chemical degradation of both host and dopant molecules is responsible of harming device's operational lifetimes.⁹ The chemical degradation products may act as charge traps, nonradiative recombination sites and/or luminescence quenchers, therefore leading to a significant luminance loss. During the last decades, many efforts have been devoted to unravel the possible intrinsic degradation mechanisms induced by electro- or photochemical reactions within a PhOLED stack.^8,10 The elucidation of the chemical degradation products as well as of the related mechanisms poses, however, significant experimental challenges due to (i) the limited amount of defects on an aged PhOLED stack, (ii) the difficult isolation of the degradation products from the organic semiconductor layers, and (iii) the intricate competition between multiple non-desired reactions (including exciton and charge carrier induced decomposition), that leads to a broad variety of chemical defects. Despite these inconveniences, multiple analytical techniques that provide insights into the chemical degradation of thin organic semiconductor films are nowadays available.⁸ One of the most powerful methods is the matrix assisted laser desorption/ionization time-of-flight mass spectroscopy (MALDI-TOF-MS) method,¹¹ which allows trace analysis of organic layers¹² or even entire devices.¹³ This technique enabled the identification of relevant degradation products for host materials as well as for phosphorescent dopants. This knowledge has paved the way to the development of host:dopant matching design principles and has therefore significantly contributed to the improvement of the operational stability of PhOLEDs materials. Nevertheless, in the majority of the cases, the actual degradation mechanisms remain unknown and thus, quantum chemical investigations can shed light into the structural features, nature of the electronically excited states and excited-state reactivity of host and dopant materials. However, to date, these investigations are scarce and limited to very specific cases.^14,15 The present work unveils, from first principles, relevant mechanisms of degradation of state-of-the-art blue Ir(III) phosphors due to photodechelation reactions. Beyond disclosing these mechanisms and providing paths for improving the design of Ir-based phosphors, this contribution illustrates how quantum chemical modeling may largely impact the field of blue Ir(III) dopants.

The degradation pathways of Ir(III) phosphors upon PhOLED operation root on parasitic annihilation processes between excited states (i.e., exciton-polaron and/or exciton–exciton) that lead to the formation of hot excited states (that is, highly energetic excited states at ≅6.0 eV above the ground-state).¹⁶ Among all possible mechanisms, triplet–triplet annihilation (TTA) is of uttermost relevance for PhOLEDs. TTA processes in PhOLEDs are thought to be mainly due to dopant:dopant aggregation in the emissive layer (EML) and occur via a diffusion-based Dexter transfer mechanism.¹⁷ In a TTA process (see Scheme 1a), according to spin statistics, one can generate 1/9 of hot singlet excited states (S_n) per 3/9 and 5/9 of hot triplet (T_n) and quintet (Q_n) states, respectively. The quintet excited states are, according to our calculations, energetically not reachable for Ir(III) complexes (exemplarily, the first quintet state for the prototypical compound 1 (see Chart 1) is located 6.11 eV above the S₀ energy at the Franck–Condon point) and, therefore, they do not contribute to the global deactivation dynamics. Hence, due to the nonradiative quenching of at least half of the initial T₁ states, TTA leads to an effective quenching of photoluminescence in PhOLEDs (also known as roll-off effect¹⁷) and to the formation of hot T_n states, since the 1/9 of S_n also lead to T_n states after efficient intersystem crossings (ISC) processes. Indeed, ISC processes occur typically with near-unity quantum yield for Ir(III) complexes.¹⁸ Having in mind that the T₁ energy for a typical deep-blue emitter is ca. 3 eV, hot T_n states of up to 6 eV can be generated through TTA (the energetic requirement for TTA is E(T_n) ≤ 2E(T₁)). The Jablonski diagram including the relevant excited states and processes is presented in Scheme 1b. While the vast majority of hot states will rapidly decay back nonradiatively¹⁶ (i.e., T_n → T₁, process 3 in Scheme 1b), those which are in a reactive excited vibrational state may lead to dissociative states (D_n, process 4 in Scheme 1b) and eventually yield the degradation of the emissive complexes. Typical bond dissociation energies of weak bonds in phosphors (see the discussion below) are well below the energy of the hot states but they are higher in energy than T₁. Therefore, it is clear that TTA is the major source of chemical degradation in PhOLEDs. We underline that often unexpected degradation events happen, since it is common that excited state reactivity greatly differs from its ground state counterpart and additionally, some groups in specific environments are more susceptible to e.g., nucleophilic substitution reactions. One typical example is the lability of the C–F bonds of the (4,6-difluorophenyl)pyridinato units upon PhOLED operation,¹⁹ which can not be explained in terms of the ground-state thermodynamics of the C(sp³)-fluorine bond, which is one of the strongest known single bonds. In short, if one aims to minimize the generation of degradation products in PhOLEDs, two possible ways are available: reducing TTA or controlling the excited state reactivity by phosphor design strategies. Efficient ways to reduce TTA processes include: (i) controlling the dopant:dopant aggregation at the EML, and (ii) attaining shorter triplet excited state lifetimes. Both approaches are challenging to implement in PhOLEDs, since obtaining triplet lifetimes of Ir(III) complexes shorter than a few μs is difficult and controlling aggregation on the vacuum deposited EML is hardly achievable.

Scheme 1 (a) TTA process and its energetic requirement. (b) Jablonski diagram of the relevant process upon PhOLED operation: (1) radiative deactivation from the lowest triplet excited state T₁, (2) TTA annihilation process between two T₁ states, (3) internal conversion (IC) and vibrational relaxation from the hot T_n state to the well of T₁, (4) population of dissociative states leading to ligand dissociation reactions.

Chart 1 Chemical structure of complexes 1–4.

In this contribution we focus on disentangling the excited state reactivity for blue Ir(III) phosphors and we explain, for the first time, why blue Ir(III) dopants are more prone to degradation than the green and red ones. We next provide some phosphor design principles to limit the formation of degradation products.

Results and discussion

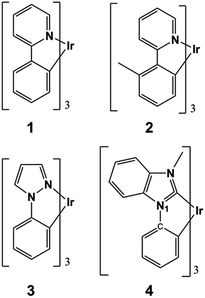
Chart 1 gathers the homoleptic Ir(III) complexes studied here, including the green fac-Ir(ppy)₃ (where ppy = phenylpyridine) and fac-Ir(mppy)₃ (where mppy = methylphenylpyridine) complexes (1 and 2, respectively) and the blue fac-Ir(ppz)₃ (where ppz = phenylpyrazole) and fac-Ir(pmb)₃ (where pmb = 1-phenyl-3-methylbenzimidazolyl) complexes (3 and 4, respectively). These complexes were selected due to the availability of experimental degradation studies and to unravel the intrinsic differences in the excited-state reactivities of blue and non-blue complexes. Experimentally, the blue complex 3 undergoes firstly dissociation of a ppz ligand and secondly it coordinates a host molecule when the device operates at moderate to high current levels.²⁰ As a result, an operational lifetime of T₉₅ < 1 h is obtained for this device. Oppositely, the green complex 1, under the same conditions, is much more photostable and its electroluminescence performances remain unchanged.²⁰ Despite the intrinsic photostability of 1, another group has reported some minor trace amounts of degradation products that involve the dissociation of the ppy cyclometallating ligand.²¹ For complex 2, the photodegradation products of aged devices have not been experimentally characterized, but when 2 is photodegradated in inert solution it undergoes enhanced deterioration processes as compared with 1,²² likely involving ligand dissociation as well. Finally, the use of N-heterocyclic carbene (NHC) ligands is beneficial not only to attain highly efficient deep-blue Ir(III) emitters but also to potentially increase their intrinsic photostabilities. Blue PhOLED devices using tris(bidentate) NHC Ir(III) complexes, such as e.g., complex 4, are known to present increased device lifetimes compared to other blue Ir(III) emitters (e.g., complex 3).²³ Although degradation is still observed in these devices, the actual degradation products have not been indentified to date. The first important criterion that should be met to avoid ligand dissociation is that the reaction from the hot excited states should be thermodynamically unfeasible. In Table 1 are listed the computed Gibbs free energies for the homolytic ligand dissociation reactions of complexes 1–4 (see computational details below). For the green complex 1, a ΔG_react of 5.01 eV is obtained. This value is nearly isoenergetic to the energy of a green hot state (which is ca. 2E(T₁) ≅ 5.0 eV) and therefore, ppy dissociation may occur only in exceptional occasions (as the minor traces experimentally detected corroborate²²). Complex 2 possesses a smaller ΔG_react value than 1 (4.80 eV), and thus it is more prone to ligand dissociation, in agreement with experimental evidences. For complex 2, another possible degradation mechanism may arise from the dissociation of a methyl group (see reaction 2′ in Table 1). Although this dissociation reaction is thermodynamically more feasible and might compete to ppy dissociation, it is likely that the latter process dominates due to the lability of the ligand dissociation in the excited states of Ir(III) complexes (see below). In the case of the blue complexes, their ΔG_react values for the photodechelation reactions (reactions 3 and 4 in Table 1) are well below the energy of a blue hot state (which is ca. 2E(T₁) ≅ 6.0 eV) and thus, their ligand dissociation reaction are in principle energetically feasible. In the case of 3 the ΔG_react value is 4.2 eV only, partly explaining the extremely fast device degradation observed experimentally.²⁰ Additionally, for 4 we explored the possibility of the self-fragmentation reaction of the pmb ligand through the N₁–C bond rupture (see Chart 1). This reaction is also thermodynamically feasible, see 4′ in Table 1 (ΔG_react = 4.6 eV).

Table 1 PWPB95-D3BJ Gibbs free ligand dissociation energies (eV) for complexes 1–5

Complex	Reaction	ΔGreact^a (2E(T1))
a Energetic threshold for a blue or a green hot state.
1	1: Ir(ppy)3 → [Ir(ppy)2]^· + [ppy]^·	5.01 (5.0)
2	2: Ir(mppy)3 → [Ir(mppy)2]^· + [mppy]^·	4.80 (5.0)
2	2′: Ir(mppy)3 → [Ir(mppy)2(ppy)]^· + [–CH3]^·	3.93 (5.0)
3	3: Ir(ppz)3 → [Ir(ppz)2]^· + [ppz]^·	4.18 (6.0)
4	4: Ir(bmp)3 → [Ir(bmp)2]^· + [bmp]^·	5.77 (6.0)
4	4′: Ir(bmp)3 → Ir(bmp)2(C6H5)^·(C8N2H7)^·	4.60 (6.0)
5	5:[Ir(mimf)(pzpyph^F)] → [Ir(mimf)]^+· + [(pzpyph^F)]^−·	10.00 (6.0)
5	5′:[Ir(mimf)(pzpyph^F)] → [Ir(pzpyph^F)]^· + [(mimf)]^·	9.06 (6.0)

---

While the thermodynamic criterion, i.e., ΔG_react > 2E(T₁), should always be met to completely avoid ligand dissociation, the excited state kinetic does play an important role in modulating the degree of degradation for complexes that do not meet such criterion. As mentioned above, the vast majority of hot T_n states rapidly decay back nonradiatively recovering the T₁ geometry. The T₁ state is usually the ³MLCT state and displays a pseudo-octahedral coordination environment (see Scheme 2b). Therefore, it seems very unlikely that ligand dissociation (which involves the breaking of two bonds, i.e., Ir–¹C and Ir–¹N) will take place at the ³MLCT structure. In this regard, spectroscopic²⁴ and computational^25–27 studies confirmed the active role of metal centred triplet excited states (³MC, see Scheme 2b) in the excited state dynamics of Ir(III) complexes, especially for blue emitters. Importantly, the ³MC state can be thermally populated from the ³MLCT state. In Scheme 2a, these pathways are represented. The pseudo-octahedral Ir(III) complexes at their T₁ geometry need to surpass a barrier (TS in Scheme 2a) to attain the ³MC state geometry. This state usually displays a trigonal bipyramid arrangement, where one iridium-heteroatom single bond is broken (see Scheme 2b). After population of the ³MC well, two processes might occur: (i) reversible return to the ³MLCT well; or (ii) irreversible radiationless recovery of the ground state (¹GS) geometry through the ¹GS/³MC minimum energy crossing point (MECP).²⁸ The MECP geometry usually exhibits a further distorted trigonal bipyramid arrangement. This kinetic scenario can be summarized as:²⁵

³MLCT⇋³MC → ¹GS. (1)

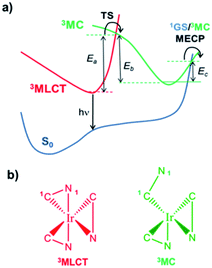Scheme 2 (a) Nonradiative pathways involving the thermal population of ³MC states for Ir(III) complexes. (b) Typical coordination environments for Ir(III) complexes at their ³MLCT and ³MC structures.

At room temperature (RT), ³MLCT − ³MC equilibration occurs for many Ir(III) complexes.²⁷ This equilibrium is controlled by the magnitude of the activation barriers (E_a, E_b and E_c in Scheme 2a). A straightforward approach to prevent the thermal population of the ³MC is to maximize the E_a value. In Table 2 are tabulated the computed E_a, E_b and E_c values for complexes 1–4 (see computational details). In the blue complex 3, the ³MC state is adiabatically located lower in energy than the emissive ³MLCT state. Additionally it is accessed in a barrierless manner, since no TS is found along the ³MLCT → ³MC reaction coordinate. Therefore, at RT, this nonradiative pathway is the most prominent deactivation channel for 3, and thus it leads experimentally to a complete quench of phosphorescence. Having in mind these kinetic considerations, and under steady-state conditions, TTA will predominantly take place in 3 between two ³MC states. Since, at the ³MC structure, one iridium–nitrogen single bond is already broken, the probability of reaching in the TTA process a reactive vibrational excited state leading to complete ppz dissociation (via the additional Ir–¹C bond cleavage, see Scheme 2b) appears quite likely for 3. This kinetic lability for 3 along with its small ΔG_react value are the ultimate reasons for its very low intrinsic photostability and its extremely fast degradation upon PhOLED operation. The use of a NHC carbene ligand (complex 4) has a great influence on the ³MLCT − ³MC equilibrium. Indeed, the combination of positive ΔE(³MC − ³MLCT) value and very large E_a value greatly prevents the formation of the ³MC state. The equilibration process between the ³MLCT and ³MC states is not plausible at RT and accordingly, TTA processes mainly occur between two ³MLCT states in the blue complex 4. Therefore, TTA will rarely lead to a direct bmp dissociation. These prognoses are in agreement with the experimental evidences, since pmb-based Ir(III) complexes do not exhibit photochemical geometrical isomerization, which also requires the formation of the ³MC state.²⁹ Nevertheless, since this process is thermodynamically feasible, one cannot fully disregard this possibility. Likewise, in view of its computed ΔG_react value, one cannot disregard either the pmb self-fragmentation reaction (4′ in Table 1). All these facts agree with the longer operational lifetimes of blue PhOLEDs using tris(bidentate) NHC Ir(III) complexes as dopant materials.²³ The green complexes (1–2) possess similar E_a values, which lie in between those of complexes 3 and 4. Their ΔE(³MC − ³MLCT) values are also positive, and, in the case of 1, quantitatively large. Under steady-state conditions, the ³MLCT − ³MC equilibration will be pushed towards the ³MLCT state at RT (especially for complex 1). Consequently, these green Ir(III) complexes are very well suited to avoid intrinsic degradation due to the confluence of favorable kinetic and thermodynamic features.

Table 2 PWPB95-D3BJ activation barriers (eV) for the temperature-dependent nonradiative channels (see Scheme 1a) and ³MLCT − ³MC adiabatic energy differences for 1–4

Complex	E a	E b	E c	ΔE(^3MC − ^3MLCT)
1	0.352	0.025	0.038	0.327
2	0.365	0.287	0.016	0.078
3	0.000	0.153	0.006	−0.153
4	0.638	0.562	0.079	0.076

---

In the previous discussion, we have assumed that dissociative states are present below the energetic threshold of the hot state. In order to ascertain this hypothesis, we scanned the triplet potential energy surfaces (PES) with time-dependent density functional theory (TD-DFT) calculations along the Ir–¹C bond cleavage reaction coordinate starting from the ³MC structure (see computational details below). In Fig. 1a, this scan is exemplarily presented for complex 3. One possible dissociative excited state is the ligand-to-metal charge transfer (³LMCT) state shown in Fig. 1b, which involves an excitation from a σ_ppz + π_Ir-ppz orbital to a 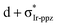orbital. At the ³MC optimized geometry this state corresponds to T₈₈ and its excitation energy is 5.84 eV, and thus it can be populated after TTA. The scan along the Ir–¹C bond cleavage reaction coordinate confirms the dissociative nature of this ³LMCT state, that potentially leads to ppz ligand dissociation upon relaxation on this PES. Note that in the real device situation, the “cage effect” exerted by the host surrounding material will favour the ligand recombination to a certain extent.

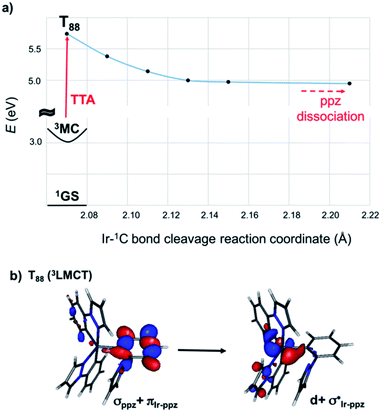Fig. 1 (a) TD-DFT scan of the T₈₈ state along the Ir–¹C bond cleavage reaction coordinate of complex 3. (b) Kohn–Sham Frontier orbitals involved in the dissociative ³LMCT state.

Let us now propose blue phosphor design principles to avoid the formation of degradation products using the thermodynamic and kinetic criteria discussed above. The most straightforward way to prevent ligand dissociation is to attain ΔG_react values above the energetic threshold of a blue hot state (i.e., >6.0 eV). To this end, the use of bis(tridentate) Ir(III) complexes,^30–32in lieu of the more popular tris(bidentate) ones, is suited, since in the former complexes ligand dissociation involves the cleavage of three Ir-heteroatom bonds. In addition, as demonstrated herein, the use of NHC ligands in a tris(bidentate) fashion is a successful strategy to decrease the kinetic liability of the dissociative processes, as their stronger Ir–C carbon bonds lead to large E_a values, consequently preventing the formation of their ³MC states. However, in view of the computed ΔG_react values for 4, it seems unlikely that the thermodynamic criterion can be met for any tris(bidentate) NHC Ir(III) complex. Nevertheless, we predict that there is still room to attain larger E_a and ΔG_react values by ligand design strategies. As an optimal way to avoid degradation, we propose to combine bis(tridentate) architectures with NHC ligands. Indeed, highly efficient deep-blue neutral Ir(III) complexes have recently been reported using this strategy.^32,33 One representative example is the heteroleptic Ir(mimf)(pzpyph^F) complex 5 shown in Chart 2 (where mimf is a pincer dicarbene ligand and pzpyph^F stands for a tridentate 6-pyrazolyl-2-phenylpyridine ligand).³³ We computed the ΔG_react values for the two possible ligand dissociation reactions of 5 (see reactions 5 and 5′ in Table 1). Both dissociations are highly endergonic (ca. 10 and 9 eV, respectively) and they are located significantly above the energetic threshold of a blue hot state. Therefore, one can anticipate that ligand dissociation cannot take place for complex 5 upon PhOLED operation. Although the presence of C–F bonds in complex 5 might be a problem for practical PhOLEDs applications, this general design approach should help improving complex stability. To our knowledge, this approach remains to be used in the PhOLEDs community.

Chart 2 Chemical structure of complex 5.

Conclusions

In this manuscript we unveil from first principles relevant degradation mechanisms of state-of-the-art blue Ir(III) complexes upon PhOLED operation. Energetically hot states (≅6.0 eV) generated after annihilation processes between excited states are responsible of the intrinsic chemical deterioration of PhOLEDs materials. These parasitic processes compromise the large-scale commercialization of PhOLEDs, especially the blue ones. Through our quantum chemical investigations, we unravel one of the most critical degradation processes, i.e., the photodechelation reaction. We found that both kinetic and thermodynamic criteria do play an important role in the degradation processes. The larger tendency to form the ³MC states in the blue complexes (enhanced kinetic liability) stands as the ultimate reason for their reduced intrinsic photostability. In view of these results we propose some blue phosphor design strategies. In particular, combining bis(tridentate) architectures with NHC ligands looks a very promising method to prevent ligand dissociation reactions. Due to their extreme robustness, these complexes may also be very good candidates to be used as hot excited state managers in managed EML.¹⁶ Finally, whilst the photodechelation mechanism is found to be common for blue and non-blue complexes, it is certainly not the exclusive mechanisms of deterioration of blue dopants. Other possible chemical reactions triggered by hot states include radical reactions occurring at the chelate ligands, as shown for complexes 2 and 4, that may potentially lead to further reactions with the host material surrounding the complexes. Another typical example found in the literature is the degradation of the picolinate ligand, where the elimination of thermodynamically stable CO₂ takes place.²¹ Therefore, phosphor design strategies should always be accompanied by a careful choice of the ligands. Computationally-guided ligand design strategies are currently under investigation in our group.

Experimental section

Computational details

All calculations rely on density functional theory (DFT). The geometries of the singlet ground state (¹GS), the triplet ³MC and ³MLCT states as well as of the transition states (TS) were optimized for complexes 1–5 using the dispersion corrected hybrid functional B3LYP-D3 (ref. 34 and 35) in combination with the 6-31G(d,p) atomic basis set for all atoms. Relativistic effects were considered for the Ir atom by using the ECP-60-mwb pseudopotential.³⁶ The Hessian was computed at the same level of theory to confirm the nature of the stationary points. The minimum energy crossing points (MECP) between the ¹GS and the ³MC potential surfaces were optimized using Harvey's algorithm,³⁷ as implemented in the ORCA software;³⁸ with the B3LYP-D3 functional in combination with the def2-svp basis set and the same pseudopotential for Ir. To obtain accurate relative energies for the PES, single-point calculations were performed with the ORCA software using the dispersion-corrected double-hybrid PWPB95-D3BJ functional³⁹ and the def2-SVP basis set (ECP-60-mwb pseudopotential for Ir). This exchange-correlation functional outperforms the majority of the available functionals for the thermodynamic properties of 5d transition metal complexes.⁴⁰ All calculations apart from the MECP optimization and the single point PWPB95-D3BJ calculations were carried out with the Gaussian09 program package.⁴¹ The same protocol (i.e., PWPB95-D3BJ/def2-svp//B3LYP-D3/6-31G(d,p)) was used to compute the ΔG_react values. For the Ir–¹C scan, gas phase TD-B3LYP-D3 vertical triplet excitation energies were obtained for 3 starting at the ³MC optimal geometry. For these calculations we used the 6-31G(d,p) atomic basis set and the ECP-60-mwb pseudopotential for Ir.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DE thanks funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 700961. This research used resources of the CCIPL (Centre de Calcul Intensif des Pays de Loire), and of a local Troy cluster.

Notes and references

1. C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048.
2. H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2001, 255, 2622–2652.
3. M. Hack, J. J. Brown, M. S. Weaver and M. Premutico, Lifetime OLED display, U.S., Patent 9257665, B2, 2016.
4. J. Zhuang, W. Li, W. Su, Y. Liu, Q. Shen, L. Liao and M. Zhou, Org. Electron., 2013, 14, 2596–2601.
5. K. P. Klubek, S.-C. Dong, L.-S. Liao, C. W. Tang and L. Rothberg, Org. Electron., 2014, 15, 3127–3136.
6. J. Zhuang, W. Li, W. Wu, M. Song, W. Su, M. Zhou and Z. Cui, New J. Chem., 2015, 39, 246–253.
7. Y. L. Kang and Y. Y. Lee, Org. Electron., 2016, 32, 109–114.
8. S. Scholz, D. Kondakov, B. Lüssem and K. Leo, Chem. Rev., 2015, 115, 8449–8503.
9. S. Schmidbauer, A. Hohenleutner and B. König, Adv. Mater., 2013, 25, 2114–2129.
10. D. Y. Kondakov, W. C. Lenhart and W. F. Nichols, J. Appl. Phys., 2007, 101, 024512.
11. M. Karas, D. Bachmann, U. Bahr and F. Hillenkamp, Int. J. Mass Spectrom. Ion Processes, 1987, 78, 53–68.
12. S. Scholz, C. Corten, K. Walzer, D. Kuckling and K. Leo, Org. Electron., 2007, 8, 709–717.
13. R. Meerheim, S. Scholz, S. Olthof, G. Schwartz, S. Reineke, K. Walzer and K. Leo, J. Appl. Phys., 2008, 104, 014510.
14. G. Treboux, J. Mizukami, M. Yabe and S. J. Nakamura, J. Photopolym. Sci. Technol., 2008, 21, 347–348.
15. T. Setzer, C. Lennartz and A. Dreuw, Dalton Trans., 2017, 46, 7194–7209.
16. J. Lee, C. Jeong, T. Batagoda, C. Coburn, M. E. Thompson and S. T. Forrest, Nat. Commun., 2017, 8, 15566.
17. C. Murawski, K. Leo and M. C. Gather, Adv. Mater., 2010, 25, 6801–6827.
18. G. J. Hedley, A. Ruseckas and I. D. W. Samuel, J. Phys. Chem. A, 2009, 113, 2–4.
19. R. Seifert, I. Rabelo de Moraes, S. Scholz, M. C. Gather, B. Lüssem and K. Leo, Org. Electron., 2013, 14, 115–123.
20. M. J. Jurow, A. Bossi, P. I. Djurovich and M. E. Thompson, Chem. Mater., 2014, 26, 6578–6584.
21. I. Rabelo de Moraes, S. Scholz, M. C. Gather, B. Lüssem and K. Leo, Org. Electron., 2011, 12, 341–347.
22. S. Schmidbauer, A. Hohenleutner and B. König, Beilstein J. Org. Chem., 2013, 9, 2088–2096.
23. J. Lee, H.-F. Chen, T. Batagoda, C. Coburn, P. I. Djurovich, M. E. Thompson and S. F. Forrest, Nat. Mater., 2016, 15, 92–98.
24. T. Sajoto, P. I. Djurovich, A. B. Tamayo, J. Oxgaard, W. A. Goddard III and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9813–9822.
25. D. Escudero and D. Jacquemin, Dalton Trans., 2015, 44, 8346–8355.
26. X. Zhou, P. L. Burn and B. J. Powell, Inorg. Chem., 2016, 55, 5266–5273.
27. D. Escudero, Chem. Sci., 2016, 7, 1262–1267.
28. D. Escudero, E. Heuser, R. J. Meier, M. Schäferling, W. Thiel and E. Holder, Chem.–Eur. J., 2013, 19, 15639.
29. K. Tsuchiya, S. Yagai, A. Kitamura, T. Karatsu, K. Endo, J. Mizukami, S. Akiyama and M. Yabe, Eur. J. Inorg. Chem., 2010, 2010, 926–933.
30. A. J. Wilkinson, A. E. Goeta, C. E. Foster and J. A. G. Williams, Inorg. Chem., 2004, 43, 6513–6515.
31. Y. Chi, T.-K. Chang, P. Ganesan and P. Rajakannu, Coord. Chem. Rev., 2017, 346, 91–100.
32. H.-H. Kuo, Y.-T. Chen, L. R. Devereux, C.-C. Wu, M. A. Fox, C.-Y. Kuei, Y. Chi and G.-H. Lee, Adv. Mater., 2017, 29, 1702464.
33. C.-Y. Kuei, W.-L. Tsai, B. Tong, M. Jiao, W.-K. Lee, Y. Chi, C.-C. Wu, S.-H. Liu, G.-H. Lee and P.-T. Chou, Adv. Mater., 2016, 28, 2795–2800.
34. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
35. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. D. Andrae, U. Häusermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141.
37. J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99.
38. F. Neese, Orca, an ab initio, DFT and semiempirical SCF-MO package 2.8.0 R2327, University of Bonn, Bonn, Germany, 2011.
39. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
40. M. Steinmetz and S. Grimme, ChemistryOpen, 2013, 2, 115–124.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009.

---