Nb₂©Au₆: a molecular wheel with a short Nb≡Nb triple bond coordinated by an Au₆ ring and reinforced by σ aromaticity

Abstract

We report a photoelectron spectroscopy and high-resolution photoelectron imaging study of a bimetallic Nb₂Au₆⁻ cluster. Theoretical calculations, in conjunction with the experimental data, reveal that Nb₂Au₆^−/0 possess high-symmetry D_6h structures featuring a Nb–Nb axis coordinated equatorially by an Au₆ ring. Chemical bonding analyses show that there are two π bonds and one σ bond in the Nb₂ moiety in Nb₂©Au₆, as well as five totally delocalized σ bonds. The Nb≡Nb triple bond is strengthened significantly by the delocalized σ bonds, resulting in an extremely short Nb–Nb bond length comparable to the quintuple bond in gaseous Nb₂. The totally delocalized σ bonding in Nb₂©Au₆ is reminiscent of σ aromaticity, representing a new bonding mode in metal–ligand systems. The unusually short Nb–Nb bond length in Nb₂©Au₆ shows that the Au₆ ring can serve as a bridging ligand to facilitate multiple bonding in transition metal dimers via delocalized σ bonding.

---

1. Introduction

Due to the strong relativistic effects,¹ negatively charged gold clusters can be planar up to a surprisingly large size.² The Au₆ cluster is very special with a huge energy gap between its highest occupied (HOMO) and lowest unoccupied molecular orbitals (LUMO), as revealed in the photoelectron spectra of Au₆⁻.^2c,3 On the basis of vibrationally-resolved photodetachment spectroscopy, Au₆ was initially deduced to have a D_6h ring structure,^3b but was later confirmed to have a D_3h triangular structure.² The high electronic stability of Au₆ is due to σ aromaticity from its delocalized σ electrons,⁴ as is also found in the isoelectronic Au₅Zn⁺ cluster.⁵ Photoelectron spectroscopy (PES) of MAu₆⁻ (M = Ti, V, Cr) along with density functional theory (DFT) calculations found these doped-clusters to have planar structures featuring an Au₆ ring with a central transition metal atom (M©Au₆⁻) with variable magnetic moments.⁶ It was shown that, while the out-of-plane 3d orbitals of the transition-metal atoms do not participate in bonding with Au, the in-plane d_xy and d_x²−y² orbitals are important to maintain the disk structure due to bonding interactions with the Au₆ ring. Subsequent DFT calculations found that Au₆ doped with 3d transition metals all have similar M©Au₆ disk structures for M = Sc–Ni,⁷ whose electronic structures were also rationalized using an electron shell model.⁸ Thus, the Au₆ ring provides a good host for a central transition metal atom with tunable magnetic properties.

In the current study, we report the observation of Nb₂©Au₆^−/0 molecular wheels, in which an Au₆ ring is hosting a Nb≡Nb triple bond equatorially. The first report in 1965 by Cotton et al. of K₂[Re₂Cl₈]·2H₂O with a quadruple bond (σ²π⁴δ²) between the two Re atoms opened the field of metal–metal multiple bonds.⁹ The σ, π, and δ bonds between two transition metal atoms (M₂) are mainly formed by the overlap of their d orbitals with the same symmetry. Employing bulky or bridging ligands, Cr₂ complexes containing a quintuple bond (σ²π⁴δ⁴) have also been successfully synthesized.¹⁰ The quintuple bonded complexes synthesized so far are mainly related to group VI metals.¹¹ Although gaseous Nb₂ is characterized to possess a quintuple Nb–Nb bond with a 1π⁴_u1σ²_g2σ²_g1δ²_g electron configuration,¹² synthesized diniobium complexes usually contain a Nb₂⁴⁺ core and maintain a Nb–Nb triple bond at the most.^9b,13 To surpass the Nb–Nb triple bond, a Nb₂ complex needs to free more d electrons from metal–ligand bonding to participate metal–metal δ bonding.

The Nb₂Au₆⁻ cluster anions were produced by a laser vaporization supersonic cluster source and characterized by a magnetic-bottle PES analyzer,¹⁴ as well as high-resolution velocity-map imaging (VMI).¹⁵ Global minimum searches along with high-level quantum calculations reveal that the D_6h Nb₂Au₆^−/0 molecular wheels are the most stable structures. Chemical bonding analyses show that there are one σ bond and two π bonds in the Nb₂ moiety, and five totally delocalized σ bonds in Nb₂Au₆. An extremely short Nb–Nb bond length is observed, showing that the Au₆ ring can serve as a bridging ligand to facilitate multiple bonding in Nb₂via delocalized σ bonding.

2. Experimental methods

The Nb₂Au₆⁻ cluster was studied using two different PES apparatuses. The experiment was first carried out using a magnetic-bottle PES apparatus equipped with a laser vaporization supersonic cluster source, details of which has been published elsewhere.¹⁴ The second harmonic radiation (532 nm) from a Nd:YAG laser was used to vaporize a disk target compressed from niobium and gold powders. A helium carrier gas seeded with 5% argon was used to quench the plasma, initiating nucleation and cluster formation. Clusters formed in the nozzle were entrained in the carrier gas and underwent a supersonic expansion. The anionic clusters were extracted from the collimated cluster beam and analyzed by a time-of-flight (TOF) mass spectrometer. The Nb₂Au₆⁻ anion of interest was mass-selected, decelerated and photodetached by a laser beam at 193 nm from an ArF excimer laser, and 266 nm from a Nd:YAG laser. Photoelectrons were collected at nearly 100% efficiency and analyzed in a 3.5 meter long electron flight tube. The photoelectron spectra were calibrated by the known spectra of Au⁻ or Bi⁻. The energy resolution of the apparatus was ΔE_k/E_k ≈ 2.5%, that is, ∼25 meV for 1 eV electrons.

High-resolution PES experiment was then performed using a VMI apparatus, which has been previously described in detail.¹⁵ The cluster source and TOF mass spectrometer are similar to the magnetic-bottle PES apparatus. The Nb₂Au₆⁻ cluster was mass selected before entering the imaging detector. A laser beam from a 355 nm pumped Deyang dye laser was used to detach electrons from the cluster anions. A voltage of −300 V was used on the repeller of the imaging lens.¹⁵ The electrons were focused onto a microchannel plate (MCP) coupled with a phosphorus screen and charged-coupled device (CCD) camera for detection. The experiments required between 30 000 and 200 000 laser shots to achieve a satisfactory signal-to-noise ratio. Images were analyzed with the maximum entropy concept using the MEVELER program.¹⁶ The detector was calibrated using the well-known detachment energy of Au⁻ at various photon energies.

3. Theoretical methods

Global minimum searches were carried out for Nb₂Au₆⁻ using the simulated annealing algorithm¹⁷ coupled with density functional theory (DFT) geometric optimization. The PW91 (ref. 18) functional with the Los Alamos basis set and effective core potential (LANL2DZ)¹⁹ on both Au and Nb atom was used in the initial structure searches. Low-lying isomers from the initial searches were refined at PW91 and PBE0 (ref. 20) levels of theory using the Def2-TZVPPD basis set²¹ and the Stuttgart–Dresden (SDD) relativistic pseudopotentials (ECP28MDF for Nb and ECP60MDF for Au).²² Vibrational frequencies of the low-lying isomers were calculated to ensure they are true energy minima. All the DFT calculations were carried out using Gaussian 09.²³ Single-point energies of the five lowest isomers were calculated using the coupled-cluster theory with single, double and perturbative triple excitations [CCSD(T)]²⁴ implemented in Molpro 2015.1.²⁵

The first vertical detachment energy (VDE) was computed as the energy difference between the neutral and the anion at the optimized geometry of the anion. The first adiabatic detachment energy (ADE) was computed as the energy difference between the optimized anion and the neutral. Further VDEs were approximated by adding excitation energies from the time-dependent density functional theory (TDDFT)²⁶ calculations to the first vertical detachment energy. The simulated spectrum was obtained by fitting a unit-area Gaussian function of 0.03 eV width to each VDE. The ezSpectrum program was employed to calculate Franck–Condon factors, which were fitted with a unit-area Gaussian function of 2 meV width (FWHM) to simulate the vibrational features.²⁷ Natural population analyses (NPA) were carried out to illustrate the charge distribution on the neutral Nb₂Au₆ cluster.²⁸ A charge decomposition analysis (CDA)²⁹ was done using the Multiwfn program³⁰ to describe the interaction between the Au₆ ring and the Nb₂ axis. Chemical bonding analyses were done using the adaptive natural density partitioning (AdNDP)³¹ method at the PBE0/Def2-TZVP level of theory. The structural and chemical bonding pictures were visualized by GaussView³² and Molekel.³³

4. Experimental results

Fig. 1 displays the photoelectron spectra of Nb₂Au₆⁻ at 266 nm and 193 nm from the magnetic-bottle PES apparatus, which are compared with the simulated spectrum. The PES bands are labeled as X, A, B… which denote detachment transitions from the ground electronic state of the anion to the ground (X) and excited electronic states (A, B…) of neutral Nb₂Au₆. The VDEs of the electronic transitions are measured from the peak maxima and summarized in Table 1, where they are compared with theoretical calculations. The high-resolution spectra shown in Fig. 2 and S1† are taken from the VMI apparatus. The peaks labeled in lower case letters (a, b, c…) represent the vibrational levels resolved for the ground electronic state of neutral Nb₂Au₆. The binding energies and the corresponding assignments for the vibrational features are summarized in Table 2.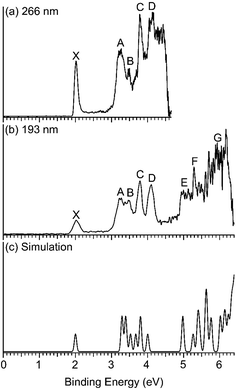

Fig. 1 Photoelectron spectra of Nb₂Au₆⁻ at (a) 266 nm (4.661 eV) and (b) 193 nm (6.424 eV) obtained from the magnetic-bottle PES apparatus, and (c) comparison with the simulated spectrum of the D_6h global minimum at PBE0/Def2-TZVPPD. The theoretical first VDE is shifted to align with the experimental first VDE, while the higher theoretical VDEs are shifted accordingly (see Table 1).

Table 1 Observed photodetachment transitions and their vertical detachment energies (VDE) for Nb₂Au₆⁻ in comparison with theoretical calculations at the TD-PBE0/Def2-TZVPPD level and the final electronic states and electron configurations. All energies are in eV

	VDE(exp)^a	Final states and electronic configuration^b	PBE0^c
a Numbers in the parentheses are the uncertainty in the last digit. b The orbitals shown in bold face indicate the major electron detachment channels. c The first VDE was computed to be 1.79 eV (see Table S2), but shifted to align with the experimental value. All higher VDEs are shifted accordingly to better compare with the experimental data.
X	1.9969(4)	^1A1g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^02u	2.00
A	3.25(3)	^3E1g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^31u2a^12u	3.29
		^3A2u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^11g5e^41u2a^12u	3.39
B	3.48(3)	^1E1g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^31u2a^12u	3.53
C	3.79(3)	^1A2u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^11g5e^41u2a^12u	3.67
		^3E2u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^32g4a^21g5e^41u2a^12u	3.80
D	4.11(5)	^1E2u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^32g4a^21g5e^41u2a^12u	4.00
E	∼5.0	^3E1g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^31u4e^42g4a^21g5e^41u2a^12u	4.98
F	∼5.3	^1E1g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^31u4e^42g4a^21g5e^41u2a^12u	5.26
		^3A1u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^12g4e^41u4e^42g4a^21g5e^41u2a^12u	5.40
		^1A1u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^12g4e^41u4e^42g4a^21g5e^41u2a^12u	5.45
		^3B2g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^11u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	5.61
		^3A2g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^11u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	5.64
		^1A2g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^11u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	5.75
		^1B2g⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^11u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	5.77
G	∼5.9	^3E1u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^31g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.02
		^1E1u⋯2e^42u3e^41u3e^42g1b^21u1b^22g2e^31g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.10
		^3E2u⋯2e^42u3e^41u3e^32g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.15
		^3B1u⋯2e^42u3e^41u3e^42g1b^21u1b^12g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.24
		^3B2g⋯2e^42u3e^41u3e^42g1b^11u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.32
		^3E2g⋯2e^32u3e^41u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.36
		^3E1g⋯2e^42u3e^31u3e^42g1b^21u1b^22g2e^41g1a^21u2b^21u1a^22g4e^41u4e^42g4a^21g5e^41u2a^12u	6.40

---

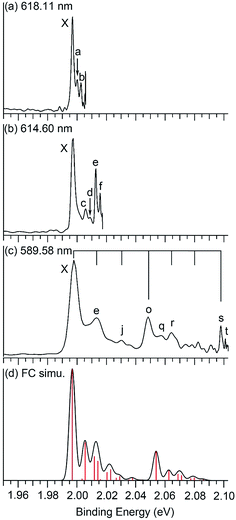Fig. 2 Photoelectron spectra of Nb₂Au₆⁻ at (a) 618.11 nm (2.0059 eV), (b) 614.60 nm (2.0173 eV), and (c) 589.58 nm (2.1029 eV) obtained from the VMI PES apparatus, and (d) the Franck–Condon simulation. The black vertical lines in (c) indicate the vibrational progressions of the two totally symmetric modes, ν₈ (short lines) and ν₁₂ (long lines) (see Fig. 4 and Table 2). The red vertical lines in (d) represent the calculated Franck–Condon factors.

Table 2 Observed vibrational peaks, binding energies (BEs), and the corresponding assignments. Vibrational levels from the totally symmetric vibrational modes are in boldface

Peak	BE (eV)	ΔE (cm^−1)	Assignment	Symmetry	Calculated^a
a The values without and with parentheses are from the PW91/Def2-TZVPPD and PBE0/Def2-TZVPPD calculations, respectively.
X	1.9969 ± 0.0004	0.0
a	2.0001 ± 0.0006	26 ± 5	ν 1	E2u	24 (26)
b	2.0027 ± 0.0003	47 ± 2	ν 3	E1g	48 (68)
c	2.0067 ± 0.0003	79 ± 2	2ν 2	A 1g	64 (70)
d	2.0092 ± 0.0002	99 ± 2	ν 7	E1u	81 (83)
e	2.0128 ± 0.0003	128 ± 2	ν 8	A 1g	121 (121)
f	2.0157 ± 0.0002	152 ± 2	4ν 2	A 1g	128 (140)
g	2.0190 ± 0.0005	178 ± 3	ν 8 + ν3	E1g	169 (189)
h	2.0215 ± 0.0013	198 ± 5	ν 8 + 2ν 2	A 1g	185 (191)
i	2.0250 ± 0.0008	227 ± 3	6ν 2	A 1g	192 (210)
j	2.0285 ± 0.0004	255 ± 2	2ν 8	A 1g	242 (242)
k	2.0349 ± 0.0003	306 ± 2	ν 8 + 4ν 2	A 1g	249 (261)
l	2.0375 ± 0.0004	328 ± 2	2ν 8 + 2ν 2	A 1g	306 (312)
m	2.0391 ± 0.0004	340 ± 2	ν 8 + 6ν 2	A 1g	313 (331)
n	2.0444 ± 0.0004	383 ± 2	2ν 8 + 4ν 2	A 1g	370 (382)
o	2.0475 ± 0.0003	408 ± 2	ν 12	A 1g	423 (460)
p	2.0509 ± 0.0002	436 ± 2	ν 12 + ν1	E2u	447 (486)
q	2.0575 ± 0.0014	489 ± 6	ν 12 + 2ν 2	A 1g	487 (530)
r	2.0643 ± 0.0011	544 ± 5	ν 12 + ν 8	A 1g	544 (581)
s	2.0979 ± 0.0005	815 ± 3	2ν 12	A 1g	846 (920)
t	2.1010 ± 0.0002	840 ± 2	2ν12 + ν1	E2u	870 (946)

---

The 266 nm spectrum (Fig. 1a) displays a sharp ground-state band X around 2.0 eV. Following a large energy gap of ∼1.25 eV, a relatively broad band A at 3.25 eV is observed, as well as three more bands (B, C, D) at VDEs of 3.48, 3.79, and 4.11 eV, respectively. Following another energy gap after band D, more congested features are observed above 5 eV in the 193 nm spectrum (Fig. 1b). The labels E, F, and G are given tentatively for the sake of discussion. The large gap between the X and A bands suggests that neutral Nb₂Au₆ is closed shell with a large HOMO–LUMO gap, indication of a very stable electronic system. A series of high-resolution spectra were obtained using the VMI PES apparatus to resolve vibrational structures for the ground-state transition. Three are shown in Fig. 2 and three more are given in Fig. S1.† The 589.58 nm spectrum (Fig. 2c) yields two main vibrational progressions with frequencies of 408 and 128 cm⁻¹. The short vibrational progressions suggest a minimal geometry change between the anionic and neutral ground states and high symmetries for Nb₂Au₆^−/0. More weak vibrational features are resolved in the spectra at even lower photon energies (Fig. 2a and b). The 618.11 nm spectrum (Fig. 2a) defines the most accurate 0–0 transition at 1.9969 ± 0.0004 eV, which represents the first VDE and ADE, as well as the electron affinity (EA) of neutral Nb₂Au₆. The peak d resolved in Fig. S1a† has a line width of 2 cm⁻¹, which is the narrowest peak resolved in PE imaging for any molecular systems.³⁴

5. Theoretical results

The optimized low-lying isomers of Nb₂Au₆⁻ within 1.5 eV of the global minimum are given in Fig. S2.† All the low-lying isomers were found to have the six Au atoms arranged around a Nb₂ moiety. Structures with two separated Nb atoms were all much higher in energy. At the PW91/Def2-TZVPPD level, the top five isomers are within 0.1 eV of each other with isomer II (D_3d, ²A_2u) being the lowest in energy. Isomer I (D_6h, ²A_2u) is a close-lying isomer, but shows a small imaginary frequency (16.5i cm⁻¹) at PW91/Def2-TZVPPD level. Distortion along this mode of imaginary frequency led to the D_3d isomer II. At the PBE0/Def2-TZVPPD level, isomer I was found to be the most stable structure, while isomers II and III optimized to isomer I. The energy difference between isomers I and II was also calculated using different density functionals, which are summarized in Table S1.† Isomer II was calculated to be slightly more stable at PW91, PBE0, BP86, B3PB6, and TPSS levels, while isomer I was calculated to be more stable at PBE0, TPSSh, and LC-ωPBE levels.³⁵ This discrepancy in relative energies and imaginary frequency suggests that the choice of density functional is important to describe the potential energy surface correctly. To establish a better relative energy order, we calculated single-point energies at the CCSD/Def2-TZVPPD and CCSD(T)/Def2-TZVPPD levels for isomers I–V at the PW91/Def2-TZVPPD structures. At the CCSD and CCSD(T) levels, we found isomer I was most stable, while the second lowest-lying isomer II was 0.029 eV and 0.066 eV higher in energy, respectively. The imaginary frequency of isomer I at PW91/Def2-TZVPPD level is likely to be a result of computational artifact. The optimized neutral structures are shown in Fig. S3,† where the D_6h structure is found to be appreciably more stable at both the PW91/Def2-TZVPPD and PBE0/Def2-TZVPPD levels of theory. The optimized structures of Nb₂Au₆⁻ and Nb₂Au₆ are nearly identical with only minor bond length changes, as shown in Fig. 3.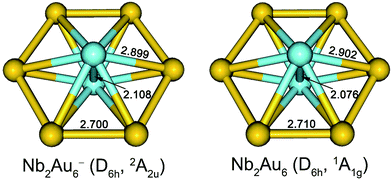

Fig. 3 The optimized structures for the global minimum D_6h Nb₂Au₆⁻ and Nb₂Au₆ at the PBE0/Def2-TZVPPD level. Bond lengths are given in Å.

6. Comparison between experiment and theory

To compare with the experimental data, we computed the first ADE and VDE of isomers I–V at the PW91 and PBE0 levels, as given in Table S2.† It was shown previously that the PW91 functional was excellent in predicting the first ADE and VDE for the M©Au₆⁻ clusters.^6a Indeed, we found that the calculated first ADE (2.01 eV) and VDE (2.02 eV) of isomer I at PW91 are in good agreement with the experimental ADE and VDE of 1.9969 eV, whereas the first VDEs computed for isomers II–V at PW91 are much larger. Furthermore, the large differences between the first ADE and VDE predicted for isomers II–V at PW91 are also inconsistent with the observed sharp band X. The first calculated VDE (1.79 eV) and ADE (1.77 eV) at the PBE0 level for isomer I are slightly lower than the experimental values. These results are consistent with previous observations that the PBE0 functional tends to underestimate the first VDEs of gold clusters by 0.1–0.3 eV.³⁶ Since isomers II–IV are not stable at the PBE0 level (Fig. S2†), their first VDE and ADE could not be computed at this level of theory. The calculated first ADE and VDE of isomer V are much larger than the experimental value at the PBE0 level. At both PW91 and PBE0 levels, only the calculated fist VDE and ADE of isomer I are consistent with the observed band X.

We further computed the vibrational frequencies for the neutral D_6h global minimum at the PW91 and PBE0 levels, as given in Table S3.† There are only two totally symmetric fundamental modes (Fig. 4) for the D_6h structure, the ring breathing (ν₈: 121 cm⁻¹ at both PW91 and PBE0) and the Nb–Nb stretching (ν₁₂: 423 cm⁻¹ at PW91 and 460 cm⁻¹ at PBE0). To better compare with the vibrationally-resolved spectra in Fig. 2 and S1,† we also calculated the Franck–Condon factors for the detachment transition from the ground state of the D_6h anion (²A_2u) to that of the D_6h neutral (¹A_1g) using output files at the PBE0 level.²⁷ The Franck–Condon simulated spectrum of isomer I is shown in Fig. 2d. Apart from the two totally symmetric fundamental modes, the totally symmetric overtone of the out-of-plane bending mode (ν₂: 32 cm⁻¹ at PW91 and 35 cm⁻¹ at PBE0) also gives a significant Franck–Condon factor. Most of the observed vibrational features can be assigned to the combination/overtone of these three modes (2ν₂, ν₈, and ν₁₂), as shown in Table 2. Several low frequency modes involving ring distortions are also observed (Fig. 2 and S1†) and the observed frequencies for these weak vibrational features are also in good agreement with the calculated frequencies (Table 2). The Franck–Condon factors of the transition from the ground state of the D_3d anion (²A_2u) to that of the D_6h neutral (¹A_1g) are negligible, ruling out the possibility of contributions from isomer II to the observed vibrational features. The excellent agreement between the computed first detachment energies and Franck–Condon factors for isomer I and the experimental data confirms firmly the D_6h global minimum for both Nb₂Au₆⁻ and Nb₂Au₆. The observation of the weak vibrational features involving the ring distortion modes indicate that the Au₆ ring is somewhat floppy in the anion.

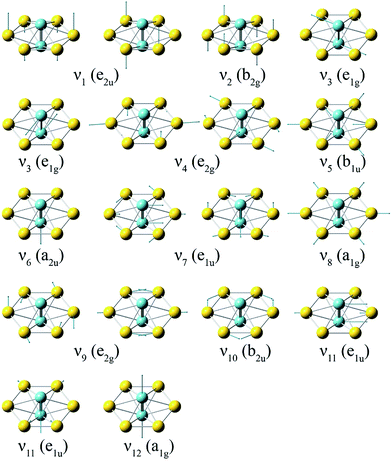Fig. 4 The normal modes and their symmetries for the D_6h Nb₂Au₆ cluster at the PBE0/Def2-TZVPPD level.

The valence canonical molecular orbital (CMO) contours of isomer I are shown in Fig. S4.† The first PES band X corresponds to electron detachment from the singly occupied molecular orbital (SOMO) (a_2u), which involves weak antibonding interactions between the two Nb atoms and weak bonding interactions between Nb and Au. Thus, the removal of the SOMO electron should lead to a slight decrease of the Nb–Nb bond length and a slight increase of the Nb–Au bond length in the Nb₂Au₆ neutral, consistent with the optimized structures (Fig. 3) and the Franck–Condon activities observed for the Au₆ ring breathing and Nb–Nb stretching modes (Fig. 2).

To help assign the PE spectra at the high photon energies (Fig. 1), we calculated higher VDEs of the D_6h global minimum of Nb₂Au₆⁻ using TDDFT at the PBE0/Def2-TZVPPD level, which are compared with the experimental VDEs in Table 1 and plotted in Fig. 1c by fitting each VDE with a unit-area Gaussian function of 0.03 eV width. The calculated VDEs from deeper orbitals are consistent with the observed bands at the higher binding energy side. We also performed TDDFT calculations for isomers I and II using different functionals and plotted the simulated spectra in the ESI (Fig. S5–S7†). Overall, only the simulated spectral pattern of isomer I is in good agreement with the experimental PE spectra (Fig. 1), lending further credence to the established D_6h global minimum for Nb₂Au₆⁻.

7. Discussion

7.1. The extremely short Nb–Nb bond length in Nb₂Au₆

The optimized structures for the global minima of Nb₂Au₆⁻ and Nb₂Au₆ at the PBE0/Def2-TZVPPD level are shown in Fig. 3. Both Nb₂Au₆⁻ and Nb₂Au₆ possess D_6h symmetry featuring an Au₆ ring building around the Nb–Nb axis. The slight bond length variations between Nb₂Au₆⁻ and Nb₂Au₆ are consistent with the nature of the SOMO of the anion (or the LUMO of the neutral), as discussed above. Interestingly, the size of the D_6h Au₆ ring in Nb₂Au₆⁻ is almost identical to that in the M©Au₆⁻ (M = Ti, V, Cr) clusters,^6a suggesting the Au₆ ring is a robust host to accommodate a dopant from a single atom to a dimer. The Nb–Nb bond lengths in Nb₂Au₆⁻ and Nb₂Au₆ are 2.108 Å and 2.076 Å, respectively. These short Nb–Nb bond lengths are similar to the observed bond length of 2.078 Å in gaseous Nb₂, which possesses a ³Σ_g⁻ ground state with a 1π⁴_u1σ²_g2σ²_g1δ²_g electron configuration.¹² With two unpaired weakly bonding electrons in the two degenerate δ orbitals, the bare Nb₂ dimer can be approximately viewed to possess a quintuple bond. The Nb–Nb bond lengths in Nb₂Au₆^−/0 are much shorter than the Nb–Nb triple bond length (2.32 Å) from Pyykkö's self-consistent covalent radii.³⁷ Indeed, the calculated Mayer bond orders³⁸ between Nb–Nb in Nb₂ and Nb₂Au₆ are 5.07 and 3.61 at the PBE0/Def2-TZVP level, respectively. This implies that the Nb–Nb bond strength in Nb₂Au₆ is beyond a triple bond. How does the Au₆ ring accommodate the Nb₂ dimer and facilitate the multiple bonding of Nb₂ in Nb₂Au₆?

7.2. Chemical bonding in Nb₂Au₆

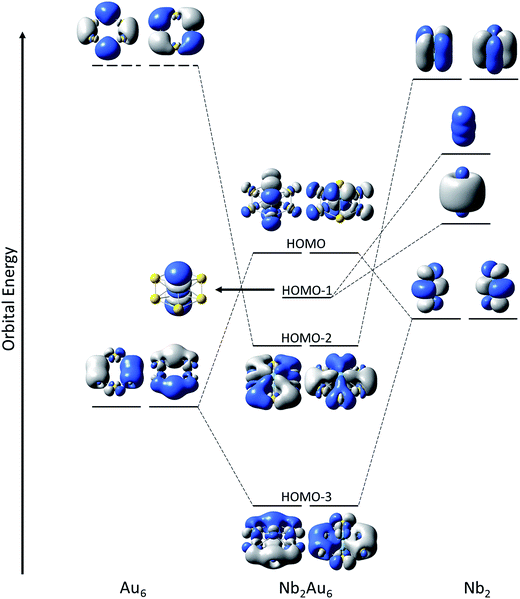
The binding energy between Nb₂ and Au₆ is calculated to be 8.71 eV at the PBE0/Def2-TZVPPD level based on Nb₂Au₆ (D_6h, ¹A_1g) → Nb₂ (D_∞h, ³Σ_g⁻) + Au₆ (D_6h, ¹A_1g), indicating strong guest–host interactions. The charge distribution on each atom in Nb₂Au₆ is shown in Table S4.† Although the Au atom is more electronegative than the Nb atom, the charge distribution shows each Nb atom actually draws electron (NPA charge: −0.195|e|; Mulliken charge: −0.457|e|) from the Au atoms in Nb₂Au₆. Using the results from the CDA analysis, we made an orbital correlation diagram about the interactions between the Nb₂ and the Au₆ fragments in Nb₂Au₆, as shown in Fig. 5. The HOMO (e_1u) and HOMO-1 (a_1g) of Nb₂Au₆ are mainly from the Nb₂ fragment, representing two π bonds and one σ bond formed by the overlap of 4d orbitals. The HOMO-2 (e_2g) of Nb₂Au₆ results from symmetric overlap between the SOMO (1δ_g) of Nb₂ and the LUMO (e_2g) of the Au₆ ring, providing the key factor to stabilize the ring structure and facilitate the multiple bonding of Nb₂ in Nb₂Au₆.

Fig. 5 Qualitative orbital correlation diagram of the interactions between the D_∞h Nb₂ fragment and the D_6h Au₆ fragment in the D_6h Nb₂Au₆. The horizontal dashed and solid lines represent virtual and occupied molecular orbitals, respectively.

However, it is difficult to establish a clear bonding picture between Nb₂ and Au₆ in the deeper CMOs due to strong hybridization. We further analyzed the bonding in Nb₂, Au₆, and Nb₂Au₆ using the AdNDP method at the PBE0/Def2-TZVPPD level. The AdNDP analysis can yield a chemically intuitive bonding picture, displaying not only localized but also delocalized bonds in complicated molecular and cluster systems.^31,39 The results of the AdNDP analyses are shown in Fig. 6. For the Au₆ ring, there are three totally delocalized σ bonds mainly from the 6s orbitals. For the isolated Nb₂, there are one 4dσ bond, two 4dπ bonds, one 5sσ bond, and two two-center one-electron (2c-1e) 5dδ bonds. In Nb₂Au₆, the one 4dσ bond and two 4dπ bonds are preserved, defining a triple bond in the Nb₂ moiety. In addition, there are five totally delocalized σ bonds, describing bonding within the Au₆ ring and the Nb₂–Au₆ guest–host bonding. These five delocalized 8c-2e bonds are remarkable, reminiscent of σ-aromaticity. The first three 8c-2e σ bonds in Nb₂Au₆ are similar to those in the Au₆ ring but contain extra contributions from 5s/5p orbitals of Nb. The first and following two 8c-2e σ bonds show the overlap between the bonding orbitals of Au₆ with the 5sσ orbital and the 5pπ orbitals of Nb₂, respectively. The last two 8c-2e bonds mainly represent interactions between the δ MOs of Nb₂ and the antibonding orbitals of Au₆. The totally delocalized bonding between Nb₂ and Au₆ represents a new mode of guest–host interactions, reinforcing the Nb≡Nb triple bond and giving rise to the extraordinarily short Nb–Nb bond length.

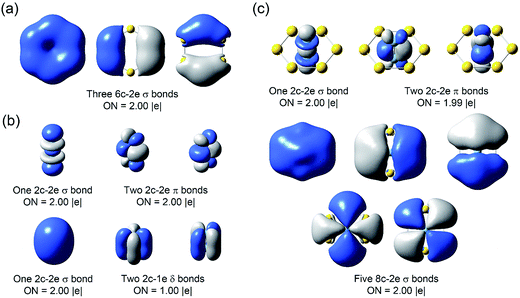Fig. 6 The AdNDP chemical bonding analyses of (a) D_6h Au₆, (b) D_∞h Nb₂, and (c) D_6h Nb₂Au₆ at the PBE0/Def2-TZVP level. ON stands for occupation number.

7.3. The Au₆ ring as a bridging ligand to facilitate metal–metal multiple bonding

It is a well-established strategy to use bridging ligands to facilitate metal–metal multiple bonding.^9b In fact, using 1,3,4,6,7,8-hexahydropyrimido[1,2-a]pyrimidinate (hpp) as bridging ligands, Cotton et al. synthesized the Nb₂(hpp)₄ complex, which contains the shortest Nb–Nb triple bond (σ²π⁴) with a bond length of 2.204 Å.¹³ This kind of complexes require four electrons of Nb₂ for metal–ligand bonding, restricting the Nb–Nb bond order to be no more than three. Note that the Nb–Nb bond length in Nb₂Au₆ is significantly shorter than that in Nb₂(hpp)₄. The δ orbitals in Nb₂ can interact with the antibonding orbitals of the equatorial Au₆ ring by symmetry, providing the key mechanism for reinforcing the Nb≡Nb triple bond. Thus, the Au₆ ring acts as a new type of bridging ligand and provides a new strategy to facilitate stronger multiple bonding in transition metal dimers.

8. Conclusions

In summary, we report the observation of highly symmetric Nb₂©Au₆^−/0 molecular wheels, in which an extremely short Nb≡Nb triple bond is coordinated equatorially by an Au₆ ring and stabilized by σ aromaticity. A large HOMO–LUMO gap is observed in the photoelectron spectra, suggesting the neutral Nb₂Au₆ cluster is a highly stable electronic system. High-resolution photoelectron spectra from velocity map imaging indicate that neutral Nb₂Au₆ is highly symmetric. Global minimum searches coupled with high-level quantum calculations show that the most stable structures of Nb₂Au₆^−/0 consist of a D_6h Au₆ ring building around a short Nb₂ axis. Chemical bonding analyses reveal one σ bond and two π bonds in the Nb₂ axis, and five totally delocalized σ bonds in Nb₂Au₆. The antibonding orbitals of the Au₆ ring can interact with the δ orbitals in Nb₂ by symmetry, which is critical for strengthening the Nb≡Nb triple bond. The Au₆ ring acts as a novel bridging ligand, providing a new strategy to facilitate stronger multiple bonding in transition metal dimers. A whole class of M₂©Au₆ type molecular wheels containing a strengthened M–M multiple bond may be possible.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation (CHE-1263745). We are indebted to Prof. Xueming Yang and Dr Tao Wang for supplying us the Deyang () dye laser system, which is critical for the high-resolution PE imaging experiment. The calculations were performed using resources at the Center for Computation and Visualization (CCV) of Brown University. T. J. wishes to thank the Chemistry Department of Brown University for the Vince Wernig Fellowship.

References

1. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
2. (a) F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990; (b) H. Hakkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89, 033401; (c) H. Hakkinen, B. Yoon, U. Landman, X. Li, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2003, 107, 6168–6175; (d) M. P. Johansson, A. Lechtken, D. Schooss, M. M. Kappes and F. Furche, Phys. Rev. A, 2008, 77, 053202; (e) W. Huang and L. S. Wang, Phys. Rev. Lett., 2009, 102, 153401.
3. (a) K. Taylor, C. L. Pettiette-Hall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 92, 3319–3329; (b) K. Taylor, C. Jin, J. Conceicao, L. S. Wang, O. Cheshnovsky, B. Johnson, P. Nordlander and R. E. Smalley, J. Chem. Phys., 1990, 93, 7515–7518.
4. I. A. Popov, A. A. Starikova, D. V. Steglenko and A. I. Boldyrev, Chem.–Eur. J., 2017 DOI:10.1002/chem.201702035.
5. H. Tanaka, S. Neukermans, E. Janssens, R. E. Silverans and P. Lievens, J. Am. Chem. Soc., 2003, 125, 2862–2863.
6. (a) X. Li, B. Kiran, L. F. Cui and L. S. Wang, Phys. Rev. Lett., 2005, 95, 253401; (b) The © sign was first proposed to designate a disk or wheel structure with a central atom in a boron ring. See C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
7. M. Zhang, L. M. He, L. X. Zhao, X. J. Feng and Y. H. Luo, J. Phys. Chem. C, 2009, 113, 6491–6496.
8. (a) W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141; (b) T. Höltzl, P. Lievens, T. Veszprémi and M. T. Nguyen, J. Phys. Chem. C, 2009, 113, 21016–21018.
9. (a) F. A. Cotton, N. F. Curtis, C. B. Harris, B. F. G. Johnson, S. J. Lippard, J. T. Mague, W. R. Robinson and J. S. Wood, Science, 1964, 145, 1305–1307; (b) F. A. Cotton, C. A. Murillo and R. A. Walton, Multiple Bonds between Metal Atoms, Springer, New York, 2005.
10. (a) T. Nguyen, A. D. Sutton, M. Brynda, J. C. Fettinger, G. J. Long and P. P. Power, Science, 2005, 310, 844–847; (b) K. A. Kreisel, G. P. Yap, O. Dmitrenko, C. R. Landis and K. H. Theopold, J. Am. Chem. Soc., 2007, 129, 14162–14163; (c) G. Frenking, Science, 2005, 310, 796–797.
11. N. V. S. Harisomayajula, A. K. Nair and Y. C. Tsai, Chem. Commun., 2014, 50, 3391–3412.
12. A. M. James, P. Kowalczyk, R. Fournier and B. Simard, J. Chem. Phys., 1993, 99, 8504–8518.
13. F. A. Cotton, J. H. Matonic and C. A. Murillo, J. Am. Chem. Soc., 1997, 119, 7889–7890.
14. (a) L. S. Wang, H. S. Cheng and J. Fan, J. Chem. Phys., 1995, 102, 9480–9493; (b) L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142.
15. I. León, Z. Yang, H. T. Liu and L. S. Wang, Rev. Sci. Instrum., 2014, 85, 083106.
16. B. Dick, Phys. Chem. Chem. Phys., 2014, 16, 570–580.
17. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680.
18. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12947.
19. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
20. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
21. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305; (b) D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
22. (a) D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244; (b) K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, USA, 2009.
24. (a) G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918; (b) G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382–7387.
25. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, et al., MOLPRO, a package of ab initio programs, see http://www.molpro.net.
26. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
27. V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, http://iopenshell.usc.edu/downloads.
28. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
29. S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352.
30. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
31. (a) D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217; (b) D. Y. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251–9258.
32. R. Dennington, T. Keith and J. Millam, GaussView, version 4.1, Semichem, Inc, Shawnee Mission, KS, 2007.
33. U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Center, Manno, Switzerland, 2009.
34. (a) I. Leon, Z. Yang and L. S. Wang, J. Chem. Phys., 2013, 138, 184304; (b) C. Hock, J. B. Kim, M. L. Weichman, T. I. Yacovitch and D. M. Neumark, J. Chem. Phys., 2012, 137, 244201.
35. (a) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (c) J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401; (d) Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433; (e) O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109–234117; (f) O. A. Vydrov, J. Heyd, A. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106–074114; (g) O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109–154117.
36. (a) L. M. Wang, R. Pal, W. Huang, X. C. Zeng and L. S. Wang, J. Chem. Phys., 2010, 132, 114306; (b) N. Shao, W. Huang, Y. Gao, L. M. Wang, X. Li, L. S. Wang and X. C. Zeng, J. Am. Chem. Soc., 2010, 132, 6596–6605.
37. P. Pyykkö, J. Phys. Chem. A, 2014, 119, 2326–2337.
38. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
39. A. I. Boldyrev and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 11589–11605.

---

Footnote

† Electronic supplementary information (ESI) available: Photoelectron spectra of Nb₂Au₆⁻ at (a) 616.86 nm, (b) 610.55 nm, (c) 603.38 nm, and (d) 589.58 nm; relative energies of low-lying isomers of Nb₂Au₆⁻ within 1.5 eV at the PW91, PBE0 (in square brackets), CCSD (in braces) and CCSD(T) (in angle brackets) levels; the four lowest-lying isomers of Nb₂Au₆ at the levels of PW91 and PBE0; valence canonical molecular orbital contours for the D_6h Nb₂Au₆⁻ at the PBE0 level; comparison between the 193 nm spectrum of Nb₂Au₆⁻ with the simulated spectra of isomers I and II at the PW91/Def2-TZVPPD and BP86/Def2-TZVPPD levels; comparison between the 193 nm spectrum of Nb₂Au₆⁻ with the simulated spectra of isomer I at PBE0/Def2-TZVPPD and TPSSh/Def2-TZVPPD levels; the energy difference between isomers I and II of Nb₂Au₆⁻ calculated at various levels of theory; the first VDEs of isomers I, II, III, IV and V of Nb₂Au₆⁻ computed at the PW91 and PBE0 levels; calculated vibrational frequencies for the D_6h global minimum of Nb₂Au₆ at PW91 and PBE0 levels; calculated bond orders and charges of D_∞h Nb₂, D_6h Au₆, and D_6h Nb₂Au₆ at the PBE0/Def2-TZVP level. See DOI: 10.1039/c7sc02881d

---