Structure and spin state of nonheme Fe^IVO complexes depending on temperature: predictive insights from DFT calculations and experiments

Abstract

The spin states (S = 1 and S = 2) of nonheme Fe^IVO intermediates are believed to play an important role in determining their chemical properties in enzymatic and biomimetic reactions. However, it is almost impossible to investigate the spin state effect of nonheme Fe^IVO species experimentally, since Fe^IVO models having the S = 1 and S = 2 spin states at the same time neither exist nor can be synthesized. However, recent synthesis of an Fe^IVO complex with an S = 1 spin state (triplet), [(Me₃NTB)Fe^IVO]²⁺ (1), and a structurally similar Fe^IVO complex but with an S = 2 spin state (quintet), [(TQA)Fe^IVO]²⁺ (2), has allowed us to compare their reactivities at 233 K. In the present study, we show that structural variants control the spin-state selectivity and reactivity of nonheme Fe^IVO complexes. While 1 and 2 were proposed to be in an octahedral geometry based on DFT calculations and spectroscopic characterization done at 4 K, further DFT calculations show that these species may well assume a trigonal bipyramidal structure by losing one coordinated solvent ligand at 233 K. Thus, the present study demonstrates that the structure and spin state of nonheme Fe^IVO complexes can be different at different temperatures; therefore, the structural and/or spin state information obtained at 4 K should be carefully used at a higher temperature (e.g., 233 K). In addition to 1 and 2, [(TPA)Fe^IVO]²⁺ (3) with an S = 1 spin state, whose spin state was determined spectroscopically and theoretically at 233 K, is included in this study to compare the chemical properties of S = 1 and S = 2 Fe^IVO complexes. The present results add another dimension to the discussion of the reactivites of nonheme Fe^IVO species, in which the structural preference and spin state of nonheme Fe^IVO species can vary depending on temperature.

---

Introduction

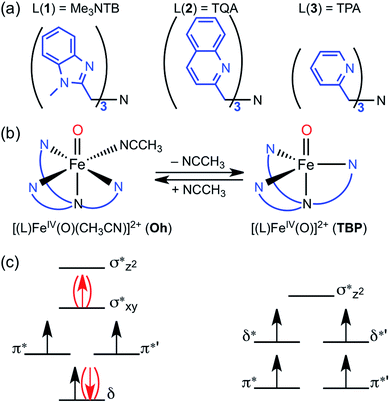
Mononuclear nonheme iron enzymes, such as taurine:α-ketoglutarate dioxygenase (TauD),¹ prolyl-4-hydroxylase,² halogenase CytC3,³ and halogenase SyrB2,⁴ utilize high-spin (S = 2, quintet) Fe^IVO intermediates in their enzymatic oxygenation reactions.⁵ In contrast, most of mononuclear nonheme Fe^IVO complexes synthesized in biomimetic model studies possess an intermediate-spin (S = 1, triplet) Fe^IVO moiety.⁶ Since the spin states (S = 1 and S = 2) of nonheme Fe^IVO intermediates are believed to play an important role in determining their chemical properties in enzymatic and biomimetic reactions, the spin state effect of nonheme Fe^IVO species has attracted much attention in the communities of bioinorganic and biological chemistry.^1–7

The high-spin configuration of nonheme Fe^IVO species is easily achieved when the Fe^IVO moiety is in a trigonal bipyramidal (TBP) geometry, which leads to the Fe d-orbitals being arranged in two groups of two energetically degenerated orbitals, with a small energy difference between the two groups (Fig. 1c).⁸ The preference of the quintet mode for TBP Fe^IVO species has been explained by the same principles governing Hund's rule; the extra energy required to populate the two higher energy d-orbitals is compensated by the lack of exchange interaction between the four α d-electrons.⁹

Fig. 1 (a) Ligands used in the synthesis of nonheme Fe^IVO complexes; [(Me₃NTB)Fe^IVO(CH₃CN)]²⁺ (1_Oh, Me₃NTB = tris((N-methyl-benzimidazol-2-yl)methyl)amine), (TQA)Fe^IVO(CH₃CN)]²⁺ (2_Oh, TQA = tris(2-quinolylmethyl)amine) and [(TPA)Fe^IVO(CH₃CN)]²⁺ (3_Oh, TPA = tris(2-pyridylmethyl)amine). (b) Structural changes between octahedral (Oh, left) and trigonal bipyramidal (TBP, right) depending on the binding of CH₃CN as a ligand. (c) The valence electron orbitals of an Oh structure (left) and those of a TBP structure (right). The Oh structures generally (but not in the case of 2_Oh) prefer an intermediate-spin configuration due to larger orbital energy differences between π* orbitals and the ones above. In contrast, the four singly occupied orbitals in the TBP structure are close in energy, favoring a high-spin conformation due to favorable electron exchange interactions.

In the case of an octahedral (Oh) geometry, the upper d-orbital energies are high, and consequently the ground state configuration is an intermediate-spin (S = 1, triplet) in most cases (Fig. 1c). Even so, during an oxygenation reaction, an electron from the abstracted hydrogen atom of the substrate reduces the iron(IV) ion, and the resulting exchange enhancement of this fifth electron allows the quintet transition state (TS) of the reaction to be lower in energy than its triplet counterpart.^8–10 Thus, for quite some time, it has been theoretically postulated that even triplet species would in fact perform the reaction through quintet surface (i.e., two-state reactivity, TSR),¹¹ unless more energy is required for spin changes due to low spin–orbit coupling.

Actual experimental proof of this two-spin state theory is in fact difficult to obtain, as TSs are not commonly observable. One is therefore limited to measure the spin states at the reactant or product states. Despite attempts to address this question by such studies,¹² this provided limited information regarding this issue, and especially so about the timing of spin change (i.e., before or after the TS). In addition, an energetically lower quintet TS may not be sufficient to guarantee a spin transition. For instance, we have earlier investigated the case of C–H activation by [(N₄Py)Fe^IVO]²⁺, where the experiments indicate that spin inversion does not occur, hence implying a low spin–orbit coupling.¹³ One rationalization for this is the large energy difference between the two spin states of the reactant compound (e.g., ΔG > 6 kcal mol⁻¹), which may lead to difficulties in changing the spin state at the beginning of the reaction. Also, in the case of using cyclohexene as a substrate, the small energy difference (e.g., ΔG < 1 kcal mol⁻¹) at the TS suggests that energy gain by the spin flip would be small.

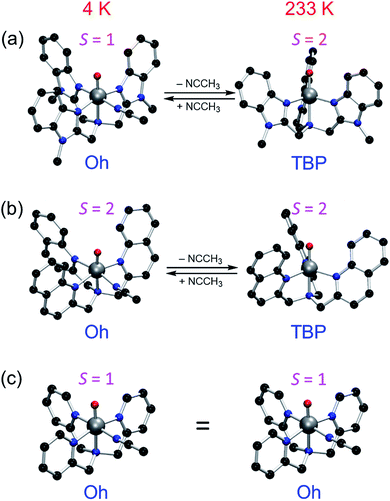
In the opposite end of the spectrum, we showed that while the ground state of [(Me₃NTB)Fe^IVO(CH₃CN)]²⁺ (1_Oh; see the ligand structure in Fig. 1a) was experimentally measured to be in the triplet state at 4.2 K; the calculated energy difference to the quintet state was almost non-existent (e.g., ΔG < 0.1 kcal mol⁻¹ at 298 K).¹⁴ At the same time, the gain at the TS was substantial (e.g., ΔG > 10 kcal mol⁻¹) when cyclohexane or cyclohexadiene was used as a substrate.¹⁴ Hence, these features constitute strong implications that 1_Oh can easily switch its spin state and perform C–H activation reactions in a high-spin mode with a large gain in reactivity. In the absence of spin–orbit couplings, this scenario remains just an implication, albeit a strong one. Moreover, we could not exclude a possibility that 1_Oh would lose its solvent ligand (e.g., CH₃CN) to form a TBP structure ([(Me₃NTB)Fe^IVO]²⁺, 1_TBP) and the reaction was then performed in the quintet state (Fig. 1b) because the TBP structure favours the quintet state by a large margin.

More recently, a quintet ground state complex with an Oh structure, [(TQA)Fe^IVO(CH₃CN)]²⁺ (2_Oh; see the ligand structure in Fig. 1a), was reported;¹⁵ the spectroscopic characterization was done at 4.2 K. The TQA ligand uses quinoline groups instead of the 1-methyl-benzimidazole groups in Me₃NTB (Fig. 1a). This small ligand modification has generated interesting questions about the differences in the chemical properties of the triplet and quintet Fe^IVO complexes, and it has been shown very recently that the reactivity rates and patterns of 1_Oh and 2_Oh were remarkably similar.¹⁶ Existing experimental comparisons, however, were limited to the spin states and structures determined at 4 K and the reactivities investigated at 233 K. A quick summary of the experimental results would be as follows: (i) when the spin states of 1_Oh and 2_Oh were determined spectroscopically at 4 K (i.e., Mössbauer), the preferred spin state of 1_Oh was the triplet,¹⁴ whereas it was the quintet for 2_Oh.¹⁵ (ii) The structures were proposed to have a solvent ligand (e.g., CH₃CN),^14,15 forming a six-coordinated octahedral structure (e.g., 1_Oh and 2_Oh) at 4 K based on density functional theory (DFT)¹⁷ calculations matching Mössbauer data. (iii) In the oxidation of cyclohexene by 1_Oh and 2_Oh, hydrogen atom transfer (HAT) (i.e., allylic C–H activation) was preferred to oxygen atom transfer (OAT) (i.e., C=C epoxidation), but some OAT products were yielded, indicating that the energy barriers for the HAT and OAT reactions are close to one another at 233 K.¹⁶ (iv) The reactivities of 1_Oh and 2_Oh were found to be comparable in oxidation reactions at 233 K.^15,16

However, as discussed above, the spectroscopic characterization of 1_Oh and 2_Oh was done at 4 K, whereas all the reactivity studies were performed at 233 K and the experimental results were interpreted with an assumption that the structures and spin states of 1_Oh and 2_Oh at 233 K were the same as those determined at 4 K.^14,15 Moreover, the temperature difference between the spectroscopic characterization and reactivity studies was not considered previously. Therefore, to gain insights into the temperature effect(s) on the structure and spin state of nonheme Fe^IVO species, we used DFT calculations as well as experiments to elucidate the experimental results obtained at a higher temperature (i.e., 233 K). In the present study, we show that the structural assignment of 1_Oh and 2_Oh with the spectroscopic data obtained at 4 K do not accurately reflect the change of structure and spin state at a higher temperature (i.e., 233 K) due to the change of the solvent-binding preference at different temperatures (Fig. 1b). Indeed, DFT calculations show that 1_Oh and 2_Oh lose one coordinated solvent ligand at 233 K, forming a trigonal bipyramidal structure (i.e., 1_TBP and 2_TBP); unfortunately, the spectroscopic determination of the spin state of the presumed 1_TBP and 2_TBP species was not successful due to the highly unstable nature of the intermediates in solution at 233 K (e.g., t_1/2 < 1 min). Thus, to validate the reliability of the DFT calculations, we have also studied the thermally more stable Fe^IVO species, [(TPA)Fe^IVO(CH₃CN)]²⁺ (3_Oh), possessing a triplet spin state at both 4 and 233 K.¹⁸ The combination of experiment and theoretical calculations lead to new insights into the temperature-structure–spin state relationship that has not been explored previously in nonheme Fe^IVO model studies.

Results and discussion

Our first set of calculations involves large basis set geometry optimizations (B3LYP/Def2-TZVPP)^19,20 to obtain accurate geometries and energies on the component structures 1, 2 and 3. Table 1 lists the relative energies for the species in both triplet and quintet spin states. Looking at the electronic energies only (ΔE), the energies show that the triplet is preferred for 1_Oh and 3_Oh, whereas the quintet is preferred for 2_Oh; all are superficially in agreement with the spin states determined spectroscopically at 4 K.^14–16,18 Hence, in this particular case, the small difference in the Me₃NTB and TQA ligands allows a slight preference of one spin state to change to a slight preference of the other (i.e., triplet for 1_Ohversus quintet for 2_Oh).

Table 1 Relative energies for 1, 2 and 3 without and with binding CH₃CN as a ligand, in kcal mol^−1a

Compound	ΔE	ΔG (4 K)	ΔG (233 K)
a Energies are relative to the separated compounds, i.e., [(L)Fe^IVO]^2+ (quintet) + CH3CN, where L is Me3NTB for 1, TQA for 2 and TPA for 3. Thus, negative energies indicate a preference for the solvent bound structure.
[1TBP/2TBP/3TBP] + CH3CN	0.0	0.0	0.0
1 Oh (triplet)	−0.6	−4.7	3.5
1 Oh (quintet)	2.2	−4.3	2.7
2 Oh (triplet)	1.6	−3.6	4.5
2 Oh (quintet)	0.9	−6.5	0.2
3 Oh (triplet)	−7.5	−11	−3.6
3 Oh (quintet)	−1.0	−3.4	3.3

---

However, a closer look into Table 1 reveals further insights. Note that the reference point (0.0 kcal mol⁻¹ in Table 1) is set at the separated components of 1_TBP, 2_TBP and 3_TBP in its quintet state + CH₃CN; therefore, these energies express the bond dissociation energies (BDE) of the CH₃CN ligand (see the equilibrium between [(L)Fe^IV(O)(CH₃CN)]²⁺ and [(L)Fe^IV(O)]²⁺ in Fig. 1b). To correlate better to experiments, one may look at the free energies (ΔG, which here includes dispersion²¹) at the experimental temperatures, instead of ΔE. Assuming that ΔG is reliable here (see ESI,† ΔG vs. k₂ comparison discussion), an interesting story develops. Mössbauer experiments at 4 K together with DFT calculations have indicated that all the Fe^IVO compounds are in an octahedral geometry, such as 1_Oh, 2_Oh and 3_Oh (i.e., with one solvent molecule ligated).^14,15,18 These results are in agreement with the current results in Table 1, which show that the octahedral complexes are stable at the free energy scale (ΔG) at 4 K. We also note that at 4 K, the experimentally determined spin states are also in agreement with the calculated ΔG (i.e., triplet for 1_Oh and 3_Oh and quintet for 2_Oh). However, at a higher temperature (i.e., 233 K) where the reactivity studies were performed, ΔG values are positive for all except triplet 3_Oh (see the column of ΔG at 233 K in Table 1). This indicates a possibility that the solvent ligand is released at some temperature higher than 4 K and the structure changes to a TBP structure in the cases of 1 and 2, where the quintet state is known to be dominant.⁸ Thus, although the preferred structure and spin state could not be determined spectroscopically at 233 K due to their instability (e.g., t_1/2 < 1 min at 233 K), TBP structures should not be disregarded at 233 K. However, different from 1 and 2, species 3 is relatively stable at 233 K, and we were able to determine a magnetic moment of 3.1 μ_B for 3 at 233 K using Evans ¹H NMR method²² and assigned a triplet spin state for 3 (see Methods section, ESI†). This result suggests the structure of 3_Oh, since the triplet 3_TBP structure + uncoordinated solvent is 11.4 kcal mol⁻¹ higher in energy (Table S1, ESI†). This is in agreement with Table 1, showing that the triplet 3_Oh is lower in energy than the quintet 3_Oh. Hence, at face value, the relative free energies ΔG seem to be in agreement with experiments at every available and verifiable points in the present system up until this stage, such as the experimental results (i) and (ii) discussed above and experiments done here for 3_Oh, even though the differences sometimes are within the error margins of the calculation methods.

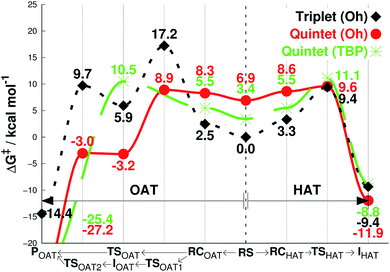
We then investigated the reactivities of 1, 2 and 3 with cyclohexene, allowing us to explore both OAT (i.e., C=C epoxidation) and HAT (i.e., allylic C–H activation).¹⁶ Since the usage of large basis set was not practical here, we used the smaller LACVP basis set^23–25 for geometry optimizations and frequency calculations, including tunneling, with Def2-TZVPP²⁰ used for single-point energy evaluation only (see Methods section, ESI†). As can be seen in Fig. 2a, the energy difference between quintet 1_TBP and 1_Oh at the center of graph (3.2 kcal mol⁻¹) indicates that binding of a sixth ligand (i.e., CH₃CN) to form an octahedral structure is endothermic with the 1_Oh triplet and 1_Oh quintet difference being within the round-off limits. These values are slightly different from that of Table 1 (3.5 and 2.7 kcal mol⁻¹ for triplet and quintet, respectively) due to the smaller basis set used in the optimization; nevertheless, they both predict that a TBP structure is preferred at 233 K.

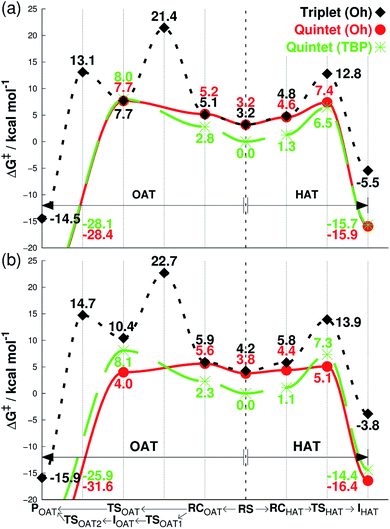Fig. 2 Free energies calculated at 233 K (ΔG, see Methods section for details†), starting from separated reactants in the center of the graph and performing OAT (going left) or HAT (going right) for the oxidation of cyclohexene by Fe^IVO complexes bearing (a) Me₃NTB and (b) TQA ligands. The energy differences in the center between quintet (TBP) and other states correspond to the CH₃CN binding energy as the sixth ligand. RS = reactants separated, RC = reactants complexed, TS = transition state, I = intermediate, P = product.

Subsequent complexation with cyclohexene and OAT reaction occurs differently for the two spin states. With triplet 1_Oh, OAT occurs in two steps, with one O–C bond formed before the other (Fig. 2a, going from the center to the left). The rate-limiting step is the first O–C bond formation with a barrier of 21.4 kcal mol⁻¹. A substrate radical intermediate bound to 1_Oh through the Fe–O–C bond is formed, and a second lower barrier (13.1 kcal mol⁻¹) is crossed when forming the second O–C bond. In comparison, the quintet state features a concerted step where the two O–C bonds are formed at the same time. This occurs over a low barrier, such as 8.0 kcal mol⁻¹ for 1_TBP and 7.7 kcal mol⁻¹ for 1_Oh (Fig. 2a).

Similarly, the HAT reaction features a high triplet barrier (12.8 kcal mol⁻¹) (Fig. 2a, going from the center to the right), compared to the quintet states (6.5 and 7.4 kcal mol⁻¹ for 1_TBP and 1_Oh, respectively). This shows that the HAT reaction may actually be mediated by 1_TBP rather than 1_Oh. However, even if the structure somehow converts to a triplet 1_Oh, a spin crossover could transpire to perform this reaction on the (much) more favorable quintet surface of 1_Oh. Indeed, we found a minimum energy crossing point (MECP) between the two spin states very close to the reactant complex geometry (Tables S2 and S3, ESI†), showing that a spin cross-over is at least geometrically plausible. In addition, at the substrate radical intermediate stage where the catalyst is an Fe^IIIOH species, the intermediate complex is clearly energetically lower in its quintet state. Hence, the only thing that would prevent the reaction from utilizing the quintet pathway is an extremely low spin–orbit coupling, something that can be excluded by comparing the reactivity with a bona fide high-spin complex, such as 2_Oh (vide infra). This corroborates the results found in the previous study that the reaction proceeds in the quintet surface regardless of being in 1_TBP or 1_Oh structure.¹⁴ In agreement with the experimental result (iii) described above, the calculations show that the lowest energy barrier in Fig. 2a is actually for the HAT reaction by 1_TBP and that the lowest epoxidation barrier is slightly higher (i.e., by 1.2 kcal mol⁻¹). Comparing the experimental k₂ directly to experiments, the ΔG barrier is somewhat low, but as shown below, this seems to be a systematic trend, not affecting relative energy comparisons (see discussion in Methods section, ESI†).

For the substrate part, an important point found in this study is the number of equivalent C–H bonds on cyclohexene. While there may seem to be four equivalent C–H bonds in cyclohexene (two each in 2 and 5 positions, as removing any of these would result in equivalent cyclohexenyl radical), the two C–H bonds attached to the same carbon are not equivalent. This can be understood by the structure of cyclohexene, a half-chair conformation, where the two C–H bonds are not at equal distance to the 3- or 4-position carbons. Calculating the vertical single-point energy by removing one of these C–H bonds at time, at the cyclohexene geometry, will show that there is a vertical BDE difference between these two C–H bonds. This vertical energy difference has the potential to change the energy barriers of an HAT reaction.²⁶ We found in this and a parallel study²⁷ that the energy barrier difference in the HAT reaction when using these two C–H bonds is around 2 kcal mol⁻¹ (see Tables S2 and S4, ESI†). Hence, the number of equivalent C–H bonds in cyclohexene is not 4 but 2, and it is potentially important to choose the “right” C–H bonds for calculations. We use the lower value of these two alternative reaction barriers henceforth. The substrate radical intermediate energy, however, is largely unaffected by the choice of C–H bonds, as the geometry optimization of the cyclohexenyl radical will allow the reorganization energy to compensate for the different vertical BDE.

As can be seen in Fig. 2b, the reaction energy profiles for OAT and HAT by 2_TBP and 2_Oh with cyclohexene are almost identical to those of 1_TBP and 1_Oh within a maximum absolute deviation of 3.7 kcal mol⁻¹ for any of the individual values. Within this small discrepancy, however, we can still find some potentially important differences. For the OAT reaction, the lowest TS is the quintet 2_Oh structure at 4.0 kcal mol⁻¹. However, as the reactant complex lies energetically higher (a consequence of adding single-point entropy and dispersion effects; see Table S5, ESI†), the rate-limiting reaction barrier can be considered to be 5.6 kcal mol⁻¹. The overall lowest energy barrier is therefore the HAT barrier performed by 2_Oh at 5.1 kcal mol⁻¹. The reacting species here is thus the octahedral structure, unlike in the case with the Me₃NTB ligand (vide supra). At the same time, the experimental result (iii) described above is still corroborated. However, the close OAT and HAT barriers suggest that any small changes in the experimental setup, for instance deuteration of the substrate, can and does change the outcome of the reactions.¹⁶ Comparing the lowest barriers from Fig. 2a and b (6.5 versus 5.1 kcal mol⁻¹), it can be seen that the energy barriers are similar, confirming the experimental result (iv) described above.

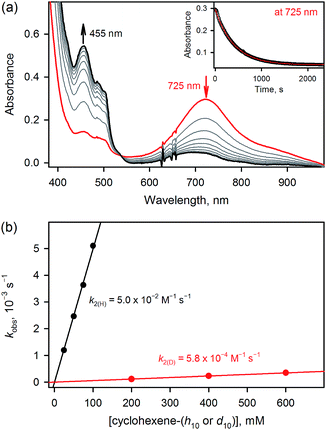
The results for species 3 are somewhat different. Our calculations correctly predict an intermediate-spin reactant state for 3_Oh (Table 1), showing that the consistent high-spin preference of 1 and 2 is not a generic artifact of the calculation methods. In fact, 3_TBP has in this system higher OAT and HAT barriers than the quintet 3_Oh (Fig. 3). Even the triplet 3_Oh is very competitive with the quintet state when it comes to HAT reaction, having a 0.2 kcal mol⁻¹ lower barrier than the quintet 3_Oh. It is therefore somewhat doubtful that it is energetically all that beneficial for 3_Oh to do a spin flip for the reaction, as the gain would be just 0.5 kcal mol⁻¹ at TS, in which case should lead to an OAT reaction rather than HAT. To shed light on this issue, we performed the oxidation reaction of cyclohexene-h₁₀ and cyclohexene-d₁₀ by 3 under an Ar atmosphere, as we have done for the oxidation of cyclohexene and cyclohexene-d₁₀ by 1 and 2.¹⁶ As the experiments show that the majority products are from HAT reactions in the oxidation of cyclohexene-h₁₀ (Table 2) with a very large kinetic isotope effect (KIE) value of ∼80 (see Table 3 and Fig. 4), a preliminary assessment is that this reaction goes on in the triplet surface due to low spin–orbit coupling as well as low energy gains, and in line with the very high KIE, which typify the S = 1 pathway.²⁸ Any spin state flip could hence occur after the rate-limiting barrier step. This is similar to what was postulated in the case of the Fe^IVO complex bearing N₄Py ligand.¹³ In addition, it is of interest to note that the reactivity patterns of the S = 1 and S = 2 Fe^IVO complexes in the cyclohexene-h₁₀ oxidation were similar, such as nonheme Fe^IVO species prefer the C–H bond activation over the C=C epoxidation irrespective of their S = 1 or S = 2 spin state.¹⁶ More interestingly, the reactivity of 3_Oh is shown here to be more than 340 times slower than that of 1_TBP and 2_TBP in the oxidation of cyclohexene-h₁₀ (Table 3). One possible explanation for this reactivity difference is the different spin states of those Fe^IVO species (i.e., S = 1 for 3_Ohversus S = 2 for 1_TBP and 2_TBP); however, other factors, such as the supporting ligand and the structure of Fe^IVO complexes, may modulate the reactivity of nonheme Fe^IVO species in oxidation reactions.²⁹

Fig. 3 Free energies calculated at 233 K (ΔG), starting from separated reactants in the center of the graph and performing OAT (going left) or HAT (going right) for the oxidation of cyclohexene by Fe^IVO complexes bearing TPA ligand. Unlike 1 or 2, this species prefer a triplet Oh structure at 233 K (center).

Table 2 Products obtained experimentally in the oxidation of substrates by 1, 2 and 3^a

Complex	Substrate	Product yield (%)
		–oxide	–ol	–one
a Reactions were run with intermediates (1.0 mM) and substrates (100 mM) under an Ar atmosphere in CH3CN at 233 K. ‘N.D.’ denotes ‘not detected’. b Product yields for 1 and 2 were taken from ref. 16.
1	Cyclohexene-h10	N.D.	27(3)	11(3)
	Cyclohexene-d10	34(3)	25(3)	4(2)
2	Cyclohexene-h10	N.D.	23(3)	14(3)
	Cyclohexene-d10	30(4)	17(4)	8(2)
3	Cyclohexene-h10	N.D.	31(3)	10(3)
	Cyclohexene-d10	19(3)	20(3)	13(2)

---

Table 3 Second-order rate constants and k_2(H)/k_2(D) ratios obtained in the oxidation of cyclohexene-h₁₀ and cyclohexene-d₁₀ by 1, 2 and 3 in CH₃CN at 233 K

Complex	Cyclohexene-h10	Cyclohexene-d10	k 2(H)/k2(D)
	k 2(H), M^−1 s^−1	k 2(D), M^−1 s^−1
a Kinetic data for 1 and 2 were taken from ref. 16.
1	17(2)	2.1(2)	8
2	1.2(1) × 10^2	5.1(4)	24
3	5.0(4) × 10^−2	5.8(4) × 10^−4	86(6)

---

Fig. 4 (a) UV-vis spectral change observed in the oxidation of cyclohexene (50 mM) by 3 (1.0 mM) in CH₃CN at 233 K. Inset shows the time course monitored at 725 nm (black circles) and the first-order fitting (red line) of the kinetic data. (b) Plots of pseudo-first-order rate constants (k_obs) against concentrations of cyclohexene-h₁₀ (black circles) and cyclohexene-d₁₀ (red circles) to determine second-order rate constants (k_2(H) and k_2(D)) in the oxidation of cyclohexene-h₁₀ (black circles) and cyclohexene-d₁₀ by 3 in CH₃CN at 233 K.

Further, we have shown earlier that nonheme M^IIIOH species (M = Cr, Mn, Fe and Ru)³⁰ prefer a dissociative reaction pathway rather than a rebound or desaturation reaction pathway after an H-atom abstraction by M^IVO species takes place.³¹ We therefore explored the rebound vs. dissociation pathways in the current cyclohexene HAT reactions, using the quintet TBP structure of [(Me₃NTB)Fe^IIIOH]²⁺ (1_TBP-OH) and the quintet Oh structure of [(TQA)Fe^IIIOH]²⁺ (2_Oh-OH) and [(TPA)Fe^IIIOH(CH₃CN)]²⁺ (3_Oh-OH). Calculations show very low dissociation energies for the cyclohexene radical (Table 4), as found in the other nonheme M^IIIOH cases.³⁰ However, different from those M^IIIOH cases, it is not immediately clear whether dissociation is favored in the current Fe^IIIOH cases. Here, the triplet values should be irrelevant as the substrate radical intermediate stage has a clear quintet ground state. In the case of 1_TBP-OH, dissociation is then indeed favored over rebound by 2.1 kcal mol⁻¹. For 2_Oh-OH and 3_Oh-OH, the differences are smaller (within the round off limits in case of 2_Oh). Since the rebound barriers are so low in these cases, it is possible that dissociation reaction may not dominate completely. It is therefore an open question which way the reaction will go; it would depend on the precise reaction conditions favoring one way or another, as we have discussed in our recent review article.³¹

Table 4 Relative free energies (ΔG) for the rebound TSs versus dissociation energy in kcal mol⁻¹ at 233 K^a

Compound	Rebound	Dissociation^b
a Energies are relative to the quintet substrate radical intermediate state. b These are equivalent to bond dissociation energies.
[(Me3NTB)Fe^III(OH)]^2+	2.0	−0.1
[(TQA)Fe^III(OH)(CH3CN)]^2+	0.00	0.00
[(TPA)Fe^III(OH)(CH3CN)]^2+	1.2	−0.7

---

The current results need to be discussed in the context of existing error margins. How to obtain correct solvation entropy is an ongoing discussion;³² however, the method used here work well for our systems (see also results of an alternative method^32e,33 in Table S6, ESI,† leading to the same conclusions). Our conclusion that both 1 and 2 perform their reactions in the quintet state should be solid enough due to the large energy differences in the rate-limiting barrier to the triplet value. There is some uncertainty in this issue in the case of 3 due to the closeness of the triplet and quintet TSs, but either path will be slower than the cases of 1 and 2. Nevertheless, the face values of ΔG for the calculations of 1, 2 and 3 are all in agreement with the experimental results (i)–(iv) as well as the experimental results obtained in this study. Similarly, the calculated TBP or Oh preference for the compounds at 4 K and 233 K is sometimes within the presumed error margins, but it does correctly predict the Oh structure of 1, 2 and 3 at 4 K and 3 at 233 K. Therefore, the TBP structure preference for 1 and 2 at 233 K should warrant serious considerations (Fig. 5).

Fig. 5 Theoretically predicted structures and spin states of (a) S = 1 1_Oh at 4 K and S = 2 1_TBP at 233 K, (b) S = 2 2_Oh at 4 K and S = 2 2_TBP at 233 K, and (c) S = 1 3_Oh at 4 K and S = 1 3_Oh at 233 K. 3_Oh retains its S = 1 3_Oh structure even at 233 K according to both calculations and experiments.

Conclusions

We have shown that (1) DFT calculations correctly reproduce the experimental data (i)–(iv) reported previously, thus validating the methodology; (2) DFT calculations predict that the structure of 1 and 2 in solution at 233 K is TBP with a quintet spin state, due to a loss of a coordinating solvent ligand; (3) reactions of 1 and 2 therefore probably occur in the quintet spin state, explaining the similar reactivity rates and patterns for the reactions of 1 and 2;^15,16 (4) DFT calculations predict that the structure of 3 is Oh with a triplet spin even at 233 K; (5) experiments performed with 3 are in agreement with the DFT calculations for the spin state, excluding a possibility that the computational results are due to inherent quintet spin bias in the methods; (6) experimental reactivities of 1 and 2 with the quintet spin state are much greater than that of 3 with the triplet spin state in oxidation reactions, proposing a possibility that the different reactivities result from the different spin states of Fe^IVO species; and (7) in the oxidation of cyclohexene-h₁₀ by the S = 2 Fe^IVO complexes (i.e., 1 and 2) and the S = 1 Fe^IVO complex (i.e., 3), they all show the preference of the allylic C–H activation rather than the C=C epoxidation.¹⁶ Finally, the present study highlights the possible influence of solvent and temperature to the structures and spin states of nonheme metal–oxo complexes synthesized in biomimetic model studies. This work is therefore predictive and at the same time explanatory for the previous reports on the nonheme S = 1 and S = 2 Fe^IVO complexes.^14–16

Acknowledgements

The authors acknowledge financial support from the NRF of Korea through the CRI (NRF-2012R1A3A2048842 to W. N.), GRL (NRF-2010-00353 to W. N.) and MSIP (NRF-2013R1A1A2062737 to K.-B. C.). The Israel Science Foundation (ISF) is acknowledged by S. S. (ISF grant 1183/13).

Notes and references

1. J. C. Price, E. W. Barr, B. Tirupati, J. M. Bollinger Jr and C. Krebs, Biochemistry, 2003, 42, 7497.
2. L. M. Hoffart, E. W. Barr, R. B. Guyer, J. M. Bollinger Jr and C. Krebs, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14738.
3. D. P. Galonic, E. W. Barr, C. T. Walsh, J. M. Bollinger Jr and C. Krebs, Nat. Chem. Biol., 2007, 3, 113.
4. S. D. Wong, M. Srnec, M. L. Matthews, L. V. Liu, Y. Kwak, K. Park, C. B. Bell III, E. E. Alp, J. Zhao, Y. Yoda, S. Kitao, M. Seto, C. Krebs, J. M. Bollinger Jr and E. I. Solomon, Nature, 2013, 499, 320.
5. C. Krebs, D. Galonić Fujimori, C. T. Walsh and J. M. Bollinger Jr, Acc. Chem. Res., 2007, 40, 484.
6. (a) X. Engelmann, I. Monte-Pérez and K. Ray, Angew. Chem., Int. Ed., 2016, 55, 7632; (b) M. Puri and L. Que Jr, Acc. Chem. Res., 2015, 48, 2443; (c) S. A. Cook and A. S. Borovik, Acc. Chem. Res., 2015, 48, 2407; (d) W. Nam, Y.-M. Lee and S. Fukuzumi, Acc. Chem. Res., 2014, 47, 1146; (e) A. R. McDonald and L. Que Jr, Coord. Chem. Rev., 2013, 257, 414; (f) S. P. de Visser, J.-U. Rohde, Y.-M. Lee, J. Cho and W. Nam, Coord. Chem. Rev., 2013, 257, 381.
7. E. Andris, J. Jašík, L. Gómez, M. Costas and J. Roithová, Angew. Chem., Int. Ed., 2016, 55, 3637.
8. K.-B. Cho, S. Shaik and W. Nam, Chem. Commun., 2010, 46, 4511.
9. D. Usharani, D. Janardanan, C. Li and S. Shaik, Acc. Chem. Res., 2013, 46, 471.
10. S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2012, 4, 511.
11. (a) S. Shaik, D. Danovich, A. Fiedler, D. Schröder and H. Schwarz, Helv. Chim. Acta, 1995, 78, 1393; (b) H. Hirao, D. Kumar, L. Que Jr and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590; (c) C. V. Sastri, J. Lee, K. Oh, Y. J. Lee, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin, J. A. Halfen, J. Kim, L. Que Jr, S. Shaik and W. Nam, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19181; (d) H. Hirao, L. Que Jr, W. Nam and S. Shaik, Chem.–Eur. J., 2008, 14, 1740.
12. (a) T. Kojima, Y. Hirai, T. Ishizuka, Y. Shiota, K. Yoshizawa, K. Ikemura, T. Ogura and S. Fukuzumi, Angew. Chem., Int. Ed., 2010, 49, 8449; (b) D. Schröder and S. Shaik, Angew. Chem., Int. Ed., 2011, 50, 3850; (c) T. Kojima and S. Fukuzumi, Angew. Chem., Int. Ed., 2011, 50, 3852.
13. Y. H. Kwon, B. K. Mai, Y.-M. Lee, S. N. Dhuri, D. Mandal, K.-B. Cho, Y. Kim, S. Shaik and W. Nam, J. Phys. Chem. Lett., 2015, 6, 1472.
14. M. S. Seo, N. H. Kim, K.-B. Cho, J. E. So, S. K. Park, M. Clémancey, R. Garcia-Serres, J.-M. Latour, S. Shaik and W. Nam, Chem. Sci., 2011, 2, 1039.
15. A. N. Biswas, M. Puri, K. K. Meier, W. N. Oloo, G. T. Rohde, E. L. Bominaar, E. Münck and L. Que Jr, J. Am. Chem. Soc., 2015, 137, 2428.
16. S. H. Bae, M. S. Seo, Y.-M. Lee, K.-B. Cho, W.-S. Kim and W. Nam, Angew. Chem., Int. Ed., 2016, 55, 8027.
17. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
18. M. H. Lim, J.-U. Rohde, A. Stubna, M. R. Bukowski, M. Costas, R. Y. N. Ho, E. Münck, W. Nam and L. Que Jr, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3665.
19. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (d) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
20. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
21. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
22. (a) D. F. Evans, J. Chem. Soc., 1959, 2003; (b) D. F. Evans and D. A. Jakubovic, J. Chem. Soc., Dalton Trans., 1988, 2927.
23. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
24. A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110.
25. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257; (b) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654.
26. W. Lai, C. Li, H. Chen and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 5556.
27. R. Gupta, X.-X. Li, K.-B. Cho, M. Guo, Y.-M. Lee, Y. Wang, S. Fukuzumi and W. Nam, J. Phys. Chem. Lett., 2017, 8, 1557.
28. D. Mandal, R. Ramanan, D. Usharani, D. Janardanan, B. Wang and S. Shaik, J. Am. Chem. Soc., 2015, 137, 722.
29. (a) G. Xue, R. De Hont, E. Münck and L. Que Jr, Nat. Chem., 2010, 2, 400; (b) D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma, K. Lee, F. Bonino, V. Crocellà, J. Yano, S. Bordiga, D. G. Truhlar, L. Gagliardi, C. M. Brown and J. R. Long, Nat. Chem., 2014, 6, 590.
30. (a) K.-B. Cho, H. Kang, J. Woo, Y. J. Park, M. S. Seo, J. Cho and W. Nam, Inorg. Chem., 2014, 53, 645; (b) K.-B. Cho, S. Shaik and W. Nam, J. Phys. Chem. Lett., 2012, 3, 2851; (c) K.-B. Cho, X. Wu, Y.-M. Lee, Y. H. Kwon, S. Shaik and W. Nam, J. Am. Chem. Soc., 2012, 134, 20222; (d) S. N. Dhuri, K.-B. Cho, Y.-M. Lee, S. Y. Shin, J. H. Kim, D. Mandal, S. Shaik and W. Nam, J. Am. Chem. Soc., 2015, 137, 8623.
31. K.-B. Cho, H. Hirao, S. Shaik and W. Nam, Chem. Soc. Rev., 2016, 45, 1197.
32. (a) J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442; (b) C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760; (c) A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, Acc. Chem. Res., 2009, 42, 489; (d) R. C. Harris and B. M. Pettitt, J. Chem. Theory Comput., 2015, 11, 4593; (e) R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556.
33. B. B. Averkiev and D. G. Truhlar, Catal. Sci. Technol., 2011, 1, 1526.

---

Footnotes

† Electronic supplementary information (ESI) available: Methods section, Tables S1–S8, all the data for DFT calculations (Tables S9–S53 for energies, Mulliken spin density distribution, and selected geometries), and coordinates. See DOI: 10.1039/c7sc01738c

‡ Present address: CSIR-Indian Institute of Toxicological Research, Lucknow 226005, India.

---