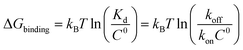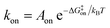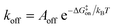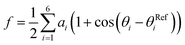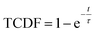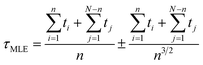Open Access Article
Open Access ArticleBiomolecular conformational changes and ligand binding: from kinetics to thermodynamics†
Yong
Wang
 ,
João Miguel
Martins
,
João Miguel
Martins
 and
Kresten
Lindorff-Larsen
and
Kresten
Lindorff-Larsen
 *
*
Structural Biology and NMR Laboratory, Linderstrøm-Lang Centre for Protein Science, Department of Biology, University of Copenhagen, Ole Maaløes Vej 5, DK-2200 Copenhagen N, Denmark. E-mail: lindorff@bio.ku.dk
First published on 12th July 2017
Abstract
The behaviour of biomolecular systems is governed by their thermodynamic and kinetic properties. It is thus important to be able to calculate, for example, both the affinity and rate of binding and dissociation of a protein–ligand complex, or the populations and exchange rates between distinct conformational states. Because these are typically rare events, calculating these properties from long molecular dynamics simulations remains extremely difficult. Instead, one often adopts a divide-and-conquer strategy in which equilibrium free-energy differences and the fastest state-to-state transition (e.g. ligand association or minor-to-major state conversion) are combined to estimate the slow rate (e.g. ligand dissociation) using a two-state assumption. Here we instead address these problems by using a previously developed method to calculate both the forward and backward rates directly from simulations. We then estimate the thermodynamics from the rates, and validate these values by independent means. We applied the approach to three systems of increasing complexity, including the association and dissociation of benzene to a fully buried cavity inside the L99A mutant variant of T4 lysozyme. In particular, we were able to determine both millisecond association and dissociation rates, and the affinity, of the protein–ligand system by directly observing dozens of rare events in atomic detail. Our approach both sheds light on the precision of methods for calculating kinetics and further provides a generally useful test for the internal consistency of kinetics and thermodynamics. We also expect our route to be useful for obtaining both the kinetics and thermodynamics at the same time in more challenging cases.
1 Introduction
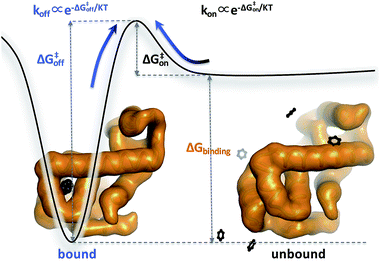
Biomolecular processes are governed by their kinetic and thermodynamic properties, and the ability to determine these properties underlies both our fundamental understanding of biology, as well as our ability to optimize drug molecules or enzymes. Calculating protein–ligand binding thermodynamics, quantified in terms of binding free energies ΔGbinding or the equilibrium dissociation constant Kd, and kinetics characterized by association and dissociation constants (kon and koff), is a problem of critical importance in computational biology and computer-aided drug design.1,2 When ligand binding can be described as a two-state system (Fig. 1), these quantities are related viawhere kB is the Boltzmann constant, T is the temperature and C0 = 1 M is the standard reference concentration.
Similarly to ligand binding, thermodynamics and kinetics are also linked in biomolecular conformational transitions, for example in protein folding. Indeed, one of the standard tests for whether protein folding conforms to a two-state model involves comparing the free energy difference estimated by equilibrium measurements with the value from kinetics.3
In principle, molecular dynamics (MD) simulations can provide a one-shot solution for calculating all of these properties. MD may, however, be limited by its inability to sample the long-timescale biological processes and the whole conformational space. Thus, although it has been possible to calculate rates (kfolding and kunfolding) and thermodynamics (ΔGfolding) from a single, long trajectory of protein folding,4 this has only been possible at temperatures where ΔG ≈ 0. To our knowledge, the same problem has so far not been solved for ligand binding or for cases where the two rates differ substantially in magnitude.
Instead of pursuing a one-shot solution, one may take a divide-and-conquer strategy in which the thermodynamics and kinetics are calculated separately using different, but complementary techniques.5–8 For the calculation of thermodynamics, several different methods have been developed. These methodologies can be categorized roughly into two types: enhanced sampling methods9 and alchemical methods.10,11 The enhanced sampling methods, including umbrella sampling (US),12 non-equilibrium approaches13 and metadynamics,14 are based on the idea that an external bias is added to the original force field so as to make rare events occur more rapidly, but in a way that the unbiased free energy difference can be calculated by reweighting techniques.15 The alchemical methods, including free-energy perturbation (FEP)16 and thermodynamic integration,17 are based on the idea that free energy differences can be calculated via a computationally convenient but not necessarily physical path because the free energy is a state function and path-independent.
While the free energy can often be calculated without knowing or studying the physical pathways that connect the reactant and product states (e.g. the bound and unbound states), the calculation of kinetics is generally more time-consuming and computationally expensive because the full physical reaction pathways have to be explored. It is still challenging but now possible to perform MD simulations up to a few milliseconds.18 Focusing on ligand-binding, it has recently been demonstrated that it is possible to observe spontaneous binding of ligands to their targets, e.g. the cancer drug dasatinib to Src kinase,19 the ‘beta blocker’ drugs propranolol and alprenolol to the β2-adrenergic receptor,6 a transition state analogue to the purine nucleoside phosphorylase enzyme8 and benzamidine to the serine protease trypsin.20–22 These observations demonstrate that the overall drug-binding process can successfully be observed starting from unbound states either in a few long trajectories6,8,19,20 or multiple shorter trajectories (analysed e.g. with the help of Markov state models or the weighted ensemble path sampling).21,23,24 The success of these examples results, in part, from the fact that the binding rate (1/τon = kon[L]) can be accelerated by simply increasing the ligand concentration [L]. However, to the best of our knowledge, unbiased MD simulations have yet not been used to determine the mechanism and kinetics of ligand escape for a tight protein–drug complex. Although it is potentially possible to determine the off rates 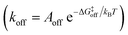 from the height of the free energy barriers, ΔG‡off, this requires good reaction coordinates that represent the entire set of slowly varying degrees of freedom and also a good estimate of the pre-exponential factor Aoff to convert barrier height to a rate. Finding good reaction coordinates and calculating the pre-exponential factor are other challenging tasks. Thus, koff has usually been estimated from ΔGbinding and kon, while assuming two-state kinetics.6,8
from the height of the free energy barriers, ΔG‡off, this requires good reaction coordinates that represent the entire set of slowly varying degrees of freedom and also a good estimate of the pre-exponential factor Aoff to convert barrier height to a rate. Finding good reaction coordinates and calculating the pre-exponential factor are other challenging tasks. Thus, koff has usually been estimated from ΔGbinding and kon, while assuming two-state kinetics.6,8
Inspired by the work of Grubmüller25 and Voter,26 Tiwary and Parrinello recently developed an enhanced sampling method, coined ‘infrequent metadynamics’,9,27 to calculate the rate of a state-to-state transition. Metadynamics is an enhanced sampling method that discourages the system from sampling already visited conformational regions by continuously adding an external history-dependent repulsive potential at the present value of a small number of slowly changing order parameters, called collective variables (CVs).14 The traditional objective of metadynamics simulations is to reconstruct the underlying free energy surface, or potential of mean force (PMF), as a function of the CVs used in the simulations or other order parameters. In standard metadynamics simulations it is very difficult to obtain kinetic properties.28,29 The key idea of infrequent metadynamics is to bias the system with a frequency slow enough so that the transition state regions are not substantially biased; therefore the sequence of basin-to-basin transitions are unaffected and rates can be estimated by applying transition state theory. This method has recently been used to reproduce the kinetics of conformational change of a mutant of T4 lysozyme,30 unbinding of the inhibitor benzamidine from trypsin,31 the unfolding of the villin head-piece,32 and state-to-state transitions of other model systems.7,27,33
Here we use MD simulations with the aid of infrequent metadynamics to address the relationship between thermodynamics and kinetics in three systems of increasing complexity. In systems of slow conformational transitions and ligand association/dissociation, we show that infrequent metadynamics provides the necessary accuracy and efficiency to determine the kinetic and thermodynamic properties. To distinguish the thermodynamic properties obtained from different sources, we term the free energies from enhanced sampling methods (e.g. metadynamics) or alchemical methods (e.g. FEP) as ‘thermodynamic ΔG’, while the free energies calculated from the forward and backward rates we call ‘kinetic ΔG’. We in particular show that thermodynamic and kinetic ΔG values are generally consistent, even in cases where the rates are estimated from biased simulations or when the free energy landscape contains multiple intermediate states. In total, we provide a novel and feasible route to calculate kinetics and thermodynamics at the same time, and a useful consistency check for the calculated kinetic and thermodynamic parameters.
2 Results and discussion
In order to examine the accuracy and applicability of the proposed strategy, we applied it to three biomolecular systems of increasing complexity. We first applied it to the conformational transition between α and β conformers of the alanine dipeptide (Ala2), a mostly two-state system. We then proceeded to study the conformational transitions between four metastable states of a five-residue peptide (Nme-Ala3-Ace). Finally, we applied the idea to the binding of a ligand to an internal, buried cavity in the L99A mutant of T4 lysozyme (L99A T4L). While the two peptide systems are sufficiently simple that the kinetics can be estimated from multiple, unbiased simulations, we demonstrate that infrequent metadynamics allows us also to determine kinetic and thermodynamic parameters for ligand binding to T4 lysozyme, further increasing the complexity of the test and the applicability of the method.2.1 First example: two-state transitions in alanine dipeptide
The alanine dipeptide is perhaps the simplest ‘biological molecule’ and has been widely used as a model system for computational biologists since the first solvation simulation by Karplus et al. almost four decades ago.34 Although this system has a simple topology, it shows a sufficiently complicated free energy landscape involving multiple conformational states (Fig. S1†). For simplicity, we projected the conformational space onto the slowest-relaxing degree of freedom, the dihedral angle Φ, to coarse-grain the system into two stable states, α and β (Fig. S2†). These two states are separated by high transition barriers, thus making the α ↔ β transition a typical rare event.We estimated the free energy difference ΔGPMFα–β between the two states to be 2.6 ± 0.1 kcal mol−1 by summing the populations on the both sides of the barrier. To calculate the kinetic ΔGkineα–β, we obtained the transition times, τα→β and τβ→α for both directions (α to β and β to α) using the statistics from 40 independent unbiased MD simulations (Table 1). Due to the low computational cost to sample this model system, these simulations could be performed without enhanced-sampling techniques. From the calculated rates, we estimated ΔGkineα–β to be kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(τβ→α/τα→β) = 2.8 ± 0.2 kcal mol−1, in excellent agreement with thermodynamic ΔGkineα–β obtained from the potential of mean force.
ln(τβ→α/τα→β) = 2.8 ± 0.2 kcal mol−1, in excellent agreement with thermodynamic ΔGkineα–β obtained from the potential of mean force.
| τ α→β (ns) | τ β→α (ns) | ΔGkineα–β (kcal mol−1) | ΔGPMFα–β (kcal mol−1) |
|---|---|---|---|
| 2.3 ± 0.6 | 231 ± 56 | 2.8 ± 0.2 | 2.6 ± 0.1 |
2.2 Second example: four-state transitions in a five-residue peptide
We then proceeded to a more complex system, a five-residue peptide Ace-Ala3-Nme, whose energy landscape has multiple local minima, and where it is non-trivial how best to describe the free energy landscape by one or a few order parameters.35,36 Using a recently described approach, called SGOOP (spectral gap optimization of order parameters), Tiwary et al. designed a one-dimensional reaction coordinate for this system (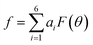 , see Methods) as a linear function of six possible dihedral torsion angles.36 We used this optimized CV in a standard metadynamics simulation (see Methods) which allowed us to obtain a converged free energy landscape (Fig. 2). The landscape reveals four free energy basins, separated by substantial barriers, indicating four conformational states that we labeled as A, B, C and D, respectively. The PMF allows us to estimate the free energy differences between states, ranging between 1.6 and 5.6 kcal mol−1 (Fig. 2).
, see Methods) as a linear function of six possible dihedral torsion angles.36 We used this optimized CV in a standard metadynamics simulation (see Methods) which allowed us to obtain a converged free energy landscape (Fig. 2). The landscape reveals four free energy basins, separated by substantial barriers, indicating four conformational states that we labeled as A, B, C and D, respectively. The PMF allows us to estimate the free energy differences between states, ranging between 1.6 and 5.6 kcal mol−1 (Fig. 2).
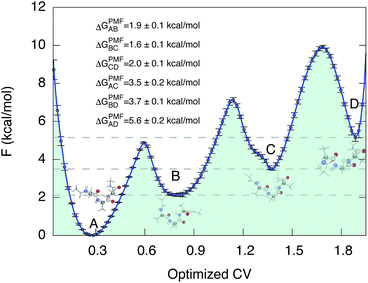 | ||
| Fig. 2 Potential of mean force of Ace-Ala3-Nme at 300 K in implicit solvent. Representative conformations are shown next to the free energy basins. The potential of mean force as a function of the optimized collective variable allows us to estimate the free energy differences ΔGPMF between these four basins. The convergence properties of free energy differences are shown in Fig. S3.† | ||
Despite its simplicity, this model system displays a more complicated free energy landscape with multiple minima, and may thus serve as a relevant model for some of the complexities that one would expect to encounter in larger biological systems. In particular, this system violates the two-state assumption, allowing us to test the practical utility of our approach and the accuracy of free energy differences estimated from the kinetics in such cases. In particular, we asked the question: can we estimate all six free energy differences between states from the transition rates between states? If so, how precisely?
We obtained each transition time (e.g. τA→B) from 40 independent unbiased MD simulations starting from the corresponding reactant state (e.g. state A) and ending with the corresponding productive state (e.g. state B) (Table 2). In all cases but one, we observed complete state-to-state transitions for all 40 simulations. In the case of A-to-D transitions we observed only 28 successful events among 50 trials and 300 μs simulation time in total, and used a maximum likelihood method37 to estimate of τAD.
| τ A→D | τ D→A | ΔGkineAD | ΔGPMFAD |
|---|---|---|---|
| 10.7 ± 2.0 μs | 7.7 ± 1.0 ns | 4.3 ± 0.2 | 5.6 ± 0.2 |
| τ A→C | τ C→A | ΔGkineAC | ΔGPMFAC |
|---|---|---|---|
| 722.4 ± 136.6 ns | 6.9 ± 0.9 ns | 2.8 ± 0.2 | 3.5 ± 0.2 |
| τ A→B | τ B→A | ΔGkineAB | ΔGPMFAB |
|---|---|---|---|
| 27.5 ± 5.1 ns | 1.4 ± 0.5 ns | 1.8 ± 0.3 | 1.9 ± 0.1 |
| τ B→C | τ C→B | ΔGkineBC | ΔGPMFBC |
|---|---|---|---|
| 23.3 ± 4.7 ns | 3.0 ± 0.6 ns | 1.2 ± 0.2 | 1.6 ± 0.1 |
| τ B→D | τ D→B | ΔGkineBD | ΔGPMFBD |
|---|---|---|---|
| 709.7 ± 130.0 ns | 6.1 ± 1.6 ns | 2.9 ± 0.2 | 3.7 ± 0.1 |
| τ C→D | τ D→C | ΔGkineCD | ΔGPMFCD |
|---|---|---|---|
| 8.1 ± 1.4 ns | 0.5 ± 0.1 ns | 1.7 ± 0.2 | 2.0 ± 0.1 |
The twelve transition times were subsequently used to estimate the six kinetic ΔGkine values (Table 2). As in the case of the dipeptide, we find here also that the values are overall in very good agreement with ΔGPMF estimated from the PMF (Fig. 3). The overall calculation of kinetic ΔG values achieved a mean absolute error (MAE) of 0.6 kcal mol−1 and a Pearson correlation coefficient of 0.99 with respect to ΔGPMF from the converged free energy landscape.
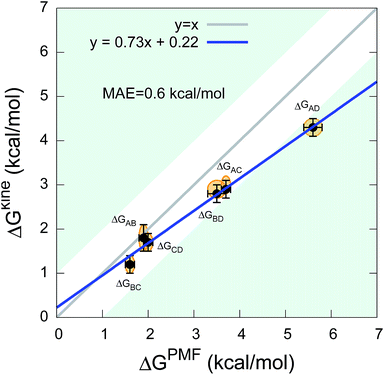 | ||
| Fig. 3 Comparison between kinetic ΔGkine and thermodynamic ΔGPMF values in the state-to-state transitions of the five-residue peptide. | ||
We note that although we find a strong, linear correlation between ΔGPMF and ΔGkine, there appears to be a systematic deviation from a unity slope. This cannot easily be explained by lack of convergence of the free energy landscape (Fig. S3†) nor by how we estimate the rates (Table S1†). Instead we note that the deviations are only observed for the largest free energy differences which also correspond to state-to-state transitions that cross one or two metastable states. In such cases, the processes will in general be multi-exponential and the dominant barrier might differ for the forward and backward reaction. Encouragingly, however, our results show that ΔGkine still provides a rather accurate estimate of the free energy difference with an acceptable overall MAE, in the current case involving two metastable states. Overall, our results suggest that in practice it is possible to estimate the ΔG even when the free energy landscape and the intermediates are not fully known.
2.3 Infrequent metadynamics can get accurate kinetics but with less cost than unbiased MD
Because of the difficulty in unbiased MD simulations to sample slow transitions such as the A → D transition in the five-residue peptide described above, we further validated the calculation of τA→D, τA→C and τB→D by employing the recently developed ‘infrequent metadynamics’ approach.9,27 We observed successful transitions in all simulations and estimated the corresponding unbiased transition times by reweighting the biased simulations (Table 3). The reliability of these estimates was analysed a posteriori by a Kolmogorov–Smirnov (KS) test,38 in which the calculated p-value is used to test the null-hypothesis that the distribution of transition times is Poissonian. Here p < 0.05 would, for example, be indicative that the biased simulations after reweighting were non-Poissonian, and hence that the biasing had substantially perturbed the kinetics. In no case do we find low p-values, and the rates calculated from the infrequent metadynamics are generally very close to those obtained by unbiased simulations but obtained at 25–100 times less computational cost (Table 3).| τ A→D | p-Value | Cost | |
|---|---|---|---|
| Unbiased MD | 10.7 ± 2.0 μs | 300 μs | |
| InMetaD | 16.4 ± 4.5 μs | 0.41 ± 0.26 | 3 μs |
| τ A→C (μs) | p-Value | Cost | |
|---|---|---|---|
| Unbiased MD | 722 ± 137 ns | 0.34 ± 0.24 | 26 μs |
| InMetaD | 553 ± 114 ns | 0.50 ± 0.28 | 1 μs |
| τ B→D (μs) | p-Value | Cost | |
|---|---|---|---|
| Unbiased MD | 709 ± 126 ns | 0.48 ± 0.25 | 25 μs |
| InMetaD | 765 ± 200 ns | 0.34 ± 0.23 | 1 μs |
2.4 Biological application: binding affinity estimation from association and dissociation times of a protein–ligand complex
The examples above, while simple, indicate that it is possible to determine thermodynamic properties from kinetics with reasonable accuracy even when intermediates are present, and that infrequent metadynamics simulations can also be used in cases where the kinetics is very slow. We thus finally proceed to illustrate the idea on a more biological and complex example of binding of a ligand to a protein. In particular, we study the L99A variant of T4 lysozyme (L99A T4L) in which the truncation of Leu99 to Ala creates a large internal cavity of volume ∼ 150 Å3. It has been shown experimentally that this cavity can bind benzene and a variety of other aromatic ligands with sub-millimolar affinities, and with association times on the order of a millisecond (at mM concentration).39–41 Since the binding site is fully buried inside the protein, ligand binding must be accompanied by conformational dynamics of the protein, and L99A T4L has thus become a model for understanding protein–ligand dynamics and interactions.42–46Despite intensive research, several questions pertaining to the mechanism of ligand binding however remain open, in particular with the conformational dynamics underlying access to the internal site remaining unclear. Previous NMR experiments have shown that L99A T4L exchanges between a ground state and an alternative, higher-energy conformational state, but further structural studies showed that both of states are sterically inaccessible to incoming ligands.41,45 This poses a long-standing question of how the ligands access the internal cavity buried in the protein core.47–49 By using metadynamics simulations to explore the native state free energy landscape of L99A T4L in the absence of ligands, we recently discovered transiently formed tunnels that connect the interior binding site to the solvent,30 and suggested these to be relevant for ligand binding.
Here we make a step forward by using enhanced sampling simulations to observe multiple events during which the ligand (benzene) either enters into or escapes from the buried cavity in L99A T4L. This not only provides us with valuable information on the ligand binding mechanism, but also allows us to determine ligand association and dissociation rates as well as binding thermodynamics. Here we focus on the kinetics and thermodynamics and analyse and describe the mechanistic aspects in future studies.
We used a total of ∼12 μs infrequent metadynamics simulations to collect 20 ligand association and 20 dissociation events. At the ligand concentration (5 mM) used in the simulation, we find τon and τoff to be 9 ± 5 ms and 168 ± 59 ms, respectively (Fig. S4†). From these values we in turn determined on- and off-rates and compared these to experiments (Table 4). Also in this case, the KS test shows compatibility of the data with a Poisson process, though the relatively lower reliability for τon estimation suggests that binding events are more difficult to sample than the unbinding events.
| Simulation | Experiment | |
|---|---|---|
| a p-Value of τon is 0.10 ± 0.12. b p-Value of τoff is 0.38 ± 0.26. c Dissociation constant of 0.8 ± 0.12 mM is from ref. 39. d Dissociation constant of 0.2 ± 0.04 mM is from ref. 50. | ||
| k on | 3.5 ± 2 × 104 M−1 s−1 | 8 × 105 M−1 s−1 |
| k off | 7 ± 2 s−1 | 800 ± 200 s−1 |
| K d | 0.3 ± 0.1 mM | 0.8 ± 0.12c/0.2 ± 0.04d mM |
| ΔGbinding | −5.0 ± 0.6 kcal mol−1 | −4.2 ± 0.1c/−5.2 ± 0.2d kcal mol−1 |
From the calculated rates we also calculated the binding affinity, which we find to be in good agreement with the two experimental estimates from either calorimetric analysis50 or NMR39 (Table 4). To obtain an independent computational estimate of the binding affinity, we also performed an alchemical free energy calculation on the L99A T4L–benzene complex using the same force field. The result obtained (ΔGFEPbinding = −4.9 ± 0.1 kcal mol−1) is within error the same as that obtained from the ligand kinetics, demonstrating consistence between these two completely different approaches. Finally, we note that even in a relatively long metadynamics simulation we were not able to obtain a converged equilibrium free energy landscape, and so could not estimate ΔGPMFbinding in this case. The fact that we can estimate the free energy difference (from the kinetics) even in the case where equilibrium sampling is not possible, suggests that the approach could be useful in cases where other free energy methods are more difficult to apply such as when charged ligand alchemical modifications are needed or exact binding poses are not well known.
Although we obtained very good agreement between experiment and simulation for the ligand-binding thermodynamics, we note that both the on- and off-rates are one-to-two orders of magnitude too slow. Because of the internal consistency between the calculated rates and thermodynamics we suspect that the error is due to remaining force field discrepancies that manifest themselves in the rates more than in thermodynamics. Indeed, when parameterizing force fields one often focuses accuracy on the populated (free) energy minima.51 Interestingly we also note a similar discrepancy between experimental rates of the conformational exchange of L99A T4L30, and suggest that future research should focus on potential systematic biases in kinetic properties.
3 Discussion and conclusions
Here we have demonstrated the practical implementation of an approach that determines free energy differences for biomolecular rearrangements using the kinetics of the process. This is also possible using e.g. Markov state models, but the simpler approach taken here provides a convenient way to use enhanced sampling simulations to estimate the kinetics. We thus show that the approach is practically feasible and rather accurate, both in systems that violate the two-state assumption or that require further enhanced sampling to calculate the slow conformational rates. In the cases studied here, the free energy differences could be independently determined either by equilibrium sampling (peptide conformational dynamics) or free energy perturbation (ligand binding), and we find good agreement between the two approaches.In other cases (such as conformational exchange in proteins30), it may be difficult to estimate the free energy difference by these methods, and as we demonstrate here the calculation from kinetics is a viable alternative. Further, our finding of internal consistency between ligand affinity and rates in T4 lysozyme lends further support to the precision of the rates calculated by the enhanced sampling method used. This suggests also that these approaches can be used more generally to estimate the kinetics of ligand binding and escape. Further, we suggest that when calculating the kinetics of ligand binding and unbinding, it is useful to validate the results by comparing the kinetic free energy difference with that obtained e.g. from free energy perturbation.
4 Methods
4.1 Collective variables
as a linear function of six possibly relevant dihedral torsion angles.36 Here θRefi is the reference dihedral angle. We used θRefi = 1.25 and the coefficients are ai = {0.6228, 0.1201, 0.5643, 0.1102, 0.5153, 0.0403} as optimized previously36 in three independent well-tempered metadynamics simulations (Fig. S3†). Gaussian hills were added every ps, with a starting height of 1.7 kJ mol−1, width of 0.03 unit, and bias factor of 15.
4.2 Kinetics calculation
Briefly described, the infrequent metadynamics approach works by performing dozens (typically 10 to 40) individual simulations to obtain first passage times between the individual basins. These are then corrected by the known acceleration factors (decrease in barrier height due to the enhanced sampling) to obtain estimates of the unbiased rates. The acceleration factor can be calculated by appealing to generalized transition state theory:54| α = τ/τM = 〈eV(s,t)/kT〉M |
As the basin-to-basin transition is a rare event, its characteristic time is expected to be a Poisson-distributed random variable. In principle, its mean μ, standard deviation σ and median tm/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 should be equal. In practice, however, they are somewhat sensitive to insufficient sampling, and so rather than simply calculating averages, we estimated the transition time τ from a fit of the empirical cumulative distribution function to the theoretical cumulative distribution function (TCDF):38
2 should be equal. In practice, however, they are somewhat sensitive to insufficient sampling, and so rather than simply calculating averages, we estimated the transition time τ from a fit of the empirical cumulative distribution function to the theoretical cumulative distribution function (TCDF):38
A bootstrap approach was used to estimate the errors. To examine whether the observed times indeed follow the expected Poisson distribution we used a KS test to obtain a p-value that quantifies the similarity between the empirical and theoretical distributions. The key parameters for infrequent metadynamics simulations, including the bias deposition pace and the initial bias height, are listed in Table 5.
In the unbiased simulations of Ace-Ala3-Nme we used a maximum likelihood method37 to estimate of τAD because not all simulations reached the D state:
4.3 Model systems and MD details
MD simulations were performed with GROMACS 5.1.2 (ref. 55) combined with the PLUMED 2.2 plugin for metadynamics.56For Ala2 and Ace-Ala3-Nme, the simulations were performed with Amber ff99SB force field57 and an implicit solvent model.58 The temperature was kept constant at 300 K using the v-rescale thermostat.59 Bonds involving hydrogens were constrained using the LINCS algorithm. A time-step of 2 fs was used.
For L99A T4L–benzene system, the simulations were performed with the CHARMM22* force field60 in the NPT ensemble using a periodic cubic box with a side length of 7 nm that includes ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules. The temperature and pressure were kept constant at 298 K using the v-rescale thermostat59 with a 1 ps coupling constant and at 1.0 bar using the Parrinello–Rahman barostat61 with a 2 ps time coupling constant, respectively. We employed the virtual sites for hydrogen atoms with a single LINCS iteration (expansion order 6)62 and constrained the bonds involving hydrogen atoms using the LINCS algorithm, allowing simulations to be performed with an integration time step of 4 fs. The long-range electrostatic interactions were calculated by the means of the particle mesh Ewald decomposition algorithm with a 0.16 nm mesh spacing.
000 water molecules. The temperature and pressure were kept constant at 298 K using the v-rescale thermostat59 with a 1 ps coupling constant and at 1.0 bar using the Parrinello–Rahman barostat61 with a 2 ps time coupling constant, respectively. We employed the virtual sites for hydrogen atoms with a single LINCS iteration (expansion order 6)62 and constrained the bonds involving hydrogen atoms using the LINCS algorithm, allowing simulations to be performed with an integration time step of 4 fs. The long-range electrostatic interactions were calculated by the means of the particle mesh Ewald decomposition algorithm with a 0.16 nm mesh spacing.
4.4 ΔGbinding calculation by alchemical transformation
The DDM methodology63 with the virtual bond algorithm64 was used for the thermodynamic cycle calculation in GROMACS 5.0.6.55 We ran three replicas for each λ value of the decoupling sequence and the results were combined using the Multistate Bennett Acceptance Ratio (MBAR).65 The restraint atoms and potentials used were kept for all protein–ligand state calculations and replicas, in accordance with the DDM-VBA method, with increasing harmonic potential restrains starting from 0 and scaled to maximums of 4184 kJ mol−1 nm−2, 41.84 kJ mol−1 rad−2 and 41.84 kJ mol−1 rad−2 for distance, angles and dihedrals respectively.Acknowledgements
We would like to thank Pratyush Tiwary and Omar Valsson for their helpful comments. The work was supported by a Hallas-Møller Stipend from the Novo Nordisk Foundation and a Sapere Aude Starting Grant from the Danish Council for Independent Research.References
- N. Ferruz and G. De Fabritiis, Mol. Inf., 2016, 35, 216–226 CrossRef CAS PubMed.
- M. De Vivo, M. Masetti, G. Bottegoni and A. Cavalli, J. Med. Chem., 2016, 59, 4035–4061 CrossRef CAS PubMed.
- S. E. Jackson and A. R. Fersht, Biochemistry, 1991, 30, 10428–10435 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- R. O. Dror, D. H. Arlow, P. Maragakis, T. J. Mildorf, A. C. Pan, H. Xu, D. W. Borhani and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 18684–18689 CrossRef CAS PubMed.
- R. O. Dror, A. C. Pan, D. H. Arlow, D. W. Borhani, P. Maragakis, Y. Shan, H. Xu and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13118–13123 CrossRef CAS PubMed.
- P. Tiwary, V. Limongelli, M. Salvalaglio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E386–E391 CrossRef CAS PubMed.
- S. Decherchi, A. Berteotti, G. Bottegoni, W. Rocchia and A. Cavalli, Nat. Commun., 2015, 6, 6155 CrossRef CAS PubMed.
- O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159–184 CrossRef CAS PubMed.
- J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Curr. Opin. Struct. Biol., 2011, 21, 150–160 CrossRef CAS PubMed.
- A. Perez, J. A. Morrone, C. Simmerling and K. A. Dill, Curr. Opin. Struct. Biol., 2016, 36, 25–31 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- P. Tiwary and M. Parrinello, J. Phys. Chem. B, 2014, 119, 736–742 CrossRef PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- R. O. Dror, R. M. Dirks, J. Grossman, H. Xu and D. E. Shaw, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed.
- Y. Shan, E. T. Kim, M. P. Eastwood, R. O. Dror, M. A. Seeliger and D. E. Shaw, J. Am. Chem. Soc., 2011, 133, 9181–9183 CrossRef CAS PubMed.
- I. Buch, T. Giorgino and G. De Fabritiis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10184–10189 CrossRef CAS PubMed.
- N. Plattner and F. Noé, Nat. Commun., 2015, 6, 7653 CrossRef PubMed.
- I. Teo, C. G. Mayne, K. Schulten and T. Lelièvre, J. Chem. Theory Comput., 2016, 12, 2983–2989 CrossRef CAS PubMed.
- D. Shukla, Y. Meng, B. Roux and V. S. Pande, Nat. Commun., 2014, 5, 3397 Search PubMed.
- M. C. Zwier, A. Pratt, J. L. Adelman, J. W. Kaus, D. M. Zuckerman and L. T. Chong, J. Phys. Chem. Lett., 2016, 7, 3440–3445 CrossRef CAS PubMed.
- H. Grubmüller, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 2893 CrossRef.
- A. F. Voter, J. Chem. Phys., 1997, 106, 4665–4677 CrossRef CAS.
- P. Tiwary and M. Parrinello, Phys. Rev. Lett., 2013, 111, 230602 CrossRef PubMed.
- F. Pietrucci, F. Marinelli, P. Carloni and A. Laio, J. Am. Chem. Soc., 2009, 131, 11811–11818 CrossRef CAS PubMed.
- F. Marinelli, F. Pietrucci, A. Laio and S. Piana, PLoS Comput. Biol., 2009, 5, e1000452 Search PubMed.
- Y. Wang, E. Papaleo and K. Lindorff-Larsen, eLife, 2016, 5, e17505 Search PubMed.
- P. Tiwary, J. Mondal, J. A. Morrone and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12015–12019 CrossRef CAS PubMed.
- H.-J. Tung and J. Pfaendtner, Mol. Syst. Des. Eng., 2016, 1, 382–390 CAS.
- D. Callegari, A. Lodola, D. Pala, S. Rivara, M. Mor, A. Rizzi and A. M. Capelli, J. Chem. Inf. Model., 2017, 57, 159–169 CrossRef CAS PubMed.
- P. J. Rossky and M. Karplus, J. Am. Chem. Soc., 1979, 101, 1913–1937 CrossRef CAS.
- O. Valsson and M. Parrinello, J. Chem. Theory Comput., 2015, 11, 1996–2002 CrossRef CAS PubMed.
- P. Tiwary and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2016, 201600917 Search PubMed.
- B. Zagrovic and V. Pande, J. Comput. Chem., 2003, 24, 1432–1436 CrossRef CAS PubMed.
- M. Salvalaglio, P. Tiwary and M. Parrinello, J. Chem. Theory Comput., 2014, 10, 1420–1425 CrossRef CAS PubMed.
- V. A. Feher, E. P. Baldwin and F. W. Dahlquist, Nat. Struct. Biol., 1996, 3, 516–521 CrossRef CAS PubMed.
- F. A. Mulder, A. Mittermaier, B. Hon, F. W. Dahlquist and L. E. Kay, Nat. Struct. Mol. Biol., 2001, 8, 932–935 CAS.
- G. Bouvignies, P. Vallurupalli, D. F. Hansen, B. E. Correia, O. Lange, A. Bah, R. M. Vernon, F. W. Dahlquist, D. Baker and L. E. Kay, Nature, 2011, 477, 111–114 CrossRef CAS PubMed.
- W. A. Baase, L. Liu, D. E. Tronrud and B. W. Matthews, Protein Sci., 2010, 19, 631–641 CrossRef CAS PubMed.
- S. E. Boyce, D. L. Mobley, G. J. Rocklin, A. P. Graves, K. A. Dill and B. K. Shoichet, J. Mol. Biol., 2009, 394, 747–763 CrossRef CAS PubMed.
- K. Wang, J. D. Chodera, Y. Yang and M. R. Shirts, J. Comput.-Aided Mol. Des., 2013, 27, 989–1007 CrossRef CAS PubMed.
- P. Vallurupalli, N. Chakrabarti, R. Pomes and L. Kay, Chem. Sci., 2016, 7, 3602–3613 RSC.
- R. Kitahara, Y. Yoshimura, M. Xue, T. Kameda and F. A. Mulder, Sci. Rep., 2016, 6, 20534 CrossRef CAS PubMed.
- F. A. Mulder, B. Hon, D. R. Muhandiram, F. W. Dahlquist and L. E. Kay, Biochemistry, 2000, 39, 12614–12622 CrossRef CAS PubMed.
- C. J. López, Z. Yang, C. Altenbach and W. L. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4306–E4315 CrossRef PubMed.
- M. Merski, M. Fischer, T. E. Balius, O. Eidam and B. K. Shoichet, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5039–5044 CrossRef CAS PubMed.
- A. Morton, W. A. Baase and B. W. Matthews, Biochemistry, 1995, 34, 8564–8575 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958 CAS.
- M. Marchi and P. Ballone, J. Chem. Phys., 1999, 110, 3697–3702 CrossRef CAS.
- D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103 CrossRef PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- A. Onufriev, D. Bashford and D. A. Case, Proteins: Struct., Funct., Bioinf., 2004, 55, 383–394 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, Biophys. J., 2011, 100, L47–L49 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- K. A. Feenstra, B. Hess and H. J. Berendsen, J. Comput. Chem., 1999, 20, 786–798 CrossRef CAS.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- S. Boresch, F. Tettinger, M. Leitgeb and M. Karplus, J. Phys. Chem. B, 2003, 107, 9535–9551 CrossRef CAS.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc01627a |
| This journal is © The Royal Society of Chemistry 2017 |