Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective arc-discharge synthesis of Dy2S-clusterfullerenes and their isomer-dependent single molecule magnetism†
Chia-Hsiang
Chen‡
a,
Denis S.
Krylov‡
a,
Stanislav M.
Avdoshenko
 a,
Fupin
Liu
a,
Fupin
Liu
 a,
Lukas
Spree
a,
Ravi
Yadav
a,
Antonis
Alvertis
a,
Liviu
Hozoi
a,
Konstantin
Nenkov
a,
Aram
Kostanyan
b,
Thomas
Greber
b,
Anja U. B.
Wolter
a and
Alexey A.
Popov
a,
Lukas
Spree
a,
Ravi
Yadav
a,
Antonis
Alvertis
a,
Liviu
Hozoi
a,
Konstantin
Nenkov
a,
Aram
Kostanyan
b,
Thomas
Greber
b,
Anja U. B.
Wolter
a and
Alexey A.
Popov
 *a
*a
aLeibniz Institute for Solid State and Materials Research Dresden, 01069 Dresden, Germany. E-mail: a.popov@ifw-dresden.de
bPhysik-Institut, Universität Zürich, Zürich, Switzerland
First published on 30th June 2017
Abstract
A method for the selective synthesis of sulfide clusterfullerenes Dy2S@C2n is developed. Addition of methane to the reactive atmosphere reduces the formation of empty fullerenes in the arc-discharge synthesis, whereas the use of Dy2S3 as a source of metal and sulfur affords sulfide clusterfullerenes as the main fullerene products along with smaller amounts of carbide clusterfullerenes. Two isomers of Dy2S@C82 with Cs(6) and C3v(8) cage symmetry, Dy2S@C72-Cs(10528), and a carbide clusterfullerene Dy2C2@C82-Cs(6) were isolated. The molecular structure of both Dy2S@C82 isomers was elucidated by single-crystal X-ray diffraction. SQUID magnetometry demonstrates that all of these clusterfullerenes exhibit hysteresis of magnetization, with Dy2S@C82-C3v(8) being the strongest single molecule magnet in the series. DC- and AC-susceptibility measurements were used to determine magnetization relaxation times in the temperature range from 1.6 K to 70 K. Unprecedented magnetization relaxation dynamics with three consequent Orbach processes and energy barriers of 10.5, 48, and 1232 K are determined for Dy2S@C82-C3v(8). Dy2S@C82-Cs(6) exhibits faster relaxation of magnetization with two barriers of 15.2 and 523 K. Ab initio calculations were used to interpret experimental data and compare the Dy-sulfide clusterfullerenes to other Dy-clusterfullerenes. The smallest and largest barriers are ascribed to the exchange/dipolar barrier and relaxation via crystal-field states, respectively, whereas an intermediate energy barrier of 48 K in Dy2S@C82-C3v(8) is assigned to the local phonon mode, corresponding to the librational motion of the Dy2S cluster inside the carbon cage.
Introduction
The discovery of single molecule magnetism in the Mn12 complex in 1993 (ref. 1) initiated an on-going chase for molecules with a high blocking temperature and large relaxation barrier of magnetization. Lanthanides entered the field in 2003 with the report on the slow relaxation of magnetization in their double–decker complexes,2 and hundreds of lanthanide-SMMs have been described since that time.3–12 Quantum tunneling of magnetization (QTM) is one of the most important mechanisms of losing the spin information by single-ion lanthanide SMMs at zero field. One of the ways to improve the situation is to increase the local symmetry of the crystal field acting on the lanthanide ion, and some of the best single-ion Dy-SMM have been obtained following this strategy.10,13–15 Another approach is to combine two or more lanthanide ions in one molecule,5,16–19 or combine lanthanides with transition metals in 3d–4f complexes.20–25 Exchange and dipolar coupling in polynuclear complexes create a manifold of additional states and an additional barrier to relaxation, thus preventing QTM. Therefore, single-ion anisotropy and inter-lanthanide interactions are the two key ingredients in improving the SMM properties.Endohedral metallofullerenes (EMFs),26,27 and in particular clusterfullerenes,28 combining lanthanides and non-metal ions in endohedral species, provide a convenient platform for creating SMMs. The presence of negatively charged non-metal ions (such as a nitride ion N3− in the nitride clusterfullerene M3N@C80) close to the lanthanide ions leads to the large magnetic anisotropy of the latter,29–33 whereas the possibility of varying the composition of the endohedral cluster by combining lanthanides with scandium or other diamagnetic analogs allows tuning the intracluster interactions.34–36 Both parameters can change strongly with variation of the central (non-metal) atom in clusterfullerenes. EMFs emerged as a new class of SMMs in 2012, when the nitride clusterfullerene DySc2N@C80 was shown to exhibit a hysteresis of magnetization with zero-field quantum tunneling of magnetization.37 Subsequent studies have shown that SMM behavior of Dy–Sc nitride clusterfullerenes strongly depends on the endohedral cluster composition, with Dy2ScN@C80 being a better SMM than DySc2N@C80 and much better than Dy3N@C80.38 The superior SMM properties of Dy2ScN@C80 are explained by the ferromagnetic exchange and dipolar coupling of Dy ions, which lead to the exchange/dipolar barrier of 10.5 K and suppress zero-field QTM. At higher temperatures, the relaxation of the magnetization in Dy2ScN@C80 proceeds via the Orbach mechanism with a high barrier of 1735 K, corresponding to the fifth Kramers doublet of the Dy3+ ion.39 The long magnetization relaxation time of Dy2ScN@C80 was partially preserved even on a metallic substrate.40 HoSc2N@C80 was also found to be a SMM, albeit with much faster relaxation than in the Dy analog.41 Other types of clusterfullerenes were also tested for SMM behavior. Ti-carbide Dy2TiC@C80 was found to exhibit hysteresis similar to Dy2ScN@C80, albeit with a lower blocking temperature.42 At the same time, addition of one more carbon atom to the cluster, such as in Dy2TiC2@C80, led to substantially worsened SMM properties.42 Field-induced SMM behavior was also demonstrated for cyano-clusterfullerenes with single metal atoms, TbNC@C82 (ref. 43) and TbNC@C76.44 As Tb3+ and Ho3+ are non-Kramers ions, the corresponding EMFs exhibit much faster relaxation of magnetization, and hence better EMF-SMMs are to be looked for among Dy-EMFs.
In this work we focus on Dy-based sulfide clusterfullerenes of the formula Dy2S@C2n to study how Dy–S bonding and inter-lanthanide coupling via the sulfide bridge affect the SMM properties. The first synthesis of the sulfide clusterfullerene Sc2S@C82 was reported in 2010.45 In that work, guanidinium thiocyanate was used as a source of nitrogen in the synthesis of nitride clusterfullerenes, and the sulfide was obtained as a by-product with much lower relative yield. Echegoyen et al. used the addition of SO2 gas to the reactor atmosphere and obtained a family of Sc2S@C2n EMFs with 2n ranging from 70 to 100 according to mass-spectrometry.46 In SO2-assisted synthesis, empty fullerenes are the main fullerene products. Thus, both synthetic routes to sulfide clusterfullerenes led to other types of fullerenes (nitride clusterfullerenes or empty fullerenes) as the main products. Isolation of sulfide clusterfullerenes then required tedious multistep chromatographic separation. The principal possibility to obtain non-Sc M2S@C82 clusterfullerenes was also demonstrated in 2010, but the isolated amounts were very small.45
The low selectivity of the arc-discharge synthesis is a serious obstacle when low-yield EMFs, such as sulfide clusterfullerenes, are the goal of the synthesis. It is therefore desirable to develop more selective approaches for the synthesis of clusterfullerenes. The first selective method for the synthesis of EMFs was developed by Dunsch and coworkers.47,48 The authors found that addition of NH3 gas to the arc-discharge reactor atmosphere dramatically reduced the yield of empty fullerenes but did not affect the formation of nitride clusterfullerenes. The latter could be thus obtained with a high degree of selectivity. High selectivity of nitride clusterfullerene formation was also achieved with the use of solid nitrogen sources (such as guanidinium thiocyanate,49 inorganic salts,50 melamine,51 or urea52) or using NOx vapor from NOx-generating solid reagents and air (known as the CAPTEAR approach).53 More recently, we have adapted a method for selective synthesis of carbide clusterfullerenes using methane as a reactive gas.42,54–57 Its influence on the arc-discharge is similar to that of NH3. Namely, hydrogen suppresses the formation of empty fullerenes, and carbide clusterfullerenes, especially Ti-carbide clusterfullerenes M2TiC@C80 and M2TiC2@C80,42,55 as well as Sc-carbide Sc3CH@C80 (ref. 54) and Sc4C2@C80,55 can be obtained with a high degree of selectivity.
In this work, we pursue two goals. First, we develop the procedure for the selective synthesis of sulfide clusterfullerenes and synthesize a new family of EMF-SMMs, Dy-based sulfide clusterfullerenes. Second, we perform a thorough analysis of the magnetic properties of the Dy-sulfide clusterfullerenes and demonstrate that they exhibit SMM behavior. Their unprecedented magnetization relaxation dynamics is analyzed as a function of temperature and the main relaxation pathways are revealed.
Results and discussion
Synthesis of clusterfullerenes
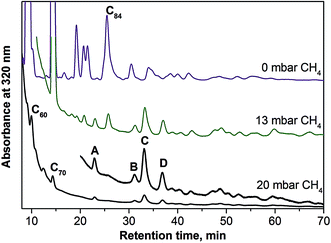
Selective synthesis of nitride and carbide clusterfullerenes was achieved via addition of hydrogen-containing compounds. Hydrogen suppresses the yield of empty fullerenes, and EMFs can be obtained with improved selectivity. To achieve a similar effect in the synthesis of sulfide clusterfullerenes, several combinations of dysprosium and sulfur sources were tested. In particular, we used (i) a mixture of Dy powder with elementary sulfur; (ii) a mixture of Dy powder with a solid organic sulfur compound, dibenzyl sulfide; (iii) Dy2S3 sulfide. The syntheses were performed in pure helium atmosphere (230 mbar), as well as with the addition of several mbar of methane. Mass-spectrometric analysis showed that all three strategies led to formation of Dy2S@C2n clusterfullerenes, albeit with quite a low yield. In all cases the presence of methane increased the relative yield of sulfide clusterfullerenes (as far as it could be decided based on laser-desorption ionization time-of flight (LDI-TOF) mass-spectra; note that conclusions on the yield of EMFs based on LDI-TOF data should be treated with caution). The best results were obtained with the use of Dy2S3 as a simultaneous source of metal and sulfur, and this route was then further optimized by varying the amount of methane. Fig. 1 compares HPLC traces of CS2 fullerene extracts obtained in the syntheses without methane and with 13 mbar and 20 mbar of CH4 (total pressure was kept at 250 mbar). In the absence of methane, empty fullerenes are formed in much larger amounts than EMFs, and the HPLC trace is very similar to that of a standard empty fullerene synthesis (not shown). Addition of 13 mbar CH4 to the reactor atmosphere immediately reduced the yield of empty fullerenes, and EMF peaks with retention times longer than 30 minutes can be well seen in the chromatogram. Their intensities are comparable to those of higher empty fullerenes (the yield of C60 and C70 is still considerably higher). In the presence of 20 mbar CH4, formation of empty fullerenes is suppressed almost completely, leaving only several well established peaks marked with block letters (A–D). Mass-spectral analysis revealed that each peak corresponds to clusterfullerenes, including Dy2S@C72 (A), Dy3N@C80 (B), and two isomers of Dy2S@C82 (C and D). Mass-spectra of the fraction collected at longer retention times (37–45 min) also showed the presence of Dy2S@C78 and Dy2S@C86, but their amounts are too low for separation. Formation of the nitride clusterfullerene Dy3N@C80 seems to be inevitable even when only traces of nitrogen are present in the generator (earlier we observed the same effect in the synthesis of carbide clusterfullerenes42). Mass-spectral analysis of the fractions C and D also showed that they contained certain amounts of carbide clusterfullerenes Dy2C2@C82. To obtain pure compounds, recycling HPLC was used at the second separation step (Fig. S1†). As a result of the chromatographic separation, pure Dy2S@C72, two isomers of Dy2S@C82, and one isomer of Dy2C2@C82 were obtained. It should be noted that the use of methane suppresses the formation of empty fullerenes and simplifies the separation of sulfide clusterfullerenes, but their overall yield remains quite low. The isolated amounts for each compound were less than 1 mg.Spectroscopic characterization and molecular structures
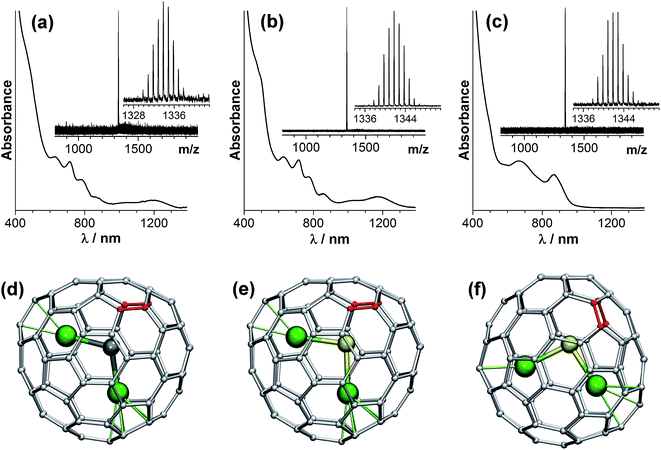
Molecular structures of the isolated clusterfullerenes are first established with the use of UV-vis-NIR absorption spectroscopy. Due to multiple π–π* transitions, the absorption spectra of EMFs are very sensitive to the isomeric structure of the fullerene cage, which can be used for structure elucidation. Fig. 2 shows that Dy2S@C82-I and Dy2C2@C82-I have very similar absorption spectra, which indicates that these two EMFs have the same carbon cage. This spectral pattern is in fact very characteristic for the EMFs with a C82-Cs(6) cage in the formal four-fold charged state, including Er2S@C82-Cs(6),58 Sc2C2@C82-Cs(6),59 Sc2S@C82-Cs(6),46 and Y2C2@C82-Cs(6).60 Thus, we can reliably assign the cage isomer of isostructural Dy2S@C82 and Dy2C2@C82 molecules as C82-Cs(6). The absorption pattern of Dy2S@C82-II closely resembles that of EMFs with the C82-C3v(8) cage in the four-fold charged state, such as sulfide clusterfullerenes Er2S@C82-C3v(8)58 and Sc2S@C82-C3v(8),45,46 or the carbide clusterfullerene M2C2@C82-C3v(8).60,61 Note that the C82-Cs(6) and C82-C3v(8) cages are rather similar and are related via two Stone–Wales transformations (i.e. via the pseudo-rotation of two C–C bonds highlighted in red in Fig. 2 by 90°).Possible orientations of the endohedral clusters in the Dy2C2@C82 and Dy2S@C82 isomers are addressed with the use of DFT calculations (Fig. 2d–f). To avoid difficulties of treating the system with partially-filled 4f-shells at the DFT level, we used Y as a model of Dy in such calculations because of their close ionic radius. For Y2C2@C82-Cs(6) and Y2S@C82-Cs(6), our calculations revealed one particular cluster orientation (identical for both carbide and sulfide clusters), which is at least 25 kJ mol−1 lower in energy than all other configurations (Fig. 2d and e). For Y2S@C82-C3v(8), the calculations revealed several energy minima, all related via rotation of the cluster around the C3 axis of the carbon cage; the lowest-energy one is shown in Fig. 2f. DFT-based Born–Oppenheimer molecular dynamics (BOMD) simulations for Y2S@C82-Cs(6) at 300 and 450 K did not reveal reorientation of the cluster on the 100 ps time scale (Fig. 3a). These data indicate that the Dy2S cluster in Dy2S@C82-Cs(6) is probably fixed, or exhibits jump-like rotations with a low rate. Note that NMR studies of Sc2C2@C82-Cs(6) revealed that the rotation of the cluster became significant at the NMR time-scale only at temperatures above 370 K.59 For Y2S@C82-C3v(8), BOMD simulations show that at room temperature the cluster rotates around the C3 axis (Fig. 3b). A similar conclusion on the rotation of the Sc2S cluster was drawn earlier for Sc2S@C82-C3v(8).45
 | ||
| Fig. 3 (a, b) Born–Oppenheimer molecular dynamics simulations of (a) Y2S@C82-Cs(6) and (b) Y2S@C82-C3v(8) at the PBE/DZVP level, T = 300 K, propagation time 100 ps. Displacements of carbon atoms are not shown. In (a), the symmetry plane of the C82-Cs(6) cage is perpendicular to the paper (in Fig. 2e, the plane is parallel to the paper). In (b), the molecule is viewed along the C3 axis of the C82-C3v(8) cage (which lies in the plane of the paper in Fig. 2f). | ||
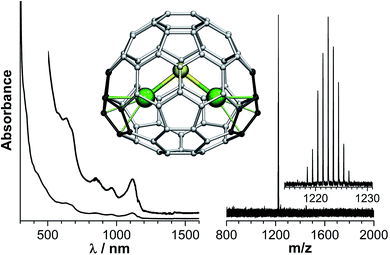
Assignment of the structure of Dy2S@C72 is based on the close similarity of its absorption spectrum (Fig. 4) to that of the non-IPR Sc2S@C72-Cs(10528) reported by Echegoyen et al.62 DFT calculations of different cage isomers of Y2S@C72 also show that C72-Cs(10528) is the most energetically favorable cage isomer for Y2S@C72 (see ESI†). The second most stable isomer, Y2S@C72-Cs(10616), is 42 kJ mol−1 less stable. Thus, based on the absorption spectra and DFT calculations, we assign the structure of isolated Dy2S@C72 to the non-IPR C72-Cs(10528) cage isomer. In this structure, the metal atoms are coordinated to adjacent pentagon pairs, and the cluster is tightly fixed inside the fullerene.
Single-crystal X-ray diffraction
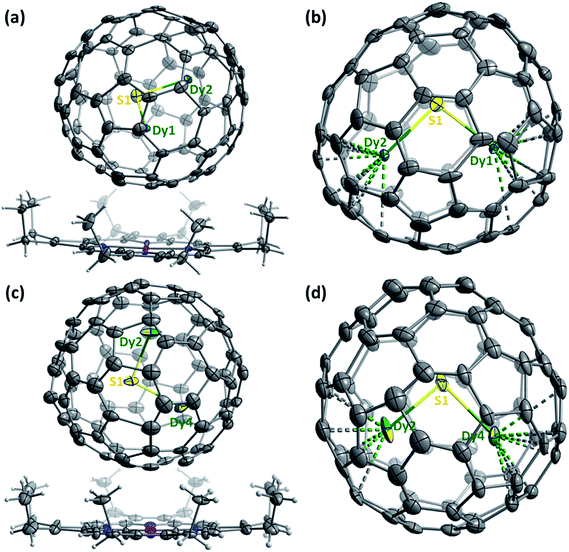
The molecular structures of Dy2S@C82-Cs(6) and Dy2S@C82-C3v(8) are further corroborated by single-crystal X-ray diffraction of the cocrystal Dy2S@C82·NiII(OEP)·2C7H8 (Fig. 5), obtained by layering a toluene solution of NiII(OEP) (OEP = octaethylporphyrin) over a CS2 solution of the fullerene following the procedure developed in ref. 63. After the two solutions diffused together over a period of one month, small black crystals suitable for X-ray crystallographic study formed. X-ray diffraction data collection for the crystal was carried out at 100 K at the BESSY storage ring (BL14.3, Berlin-Adlershof, Germany)64 using a MAR225 CCD detector, λ = 0.89429 Å. Processing the diffraction data was done with the XDSAPP2.0 suite.65 The structure was solved by direct methods and refined using all data (based on F2) by SHELX 2016.66 Hydrogen atoms were located in a difference map, added geometrically, and refined with a riding model. The data can be obtained free of charge from The Cambridge Crystallographic Data Centre with CCDC No. 1546957 and 1551313.†The asymmetric unit cells of both crystals contain a half of the NiII(OEP) molecule and two halves of the C82-Cs(6) or C82-C3v(8) cage. The fully ordered NiII(OEP) molecule is perpendicular to the crystal mirror plane, so the intact molecule was generated by combining the existing half-molecule with its mirror image. Complete fullerene cages in both crystals were generated by combining one of the halves of the fullerene cage with the mirror image of the other. Accordingly, the occupancies of the two cage orientations in both crystals are 0.50 and 0.50, respectively.
For Dy2S@C82-Cs(6), two symmetry-related sulfur positions with 0.50/0.50 occupancies were refined. Dy is disordered over 9 sites with occupancies of 2 × 0.35 (Dy1), 2 × 0.34 (Dy2), 0.11 (Dy3), 0.11 (Dy4), 2 × 0.09 (Dy5), and 0.23 (Dy6) (Dy1, Dy2, and Dy5 are located in general positions and their sites are duplicated by the crystallographic mirror plane, see ESI† for details). The major configuration of the cluster shown in Fig. 5b (Dy1–S–Dy2, 68% of all Dy2S sites) corresponds to the lowest energy structure found by DFT (Fig. 2e) and is similar to that in the crystal structure of Sc2S@C82-Cs(6).67
For Dy2S@C82-C3v(8), S is disordered over 3 sites with occupancies of 2 × 0.31 (S1) and 0.38 (S2). Dy is disordered over 12 sites with occupancies of 0.25 (Dy1), 0.38 (Dy2), 2 × 0.24 (Dy3), 2 × 0.18 (Dy4), 2 × 0.16 (Dy5), 2 × 0.04 (Dy6), and 2 × 0.07 (Dy7) (S1, Dy3, Dy4, Dy5, Dy6 and Dy7 are located in general positions and their sites are duplicated by the crystallographic mirror plane, see ESI† for details). Two configurations of the cluster (Dy2–S1–Dy4 shown in Fig. 5d, and Dy1–S1–Dy3) covering 61% of all Dy2S sites have the same orientation of the cluster inside the cage as in the lowest energy conformer found by DFT (Fig. 2f). This configuration is also similar to the major site (60%) of the Sc2S cluster in the co-crystal of Sc2S@C82-C3v(8) with NiII(OEP).67
Magnetic properties of Dy-clusterfullerenes
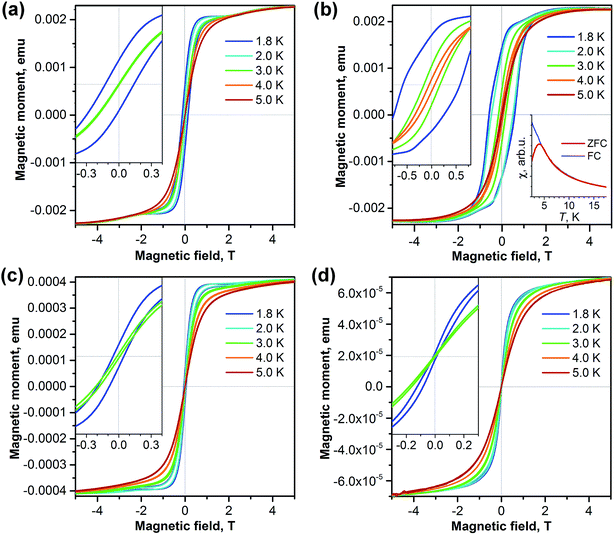
The isolation of two isomers of Dy2S@C82 and the isomer of the carbide Dy2C2@C82 with the same carbon cage as one of the sulfide clusterfullerenes allows us to address the question of how the carbon cage and type of internal cluster affect the magnetic properties of EMFs. Fig. 6 shows magnetization curves for each sample measured in the temperature range from 1.8 to 5 K. Quite remarkable is the difference between the two isomers of Dy2S@C82. The Cs isomer exhibits narrow hysteresis at 1.8 K (coercive field 0.12 T), which closes at 3 K. The hysteresis of the C3v isomer is significantly broader at 1.8 K (coercive field 0.58 T, Fig. 6b), and the closing temperature is between 4 and 5 K. For Dy2S@C82-C3v we could also measure the blocking temperature TB = 4 K as the temperature of the peak in the susceptibility of the zero-field-cooled (ZFC) sample (Fig. 6b); for other samples the TB values are near 2 K, which is too low to be reliably measured. Another SMM characteristic, the temperature at which the relaxation time of magnetization is 100 s, is determined for Dy2S@C82-C3v to be TB100 = 2 K.The magnetization behavior of Dy2C2@C82-Cs is similar to that of the isostructural sulfide. The hysteresis is narrower but closes at a slightly higher temperature (Fig. 6c). Finally, Dy2S@C72 has the smallest opening of hysteresis among all studied samples (Fig. 6d). Thus, all four studied clusterfullerenes exhibited hysteresis of magnetization below 3 K and can be classified as single molecule magnets. Importantly, we observe considerably different SMM properties of sulfide clusterfullerenes with different fullerene cages.
Dynamics of the relaxation of magnetization
To study the dynamics of the relaxation of magnetization at temperatures up to 60–70 K, we performed AC-susceptibility measurements for Dy2C2@C82 and the two isomers of Dy2S@C82 (the amount of isolated Dy2S@C72 was not sufficient for such measurements). Characteristic temperature-dependent peaks in the out-of-phase susceptibility were found for all samples. As an example, Fig. 7 shows χ″ susceptibility for Dy2S@C82-Cs; analogous data for other compounds are available in the ESI.† Magnetization relaxation times τ shorter than 10 s were determined from the AC-data using a generalized Debye model (see Cole–Cole plots in the ESI†). The longer τ values at the lowest temperatures were determined directly by measuring the relaxation of magnetization in a DC mode.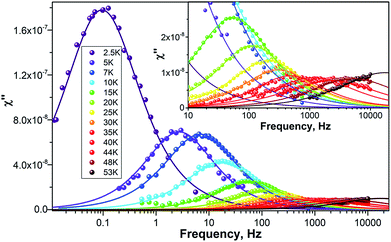 | ||
| Fig. 7 χ″ of Dy2S@C82-Cs measured at different temperatures as a function of AC frequency. Dots are experimental points, lines are results of the fit with a generalized Debye model. | ||
Fig. 8 shows the plots of magnetization relaxation times of Dy2S@C82-Cs, Dy2C2@C82-Cs, and Dy2S@C82-C3v as a function of reciprocal temperature. The two isomers of Dy2S@C82 exhibit strikingly different relaxation dynamics, which in both cases can be described as a combination of Orbach relaxation processes via two or three thermal barriers. The relaxation rate for the Orbach relaxation mechanism is the exponential function of the reciprocal temperature and the energy of an excited state, which defines the effective relaxation barrier Ueff:
τOrbach−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/T) exp(−Ueff/T) | (1) |
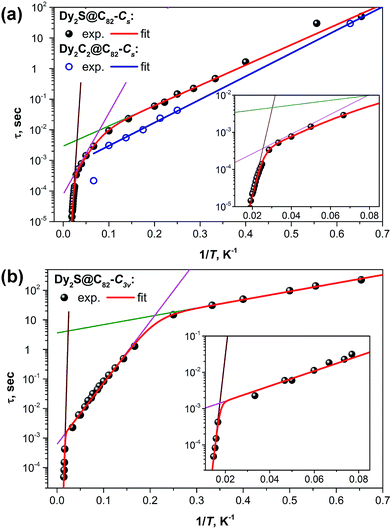 | ||
| Fig. 8 Magnetization relaxation times of (a) Dy2C2@C82-Cs and Dy2S@C82-Cs and (b) Dy2S@C82-C3v. Dots are experimental points, red lines are results of a global fit with three Orbach processes; green, magenta, and brown lines represent contributions of individual Orbach processes. For Dy2C2@C82-Cs with a limited number of data points, a single Orbach process was considered (blue line). Insets show enhancement of the high-temperature range for Dy2S@C82-Cs and Dy2S@C82-C3v. Fitting of the magnetization relaxation of Dy2S@C82-Cs with two Orbach processes and one Raman process is shown in the ESI.† | ||
In the log(τ) vs. 1/T coordinates, relaxation via the Orbach mechanism appears as a straight line. A combination of several Orbach relaxation processes and relaxation via the Raman mechanism would be then described by the equation:
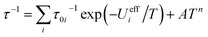 | (2) |
| Dy2C2@C82-Cs | Dy2S@C82-Csb | Dy2S@C82-Csc | Dy2S@C82-C3v | Dy2ScN@C80-Ihd | |
|---|---|---|---|---|---|
| a Effective barriers Ueffi are given in Kelvin, τ0i values are given in seconds. b Modelling magnetization relaxation rate of Dy2S@C82-Cs with three Orbach processes. c Modelling magnetization relaxation rate of Dy2S@C82-Cs with two Orbach processes and an intermediate Raman process; for Dy2S@C82-C3v, the Raman relaxation mechanism could not give an acceptable fit (see ESI). d From ref. 39. e The highest temperature of the range is determined by the frequency and sensitivity limits of the PPMS system. | |||||
| U eff1 | 17.4 ± 0.2 | 15.2 ± 0.3 | 18.0 ± 0.5 | 6.5 ± 0.5 | 10.7 ± 0.3 |
| τ 01 | (5.2 ± 0.3) × 10−4 | (2.9 ± 0.3) × 10−3 | (1.6 ± 0.2) × 10−3 | 3.6 ± 0.8 | 11.9 ± 1.5 |
| T range | 1.6–10 | 1.6–10 | 1.8–15 | 1.6–4 | 1.8–5 |
| U eff2 | 61 ± 6 | 48 ± 1 | |||
| τ 02 | (7.8 ± 2.3) × 10−5 | (6.2 ± 0.6) × 10−4 | |||
| T range | 15–35 | 5–47 | |||
| A | (2.5 ± 0.6) × 10−3 | ||||
| n | 3.97 ± 0.08 | ||||
| T range | ≤1.6, 20–43 | ||||
| U eff3 | 523 ± 35 | 696 ± 86 | 1232 ± 160 | 1735 ± 21 | |
| τ 03 | (6.0 ± 4.4) × 10−10 | (2.5 ± 4.3) × 10−11 | (0.6 ± 1.5) × 10−12 | (2.4 ± 0.8) × 10−15 | |
| T range | 40–53 | 47–53 | 47–70 | 63–76 | |
At the lowest accessible temperatures (1.6–5 K), all three Dy-EMFs exhibit a linear regime with a relatively small barrier, Ueff1, presumably corresponding to the energy difference between the states with ferromagnetically and antiferromagnetically coupled Dy ions (it has contributions from both dipolar and exchange interactions, see more detailed discussion below). Magnetization relaxation pathways proceeding through excited “exchange states” are well documented for 3d–4f complexes, albeit usually with much shorter τ0 values than those observed in EMFs.20,21,23,68–71 In Dy2S@C82-C3v, the Ueff1 barrier amounts to 6.5 K versus 15.2 K in Dy2S@C82-Cs and 17.4 K in Dy2C2@C82-Cs. At the same time, Dy2S@C82-C3v has the longest attempt time τ01 of 3.6 s, which is 3–4 orders of magnitude longer than that of the EMFs with the Cs cage isomer (2.9 ms in Dy2S@C82-Cs and 0.5 ms in Dy2C2@C82-Cs). Thus, due to the smaller barrier, the C3v isomer has a moderate inclination in log(τ) vs. 1/T and hence smaller variation of the relaxation rate with temperature, whereas its much longer τ01 value leads to the considerably longer magnetization relaxation times. The difference between the two isomers of Dy2S@C82 reaches two orders of magnitude near 5 K. In due turn, the magnetization of Dy2C2@C82-Cs relaxes ca. two times faster than that of the isostructural Dy2S@C82-Cs showing that the acetylide C22− central unit in the Dy2C2 cluster is inferior for the SMM properties compared to the sulfide ion S2− in the Dy2S cluster within the same fullerene cage. This finding agrees with our earlier study of Dy2TiC@C80 and Dy2TiC2@C80, which also showed that the single carbide ion in the endohedral cluster leads to much better SMMs than the C2 unit.42 The best EMF-SMM molecule so far is the nitride clusterfullerene Dy2ScN@C80-Ih. It also has a Ueff1 barrier of 10.5 K and a long τ01 value of 12 s (see Table 1).39 Thus, the comparison between sulfide, carbide, and nitride clusterfullerenes with two Dy atoms shows that their magnetization relaxation dynamics at low temperatures is determined by the Orbach process with the “exchange” barrier. The height of the barrier appears to be less important than the attempt time, which varies by several orders of magnitude between the EMFs. The best SMM in the series is not the EMF with the largest exchange barrier, but the molecule with the longest τ01 value.
Above 5 K, the magnetization relaxation mechanisms for the C3v and Cs isomers become significantly different. Between 5 and 47 K, the magnetization relaxation of Dy2S@C82-C3v is driven by another Orbach process with Ueff2 = 48 K and τ02 = 0.36 ms. As will be discussed below in more detail, this barrier is too small to be assigned to one of the crystal-field (CF) states, and the τ02 value is likewise too long for the Orbach processes via CF states normally observed for Dy-SMMs. Above 47 K and up to the instrumental frequency limit at 70 K, the magnetization relaxation of Dy2S@C82-C3v is determined by the energy barrier of 1232 K and the corresponding τ03 value of 0.6 × 10−12 s. Unfortunately, the measurements in this temperature range and frequencies, with the small amount of the available sample, are performed near the sensitivity limit of the PPMS system, which leads to large uncertainties in the determined values. Yet, there is no doubt that the barrier is rather high, but smaller than the barrier of the analogous relaxation process in Dy2ScN@C80, 1735 K. For comparison, the highest thermal relaxation barrier among lanthanide-only dimers, 721 K, was reported recently by Gao et al. for hydroxide-bridged five-coordinate DyIII dimer.18 The highest barrier among non-fullerene polynuclear Dy complexes is 888 K,72 whereas in single-ion Dy SMMs, the largest reported barrier is 1815 K.13
For the Cs isomers, the linear regime with the “exchange” barrier is operative up to ca. 10–15 K. Above ca. 45 K, Dy2S@C82-Cs exhibits a high-energy Orbach process with the parameters typical for the relaxation via a CF state, i.e. large Ueff3 of several hundred K and a τ03 value in the range of 10−10–10−11 s. However, the relaxation dynamics between the temperature ranges of the two Orbach processes, i.e. 15–40 K, are not uniquely defined. Equally good fits were obtained for either an intermediate Orbach process (Ueff2 = 61 K and τ02 = 0.08 ms; see Fig. 8a) or for the Raman relaxation process (A = 2.5 ms K−n and n = 3.97, see Fig. S20†). The choice of either an Orbach or Raman process also affects the parameters of other Orbach processes, especially the Ueff3 and τ03 values (Table 1). The high energy Orbach process is observed at AC frequencies close to the frequency and sensitivity limits of the instrument, which significantly affects the accuracy of the fit and leads to large uncertainties for the Ueff3 and τ03 values. It is very likely that the third linear regime for Dy2S@C82-Cs is not fully reached at accessible temperatures, and that the actual energy barrier for the relaxation via CF state is higher.
To summarize, although Dy2S@C82-C3v and Dy2S@C82-Cs have a similar structure of the encapsulated Dy2S cluster, the differences in their fullerene cages have paramount effect on the magnetization relaxation dynamics. In the whole temperature range accessible for our measurements, relaxation times of the C3v isomer are considerably longer than those of the Cs isomer, from a factor of 5 to two orders of magnitude. The difference in the relaxation behavior of Dy2S@C82-Cs and Dy2C2@C82-Cs is not as pronounced as between the isomers of Dy2S@C82, which shows that the influence of the cage isomerism may be stronger than the influence of the central atom(s) in the endohedral clusters.
Few SMMs with sulfur-ligated Dy have been reported so far,73–75 and all of them have substantially faster relaxation times and smaller relaxation barriers than in the Dy2S@C82 system reported in this work. In the EMF molecules, sulfur bears a substantially larger negative charge and the Dy–S sulfur distances are at the same time much shorter, which altogether leads to a stronger crystal field in sulfide clusterfullerenes.
Effective spin Hamiltonian for di-nuclear Dy EMFs
The system with two Dy centers with magnetic moments J1,2 weakly coupled through exchange/dipolar interactions can be described by the following effective spin Hamiltonian:| Ĥtot = ĤCF1 + ĤCF2 − 2j12Ĵ1Ĵ2 | (3) |
Ab initio calculations of single-ion magnetic anisotropy in Dy-EMFs
Single-point ab initio calculations discussed in this section were performed using a complete active space self-consistent field with spin–orbit interactions (CASSCF/SO-RASSI level of theory) as implemented in MOLCAS 8.0.76 In all systems, Dy3+ has a 6H15/2 ground state multiplet, resulting in eight low-lying Kramers doublets. The active space of the CASSCF calculations includes nine active electrons and seven active orbitals (e.g. CAS (9,7)). The single ion CF-parameters were then obtained with the use of the SINGLE_ANISO module77 and transferred to the PHI code78 for further pseudospin analysis of single ion as well total spin states. The crystal structures of EMFs often exhibit strong disorder of the cage and cluster positions, thus limiting the use of X-ray determined geometries for accurate analysis of the crystal field splitting. Besides, crystal structures are not always available. In this work, molecular geometries were optimized by DFT for Y analogs, and then one of the Y ions was replaced by Dy for the subsequent ab initio calculations. Table 2 lists the CF energy levels for each Dy ion in Dy2S@C72, the two isomers of Dy2S@C82, and Dy2C2@C82-Cs. Note that the term “crystal field” is somewhat ambiguous here since de facto we discuss splitting of the Jz levels by the intramolecular interactions between the Dy ion and surrounding ions. The term “crystal field” is inherited in the field of SMMs from the earlier studies of lanthanide solids and broadly used in the literature, and we follow this convention.| KD | Dy2S@C72 | Dy2C2@C82-Cs | Dy2S@C82-Cs | Dy2S@C82-C3v | |||
|---|---|---|---|---|---|---|---|
| Dy1 | Dy2 | Dy1 | Dy2 | Dy1 | Dy2 | ||
| a Energies are given in cm−1, the conversion factor of cm−1 to Kelvin units is 1.439. b X is either a sulfide ion in sulfide clusterfullerenes or a center of the acetylide unit in Dy2C2@C82. | |||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 181 | 225 | 185 | 228 | 221 | 269 | 295 |
| 3 | 398 | 354 | 393 | 381 | 450 | 424 | 459 |
| 4 | 572 | 469 | 551 | 512 | 622 | 549 | 593 |
| 5 | 658 | 588 | 668 | 648 | 723 | 653 | 701 |
| 6 | 691 | 688 | 747 | 764 | 799 | 743 | 788 |
| 7 | 765 | 742 | 791 | 848 | 857 | 806 | 858 |
| 8 | 876 | 806 | 868 | 913 | 905 | 881 | 967 |
| d(Dy–Xb), Å | 2.456 | 2.313 | 2.329 | 2.484 | 2.506 | 2.509 | 2.486 |
| ∠(Dy–Xb–Dy)° | 104.7 | 112.1 | 99.4 | 97.2 | |||
The ground states of the Dy ions in all studied EMFs feature a highly anisotropic g-tensor with gzz near 19.8–19.9 and vanishingly small gxx and gyy components (see ESI† for more details), which corresponds to the “pure” state with Jz = ±15/2. The overall CF splitting (ΔE1–8 hereafter) is in the range of 810–970 cm−1. The smallest energy difference between the ground and the first excited state, ΔE1–2 = 181 cm−1, is found in Dy2S@C72; for all other EMFs the ΔE1–2 energies are larger and reach 295 cm−1 for one of the Dy centers in Dy2S@C82-C3v. These values are sufficiently high to conclude that the magnetic properties of these EMFs at liquid helium temperatures are determined solely by the ground state and intramolecular exchange/dipolar coupling between magnetic moments.
Although the central non-metal ion is the main “source” of magnetic anisotropy, the CF splitting in sulfide clusterfullerenes is not a simple function of the metal-sulfur distance. With a considerably shorter Dy–S distance, Dy2S@C72 has the smallest ΔE1–2 energy gap among the studied sulfide clusterfullerenes. Likewise, with almost identical Dy–S bond lengths and cluster geometry, the ΔE1–2 values in Dy2S@C82-C3v are larger than those in Dy2S@C82-Cs. Thus, despite the relatively small charges of individual carbon atoms, the fullerene cage (and in particular, the coordination mode of Dy ions to the nearby carbons) also plays a certain role, which may have a critical effect on the difference between the otherwise similar isomers.
The influence of the non-metal species on the magnetic anisotropy can be clearly seen from the comparison of Dy2C2@C82-Cs and Dy2S@C82-Cs. The Dy atoms in both molecules have virtually identical metal-cage coordination. Besides, the orientations of the anisotropy axes for each metal center are also very similar (along the Dy–S axes in Dy2S@C82 and along the axes connecting Dy and the midpoint between the two carbons in Dy2C2@C82). Finally, the acetylide unit and the sulfide ion have the same formal charge, −2. But in the Dy2S cluster, the negative charge is localized on the single sulfur atom, whereas in the Dy2C2 cluster the charge is shared between the two carbons. As a result, the CF splitting in the carbide clusterfullerene is systematically smaller than that in the sulfide clusterfullerene by 10%.
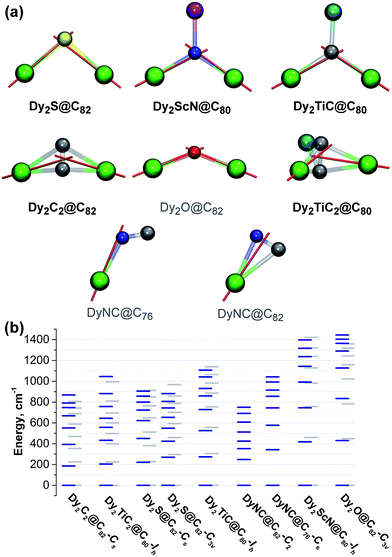
To place these results into a broader context, we performed ab initio calculations for Dy centers in other di-Dy clusterfullerenes known to exhibit SMM properties, including Dy2ScN@C80-Ih, Dy2TiC@C80-Ih, and Dy2TiC2@C80-Ih. Also studied were hypothetical DyNC@C82-C2(5), DyNC@C76-C2v(19138), and Dy2O@C82-C3v(8), whose synthesis appears feasible based on the literature reports on analogous EMFs with other metals (such as cyano clusterfullerenes TbNC@C76 (ref. 44) and three cage isomers of TbNC@C82,43,79 or oxide clusterfullerenes Sc2O@C2n,80–82 Y2O@C2n, and Lu2O@C2n (ref. 83)).
In clusterfullerenes with a single non-metal atom, the magnetic anisotropy axis is aligned along the bond connecting Dy to the central atom, sometimes with a slight deviation of a few grad (Fig. 9). In carbide clusterfullerenes with an acetylide unit, the anisotropy axis is directed towards the point between the two carbon atoms, whereas in clusterfullerenes with CN− ions the axis is directed towards more negatively charged nitrogen, but significantly deviates from the metal-nitrogen axis.
Among the EMFs with experimentally studied magnetic properties, Dy2ScN@C80-Ih has the largest ΔE1–2 and ΔE1–8 values (418/460 and 1397/1421 cm−1, respectively; similar values were predicted for this molecule by Chibotaru et al.32). The Dy–N distances in Dy2ScN@C80, 2.107/2.111 Å, are much shorter than the Dy–S distances in clusterfullerenes, whereas the formal charge of the nitride ion is higher, which altogether explains the substantially larger CF splitting. Dy2TiC@C80 is very similar to Dy2ScN@C80 in its charge distribution and has slightly longer bonds between Dy and the central carbon (2.176/2.192 Å) than in the nitride clusterfullerene. Nonetheless, it has considerably smaller ΔE1–2 and ΔE1–8 splitting (273/304 and 1106/1139 cm−1, respectively) than in Dy2ScN@C80-Ih, but still slightly higher than in the sulfide clusterfullerenes. In Dy2TiC2@C80-Ih, the CF splitting is much smaller (204/224 and 1045/994 cm−1 for ΔE1–2 and ΔE1–8, respectively), which makes it similar to Dy2C2@C82-Cs.
Interestingly, although none of the relaxation processes described in the EMF-SMMs so far involve the first CF excited state, there is an empirical correlation between the strength of the EMF-SMM and the ΔE1–2 gap. Dy2ScN@C80-Ih is the best EMF-SMM so far followed by Dy2TiC@C80-Ih, which is comparable to Dy2S@C82-C3v. Dy2S@C82-Cs has a smaller ΔE1–2 energy than the C3v isomer and exhibits poorer SMM properties, and Dy2C2@C82-Cs is inferior to Dy2S@C82-Cs. If this correlation holds for other EMFs, then the oxide clusterfullerene Dy2O@C82-C3v may become a superior SMM than Dy2ScN@C80 as it has the largest ΔE1–2 and ΔE1–8 values (430/448 and 1358/1444 cm−1, respectively) in the whole group of computed EMFs. The reasons are the short Dy–O distances (2.041/2.029 Å) and rather large Dy–O–Dy angle of 134°. Even larger CF splitting was predicted recently in mixed-metal Dy–Sc and Dy–Lu oxide clusterfullerenes by Rajaraman et al.84 Thus, Dy-oxide clusterfullerenes seem to be a reasonable target for the SMM-EMF synthesis. Dy-cyano clusterfullerenes are expected to be comparable to sulfide clusterfullerenes in terms of the CF splitting. Flexible cluster geometry from almost linear in MNC@C76 to triangular in MNC@C82 leads to a large variation of the CF splitting (Fig. 9).
To evaluate the effect of dynamical correlation on CF splitting, a series of additional calculations were performed for simpler model systems, in which all cage carbon atoms were replaced by point charges corresponding to their formal charges in the respective EMFs. When 18 sextets and 15 quartets are used in the CASSCF computations, the model gives a reasonable agreement with full-molecule calculations at only a fraction of the computational cost. Subsequent multi-reference configuration interaction (MRCI) calculations were then performed with 18 sextets and 8 quartets using the Molpro code.85 MRCI calculations show that dynamic correlation increases the ΔE1–2 energy by ca. 10–15% (see ESI†). We can tentatively suggest that due to the lack of dynamical correlation, the CASSCF calculations for Dy-EMFs described above underestimate the CF splitting in a similar manner.
The strength of the molecular magnet is determined not only by the CF splitting, but also by the transition probabilities between the states with opposite spin, which are determined by transverse components (gxx and gyy) of the g-tensor. Our calculations show that the nature of the central atom(s) and the cluster geometry strongly affect the transverse components of the g-tensor (see Tables S6–S15† for transition probabilities between single-ion states in all computed Dy-clusterfullerenes). The clusters with compact single non-metal atoms, such as oxide and nitride clusterfullerenes, have the smallest transverse components for several lowest excited states, which leads to the low transition probabilities. Our recent experimental study of the relaxation mechanism in Dy2ScN@C80-Ih revealed that the Orbach relaxation process observed at high temperatures corresponds to the relaxation via the fifth Kramers doublet.39 On the other hand, the clusters with diatomic central units have a considerably higher transverse component of the g-tensor, which substantially increases transition probabilities for lower-energy KDs. For C2 and CN central units, larger transverse components are observed already for the ground state (which may be another reason for the poorer SMM properties of carbide clusterfullerenes). Sulfide clusterfullerenes with relatively large sulfide ions are inferior to oxide and nitride clusterfullerenes, but are better than carbide and cyano-clusterfullerenes.
Exchange and dipolar interactions in Dy-EMFs
The low-temperature relaxation dynamics of all three EMF-SMMs with two Dy ions are determined by the exchange/dipolar barrier Ueff1. That is, due to the dipolar and exchange interactions between the Dy ions, the ground and the first excited state of the dinuclear system are the states in which Dy ions in their single-ion ground state (Jz = ±15/2) are coupled ferromagnetically and antiferromagnetically, respectively, and the Orbach process proceeds via the antiferromagnetic state. Knowing the Ueff1 values, the j12 coupling constants in eqn (2) can be computed by matching the lowest excited state energy (Table 3).| U eff1, K | j exp12, cm−1 | α, ° | ΔEdip, K | j dip12, cm−1 | j ex12,a cm−1 | |
|---|---|---|---|---|---|---|
a To compute exchange coupling constants, jex12(Gd–Gd) values in Gd-EMF analogs were first computed using Orca code86 at the PBE0/TZVP-DKH87,88 level within the broken-symmetry approximation, and then scaled by a factor of 25/49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α). cos(α).
|
||||||
| Dy2S@C72 | 78.8 | 3.4 | 0.051 | 0.013 | ||
| Dy2S@C82-Cs | 15.2 | 0.220 | 77.6 | 3.6 | 0.051 | 0.136 |
| Dy2S@C82-C3v | 6.5 | 0.104 | 78.9 | 3.7 | 0.059 | 0.063 |
| Dy2C2@C82-Cs | 17.4 | 0.175 | 71.8 | 3.7 | 0.025 | 0.108 |
| Dy2ScN@C80 | 10.5 | 0.073 | 62.8 | 4.6 | 0.031 | 0.128 |
| Dy2TiC@C80 | 62.3 | 4.4 | 0.029 | 0.159 | ||
| Dy2TiC2@C80 | 71.8 | 5.0 | 0.050 | 0.073 | ||
| Dy2O@C82-C3v | 45.7 | 4.4 | 0.018 | 0.110 | ||
Dipolar contributions to Ueff1 energies (Table 3) are calculated straightforwardly using the equation:
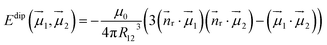 | (4) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) r is the normal of the radius vector connecting two magnetic moments µ1 and µ2, and R12 is the distance between them. The angles between the moments are taken from ab initio calculations. The ΔEdip values listed in Table 3 show that for all EMFs the dipolar contribution is in the range of 3.4–5 K. ΔEdip constitutes roughly a half of the Ueff1 barriers in Dy2S@C82-C3v and Dy2ScN@C80, but is below 25% of that in Dy2S@C82-Cs and Dy2C2@C82-Cs. From ΔEdip, the dipolar contribution jdip12 to the j12 constant in eqn (3) is computed by scaling with the factor of 152
r is the normal of the radius vector connecting two magnetic moments µ1 and µ2, and R12 is the distance between them. The angles between the moments are taken from ab initio calculations. The ΔEdip values listed in Table 3 show that for all EMFs the dipolar contribution is in the range of 3.4–5 K. ΔEdip constitutes roughly a half of the Ueff1 barriers in Dy2S@C82-C3v and Dy2ScN@C80, but is below 25% of that in Dy2S@C82-Cs and Dy2C2@C82-Cs. From ΔEdip, the dipolar contribution jdip12 to the j12 constant in eqn (3) is computed by scaling with the factor of 152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α), where α is the angle between the anisotropy axes of individual Dy ions.
cos(α), where α is the angle between the anisotropy axes of individual Dy ions.
The calculation of the exchange contribution to the coupling constant for Dy is not straightforward, and it is a common praxis to use Gd analogs to estimate jex12. For the latter, exchange coupling constants are computed using broken-symmetry approximation at the DFT level, and the different spin moments of Dy and Gd as well as non-collinearity of magnetic moments is accounted for by multiplying with the factor of 25/49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α).32 The values calculated this way for Dy-EMFs (Table 3) are in reasonable agreement with experiment. Similar jex12 values are predicted for all other Dy-EMFs, showing that the extent of the exchange/dipolar coupling between the magnetic moment of Dy ions in clusterfullerenes is not dramatically changing with variation of the central atom(s). Remarkably, the jex12 value in Dy2S@C82-C3v is predicted to be considerably smaller than that in the Cs isomer.
cos(α).32 The values calculated this way for Dy-EMFs (Table 3) are in reasonable agreement with experiment. Similar jex12 values are predicted for all other Dy-EMFs, showing that the extent of the exchange/dipolar coupling between the magnetic moment of Dy ions in clusterfullerenes is not dramatically changing with variation of the central atom(s). Remarkably, the jex12 value in Dy2S@C82-C3v is predicted to be considerably smaller than that in the Cs isomer.
Once the CF and coupling parameter in the spin Hamiltonian are known or estimated, the solution of eqn (3) allows simulation of the magnetization curves. Low-temperature experimental magnetization curves (Fig. 6 and S23†) have peculiarities at 1.5–2 T, whose presence is caused by exchange/dipolar interactions and hence can be used to verify the computational model. For Dy2C2@C82-Cs and Dy2S@C82-Cs, the use of j12 parameters fitted to match the experimental Ueff1 values (0.175 and 0.220 cm−1, respectively) leads to good agreement between simulated and experimental curves, confirming the assignment of Ueff1 to the exchange/dipolar barrier. However, for Dy2S@C82-C3v, the agreement with experiment is less satisfactory (Fig. S23†). To match the experimental magnetization curve, the j12 parameter should be increased from 0.104 cm−1 to 0.18 cm−1, which amounts to the calculated Ueff1 barrier of 11 K. The discrepancy between experimental and calculated Ueff1 is likely to be caused by the not-well defined geometry of the Dy2S cluster as exchange parameters are very sensitive to the Dy–S–Dy angle, and for the C3v isomer the cluster is not fixed in one positon but is rather disordered between several ones.
Orbach relaxation via CF states
The large Ueff3 barriers of hundreds of K observed in both isomers of Dy2S@C82 are indicative of the relaxation via CF states. It is usually assumed that in polynuclear systems, the Orbach mechanism involves CF states of the individual lanthanide ion. In Dy2S@C82-C3v, ab initio CF splitting and transition probability calculations show that the barriers for the relaxation via individual CF states of single Dy ions unperturbed by interaction with another Dy center may be expected in the range of up to 1000 K (corresponding to the fifth Kramer doublet), whereas the total CF splitting is exceeding 1300 K (Fig. 9). Within the limits of rather high experimental uncertainties, the experimental value is in line with this expectation. For Dy2S@C82-Cs, ab initio calculations show that relaxation via lower-energy Kramers doublets can also be efficient (see Table S6†). This expectation is also in line with the lower Ueff3 value observed for this compound experimentally (Table 1), but currently impossible higher-frequency AC measurements would be necessary to confirm the Ueff3 barrier in Dy2S@C82-Cs.Intermediate barrier
The nature of the Orbach relaxation processes in Dy2S@C82 isomers with barriers of 50–60 K cannot be explained based on the energy spectrum of the Hamiltonian (3). The Ueff2 values are clearly above the exchange/dipolar barrier and yet well below the energies of the CF-derived excited states. Besides, τ02 values are also much longer than would be expected for the relaxation through CF excited states.Multiple studies of the electron spin-lattice relaxation times in salts of transition metals and lanthanides starting from the early 1960s and later on revealed that relaxation via the Raman mechanism in the presence of the so-called localized phonon of frequency ω (usually associated with defects in those studies) can take an exponential form proportional to exp(−ħω/kBT).89–91 In other words, it can be described as an Orbach relaxation process with the energy barrier corresponding to the phonon excited state. Orbach relaxation processes with barriers corresponding to the frequencies of molecular vibrations were also observed in N@C60 (ref. 92) and other paramagnetic solids and host–guest systems.93–95 Very recently, Sanvito et al. studied the role of phonons in the under-barrier spin relaxation of SMMs and found that an anharmonic phonon with finite linewidth may result in the Arrhenius behavior with the barrier corresponding to a half of the phonon frequency.96
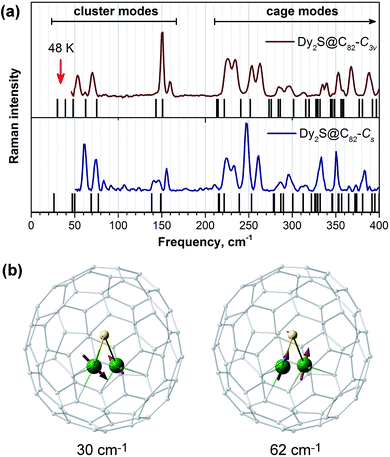
To our knowledge, the possibility of Orbach relaxation via an excited phonon state has not been widely considered for SMMs. Usually, SMMs have rather high vibrational density of states in the low frequency range due to the presence of “floppy” fragments and side chains in the ligands. However, fullerene molecules are quite rigid, and their lowest frequency vibrations occur above 200 cm−1. In EMFs, encapsulated clusters with heavy lanthanide atoms have few low-frequency vibrational modes due to frustrated rotations and translation as well as internal cluster vibrations. In the Raman spectra of Dy2S@C82 isomers shown in Fig. 10a, the cage (above 220 cm−1) and the cluster (between 50 and 160 cm−1) vibrational features are well separated. The frequencies of ∼40 cm−1 corresponding to Ueff2 values lie outside the accessible range of our spectrometer, but DFT computations show the presence of cluster vibrations in this frequency range, mainly of the librational character (in Dy2S@C82-C3v such modes are predicted at 30, 39, and 48 cm−1). It is reasonable to suggest that the lowest-frequency librational mode may be responsible for the Orbach relaxation process with a barrier of 48 K (33 cm−1). On the other hand, if following Sanvito et al. we suggest that the observed barrier corresponds to a half of the phonon frequency,96 then the relaxation of magnetization in Dy2S@C82 may be induced by the mixed translation/deformation mode of the Dy2S cluster with the calculated frequency of 62 cm−1 (Fig. 10b).
Thus, shielding of endohedral species by the carbon cage not only stabilizes the otherwise “improper” endohedral species (none of the clusters discussed in this work can exist outside the fullerene), but also isolates the Dy spin system from the lattice phonon bath, resulting in a kind of phonon bottlenecking at low temperatures. When the local vibrational modes gain certain thermal population, a new Orbach relaxation pathway is open and the rate of relaxation is accelerated. The sparse vibrational density of states in EMFs may be the reason for the long relaxation times that these molecules exhibit at low temperatures. Further studies of the low-frequency vibrational density of states as well as development of a rigorous theory of the spin-phonon relaxation in SMMs are required to confirm this hypothesis.
Conclusions
In this article, we report a new method for the selective synthesis of sulfide clusterfullerenes. We utilized the suppressing influence of hydrogen on the empty fullerene formation and performed arc-discharge synthesis in the presence of methane. Under optimized conditions, and with the use of dysprosium sulfide as a source of metal and sulfur, Dy2S@C2n clusterfullerenes could be synthesized with a high degree of selectivity, and molecular structures of the most abundant Dy-sulfide clusterfullerenes, Dy2S@C82 isomers with Cs(6) and C3v(8) cage symmetry, were elucidated by single-crystal X-ray diffraction. The yield of carbide clusterfullerenes appears to be much lower when sulfur is present in the system. This finding shows that the clusterfullerenes with other central atoms may also be selectively synthesized this way with the proper choice of arc-discharge conditions.The magnetic properties of Dy-sulfide clusterfullerenes, Dy2S@C82-Cs and Dy2S@C82-C3v, and of one Dy-carbide clusterfullerene, Dy2C2@C82-Cs, have been further studied by DC and AC magnetometry and ab initio calculations. All molecules were found to be single molecule magnets with hysteresis of magnetization below 3–4 K, and with substantially different cage- and cluster-dependent relaxation rates. Among the two isomers of Dy2S@C82, the one with the C3v(8) carbon cage is a far more superior SMM than the analogous molecule with the Cs(6) carbon cage, whereas among the two EMFs with the C82-Cs(6) fullerene cage, the sulfide clusterfullerene Dy2S@C82 has longer relaxation times than the carbide clusterfullerene Dy2C2@C82. Ab initio calculations for different types of clusterfullerenes showed that the clusters with a single non-metal ion are more preferable for the better SMM performance than the clusterfullerenes with diatomic non-metal units, and oxide clusterfullerenes were found to have the highest crystal field splitting.
Dynamic magnetic studies showed that the relaxation of magnetization in Dy2S@C82 isomers unprecedentedly involves three Orbach processes operative at different temperatures. Below 5–10 K, the dominant process is the relaxation via the exchange/dipolar excited state with antiferromagnetic coupling of Dy ions. At temperatures above 40–50 K, Orbach relaxation via crystal-field excited states with relative energies exceeding 500 K is observed. The CF barriers in sulfide clusterfullerenes are among the highest magnetization relaxation barriers observed in dinuclear Dy-SMMs so far. For the intermediate temperatures, we have discovered an unusual Orbach process, whose energy barrier of 50–60 K corresponds to the intramolecular vibrations of the EMF molecules involving librational motions of the endohedral cluster.
Acknowledgements
The authors acknowledge funding by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 648295 “GraM3”). Main computational resources were provided by the Center for Information Services and High Performance Computing (ZIH) in TU Dresden. The authors thank Ulrike Nitzsche for technical assistance with computational resources at IFW Dresden, Sebastian Gaß for help with the magnetic measurements, and Frank Ziegs and Sandra Schiemenz for assistance with the spectroscopic measurements. Manfred Weiss and Karine M. Röwer are acknowledged for their help with crystallographic measurements at BESSY.References
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33 CrossRef CAS.
- R. A. Layfield, Organometallics, 2014, 33, 1084–1099 CrossRef CAS.
- F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288 RSC.
- P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923–3929 RSC.
- J. Dreiser, J. Phys.: Condens. Matter, 2015, 27, 183203 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556–13567 RSC.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed. Engl., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed.
- W. Huang, F.-X. Shen, S.-Q. Wu, L. Liu, D. Wu, Z. Zheng, J. Xu, M. Zhang, X.-C. Huang, J. Jiang, F. Pan, Y. Li, K. Zhu and O. Sato, Inorg. Chem., 2016, 55, 5476–5484 CrossRef CAS PubMed.
- J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Chem. Sci., 2017, 8, 1288–1294 RSC.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- H.-H. Zou, L.-B. Sheng, F.-P. Liang, Z.-L. Chen and Y.-Q. Zhang, Dalton Trans., 2015, 44, 18544–18552 RSC.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. Sci., 2014, 5, 3246–3256 RSC.
- M. Andruh, J. P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342–3359 CrossRef CAS PubMed.
- X.-L. Li, F.-Y. Min, C. Wang, S.-Y. Lin, Z. Liu and J. Tang, Inorg. Chem., 2015, 54, 4337–4344 CrossRef CAS PubMed.
- L. Rosado Piquer and E. C. Sanudo, Dalton Trans., 2015, 44, 8771–8780 RSC.
- K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289–290, 74–122 CrossRef CAS.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760 RSC.
- S. Yang, F. Liu, C. Chen, M. Jiao and T. Wei, Chem. Commun., 2011, 47, 11822–11839 RSC.
- M. Wolf, K. H. Muller, Y. Skourski, D. Eckert, P. Georgi, M. Krause and L. Dunsch, Angew. Chem., Int. Ed., 2005, 44, 3306–3309 CrossRef CAS PubMed.
- Y. Zhang, D. Krylov, M. Rosenkranz, S. Schiemenz and A. A. Popov, Chem. Sci., 2015, 6, 2328–2341 RSC.
- Y. Zhang, D. Krylov, S. Schiemenz, M. Rosenkranz, R. Westerstrom, J. Dreiser, T. Greber, B. Buchner and A. A. Popov, Nanoscale, 2014, 6, 11431–11438 RSC.
- V. Vieru, L. Ungur and L. F. Chibotaru, J. Phys. Chem. Lett., 2013, 4, 3565–3569 CrossRef CAS.
- F. Cimpoesu, N. Dragoe, H. Ramanantoanina, W. Urland and C. Daul, Phys. Chem. Chem. Phys., 2014, 16, 11337–11348 RSC.
- A. L. Svitova, Y. Krupskaya, N. Samoylova, R. Kraus, J. Geck, L. Dunsch and A. A. Popov, Dalton Trans., 2014, 43, 7387–7390 RSC.
- C. F. Hermanns, M. Bernien, A. Krüger, C. Schmidt, S. T. Waßerroth, G. Ahmadi, B. W. Heinrich, M. Schneider, P. W. Brouwer, K. J. Franke, E. Weschke and W. Kuch, Phys. Rev. Lett., 2013, 111, 167203 CrossRef PubMed.
- B. Náfrádi, Á. Antal, Á. Pásztor, L. Forró, L. F. Kiss, T. Fehér, É. Kováts, S. Pekker and A. Jánossy, J. Phys. Chem. Lett., 2012, 3, 3291–3296 CrossRef.
- R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, J. Am. Chem. Soc., 2012, 134, 9840–9843 CrossRef PubMed.
- R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060406 CrossRef.
- D. S. Krylov, F. Liu, S. M. Avdoshenko, L. Spree, B. Weise, A. Waske, A. U. B. Wolter, B. Büchner and A. A. Popov, Chem. Commun., 2017, 53, 7901–7904 RSC.
- R. Westerström, A.-C. Uldry, R. Stania, J. Dreiser, C. Piamonteze, M. Muntwiler, F. Matsui, S. Rusponi, H. Brune, S. Yang, A. Popov, B. Büchner, B. Delley and T. Greber, Phys. Rev. Lett., 2015, 114, 087201 CrossRef PubMed.
- J. Dreiser, R. Westerström, Y. Zhang, A. A. Popov, L. Dunsch, K. Krämer, S.-X. Liu, S. Decurtins and T. Greber, Chem.–Eur. J., 2014, 20, 13536–13540 CrossRef CAS PubMed.
- K. Junghans, C. Schlesier, A. Kostanyan, N. A. Samoylova, Q. Deng, M. Rosenkranz, S. Schiemenz, R. Westerström, T. Greber, B. Büchner and A. A. Popov, Angew. Chem., Int. Ed. Engl., 2015, 54, 13411–13415 CrossRef CAS PubMed.
- F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771 CrossRef CAS PubMed.
- F. Liu, S. Wang, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, F. Jin, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, Angew. Chem., Int. Ed. Engl., 2017, 56, 1830–1834 CrossRef CAS PubMed.
- L. Dunsch, S. Yang, L. Zhang, A. Svitova, S. Oswald and A. A. Popov, J. Am. Chem. Soc., 2010, 132, 5413–5421 CrossRef CAS PubMed.
- N. Chen, M. N. Chaur, C. Moore, J. R. Pinzon, R. Valencia, A. Rodriguez-Fortea, J. M. Poblet and L. Echegoyen, Chem. Commun., 2010, 46, 4818–4820 RSC.
- L. Dunsch, M. Krause, J. Noack and P. Georgi, J. Phys. Chem. Solids, 2004, 65, 309–315 CrossRef CAS.
- L. Dunsch, P. Georgi, M. Krause and C. R. Wang, Synth. Met., 2003, 135, 761–762 Search PubMed.
- S. Yang, L. Zhang, W. Zhang and L. Dunsch, Chem.–Eur. J., 2010, 16, 12398–12405 CrossRef CAS PubMed.
- F. Liu, J. Guan, T. Wei, S. Wang, M. Jiao and S. Yang, Inorg. Chem., 2013, 52, 3814–3822 CrossRef CAS PubMed.
- A. L. Svitova, A. A. Popov and L. Dunsch, Inorg. Chem., 2013, 52, 3368–3380 CrossRef CAS PubMed.
- M. Jiao, W. Zhang, Y. Xu, T. Wei, C. Chen, F. Liu and S. Yang, Chem.–Eur. J., 2012, 18, 2666–2673 CrossRef CAS PubMed.
- S. Stevenson, M. C. Thompson, H. L. Coumbe, M. A. Mackey, C. E. Coumbe and J. P. Phillips, J. Am. Chem. Soc., 2007, 129, 16257–16262 CrossRef CAS PubMed.
- K. Junghans, M. Rosenkranz and A. A. Popov, Chem. Commun., 2016, 52, 6561–6564 RSC.
- K. Junghans, K. B. Ghiassi, N. A. Samoylova, Q. Deng, M. Rosenkranz, M. M. Olmstead, A. L. Balch and A. A. Popov, Chem.–Eur. J., 2016, 22, 13098–13107 CrossRef CAS PubMed.
- Q. Deng, K. Junghans and A. A. Popov, Theor. Chem. Acc., 2015, 134, 10 CrossRef.
- A. L. Svitova, K. Ghiassi, C. Schlesier, K. Junghans, Y. Zhang, M. Olmstead, A. Balch, L. Dunsch and A. A. Popov, Nat. Commun., 2014, 5, 3568 CAS.
- N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. Kirkhorn, M. Rosenkranz, S. Schiemenz, F. Ziegs, A. U. B. Wolter, S. Yang, S. Stevenson and A. A. Popov, Nanoscale, 2017, 9, 7977–7990 RSC.
- X. Lu, K. Nakajima, Y. Iiduka, H. Nikawa, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2011, 133, 19553–19558 CrossRef CAS PubMed.
- T. Inoue, T. Tomiyama, T. Sugai, T. Okazaki, T. Suematsu, N. Fujii, H. Utsumi, K. Nojima and H. Shinohara, J. Phys. Chem. B, 2004, 108, 7573–7579 CrossRef CAS.
- Y. Iiduka, T. Wakahara, K. Nakajima, T. Tsuchiya, T. Nakahodo, Y. Maeda, T. Akasaka, N. Mizorogi and S. Nagase, Chem. Commun., 2006, 2057–2059 RSC.
- N. Chen, C. M. Beavers, M. Mulet-Gas, A. Rodriguez-Fortea, E. J. Munoz, Y.-Y. Li, M. M. Olmstead, A. L. Balch, J. M. Poblet and L. Echegoyen, J. Am. Chem. Soc., 2012, 134, 7851–7860 CrossRef CAS PubMed.
- M. M. Olmstead, D. A. Costa, K. Maitra, B. C. Noll, S. L. Phillips, P. M. Van Calcar and A. L. Balch, J. Am. Chem. Soc., 1999, 121, 7090–7097 CrossRef CAS.
- U. Mueller, R. Förster, M. Hellmig, F. U. Huschmann, A. Kastner, P. Malecki, S. Pühringer, M. Röwer, K. Sparta, M. Steffien, M. Ühlein, P. Wilk and M. S. Weiss, Eur. Phys. J. Plus, 2015, 130, 141 CrossRef.
- K. M. Sparta, M. Krug, U. Heinemann, U. Mueller and M. S. Weiss, J. Appl. Crystallogr., 2016, 49, 1085–1092 CAS.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 CrossRef PubMed.
- B. Q. Mercado, N. Chen, A. Rodriguez-Fortea, M. A. Mackey, S. Stevenson, L. Echegoyen, J. M. Poblet, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 6752–6760 CrossRef CAS PubMed.
- K. C. Mondal, A. Sundt, Y. Lan, G. E. Kostakis, O. Waldmann, L. Ungur, L. F. Chibotaru, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed. Engl., 2012, 51, 7550–7554 CrossRef CAS PubMed.
- X.-L. Li, F.-Y. Min, C. Wang, S.-Y. Lin, Z. Liu and J. Tang, Dalton Trans., 2015, 44, 3430–3438 RSC.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed. Engl., 2013, 52, 12014–12019 CrossRef CAS PubMed.
- J. Li, R.-M. Wei, T.-C. Pu, F. Cao, L. Yang, Y. Han, Y.-Q. Zhang, J.-L. Zuo and Y. Song, Inorg. Chem. Front., 2017, 4, 114–122 RSC.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed. Engl., 2012, 51, 6976–6980 CrossRef CAS PubMed.
- S.-S. Liu, K. Lang, Y.-Q. Zhang, Q. Yang, B.-W. Wang and S. Gao, Dalton Trans., 2016, 45, 8149–8153 RSC.
- W. Cao, C. Gao, Y.-Q. Zhang, D. Qi, T. Liu, K. Wang, C. Duan, S. Gao and J. Jiang, Chem. Sci., 2015, 6, 5947–5954 RSC.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- F. Liu, S. Wang, J. Guan, T. Wei, M. Zeng and S. Yang, Inorg. Chem., 2014, 53, 5201–5205 CrossRef CAS PubMed.
- M. Zhang, Y. Hao, X. Li, L. Feng, T. Yang, Y. Wan, N. Chen, Z. Slanina, F. Uhlik and H. Cong, J. Phys. Chem. C, 2014, 118, 28883–28889 CAS.
- B. Q. Mercado, M. A. Stuart, M. A. Mackey, J. E. Pickens, B. S. Confait, S. Stevenson, M. L. Easterling, R. Valencia, A. Rodriguez-Fortea, J. M. Poblet, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2010, 132, 12098–12105 CrossRef CAS PubMed.
- Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2016, 55, 1926–1933 CrossRef CAS PubMed.
- S. Stevenson, in Endohedral Fullerenes. From Fundamentals to Applications, ed. S. Yang and C.-R. Wang, World Scientific, Singapore, 2014, pp. 179–210 Search PubMed.
- M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047–14050 RSC.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef CAS PubMed.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- P. G. Klemens, Phys. Rev., 1962, 125, 1795–1798 CrossRef.
- D. L. Mills, Phys. Rev., 1966, 146, 336–343 CrossRef CAS.
- M. B. Walker, Phys. Rev., 1967, 162, 199–208 CrossRef CAS.
- J. J. L. Morton, A. M. Tyryshkin, A. Ardavan, K. Porfyrakis, S. A. Lyon and G. A. D. Briggs, J. Chem. Phys., 2006, 124, 014508 CrossRef PubMed.
- J. Goslar, S. K. Hoffmann and W. Hilczer, Solid State Commun., 2002, 121, 423–427 CrossRef CAS.
- S. K. Hoffmann and J. Goslar, J. Phys.: Condens. Matter, 2015, 27, 265402 CrossRef CAS PubMed.
- J. Goslar, S. Lijewski, S. K. Hoffmann, A. Jankowska and S. Kowalak, J. Chem. Phys., 2009, 130, 204504 CrossRef PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1546957 and 1551313. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc02395b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2017 |