Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CdS/ZnS core–shell nanocrystal photosensitizers for visible to UV upconversion†
Victor
Gray
 a,
Pan
Xia
a,
Pan
Xia
 b,
Zhiyuan
Huang
c,
Emily
Moses
c,
Alexander
Fast
d,
Dmitry A.
Fishman
d,
Valentine I.
Vullev
b,
Zhiyuan
Huang
c,
Emily
Moses
c,
Alexander
Fast
d,
Dmitry A.
Fishman
d,
Valentine I.
Vullev
 c,
Maria
Abrahamsson
c,
Maria
Abrahamsson
 a,
Kasper
Moth-Poulsen
a,
Kasper
Moth-Poulsen
 a and
Ming
Lee Tang
a and
Ming
Lee Tang
 *c
*c
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden
bMaterials Science & Engineering Program, University of California, Riverside, 900 University Ave., Riverside, CA 92521, USA
cDepartment of Chemistry, University of California, Riverside, 900 University Ave., Riverside, CA 92521, USA. E-mail: mltang@ucr.edu
dDepartment of Chemistry, University of California, Irvine, CA 92697, USA
First published on 31st May 2017
Abstract
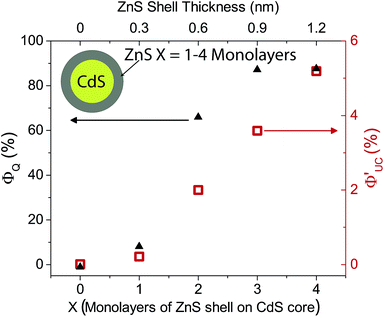
Herein we report the first example of nanocrystal (NC) sensitized triplet–triplet annihilation based photon upconversion from the visible to ultraviolet (vis-to-UV). Many photocatalyzed reactions, such as water splitting, require UV photons in order to function efficiently. Upconversion is one possible means of extending the usable range of photons into the visible. Vis-to-UV upconversion is achieved with CdS/ZnS core–shell NCs as the sensitizer and 2,5-diphenyloxazole (PPO) as annihilator and emitter. The ZnS shell was crucial in order to achieve any appreciable upconversion. From time resolved photoluminescence and transient absorption measurements we conclude that the ZnS shell affects the NC and triplet energy transfer (TET) from NC to PPO in two distinct ways. Upon ZnS growth the surface traps are passivated thus increasing the TET. The shell, however, also acts as a tunneling barrier for TET, reducing the efficiency. This leads to an optimal shell thickness where the upconversion quantum yield (Φ′UC) is maximized. Here the maximum Φ′UC was determined to be 5.2 ± 0.5% for 4 monolayers of ZnS shell on CdS NCs.
1 Introduction
It remains a challenge to utilize visible light directly in photocatalysis for the production of solar fuels. Since Honda and Fujishima's pioneering work,1 it has been shown that wide bandgap semiconductors like titania2 or NiO/NaTaO3:La in combination with ultra-violet (UV) radiation can perform efficient chemical transformations. For example, combining NiO/NaTaO3:La with 270 nm light results in an extremely high quantum yield of 56% for water splitting.3 Various methods to extend the response of these materials to the entire solar spectrum have focused on extending the absorption of the semiconductor, mostly without a commensurate increase in photocatalytic efficiency, due to the introduction of trap states that compromise carrier mobility.4,5 The record thus far is a solid solution of GaN/ZnO that can absorb visible light shorter than 500 nm, and split water with a quantum yield >3%. These photocatalysts by Domen and co-workers remain the state of the art in the field.6–8It may be possible to extend the response of photocatalysts to the entire solar spectrum, by using semiconductor nanocrystals (NCs) to absorb the low energy photons, and transferring them to molecular triplet states. With their high absorption coefficients, semiconductor NCs or quantum dots (QDs) have been employed as light absorbers in photovoltaic (PV) cells9 and photocatalytic H2 production10,11 as well as labels for biosensing and imaging.12 It has recently been shown that semiconductor NCs can donate13,14 and accept15,16 triplet excitons to and from molecular species, respectively. Thus semiconductor NCs can be used as triplet sensitizers for triplet–triplet annihilation (TTA) based photon upconversion.13,14,17–21 By enabling the use of sub-bandgap photons, TTA photon upconversion can potentially extend the absorption of light harvesting devices,22,23 leading to improved efficiencies.24–35 For example, in commercially relevant solar cells, up to 34% of the photons from the Sun are wasted in PV platforms where the light absorber has band gaps above 1.1 eV. Therefore, sensitizers capable of efficiently absorbing NIR photons for improving PV efficiency, or for subsequent upconversion to UV photons for photocatalysis are sought after. Indeed, efficient TTA photon upconversion of NIR photons to visible (vis) has been achieved at sub-solar excitation intensities by using NCs as triplet sensitizers.20,36 NC based triplet sensitizers are particularly interesting in this aspect as they have high molar absorptivities, good photostability and size-tunable optical profiles.37,38 However, to the best of our knowledge, there has been no report of NC sensitized triplet–triplet annihilation based photon upconversion from the vis-to-UV. It is not trivial to develop NCs for efficient triplet sensitization since there is a lot left to unravel regarding the mechanism for efficient triplet energy transfer from NCs to organic molecules. Furthermore, even in purely molecular TTA systems vis-to-UV upconversion is scarce,39–41 as suitable annihilator–sensitizer pairs are elusive. This is because the ideal annihilator has to fulfill two requirements: a high fluorescence QY, and a first triplet excited state, T1, slightly higher in energy than twice the first singlet excited state, S1, i.e. 2 × E(T1) > E(S1). UV emitters, however, have relatively small exchange energies compared to their more conjugated counterparts. This translates into a relatively high T1 compared to S1. Since the sensitizer S1 and T1 both must lie between the annihilator S1 and T1, it is difficult to find molecular triplet donors that can sensitize these states to achieve efficient photon upconversion. The difficulty in predicting excited state properties, like intersystem crossing efficiencies, makes designing triplet sensitizers with high extinction coefficients, high triplet yields and suitable triplet energies challenging.42 In contrast, the exchange energy is on the order of meV for quantum confined semiconductor nanocrystal sensitizers, hence thermodynamic restrictions are relaxed for this class of materials as triplet exciton donors.43,44
Herein we demonstrate the first example of vis-to-UV photon upconversion with quantum yields of up to 5.2% utilizing a hybrid organic–inorganic system with a series of CdS/ZnS core–shell nanocrystals as sensitizers. We find that a ZnS shell on CdS cores of 3.6–4.3 nm in diameter is necessary for any appreciable upconversion. Using transient absorption spectroscopy and photoluminescence (PL) lifetime measurements, we show that the ZnS shell removes the trap states on the core, while facilitating triplet energy transfer to molecular annihilators. The optimal shell-thickness occurred at 4 monolayers, corresponding to ∼1.2 nm of ZnS, which is surprisingly thick considering the shell is a tunneling barrier for triplet excitons. We found, unexpectedly, that a transmitter ligand did not enhance the photon upconversion quantum yields. Typically, in these hybrid photon upconversion platforms, a transmitter ligand can increase the upconversion quantum yield by up to 3 orders of magnitude by introducing an energy cascade and improving orbital overlap between the NC donor and the molecular acceptor.13,14 This work shows that energy transfer between nanocrystals and conjugated organic molecules is very sensitive to the atomic and molecular details at this hybrid interface.
2 Results and discussion
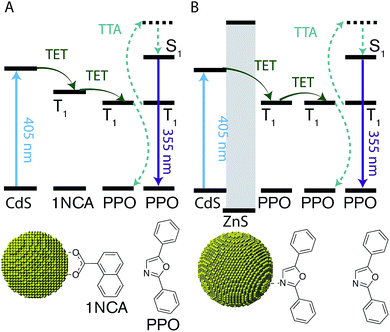
A scheme of all the components involved in the energy transfer during photon upconversion is presented in Fig. 1. The energy offsets of the three components are also illustrated. In this study we employed the scintillator 2,5-diphenyloxazole (PPO) as the annihilator. PPO emits UV photons with an emission maxima of 355 nm (3.49 eV) in hexane and has a high fluorescence quantum yield close to unity.45 The first excited triplet state, T1, of PPO lies in the range of 2.3–3.0 eV,39,46 corresponding to the visible wavelength range of 400–540 nm. Therefore, CdS NCs with the appropriate band-gap slightly higher in energy than this T1 state were used as photosensitizers for PPO.2.1 Nanocrystal synthesis and characterization
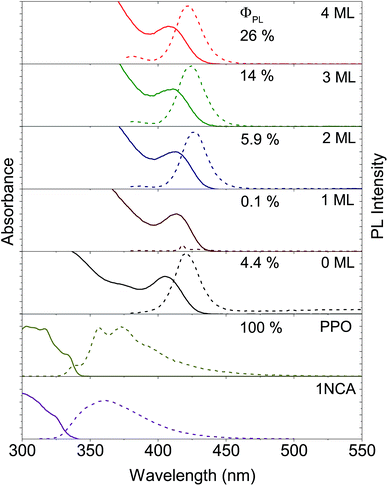
Two sets of CdS NCs were synthesized from CdO and elemental sulfur via the hot injection method,47 yielding NCs with a diameter of 3.6 nm and 4.3 nm, according to the first exciton absorption maxima at 405 nm and 427 nm respectively.48 The 3.6 nm and 4.3 nm CdS cores were subsequently coated with 1–4 and 3–5 monolayers of ZnS respectively using zinc-diethyldithiocarbamate as the precursor, similar to the procedure reported by Chen et al.49 In the rest of the text, shell thickness for the CdS/ZnS core–shell NCs will be indicated by XML, where X = 0, 1, 2, 3, 4 and 5 and ML = monolayers.Growth of the first ZnS monolayer (1ML) red-shifts the excitonic absorption maxima about 9 nm compared to the CdS core. Table 1 lists the optical properties for the core–shell NCs derived from the 3.6 nm diameter CdS cores. This bathochromic shift is expected for cation terminated NCs as the addition of an outer layer of sulfide anions delocalizes the exciton compared to the original core.38 Further growth of the ZnS shell results in a gradual blue-shift (Table 1, Fig. 2 and S1†), suggesting the formation of an alloy.49,50 TEM images of the 4.3 nm CdS core and 3–5ML core–shell NCs can be found in the ESI, Fig. S2.†
| NC | Absmax (nm) | Emmax (nm) | Φ PL (%) | k r (s−1) | k nr (s−1) | 〈τ0〉 (ns) | 〈τPPO〉 (ns) |
|---|---|---|---|---|---|---|---|
a All measurements were done in hexane.
b
k
r and knr are calculated from the intensity weighted average lifetimes ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) as described in the ESI. as described in the ESI.
|
|||||||
| 0ML | 405 | 421 | 4.4 | 5.3 × 105 | 0.1 × 108 | 16.9 | 17.1 |
| 1ML | 414 | 418 | 0.1 | 4.2 × 105 | 7.0 × 108 | 0.25 | 0.23 |
| 2ML | 413 | 427 | 5.9 | 1.1 × 107 | 1.8 × 108 | 1.35 | 0.46 |
| 3ML | 411 | 425 | 14 | 1.6 × 107 | 1.0 × 108 | 4.11 | 0.53 |
| 4ML | 407 | 422 | 26 | 2.8 × 107 | 0.8 × 108 | 5.80 | 0.72 |
Photoluminescence from both the band-edge and trap states is observed (Fig. 2 and S1†) for both CdS core NCs. For the 3.6 nm CdS core the band-edge emission is observed as a sharp peak at about 420 nm and the trap state emission as a broad peak in the range of 450–650 nm. The latter is ascribed to surface-based trap states arising from sulfur vacancies.51 This trap-state emission was completely removed with the growth of more than 2 monolayers of ZnS shell on the CdS core, indicating that shell growth passivates the surface traps. This results in higher photoluminescence quantum yields (ΦPL), up to 26% for the 4ML core–shell NCs, compared to 4.4% for the 3.6 nm CdS core, as summarized in Fig. 2 and Table 1. For 1ML core–shell NCs, almost no emission could be detected, possibly due to an incomplete shell, in line with previous results.49,52
2.2 Visible to UV upconversion
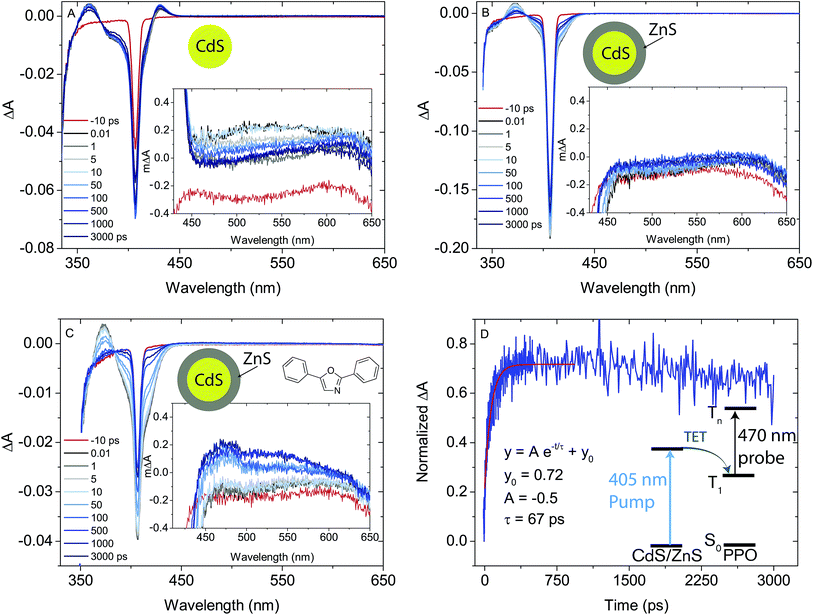
Much like triplet energy transfer (TET) between molecules in solution, which is governed by the Dexter exchange mechanism and limited by diffusion, the TET here depends on both the acceptor concentration and sensitizer lifetime. Thus, a long triplet lifetime of the sensitizer is desired to achieve high TET efficiencies. Typically a molecular triplet sensitizer has a lifetime of 10–100 s of μs. As NCs generally have shorter lifetimes, a transmitter ligand with a long-lived triplet state is helpful.13,14,53 Carboxylic acid functionalized ligands, such as 9-anthracenecarboxylic acid (9ACA) and 5-tetracenecarboxylic acid (5CT) are effective triplet transmitters for CdSe and PbS(Se) NCs, respectively.13,14,19,54 The carboxylic functionality allows for binding to chalcogenide nanoparticles without quenching the NC PL and the fused aromatic system has a triplet energy level suitable for it to act as an acceptor to enable triplet energy transfer from NC to ligand. Therefore our first choice of transmitter ligand was a molecule with a carboxylic acid binding group and a naphthalene core in the form of 1-naphthoic acid (1NCA) as its triplet energy is about 2.48 eV (corresponding to 500 nm),55 which is within the range of the reported T1 levels of the PPO annihilator (400–540 nm).For comparison between photon upconversion systems the upconversion quantum yield (ΦUC) is typically the main figure of merit. It can be determined relative to a standard according to eqn (1),
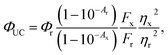 | (1) |
An upconverting system consisting of CdS NCs (core only, 0ML) as photosensitizer, 1NCA as transmitter ligand bound to the NC and PPO as annihilator yielded only low Φ′UC of ∼0.8%. No photon upconversion was detected without the 1NCA transmitter ligand bound to the CdS NCs, nor was it observed without the CdS NCs. Furthermore, CdSe NC sensitizers of various sizes (absorption maxima in the range of 480–520 nm) did not afford any detectable upconversion.
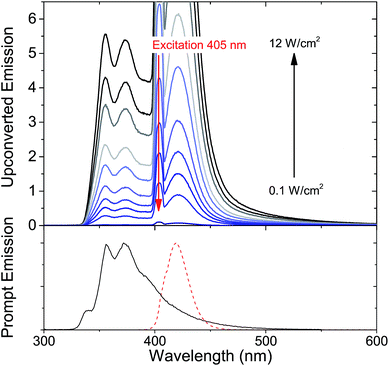
Since it is well known that core–shell NCs have fewer surface trap-states compared to core only NC10,11,21,37,38 we expected CdS/ZnS core–shell NCs to be more efficient for photosensitization. The entire series of CdS/ZnS core/shell NCs with 1–4ML of ZnS shell did not require the transmitter ligand 1NCA to achieve detectable upconversion. In fact, there was no difference in the upconversion quantum yield (Φ′UC) with and without the 1NCA transmitter. This is most likely due to the possibility of PPO binding to the ZnS shell through the oxazole nitrogen and a mismatch between the triplet energy levels of 1NCA and PPO. Upon 405 nm excitation of 4ML core–shell NCs (1 μM) with PPO (5.7 mM in hexane) upconverted PPO emission was readily detected, as seen in Fig. 3, and Φ′UC was determined to 5.2 ± 0.5% at 7.1 W cm−2, in the linear excitation regime (Fig. S3†). The linear regime is reached at a rather high excitation power density (>1 W cm−2), Fig. S3,† and for practical applications it must be reduced.
Φ′UC increases with ZnS shell thickness up to 4 monolayers. Further ZnS shell growth leads to a decrease in the photon upconversion quantum yield. This trend was observed for both sets of CdS/ZnS core–shell NCs. Data for the 3.6 nm diameter series is summarized in Fig. 4, while that for the 4.3 nm diameter series is in Fig. S4.† It is somewhat surprising that Φ′UC initially increases with the layer thickness as it has been reported previously that both CdS and ZnS shells acts as a tunneling barrier for hole transport from CdSe NCs to surface bound ligands.56,57 Hence, after passivation of the trap states, the ZnS shell is expected to decrease TET from the CdS core to the molecular acceptors. Charge and energy transfer are dictated by the energy offset between the donor and acceptor as well as the tunneling barrier. Comparing 0ML core only CdS NCs and 4ML CdS/ZnS core–shell NCs, both have similar absorption maxima (405 nm and 407 nm, respectively). Therefore the driving force for TET is the same for both NC sensitizers, and only depends on the energetics of the triplet state of the molecular acceptor. TET is downhill by ∼0.5 eV and ∼0.7 eV for 1NCA and PPO respectively. It should, however, be noted that the spread of reported PPO triplet energy levels in the literature is wide and the driving force for PPO could, in fact, be lower than 1NCA.
2.3 Effect of ZnS shell
To increase our understanding of the effect of the ZnS shell and how it affects TET and therefore photon upconversion, we performed time-resolved PL (TRPL) of the NCs both with and without PPO. NCs often show multi-exponential decays, even after shell growth11,58,59 and a three exponential fit was required to achieve a satisfactory fit to the data. Both amplitude and intensity weighted average lifetimes, 〈τ〉 and![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) respectively, were extracted from the fits. 〈τ〉 values were used to calculate the quenching efficiencies whereas the radiative decay rates kr were obtained from
respectively, were extracted from the fits. 〈τ〉 values were used to calculate the quenching efficiencies whereas the radiative decay rates kr were obtained from ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) , as described in the ESI.† Fig. S5 and S6† show the decays and fits. In Table 1 the amplitude weighted average lifetime 〈τ〉 is listed. A similar trend is observed for
, as described in the ESI.† Fig. S5 and S6† show the decays and fits. In Table 1 the amplitude weighted average lifetime 〈τ〉 is listed. A similar trend is observed for ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) and can be found in the ESI, Table S1.† As can be seen in Table 1, 2–4 monolayers of ZnS shell increase the radiative decay rates by an order of magnitude with respect to the shell. In a type I core–shell NC, both the electron and hole are confined to the core due to its band offsets with respect to the shell, thus increasing the radiative rate due to enhanced wavefunction overlap. A type I structure is expected for CdS/ZnS core–shell NCs since the bandgap of bulk CdS lies within the bandgap of bulk ZnS.38,60 The ZnS shell eliminates the trap state emission to the red of the excitonic absorption maxima seen in the CdS NCs (Fig. 2 and S1†). This passivation of surface trap states explains the increase in ΦPL with respect to the CdS core only NCs.60
and can be found in the ESI, Table S1.† As can be seen in Table 1, 2–4 monolayers of ZnS shell increase the radiative decay rates by an order of magnitude with respect to the shell. In a type I core–shell NC, both the electron and hole are confined to the core due to its band offsets with respect to the shell, thus increasing the radiative rate due to enhanced wavefunction overlap. A type I structure is expected for CdS/ZnS core–shell NCs since the bandgap of bulk CdS lies within the bandgap of bulk ZnS.38,60 The ZnS shell eliminates the trap state emission to the red of the excitonic absorption maxima seen in the CdS NCs (Fig. 2 and S1†). This passivation of surface trap states explains the increase in ΦPL with respect to the CdS core only NCs.60
With a thicker shell, however, the tunneling barrier for TET from NC core to the molecular acceptors would increase, leading to a decrease in the TET rate.56,57 These two opposing effects on the TET with shell thickness would explain why there is an optimum shell thickness where the maximum Φ′UC is observed.
2.4 Triplet energy transfer from NC to PPO
From the PL lifetimes the quenching efficiency (ΦQ) of PPO on the NCs can be calculated according to eqn (2),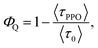 | (2) |
Furthermore, for 4ML CdS/ZnS core–shell NCs with PPO, there is also a new positive feature at 450–600 nm, ascribed to the T1–Tn absorption of PPO,66–68 verifying TET from the core–shell NC to PPO. The rise of the T1–Tn feature can be fit to a monoexponential with a rise-time of 67 ps, corresponding to a rate constant of 14.9 × 109 s−1, an order of magnitude faster than that reported previously for TET from CdSe NCs to 9-anthracenecarboxylic acid.14 The fast TET is in agreement with the efficient PL quenching of the NC by PPO.
The upconversion quantum yield depends on the efficiencies of the processes involved and can be described by eqn (3),
| Φ′UC = 2ΦISCΦTETΦTTA, | (3) |
Triplet–triplet annihilation can be limited by spin-statistics if the second triplet state (T2) and the first quintet state (Q1) are lower in energy than 2 × E(T1), resulting in Φ′UC less than 11%.69 Furthermore, we have recently shown that there are other loss factors influencing the TTA process.70 PPO has been used previously as an annihilator with two different molecular sensitizers and the reported Φ′UC values are low, <1%.39,40 This could indicate that PPO does have intrinsic limitations as the annihilator, possibly originating from its high T1 energy. The relatively high T1 energy also limits the efficiency of energy conversion in the present system to blue-to-UV upconversion. Finding a better annihilator, with 2 × E(T1) only slightly exceeding E(S1), a larger part of the visible spectrum could be converted with a higher efficiency. This is currently under investigation in our lab. With the efficient sensitization by core–shell NCs demonstrated here, we have, however, increased the upconversion efficiency (Φ′UC) by a factor of 5 compared to the all-molecular systems employing PPO as the annihilator.
3 Conclusion
Herein we demonstrate the first example of visible to UV upconversion using NC sensitizers for TTA-based photon upconversion. This work extends the broad range of wavelengths possible for photon upconversion based on triplet fusion sensitized by NCs from the NIR and visible into the UV. Sensitization of the annihilator PPO was achieved efficiently by CdS/ZnS core–shell NCs with the optimal shell thickness of 4 monolayers. The effect of the ZnS shell is twofold. First the surface traps of the CdS core are removed, secondly the large bandgap shell acts as a tunneling barrier for TET, as observed for hole and electron transfer.56,57 The former has a positive effect on TET and consequently Φ′UC, the latter on the other hand decreases TET as the shell thickness increases. Our data suggests that there is an optimal thickness where these two effects are balanced, resulting in the most efficient TET and Φ′UC. These results contribute to the ongoing investigation of TET from NCs to organic ligands. In particular, it improves the understanding of the requirements for efficient triplet energy transfer (TET) between semiconductor NCs and organic molecules necessary for future design of efficient triplet sensitizer NCs.4 Experimental section
4.1 Chemicals
Zinc diethyldithiocarbamate (Zn(DDTC)2, 99.0%) was purchased from TCI America, washed with water and dried under vacuum for 8 h before use. Cadmium oxide (CdO, 99.99%), 2,5-diphenyloxazole (PPO, for scintillation), 1-naphthoic acid (1NCA, 96%) were all purchased from Sigma-Aldrich. Sulfur powder (99%) was purchased from Strem Chemicals, oleic acid (90%) was purchased from Alfa Aesar. 1-Octadecene (ODE, tech. grade 90%) was purchased from Acros Organics. All chemicals were used without further purification if not stated otherwise.4.2 Synthesis of CdS core NCs
Synthesis of CdS cores was based on the procedure by Li et al.47 CdO, 257 mg (2 mmol), 6 ml oleic acid and 15.8 ml ODE was mixed in a 50 ml, three-necked flask equipped with condenser and temperature controller. The reaction mixture was degassed under vacuum at 110 °C for 1 hour. The mixture was then stirred and heated to 260 °C under argon, until it turned clear and colorless. 32 mg of sulfur powder in 3 ml ODE was prepared in a glove box and sonicated. The sulfur precursor was injected to the reaction mixture at 240 °C (260 °C for larger NCs), stirred for 25 s, then cooled with compressed air to room temperature yielding a pale, colorless reaction mixture with NC absorption maxima at 405 nm (427 nm for larger NCs). The particles were purified in an Ar(g) glove box with extraction by methanol, hexane and butylamine (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7
0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04, v/v/v). The organic fraction was collected and extracted again with methanol and hexane (1
0.04, v/v/v). The organic fraction was collected and extracted again with methanol and hexane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v). The organic fraction was then precipitated using acetone with a few drops of butylamine. After re-dispersing the NC pellet in hexane, the NCs were precipitated twice more with acetone and stored in hexane at micromolar concentrations.
2, v/v). The organic fraction was then precipitated using acetone with a few drops of butylamine. After re-dispersing the NC pellet in hexane, the NCs were precipitated twice more with acetone and stored in hexane at micromolar concentrations.
4.3 Growth of ZnS shell
Using the CdS core, synthesized as described above, the ZnS shells were grown according to the procedure by Chen et al.49 Zn(DDTC)2 was dissolved in oleylamine to prepare a 0.1 M solution. In the glove box, 0.13 μmol CdS core in ODE was dissolved in 8.5 ml ODE in a 27 ml vial. For the first monolayer, 0.47 ml Zn(DDTC)2 (0.1 M) was added and the mixture was stirred and heated to 185 °C for 25 min. A second portion of Zn(DDTC)2 was added at 50 °C to grow the second monolayer, followed by heating to 185 °C for 30 min. This procedure was repeated until the number of desired monolayers was achieved. The amount of Zn(DDTC)2 needed for each layer was calculated as described in the ESI.†The core–shell NCs were purified by extraction with methanol and hexane (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) twice, followed by precipitation of the core–shell NCs by addition of acetone to the organic phase. The particles were re-dissolved in hexane and precipitated twice more with acetone and stored in hexane at micromolar concentrations.
1, v/v) twice, followed by precipitation of the core–shell NCs by addition of acetone to the organic phase. The particles were re-dissolved in hexane and precipitated twice more with acetone and stored in hexane at micromolar concentrations.
4.4 Steady-state absorption, photoluminescence and upconversion experiments
Steady-state UV/vis absorption was recorded in 10 mm path length quartz cuvettes on a Jasco 670 spectrophotometer. Photoluminescence spectra were recorded on a Horiba SpexFluorolog 3 fluorescence spectrophotometer using a right-angle sample geometry. Photoluminescence quantum yields, ΦPL, were determined relative to 9,10-diphenylanthracene in hexane (ΦPL = 0.95 (ref. 71)).Upconverted emission was detected on an Ocean Optics Maya2000 Pro spectrometer. Excitation of the upconversion samples was a 405 nm cw OBIS laser with a beam radius of 0.2 mm. Samples were prepared in a glove box by adding 15 nmol core–shell NCs (10–80 μl) to 100 μl THF and precipitated with 1 ml acetone, then half of the particles were re-dissolved in 0.7 ml PPO stock solution (5.7 mM) for upconversion experiments and the other half was re-dissolved in 3 ml hexane for PL measurements. Samples were sealed in quartz cuvettes using Teflon backed screw caps to ensure an air-free solution. Herein we have chosen to report the normalized upconversion quantum yield (Φ′UC = 2ΦUC) with the theoretical maximum upconversion quantum yield being 100%. Reported Φ′UC values are the average of at least 2 measurements. The upconversion quantum yield Φ′UC was determined relative to perylene in degassed ethanol (ΦPL = 92% (ref. 72)).
4.5 Transient absorption measurements
Transient absorption were performed using the Ti:sapphire chirped pulse amplified system Spitfire-ACE (Spectra Physics, Newport Corp, 6 mJ@800 nm, 100 fs, 1 kHz) and Transient Absorption Spectrometer (TAS, Newport Corp.). The amplifier system is pumped using an Empower® Q-switched DPSS laser and seeded by a Mai Tai SP oscillator (90 fs, 80 MHz). The outcome of the regenerative amplifier was split in multiple paths. One beam was coupled to optical parametric amplifiers (OPA, Lightconversion TOPAS™) to generate a pump pulse at 405 nm (100 fs pulse duration). A small portion of the fundamental 800 nm beam was picked off and sent through a delay line and then focused into a 2 mm CaF2 crystal to generate a white light continuum. The generated supercontinuum is then focused onto the sample and overlapped with the pump beam. The transient spectra were detected with fiber-coupled CCD-based monochromator (Oriel, Newport). The excitation power was set to 200 μW, which was below the multi-photon annihilation regime, see ESI† for further details.4.6 Time-correlated single photon counting (TCSPC)
Photoluminescence lifetimes were recorded on a JY Horiba Fluorolog time-correlated single photon counting setup, with a NANOLed laser diode with peak wavelength at 406 nm and a repetition rate of 10 MHz. For detection a 512 channel PMT (TBX Picosecond Photon Detection Module from JY Horiba) was used and a count rate of <1% was maintained. Fits were made to three exponential decays with an y-offset and the amplitude averaged lifetime 〈τ〉 was extracted from the fits, see the ESI† for further details.4.7 TEM imaging
TEM images were recorded on a FEI Titan Themis 300 with an X-FEG electron gun.Acknowledgements
The author MLT acknowledges U.S. Army W911NF-16-1-0523 for instrumentation and CHE-1351663 for supplies and personnel. KMP and VG thank the Knut & Alice Wallenberg foundation and the Swedish Foundation for Strategic Research for financial support. The author VG acknowledges the financial support from Sixten Gemzéus Stiftelse. DAF acknowledges NSF grant 1532125. VV acknowledges NSF grant CHE 1465284.References
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- E. Smotkin, A. J. Bard, A. Campion, M. A. Fox, T. Mallouk, S. E. Webber and J. M. White, J. Phys. Chem., 1986, 90, 4604–4607 CrossRef CAS.
- H. Kato, K. Asakura and A. Kudo, J. Am. Chem. Soc., 2003, 125, 3082–3089 CrossRef CAS PubMed.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed.
- R. Augustynski, J. Alexander and B. D. Solarska, in Top. Curr. Chem., ed. C. A. Bignozzi, Springer-Verlag, Berlin Heidelberg, 2011, ch. Photocatal, pp. 1–38 Search PubMed.
- K. Maeda, K. Teramura, T. Takata, M. Hara, N. Saito, K. Toda, Y. Inoue, H. Kobayashi and K. Domen, J. Phys. Chem. B, 2005, 109, 20504–20510 CrossRef CAS PubMed.
- K. Maeda, K. Teramura, D. Lu, T. Takata, N. Saito, Y. Inoue and K. Domen, Nature, 2006, 440, 295 CrossRef CAS PubMed.
- K. Maeda, K. Teramura and K. Domen, J. Catal., 2008, 254, 198–204 CrossRef CAS.
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295, 2425–2428 CrossRef CAS PubMed.
- A. Thibert, F. A. Frame, E. Busby, M. A. Holmes, F. E. Osterloh and D. S. Larsen, J. Phys. Chem. Lett., 2011, 2, 2688–2694 CrossRef CAS.
- L. Huang, X. Wang, J. Yang, G. Liu, J. Han and C. Li, J. Phys. Chem. C, 2013, 117, 11584–11591 CAS.
- I. L. Medintz, U. Tetsuo, E. R. Goldman and H. Mattoussi, Nat. Mater., 2005, 4, 435–446 CrossRef CAS PubMed.
- Z. Huang, X. Li, M. Mahboub, K. Hanson, V. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 5552–5557 CrossRef CAS PubMed.
- C. Mongin, S. Garakyaraghi, N. Razgoniaeva, M. Zamkov and F. N. Castellano, Science, 2016, 351, 369–371 CrossRef CAS PubMed.
- M. Tabachnyk, B. Ehrler, S. Gélinas, M. L. Böhm, B. J. Walker, K. P. Musselman, N. C. Greenham, R. H. Friend and A. Rao, Nat. Mater., 2014, 13, 1033–1038 CrossRef CAS PubMed.
- N. J. Thompson, M. W. B. Wilson, D. N. Congreve, P. R. Brown, J. M. Scherer, T. S. Bischof, M. Wu, N. Geva, M. Welborn, T. V. Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Mater., 2014, 13, 1039–1043 CrossRef CAS PubMed.
- Z. Huang, X. Li, B. D. Yip, J. M. Rubalcava, C. J. Bardeen and M. L. Tang, Chem. Mater., 2015, 27, 7503–7507 CrossRef CAS.
- G. B. Piland, Z. Huang, M. L. Tang and C. J. Bardeen, J. Phys. Chem. C, 2016, 120, 5883–5889 CAS.
- M. Mahboub, H. Maghsoudiganjeh, A. M. Pham, Z. Huang and M. L. Tang, Adv. Funct. Mater., 2016, 26, 6091–6097 CrossRef CAS.
- M. Mahboub, Z. Huang and M. L. Tang, Nano Lett., 2016, 16, 7169–7175 CrossRef CAS PubMed.
- K. Okumura, K. Mase, N. Yanai and N. Kimizuka, Chem.–Eur. J., 2016, 22, 7721–7726 CrossRef CAS PubMed.
- J. de Wild, A. Meijerink, J. K. Rath, W. G. J. H. M. van Sark and R. E. I. Schropp, Energy Environ. Sci., 2011, 4, 4835–4848 CAS.
- J. C. Goldschmidt and S. Fischer, Adv. Opt. Mater., 2015, 3, 510–535 CrossRef CAS.
- Y. Y. Cheng, B. Fückel, R. W. MacQueen, T. Khoury, R. G. C. R. Clady, T. F. Schulze, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Energy Environ. Sci., 2012, 5, 6953–6959 CAS.
- T. F. Schulze, Y. Y. Cheng, B. Fckel, R. W. MacQueen, A. Danos, N. J. L. K. Davis, M. J. Y. Tayebjee, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley, B. Stannowski, K. Lips and T. W. Schmidt, Aust. J. Chem., 2012, 65, 480–485 CrossRef CAS.
- T. F. Schulze, J. Czolk, Y.-Y. Cheng, B. Fückel, R. W. MacQueen, T. Khoury, M. J. Crossley, B. Stannowski, K. Lips, U. Lemmer, A. Colsmann and T. W. Schmidt, J. Phys. Chem. C, 2012, 116, 22794–22801 CAS.
- J.-h. Kim and J.-h. Kim, J. Am. Chem. Soc., 2012, 134, 17478–17481 CrossRef CAS PubMed.
- R. S. Khnayzer, J. Blumhoff, J. a. Harrington, A. Haefele, F. Deng and F. N. Castellano, Chem. Commun., 2012, 48, 209 RSC.
- A. Nattestad, Y. Cheng, R. Macqueen, T. Schulze, F. Thompson, A. Mozer, B. Fu, T. Khoury, M. Crossley, K. Lips, G. Wallace and T. W. Schmidt, J. Phys. Chem. Lett., 2013, 4, 2073–2078 CrossRef CAS PubMed.
- K. Börjesson, D. Dzebo, B. Albinsson and K. Moth-Poulsen, J. Mater. Chem. A, 2013, 1, 8521–8524 Search PubMed.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC.
- C. Simpson, T. Clarke, R. MacQueen, Y.-Y. Cheng, A. Trevitt, A. Mozer, P. Wagner, T. Schmidt and A. Nattestad, Phys. Chem. Chem. Phys., 2015, 17, 24826–24830 RSC.
- S. P. Hill, T. Dilbeck, E. Baduell and K. Hanson, ACS Energy Lett., 2016, 1, 3–8 CrossRef CAS.
- T. Dilbeck, S. P. Hill and K. Hanson, J. Mater. Chem. A, 2017 10.1039/c7ta00317j.
- L. Frazer, J. K. Gallaher and T. W. Schmidt, ACS Energy Lett., 2017, 2, 1346–1354 CrossRef CAS.
- M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. V. Voorhis, V. Bulovi, M. G. Bawendi and M. A. Baldo, Nat. Photonics, 2015, 10, 31–34 CrossRef.
- A. P. Alivisatos, J. Phys. Chem., 1996, 100, 13226–13239 CrossRef CAS.
- C. de Mello Donegá, Chem. Soc. Rev., 2011, 40, 1512–1546 RSC.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2009, 113, 5912–5917 CrossRef CAS PubMed.
- P. B. Merkel and J. P. Dinnocenzo, J. Lumin., 2009, 129, 303–306 CrossRef CAS.
- N. Yanai, M. Kozue, S. Amemori, R. Kabe, C. Adachi and N. Kimizuka, J. Mater. Chem. C, 2016, 4, 6447–6451 RSC.
- J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 43, 5323–5351 RSC.
- A. L. Efros, M. Rosen, M. Kuno, M. Nirmal, D. J. Norris and M. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4843–4856 CrossRef CAS.
- G. D. Scholes, Adv. Funct. Mater., 2008, 18, 1157–1172 CrossRef CAS.
- I. Berlman, Handbook of Fluorescence Spectra of Aromatic Molecules, Academic Press, New York and London, 2nd edn, 1971 Search PubMed.
- J. C. Lecoq, R. Mechin, C. Tanielian, M. Bazin and R. Santus, Chem. Phys. Lett., 1978, 54, 616–618 CrossRef CAS.
- Z. Li, Y. Ji, R. Xie, S. Y. Grisham and X. Peng, J. Am. Chem. Soc., 2011, 133, 17248–17256 CrossRef CAS PubMed.
- W. W. Yu, L. Qu, W. Guo and X. Peng, Chem. Mater., 2003, 15, 2854–2860 CrossRef CAS.
- D. Chen, F. Zhao, H. Qi, M. Rutherford and X. Peng, Chem. Mater., 2010, 22, 1437–1444 CrossRef CAS.
- X. Peng, M. C. Schlamp, A. V. Kadavanich and A. P. Alivisatos, J. Am. Chem. Soc., 1997, 119, 7019–7029 CrossRef CAS.
- A. Veamatahau, B. Jiang, T. Seifert, S. Makuta, K. Latham, M. Kanehara, T. Teranishi and Y. Tachibana, Phys. Chem. Chem. Phys., 2015, 17, 2850–2858 RSC.
- V. Kocevski, O. Eriksson, C. Gerard, D. D. Sarma and J. Rusz, J. Chem. Phys., 2015, 143, 164701 CrossRef CAS PubMed.
- Z. Huang, D. E. Simpson, M. Mahboub, X. Li and M. L. Tang, Chem. Sci., 2016, 7, 4101–4104 RSC.
- P. Xia, Z. Huang, X. Li, J. J. Romero, V. I. Vullev, G. S. H. Pau and M. L. Tang, Chem. Commun., 2017, 53, 1241–1244 RSC.
- R. M. Hochstrasser, Can. J. Chem., 1961, 39, 1776–1782 CrossRef CAS.
- H. Zhu, N. Song and T. Lian, J. Am. Chem. Soc., 2010, 132, 15038–15045 CrossRef CAS PubMed.
- T. X. Ding, J. H. Olshansky, S. R. Leone and A. P. Alivisatos, J. Am. Chem. Soc., 2015, 137, 2021–2029 CrossRef CAS PubMed.
- S. J. Lim, B. Chon, T. Joo and S. K. Shin, J. Phys. Chem. C, 2008, 112, 1744–1747 CAS.
- K. L. Sowers, Z. Hou, J. J. Peterson, B. Swartz, S. Pal, O. Prezhdo and T. D. Krauss, Chem. Phys., 2016, 471, 24–31 CrossRef CAS.
- H. Zhu and T. Lian, Energy Environ. Sci., 2012, 5, 9406–9418 CAS.
- E. F. Hilinski, P. A. Lucas and Y. Wang, J. Chem. Phys., 1988, 89, 3435–3441 CrossRef CAS.
- S. H. Park, R. A. Morgan, Y. Z. Hu, M. Lindberg, S. W. Koch and N. Peyghambarian, J. Opt. Soc. Am. B, 1990, 7, 2097–2105 CrossRef CAS.
- V. Klimov, S. Hunsche and H. Kurz, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 8110–8113 CrossRef CAS.
- D. J. Norris, A. Sacra, C. B. Murray and M. G. Bawendi, Phys. Rev. Lett., 1994, 72, 2612–2615 CrossRef CAS PubMed.
- V. I. Klimov, J. Phys. Chem. B, 2000, 104, 6112–6123 CrossRef CAS.
- F. Dainton, T. Morrow, G. A. Salmon and G. F. Thompson, Proc. R. Soc. A, 1972, 328, 457–479 CrossRef CAS.
- D. N. Dempster, T. Morrow and M. F. Quinn, J. Photochem., 1973, 2, 329–341 CrossRef.
- T. G. Pavlopoulos and P. R. Hammond, J. Am. Chem. Soc., 1974, 96, 6568–6579 CrossRef CAS.
- T. W. Schmidt and F. N. Castellano, J. Phys. Chem. Lett., 2014, 5, 4062–4072 CrossRef CAS PubMed.
- V. Gray, A. Dreos, P. Erhart, B. Albinsson, K. Moth-poulsen and M. Abrahamsson, Phys. Chem. Chem. Phys., 2017, 19, 10931–10939 RSC.
- J. V. Morris, M. A. Mahaney and J. R. Huberr, J. Phys. Chem., 1975, 80, 969–974 CrossRef.
- J. N. Demas and G. A. Crosby, J. Phys. Chem., 1971, 75, 991–1024 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc01610g |
| This journal is © The Royal Society of Chemistry 2017 |