Open Access Article
Open Access ArticleForce-induced retro-click reaction of triazoles competes with adjacent single-bond rupture†
Tim
Stauch
 * and
Andreas
Dreuw
* and
Andreas
Dreuw
 *
*
Interdisciplinary Center for Scientific Computing, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany. E-mail: tim.stauch@iwr.uni-heidelberg.de; dreuw@uni-heidelberg.de
First published on 13th June 2017
Abstract
The highly controversial force-induced cycloreversion of 1,2,3-triazole, its well-known retro-click reaction, is shown to be possible only for 1,5-substituted triazoles, but competes with rupture of an adjacent single-bond. We draw this conclusion from both static and dynamic calculations under external mechanical forces applied to unsubstituted and 1,4- and 1,5-substituted triazoles. The JEDI (Judgement of Energy DIstribution) analysis, a quantum chemical tool quantifying the distribution of strain energy in mechanically deformed molecules, is employed to identify the key factors facilitating the force-induced retro-click reaction in these systems. For 1,4-substituted triazoles it is shown to be impossible, but the parallel alignment of the scissile bond in 1,5-substituted triazoles with the acting force makes it generally feasible. However, the weakness of the carbon–nitrogen bond connecting the triazole ring to the linker prevents selective cycloreversion.
1 Introduction
The 1,3-dipolar cycloaddition of an azide and an alkyne falls into the category of click chemistry.1,2 The resulting 1,2,3-triazoles are versatile building blocks finding numerous applications in biology3–9 as well as in polymer and materials science.9–15 Considering the thermodynamic stability of the triazole moiety, it came as a surprise when sonochemical cycloreversion of 1,2,3-triazoles incorporated in poly(methyl acrylate) was presented in 2011 (Fig. 1).16 As polymers in an ultrasound bath are known to be subject to mechanical forces,17–22 this reaction was interpreted as a mechanically induced cycloreversion. Although the original publication16 has been retracted,23 the mechanical cycloreversion of triazoles has attracted considerable interest within the past few years.24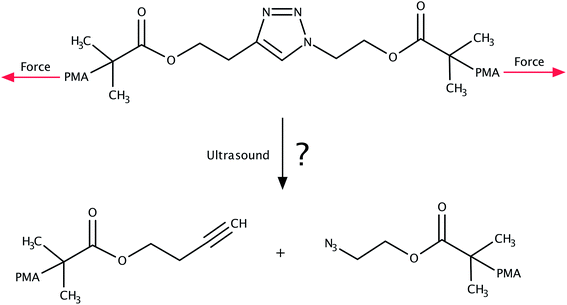 | ||
| Fig. 1 System investigated in ref. 16, in which the mechanochemical retro-click reaction of triazole that is substituted by poly(methyl acrylate) (PMA) chains in an ultrasound bath was reported. We investigate the feasibility of this reaction in this paper. | ||
Using sonochemical experiments and extended Bell theory,25 for example, the application of an external force to the triazole ring was found to indeed lower the activation energy barrier for cycloreversion.26 In a purely theoretical work, on the contrary, the cycloreversion has been shown to be only favored for pulling forces below 1 nN and rupture at the α bond to be preferred at higher forces.27 It was concluded that mechanical force alone is insufficient to explain cycloreversion of 1,2,3-triazoles. In yet another computational study of triazoles resulting from strained alkynes, the pulling geometry was identified as the key factor for successful cycloreversion.28 The possibility of metal-assisted mechanical cycloreversion of triazoles has also been discussed recently.29 Experimentally, cycloreversion was observed for forces below 860 pN in an Atomic Force Microscope (AFM).30 On the other hand, in another AFM study, it was not possible to determine reliably whether cycloreversion did indeed take place, but it was pointed out that forces in the nN regime would be needed.31 As can be seen from such contradictory experimental and theoretical findings, the feasibility of mechanical cycloreversion of 1,2,3-triazoles is widely debated.24
Here we apply static quantum chemical calculations under a constant stretching force32–34 in combination with the JEDI (Judgement of Energy DIstribution) analysis.35–37 This allows us to quantify the distribution of mechanical strain energy in deformed molecules in general, and here to answer the specific question under which circumstances cycloreversion of 1,4- and 1,5-substituted triazoles is possible. Although the JEDI analysis is based on the harmonic approximation, it has been used successfully to gain detailed insights into the rupture mechanisms of knotted polymer strands38 and mechanophores.39 We first study several pulling coordinates within the isolated triazole to identify relevant coordinates triggering cycloreversion most efficiently. Then the mechanical properties and possible cycloreversion of triazoles substituted with aliphatic linkers are investigated. Therefore, the linkers are pulled in opposite directions to simulate the mechanical force acting in sonochemical experiments that is transmitted to the triazole via the linkers. In addition, Born–Oppenheimer Molecular Dynamics (BOMD) calculations under external forces are performed to simulate the experimental conditions more realistically. From an energetic point of view, the cycloreversion of 1,4-substituted triazoles is strongly disfavored. 1,5-Substituted triazoles, on the contrary, can in principle undergo cycloreversion, but this process competes with rupture of the carbon–nitrogen single-bond connecting the triazole ring to the aliphatic linker.
2 Computational methods
Static isotensional stretching32–34 was simulated using the EFEI (External Force is Explicitly Included)33 method as implemented in the Q-Chem 4.3 program package.40 Bond rupture forces were determined iteratively with a precision of 50 pN. For the Born–Oppenheimer Molecular Dynamics (BOMD) simulations, the Q-Chem 4.0.1 program package41 was used. In the BOMD simulations, forces were applied to the terminal carbon atoms of the linkers in a manner analogous to the EFEI approach. All calculations were carried out using Density Functional Theory (DFT)42,43 at the PBE44/cc-pVDZ45 level of theory, since this method has been shown to deliver satisfactory results in various mechanochemical pulling scenarios within reasonable computation times.46,47 We used custom Python routines interfaced with the Q-Chem program package to carry out the JEDI analysis. In particular, the strain energies in all internal coordinates i, i.e. all bonds, bendings and torsions of the molecule, were calculated via35–37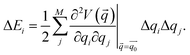 | (1) |
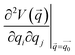 is the Hessian matrix in redundant internal coordinates at the equilibrium geometry and Δqi is the change in internal coordinate i upon mechanical deformation. M denotes the number of internal coordinates in the molecule. As the JEDI analysis is based on the harmonic approximation, it is useful to compare the harmonic strain energy ΔEharm, i.e. the sum of the individual contributions ΔEi, to the energy difference ΔEDFT between the relaxed and the strained geometry, calculated with DFT. This allows an error estimation of the harmonic approximation.
is the Hessian matrix in redundant internal coordinates at the equilibrium geometry and Δqi is the change in internal coordinate i upon mechanical deformation. M denotes the number of internal coordinates in the molecule. As the JEDI analysis is based on the harmonic approximation, it is useful to compare the harmonic strain energy ΔEharm, i.e. the sum of the individual contributions ΔEi, to the energy difference ΔEDFT between the relaxed and the strained geometry, calculated with DFT. This allows an error estimation of the harmonic approximation.
3 Results and discussion
3.1 Static stretching
In a previous study,28 a number of different pulling geometries in triazoles resulting from strained alkynes were investigated. Here, on the contrary, we first concentrate on several conceivable pulling geometries in isolated, unsubstituted 1,2,3-triazole to gain fundamental insight into the mechanical properties of triazole itself, and subsequently move to triazoles substituted by alkyl chains in order to model the original experimental setup16 more realistically. The coordinates tested (Fig. 2) include a symmetric expansion of the triazole ring (the “breathing” coordinate c1), two distinct shearing coordinates (c2 and c3), two additional symmetric stretching coordinates, in which the azide is being removed from the alkyne (c4 and c5), and two unzipping coordinates (c6 and c7).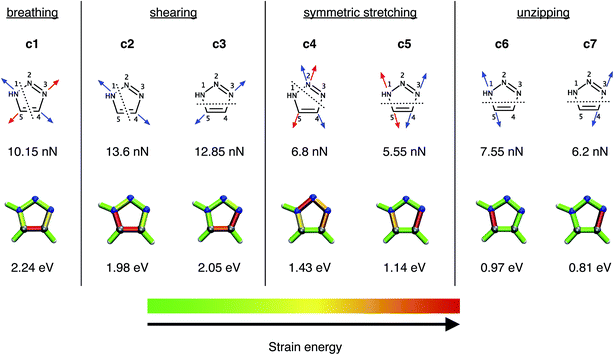 | ||
| Fig. 2 The investigated breathing coordinate c1, the shearing coordinates c2 and c3, the symmetric stretching coordinates c4 and c5 as well as the unzipping coordinates c6 and c7. Forces were applied to the atoms indicated by the arrows, with arrows of the same color signifying the same EFEI stretching coordinate. Dotted lines indicate scissile bonds. The rupture forces are given below the coordinates. The results of the JEDI analysis are shown qualitatively by color-coded structures (gray : carbon, blue : nitrogen, white : hydrogen), the generation of which is described in detail in ref. 37. The rupture energies ΔEDFT, calculated at the PBE/cc-pVDZ level of theory, are given below the color-coded structures. | ||
At the PBE/cc-pVDZ level of theory, only four of the seven investigated coordinates (c3 and c5–c7) lead to cycloreversion. Of these coordinates, cycloreversion via c3 requires approximately twice the applied force (12.85 nN) and energy (2.05 eV) that is needed for cycloreversion via the other coordinates. This finding can be rationalized using the JEDI analysis (Fig. 2), which reveals that the entire triazole ring needs to be mechanically activated for cycloreversion via c3. Upon inspection of the results of the JEDI analysis for the coordinates c5–c7, by contrast, it becomes apparent that it is sufficient to activate one of the carbon–nitrogen bonds in the triazole ring to trigger cycloreversion. In the case of c5, both carbon–nitrogen bonds are activated and therefore the force needed to stretch each one of them (5.55 nN) is particularly low. However, since two bonds are elongated, the energy that is needed for cycloreversion (1.14 eV) is higher than in the case of c6 (0.97 eV) and c7 (0.81 eV). Moreover, the N3–C4 bond is especially weak, since it stores more energy in c5 than the N1–C5 bond. In other words, stretching by the same force leads to a storage of more energy in the N3–C4 bond. This picture is supported by a comparison of the unzipping coordinates c6 and c7, since more force and energy is needed for rupture of the N1–C5 bond via c6 than the N3–C4 bond via c7. In the coordinates c5–c7, more than 90% of the strain energy is stored in the scissile bonds, while in the other stretching coordinates multiple bonds and bendings in the triazole ring store significant amounts of strain energy. Hence, cycloreversion proceeds only very inefficiently (c3) or is not triggered at all (c1, c2 and c4).
Since the N3–C4 bond is ruptured most easily by an external force via c7 and, as a result, the lowest amount of energy is needed for cycloreversion, the specific activation of this bond in experimental setups would lead to cycloreversion most efficiently. However, it is hard to imagine an experimental setup involving 1,4- or 1,5-substituted 1,2,3-triazoles, in which the N3–C4 bond is stretched in an isolated or at least in a preferred manner. Similar restrictions apply for the mechanically favored coordinate c5, i.e. simultaneous rupture of both carbon–nitrogen bonds. The bond that can arguably be activated most easily in an experiment is the N1–C5 bond by adding aliphatic linkers in a 1,5-substitution pattern. Upon stretching such molecules end-to-end, it is reasonable to expect a significant activation of the N1–C5 bond in analogy to the unzipping coordinate c6. End-to-end stretching in the case of a 1,4-substitution, however, resembles the shearing coordinate c2 most closely, which may not lead to cycloreversion. Such scenarios are discussed in detail below.
In closing the discussion of the stretching coordinates within the isolated triazole ring it should be noted that the mere presence of a linker influences the forces and energies that are needed for rupture in a nontrivial manner (cf. the ESI, Fig. S1†). The linkers do not only fulfill the role of a transmitter of strain energy from the environment to the triazole ring, but have an electronic influence as well. Similar effects have been documented previously in literature.48,49
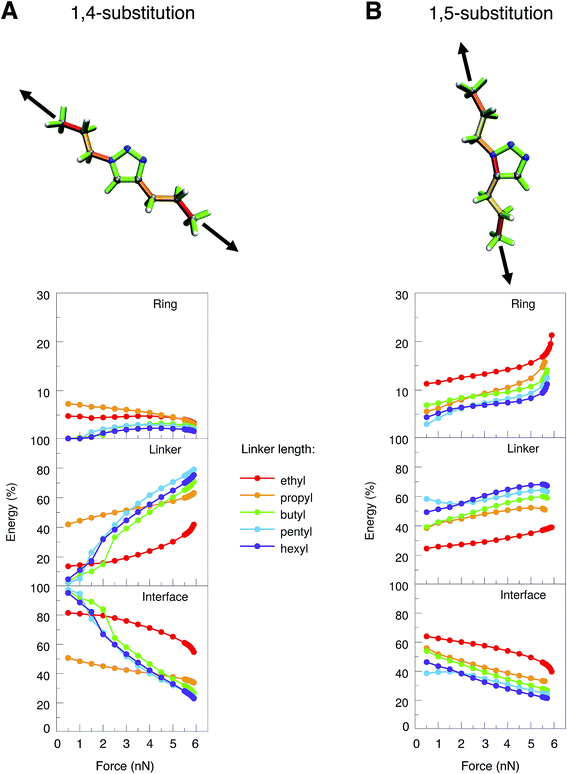
To simulate experimental conditions more realistically, alkyl linkers of different lengths (ethyl to hexyl) were introduced at positions 1 and 4 or 1 and 5 of the triazole ring, respectively (Fig. 3). The JEDI analysis reveals the triazole ring of the 1,4-isomer to be hardly strained when the molecule is stretched end-to-end (Fig. 3A, top). As a result, cycloreversion was not observed in any of the 1,4-substituted triazole systems under investigation. In the 1,5-isomer, on the contrary, the N1–C5 bond in the triazole ring is significantly strained (Fig. 3B, top), so that cycloreversion takes place in each case.
To study these effects more closely, the internal coordinates of the molecules, i.e. their bond lengths, bond angles and dihedral angles, were partitioned into three groups. The first group consists of internal coordinates in which the involved atoms are located solely in the ring. Analogously, the second group comprises internal coordinates in which the atoms are located solely in the linker. The third group consists of internal coordinates that involve atoms from both the ring and the linker (e.g. the bond between the ring and the linker). The application of this partitioning scheme in the JEDI analysis reveals that the strain energy in the triazole ring of the 1,4-isomer is rather low during the entire end-to-end stretching process and becomes even lower at higher forces (Fig. 3A). This demonstrates that triazoles are mechanically robust in general, and cycloreversion cannot be achieved by a purely mechanical activation of the entire ring via a shearing geometry. If the forces pulling at the terminal carbon atoms are low, most strain energy is stored in the interface between ring and linker, but this energy percentage decreases with increasing force, whereas the energy percentage in the linkers increases. Bond rupture in the 1,4-substituted triazoles was observed exclusively at the chain ends, which can be rationalized by the observation that the terminal bond angles of an aliphatic chain are typically softer than in its central part, thus leading to better alignment of the terminal bonds with the external force.50
Apparently, the end-to-end stretching coordinate in 1,4-substituted triazole is similar to the shearing coordinate c2 within the triazole ring. Rupture upon stretching the 1,4-isomer end-to-end occurs in the linker and not, as in the case of the shearing coordinate c2, within the ring, because very large forces and energies are needed to initiate rupture in the triazole ring via the c2 shearing coordinate (Fmax = 13.6 nN). Rupture in the linker, on the other hand, requires much less force and energy (Fmax ≈ 6 nN), this process is thus triggered in the end-to-end stretching coordinate.
In 1,5-substituted triazoles (Fig. 3B), on the other hand, the N1–C5 bond is activated directly. The increase in strain energy in the triazole ring at higher stretching forces can be traced back to the error of the harmonic approximation resulting from rupture of the N1–C5 bond, which leads to cycloreversion. Initially, however, a large amount of strain energy is also stored in the linker and the interface, but this proportion generally decreases towards the end of the stretching coordinate. Of course, the longer the linker the more energy is stored in it, since there are more internal coordinates that can act as reservoirs of strain energy.
We conclude from these considerations that cycloreversion of 1,5-substituted triazoles is much more feasible than cycloreversion of the 1,4-isomers, since, in the former case, the activation of the entire mechanically robust triazole ring can be circumvented due to the optimal coupling between the end-to-end stretching coordinate and a scissile bond in the triazole ring. Thus, the results of the JEDI analysis provide the quantitative basis for straightforward geometric arguments.26 If cycloreversion of the 1,4-isomers indeed occurs in the experiment, mechanical forces resulting from longitudinal waves in an ultrasound bath cannot play the key role. An earlier study suggested rapid heating due to the collapse of cavitational bubbles, electronically excited states, solvent-assisted cycloreversion or processes including radicals as additional factors influencing scission of 1,2,3-triazole in an ultrasound bath,27 all of which were not considered here. Since this study focuses on the mechanochemical aspect of the cycloreversion of triazoles, we concentrate on the 1,5-substitution pattern in the following.
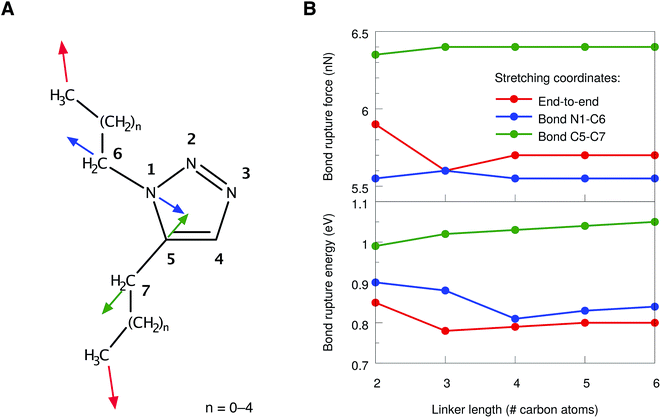
However, even in 1,5-substituted triazoles it is not possible to activate the N1–C5 bond exclusively by stretching the aliphatic linkers. We found that the bonds connecting the linker to the ring are significantly strained as well. Therefore, two additional stretching coordinates, in which these bonds were pulled apart in an isolated manner (cf. the blue and green arrows in Fig. 4A), were investigated. In all cases, linkers of different sizes were considered and the bond rupture forces and energies were compared. We refrained from an isolated stretching of the terminal carbon–carbon bonds, since the rupture probability of polymer chains in an ultrasound bath is highest within the central 15% of the chain.21,22
In general, the rupture forces change only slightly when the linker length is altered (Fig. 4B, top panel). Interestingly, the scission of one of the interface bonds (N1–C6) requires less force when stretched in an isolated manner than the scission of the N1–C5 bond when stretched end-to-end. Nevertheless, it is the N1–C5 bond in the triazole ring that breaks when the molecule is stretched end-to-end, thereby initiating cycloreversion, since the N1–C5 bond is aligned optimally with the force vector in this stretching scenario. As a result, only rupture events of the N1–C5 bond in the end-to-end stretching coordinate have been observed, regardless of the linker length. Breaking the other interface bond (C5–C7), however, requires significantly more force, which is in agreement with the previous observations that the carbon–nitrogen bonds in the molecule are weaker than the carbon–carbon bonds.
In addition to the comparison of bond rupture forces, it is insightful to compare the energies needed for bond rupture in each of the three coordinates using the JEDI analysis. Since the JEDI analysis is based on the harmonic approximation, the bond rupture energies yielded by the JEDI analysis for the coordinates shown in Fig. 4A overestimate ΔEDFT due to pronounced anharmonic effects. However, a satisfactory correction of the energies is possible.37 In the case of end-to-end stretching, for example, we are primarily interested in the energy stored in the scissile N1–C5 bond. As a step towards correcting this value, the bond length immediately prior to rupture was adjusted in an isolated bond stretching scenario, which corresponds to the coordinate c6. Subsequently, a COGEF (COnstrained Geometries simulate External Force)51,52 calculation was carried out. The harmonic error within this isolated stretching setup was used to compensate the error of the energy stored in the N1–C5 bond in the end-to-end stretching scenario. In the case of the interface bonds N1–C6 and C5–C7, the energy correction is much more straightforward, since only one bond is stretched and the overestimation of ΔEDFT by ΔEharm can be used directly to correct the energy.
The resulting corrected energies from the JEDI analysis are shown in Fig. 4B (bottom panel). As expected, similar energies are needed to rupture the bonds N1–C5 and N1–C6. Although the N1–C6 interface bond breaks at slightly lower forces, the energy needed to rupture the N1–C5 bond in the triazole ring and to achieve cycloreversion is lower. A straightforward explanation of this effect is that the energy is proportional to the bond elongation and the N1–C5 bond does not need to be elongated as much as the N1–C6 bond in order to achieve rupture. The C5–C7 bond is again found to be significantly more stable. Interestingly, the rupture forces and energies correlate only weakly with the length of the linker, although the total amount of strain in the molecule increases linearly with the chain length (Fig. S2†).
Hence, from a static point of view, rupture of the bonds N1–C5 and N1–C6 require similar amounts of force and energy. From these considerations we predict that, if cycloreversion takes place in the 1,5-substituted triazole, it is a statistical process that competes with rupture of the adjacent single-bonds connecting the linker to the ring. However, these conclusions were drawn entirely from static considerations and thus we now turn to a discussion of the end-to-end stretching process based on dynamics calculations.
3.2 Dynamic stretching
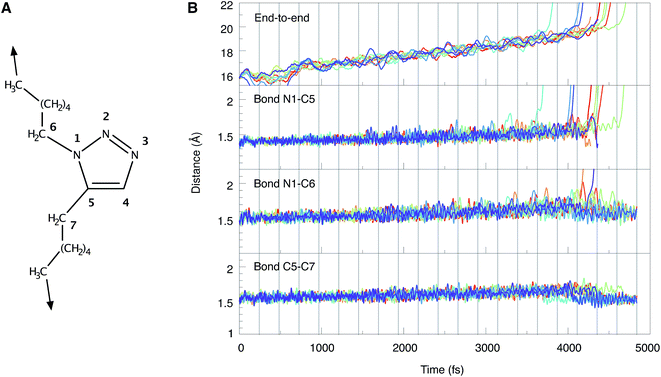
As dynamics simulations have proven to be valuable tools in the description of mechanochemical bond rupture processes,53–55 Born–Oppenheimer Molecular Dynamics (BOMD) simulations have been carried out, in which a stretching force was applied to the terminal carbon atoms of 1,5-hexyl triazole. To mimic experimental conditions, the stretching force was increased by 250 pN each 500 time steps (1 time step = 0.484 fs), until a maximum force of 5 nN was reached. Thus, the total simulation time amounted to 4.84 ns. With this setup, a loading rate of approximately 109 nN s−1 was simulated, which lies in the range estimated for ultrasound baths (108–1010 nN s−1).28 Since elevated temperatures play a major role in sonochemistry56,57 and thermal oscillations have a significant impact on bond rupture in general,58–61 we adjusted the temperature in the BOMD simulations to 500 K and sampled the initial velocities via a Boltzmann distribution. Due to the size of the system and the immense computational cost, only ten BOMD simulations could be conducted, although a larger number of trajectories would be beneficial for a more robust statistical evaluation. We are aware that our setup does not model the experimental conditions in an ultrasound bath fully realistically, since solvent effects, radicals and the influence of pressure are not simulated. However, we concentrate on the mechanical component of ultrasound baths and note that a computational protocol for modeling sonochemical experiments realistically is not available.24The end-to-end distances and the lengths of the bonds N1–C5, N1–C6 and C5–C7 during the BOMD simulations are shown in Fig. 5. In the ten trajectories, eight cycloreversions, initiated by rupture of the N1–C5 bond, and two ruptures of the N1–C6 bond have occurred. Scission of the C5–C7 bond was not observed. The forces needed to achieve bond rupture lie between 3.75 and 4.75 nN. In general, the gradual application of a stretching force leads to a gradual increase in bond lengths. After rupture of a bond, the other bond lengths relax. An example of this effect is provided by the two cases in which rupture of the N1–C6 bond occurs and the N1–C5 bond length relaxes as a consequence (cf. the orange and purple lines in Fig. 5B). Although the inclusion of a wider variety of experimental parameters and the calculation of a larger number of trajectories would be beneficial for a quantitative discussion of the behavior of triazoles in ultrasound baths, the results are in qualitative agreement with the static EFEI calculations (Fig. 4B), where it was found that the forces needed for rupture of the bonds N1–C5 and N1–C6 are very similar.
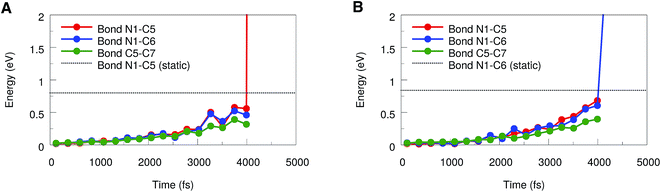
To draw more quantitative conclusions, we used the JEDI analysis to investigate the distribution of potential energy among the internal coordinates of the molecule in the course of the BOMD simulations. For this, we averaged the geometries over 500 consecutive time steps in order to minimize the influence of thermal oscillations and used these mean geometries as the mechanically strained structures within the JEDI analysis.37 The full set of JEDI analyses for all BOMD simulations can be found in the ESI (Fig. S3†). The results of a typical trajectory, in which cycloreversion occurs, are shown in Fig. 6A. The energies in the bonds N1–C5, N1–C6 and C5–C7 are similar throughout a large part of the simulation. As soon as cycloreversion occurs after approximately 4 ns, however, anharmonic effects result in a sharp increase in energy of the N1–C5 bond and the results are no longer quantitative. Up to this point, however, the energies in the bonds N1–C5 and N1–C6 are almost the same, thus supporting our conclusion that rupture of one of these bonds is a statistical phenomenon.
Similar effects can be observed in the JEDI analysis of one of the trajectories in which rupture of the N1–C6 bond occurs (Fig. 6B): the energies in the bonds N1–C5 and N1–C6 are very similar throughout the simulation, but the sharp increase in the N1–C6 bond energy indicates rupture at approximately 4 ns. The observation of both cycloreversion and interface rupture events are in good agreement with the results from the static JEDI analyses based on EFEI calculations (Fig. 4B), where it was found that the energies needed for the rupture of the bonds N1–C5 and N1–C6 are almost the same.
Finally, we note that the forces needed to induce rupture are larger by almost a factor of 2 when they are applied gradually in comparison to a BOMD simulation in which the force is applied suddenly (Fig. S4†). If the force is applied gradually, the molecule has time for equilibration, i.e. for a redistribution of strain energy among all internal coordinates. If the fore is applied suddenly, by contrast, the strain propagates rapidly from the linkers to the central triazole moiety, where constructive interference results in efficient bond rupture. Hence, one way of reducing the forces required for rupture in triazoles would be to increase the loading rate. However, the close proximity of the bonds N1–C5 and N1–C6 impedes selective cycloreversion (see ESI†).
4 Conclusions and outlook
In this paper, we have applied static EFEI and dynamic BOMD calculations in combination with the JEDI analysis to answer the question whether mechanically induced cycloreversion of 1,4- and 1,5-substituted 1,2,3-triazoles is generally possible. We have found that cycloreversion of 1,4-substituted 1,2,3-triazoles is impossible if stretching forces are applied to the ends of the aliphatic linkers, since the entire mechanically robust triazole ring would need to be activated. This process is energetically much less favorable than rupture somewhere in the aliphatic chain. In contrast, mechanical cycloreversion of 1,5-substituted 1,2,3-triazoles is possible, since the N1–C5 bond in the triazole ring, which needs to be ruptured for cycloreversion, can be activated efficiently by stretching forces due to the optimal alignment of the scissile bond with the force vector.Cycloreversion in 1,5-substituted triazoles, however, competes with rupture of the carbon–nitrogen bond connecting the triazole ring to the aliphatic linker. The forces and energies needed to rupture these bonds are very similar, so that a statistical mixture of cycloreversions and rupture events of the interface bond in stretching experiments is expected. Since only a few BOMD trajectories could be calculated and several important experimental parameters (e.g. temperature, pressure, solvent effects, loading rate, length and nature of the linkers) have been neglected or sampled only insufficiently, we cannot predict the distribution of cycloreversion and interface rupture events in experiments quantitatively. In the future, experimental conditions need to be modeled more realistically and a larger number of ab initio molecular dynamics simulations need to be carried out to predict the probability of mechanical triazole cycloreversion in a given experimental setup.
References
- V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, A Stepwise Huisgen Cycloaddition Process: Copper(I)-Catalyzed Regioselective “Ligation” of Azides and Terminal Alkynes, Angew. Chem., Int. Ed., 2002, 41, 2596–2599 CrossRef CAS PubMed.
- C. W. Tornøe, C. Christensen and M. Meldal, Peptidotriazoles on Solid Phase: [1,2,3]-Triazoles by Regiospecific Copper(I)-Catalyzed 1,3-Dipolar Cycloadditions of Terminal Alkynes to Azides, J. Org. Chem., 2002, 67, 3057–3064 CrossRef.
- M. F. Debets, S. S. Van Berkel, J. Dommerholt, A. J. Dirks, F. P. J. T. Rutjes and F. L. Van Delft, Bioconjugation with Strained Alkenes and Alkynes, Acc. Chem. Res., 2011, 44, 805–815 CrossRef CAS PubMed.
- T. Yamada, C. G. Peng, S. Matsuda, H. Addepalli, K. N. Jayaprakash, M. R. Alam, K. Mills, M. A. Maier, K. Charisse and M. Sekine, et al., Versatile Site-Specific Conjugation of Small Molecules to siRNA Using Click Chemistry, J. Org. Chem., 2011, 76, 1198–1211 CrossRef CAS PubMed.
- G. Pourceau, A. Meyer, J. J. Vasseur and F. Morvan, Azide Solid Support for 3′-Conjugation of Oligonucleotides and Their Circularization by Click Chemistry, J. Org. Chem., 2009, 74, 6837–6842 CrossRef CAS PubMed.
- J. C. Jewett and C. R. Bertozzi, Cu-free click cycloaddition reactions in chemical biology, Chem. Soc. Rev., 2010, 39, 1272–1279 RSC.
- E. Lallana, A. Sousa-Herves, F. Fernandez-Trillo, R. Riguera and E. Fernandez-Megia, Click Chemistry for Drug Delivery Nanosystems, Pharm. Res., 2012, 29, 1–34 CrossRef CAS PubMed.
- K. Lang and J. W. Chin, Bioorthogonal Reactions for Labeling Proteins, ACS Chem. Biol., 2014, 9, 16–20 CrossRef CAS PubMed.
- X. Deng and J. Lahann, Orthogonal Surface Functionalization Through Bioactive Vapor-Based Polymer Coatings, J. Appl. Polym. Sci., 2014, 131, 40315 CrossRef.
- W. H. Binder and R. Sachsenhofer, ‘Click’ Chemistry in Polymer and Materials Science, Macromol. Rapid Commun., 2007, 28, 15–54 CrossRef CAS.
- H. Nandivada, X. Jiang and J. Lahann, Click Chemistry: Versatility and Control in the Hands of Materials Scientists, Adv. Mater., 2007, 19, 2197–2208 CrossRef CAS.
- R. K. Iha, K. L. Wooley, A. M. Nyström, D. J. Burke, M. J. Kade and C. J. Hawker, Applications of Orthogonal “Click” Chemistries in the Synthesis of Functional Soft Materials, Chem. Rev., 2009, 109, 5620–5686 CrossRef CAS PubMed.
- P. L. Golas and K. Matyjaszewski, Marrying click chemistry with polymerization: expanding the scope of polymeric materials, Chem. Soc. Rev., 2010, 39, 1338–1354 RSC.
- P. Antoni, M. J. Robb, L. Campos, M. Montanez, A. Hult, E. Malmström, M. Malkoch and C. J. Hawker, Pushing the Limits for Thiol–Ene and CuAAC Reactions: Synthesis of a 6th Generation Dendrimer in a Single Day, Macromolecules, 2010, 43, 6625–6631 CrossRef CAS.
- W. Xi, T. F. Scott, C. J. Kloxin and C. N. Bowman, Click Chemistry in Materials Science, Adv. Funct. Mater., 2014, 24, 2572–2590 CrossRef CAS.
- J. N. Brantley, K. M. Wiggins and C. W. Bielawski, Unclicking the Click: Mechanically Facilitated 1,3-Dipolar Cycloreversions, Science, 2011, 333, 1606–1609 CrossRef CAS PubMed.
- P. Cintas, G. Cravotto, A. Barge and K. Martina, Interplay Between Mechanochemistry and Sonochemistry, Top. Curr. Chem., 2015, 369, 239–284 CrossRef CAS PubMed.
- G. Cravotto, E. C. Gaudino and P. Cintas, On the mechanochemical activation by ultrasound, Chem. Soc. Rev., 2013, 42, 7521–7534 RSC.
- G. Cravotto and P. Cintas, Forcing and Controlling Chemical Reactions with Ultrasound, Angew. Chem., Int. Ed., 2007, 46, 5476–5478 CrossRef CAS PubMed.
- G. Cravotto and P. Cintas, Power ultrasound in organic synthesis: moving cavitational chemistry from academia to innovative and large-scale applications, Chem. Soc. Rev., 2006, 35, 180–196 RSC.
- P. A. R. Glynn, B. M. E. van der Hoff and P. M. Reilly, A General Model for Prediction of Molecular Weight Distributions of Degraded Polymers. Development and Comparison with Ultrasonic Degradation Experiments, J. Macromol. Sci., Chem., 1972, 6, 1653–1664 CrossRef CAS.
- P. A. R. Glynn and B. M. E. van der Hoff, Degradation of Polystyrene in Solution by Ultrasonication – A Molecular Weight Distribution Study, J. Macromol. Sci., Chem., 1973, 7, 1695–1719 CrossRef CAS.
- M. McNutt, Editorial retraction, Science, 2015, 347, 834 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Advances in Quantum Mechanochemistry: Electronic Structure Methods and Force Analysis, Chem. Rev., 2016, 116, 14137–14180 CrossRef CAS PubMed.
- S. S. M. Konda, J. N. Brantley, C. W. Bielawski and D. E. Makarov, Chemical reactions modulated by mechanical stress: extended Bell theory, J. Chem. Phys., 2011, 135, 164103 CrossRef PubMed.
- J. N. Brantley, S. S. M. Konda, D. E. Makarov and C. W. Bielawski, Regiochemical Effects on Molecular Stability: A Mechanochemical Evaluation of 1,4- and 1,5-Disubstituted Triazoles, J. Am. Chem. Soc., 2012, 134, 9882–9885 CrossRef CAS PubMed.
- H. S. Smalø and E. Uggerud, Ring opening vs. direct bond scission of the chain in polymeric triazoles under the influence of an external force, Chem. Commun., 2012, 48, 10443–10445 RSC.
- M. J. Jacobs, G. Schneider and K. G. Blank, Mechanical Reversibility of Strain-Promoted Azide–Alkyne Cycloaddition Reactions, Angew. Chem., Int. Ed., 2016, 55, 2899–2902 CrossRef CAS PubMed.
- M. Krupička, P. Dopieralski and D. Marx, Unclicking the Click: Metal-Assisted Mechanochemical Cycloreversion of Triazoles is Possible, Angew. Chem., Int. Ed., 2017 DOI:10.1002/anie.201612507.
- A. Khanal, F. Long, B. Cao, R. Shahbazian-Yassar and S. Fang, Evidence of Splitting 1,2,3-Triazole into an Alkyne and Azide by Low Mechanical Force in the Presence of Other Covalent Bonds, Chem.–Eur. J., 2016, 22, 9760–9767 CrossRef CAS PubMed.
- D. Schütze, K. Holz, J. Müller, M. K. Beyer, U. Lüning and B. Hartke, Pinpointing Mechanochemical Bond Rupture by Embedding the Mechanophore into a Macrocycle, Angew. Chem., Int. Ed., 2015, 54, 2556–2559 CrossRef PubMed.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene, J. Am. Chem. Soc., 2009, 131, 6377–6379 CrossRef CAS PubMed.
- J. Ribas-Arino, M. Shiga and D. Marx, Understanding Covalent Mechanochemistry, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- K. Wolinski and J. Baker, Theoretical predictions of enforced structural changes in molecules, Mol. Phys., 2009, 107, 2403–2417 CrossRef CAS.
- T. Stauch and A. Dreuw, A quantitative quantum-chemical analysis tool for the distribution of mechanical force in molecules, J. Chem. Phys., 2014, 140, 134107 CrossRef PubMed.
- T. Stauch and A. Dreuw, On the use of different coordinate systems in mechanochemical force analyses, J. Chem. Phys., 2015, 143, 074118 CrossRef PubMed.
- T. Stauch and A. Dreuw, Quantum Chemical Strain Analysis For Mechanochemical Processes, Acc. Chem. Res., 2017, 50, 1041–1048 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Knots “Choke Off” Polymers upon Stretching, Angew. Chem., Int. Ed., 2016, 55, 811–814 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Stiff-stilbene photoswitch ruptures bonds not by pulling but by local heating, Phys. Chem. Chem. Phys., 2016, 18, 15848–15853 RSC.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al., Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2014, 113, 184–215 CrossRef.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko and D. P. O'Neill, et al., Advances in methods and algorithms in a modern quantum chemistry program package, Phys. Chem. Chem. Phys., 2006, 3172–3191 RSC.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. F. Iozzi, T. Helgaker and E. Uggerud, Assessment of theoretical methods for the determination of the mechanochemical strength of covalent bonds, Mol. Phys., 2009, 107, 2537–2546 CrossRef CAS.
- G. S. Kedziora, S. A. Barr, R. Berry, J. C. Moller and T. D. Breitzman, Bond breaking in stretched molecules: multi-reference methods versus density functional theory, Theor. Chem. Acc., 2016, 135, 79 CrossRef.
- J. Ribas-Arino, M. Shiga and D. Marx, Mechanochemical Transduction of Externally Applied Forces to Mechanophores, J. Am. Chem. Soc., 2010, 132, 10609–10614 CrossRef CAS PubMed.
- P. Dopieralski, P. Anjukandi, M. Rückert, M. Shiga, J. Ribas-Arino and D. Marx, On the role of polymer chains in transducing external mechanical forces to benzocyclobutene mechanophores, J. Mater. Chem., 2011, 21, 8309–8316 RSC.
- H. S. Smalø and E. Uggerud, Breaking covalent bonds using mechanical force, which bond breaks?, Mol. Phys., 2013, 111, 1563–1573 CrossRef.
- M. K. Beyer, The mechanical strength of a covalent bond calculated by density functional theory, J. Chem. Phys., 2000, 112, 7307–7312 CrossRef CAS.
- E. A. Nikitina, V. D. Khavryutchenko, E. F. Sheka, H. Barthel and J. Weis, Deformation of Poly(dimethylsiloxane) Oligomers under Uniaxial Tension: Quantum Chemical View, J. Phys. Chem. A, 1999, 103, 11355–11365 CrossRef CAS.
- J. Ribas-Arino and D. Marx, Covalent Mechanochemistry: Theoretical Concepts and Computational Tools with Applications to Molecular Nanomechanics, Chem. Rev., 2012, 112, 5412–5487 CrossRef CAS PubMed.
- H. S. Smalø, V. V. Rybkin, W. Klopper, T. Helgaker and E. Uggerud, Mechanochemistry: The Effect of Dynamics, J. Phys. Chem. A, 2014, 118, 7683–7694 CrossRef PubMed.
- P. Dopieralski and Z. Latajka, in Practical Aspects of Computational Chemistry IV, ed. J. Leszczynski and M. K. Shukla, Springer, US, New York, 1st edn, 2016, pp. 233–243 Search PubMed.
- K. S. Suslick, D. A. Hammerton and R. E. Cline, The Sonochemical Hot Spot, J. Am. Chem. Soc., 1986, 108, 5641–5642 CrossRef CAS.
- K. S. Suslick, Sonochemistry, Science, 1990, 247, 1439–1445 CAS.
- E. Evans, Probing the Relation Between Force – Lifetime – and Chemistry in Single Molecular Bonds, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS PubMed.
- Y. S. Lo, J. Simons and T. P. Beebe, Temperature Dependence of the Biotin–Avidin Bond-Rupture Force Studied by Atomic Force Microscopy, J. Phys. Chem. B, 2002, 106, 9847–9852 CrossRef CAS.
- I. Schumakovitch, W. Grange, T. Strunz, P. Bertoncini, H.-J. Güntherodt and M. Hegner, Temperature Dependence of Unbinding Forces between Complementary DNA Strands, Biophys. J., 2002, 82, 517–521 CrossRef CAS PubMed.
- P. Dopieralski, J. Ribas-Arino and D. Marx, Force-Transformed Free-Energy Surfaces and Trajectory-Shooting Simulations Reveal the Mechano-Stereochemistry of Cyclopropane Ring-Opening Reactions, Angew. Chem., Int. Ed., 2011, 50, 7105–7108 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc01562c |
| This journal is © The Royal Society of Chemistry 2017 |