Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical tuning of dynamic cation off-centering in the cubic phases of hybrid tin and lead halide perovskites†
Geneva
Laurita
a,
Douglas H.
Fabini
 ab,
Constantinos C.
Stoumpos
d,
Mercouri G.
Kanatzidis
d and
Ram
Seshadri
ab,
Constantinos C.
Stoumpos
d,
Mercouri G.
Kanatzidis
d and
Ram
Seshadri
 *abc
*abc
aMaterials Research Laboratory, University of California, Santa Barbara, California 93106, USA
bMaterials Department, University of California, Santa Barbara, California 93106, USA
cDepartment of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106, USA. E-mail: seshadri@mrl.ucsb.edu
dDepartment of Chemistry, Argonne-Northwestern Solar Energy Research (ANSER) Center, Northwestern University, Evanston, Illinois 60208, USA
First published on 16th June 2017
Abstract
Hybrid halide perovskites combine ease of preparation and relatively abundant constituent elements with fascinating photophysical properties. Descriptions of the chemical and structural drivers of the remarkable properties have often focused on the potential role of the dynamic order/disorder of the molecular A-site cations. We reveal here a key aspect of the inorganic framework that potentially impacts the electronic, thermal, and dielectric properties. The temperature evolution of the X-ray pair distribution functions of hybrid perovskites ABX3 [A+ = CH3NH3 (MA) or CH(NH2)2 (FA); B2+ = Sn or Pb; X− = Br, or I] in their cubic phases above 300 K reveals temperature-activated displacement (off-centering) of the divalent group 14 cations from their nominal, centered sites. This symmetry-lowering distortion phenomenon, previously dubbed emphanisis in the context of compounds such as PbTe, is attributed to Sn2+ and Pb2+ lone pair stereochemistry. Of the materials studied here, the largest displacements from the center of the octahedral sites are found in tin iodides, a more moderate effect is found in lead bromides, and the weakest effect is seen in lead iodides. The A-site cation appears to play a role as well, with the larger FA resulting in greater off-centering for both Sn2+ and Pb2+. Dynamic off-centering, which is concealed within the framework of traditional Bragg crystallography, is proposed to play a key role in the remarkable defect-tolerant nature of transport in these semiconductors via its effect on the polarizability of the lattice. The results suggest a novel chemical design principle for future materials discovery.
1 Introduction
Inorganic and hybrid organic–inorganic halide perovskites ABX3 [A+ = Cs, CH3NH3 (MA), or CH(NH2)2 (FA); B2+ = Ge, Sn, or Pb; X− = Cl, Br, or I] have attracted significant research attention of late due to their impressive optoelectronic performance, ease of preparation, and abundant constituent elements. Since the first application of hybrid lead iodides in photovoltaic (PV) devices in 2009,1 the conversion efficiency of record perovskite PV cells has risen to over 20%,2 and the field has broadened substantially to include the pursuit of lead-free materials,3–11 bromides and mixed halides for light emission and detection applications,12–17 and layered perovskite-derivatives for enhanced stability.18–20 However, key aspects regarding the origins of the remarkable functionality of these materials remain enigmatic. Among them are: why do the low rates of carrier trapping and recombination16,17,21–23 in these relatively soft, solution-processed materials approach those of the best high purity III–V semiconductors, leading to long carrier lifetimes and long diffusion lengths?21,24 Why are the carrier mobilities so modest21,22,25 relative to the calculated carrier effective masses and typical scattering rates? In answering these questions, much attention has focused on the potential importance of the A-site organic molecular cations in the hybrid systems,26–28 but recent reports suggest that all-inorganic analogues exhibit many of the same structural tendencies29,30 and favorable transport properties.23,31–34A clue then to the unusual properties potentially lies in these systems being proximate in phase space (composition, temperature, pressure, strain) to symmetry-lowering distortions of the octahedral coordination environment of the group 14 divalent cation. The presence of this instability and the role that it may play in the properties of the perovskites have been hinted at in prior reports,29,35–37 but have not been explored in detail, nor have the impacts on the properties been fully considered. The strength of this effect is dictated by the stability of the ns2 level of the isolated lone-pair bearing cation and the electronegativity of the halogen. In the case of the perovskites studied here, the Goldschmidt tolerance factor, as influenced by the size of the A-site cation and potentially the shape of the A cation, is also likely to play a role, providing guidelines for tuning these effects in a rational manner.
Main-group cations with a valence state that is two fewer than the group valence (e.g. Sn2+, Sb3+, Tl+, Pb2+ and Bi3+) possess the lone pair s2p0 electronic configuration and are prone to symmetry-lowering distortions associated with the pseudo- or second-order-Jahn–Teller effects.38,39 Heavier cations have deep ns2 levels due to relativistic stabilization, reducing the strength of the on-site s–p hybridization. The higher energy of the ns2 levels of lighter cations, as well as the mixing with the anion p orbitals, leads to stereochemical expression of the lone pair.40–44 This is exemplified in the AGeI3 (A+ = Cs, MA, FA) perovskite analogs,45 where the strong tendency for the activity of the 4s2 electrons of Ge results in room-temperature structures with highly distorted Ge environments, which also happen to be polar. In contrast, the heavier Sn and Pb atoms form halide perovskite compounds that can crystallize with these cations in nominally regular octahedral environments.
The choice of ligand is also a key factor with more electronegative anions resulting in greater interaction of the anion p states with the orbitals of the cation and thus greater propensity for the off-centered coordination polyhedra associated with lone pair stereochemical activity.43 When the propensity for lone pair stereochemical activity is not sufficiently strong relative to the thermal energy to produce a ferroically distorted phase, uncorrelated, local off-centering displacements of the main-group cation can result. Such displacements have recently been observed to emerge from a high symmetry phase upon heating in rock-salt group 14 chalcogenides,46–48 and this phenomenon has been termed emphanisis. This phenomenon leads to substantial anharmonicity of the lattice dynamics, contributing to the observed ultralow thermal conductivity important for thermoelectrics,49 and has been a topic of intense interest since the first reports.50–57 Our recent work has shown a similar dynamic displacement of Sn2+ in CsSnBr3 at ambient and elevated temperatures,29 suggesting that an emphanitic local distortion of the metal halide network may also be present in the technologically important hybrid halide perovskites.
We show here that the tendency for symmetry-lowering local distortions of the group 14 cation coordination environment exists across the hybrid halide perovskites. The pair distribution functions for ABX3 (A+ = MA or FA; B2+ = Sn or Pb; X− = Br or I) calculated from X-ray scattering at and above 300 K reveal temperature-activated, dynamic off-centering of the lone pair-bearing Sn2+ and Pb2+ cations that is not observed through traditional crystallographic techniques. This local off-centering is described by displacements along <111>, and we find the largest degree of off-centering in lead-free tin iodides, a moderate degree in lead bromides, and the smallest degree in the lead iodide compositions. This qualitative agreement with the chemical predictors of the lone pair stereochemical activity as enumerated for the group 14 chalcogenides,43 together with our prior ab initio studies of the perovskite CsSnBr3,29 implicates the lone pairs as the driving force for this behavior. This phenomenon has profound implications on understanding the properties: systems displaying this proximal instability exhibit strongly anharmonic lattice dynamics leading to an elevated static dielectric response, which reduces carrier scattering, trapping, and recombination,58–60 as well as high coefficients of volumetric thermal expansion29,61–63 and unusual temperature evolution of the bandgap.29 The substantial lattice polarizability associated with this proximal instability is of particular importance as it may explain why the carrier mobilities are limited by scattering from phonons rather than charged defects22,64,65 and why carrier trapping and recombination rates are so low.21–23 This additionally lends credence to the hypothesis of large polaron formation60 that reconciles the small carrier effective masses from band theory with the modest mobilities observed in the experiment. Chemical control of this phenomenon, as demonstrated by the qualitative composition trends observed here, offers new design principles in the search for defect-tolerant semiconductors.
2 Experimental section
2.1 Sample synthesis
The hybrid perovskites were prepared following modifications of the previously reported procedures.66 PbO and CH3NH3Cl were purchased from Sigma-Aldrich. HC(NH2)2Cl was prepared by stoichiometric addition of solid HC(NH2)2(O2CCH3) in 37% aqueous HCl, followed by rotary evaporation and washing with toluene to remove excess acetic acid.63 Black SnO was prepared following a modification of the literature procedure.67 The detailed procedures for the preparation of the polycrystalline samples of CH3NH3PbI3, HC(NH2)2PbI3, CH3NH3SnI3, HC(NH2)2SnI3, CH3NH3PbBr3, and HC(NH2)2PbBr3 can be found in the ESI.†2.2 X-ray scattering data collection and modeling
For the synchrotron total scattering measurements, samples of fine powder, obtained by the means described above, were transferred into Kapton capillaries (0.81 mm OD, 0.8 mm ID) and tightly compacted to ensure a maximum packing fraction. Both ends of the capillaries were sealed with epoxy and stored in a N2 atmosphere prior to the measurement.The synchrotron X-ray total scattering measurements were recorded on the 11-ID-B beam line at the Advanced Photon Source located at Argonne National Laboratory. The 2D scattering data were collected on a Perkin-Elmer amorphous Si-based area detector. A photon wavelength of 0.2114 Å (58.66 keV) was used for MAPbI3 (collected from 360 K to 300 K), FAPbI3 (collected from 480 K to 300 K to ensure conversion from the yellow δ phase to the black perovskite phase, and verified by analysis of the reciprocal space data, shown in Fig. S1† at 360 K), MAPbBr3 (collected from 360 K to 300 K), and FAPbBr3 (collected from 360 K to 300 K). A photon wavelength of 0.1430 Å (86.70 keV) was used for MASnI3 (collected from 360 K to 300 K) and FASnI3 (collected from 360 K to 300 K) to avoid the Sn fluorescence edge at 29.21 keV. The data were collected every 2 minutes upon cooling at a rate of 6 K min−1. Fit2D68 was utilized to integrate the 2D data to the 1D diffraction patterns. Corrections to obtain the S(Q) and subsequent Fourier transform with a Qmax of 23 Å−1 and an r-grid of 0.01 Å to obtain the X-ray pair distribution function (PDF, G(r)) were performed using the program PDFgetX2.69 These parameters were chosen to optimize the r-resolution while minimizing the Fourier termination ripples satisfactorily for all samples across the series, and an example of the optimization process is shown in Fig. S2† for FASnI3. The instrumental parameters used in the fits were Qbroad = 0.06 Å−1 and Qdamp = 0.01 Å−1, as determined from a CeO2 standard.
For all samples, the A-site cations were modeled as a pseudo-atom with an equivalent scattering power (K for CH3NH3 and Mn for CH(NH2)2) placed in the center of the A site at (0, 0, 0) and given a large (between 0.2 and 0.4 Å2) atomic displacement parameter (ADP). For all fit ranges, the fits of the XPDF data were first performed against the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model to obtain the lattice parameters. The ADPs for the A- and B-site cations were refined isotropically, while the ADPs for the halide atoms were allowed to refine anisotropically. The cubic space groups were subsequently transformed into the respective I4cm and R3m space groups using the “TRANSTRU” tool on the Bilbao Crystallographic Server.70–72 Fits against the I4cm model were first performed over an r-range of 2 Å to 25 Å. The lattice parameters were fixed to the transformed values from the cubic fit. The halide positions and anisotropic ADPs were allowed to refine, while the A-site ADPs were fixed to those obtained from the cubic fit. The B-site ADPs were fixed to 0.008 Å2. For fits against the remaining r-ranges (2 Å to 5 Å and all incremental fits), the lattice parameters were fixed to the values obtained from the transformed structures, the halide ADPs and displacements were fixed to the values obtained from the 2 Å to 25 Å fits while the B-site displacement in the 4a Wyckoff position (0, 0, z) was allowed to refine. Fits against the R3m model were first performed over an r-range of 2 Å to 25 Å. The lattice parameters were fixed to the transformed values from the cubic fit. The halide anisotropic ADPs were allowed to refine, while the A-site ADPs were fixed to those obtained from the cubic fit. The B-site ADPs were fixed to 0.008 Å2. For fits against the remaining r-ranges (2 Å to 5 Å and all incremental fits), the lattice parameters were fixed to the values obtained from the transformed structures, the halide ADPs were fixed to the values obtained from the 2 Å to 25 Å fits while the B-site displacement in the 3a Wyckoff position (0, 0, z) was allowed to refine.
m model to obtain the lattice parameters. The ADPs for the A- and B-site cations were refined isotropically, while the ADPs for the halide atoms were allowed to refine anisotropically. The cubic space groups were subsequently transformed into the respective I4cm and R3m space groups using the “TRANSTRU” tool on the Bilbao Crystallographic Server.70–72 Fits against the I4cm model were first performed over an r-range of 2 Å to 25 Å. The lattice parameters were fixed to the transformed values from the cubic fit. The halide positions and anisotropic ADPs were allowed to refine, while the A-site ADPs were fixed to those obtained from the cubic fit. The B-site ADPs were fixed to 0.008 Å2. For fits against the remaining r-ranges (2 Å to 5 Å and all incremental fits), the lattice parameters were fixed to the values obtained from the transformed structures, the halide ADPs and displacements were fixed to the values obtained from the 2 Å to 25 Å fits while the B-site displacement in the 4a Wyckoff position (0, 0, z) was allowed to refine. Fits against the R3m model were first performed over an r-range of 2 Å to 25 Å. The lattice parameters were fixed to the transformed values from the cubic fit. The halide anisotropic ADPs were allowed to refine, while the A-site ADPs were fixed to those obtained from the cubic fit. The B-site ADPs were fixed to 0.008 Å2. For fits against the remaining r-ranges (2 Å to 5 Å and all incremental fits), the lattice parameters were fixed to the values obtained from the transformed structures, the halide ADPs were fixed to the values obtained from the 2 Å to 25 Å fits while the B-site displacement in the 3a Wyckoff position (0, 0, z) was allowed to refine.
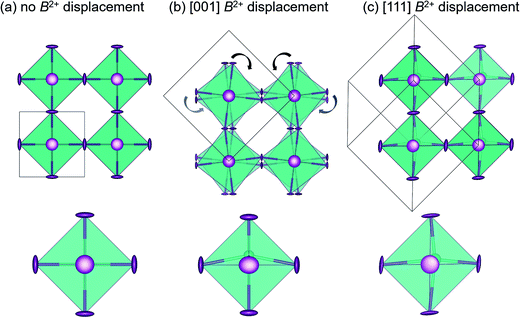
3 Results & discussion
Dynamic octahedral rotations have been observed through local techniques at elevated temperatures in several halide perovskite systems29,37 which may be active in conjunction with dynamic off-centering of the B-site cations. To investigate the interplay between the octahedral rotations and B-site stereochemical activity (and subsequent off-centering), three crystallographic models (Fig. 1) were chosen to fit against the X-ray PDF data over the various r-ranges: cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, which allows neither octahedral rotations nor B-site off-centering; tetragonal I4cm, which allows for simultaneous octahedral rotations and B-site off-centering along the c-axis; rhombohedral R3m, which allows for no octahedral rotations but does allow for B-site off-centering along the [111] crystallographic direction. The space groups chosen to model the local symmetry of the PDF data were based on the crystallographic structures with prototypical ferroic displacements in perovskite systems. In an effort to qualitatively describe the local structure, we have chosen known models that systematically lower the symmetry without drastically increasing the number or correlation of refined parameters. We have previously reported the R3m structure as an approximate description of the dynamic off-centering of Sn2+ in CsSnBr3 (in comparison to the Pm
m, which allows neither octahedral rotations nor B-site off-centering; tetragonal I4cm, which allows for simultaneous octahedral rotations and B-site off-centering along the c-axis; rhombohedral R3m, which allows for no octahedral rotations but does allow for B-site off-centering along the [111] crystallographic direction. The space groups chosen to model the local symmetry of the PDF data were based on the crystallographic structures with prototypical ferroic displacements in perovskite systems. In an effort to qualitatively describe the local structure, we have chosen known models that systematically lower the symmetry without drastically increasing the number or correlation of refined parameters. We have previously reported the R3m structure as an approximate description of the dynamic off-centering of Sn2+ in CsSnBr3 (in comparison to the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, P4mm, and Amm2 models),29 while the local coexistence of rotations and Pb2+ off-centering described by I4cm has been reported for crystallographically cubic MAPbI3.37
m, P4mm, and Amm2 models),29 while the local coexistence of rotations and Pb2+ off-centering described by I4cm has been reported for crystallographically cubic MAPbI3.37
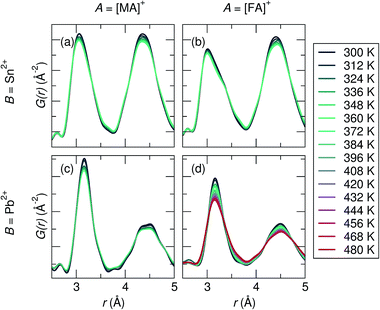
The X-ray PDF data was analyzed from 300 K to 360 K (480 K for FAPbI3), shown in Fig. 2. The temperature at which the cubic perovskite phase is present varies for each composition: for MASnI3T > 275 K,73 for FASnI3T > 250 K,66 for MAPbI3T > 327 K,74 for FAPbI3T > 285 K,63 for MAPbBr3T > 237 K,74 and for FAPbBr3T > 265 K (unpublished reference). Therefore, quantitative studies were only performed in the known cubic phase regimes of each sample. Qualitatively, for all compositions the first B–I peak becomes broader and more asymmetric upon warming, and the effect is most pronounced for the Sn2+ samples. Peak broadening and asymmetry are expected to further increase with higher collection temperatures, which is evidenced in FAPbI3, the only composition collected up to 480 K.
Fits against the X-ray PDF for each sample were performed carefully to avoid excessive correlation of the refined parameters, and the modeling is described in detail in the experimental section. To verify that the samples are crystallographically cubic, the X-ray PDF data were fit over an r-range of 10 Å to 25 Å against the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model at the various reported cubic phase temperatures, and the representative fits for each sample are shown in the ESI Fig. S3.† Reasonable goodness-of-fit (Rw) values (between 8 and 12%) were obtained for all compositions, suggesting that the data are well described by the expected cubic symmetry as we approach the average, crystallographic length scale. The corresponding reciprocal space data from the total scattering experiment, shown in Fig. S1† at 360 K, is additionally consistent with the cubic perovskite structure and does not indicate the presence of any impurity phases.
m model at the various reported cubic phase temperatures, and the representative fits for each sample are shown in the ESI Fig. S3.† Reasonable goodness-of-fit (Rw) values (between 8 and 12%) were obtained for all compositions, suggesting that the data are well described by the expected cubic symmetry as we approach the average, crystallographic length scale. The corresponding reciprocal space data from the total scattering experiment, shown in Fig. S1† at 360 K, is additionally consistent with the cubic perovskite structure and does not indicate the presence of any impurity phases.
Fits of the X-ray PDF data at 360 K against the candidate space group models over a 2.0 Å to 5.0 Å range indicate the poorest fit for all samples against the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model. Fits for the most extreme cases, FASnI3 (the most distorted B–I peak) and MAPbI3 (the least distorted B–I peak), are shown in Fig. 3. For both Sn2+ samples, the best description of the Sn–I correlation is with the R3m model, indicating off-centering best described by rhombohedral symmetry. It should be noted that the goodness-of-fit for the Sn2+ compositions is heavily influenced by the fit to the I–I correlations due to the stronger scattering power of I vs. Sn (in comparison to I vs. Pb). This appears to result in a poorer fit in the Sn–I correlation of these samples; however, this does not change the result that the local symmetry of the Sn2+ compositions is best modeled with a rhombohedral off-centering of Sn2+. It should also be noted that the use of anisotropic displacement parameters is necessary to fit the I–I correlation around 4.5 Å. However, the implementation of the large anisotropic displacements of the halides perpendicular to the B–I bond does not account for the observed peak asymmetry of the first B–X correlation, even with highly exaggerated anisotropic components, as we demonstrated for CsSnBr3.29 For both the Pb2+ samples, a similar description of the Pb–I correlation is obtained with both the I4cm and R3m models. This indicates that cation off-centering is present in the Pb2+ samples; however, it is minor compared to that of the Sn2+ samples, and complicated by a greater degree of correlation with the refined halide parameters. Regardless, the crystallographic cubic phase is an insufficient model of the local symmetry of the Sn2+ and Pb2+ coordination environment for all compositions.
m model. Fits for the most extreme cases, FASnI3 (the most distorted B–I peak) and MAPbI3 (the least distorted B–I peak), are shown in Fig. 3. For both Sn2+ samples, the best description of the Sn–I correlation is with the R3m model, indicating off-centering best described by rhombohedral symmetry. It should be noted that the goodness-of-fit for the Sn2+ compositions is heavily influenced by the fit to the I–I correlations due to the stronger scattering power of I vs. Sn (in comparison to I vs. Pb). This appears to result in a poorer fit in the Sn–I correlation of these samples; however, this does not change the result that the local symmetry of the Sn2+ compositions is best modeled with a rhombohedral off-centering of Sn2+. It should also be noted that the use of anisotropic displacement parameters is necessary to fit the I–I correlation around 4.5 Å. However, the implementation of the large anisotropic displacements of the halides perpendicular to the B–I bond does not account for the observed peak asymmetry of the first B–X correlation, even with highly exaggerated anisotropic components, as we demonstrated for CsSnBr3.29 For both the Pb2+ samples, a similar description of the Pb–I correlation is obtained with both the I4cm and R3m models. This indicates that cation off-centering is present in the Pb2+ samples; however, it is minor compared to that of the Sn2+ samples, and complicated by a greater degree of correlation with the refined halide parameters. Regardless, the crystallographic cubic phase is an insufficient model of the local symmetry of the Sn2+ and Pb2+ coordination environment for all compositions.
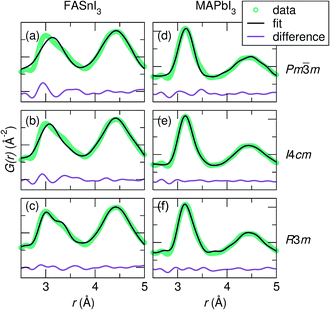 | ||
Fig. 3 Fits of the X-ray PDF data at 360 K from 2.0 Å to 5.0 Å against the various space groups for representative samples FASnI3 [(a) Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, (b) I4cm, and (c) R3m] and MAPbI3 [(d) Pm m, (b) I4cm, and (c) R3m] and MAPbI3 [(d) Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, (e) I4cm, and (f) R3m]. For both FASnI3 and MASnI3 (shown in Fig. S2†), the peak shape of the first Sn–I correlation is best captured by Sn off-centering along <111> as in the R3m model, while FAPbI3 and MAPbI3 (shown in Fig. S2†) are equally well-described by both the I4cm and R3m models. m, (e) I4cm, and (f) R3m]. For both FASnI3 and MASnI3 (shown in Fig. S2†), the peak shape of the first Sn–I correlation is best captured by Sn off-centering along <111> as in the R3m model, while FAPbI3 and MAPbI3 (shown in Fig. S2†) are equally well-described by both the I4cm and R3m models. | ||
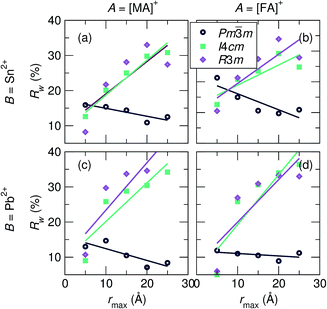
To investigate the coherence length of distortions in the samples, 10 Å incremental fits of the PDF data at 360 K were performed (r-ranges = 1 Å to 10 Å, 5 Å to 15 Å, 10 Å to 20 Å, and 15 Å to 25 Å). Rw values of the fits against the various space group models as a function of rmax are shown in Fig. 4. Rw values of the 2 Å to 5 Å fits are also plotted to illustrate the best representation of the local B-site coordination environment. It is observed for all samples that the cubic model quickly becomes the best description of the data as the incremental series progresses, even at an r-max of only 10 Å, and the Rw for the cubic fit continues to decrease with increasing rmax, further illustrating cubic symmetry as the fit range tends towards the average crystallographic structure.
In CsSnBr3, we determined the presence of a dynamic displacement of the Sn2+ cation of approximately 0.2 Å along the [111] crystallographic direction at 420 K.29 Fits of the local structure of the compositions studied herein indicate a similar local cation displacement. The presence of cation displacement with increasing temperature was investigated by fitting the temperature-dependent data of all samples against the R3m model over a range of 2 Å to 5 Å, shown in Fig. 5. The refined local structures indicate that large displacements are present for the Sn2+-containing samples, while they are minimal in the Pb2+ samples. At 360 K the maximum displacement for each composition, from largest to smallest, is approximately 0.24 Å in FASnI3, 0.22 Å in MASnI3, 0.06 Å in FAPbI3, and 0.01 Å in MAPbI3. This goes with the expected trend of larger displacements in Sn2+ than Pb2+ due to the larger relativistic effects in Pb and larger displacements with increasing lattice parameter from MA to FA. In addition to these cationic effects, the chemical identity of the anion and subsequent interaction between its orbitals and those of the B-site cation affect the propensity for stereochemical activity. Increasing the hardness of the anion (i.e. APbBr3 instead of APbI3) increases the interaction of the anion p states with the B-site s orbitals,43 thus increasing the tendency for activity of the lone pair. Therefore, a larger rhombohedral distortion of Pb2+ should be observed in MAPbBr3 and FAPbBr3 in comparison to their iodide counterparts. Indeed, fitting of the X-ray PDF data of MAPbBr3 and FAPbBr3 at 360 K against the R3m model (Fig. S6†) indicates a Pb2+ displacement of approximately 0.15 Å. Based on the magnitudes of displacement resulting from the fits, it appears that the identity of the A-site cation, which plays a role in the lattice parameter and influences the octahedral rotations observed upon cooling, has the smallest effect on the stereochemical activation of the lone pair, and the compositions of the B-site cation and X-site anion are the largest drivers for the stereochemical activity of the ns2 electrons, highlighting the importance of the B–X cation–anion orbital interaction. However, the displacement magnitudes reported for CsSnBr3 (ref. 29) are essentially indistinguishable from those we find for MAPbBr3 and FAPbBr3, suggesting that the A-site shape may matter in addition to the size, as one would expect greater displacements for Sn2+ than for Pb2+ given the same anion. We expect these chemical trends to be universal in the halide perovskite materials, even extending to the layered perovskites, which are known to exhibit distortions of the MX6 octahedra.75–78 However, the dimensionality of layered perovskites may play an additional role in octahedral distortions and warrants further consideration.
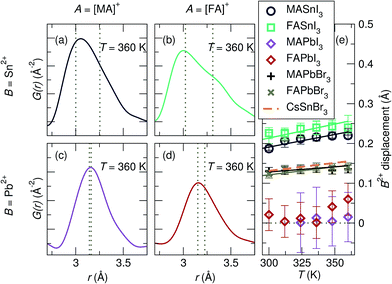 | ||
| Fig. 5 X-ray pair distribution functions for (a) MASnI3, (b) FASnI3, (c) MAPbI3, and (d) FAPbI3 at 360 K of the nearest B–I correlation. (e) Refined displacements of the B-site cation in space group R3m as a function of the temperature indicate large displacements for Sn2+ iodides and minimal displacements for Pb2+ iodides. Refined displacements for the APbBr3 analogs indicate moderate off-centering. Reported Sn2+ displacements in CsSnBr3 are overlaid for comparison.29 The dashed lines in (a–d) indicate the distinct bond lengths extracted from modeling the local structure in the space group R3m ([111] displacement). | ||
4 Conclusions
We have shown through the analysis of pair distribution functions calculated from X-ray scattering experiments that dynamic, temperature-activated B-site cation off-centering displacements occur at and above ambient temperature in the hybrid halide perovskites MASnI3, FASnI3, MAPbI3, FAPbI3, MAPbBr3, and FAPbBr3 as a consequence of the lone pair stereochemical activity. The propensity for stereochemical activity can be tuned through chemical substitution on all sites of the ABX3 perovskite structure: the substitution of a larger A-site cation (FA+ for MA+), a lighter B-site cation (Sn2+ for Pb2+), and a harder anion (Br− for I−) all enhance the magnitude of these displacements. This tendency arises directly from the inherent instability of high-symmetry coordination for ns2p0 cations with significant impact on the properties.29Importantly, these observations are consistent with the emerging hypothesis that the remarkable defect-tolerance of these semiconductors is related to the lattice polarizability, and does not require the strongly dipolar [CH3NH3]+ cation of the hybrid compositions. Recent reports have focused on the possibility of large60 and small79 polaron formation, and the measurements of lifetimes and recombination constants for both hot28 and band-edge23 carriers point to important differences and similarities across compositions. Zhu and coworkers find that hot carriers are much longer lived in MAPbBr3 and FAPbBr3 than in CsPbBr3 and ascribe this to the dipolar molecular cations.28 However, this ignores the negligible FA dipole moment (0.21 D)26 compared to that of MA (2.29 D)26 and the fact that, unlike the hybrid compositions, CsPbBr3 is tilted (orthorhombic, a+b−b−) rather than cubic at room temperature,31,80 which will affect the lattice dynamics and polarizability both directly and via the suppression of the lone pair stereochemical activity through reduced orbital overlap. In a separate report, Zhu and coworkers find extremely low trapping and recombination constants for the band-edge carriers in all three compositions, suggesting the importance of the lead–halogen sublattice, rather than the molecular cations, for defect tolerance.23 Additionally, the large static dielectric response of the halide perovskites is well known63,81–85 and likely contributes to the effective screening of charged defects,86 as has been postulated for thallium halides58 and demonstrated for doped complex oxides.59 Our findings are consistent with these ideas, suggesting that the desired optoelectronic properties are in large part a consequence of the behavior of the metal–halogen network.
An analogous system where proximal instabilities impact the transport properties may be seen in SrTiO3. This d0 system—which has attracted renewed attention in recent years, because of the rich electrical transport phenomena doped variants display, particularly in thin film form87—is also subject to off-centering instabilities due to second-order Jahn–teller effects.39 However, due to the balance of size effects and the perovskite tolerance factor, the expected off-centering transition is pushed down to low enough temperatures that quantum fluctuations suppress any phase transition to a structure with distorted TiO6 octahedra.88 The dielectric constant is anomalously high, however, resulting in unusual transport behavior in the doped phases.89,90 Most notably, polaronic effects, as in the halide perovskites, have been implicated in yielding a measured effective mass that appears larger than one would expect from band structure calculations.91
The elevated polarizability conferred by the proximal instability in Sn2+ and Pb2+ halide perovskites, together with the shallow nature of the defect states due to the antibonding character of the valence band92–94 and the possible separation of the excited carriers in reciprocal space due to the spin–orbit interactions,95–97 is proposed to imbue these materials with their remarkable defect-tolerance. Actively profiting from the phenomena of proximal instabilities due to lone pairs offers a new paradigm for the chemical design of defect-tolerant semiconductors: other compounds with lone pair-bearing ions in high symmetry environments may exhibit similarly favorable transport and recombination properties.
Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under the award number DE-SC-0012541. This research used the resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. GL and CCS would like to thank Hayden Evans, Kevin Beyer and Karena Chapman for their assistance and helpful discussions during beam line experiments. DHF thanks the National Science Foundation Graduate Research Fellowship Program for support under Grant DGE 1144085.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997 CAS.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489–494 CrossRef CAS.
- M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127 CrossRef CAS PubMed.
- B. Saparov, F. Hong, J.-P. Sun, H.-S. Duan, W. Meng, S. Cameron, I. G. Hill, Y. Yan and D. B. Mitzi, Chem. Mater., 2015, 27, 5622–5632 CrossRef CAS.
- A. J. Lehner, H. Wang, D. H. Fabini, C. D. Liman, C.-A. Hébert, E. E. Perry, M. Wang, G. C. Bazan, M. L. Chabinyc and R. Seshadri, Appl. Phys. Lett., 2015, 107, 131109 CrossRef.
- A. J. Lehner, D. H. Fabini, H. A. Evans, C.-A. Hébert, S. R. Smock, J. Hu, H. Wang, J. W. Zwanziger, M. L. Chabinyc and R. Seshadri, Chem. Mater., 2015, 27, 7137–7148 CrossRef CAS.
- S. Gupta, T. Bendikov, G. Hodes and D. Cahen, ACS Energy Lett., 2016, 1, 1028–1033 CrossRef CAS.
- L. Ma, F. Hao, C. C. Stoumpos, B. T. Phelan, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 14750–14755 CrossRef CAS PubMed.
- W. Liao, D. Zhao, Y. Yu, C. R. Grice, C. Wang, A. J. Cimaroli, P. Schulz, W. Meng, K. Zhu, R.-G. Xiong and Y. Yan, Adv. Mater., 2016, 28, 1–8 CrossRef PubMed.
- A. M. Ganose, C. N. Savory and D. O. Scanlon, Chem. Commun., 2017, 53, 20–44 RSC.
- Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Nat. Nanotechnol., 2014, 9, 687–692 CrossRef CAS PubMed.
- F. Deschler, M. Price, S. Pathak, L. E. Klintberg, D.-D. Jarausch, R. Higler, S. Hüttner, T. Leijtens, S. D. Stranks, H. J. Snaith, M. Atatüre, R. T. Phillips and R. H. Friend, J. Phys. Chem. Lett., 2014, 5, 1421–1426 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. S. Lim, N. Yantara, X. Liu, D. Sabba, M. Grätzel, S. Mhaisalkar and T. C. Sum, Nat. Mater., 2014, 13, 476–480 CrossRef CAS PubMed.
- Y.-H. Kim, H. Cho, J. H. Heo, T.-S. Kim, N. Myoung, C.-L. Lee, S. H. Im and T.-W. Lee, Adv. Mater., 2015, 27, 1248–1254 CrossRef CAS PubMed.
- C. C. Stoumpos and M. Kanatzidis, Acc. Chem. Res., 2015, 48, 2791–2802 CrossRef CAS PubMed.
- C. C. Stoumpos and M. Kanatzidis, Adv. Mater., 2016, 28, 5778–5793 CrossRef CAS PubMed.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235 CrossRef CAS PubMed.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843–7850 CrossRef CAS PubMed.
- H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, Nature, 2016, 536, 312–316 CrossRef CAS PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- H. Oga, A. Saeki, Y. Ogomi, S. Hayase and S. Seki, J. Am. Chem. Soc., 2014, 136, 13818–13825 CrossRef CAS PubMed.
- H. Zhu, M. T. Trinh, J. Wang, Y. Fu, P. P. Joshi, K. Miyata, S. Jin and X.-Y. Zhu, Adv. Mater., 2016, 29, 1603072 CrossRef PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS PubMed.
- T. M. Brenner, D. A. Egger, A. M. Rappe, L. Kronik, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 4754–4757 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. Van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S.-H. Lee, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286 RSC.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820–11832 CrossRef CAS PubMed.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 136001 CrossRef PubMed.
- C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Cryst. Growth Des., 2013, 13, 2722–2727 CAS.
- M. Kulbak, D. Cahen and G. Hodes, J. Phys. Chem. Lett., 2015, 6, 2452–2456 CrossRef CAS PubMed.
- G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695 CAS.
- R. E. Beal, D. J. Slotcavage, T. Leijtens, A. R. Bowring, R. A. Belisle, W. H. Nguyen, G. Burkhard, E. T. Hoke and M. D. McGehee, J. Phys. Chem. Lett., 2016, 7, 746–751 CrossRef CAS PubMed.
- R. J. Worhatch, H. Kim, I. P. Swainson, A. L. Yonkeu and S. J. L. Billinge, Chem. Mater., 2008, 20, 1272–1277 CrossRef CAS.
- J. Brgoch, A. J. Lehner, M. L. Chabinyc and R. Seshadri, J. Phys. Chem. C, 2014, 18, 27721–27727 Search PubMed.
- A. N. Beecher, O. E. Semonin, J. M. Skelton, J. M. Frost, M. W. Terban, H. Zhai, A. Alatas, J. S. Owen, A. Walsh and S. J. L. Billinge, ACS Energy Lett., 2016, 1, 880–887 CrossRef CAS.
- I. Bersuker, Phys. Lett., 1966, 20, 589–590 CrossRef CAS.
- I. B. Bersuker, Chem. Rev., 2013, 113, 1351–1390 CrossRef CAS PubMed.
- G. W. Watson, S. C. Parker and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8481 CrossRef CAS.
- R. Seshadri and N. A. Hill, Chem. Mater., 2001, 13, 2892–2899 CrossRef CAS.
- R. Seshadri, J. Chem. Sci., 2001, 113, 487–496 CrossRef CAS.
- U. V. Waghmare, N. A. Spaldin, H. C. Kandpal and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125111 CrossRef.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. b. Ketterson, J. I. Jang and M. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 CrossRef CAS PubMed.
- E. S. Bozin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. L. Billinge, Science, 2010, 330, 1660–1663 CrossRef CAS PubMed.
- K. M. Ø. Jensen, E. S. Božin, C. D. Malliakas, M. B. Stone, M. D. Lumsden, M. G. Kanatzidis, S. M. Shapiro and S. J. L. Billinge, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085313 CrossRef.
- K. R. Knox, E. S. Bozin, C. D. Malliakas, M. G. Kanatzidis and S. J. L. Billinge, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014102 CrossRef.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS PubMed.
- Y. Zhang, X. Ke, P. R. C. Kent, J. Yang and C. Chen, Phys. Rev. Lett., 2011, 107, 175503 CrossRef PubMed.
- T. Keiber, F. Bridges and B. C. Sales, Phys. Rev. Lett., 2013, 111, 095504 CrossRef CAS PubMed.
- S. Kastbjerg, N. Bindzus, M. Søndergaard, S. Johnsen, N. Lock, M. Christensen, M. Takata, M. A. Spackman and B. Brummerstedt Iversen, Adv. Funct. Mater., 2013, 23, 5477–5483 CrossRef CAS.
- C. W. Li, J. Ma, H. B. Cao, A. F. May, D. L. Abernathy, G. Ehlers, C. Hoffmann, X. Wang, T. Hong, A. Huq, O. Gourdon and O. Delaire, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214303 CrossRef.
- Y. Chen, X. Ai and C. A. Marianetti, Phys. Rev. Lett., 2014, 113, 105501 CrossRef PubMed.
- K. S. Knight, J. Phys.: Condens. Matter, 2014, 26, 385403 CrossRef CAS PubMed.
- K. V. Mitrofanov, A. V. Kolobov, P. Fons, M. Krbal, T. Shintani, J. Tominaga and T. Uruga, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 1–6 CrossRef.
- L. Aggarwal, A. Banik, S. Anand, U. V. Waghmare, K. Biswas and G. Sheet, J. Materiomics, 2016, 2, 196–202 CrossRef.
- M.-H. Du and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144114 CrossRef.
- W. Siemons, M. A. McGuire, V. R. Cooper, M. D. Biegalski, I. N. Ivanov, G. E. Jellison, L. A. Boatner, B. C. Sales and H. M. Christen, Adv. Mater., 2012, 24, 3965–3969 CrossRef CAS PubMed.
- X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- Y. Kawamura, H. Mashiyama and K. Hasebe, J. Phys. Soc. Jpn., 2002, 71, 1694–1697 CrossRef CAS.
- I. Chung, J.-H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579–8587 CrossRef CAS PubMed.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Angew. Chem., Int. Ed., 2016, 55, 15392–15396 CrossRef CAS PubMed.
- T. J. Savenije, C. S. Ponseca, L. Kunneman, M. Abdellah, K. Zheng, Y. Tian, Q. Zhu, S. E. Canton, I. G. Scheblykin, T. Pullerits, A. Yartsev and V. Sundström, J. Phys. Chem. Lett., 2014, 5, 2189–2194 CrossRef CAS PubMed.
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- W. Kwestroo and P. Vromans, J. Inorg. Nucl. Chem., 1967, 29, 2187–2190 CrossRef CAS.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Häusermann, High Pressure Res., 1996, 14, 235–248 CrossRef.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS.
- M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. De La Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr., 2006, 221, 15–27 CAS.
- M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128 CrossRef PubMed.
- Y. Takahashi, R. Obara, Z.-Z. Lin, Y. Takahashi, T. Naito, T. Inabe, S. Ishibashi and K. Terakura, Dalton Trans., 2011, 40, 5563 RSC.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- Z. Tang, J. Guan and A. M. Guloy, J. Mater. Chem., 2001, 11, 479–482 RSC.
- Y. Y. Li, C. K. Lin, G. L. Zheng, Z. Y. Cheng, H. You, W. D. Wang and J. Lin, Chem. Mater., 2006, 18, 3463–3469 CrossRef CAS.
- Y. Takahashi, R. Obara, K. Nakagawa, M. Nakano, J. Tokita and T. Inabe, Chem. Mater., 2007, 19, 6312–6316 CrossRef CAS.
- M. D. Smith, A. Jaffe, E. R. Dohner, A. M. Lindenberg and H. I. Karunadasa, Chem. Sci., 2017, 8, 4497–4504 RSC.
- A. J. Neukirch, W. Nie, J.-C. Blancon, K. Appavoo, H. Tsai, M. Y. Sfeir, C. Katan, L. Pedesseau, J. Even, J. J. Crochet, G. Gupta, A. D. Mohite and S. Tretiak, Nano Lett., 2016, 16, 3809–3816 CrossRef CAS PubMed.
- S. Hirotsu, J. Harada, M. Iizumi and K. Gesi, J. Phys. Soc. Jpn., 1974, 37, 1393–1398 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 935–939 CrossRef CAS.
- L.-Y. Huang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165203 CrossRef.
- L.-Y. Huang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195201 CrossRef.
- Q. Lin, A. Armin, R. Chandra, R. R. C. R. Nagiri, P. L. Burn and P. Meredith, Nat. Photonics, 2014, 9, 106–112 CrossRef.
- D. H. Fabini, T. Hogan, H. A. Evans, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, J. Phys. Chem. Lett., 2016, 7, 376–381 CrossRef CAS PubMed.
- M. H. Du, J. Mater. Chem. A, 2014, 2, 9091 CAS.
- S. Stemmer and S. James Allen, Annu. Rev. Mater. Res., 2014, 44, 151–171 CrossRef CAS.
- K. A. Müller and H. Burkard, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 3593 CrossRef.
- H. P. R. Frederikse, W. R. Thurber and W. R. Hosler, Phys. Rev., 1964, 134, A442–A445 CrossRef.
- A. Spinelli, M. A. Torija, C. Liu, C. Jan and C. Leighton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155110 CrossRef.
- S. J. Allen, B. Jalan, S. Lee, D. G. Ouellette, G. Khalsa, J. Jaroszynski, S. Stemmer and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045114 CrossRef.
- W.-J. Yin, T. Shi and Y. Yan, Appl. Phys. Lett., 2014, 104, 063903 CrossRef.
- A. Zakutayev, C. M. Caskey, A. N. Fioretti, D. S. Ginley, J. Vidal, V. Stevanovic, E. Tea and S. Lany, J. Phys. Chem. Lett., 2014, 5, 1117–1125 CrossRef CAS PubMed.
- R. E. Brandt, V. Stevanović, D. S. Ginley and T. Buonassisi, MRS Commun., 2015, 5, 265–275 CrossRef CAS.
- M. Kim, J. Im, A. J. Freeman, J. Ihm and H. Jin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6900–6904 CrossRef CAS PubMed.
- D. Niesner, M. Wilhelm, I. Levchuk, A. Osvet, S. Shrestha, M. Batentschuk, C. Brabec and T. Fauster, Phys. Rev. Lett., 2016, 117, 126401 CrossRef PubMed.
- P. Azarhoosh, S. McKechnie, J. M. Frost, A. Walsh and M. van Schilfgaarde, APL Mater., 2016, 4, 091501 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the sample synthesis. LeBail fits of the X-ray diffraction data at 360 K. Fourier transform optimization of the X-ray total scattering data. Cubic fits of the XPDF data over 10 Å to 20 Å. Fits of the XPDF data over 2 Å to 5 Å against all models. Cubic and rhombohedral fits of APbBr3 at 300 K and 360 K. See DOI: 10.1039/c7sc01429e |
| This journal is © The Royal Society of Chemistry 2017 |