Open Access Article
Open Access ArticleDynamic, structural and thermodynamic basis of insulin-like growth factor 1 kinase allostery mediated by activation loop phosphorylation†
Yaozong
Li
 a and
Kwangho
Nam
a and
Kwangho
Nam
 *ab
*ab
aDepartment of Chemistry, Umeå University, SE-901 87 Umeå, Sweden
bDepartment of Chemistry and Biochemistry, University of Texas at Arlington, Arlington, TX 76019-0065, USA. E-mail: kwangho.nam@uta.edu; Tel: +1-817-272-1091
First published on 20th March 2017
Abstract
Despite the importance of kinases' catalytic activity regulation in cell signaling, detailed mechanisms underlying their activity regulation are poorly understood. Herein, using insulin-like growth factor 1 receptor kinase (IGF-1RK) as a model, the mechanisms of kinase regulation by its activation loop (A-loop) phosphorylation were investigated through molecular dynamics (MD) and alchemical free energy simulations. Analyses of the simulation results and free energy landscapes determined for the entire catalytic cycle of the kinase revealed that A-loop phosphorylation affects each step in the IGF-1RK catalytic cycle, including conformational change, substrate binding/product release and catalytic phosphoryl transfer. Specifically, the conformational equilibrium of the kinase is shifted by 13.2 kcal mol−1 to favor the active conformation after A-loop phosphorylation, which increases substrate binding affinity of the activated kinase. This free energy shift is achieved primarily via destabilization of the inactive conformation. The free energy of the catalytic reaction is also changed by 3.3 kcal mol−1 after the phosphorylation and in the end, facilitates product release. Analyses of MD simulations showed that A-loop phosphorylation produces these energetic effects by perturbing the side chain interactions around each A-loop tyrosine. These interaction changes are propagated to the remainder of the kinase to modify the orientations and dynamics of the αC-helix and A-loop, and together yield the observed free energy changes. Since many protein kinases share similar interactions identified in this work, the mechanisms of kinase allostery and catalysis unraveled here can be applicable to them.
Introduction
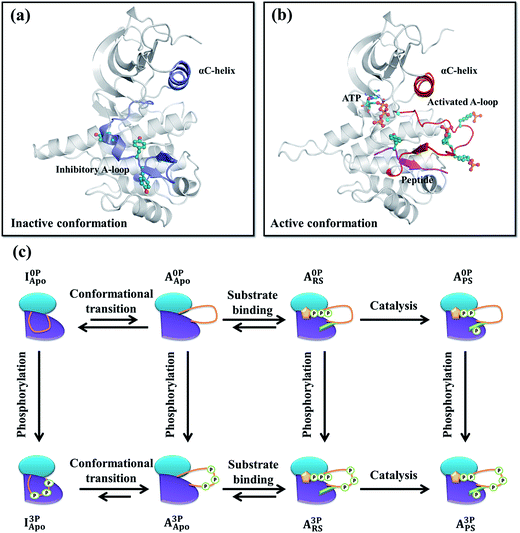
Insulin-like growth factor 1 receptor kinase (IGF-1RK) is a key member of the IGF-1 signal transduction pathway controlling cell proliferation, differentiation, and motility.1,2 Owing to its importance in cell survival, dysfunction of this signaling cascade is associated with a number of human diseases, including cancers3,4 and rheumatoid arthritis.5 IGF-1 signaling proceeds by binding of an extracellular hormone to the receptor's ectodomain and dimerization of the intracellular kinase domains (i.e., IGF-1RK).6,7 Next, autophosphorylation takes place in trans at three tyrosine residues (i.e., Tyr1131, Tyr1135, and Tyr1136) of the activation loop (A-loop) of the kinase, and yields a fully activated kinase.8X-ray crystallography has established that IGF-1RK exists in two conformations: one referred to as inactive and the other active.9–11 Without A-loop phosphorylation, the kinase adopts the inactive conformation.10 This conformation is characterized by an inhibitory conformation of the A-loop, which sterically blocks the binding pocket of adenosine triphosphate (ATP) and occludes the docking site of a downstream substrate protein (Fig. 1a). In addition, the conserved Asp–Phe–Gly (DFG) motif and αC-helix rotate away from the active site, disabling its catalytic activity. In the active conformation,11 the A-loop is fully phosphorylated and adopts an extended conformation to enable ATP and substrate binding (Fig. 1b), which together with the in-orientation DFG and αC-helix forms the catalytically competent active site of the kinase.
The activity of IGF-1RK is enhanced by ∼120 fold after its A-loop phosphorylation,11 of which 11 fold is contributed by increased catalytic rate (i.e., kcat) and the rest by increased substrate binding affinities. Similar enhancement of the catalytic activity has been reported in the insulin receptor kinase (IRK).12 These kinetic data have two implications for IGF-1RK activation and catalysis. First, the enzyme has a basal level catalytic activity in its unphosphorylated form, which enables the kinase's autophosphorylation upon receiving its activation signal. Second, the unphosphorylated kinase can adopt the catalytically competent (active) conformation to display the basal level catalytic activity. Otherwise, much larger change is expected than the reported 11 fold change in catalytic rate. These imply that the kinase interconverts between the inactive and active conformations, and that A-loop phosphorylation shifts the relative population between them.13
Owing to the importance of kinases in human health and drug development, many studies, both experimental and theoretical, were conducted to understand the mechanisms underlying the effects of ligands or regulatory domains on the protein dynamics and activities,14–20 cancer-causing mutations on kinase activities21–24 and kinase conformational changes.25–29 On the other hand, relatively few studies have been carried out to understand the allosteric regulation of A-loop phosphorylation on kinase conformational dynamics22,30–32 and catalytic activities.33 Thus, detailed mechanisms of kinase allostery mediated by A-loop phosphorylation remain poorly understood.
In the present study, the effects of A-loop phosphorylation on the protein dynamics, structure, stability and free energy landscape were examined using molecular dynamics (MD) and alchemical free energy simulations. Specifically, four different conformational and ligand bound states of IGF-1RK were simulated to cover the entire catalytic cycle, including the conformational change, substrate binding, phosphoryl transfer and product release. By using these states, we examined differences in the protein dynamics, side chain interactions and thermodynamics. The study provided a molecular level understanding of how A-loop phosphorylation affects different steps in the IGF-1RK catalytic cycle for allosteric control of its catalytic activity.
Methods
System preparation
All systems (residues between 958 and 1255) were prepared based on either the inactive (PDB code 1P4O10) or active (PDB code 1K3A11) conformation X-ray structure. All prepared systems and their notations are summarized in Fig. 1c and Table S1.† In the inactive conformation systems, the first monomer (chain A) of the 1P4O structure, including all corresponding crystal waters, were used. Protonation states of all ionizable residues were determined on the basis of their pKa values in water and hydrogen bonding networks deduced from both the inactive and active conformation X-ray structures. In the phosphorylated inactive conformation system, the three A-loop tyrosines (Tyr1135, Tyr1131 and Tyr1136) were modified to their phosphorylated forms. All missing atomic coordinates were then generated using the CHARMM27 force field parameters.34,35 Each system was solvated with an 80 Å rhombic dodecahedron box of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 TIP3P waters36 followed by removal of waters that overlapped with protein atoms. To neutralize and set the ionic concentration of each system to 150 mM, different numbers of Na+ and Cl− ions were placed at random positions. For example, in the I0PApo system, 33 Na+ and 24 Cl− ions were added, resulting in a total of 35
043 TIP3P waters36 followed by removal of waters that overlapped with protein atoms. To neutralize and set the ionic concentration of each system to 150 mM, different numbers of Na+ and Cl− ions were placed at random positions. For example, in the I0PApo system, 33 Na+ and 24 Cl− ions were added, resulting in a total of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868 atoms in the system.
868 atoms in the system.
All active conformation systems were prepared based on the 1K3A X-ray structure, in which the residues between 1067 and 1076 were model built based on the 3NW5 X-ray structure.37 In the reactant state systems, the AMP–PCP (ATP analogue) was replaced with ATP. The substrate peptide found in the X-ray structure was included without modification. In the product state systems, AMP–PCP and the tyrosine residue of the substrate peptide were replaced with ADP and phosphotyrosine, respectively. In both systems, two Mg2+ ions and their coordinating waters were model built in the active site based on their positions in the active conformation IRK structure (PDB code 1IR3 (ref. 38)). All unphosphorylated systems were prepared by restoring each phosphorylated A-loop tyrosine to tyrosine. The rest of the system preparation was the same as the inactive conformation system preparation.
Each system was first energy minimized for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with a series of constraints and restraints to relieve high-energy contacts. Then, while keeping similar restraints, each system was equilibrated for 310 ps at temperatures ranging between 300 K and 600 K. During the last 100 ps, the restraints that were applied to the protein were slowly removed, followed by additional 500 ps equilibration without restraints. Details of the energy minimizations and equilibration MD simulations are provided in ESI.†
000 steps with a series of constraints and restraints to relieve high-energy contacts. Then, while keeping similar restraints, each system was equilibrated for 310 ps at temperatures ranging between 300 K and 600 K. During the last 100 ps, the restraints that were applied to the protein were slowly removed, followed by additional 500 ps equilibration without restraints. Details of the energy minimizations and equilibration MD simulations are provided in ESI.†
Molecular dynamics (MD) simulations and trajectory analysis
For each system, a production MD simulation was performed for 300 ns at 1 atm and 300 K. All simulations were carried out using the leap-frog Verlet with 2 fs integration time. The temperature and pressure were maintained using the Langevin thermostat and Nosé–Hoover Langevin piston algorithms,39,40 respectively. Throughout, the protein, substrate peptide, ATP/ADP and ions were represented by the CHARMM27 force fields35,41 with the CMAP correction on protein backbone dihedrals,34,42 and water molecules by the TIP3P model.36 The SHAKE algorithm43 was applied to all bonds involving hydrogen atoms. The particle mesh Ewald summation (PME) method44 was used for electrostatic interactions with an 11 Å real-space cutoff. The switching function45 was applied between 9 Å and 11 Å for the van der Waals interactions. During each MD simulation, atomic coordinates were saved at 2 ps time intervals for later analysis (see the ESI† for details of the trajectory analyses).All system preparation, energy minimizations and equilibration MD simulations was carried out using the CHARMM program (version c38a1)46 and CHARMM-GUI web interface.47 The production MD simulations were performed using the NAMD program (version 2.9).48 Trajectory analyses, including principle component analysis (PCA),49 protein motion projection,50,51 covariance matrix analysis, root-mean-square deviation (RMSD) and distance measurements, were carried out using the CHARMM program. Community network analysis was performed according to the protocol of Sethi et al.52 All protein structure figures were prepared using PyMOL software.53
Alchemical free energy simulations of A-loop phosphorylation
Free energy differences between the unphosphorylated and phosphorylated systems were determined using the alchemical free energy simulation method.54,55 These simulations were carried out by alchemically mutating each phosphotyrosine to its corresponding tyrosine (or vice versa) at four different functional states of IGF-1RK (i.e., the inactive conformation, active apo conformation and both the reactant and product state systems). To minimize the total number of simulations, all three A-loop tyrosines were mutated simultaneously. As a reference, we also performed alchemical simulations for the mutation of a single phosphotyrosine to tyrosine in water.Each mutation simulation was carried out in three steps. In the first step, the charges on the tyrosine residues were removed (i.e., uncharging step). In the second step, the uncharged tyrosines were transformed to the uncharged phosphotyrosines with the soft-core potential56 for enhanced endpoint configuration samplings. In the final step, the charges on the phosphotyrosines were restored (i.e., charging step). In the latter step, the background charge correction57 was applied and the net charge of each system was set to the midpoint charge between the uncharged and fully charged pTyr residues by adjusting the total number of counter ions, to minimize the net charge artifact. Each transformation was accomplished in 11λ steps (i.e., λ = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0 values), where λ is the coupling parameter for a linear transformation between the starting and end points.54 At each λ value, a total of 1 ns simulation was carried out and the last 800 ps was used for free energy calculations by thermodynamic integration (TI).58 To remove bias when estimating the free energy change, uncorrelated data were extracted based on their correlation time and the bootstrapping protocol59,60 was applied to obtain the free energy error with 1000 repetitions for each transformation. The convergence of the determined free energy values was checked by extending the simulation length to 2 ns for each system. All simulations were carried out using the PERT module in the CHARMM program (version c38a1).
Results
Effects of A-loop phosphorylation on low frequency protein motions
During the 300 ns MD simulations, none of the systems underwent large-scale structural reorganization. Instead, small and localized changes were observed near the A-loop of all phosphorylated inactive conformation and unphosphorylated active conformation systems (see ESI for detailed descriptions and Fig. S1–S3†). To gain insights into how such local changes induce large conformational changes, we performed the principal component analysis (PCA)49 and identified low frequency protein motions. In Fig. S4,† the three lowest frequency motions and projection of each saved coordinates onto the two lowest frequency motions are presented for each system. These analyses revealed differences in the A-loop motions before and after A-loop phosphorylation in all system pairs and αC-helix motions in most system pairs. The remainder of the kinase showed similar motions.In the inactive conformation, the A-loop, particularly the end of it, showed enhanced motions after the phosphorylation (Fig. S4a and b†). The perturbation is clearly visible in the plots showing the overall RMSF and the lowest-frequency motion contribution to it61 (Fig, S2a and b†). Our analysis of side chain interactions between the A-loop and the rest of the kinase identified several interactions that changed after the phosphorylation, which likely caused the large amplitude A-loop motion (Fig. S5 and S6†). One representative interaction was the Lys1058–Asp1134 salt bridge, which was formed in I0PApo but destroyed in I3PApo. A similar interaction is also found in the inactive conformation IRK between its Lys1085 and Asp1161. This conservation supports the importance of this interaction to stabilize the inhibitory conformation A-loop. Moreover, because these residues are located near the A-loop tyrosines, any changes in the A-loop tyrosines such as by phosphorylation can easily disturb these interactions. Removal of these interactions can thus enhance the mobility of A-loop as evidenced by a mutation study in IRK.62
In the active conformation (both the apo and holo kinases), protein motions near the A-loop tyrosines were suppressed after the kinase phosphorylation (Fig. S4c–h†). This is consistent with the decreased RMSDs of the phosphorylated A-loop tyrosines (Fig. S3†). In the holo form kinase, the αC-helix motions were also suppressed after the phosphorylation. In contrast, such suppression of αC-helix motions was not observed in the active conformation apo form kinase (Fig. S4c and d†). This difference in αC-helix motions suggests that substrate binding imposes some restraints on αC-helix motion only in the phosphorylated kinase. We found several interactions that are potentially connected to this αC-helix motion suppression. They are discussed in details in the section entitled “Interactions in the active conformations controlling the stability and dynamics of the A-loop and αC-helix”.
Contribution of low frequency protein motions to kinase conformational change
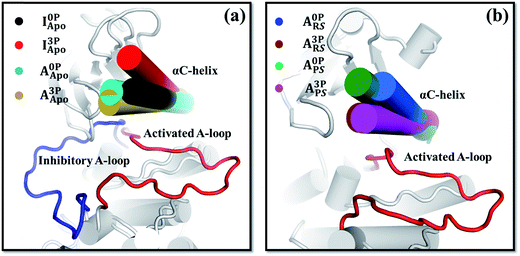
The above analysis of the MD simulations suggests that A-loop phosphorylation induces only local and relatively small changes in protein motions. Can these changes lead to a large conformational change of the kinase? To quantify, at least approximately, the contribution of each protein motion to the global conformational change, vibrational projection analysis of protein motion51 was performed by projecting each PCA mode onto a unit displacement vector defined by the active versus inactive conformations (Fig. S7†). The results are presented in Fig. 2 as the cumulative sum of the projection square for the first 200 lowest frequency motions. Among the studied systems, the fully phosphorylated inactive conformation system (I3PApo) showed the most pronounced difference. In I3PApo, the cumulative sum increased early, such that the first 100 (lowest frequency) PCA modes accounted for ∼70% of the total projection. In contrast, the same number of modes contributed only ∼40% in the other systems. Because the difference of the A-loop orientation between the two conformations was the major contributor to the displacement vector, the early rise in I3PApo implies enhanced A-loop motions directed toward the active conformation.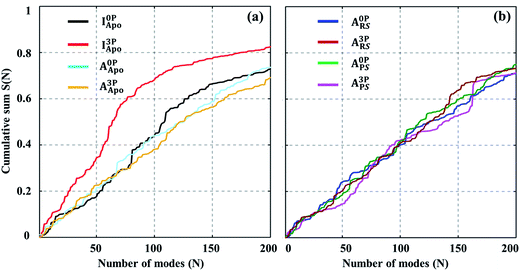 | ||
Fig. 2 Cumulative sum of projection square for (a) apo and (b) holo systems. In the X-axis, the PCA modes were arranged in ascending order by mode frequency. The cumulative sum was calculated as 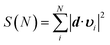 , where d and υi denote the unit displacement vector (Fig. S6†) and PCA mode vector, respectively. , where d and υi denote the unit displacement vector (Fig. S6†) and PCA mode vector, respectively. | ||
Network connectivity and its variation between different simulated systems
In parallel to PCA, community network52 and covariance matrix analyses (Fig. S8 and S9†) were carried out to gain insight into the structural and dynamical coupling between different regions, e.g., the αC-helix and A-loop, of the kinase. The community network analysis revealed that the entire kinase was partitioned roughly into 9 communities, ignoring isolated communities formed by a small number of residues (Fig. S10†). This partitioning was similar to the pattern observed in protein kinase A (PKA),63 in which each community has some associated roles in kinase structure and function.Despite seemingly similar global partitioning in all simulated states, pronounced community variations were found in the inactive and reactant states, especially, near their A-loop and αC-helix. In I0PApo, for example, a substantial fraction of the A-loop merged with the αD-helix to form a single community (Fig. S10a†). This changed after phosphorylation; i.e., the A-loop detached from the αD-helix and disintegrated into several isolated communities (Fig. S10e†). This community variation suggests that kinase phosphorylation perturbs the contacts between the A-loop and the rest of the protein, making the A-loop structurally and dynamically independent. This finding is consistent with the results of covariance analysis of atomic fluctuations, which showed the decreased correlation of A-loop, while the correlation of αC-helix was increased after the A-loop phosphorylation (Fig. S9†).
In the reactant state, the connectivity between the A-loop and αC-helix was enhanced in the fully phosphorylated kinase, compared with the connectivity in the unphosphorylated kinase (Fig. S10c and g†). Similarly enhanced connectivity was also observed in the phosphorylated product state. The enhanced connectivity, together with the covariance analysis results (Fig. S9†), indicates that in the holo kinase, A-loop phosphorylation increases both the structural and dynamical coupling between the A-loop and αC-helix. This increased coupling provides a rational explanation to the enhanced catalytic activity of the fully activated kinase.
Changes in αC-helix orientation after A-loop phosphorylation and ligand binding
In addition to the A-loop, the orientation and dynamics of the αC-helix changed after A-loop phosphorylation (Fig. 3, S11 and S12†). These changes appeared to induce the kinase's conformational change and thus affect its catalytic activity. For example, in I3PApo, the αC-helix rotated outward relative to that in I0PApo (Fig. 3a), which resulted in a more open active site. Since some space is required in the active site of the kinase for the inhibitory A-loop, especially the DFG motif, to flip toward that of the active form,64 the outward αC-helix rotation may provide such space to facilitate the large conformational change. This is consistent with the partial flipping of the DFG motif observed from the I3PApo system MD simulations, which occurred in concert with the outward αC-helix rotation (Fig. S13†).In the active conformation, the response of the αC-helix to A-loop phosphorylation was different between the apo and holo states. In the apo state, both the phosphorylated and unphosphorylated kinases adopted very similar αC-helix orientations (Fig. 3a). In the holo systems, in contrast, the αC-helix of the phosphorylated kinase rotated more inward than that of the unphosphorylated kinase (Fig. 3b). The inward rotation resulted in a narrower orientation distribution of the αC-helix (Fig. S12b†). To confirm this difference, we carried out accelerated MD (aMD) simulations65 and found similarly inward oriented αC-helix (Fig. S12c and d†), consistent with the equilibrium MD simulation results (Fig. 3). This difference of αC-helix orientation suggests that A-loop phosphorylation restricts the αC-helix close to the active site in the holo form kinase, which is further supported by the covariance (Fig. S9g†) and community network analyses (Fig. S10g†). The restricted αC-helix in the phosphorylated reactant state may stabilize the catalytically competent active site of the kinase with enhanced catalytic activity.
Interactions in the inactive conformations controlling the stability and dynamics of the A-loop and αC-helix
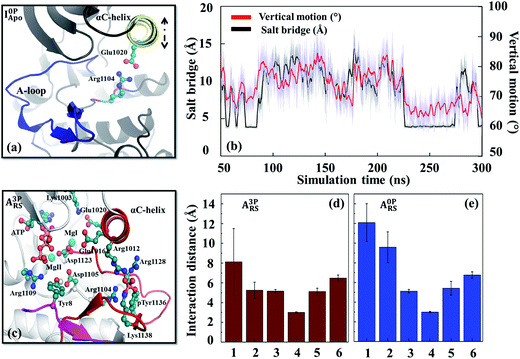
From the interaction analysis, we have identified several interactions that are important for controlling the stability of the inhibitory conformation A-loop. One particular set of interactions were the hydrogen bonds formed between the A-loop tyrosines (Tyr1131, Tyr1135 and Tyr1136) and nearby aspartate/glutamate residues (Asp1056, Asp1105 and Glu1189) (Fig. S14†). Not only these hydrogen bonds were observed from the inactive conformation X-ray structure of IGF-1RK,10 they persisted during the simulations and stabilized the inhibitory conformation A-loop. The importance of these interactions were confirmed previously by the Tyr-to-Phe mutation experiments of the three A-loop tyrosines with increased activity.66 More importantly, when the A-loop tyrosines were phosphorylated, their interactions with the Asp/Glu residues changed to repulsive ones. This repulsion destabilized the inhibitory A-loop, causing the A-loop to detach from the main body of the kinase (Fig. S10e†). Analysis of the interactions between the A-loop tyrosines and surrounding residues confirmed this destabilization; i.e., their interactions were repulsive in I3PApo but attractive in I0PApo (Fig. S15†). In addition, since similar residues were conserved in other protein tyrosine kinases, especially in their inhibitory conformations (Table S2 and Fig. S16†), this attraction-to-repulsion switch can be a common strategy to control their inhibitory conformation stability.Besides the Lys1058–Asp1134 interaction (Fig. S5 and S6†) discussed above, there were other interactions that affected the inactive conformation stability. One example was the Glu1020–Arg1104 salt bridge. In the I0PApo system, this salt bridge was formed transiently with concurrent inward rotation of the αC-helix (Fig. 4a and b). This suggests some sort of coupling between the salt bridge and αC-helix motion. We verified this coupling by MD simulations with the Arg1104Ala mutant, which showed no inward αC-helix rotation (Fig. S17 and Table S3†). Because the inward oriented αC-helix can hinder flipping of the inhibitory A-loop, the identified coupling suggests that this salt bridge plays a role in stabilizing the inactive conformation. In contrast, the salt bridge and inward αC-helix rotation did not occur in the phosphorylated kinase, likely due to altered interactions around Arg1104, resulting in an “out”-oriented αC-helix (Fig. 3a). The importance of the similar salt bridge to Glu1020–Arg1104 for the inactive conformation stability has been suggested previously based on comparison of HCK structures.67
Interactions in the active conformations controlling the stability and dynamics of the A-loop and αC-helix
In the active conformation systems, all phosphorylated A-loop tyrosines interacted attractively with neighboring positively charged residues, such as, Lys1100, Arg1102, Arg1104, Arg1128 and Arg1137, several of them via salt bridges (Fig. S6d†). When these tyrosines were dephosphorylated, their interactions weakened compared with the salt bridges of the phosphorylated tyrosines (Fig. S15†). This change of interactions resulted in a diminished contribution of the dephosphorylated A-loop to the active conformation stability. This finding and the conservation of similar interactions in other kinases, including JAK2,68 FGFR1 (ref. 69) and RETK,70 suggest the importance of these salt bridges in controlling active conformation A-loop stability.In addition to the interactions with the A-loop tyrosines, several other interactions formed in the holo form kinase influenced the αC-helix orientation and dynamics. One example was the interaction between Glu1016 and Arg1012 on the αC-helix (Fig. S18†). These two residues formed an intra-helix salt bridge in the unphosphorylated (holo) kinase. When the kinase was phosphorylated, Arg1012 disengaged from Glu1016 and extended toward the phosphorylated Tyr1136 (pTyr1136) to interact with it in the reactant state (Fig. S18b†). The estranged Glu1016 then oriented toward the active site to form a secondary coordination sphere interaction with an Mg2+ cofactor (MgI). These two interactions anchored the αC-helix to the active site and A-loop, thereby aiding proper positioning of the catalytic residues (e.g., Aps1123 and Asp1105) as well as substrate tyrosine for efficient phosphoryl transfer (Fig. 4c–e). These interactions also explain the diminished αC-helix dynamics (Fig. S1b and S12b†), enhanced correlation of the active site (Fig. S9g†) and stronger connectivity between the αC-helix and A-loop in the phosphorylated holo form kinase (Fig. S10g†). To confirm the role of these two residues in regulating αC-helix orientation and dynamics, MD simulations were performed with the double mutant (Arg1012Ala/Glu1016Ala). The mutant (in its phosphorylated holo state) showed outward rotation of the αC-helix (Fig. S19†), similar to that observed in the wild-type unphosphorylated holo form kinases (Fig. 3b). The conservation of similar interactions in other protein kinases (Fig. S20†) and previous kinetic analysis performed with a PKA mutant71 support the role of the coupling between the αC-helix and A-loop in fine-tuning the catalytic activity of IGF-1RK and other related kinases.
The salt bridge between Glu1020 and Lys1003 has been used widely as an indicator of the active form kinase, which switches to Gly1020–Arg1128 salt bridge in the inactive kinase.14,21,72–74 We utilized aMD simulations75 to probe effects of A-loop phosphorylation on these two interactions and αC-helix dynamics. The results showed that A-loop dephosphorylation facilitated the salt-bridge switch and enhanced the αC-helix dynamics (Fig. S21 and S22†). They suggest that the unphosphorylated kinase exhibits enhanced conformational dynamics in its active conformation, which may facilitate the kinase's conformational change to the inactive conformation.
Free energies of A-loop phosphorylation in different functional and conformational states of IGF-1RK
To determine the effects of A-loop phosphorylation on kinase stability, four alchemical transformation simulations, i.e., I0P→3PApo, A0P→3PApo, A0P→3PRS and A0P→3PPS, were performed by mutating each A-loop tyrosine (Tyr) to phosphotyrosine (pTyr). We also performed the phosphorylation transformation of a tyrosine residue in water. For each transformation, the reliability of the results was examined by checking convergence of the computed free energy values (Table S4†) and free energy gradients (Fig. S23†). Then, using the free energy value for a tyrosine in water as a reference, the free energy change was determined for each system pair. The results are presented in Table S4† as ΔΔF, which can be considered as the free energy contribution of A-loop phosphorylation to the kinase stability (relative to the unfolded protein). For example, a positive value of 12.7 kcal mol−1 in I0P→3PApo indicates the destabilization of the inactive conformation and −0.5 kcal mol−1 in A0P→3PApo the stabilization of the active conformation by A-loop phosphorylation, respectively (Fig. 5a).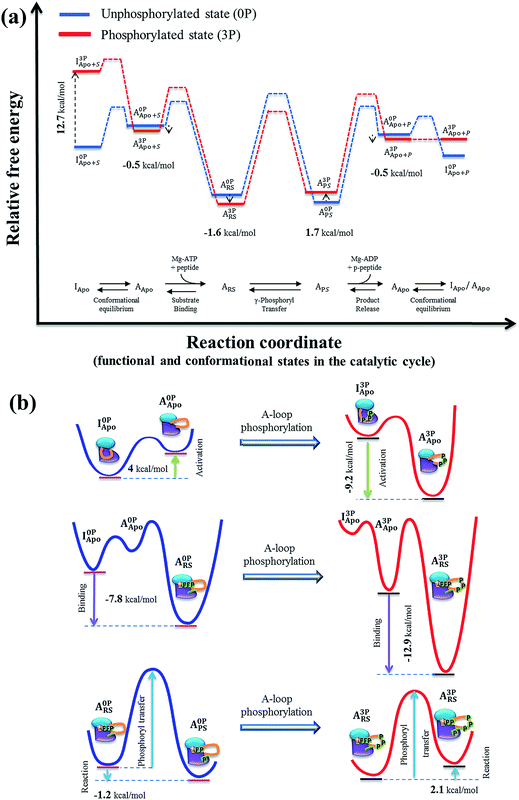 | ||
| Fig. 5 (a) Proposed IGF-1RK catalytic cycle and associated free energy changes. The free energy profile was constructed first for the unphosphorylated kinase (blue), based on the previous experimental and theoretical results on IRK family and other protein kinases (Table 1). The free energy profile for the fully phosphorylated kinase (red) were then constructed by applying the free energy values determined in the present study (Table S4†). In both profiles, the solid lines indicates metastable conformational states, and the dashed lines represent proposed changes between two neighboring metastable states (i.e., conformation change, ligand bindings and catalysis). (b) Schematic representations of the free energy changes of the IGF-1RK conformational change (top), substrate binding (middle) and phosphoryl transfer reaction (bottom). In each diagram, the changes of free energy are indicated with the arrow, and the red- and blue-lines represent the free energy profiles of fully activated and inactive form kinases, respectively. | ||
In addition, the results provided information about the effects of A-loop phosphorylation on substrate/product binding. For example, the free energy difference of −1.1 kcal mol−1 between A0P→3PRS and A0P→3PApo (Table S4†) indicates that the phosphorylated kinase has a slightly higher substrate binding affinity than the unphosphorylated kinase in the active conformation. Similarly, the 2.2 kcal mol−1 change between A0P→3PPS and A0P→3PApo indicates a lower product binding affinity in the phosphorylated kinase than the corresponding unphosphorylated kinase. However, these values cannot be directly compared with the experimentally estimated substrate/product binding free energies, because those values for the unphosphorylated kinase correspond to the inactive conformation. To compare with experimental values, the present values have to be corrected by the free energy difference between the active and inactive conformations (i.e., 4.0 kcal mol−1 in Table 1). The resultant values were intriguingly very close to the experimental estimations (Table 1).12
| Step | 0P state | 3P state | ||
|---|---|---|---|---|
| Process | ΔF (kcal mol−1) | Process | ΔF (kcal mol−1) | |
a This value was estimated as the average of the Src,25 EGFR,76 and CDK5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 simulation results.
b This value was determined based on the experimental results that >90% of IRK is in the inactive conformation in its basally active kinase form.81
c Binding free energies were estimated based on the KM values of substrates in IRK.12 In this estimation, binding of ATP and substrate peptide to the kinase was assumed to follow a rapid-equilibrium-random-order mechanism. Then, the total binding free energy is the sum of the two binding energies, as ΔF = RT 29 simulation results.
b This value was determined based on the experimental results that >90% of IRK is in the inactive conformation in its basally active kinase form.81
c Binding free energies were estimated based on the KM values of substrates in IRK.12 In this estimation, binding of ATP and substrate peptide to the kinase was assumed to follow a rapid-equilibrium-random-order mechanism. Then, the total binding free energy is the sum of the two binding energies, as ΔF = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KM,ATP) + RT ln(KM,ATP) + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KM,peptide), where R and T are the gas constant and temperature (298 K in the present work), respectively. For the unphosphorylated kinase, since substrate binding was assumed to occur from the inactive conformation, the substrate binding free energy between the active conformations (i.e., A0PApo → A0PRS) required a correction by the free energy difference between the active and inactive conformations (i.e., I0PApo → A0PApo).
d The phosphoryl transfer barrier heights were estimated based on the catalytic rates reported for IRK12 and using the Eyring's transition state theory.
e To determine the reaction free energy in the active site of IGF-1RK, we first estimated the total reaction free energy of the uncatalyzed reaction (i.e., the same reaction in water) based on the kinetic data reported for Src.82 The free energies of substrate binding and product release for IRK were then applied.
f Free energy values for product binding were estimated based on the Ki values of ADP and phosphorylated peptide in IRK,12 using ΔF = RT ln(KM,peptide), where R and T are the gas constant and temperature (298 K in the present work), respectively. For the unphosphorylated kinase, since substrate binding was assumed to occur from the inactive conformation, the substrate binding free energy between the active conformations (i.e., A0PApo → A0PRS) required a correction by the free energy difference between the active and inactive conformations (i.e., I0PApo → A0PApo).
d The phosphoryl transfer barrier heights were estimated based on the catalytic rates reported for IRK12 and using the Eyring's transition state theory.
e To determine the reaction free energy in the active site of IGF-1RK, we first estimated the total reaction free energy of the uncatalyzed reaction (i.e., the same reaction in water) based on the kinetic data reported for Src.82 The free energies of substrate binding and product release for IRK were then applied.
f Free energy values for product binding were estimated based on the Ki values of ADP and phosphorylated peptide in IRK,12 using ΔF = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ki,ADP) + RT ln(Ki,ADP) + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ki,phosphopeptide), as in the substrate binding free energy estimation. For the inactive conformation, we applied the same correction that was applied to the substrate binding free energy, to determine the free energy of product binding to the active conformation (i.e., A0PApo → A0PPS). The free energy of product release was the negative of the product binding free energy. ln(Ki,phosphopeptide), as in the substrate binding free energy estimation. For the inactive conformation, we applied the same correction that was applied to the substrate binding free energy, to determine the free energy of product binding to the active conformation (i.e., A0PApo → A0PPS). The free energy of product release was the negative of the product binding free energy.
|
||||
| Conformational change | I0PApo → A0PApo | 4.0a (≥1.3)b | I3PApo → A3PApo | −9.2 |
| Substrate bindingc | I0PApo → A0PRS | −7.8 | A3PApo → A3PRS | −12 (−12.9) |
| (A0PApo → A0PRS) | (−11.8) | |||
| Barrier for the phosphoryl transferd | A0PRS → A0PPS | 17.7 | A3PRS → A3PPS | 15.4 |
| Catalytic phosphoryl transfer equilibrium | A0PRS → A0PPS | −1.2e | A3PRS → A3PPS | 2.1 |
| Product releasef | A0PPS → I0PApo | 7.6 | A3PPS → A3PApo | 10 (9.4) |
| (A0PPS → A0PApo) | (11.6) | |||
Discussion
In Fig. 5a, we present the free energy profiles of both the inactive (0P) and fully active (3P) kinases along their entire catalytic cycle, encompassing the conformational change, substrate binding, γ-phosphoryl transfer and product release. These profiles were constructed by combining the present simulation results with previously published data on IRK family and other kinases (Table 1). Based on the figure, we discuss below the impacts of A-loop phosphorylation on each step of the IGF-1RK catalytic cycle from the perspective of protein dynamics, side chain interactions and thermodynamics.Conformational change between the active and inactive conformations
Fig. 5a clearly demonstrates the population shift from the inactive to the active conformation upon A-loop phosphorylation. Our analysis shows that this occurs by destabilization of the inactive conformation by 12.7 kcal mol−1, whereas the active conformation contributes only 0.5 kcal mol−1 to the conformational change. In the absence of the phosphorylation, the inactive conformation is favored by ∼4.0 kcal mol−1 (based on the Src,25 EGFR76 and CDK5 (ref. 29) results). Based on these values, we can estimate −9.2 kcal mol−1 as the free energy difference between the active and inactive conformations of the fully phosphorylated kinase and −13.2 kcal mol−1 as the total allosteric effects of A-loop phosphorylation (Table 1). This large free energy change suggests that A-loop phosphorylation provides a sufficient driving force for the conformational change to the active state, primarily via destabilization of the inactive conformation.The interaction and protein dynamics analyses supported the determined free energy changes. In the inactive conformation, two types of interactions were found to be important for controlling the inhibited conformation stability, i.e., the hydrogen bonds between the A-loop tyrosines and neighboring Asp/Glu residues (Fig. S14†) and the Glu1020–Arg1104 (Fig. 4a and b) and Asp1134–Lys1058 salt bridges (Fig. S6†). A-loop phosphorylation disrupts these interactions and yields a flexible A-loop. This then, in concert with outward rotation of αC-helix, triggers flipping of the DFG motif towards the active conformation orientation. In the active conformation, A-loop phosphorylation forms multiple salt bridges (Fig. S6d†), and stabilizes the active conformation A-loop.
The mechanisms presented by IGF-1RK can be applicable to other protein kinases. For example, in Src kinase, although different set of interactions are involved in the conformational change upon A-loop phosphorylation (at Tyr416),64,77 the conserved Asp386 interacts repulsively with pTyr416 (Fig. S16†). This repulsion in conjunction with the release of its SH2/SH3 regulatory domains destabilizes the inactive conformation of the kinase and ultimately, induces its conformational change.78 In Fig. S16 and Table S2,† we presents more examples of such negative residues surrounding A-loop tyrosines, which potentially contribute to their activation.
Substrate binding and product release steps
The estimated free energy contribution of A-loop phosphorylation to ligand binding (in the active conformation) was −1.1 kcal mol−1 for substrates and 2.2 kcal mol−1 for products (Table 1). For the substrate binding, the relatively small free energy change suggests that A-loop phosphorylation has a small impact on substrate binding once the kinase adopts the active conformation. As noted, however, this value cannot be directly compared with the experimental value of −4.2 kcal mol−1 (−7.8 kcal mol−1 of the 0P state vs. −12.0 kcal mol−1 of the 3P state; Table 1),12 because the more favored conformation is different between the fully phosphorylated and unphosphorylated kinases. In the experimentally determined values, the effects of the difference of favored conformations were naturally included, whereas the calculated values were only based on the active conformation. We corrected this discrepancy by applying the free energy difference between the active and inactive conformations (i.e., 4.0 kcal mol−1) to the unphosphorylated kinase result. This yielded a value of −5.1 kcal mol−1 (Table 1) as the phosphorylation contribution to substrate binding, which agrees with the experimental estimation of −4.2 kcal mol−1. This result suggests that substrate binding is favored by A-loop phosphorylation, mainly because the active conformation is thermodynamically favored in the phosphorylated kinase.Regarding product binding, the same free energy correction was applied, yielding −1.8 kcal mol−1 as the phosphorylation contribution to product binding. This value is comparable to −2.4 kcal mol−1, estimated based on the IRK Ki values (−7.6 kcal mol−1 of 0P state versus −10.0 kcal mol−1 of 3P state in Table 1). On the other hand, if the product binding only to the active conformation was considered, a value of 2.2 kcal mol−1 of unfavorable free energy was obtained. This value implies that A-loop phosphorylation lowers the product binding affinity in the active conformation. This decrease of binding affinity is due to the destabilization of the product state by the phosphorylation (1.7 kcal mol−1), whereas the other two active conformation states were stabilized by A-loop phosphorylation (Table S4†). Our interaction analysis rationalizes the destabilization in the product state. Specifically, as presented in Fig. S18,† the pTyr1136–Arg1012 interaction was disrupted in A3PPS, whereas it remained intact in A3PRS. This change occurred because the γ-phosphoryl transfer induced local rearrangement of the active site of the kinase, in particular, in the orientations of the β-phosphate of ADP and Mg2+ cofactors. Consequently, the coupling between the αC-helix and A-loop was weakened, lowering the stability of the A-loop relative to the reactant state. This lowered binding affinity in the product state indicates that product release is thermodynamically enhanced via the phosphorylation, which would benefit the kinase's catalytic turnover.
Catalytic step and free energy of catalytic reaction
Previously, we have shown that kinase phosphorylation enhances correlated protein motions in IRK, thereby increasing its catalytic activity.33 The present study identified similarly enhanced protein dynamics and strong community connectivity between the αC-helix and A-loop in the reactant state of IGF-1RK (Fig. S9g and S10g†), suggesting a similar role of protein dynamics in kinase allostery. As discussed above, changes in side chain interactions underlie the protein dynamics and connectivity changes caused by A-loop phosphorylation and control the αC-helix orientation (Fig. 3b). For example, in A3PRS, the αC-helix is held close to the active site and A-loop via the pTyr1136–Arg1012 and Glu1016–MgI interactions (Fig. 4c). In this way, the kinase can assemble the catalytic residues, e.g., Asp1123 and Asp1105 (Fig. 4c–e), properly for catalysis. However, once the kinase is dephosphorylated, these interactions are lost and a less organized active site is formed (Fig. S18a†).In addition to the changes of catalytic rates,11 A-loop phosphorylation changes the free energy of catalytic reaction from −1.2 kcal mol−1 to 2.1 kcal mol−1 (Fig. 5 and Table 1). This change indicates that A-loop phosphorylation thermodynamically disfavors the chemical reaction. Since the increased reaction free energy is directly connected with the decreased product binding affinity in the fully phosphorylated kinase (Fig. 5a and Table 1), the same interaction changes in the product state are responsible for the changes of both the catalytic reaction free energy and product binding affinity. Taken together, the results suggest that A-loop phosphorylation fine-tunes the chemical step via modifications of interactions that couple the αC-helix with the A-loop and active site. These interactions not only assist the formation of a catalytically competent active site but also suppress their fluctuations during catalysis.
Proposed allosteric mechanism of IGF-1RK activation
By summarizing all results described thus far, we propose a mechanism of IGF-1RK activation mediated by A-loop phosphorylation, which is achieved in two steps. In the first step, the favored conformation of the kinase is changed to the active conformation after A-loop phosphorylation (Fig. 5b upper panel). We have shown that this change is mainly driven by destabilization of the inactive conformation. In particular, the electrostatic repulsion between the kinase and phosphorylated A-loop tyrosines destabilizes the kinase and disturbs the structure and dynamics of A-loop. These local perturbations propagate along the A-loop and in concert with the change of αC-helix orientation induce flipping of the DFG motif, which in turn trigger the global conformational change. This mechanism is consistent with the previous simulation results suggesting the importance of DFG flipping to the conformational change of Abl kinase.79 In addition, as depicted in Fig. 5b (middle panel), the shift of favored kinase conformation results in the increase of substrate binding affinity in the activated kinase.In the second step, the interactions between A-loop and αC-helix are altered after A-loop phosphorylation to fine tune the organization of the active site and coordinated protein motions of the active form kinase. The changes in the active site enhance the catalytic activity of the kinase (Fig. 5b lower panel). For example, after the substrate binding, the increased coupling between the A-loop and αC-helix in the fully phosphorylated kinase tightens the local structure of the active site, making it better organized for catalytic reaction. On the other hand, in the product state, the coupling between the A-loop and αC-helix is weakened to reduce the stability of the kinase relative to that of the unphosphorylated kinase. As a consequence of the change, the reaction free energy is increased.
Taken together, the IGF-1RK activity is modulated not only by changes of favored kinase conformations but also by changes of active site architecture and dynamics. The proposed roles of A-loop phosphorylation can be tested, for example, by introducing mutations at the negatively charged residues that interact with the inactive conformation A-loop tyrosines and measuring variation of their kinetic parameters (i.e., kcat and KM values) at different A-loop phosphorylation levels. Such experiment in conjunction with existing simulation and experimental data will increase our understanding of the mechanisms of IGF-1RK regulation and also generally kinase allostery.80
Conclusions
In this study, molecular dynamics and alchemical free energy simulations were performed to understand the protein dynamics, structural and thermodynamic basis of IGF-1RK regulation by activation loop (A-loop) phosphorylation. By integrating the present simulation data with previous experimental and theoretical data, free energy landscapes representing the entire catalytic cycle of IGF-1RK were constructed for both the fully activated and basally active enzymes. The constructed free energy profiles together with analyses of MD simulations revealed that A-loop phosphorylation drives the population shift of the kinase to favor the active conformation over the inactive one by 9.2 kcal mol−1, and enhances substrate binding affinity of the kinase. In addition, A-loop phosphorylation exerts its effects on the phosphoryl transfer and product release via stabilization of the reactant state by 1.1 kcal mol−1 and destabilization of the product state by 2.2 kcal mol−1, respectively, relative to the apo active conformation kinase. Analysis of the side chain interactions and dynamics of the αC-helix and A-loop supported the thermodynamic results and provided a detailed model explaining the IGF-1RK allostery leading to the kinase activation via inducing population shift and fine-tuning active site organization. In particular, A-loop phosphorylation induces changes in multiple side chain interactions and protein motions in the A-loop and αC-helix. These changes are propagated to the rest of the kinase to perturb the conformational equilibrium and ultimately increase catalytic activity of the kinase.Conflict of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge Drs Pedro Ojeda-May and Tatiana Shutova for helpful discussions. This study was financed by grants from Umeå University, University of Texas at Arlington, and the Swedish Research Council (VR 2015-04114). Computer resources were provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N) and National Supercomputing Center (NSC) and by the National Energy Resource Scientific Computer Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- K. Siddle, J. Mol. Endocrinol., 2011, 47, R1–R10 CrossRef CAS PubMed.
- P. Blume-Jensen and T. Hunter, Nature, 2001, 411, 355–365 CrossRef CAS PubMed.
- C. Bahr and B. Groner, Growth Horm. IGF Res., 2004, 14, 287–295 CrossRef CAS PubMed.
- E. Foulstone, S. Prince, O. Zaccheo, J. L. Burns, J. Harper, C. Jacobs, D. Church and A. B. Hassan, J. Pathol., 2005, 205, 145–153 CrossRef CAS PubMed.
- J. A. Gomez-Puerta and A. Mocsai, Curr. Top. Med. Chem., 2013, 13, 760–773 CrossRef CAS PubMed.
- S. R. Hubbard, Nat. Rev. Mol. Cell Biol., 2004, 5, 464–471 CrossRef CAS PubMed.
- S. R. Hubbard and J. H. Till, Annu. Rev. Biochem., 2000, 69, 373–398 CrossRef CAS PubMed.
- J. H. Wu, W. Li, B. P. Craddock, K. W. Foreman, M. J. Mulvihill, Q. S. Ji, W. T. Miller and S. R. Hubbard, EMBO J., 2008, 27, 1985–1994 CrossRef CAS PubMed.
- J. A. Endicott, M. E. Noble and L. N. Johnson, Annu. Rev. Biochem., 2012, 81, 587–613 CrossRef CAS PubMed.
- S. Munshi, D. L. Hall, M. Kornienko, P. L. Darke and L. C. Kuo, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 1725–1730 CrossRef.
- S. Favelyukis, J. H. Till, S. R. Hubbard and W. T. Miller, Nat. Struct. Biol., 2001, 8, 1058–1063 CrossRef CAS PubMed.
- A. J. Ablooglu and R. A. Kohanski, Biochemistry, 2001, 40, 504–513 CrossRef CAS PubMed.
- B. Y. Ma, S. Kumar, C. J. Tsai and R. Nussinov, Protein Eng., 1999, 12, 713–720 CrossRef CAS PubMed.
- Z. H. Foda, Y. B. Shan, E. T. Kim, D. E. Shaw and M. A. Seeliger, Nat. Commun., 2015, 6, 5939 CrossRef CAS PubMed.
- Y. Tokunaga, K. Takeuchi, H. Takahashi and I. Shimada, Nat. Struct. Mol. Biol., 2014, 21, 704–711 CAS.
- L. R. Masterson, C. Cheng, T. Yu, M. Tonelli, A. Kornev, S. S. Taylor and G. Veglia, Nat. Chem. Biol., 2010, 6, 821–828 CrossRef CAS PubMed.
- A. Narayanan and M. P. Jacobson, Curr. Opin. Struct. Biol., 2009, 19, 156–163 CrossRef CAS PubMed.
- C. Hyeon, P. A. Jennings, J. A. Adams and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3023–3028 CrossRef CAS PubMed.
- S. Wiesner, L. E. Wybenga-Groot, N. Warner, H. Lin, T. Pawson, J. D. Forman-Kay and F. Sicheri, EMBO J., 2006, 25, 4686–4696 CrossRef CAS PubMed.
- M. A. Young, S. Gonfloni, G. Superti-Furga, B. Roux and J. Kuriyan, Cell, 2001, 105, 115–126 CrossRef CAS PubMed.
- L. Sutto and F. L. Gervasio, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10616–10621 CrossRef CAS PubMed.
- Y. Shan, M. P. Eastwood, X. Zhang, E. T. Kim, A. Arkhipov, R. O. Dror, J. Jumper, J. Kuriyan and D. E. Shaw, Cell, 2012, 149, 860–870 CrossRef CAS PubMed.
- S. Wan and P. V. Coveney, J. Comput. Chem., 2011, 32, 2843–2852 CrossRef CAS PubMed.
- E. D. Lew, J. H. Bae, E. Rohmann, B. Wollnik and J. Schlessinger, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19802–19807 CrossRef CAS PubMed.
- D. Shukla, Y. L. Meng, B. Roux and V. S. Pande, Nat. Commun., 2014, 5, 3397 Search PubMed.
- Y. Shan, A. Arkhipov, E. T. Kim, A. C. Pan and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7270–7275 CrossRef CAS PubMed.
- H. Vashisth, L. Maragliano and C. F. Abrams, Biophys. J., 2012, 102, 1979–1987 CrossRef CAS PubMed.
- H. Huang, E. Ozkirimli and C. B. Post, J. Chem. Theory Comput., 2009, 5, 1304–1314 CrossRef CAS PubMed.
- A. Berteotti, A. Cavalli, D. Branduardi, F. L. Gervasio, M. Recanatini and M. Parrinello, J. Am. Chem. Soc., 2009, 131, 244–250 CrossRef CAS PubMed.
- P. G. Jambrina, N. Rauch, R. Pilkington, K. Rybakova, L. K. Nguyen, B. N. Kholodenko, N. V. Buchete, W. Kolch and E. Rosta, Angew. Chem., Int. Ed. Engl., 2016, 55, 983–986 CrossRef CAS PubMed.
- N. P. Damle and D. Mohanty, Biochemistry, 2014, 53, 4715–4726 CrossRef CAS PubMed.
- E. S. Groban, A. Narayanan and M. P. Jacobson, PLoS Comput. Biol., 2006, 2, 238–250 CAS.
- P. Ojeda-May, Y. Li, V. Ovchinnikov and K. Nam, J. Am. Chem. Soc., 2015, 137, 12454–12457 CrossRef CAS PubMed.
- A. D. Mackerell Jr, M. Feig and C. L. Brooks 3rd, J. Comput. Chem., 2004, 25, 1400–1415 CrossRef PubMed.
- N. Foloppe and A. D. MacKerell, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. J. Sampognaro, M. D. Wittman, J. M. Carboni, C. Chang, A. F. Greer, W. W. Hurlburt, J. S. Sack and D. M. Vyas, Bioorg. Med. Chem. Lett., 2010, 20, 5027–5030 CrossRef CAS PubMed.
- S. R. Hubbard, EMBO J., 1997, 16, 5572–5581 CrossRef CAS PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- A. D. MacKerell, M. Feig and C. L. Brooks, J. Am. Chem. Soc., 2004, 126, 698–699 CrossRef CAS PubMed.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- P. J. Steinbach and B. R. Brooks, J. Comput. Chem., 1994, 15, 667–683 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- B. R. Brooks, D. Janezic and M. Karplus, J. Comput. Chem., 1995, 16, 1522–1542 CrossRef CAS.
- A. K. Grafton and R. A. Wheeler, J. Comput. Chem., 1998, 19, 1663–1674 CrossRef CAS.
- O. Marques and Y. H. Sanejouand, Proteins, 1995, 23, 557–560 CrossRef CAS PubMed.
- A. Sethi, J. Eargle, A. A. Black and Z. Luthey-Schulten, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6620–6625 CrossRef CAS PubMed.
- PyMOL (version 0.99 ed.), DeLano Scientific LLC, South San Francisco, CA, 2006 Search PubMed.
- P. Kollman, Chem. Rev., 1993, 93, 2395–2417 CrossRef CAS.
- J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Curr. Opin. Struct. Biol., 2011, 21, 150–160 CrossRef CAS PubMed.
- M. Zacharias, T. P. Straatsma and J. A. McCammon, J. Chem. Phys., 1994, 100, 9025–9031 CrossRef CAS.
- B. R. Morgan and F. Massi, J. Chem. Theory Comput., 2010, 6, 1884–1893 CrossRef CAS PubMed.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- S. E. Boyce, D. L. Mobley, G. J. Rocklin, A. P. Graves, K. A. Dill and B. K. Shoichet, J. Mol. Biol., 2009, 394, 747–763 CrossRef CAS PubMed.
- S. M. Hanson, S. Ekins and J. D. Chodera, J. Comput.-Aided Mol. Des., 2015, 29, 1073–1086 CrossRef CAS PubMed.
- H. F. Lou and R. I. Cukier, J. Phys. Chem. B, 2006, 110, 12796–12808 CrossRef CAS PubMed.
- J. H. Till, A. J. Ablooglu, M. Frankel, S. M. Bishop, R. A. Kohanski and S. R. Hubbard, J. Biol. Chem., 2001, 276, 10049–10055 CrossRef CAS PubMed.
- C. L. McClendon, A. P. Kornev, M. K. Gilson and S. S. Taylor, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4623–4631 CrossRef PubMed.
- Y. Meng and B. Roux, J. Mol. Biol., 2014, 426, 423–435 CrossRef CAS PubMed.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- W. Q. Li and W. T. Miller, J. Biol. Chem., 2006, 281, 23785–23791 CrossRef CAS PubMed.
- F. Sicheri, I. Moarefi and J. Kuriyan, Nature, 1997, 385, 602–609 CrossRef CAS PubMed.
- F. Baffert, C. H. Regnier, A. De Pover, C. Pissot-Soldermann, G. A. Tavares, F. Blasco, J. Brueggen, P. Chene, P. Drueckes, D. Erdmann, P. Furet, M. Gerspacher, M. Lang, D. Ledieu, L. Nolan, S. Ruetz, J. Trappe, E. Vangrevelinghe, M. Wartmann, L. Wyder, F. Hofmann and T. Radimerski, Mol. Cancer Ther., 2010, 9, 1945–1955 CrossRef CAS PubMed.
- J. H. Bae, E. D. Lew, S. Yuzawa, F. Tome, I. Lax and J. Schlessinger, Cell, 2009, 138, 514–524 CrossRef CAS PubMed.
- L. Mologni, R. Rostagno, S. Brussolo, P. P. Knowles, S. Kjaer, J. Murray-Rust, E. Rosso, A. Zambon, L. Scapozza, N. Q. McDonald, V. Lucchini and C. Gambacorti-Passerini, Bioorg. Med. Chem., 2010, 18, 1482–1496 CrossRef CAS PubMed.
- S. Cox and S. S. Taylor, Biochemistry, 1995, 34, 16203–16209 CrossRef CAS PubMed.
- Y. Li, X. Li, W. Ma and Z. Dong, J. Chem. Theory Comput., 2014, 10, 3503–3511 CrossRef CAS PubMed.
- E. Ozkirimli, S. S. Yadav, W. T. Miller and C. B. Post, Protein Sci., 2008, 17, 1871–1880 CrossRef CAS PubMed.
- E. Ozkirimli and C. B. Post, Protein Sci., 2006, 15, 1051–1062 CrossRef CAS PubMed.
- D. Hamelberg, C. A. F. de Oliveira and J. A. McCammon, J. Chem. Phys., 2007, 127, 155102 CrossRef PubMed.
- J. Park, J. J. McDonald, R. C. Petter and K. N. Houk, J. Chem. Theory Comput., 2016, 12, 2066–2078 CrossRef CAS PubMed.
- Y. Meng and B. Roux, Protein Sci., 2016, 25, 219–230 CrossRef CAS PubMed.
- R. Roskoski, Biochem. Biophys. Res. Commun., 2004, 324, 1155–1164 CrossRef CAS PubMed.
- N. M. Levinson, O. Kuchment, K. Shen, M. A. Young, M. Koldobskiy, M. Karplus, P. A. Cole and J. Kuriyan, PLoS Biol., 2006, 4, 753–767 CAS.
- C. J. Tsai and R. Nussinov, PLoS Comput. Biol., 2014, 10, e1003394 Search PubMed.
- M. Frankel, S. M. Bishop, A. J. Ablooglu, Y. P. Han and R. A. Kohanski, Protein Sci., 1999, 8, 2158–2165 CrossRef CAS PubMed.
- R. J. Boerner, S. C. Barker and W. B. Knight, Biochemistry, 1995, 34, 16419–16423 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation and analysis details are provided. See DOI: 10.1039/c7sc00055c |
| This journal is © The Royal Society of Chemistry 2017 |