Open Access Article
Open Access ArticleResonances of the anthracenyl anion probed by frequency-resolved photoelectron imaging of collision-induced dissociated anthracene carboxylic acid†
Laurence H.
Stanley
 ,
Cate S.
Anstöter
,
Cate S.
Anstöter
 and
Jan R. R.
Verlet
and
Jan R. R.
Verlet
 *
*
Department of Chemistry, Durham University, Durham DH1 3LE, UK. E-mail: j.r.r.verlet@durham.ac.uk
First published on 2nd February 2017
Abstract
Resonances in polyaromatic hydrocarbon (PAH) anions are key intermediates in a number of processes such as electron transfer in organic electronics and electron attachment in the interstellar medium. Here we present a frequency- and angle-resolved photoelectron imaging study of the 9-anthracenyl anion generated through collision induced dissociation (CID) of its electrosprayed deprotonated anthracene carboxylic acid anion. We show that a number of π* resonances are active in the first 2.5 eV above the threshold. The photoelectron spectra and angular distributions revealed that nuclear dynamics compete with autodetachment for one of the resonances, while higher-lying resonances were dominated by prompt autodetachment. Based on electronic structure calculations, these observations were accounted for on the basis of the expected autodetachment rates of the resonances. Virtually no ground state recovery was observed, suggesting that the smallest deprotonated PAH that leads to ground state recovery is the tetracenyl anion, for which clear thermionic emission has been observed. The use of CID and photodissociation of organic carboxylic acid anions is discussed as a route to studying the dynamics of resonances in larger PAH anions.
Introduction
Polyaromatic hydrocarbons (PAHs) are present in many different chemical environments, where they play critical roles such as in coal1 and as a nucleation point in soot formation relevant to atmospheric chemistry.2,3 As PAHs are both carcinogenic and mutagenic,4,5 it is prudent to establish an understanding of their part in anthropogenic pollution. From a technological perspective, PAHs have been considered as a basis for new organic electronics such as OLEDs, photo-voltaic cells, and organic field effect transistors.6,7 For such devices, a fundamental knowledge of the electronic and redox properties of PAHs is essential. This is also the case for gas-phase PAHs, which have long been considered to be a key source of carbon in the interstellar medium and their presence has been inferred from unidentified IR bands.8–10 It has also been predicted that a significant fraction of interstellar PAHs are in an ionised state,10,11 which is not surprising given that the overwhelming majority of normal matter in the universe is in a plasma state. As an example, C60+ was recently identified to contribute to the IR bands.12 In regions of increased electron density, anionic PAHs are also expected and other hydrocarbon based anions, such as C6H− and C4H−, have been observed with abundances in the order of a few percent of that of their neutral precursors.13–15 The mechanism of anion formation in the interstellar medium is still unclear. Low energy electron attachment via a non-valence dipole-bound state has been the most commonly invoked mechanism.16,17 However, the minimum dipole moment required for a dipole-bound state is ∼2.5 D,18 so most neutral PAHs do not possess a sufficient dipole moment to support this mechanism. An alternative process involves electron attachment via the valence excited states of the anion embedded in the continuum. Although autodetachment is the most likely outcome following electron attachment into such a resonance, excited state processes including internal conversion can compete and may eventually form the anionic ground state.19–22 Valence resonances are particularly prevalent in highly π-conjugated systems.18,23,24 Electron impact studies have confirmed that such resonance-mediated decay processes occur23 and ground state anions of tetracene (C18H12) and pentacene (C22H14) have been observed following electron impact energies of ∼3 eV.25All of the molecular anions that have been confirmed to exist in the interstellar medium are closed-shell13,15,26–31 and therefore, PAH anions that are believed to exist in the interstellar medium are also likely to be closed-shell. Hence, deprotonated PAH anions are likely candidates. Over the past few years, we have developed anion photoelectron spectroscopy as a probe for resonances in a range of radical20,20,21,32–34 and closed-shell anions,35–37 including the tetracenyl anion, C18H11−.19 Following excitation to a resonance, C18H11− showed a preference for internal conversion back to the ground state of the anion rather than autodetachment from the resonance. Hence, from an anion formation perspective, when neutral C18H11 is approached by a low-energy electron with a kinetic energy that matches the anionic resonance, then the electronic ground state of the anion can be formed despite the unbound nature of the resonance. As these dynamics are enabled by the presence of a large number of π* resonances, it is not unreasonable to expect that the same processes may also occur in larger polyacenes. However, for smaller polyacenes fewer low-lying resonances exist, which leads to the question – how small can a polyacene be to efficiently recover the ground electronic state from an anion resonance? Here we present a study of the frequency- and angle-resolved photoelectron imaging of the anthracenyl anion, C14H9−, and show that, although resonance dynamics can be clearly identified, ground state recovery is inefficient as evidenced by a low yield of thermionic emission.
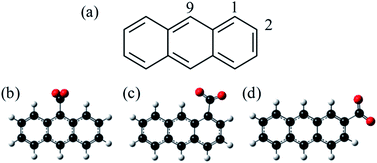
C18H11− was previously generated using electrospray ionisation of C18H12 dissolved in toluene. However, this produced the deprotonated anion in low yield and the overall ion signal suffered from instability. Furthermore, electrospray ionisation offers no selectivity over the isomeric form produced and generally forms the most stable species. In applying the same methodology to produce C14H9−, we found that the yield was too low and so here we employ an alternative method for producing the anthracenyl anion. Within the mass-spectrometry community, two main methods have been developed to generate carbanions.38,39 The first is based on the reaction of F− with a trimethyl-silanated molecule.40,41 This was recently used by the Neumark group to study the neutral ground and first excited states of the three isomers n-C14H9 (with n = 1, 2, and 9) by slow-electron velocity map imaging (SEVI) of C14H9− generated through molecular beam co-expansion of NF3 and n-(trimethylsilyl)-anthracene in He carrier gas in the presence of excess electrons.42 A second commonly employed method in mass spectrometry is decarboxylation of a deprotonated carboxylic acid anion through collision induced dissociation (CID) in a buffer cell.43 Because CO2 is very stable and has a negative electron affinity, decarboxylation is often the lowest energy path and leaves the charge at the location of the CO2 loss. Here, we employ this method, starting with the three isomeric forms of anthracene carboxylic acid (n-C14H9–CO2H, where n = 1, 2, or 9 as shown in Fig. 1), and employ frequency- and angle-resolved photoelectron imaging to probe the resonance dynamics of the 9-C14H9− fragment ion produced through CID.
Methodology
Experimental
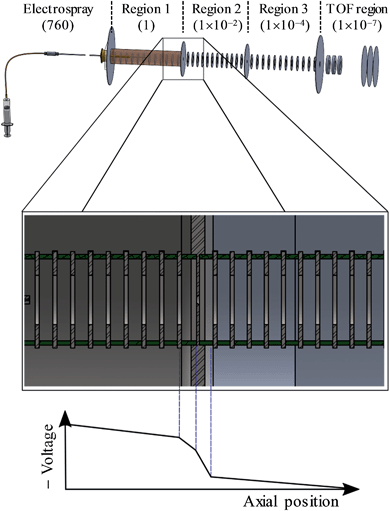
A detailed description of the experiment has been presented elsewhere.44–46 Here, a brief overview is presented of the instrument used and we detail the changes that have been implemented to enable CID prior to photoelectron imaging. A schematic of the new elements of the instrument is shown in Fig. 2. Anions were produced by electrospray ionisation of a 1 mM solution of n-C14H9–CO2H (procured from Tokyo Chemical Industry and used without further purification) in methanol. The electrospray plume was drawn into the first of several vacuum regions through a long (20 cm) capillary tube (0.6 mm inner diameter). This first region is connected to the next regions by pin-holes which incrementally reduce the pressure from 1 Torr in the first, to 10−2 Torr in the second, and 10−4 Torr in the third differentially pumped region. Each region houses sequential ring-electrode ion guides, consisting of both radially-confining RF fields and longitudinal DC ramps. This effectively forms a tube where potential energy guides the ions along by means of the DC ramps. An additional potential can be applied to encourage the ions to pass through the differential apertures, while at the end of the ion guide in the third region, a potential barrier was used to stop and trap the ions. The arrangement allows for a considerable increase in the transmission from the capillary to the trap as well as a much increased trapping volume.46 The trapping voltage was rapidly switched to extract the ions in the trap and these were then injected into a collinear Wiley-McLaren time-of-flight mass spectrometer.47 Mass-selected ion packets then entered a continuous mode velocity map imaging spectrometer,44,48 where the ions were subject to a tuneable ∼6 ns laser pulse from a Nd:YAG pumped OPO (Continuum Surelite II-10, Horizon I) and the resultant photoelectrons were collected on a position sensitive detector.49 Raw images were analysed using the Polar Onion Peeling algorithm to determine both the photoelectron spectrum and the angular distribution.49 Photoelectron spectra were calibrated using the known photoelectron spectrum of I− and the resolution of the spectrometer was around 5%.Under normal operating conditions, anions experience only a small DC voltage drop from the last electrode of the first ion guide to the pinhole, and the same on the other side. By increasing the magnitude of this voltage drop into the second ion guide, significant CID can be induced as evidenced by fragments appearing in the time-of-flight mass spectrum. The most prominent fragment was an ion with a m/z 44 less than the parent anion n-C14H9–CO2−, corresponding to CO2 loss.
Computational
Density functional theory (DFT) calculations were performed using the Gaussian 09 computational package50 and the B3LYP functional with the 6-31+G** basis set, which has been shown to perform well on anionic PAHs.42 The geometries of 1-, 2- and 9-C14H9− and their corresponding radical neutral species were optimized, and were confirmed to represent the geometric minima through vibrational frequency analysis. All of the geometries of n-C14H9− were confirmed to have planar minimum energy structures, in agreement with the previous literature.11,42,51 The calculated energetics have been corrected for zero-point energy. Calculations using time-dependent (TD) DFT employing the Tamm–Dancoff approximation52 provided energetics and information about the character of both the anionic and neutral excited states accessed experimentally for 9-C14H9− which has C2V symmetry.Additional ab initio calculations were carried out to predict the photoelectron angular distributions using the coupled-cluster equations of motion (EOM) formalism53 and employing the QChem 4.4 package.54 Specifically, EOM-IP-CCSD calculations (using the same basis set as before) were used to determine the Dyson orbital with the anion ground state as the initial reference wavefunction, ΨN, and the neutral ground state as the final wavefunction, ΨN−1.55,56 The photoelectron angular distribution for this direct detachment channel was modelled using the ezDyson program (version 3.2) developed by Krylov and coworkers.57,58
Results and discussion
Production of 9-C14H9− from the CID of 9-C14H9–CO2−
By altering the voltage drop between regions 1 and 2 in Fig. 2, both the parent anion and a mass-peak at a m/z 44 below the parent anion could be produced. The ratio of the fragment to the parent anion could be increased by increasing the voltage drop, which corresponds to increasing the kinetic energy of the parent anion through a high pressure (∼1 Torr) region of the instrument causing CID. It is well known that the CID of an organic carboxylic acid generally removes the CO2 group to produce the deprotonated carbanion.38,39 Under low-pressure conditions and “soft” CID, the negative charge generally remains localised in the location where the CO2 was removed. However, in the present case, CID occurs in a region of higher pressure than that of a typical CID mass-spectrometric experiment and the timescales in our experiment are also very different (with the time from CID to photoelectron spectroscopy being several milliseconds). The consequence of this “in-source” CID was that we could only produce the lowest energy isomer (9-C14H9−) in isolation, regardless of the starting n-C14H9–CO2− isomer. We also found it necessary to flow dry Ar over the inlet of the mass-spectrometer (see Fig. 2) as O2 and H2O in the air led to several additional fragments, presumably produced by in-source reactions of CID-produced reactive intermediates. Note that even though 9-C14H9− is formed vibrationally hot by CID, the anion is eventually thermalized to room temperature within the second and third ion guide regions of the instrument. Under the mildest conditions using 1-C14H9–CO2− that resulted in sufficient CID to perform photoelectron spectroscopy, some 1-C14H9− could be formed, but the ion packet contained significant contamination from the 9-isomer too (see the ESI†).Although in the present experiment only a single isomer could be formed exclusively, the use of CID in forming decarboxylated fragment anions is appealing because it relies on electrosprayed anions for which there is essentially no size or volatility limit of the precursor anion. For larger PAHs, the vapour pressure rapidly reduces. For example, perylene has a vapour pressure of ∼4 × 10−2 Pa at 400 K (ref. 59) and needs to be heated to very high temperatures for molecular beam studies. In contrast, electrospray ionisation of the perylene carboxylic acid is readily achieved.
Frequency- and angle-resolved photoelectron spectra of 9-C14H9−
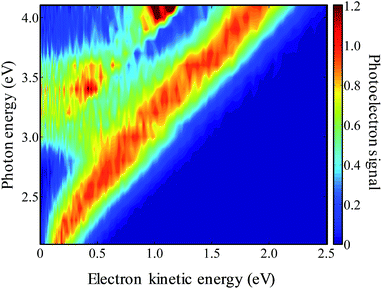
The frequency-resolved photoelectron spectra are shown in Fig. 3 as a false-colour plot. It is composed of 21 photoelectron spectra at 0.1 eV intervals (the individual photoelectron spectra are given in the ESI†). Each spectrum has been normalised so that the highest energy peak has a unit maximum intensity. As the photon energy is increased, the eKE of the highest energy peak increases by the same amount indicating that this is a direct detachment feature. Extrapolation of the high eKE edge yields ADE = 1.7(1) eV, which is in agreement with the value of 1.7155(2) eV determined by Neumark and coworkers.42 At around hν ∼ 3.0 eV, a second channel opens up which also leads to a peak that increases linearly with hν. This feature can be assigned to the first excited state of the 9-C14H9 neutral radical. The energy gap between these values from our measurements is 1.2(1) eV, which is in agreement with the gap of 1.205(6) eV determined by Neumark and coworkers.42In addition to the two direct detachment features, there is evidence of delayed autodetachment at 2.8 < hν < 3.5 eV. Instead of the expected increase of eKE with hν, the photoelectron spectra show signals at a lower eKE, indicating that some of the available eKE has been converted to kinetic energy of the nuclei.60 Hence, in the 2.8 < hν < 3.5 eV energy range, a resonance appears to be excited and its nuclear wavepacket and/or internal conversion dynamics are in competition with autodetachment from the resonance.
For hν > 3.8 eV, there also appears to be a dramatic change in the branching ratio of formation of the neutral species in the ground or first excited state following electron detachment.
Specifically, the neutral excited state appears to be produced more favourably compared to the ground state. As discussed below, this arises from the presence of a resonance for which autodetachment to the first excited state may be more favourable.
Additional insight can be gained by considering the photoelectron angular distributions at all hν and eKE values. The angular distribution can be quantified using the anisotropy parameter, β2, defined from a fit to the photoelectron angular distribution at a given eKE to61,62
I(θ, eKE) ∝ 1 + ½[β2P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)], θ)], |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) = 3
θ) = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1 is the second order Legendre polynomial. The two limiting values of β2 are −1 and +2, which correspond to photoelectron emission predominantly perpendicular and parallel to the polarisation axis of the laser.
θ − 1 is the second order Legendre polynomial. The two limiting values of β2 are −1 and +2, which correspond to photoelectron emission predominantly perpendicular and parallel to the polarisation axis of the laser.
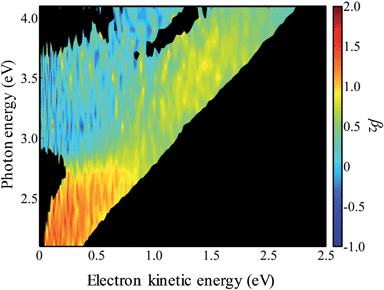
In Fig. 4, the frequency-resolved β2 parameters are plotted as a false colour plot (the raw photoelectron images are in the ESI†). The photoelectron spectra show strong anisotropy in certain spectral regions. The direct detachment feature that forms the neutral ground state exhibits an overall positive β2. At low hν, the direct detachment has β2 = +1.3 ± 0.1. This is consistent with the observation of the Neumark group. The photoelectrons arising from delayed autodetachment (lower eKE) in the 2.8 < hν < 3.5 eV range are predominantly isotropic with β2 ∼ 0. Similarly, detachment to form the first excited state of the neutral species appears to be isotropic.
 | ||
| Fig. 4 False-colour plot of the frequency-resolved β2 spectra of 9-C14H9−. The signals below an intensity of 0.2 in Fig. 3 have been blacked out because the signal levels were too low to determine a reliable β2 parameter. | ||
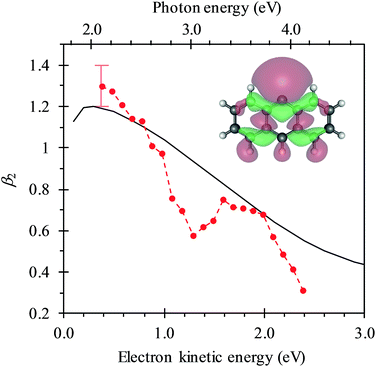
Upon closer inspection, the anisotropy of the direct detachment feature that leaves the neutral radical in its ground state appears to change quite abruptly across the hν range studied. In Fig. 5, the β2 parameter averaged over this direct detachment peak is shown as a function of hν (and of eKE of the photoelectron). If direct detachment was the only available channel, then one would expect to see slow variations with increasing hν. However, over the regions 2.8 < hν < 3.5 eV and hν > 3.8 eV, there are strong deviations from this expected behaviour, which supports our earlier suggestion that resonances are excited in these regions.
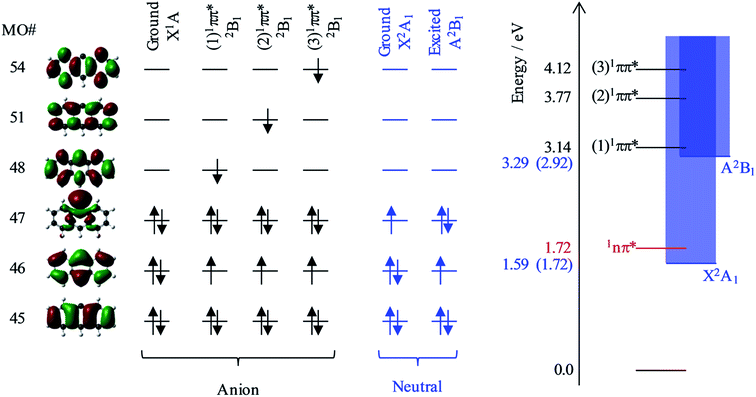
Fig. 6 shows the relevant calculated molecular orbitals (MOs) of 9-C14H9−. The highest occupied MO (HOMO) corresponds to the n-orbital localised primarily at the C9 position (see Fig. 1), while the lowest unoccupied MO (LUMO) is a delocalised π* orbital. Our calculations show that there are several excited states and resonances of 9-C14H9− that can be accessed in the hν range used in the present experiments. Fig. 6 also shows an overview of the most relevant excited states (those with significant oscillator strengths) and their dominant orbital contributions are given in the ESI.† Many of the lowest lying excited states involve 1nπ* states and consequently have very low oscillator strengths; the lowest lying anion 1nπ* resonance is included in the energy level diagram.
Based on our calculations, the most likely resonances that are excited around 2.8 < hν < 3.5 eV and hν > 3.8 eV are the three lowest 1ππ* transitions. The lowest (1)1ππ* transition is calculated to be at 3.14 eV. This calculated energy is consistent with the 2.8 < hν < 3.5 eV range over which the deviation of the β2 parameter was noted in Fig. 5 and with the resonance signatures in the frequency-resolved photoelectron spectra in Fig. 3. For hν > 3.8 eV, deviations from the expected β2 behaviour were also noted in Fig. 5, which is consistent with the next two 1ππ* resonances: (2)1ππ* was calculated at 3.77 eV and (3)1ππ* at 4.12 eV photon energy. Interestingly, only the (1)1ππ* resonance shows evidence of nuclear dynamics in competition with autodetachment (Fig. 3).
Fig. 6 additionally shows the orbital configurations associated with the neutral ground state (X2A1) and its first excited state (A2B1). The ground state is formed by the loss of the n-electron in the HOMO, while the first excited state is formed by the loss of a π-electron from the HOMO−1. All three 1ππ* states predominantly involve the excitation of the HOMO−1 π-electron into a π* MO. Hence, these resonances are of Feshbach character with respect to the electron loss channel that forms the neutral ground state, but are of shape character with respect to the electron loss channel that leaves the neutral species in its first excited state. Because a Feshbach resonance involves a 2-electron transition, the autodetachment lifetimes are typically longer compared to shape resonances for which only a single electron transition is required.
The adiabatic energy of the neutral excited state lies very close to the onset of the (1)1ππ* resonance, while the vertical energy of the neutral species (at the anion geometry) will be higher and was calculated to be at hν = 3.29 eV. Because excitation occurs in the vertical region and the electron loss cross section is small for low eKE electrons, the (1)1ππ* resonance will predominantly decay by autodetachment to the ground state of the neutral species. But as this is a 2-electron transition, autodetachment may be expected to be relatively slow. Therefore, one might anticipate that nuclear dynamics could compete with autodetachment, which is consistent with the observations in Fig. 3. The (2)1ππ* and (3)1ππ* resonances are some way above the threshold region for the autodetachment channel that leaves the neutral species in its excited state. Therefore, loss of the electron can proceed through a one electron process (excited shape resonance) and the consequential increased autodetachment rate appears to outcompete the nuclear dynamics of the (2)1ππ*/(3)1ππ* resonances so that the photoelectron peak essentially takes the spectral form of a direct detachment process as seen in Fig. 3. We also previously noted the increase in yield of the neutral excited state when hν > 3.8 eV (see Fig. 3), and this is fully consistent with the fact that the (2)1ππ* and (3)1ππ* resonances are only of shape character with respect to the neutral excited state, but Feshbach with respect to the ground state. Hence autodetachment into the former channel is faster and therefore has a higher yield. Note that we cannot determine the branching ratios accurately because of the additional direct detachment channel that is always open for hν > ADE.
One aspect of the direct photodetachment from 9-C14H9− that is particularly clear is its anisotropy. This has previously been discussed by the Neumark group in their interpretation of their SEVI experiment.42 The photoelectron angular distribution for directed detachment in the 0.0 < eKE < 0.3 eV range was measured to be β2 = +1.3.42 This is in agreement with the β2 parameters determined here in the same energy range (Fig. 5). For higher eKE values, we observe a gradual decrease in β2 as well as rapid changes. In order to confirm that the rapid changes correspond to the deviation of a smoothly varying β2 parameter due to direct detachment, we have performed similar calculations to the Neumark group but over a wider eKE range. The results from these calculations are included in Fig. 5 (solid line). The data are not scaled in any way and yield β2 = +1.2 for low eKE electrons, in excellent agreement with the experiment.‡ As eKE increases, the β2 parameter smoothly decreases as anticipated. This overall trend is reproduced in the experimental data. However, over the ranges where resonance dynamics were noted (2.8 < hν < 3.5 eV and hν > 3.8 eV), the measured photoelectron angular distributions are significantly more isotropic than that predicted for direct detachment, confirming that the frequency-resolved β2 parameter has identified the resonances.
The quantitative agreement between the experiment and theory here is very encouraging. Our group has previously shown similar rapid changes in β2 for para-benzoquinone radical anions,33 which could also be correlated with the excitation and electron emission from resonances. However, in chemical derivatives of para-benzoquinone, the overall anisotropy tended to zero so that changes were difficult to discern.20,21 For 9-C14H9−, the clear anisotropy arises from its high (C2V) symmetry, enabling full use of the angular dimension. Further theoretical developments to accurately predict photoelectron distributions for photo-detachment and specifically autodetachment may assist in identifying the nature of the resonances in favourable cases such as 9-C14H9−.
Resonance dynamics in 9-C14H9− compared to 1-C18H11−
The frequency- and angle-resolved photoelectron spectra clearly show that nuclear resonance dynamics can compete with autodetachment from the (1)1ππ* resonance of 9-C14H9−. The dynamics of the resonance involves nuclear wavepacket motion on the (1)1ππ* potential energy surface. Hence, autodetachment may occur along different coordinates of the (1)1ππ* surface which leads to different Franck–Condon factors to the neutral ground state and consequently to photoelectrons with a lower eKE relative to that for direct detachment. Additionally, internal conversion can occur from the (1)1ππ* resonance to lower-lying 1nπ* resonances. Several such resonances were identified in our calculations. The population of the 1nπ* resonances following a non-adiabatic transition from the (1)1ππ* state is expected to result in very fast autodetachment as these are of shape character relative to the neutral ground state. Unfortunately, we cannot determine whether such internal conversion processes are occurring from the present data.Internal conversion to repopulate the ground electronic state of the anion is barely observed: this would be evidenced by the presence of very low energies in the photoelectron spectra that are statistically emitted (thermionic emission) from the hot anion. There is the suggestion of thermionic emission in the photoelectron images (ESI†), but the yield is very low. Hence, unlike the case of the tetracenyl anion, C18H11−, for which intense thermionic emission was clearly seen, resonances in 9-C14H9− are not efficient in recovering the ground state. While 1-C18H11− has a higher density of resonances than 9-C14H9−, a key additional difference between the two systems is that 1-C18H11− has several bound singlet excited electronic states. This is partly due to its higher ADE and partly due to the greater π-electron delocalisation in 1-C18H11−. We have previously shown that in the menadione radical anion, efficient anion ground state recovery was facilitated by a bound excited state, which acted as an intermediate in an internal conversion cascade.20 Hence, we suggest that 9-C14H9− does not efficiently reform the anion ground state in part because of the lack of anion bound states. We can therefore also suggest that 1-C18H11− is the smallest astrophysically relevant polyacenyl anion for which efficient ground state recovery can occur. Note that 1-C14H9−, 2-C14H9−, 2-C18H11− and 3-C18H11− may prove to be more efficient in this regard, but only the lowest energy isomers (9-C14H9− and 1-C18H11−) are expected to be prevalent in the interstellar medium; these can be formed by H-atom tunnelling from the other higher-lying isomers, which proceeds on timescales faster than the astronomically relevant ones.63
The observation of resonances in 9-C14H9− and their dynamics also has implications for the SEVI work reported by the Neumark group. Specifically, the SEVI experiment assumes that direct detachment into the continuum determines the vibrational structure of the neutral species. However, as the direct detachment cross section is low near the threshold, even optically weak transitions may become important, and we note that our calculations suggest that the lowest 1nπ* resonance is close to the neutral state energy. If a resonance was accessed at the SEVI detachment energy, then this would lead to changes in the Franck–Condon factors of the neutral species, as was shown by Schiedt and Weinkauf in para-benzoquinone radical anions.64 This should be apparent from changes in the peak intensities as the photon energy was changed and perhaps in the β2 parameters associated with specific photoelectron peaks. In the data presented for the neutral ground state of 9-C14H9−, there is no evidence of the participation of resonance excitation, however, the same is certainly not true for the first excited state of the neutral species. Fig. 3 clearly shows that the (1)1ππ* resonance produces photoelectrons essentially over the entire eKE < hν − ADE range. Indeed, it is noted in their work that the β2 parameters are likely distorted because of high-eKE electrons that are arising from direct detachment into the neutral ground state.42 From our data, these “distorting” electrons are actually also at low-eKE because of the resonance dynamics of the (1)1ππ* state.
Conclusions
A new methodology for studying the resonances of closed shell PAH anions has been presented based on the CID of their respective carboxylic acids formed by electrospray ionisation. For different anthracene carboxylic acid isomers, only the most stable isomer of the anthracenyl anion (9-C14H9−) is formed. Frequency- and angle-resolved photoelectron imaging of 9-C14H9− was used to identify and characterise the dynamics of a number of resonances. The lowest lying π* resonance shows rapid nuclear dynamics that are in competition with autodetachment. However, ground state recovery was observed to be inefficient. Two higher-lying π* resonances were observed to rapidly decay by autodetachment. All observations could be accounted for using supporting electronic structure calculations. In particular, our data and calculations show how photoelectron anisotropy can be used to identify the presence of resonances.Closed shell PAH anions have been implicated to exist in the interstellar medium, where, in the absence of a sufficiently large dipole moment, electron attachment through resonances may be a key formation mechanism. Our results show that the predominant decay mechanism for resonances in 9-C14H9− is autodetachment, which is in contrast to the next polyacene increment, the tetracenyl anion, for which ground state recovery has been reported previously.19 Therefore, the latter is the smallest polyacenyl anion for which this process can occur and therefore is also the smallest likely polyacenyl anion to be found in the interstellar medium. With the development of this new methodology, we will now be able to explore a wide range of large PAHs to determine the role of resonances in their anion formation.
Acknowledgements
We thank Berwyck Poad for many insightful discussions concerning CID and bringing it and its versatility to our attention. This work was supported by the European Research Council (Starting Grant 306536).Notes and references
- C. Barckholtz, T. A. Barckholtz and C. M. Hadad, J. Am. Chem. Soc., 1999, 121, 491–500 CrossRef CAS.
- H. F. Calcote, Combust. Flame, 1981, 42, 215–242 CrossRef CAS.
- H. Richter, O. A. Mazyar, R. Sumathi, W. H. Green, J. B. Howard and J. W. Bozzelli, J. Phys. Chem. A, 2001, 105, 1561–1573 CrossRef CAS.
- R. G. Harvey and N. E. Geacintov, Acc. Chem. Res., 1988, 21, 66–73 CrossRef CAS.
- J. L. Durant, W. F. Busby, A. L. Lafleur, B. W. Penman and C. L. Crespi, Mutat. Res., Genet. Toxicol., 1996, 371, 123–157 CrossRef CAS.
- T. M. Figueira-Duarte and K. Müllen, Chem. Rev., 2011, 111, 7260–7314 CrossRef CAS PubMed.
- X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- J. L. Puget and A. Léger, Annu. Rev. Astron. Astrophys., 1989, 27, 161–198 CrossRef CAS.
- L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., Suppl. Ser., 1989, 71, 733–775 CrossRef CAS PubMed.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- H. A. Galué and J. Oomens, Astrophys. J., 2012, 746, 83 CrossRef.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- S. Brünken, H. Gupta, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, Astrophys. J., Lett., 2007, 664, L43 CrossRef.
- M. C. McCarthy, C. A. Gottlieb, H. Gupta and P. Thaddeus, Astrophys. J., Lett., 2006, 652, L141 CrossRef CAS.
- J. Cernicharo, M. Guélin, M. Agúndez, K. Kawaguchi, M. McCarthy and P. Thaddeus, Astron. Astrophys., 2007, 467, L37–L40 CrossRef CAS.
- P. J. Sarre, Mon. Not. R. Astron. Soc., 2000, 313, L14–L16 CrossRef CAS.
- K. D. Jordan and F. Wang, Annu. Rev. Phys. Chem., 2003, 54, 367–396 CrossRef CAS PubMed.
- J. Simons, J. Phys. Chem. A, 2008, 112, 6401–6511 CrossRef CAS PubMed.
- J. N. Bull, C. W. West and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2015, 17, 32464–32471 RSC.
- J. N. Bull, C. W. West and J. R. R. Verlet, Chem. Sci., 2015, 6, 1578–1589 RSC.
- J. N. Bull, C. W. West and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2015, 17, 16125–16135 RSC.
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- K. D. Jordan and P. D. Burrow, Chem. Rev., 1987, 87, 557–588 CrossRef CAS.
- H. S. Taylor, G. V. Nazaroff and A. Golebiewski, J. Chem. Phys., 1966, 45, 2872–2888 CrossRef CAS.
- R. V. Khatymov, R. F. Tuktarov and M. V. Muftakhov, JETP Lett., 2011, 93, 437–441 CrossRef CAS.
- M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 66901 CrossRef CAS PubMed.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- G. Israël, C. Szopa, F. Raulin, M. Cabane, H. B. Niemann, S. K. Atreya, S. J. Bauer, J.-F. Brun, E. Chassefière, P. Coll, E. Condé, D. Coscia, A. Hauchecorne, P. Millian, M.-J. Nguyen, T. Owen, W. Riedler, R. E. Samuelson, J.-M. Siguier, M. Steller, R. Sternberg and C. Vidal-Madjar, Nature, 2005, 438, 796–799 CrossRef PubMed.
- A. J. Coates, F. J. Crary, G. R. Lewis, D. T. Young, J. H. Waite and E. C. Sittler, Geophys. Res. Lett., 2007, 34, L22103 CrossRef.
- C. Walsh, N. Harada, E. Herbst and T. J. Millar, Astrophys. J., 2009, 700, 752 CrossRef CAS.
- R. C. Fortenberry, J. Phys. Chem. A, 2015, 119, 9941–9953 CrossRef CAS PubMed.
- J. N. Bull, C. W. West and J. R. R. Verlet, Chem. Sci., 2016, 7, 5352–5361 RSC.
- C. W. West, J. N. Bull, E. Antonkov and J. R. R. Verlet, J. Phys. Chem. A, 2014, 118, 11346–11354 CrossRef CAS PubMed.
- D. A. Horke, Q. Li, L. Blancafort and J. R. R. Verlet, Nat. Chem., 2013, 5, 711–717 CrossRef CAS PubMed.
- C. W. West, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Chem. Phys., 2013, 139, 71104 CrossRef PubMed.
- C. W. West, J. N. Bull, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Phys. Chem. B, 2015, 119, 3982–3987 CrossRef CAS PubMed.
- C. W. West, J. N. Bull and J. R. R. Verlet, J. Phys. Chem. Lett., 2016, 7, 4635–4640 CrossRef CAS PubMed.
- R. R. Squires, Acc. Chem. Res., 1992, 25, 461–467 CrossRef CAS.
- Z. Tian and S. R. Kass, Chem. Rev., 2013, 113, 6986–7010 CrossRef CAS PubMed.
- C. H. DePuy, V. M. Bierbaum, L. A. Flippin, J. J. Grabowski, G. K. King, R. J. Schmitt and S. A. Sullivan, J. Am. Chem. Soc., 1980, 102, 5012–5015 CrossRef CAS.
- I. H. Krouse and P. G. Wenthold, J. Am. Soc. Mass Spectrom., 2005, 16, 697–707 CrossRef CAS PubMed.
- M. L. Weichman, J. A. DeVine, D. S. Levine, J. B. Kim and D. M. Neumark, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1698–1705 CrossRef CAS PubMed.
- S. W. Froelicher, B. S. Freiser and R. R. Squires, J. Am. Chem. Soc., 1986, 108, 2853–2862 CrossRef CAS.
- D. A. Horke, G. M. Roberts, J. Lecointre and J. R. R. Verlet, Rev. Sci. Instrum., 2012, 83, 63101 CrossRef PubMed.
- G. Roberts, Doctoral, Durham University, 2010.
- J. Lecointre, G. M. Roberts, D. A. Horke and J. R. R. Verlet, J. Phys. Chem. A, 2010, 114, 11216–11224 CrossRef CAS PubMed.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 53104 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, T. Vreven, J. A. Montgomery, G. A. Petersson, G. E. Scuseria, H. B. Schlegel, H. Nakatsuji, A. F. Izmaylov, R. L. Martin, J. L. Sonnenberg, J. E. Peralta, J. J. Heyd, E. Brothers, F. Ogliaro, M. Bearpark, M. A. Robb, B. Mennucci, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, A. Rendell, R. Gomperts, V. G. Zakrzewski, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao and H. Nakai, Gaussian 09 Search PubMed.
- J. Schiedt and R. Weinkauf, Chem. Phys. Lett., 1997, 266, 201–205 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- Y. Liu and C. Ning, J. Chem. Phys., 2015, 143, 144310 CrossRef PubMed.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2009, 131, 124114 CrossRef PubMed.
- A. I. Krylov and S. Gozem, ezDyson Search PubMed.
- J. L. Goldfarb and E. M. Suuberg, J. Chem. Eng. Data, 2008, 53, 670–676 CrossRef CAS.
- C. S. Anstöter, J. N. Bull and J. R. R. Verlet, Int. Rev. Phys. Chem., 2016, 35, 509–538 CrossRef.
- R. N. Zare, Mol. Photochem., 1972, 4, 1 CAS.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
- F. Trixler, Curr. Org. Chem., 2013, 17, 1758–1770 CrossRef CAS PubMed.
- J. Schiedt and R. Weinkauf, J. Chem. Phys., 1999, 110, 304–314 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Raw photoelectron spectra and images; fragment photoelectron spectra from 9- and 1-C14H9–CO2− precursors; and excited state molecular orbital contributions. See DOI: 10.1039/c6sc05405f |
| ‡ We believe that this specific β2 parameter calculated by Neumark and coworkers may be erroneous because of the older version of QChem and/or ezDyson used in their calculations. In fact, visual inspection of the Dyson orbital shows that, while a large component of the orbital is of n-character which would lead to β2 = +2, there is also significant π-character which should reduce this substantially, which is consistent with the predicted and observed β2 parameter presented here. |
| This journal is © The Royal Society of Chemistry 2017 |