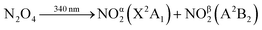Unravelling the mechanisms of vibrational relaxation in solution

Abstract

We present a systematic study of the mode-specific vibrational relaxation of NO₂ in six weakly-interacting solvents (perfluorohexane, perfluoromethylcyclohexane, perfluorodecalin, carbon tetrachloride, chloroform, and d-chloroform), chosen to elucidate the dominant energy transfer mechanisms in the solution phase. Broadband transient vibrational absorption spectroscopy has allowed us to extract quantum state-resolved relaxation dynamics of the two distinct NO₂ fragments produced from the 340 nm photolysis of N₂O₄ → NO₂(X) + NO₂(A) and their separate paths to thermal equilibrium. Distinct relaxation pathways are observed for the NO₂ bending and stretching modes, even at energies as high as 7000 cm⁻¹ above the potential minimum. Vibrational energy transfer is governed by different interaction mechanisms in the various solvent environments, and proceeds with timescales ranging from 20–1100 ps. NO₂ relaxation rates in the perfluorocarbon solvents are identical despite differences in acceptor mode state densities, infrared absorption cross sections, and local solvent structure. Vibrational energy is shown to be transferred to non-vibrational solvent degrees of freedom (V-T) through impulsive collisions with the perfluorocarbon molecules. Conversely, NO₂ relaxation in chlorinated solvents is reliant on vibrational resonances (V-V) while V-T energy transfer is inefficient and thermal excitation of the surrounding solvent molecules inhibits faster vibrational relaxation through direct complexation. Intramolecular vibrational redistribution allows the symmetric stretch of NO₂ to act as a gateway for antisymmetric stretch energy to exit the molecule. This study establishes an unprecedented level of detail for the cooling dynamics of a solvated small molecule, and provides a benchmark system for future theoretical studies of vibrational relaxation processes in solution.

---

Introduction

Chemical reactions in solution are commonplace in living organisms, the natural environment, and in synthetic and industrial processes. The rates of these reactions can be strongly dependent upon the internal energy of the reactants, and hence upon the mechanisms and rates with which energy flows between solute and solvent molecules. The solute molecules are continuously exposed to forces from the surrounding solvent, and the interplay of these solute–solvent interactions can stabilise or destabilise reactive intermediates, and control the exchange of energy and reaction mechanisms. Measurements of the flow of energy from a solute to the solvent probe the intermolecular interactions, but are challenging given their complexity and frequency.

The timescale of vibrational energy relaxation in solution can range from a few picoseconds up to several seconds in some instances, and a reliably predictive theoretical model for these widely varying relaxation processes is still out of reach.^1–3 Here we present a systematic study of the (mode-specific) vibrational cooling dynamics of energized solute molecules (NO₂) in six simple solvents, chosen to allow systematic examination of the mechanisms by which energy relaxation occurs in solution, and to distinguish between competing solute-to-solvent energy transfer pathways.

Highly vibrationally excited NO₂ can be generated promptly from the photolysis of N₂O₄, which dissolves readily in all of the solvents used and is formed by bubbling in gaseous NO₂. Photolysis at 340 nm generates two NO₂ molecules: one (α) in the ground X²A₁ state, the other (β) in the first excited A²B₂ state.⁴

The NO^α₂ fragment is produced with modest vibrational excitation. The NO^β₂ fragment is formed with both electronic and vibrational excitation, but rapidly internally converts to high vibrational levels of the ground state. This second pathway provides a source of highly vibrationally excited non-thermal NO₂.

Vibrational energy transfer is generally discussed in terms of donating and accepting modes. Two broad categories describe the nature of the donating–accepting pair interaction in the previous literature: solute vibration to solvent vibration energy transfer (V-V) and solute vibration to solvent translation/rotation/libration transfer (V-T).^1,5–8 Three primary energy transfer mechanisms are useful for the current discussion. These mechanisms for solute vibrational energy relaxation to the solvent are identified through their interaction type:

(1) Impulsive coupling (V-T and/or V-V): energy transfer through short-range repulsive interactions. This coupling is more efficient for ‘hard’ collisions.^9,10

(2) Anharmonic coupling (V-V): vibrational energy is transferred via short-range attractive interactions. This mechanism requires some degree of solute–solvent complexation, most notably through hydrogen bonding.¹¹

(3) Förster coupling (V-V): vibrational energy is transferred through transition dipole–dipole interactions, as a virtual photon. Förster coupling requires spectral overlap of the solute infrared (IR) emission and solvent IR absorption spectra, and decays with increasing solute–solvent distance (R) with R⁻⁶ dependence.^12–14

The solvents used in the current studies were chosen to enhance specific energy transfer mechanisms. The three perfluorinated solvent molecules – perfluorohexane, perfluoromethylcyclohexane, and perfluorodecalin – have negligible dipole moments and minimal polarizability, and thus experience only weak attractive interactions with solute molecules. However, each solvent possesses unique vibrational frequencies and bulk/molecular solvent structures, which can affect Förster and impulsive coupling mechanisms. Perfluorodecalin contains 1.4 times as many internal degrees of freedom as the other perfluorinated solvents, and thus should accept energy faster in any purely statistical picture. Carbon tetrachloride (CCl₄) also has no permanent molecular dipole moment, but is significantly more polarizable than the perfluorocarbons (PFCs) and thus experiences stronger dispersion interactions with the solute. Chloroform (CHCl₃) is similar to CCl₄ in terms of vibrational modes and dispersion interaction strength, but possesses a permanent dipole moment (∼1.04 D)¹⁵ which facilitates stronger complexation with a polar solute molecule. Deuterated chloroform (CDCl₃) is chemically identical to CHCl₃, but some of its vibrational frequencies are shifted by the heavier deuterium atom. The effects of these different solute–solvent interactions are clearly distinguished in our ultrafast time-resolved IR absorption measurements of the vibrational cooling of internally hot NO₂ in the various solvents.

Results and discussion

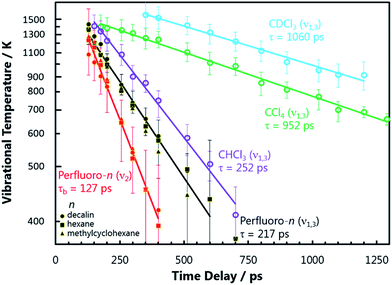
Steady state electronic absorption spectra of NO₂ dissolved in perfluorodecalin (which was indistinguishable from the spectra of NO₂ dissolved in perfluorohexane and perfluoromethylcyclohexane), CCl₄, and CHCl₃ are shown in Fig. 1 alongside the gas phase spectrum (at 1 atm). The gas-phase vibronic structure of the NO₂ is partially or completely lost through inhomogeneous broadening by solvent interactions, which can be modelled by convoluting the gas phase spectrum with a Gaussian function. The degree of spectral broadening provides valuable information about the local solvation environment of the NO₂ in these solutions. The solution phase electronic spectra of NO₂ show an increasing Gaussian linewidth (FWHM) with the intermolecular interaction strength of the solvent, from PFCs (∼230 cm⁻¹), to CCl₄ (∼500 cm⁻¹), and CHCl₃ (∼600 cm⁻¹).

Fig. 1 IR absorption spectra (bottom) of the solvents used in the present experiments. The translucent vertical bands overlaid on the solvent spectra indicate the wavenumbers of the three vibrational modes of NO₂, and highlight potential resonant vibrational modes of the solvent. The IR absorption spectra of the NO₂ (ν₃ = 1 ← 0) fundamental transition in perfluorohexane, perfluorodecalin, and chloroform are shown (top right) with their central wavenumbers shifted to the same value for the sake of comparison. The true central wavenumbers of this transition (ν₃), the Lorentzian linewidth Γ, and ratio of rotationally hindered to unhindered spectral contributions (see ESI‡) are provided in the table. The visible spectra of NO₂ in the gas phase, in perfluorodecalin, carbon tetrachloride, and in chloroform (top left) demonstrate the increasing degree of inhomogeneous broadening induced by solute–solvent interactions in this sequence of environments.

The shapes of individual bands in the infrared (IR) vibrational spectrum also inform about the local solvation of the NO₂. Spectra of the ∼1610 cm⁻¹ transition of NO₂ in perfluorohexane, perfluorodecalin, and chloroform are shown in Fig. 1. Each spectrum has been shifted to the same central transition wavenumber for better comparison of the lineshapes, but the true transition wavenumbers (ν₃ in Fig. 1) are provided in the accompanying table. All of the transitions are Lorentzian broadened, indicating that homogeneous broadening dominates the line shape. The Lorentzian linewidth Γ reflects the magnitude and timescale of solvent-induced perturbations to the solute transition frequency. The similarity of these linewidths and the solvent-induced band shifts (Fig. 1) indicates comparable solute–solvent interaction potentials for the three PFC solvents, albeit with some subtle differences in the local solvation environments of the NO₂. Significant signal contributions were observed in the wings of the spectral band that cannot be captured by a single Lorentzian function, but can be fit when some P/R branch rotational character is included in the lineshape. We recently established that (small molecule) solute rotation is relatively unhindered in PFC solutions, leading to the observation of significant rotational band structure in the absorption spectrum.¹⁶ The degree to which the solute rotation is hindered in each solvent provides further insights about the local solute environment. Further discussion of this effect is provided in the ESI.‡

NO₂ vibration is described by three normal modes: the symmetric stretch (ν₁ = 1320 cm⁻¹), bend (ν₂ = 750 cm⁻¹), and antisymmetric stretch (ν₃ = 1617 cm⁻¹).¹⁷ The vibrational state-populations of both NO₂ fragments from N₂O₄ photolysis were tracked as a function of time through the IR absorption of the ν₃ transitions with sub-picosecond temporal resolution, using broadband Transient Vibrational Absorption Spectroscopy. While the ν₃ mode is probed directly, the ν₂ and ν₁ state populations can also be observed through their anharmonic coupling to the antisymmetric stretch (x₃₃ = −16.6 cm⁻¹, x₂₃ = −11.1 cm⁻¹, x₁₃ = −26.9 cm⁻¹).¹⁷ The way this coupling reveals itself in the vibrational spectra is shown by the superimposed combs in Fig. 2.

Fig. 2 Transient vibrational absorption spectra of the antisymmetric stretch vibration (ν₃) of NO₂ X²A₁ produced from N₂O₄ photolysis at 340 nm in a liquid solution of CCl₄ (top) and perfluorodecalin (bottom). Excitation of the symmetric stretch (ν₁) and bend (ν₂) modes can also be observed due to anharmonic coupling with ν₃. The combs identify the absorption bands corresponding to NO₂ molecules with different degrees of excitation in the three vibrational modes. The inset shows schematically how N₂O₄ dissociation produces two NO₂ molecules with different electronic and vibrational character, labelled as NO^α₂ and NO^β₂ in the main text.

Fig. 2 shows transient vibrational spectra of the NO₂ antisymmetric stretch as a function of pump–probe delay time after the photolysis of N₂O₄ at 340 nm in CCl₄ and perfluorodecalin solutions. The initial internal energy of the NO^α₂ fragment can be clearly observed from the breadth of the dark blue 0.5 ps trace, and is well described by a 1350 K Boltzmann vibrational distribution across all three vibrational modes. The initial distribution is not dependent on the choice of solvent, indicating the solvent environment has little effect on the N₂O₄ dissociation dynamics. The NO^β₂ fragment is not observed until after it internally converts to high vibrational levels of the X²A₁ state and subsequently cools to ν₃ ≤ 7 (levels with ν₃ ≤ 4 are revealed in the spectral region presented in Fig. 2). This delayed observation is especially evident in the perfluorinated solvents, where the signal from this fragment moves into the spectral window from the low wavenumber side as a localized envelope of absorption signal (see ESI‡ for animated transient spectra in all solvents, and for spectra showing the earlier time cooling among higher vibrational levels in the region to lower wavenumber).

Vibrational relaxation in the X²A₁ state

After pump–probe time delays Δt > 150 ps, both NO₂ fragments are sufficiently vibrationally relaxed that their combined spectral contributions can be described by a Boltzmann distribution of NO₂ vibrational state populations. In all solvents, the spectra reveal that the populations of the ν₁ and ν₃ vibrational modes evolve concurrently, indicating that intramolecular vibrational redistribution (IVR) between the two stretching modes is faster than the dissipation of vibrational energy to the solvent. Fig. 2 shows that the signal attributable to population in ν₂ = 1 at 1590 cm⁻¹ in CCl₄ rapidly disappears; however, it persists as a shoulder on the ν₃ = 1 ← 0 absorption feature in perfluorodecalin for 100 s of ps demonstrating that population in the NO₂ bending mode evolves on different timescales in different solvents. The populations of the various vibrational levels within each mode are always well-described by a Boltzmann distribution of states after Δt > 150 ps, and all subsequent Δt spectra could be reproduced with a simple model where the vibrational temperatures of the ν_1,3 and ν₂ modes were the only variables. The thermalization within each mode provides an important constraint when extracting state populations from the transient spectra, which are otherwise underdetermined for transitions in the 1480–1560 cm⁻¹ spectral range where the density of spectral transitions becomes large.

Each transient spectrum after Δt = 150 ps was simulated with a best-fit model spectrum, in which the only adjustable parameters were the Boltzmann temperatures for the stretching and bending modes. The anharmonically coupled transition wavenumbers were calculated under the assumption that the gas-phase x_e values did not change in solution, but the central wavenumber of the ν₃ = 1 ← 0 transition was shifted to match the observed experimental wavenumber in each solvent (Fig. 1). The intensity of each ν(n₁, n₂, n₃) → ν(n₁, n₂, n₃ + 1) transition (with n₁, n₂, n₃ denoting numbers of quanta of the three modes) was set to depend on the difference in population between the ν(n₁, n₂, n₃) and ν(n₁, n₂, n₃ + 1) states, to include the balance of absorption and stimulated emission. Each transition intensity was further scaled by a factor of n₃ + 1, to account for the predicted linestrength enhancement from vibrational excitation in a harmonic oscillator.¹⁸ This manner of calculating the transition strengths accurately predicts an integrated intensity from the simulated fit of the initial spectrum (only NO^α₂) that is equal to half that of the fully relaxed spectrum at Δt = 1200 ps (by which time the NO^α₂ + NO^β₂ fragments are both contributing to the observed spectrum in equal numbers).

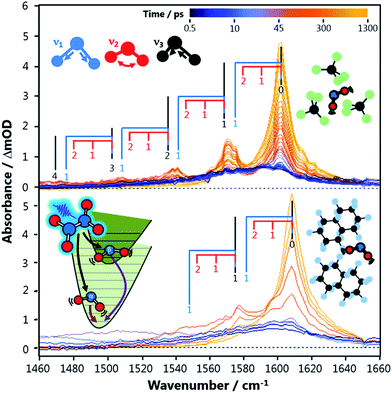
The resulting vibrational temperatures from the best-fit simulations are shown in Fig. 3. The temperature of each vibrational mode in each solvent is observed to cool exponentially in time, as evidenced by the linear slopes of the ln(T_vib − 293) vs. Δt plots. An analysis of the NO₂ stretch vibrational relaxation as a function of N₂O₄ concentration is provided in the ESI.‡ The vibrational temperatures presented in Fig. 3 were observed at N₂O₄ concentrations on the order of 200 mM in each solvent, and are found to be only weakly concentration dependent. Hence, semi-quantitative comparisons can be drawn between NO₂ vibrational temperature relaxation time coefficients in the different solvent environments. NO₂ bend relaxation in the three chlorinated solvents does not appear on the plot as all excitation in this mode is completely thermalized to 293 K before Δt = 150 ps. A relaxation time constant of τ_b ∼ 20–50 ps is estimated for this process based on the earlier Δt spectra.

Fig. 3 The NO₂ vibrational temperature (T_vib), extracted from modelling the transient vibrational spectra as a function of pump–probe delay time, plotted using a ln(T_vib − 293) scale. The slopes of the best-fit lines yield the vibrational temperature relaxation rate coefficients of the modes in parentheses for the indicated solvents. The time constants τ are reciprocals of these rate coefficients. NO₂ vibrational temperatures obtained in each PFC solvent are represented by different symbols, but show the same behaviour and thus are fit with a single line. Only spectra with Δt > 150 ps were used for this analysis, when the vibrational populations have thermalized sufficiently to be well-described by a Boltzmann distribution of states. The error bars represent the range of T_vib that result in a residual sum of squares between the experimental and model spectrum less than double the best-fit minimum value.

Despite differences in solvent molecular structure, the vibrational relaxation timescales found in the three PFC environments are the same. The significance of the identical NO₂ bend relaxation time in the three PFC solvents (τ_b = 127 ps) is first considered. The IR absorption spectra of the three solvents are very different in the 700–750 cm⁻¹ range corresponding to intervals between NO₂ bending levels. The relative integrated absorptions of perfluorohexane, perfluoromethylcyclohexane, and perfluorodecalin respectively are: 1, 0.4, and 0.12 in this wavenumber interval (or 0.67, 1, 0.37 if the range is extended to 650–800 cm⁻¹). The large differences in integrated absorption are at odds with the small difference between ν₂ relaxation rates in the three solvents, implying Förster coupling has a negligible effect on this relaxation. Attractive forces in the PFCs are weak, and thus direct anharmonic coupling is not expected to be significant either. Thus we deduce that NO₂ bend energy is transferred to the perfluorinated solvents primarily through impulsive interactions. It is anticipated that this energy is transferred to non-vibrational degrees of freedom (V-T), since the rate is independent of the solvent's total number of vibrational modes and the density of vibrational states in the 700–750 cm⁻¹ range. The energy transfer timescale can be fully explained by the local, repulsive potential energy surfaces of the solute–solvent collisions, which are similar in all three solvents.

Assuming the impulsive model is applicable to all NO₂ (ν) in perfluorinated solvents, the relaxation rates of the higher frequency NO₂ stretching modes can be predicted using semi-classical theories. Landau–Teller theory, which describes a quantum oscillator in a classical bath, predicts the vibrational relaxation time τ to be directly proportional to the frequency of the oscillator ω.¹ Therefore, the ratio of the NO₂ bend to stretch frequency should give the ratio of their relative relaxation times. The lower ν₁ stretch frequency is used in this analysis because IVR between ν₁ and ν₃ is rapid. This comparison predicts a stretch relaxation time of 225 ps, which is almost exactly what is observed experimentally (τ_s = 217 ps). So, despite the PFCs having a number of intense IR transitions throughout the 1250–1350 cm⁻¹ range, the relaxation time does not appear to be accelerated by these vibrational resonances. Thus, NO₂ stretch energy is also shown to be lost through impulsive interactions and dissipated to non-vibrational degrees of freedom (V-T) in the PFC solvents.

NO₂ relaxation in chlorinated solvents is a completely different story. First, it is clear that energy transfer through impulsive interactions is much less efficient than in PFCs. The fastest vibrational energy transfer pathway available for the NO₂ stretch in CCl₄ and CDCl₃ is ∼900 ps, much longer than in the perfluorinated solvents. This is qualitatively expected since the chlorine atoms have a softer repulsive interaction than fluorine atoms. The much faster relaxation of the NO₂ stretch in CHCl₃ (τ_s = 252 ps) compared to CDCl₃ (τ_s = 1060 ps), however, is unambiguous evidence of a resonant vibrational enhancement. The C–H bend wavenumber (1220 cm⁻¹) in CHCl₃ is nearly resonance with the NO₂ν₁ fundamental transition (1320 cm⁻¹), while the C–D bend mode is red-shifted (907 cm⁻¹). The resonant effect between NO₂ and CHCl₃ occurs even with a vibrational energy mismatch of 100 cm⁻¹, and thus coupling to other solvent degrees of freedom may be important in helping bridge this energy gap.

The NO₂ bend relaxation (20 ps < τ_b < 50 ps) in chlorinated solvents must also be resonantly enhanced, since this timescale is faster than predicted by the stretch: bend frequency ratio and over four times as fast as in the PFCs. All of the chlorinated solvents have an intense IR absorption from a C–Cl_n stretching vibration near-resonant with the NO₂ bend mode in the vicinity of 750 cm⁻¹, and thus Förster coupling may be significant. The integrated absorption intensity of this band in CHCl₃ is nearly 10 times larger than that of the 1210 cm⁻¹ band that is near-resonant with the NO₂ stretch, consistent with the relative ν₂ and ν_1,3 relaxation rates in this solvent and the predictions of Förster theory.

The relaxation of thermally excited NO₂ formed through the UV photodissociation of N₂O₄ can be directly compared to the relaxation timescale of NO₂ prepared (by IR excitation) with a single quantum of antisymmetric stretch vibration. The majority of the excited population with ν₃ = 1 relaxes with a significantly smaller time constant in CCl₄ (62 ± 10 ps), CHCl₃ (23 ± 2 ps) and CDCl₃ (24 ± 3 ps) than observed for the final ν_1,3ν = 1 → ν = 0 step of NO₂ formed through UV photodissociation of N₂O₄ after all higher vibrational levels have relaxed (>1 ns, 180 ps, and >1 ns in the three respective solvents) – see ESI.‡ The apparent discrepancy in these ν_1,3ν = 1 → ν = 0 vibrational relaxation times measured in chlorinated solvents is not seen when using the PFC solvents. Instead, the final ν_1,3ν = 1 → ν = 0 relaxation of NO₂ from UV photodissociation of N₂O₄ in a PFC solvent occurs with a time constant (120 ± 30 ps) similar to that (89 ± 7 ps) measured for the relaxation of the NO₂ (ν₃ = 1) molecules prepared by direct IR excitation.

Most of the UV photon energy (29 400 cm⁻¹) used to dissociate N₂O₄ must be taken up by the solvent molecules in close proximity to the photoexcited solute, resulting in a significant increase in local temperature. Vibrational relaxation is typically accelerated by higher temperature due to increased occupancy of bath modes.^11,19 However, solute–solvent intermolecular interaction potentials which facilitate solute cooling through anharmonic coupling can be overcome by excess solute or solvent internal energy, thereby increasing the timescale for solute vibrational relaxation.¹¹ NO₂ induces a dipole–dipole interaction with the polarizable CCl₄, and can interact with the permanent dipole moment of CHCl₃. Quantum mechanical calculations predict NO₂–CCl₄ and NO₂–CHCl₃ complexes with intermolecular well depths of a few hundred wavenumbers (cm⁻¹) – see ESI.‡ These attractive interactions between NO₂ and chlorinated solvents are easily disrupted by the thermal energy released during the photodissociation of N₂O₄ and subsequent vibrational relaxation of NO₂ molecules, which inhibits an efficient pathway for solute-to-solvent vibrational energy transfer until the initially hot NO₂ and its local solvent shell have cooled sufficiently to associate into complexes. The long cooling timescales suggest the energy released by N₂O₄ photolysis significantly distorts the local solvent environment, resulting in energy relaxation pathways which are less effective than those that dominate the more weakly perturbing IR-pump measurements. The relaxation of IR-excited NO₂ is instead controlled by the intermolecular interactions within NO₂-solvent complexes. Analogous complexes in PFC solvents will only be very weakly bound because of the lower solvent polarizabilities, and are unlikely to contribute significantly to vibrational cooling rates.

Relaxation of the NO^β₂ fragment

The signal contributions from initially generated NO^α₂ and NO^β₂ fragments can be separated using the vibrational relaxation rates obtained from Fig. 3. The NO^α₂ fragment accounts for the entire signal in the spectral window at Δt < 5 ps, and is generated with a vibrational temperature of 1350 K. This distribution was simulated in the same manner as in the previous section, but instead of optimizing the vibrational temperatures at each Δt to find the best fit, the vibrational temperatures were fixed to relax with the time constants acquired from Fig. 3. The signal arising from the NO^β₂ state fragment was then obtained from the difference between the experimental transient absorption signal and this fixed simulation (Fig. 4). The tiny bleach evident at 1610 cm⁻¹ in the transient spectra recorded at Δt < 100 ps arises from the 340 nm photolysis of some of the small amount of NO₂ that is present in the sample in equilibrium with N₂O₄. The NO^β₂ fragment signal can first be observed after Δt = 5 ps in the PFC solvents, as a localized envelope of absorption signal at the low wavenumber end of the spectral window of Fig. 4 (around the ν₃ = 7 → 8 transition). The NO^β₂ fragment signal also appears after Δt = 5 ps in chloroform and CCl₄, but the broad signal packet rapidly localizes into stretching vibrational modes due to the much faster bend relaxation rates. Transient absorption data showing the signal packet to lower wavenumbers (for higher vibrational levels) in chlorinated solvents are presented in the ESI.‡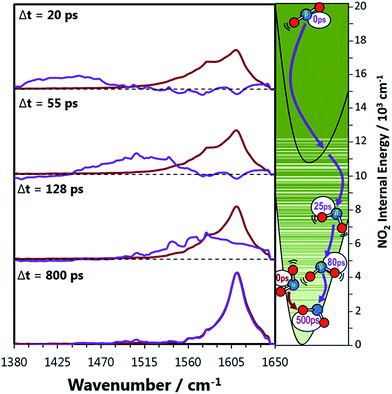

Fig. 4 Decomposed transient vibrational spectra of the two NO₂ product fragments in perfluorohexane. The red lines represent NO^α₂ which is produced immediately with a thermal population of vibrational states described by a 1350 K Boltzmann distribution. The vibrational populations are simulated to evolve exponentially in time with the relaxation time constants obtained from Fig. 3. The difference between the experimental transient spectra and this simulation are shown as the purple lines, which represent the signal contribution from the NO^β₂ fragments. The right hand panel represents the two NO₂ fragments relaxing to the ground state where the solid green lines are vibrational energy levels of NO₂. These lines demonstrate how the vibrational levels of NO₂ become a near continuum above the A state minimum.

From the energy of the 340 nm photon (29 400 cm⁻¹), the N–N bond strength in N₂O₄ (4500 cm⁻¹),²⁰ and the average vibrational energy of the NO^α₂ fragment observed (〈E_vib〉 = 2815 cm⁻¹ at 1350 K) the internal energy of the NO^β₂ fragment is estimated to be at most 22 000 cm⁻¹. This value is consistent with the shortest wavelengths observed from fluorescence measurements of gas-phase N₂O₄ photolysis products.⁴ These fluorescence experiments measured an internal energy distribution peaked at approximately 19 000 cm⁻¹ for this fragment, corresponding to A²B₂ state NO₂ (T₀₀(A–X) = 9710 cm⁻¹) born with ∼10 000 cm⁻¹ of vibrational energy. The A²B₂ state is strongly coupled to the X²A₁ state which leads to long radiative lifetimes in a collisionless environment, but internally converts to high vibrational levels of the X²A₁ state after only a few collisions in the gas phase.²¹ Gas-phase thermal lensing measurements of excited NO₂ colliding with atomic gases (and thus only sensitive to V-T energy transfer), and further IR emission measurements,⁸ found that the vibrational relaxation rate of NO₂ is considerably faster when it contains >10 000 cm⁻¹ of vibrational energy. The authors attributed this enhanced energy transfer to larger amplitude vibrations arising from the mixed electronic character of the molecule above the A²B₂ state threshold.

The gas phase picture is consistent with the observations in solution, which imply rapid transfer of >7000 cm⁻¹ of vibrational energy to the solvent bath in the first 5 ps after dissociation. The highest X state vibrational level observable in the probe window of Fig. 4 is ν(0, 0, 7) with 11 950 cm⁻¹ of vibrational energy, just above the A state threshold. NO^β₂ further relaxes below the A state threshold populating ν(0, 0, 5) by 10 ps, after which considerable diversity in vibrational relaxation timescales is observed between different solvents. The mixing of the X and A electronic states results in a high density of vibrational levels, which favours semi-classical energy transfer dynamics. We propose that both the large amplitude motions associated with vibrational levels with character typical of a polyatomic molecule high in its ground electronic state potential, and the quasi-continuum of NO₂ vibrational levels, will promote efficient energy transfer through hard collisions. Consequently, the relaxation rates are similar in all of the solvents up to 10 ps, with V-T energy transfer through impulsive interactions providing the dominant energy transfer mechanism in all solvents when NO^β₂ has >10 000 cm⁻¹ of internal energy. This energy transfer mechanism is the least efficient in CCl₄, as the appearance of the NO^β₂ fragment signal within our observation window is delayed by ∼5 ps compared to the other solvents.

Conclusions

The detailed relaxation dynamics of both NO₂ fragments resulting from N₂O₄ photolysis in solution have been observed using transient vibrational absorption spectroscopy. The NO^β₂ fragment is produced with nearly 20 000 cm⁻¹ of internal (vibronic) energy, the first 10 000 cm⁻¹ of which is dissipated to the solvent bath via impulsive interactions within the first 10 ps (15 ps in CCl₄) after its formation. Once the internal energy of NO^β₂ drops below the A²B₂ state threshold, the relaxation rate slows dramatically and the bending and stretching modes relax independently and through mechanisms which are highly solvent dependent. The ν₁ and ν₃ stretching modes are coupled, and the energy of the high frequency ν₃ mode appears to be funnelled out of the molecule through ν₁ relaxation in most cases.

NO₂ vibrational relaxation rates in perfluorohexane, perfluoromethylcyclohexane, and perfluorodecalin are nearly identical and are governed by impulsive V-T interactions with the solvent. The relative relaxation rates of the bending and stretching modes of NO₂ match their relative frequencies, consistent with semiclassical theories of quantized cooling in a classical bath.

Below the A²B₂ state threshold, NO₂ relaxation through impulsive V-T interactions becomes inefficient in the chlorinated solvents. Vibrational resonances become important, leading to rapid bend relaxation in all three chlorinated solvents, and faster stretch relaxation in chloroform where the C–H bend vibrational frequency is near resonant with the NO₂ symmetric stretch. The relative relaxation rates of the bending and stretching modes are consistent with expectations from Förster theory, however, rapid cooling of vibrational energy through anharmonic coupling to the chlorinated solvents at room temperature is impeded by solvent heating.

These detailed observations regarding the solvent-dependent relaxation mechanisms of NO₂ provide a benchmark against which theoretical models can be tested. In turn, these models will provide better understanding of how the excess energy released by exothermic reactions dissipates in a solvent, and whether it influences branching between competing product channels.

Experimental section

Vibrational transient absorption spectra were collected using the ultrafast laser system at the University of Bristol.²² All chemicals were sourced from Sigma-Aldrich. N₂O₄ solutions were prepared in perfluorohexane (99%), perfluorodecalin (95%), perfluoromethylcyclohexane (90%), carbon tetrachloride (≥99.9%), chloroform (≥99%), and d-chloroform (99.8% D) by bubbling NO₂ (≥99.5%) through the pure solvents. The solvents were degassed prior to bubbling by a freeze–pump–thaw method using liquid nitrogen. N₂O₄ was photolysed using a 340 nm pump pulse of approximately 120 fs duration and 1 μJ of energy with a repetition frequency of 500 Hz. A broad band (300 cm⁻¹) IR pulse was used to probe the samples at 1 kHz and then focused onto a 128 element array detector. The pump–probe time delay was varied using a motorized translation stage while the sample was circulated through a PTFE cell with CaF₂ windows and a 250 μm path length using a peristaltic pump. The wavelength scales of the transient vibrational absorption spectra were calibrated using a sample of (E)-stilbene. Steady state IR spectra were obtained using a Perkin-Elmer Spectrum II ATR-FTIR spectrometer, and steady state UV-vis spectra were acquired using a Thermo Scientific GENYSIS spectrophotometer. Approximate concentrations of N₂O₄ were determined to be on the order of 200 mM from steady state UV-vis spectra, using gas-phase absorption cross-sections.^11,23 Density functional theory and MP2 calculations of the CHCl₃–NO₂ and CCl₄–NO₂ complexes were performed in Gaussian 09.²⁴

Acknowledgements

AJOE is grateful to the ERC for the award of Advanced Grant 290966 CAPRI, and both MNRA and AJOE thank the EPSRC for the award of a Programme Grant (EP/L005913). MPG was supported by a Marie Curie International Incoming Fellowship (PIIF-GA-2012-326988).

Notes and references

1. J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Annu. Rev. Phys. Chem., 1994, 45, 519–555.
2. J. L. Skinner, Theor. Chem. Acc., 2011, 128, 147–155.
3. Y. Q. Deng and R. M. Stratt, J. Chem. Phys., 2002, 117, 1735–1749.
4. W. N. Sisk, C. E. Miller and H. S. Johnston, J. Phys. Chem., 1993, 97, 9916–9923.
5. S. R. J. Brueck and R. M. Osgood, Chem. Phys. Lett., 1976, 39, 568–572.
6. P. Hess and C. B. Moore, J. Chem. Phys., 1976, 65, 2339–2344.
7. A. Pigliucci, G. Duvanel, L. M. L. Daku and E. Vauthey, J. Phys. Chem. A, 2007, 111, 6135–6145.
8. G. V. Hartland, D. Qin and H. L. Dai, J. Chem. Phys., 1994, 100, 7832–7835.
9. D. J. Nesbitt and J. T. Hynes, J. Chem. Phys., 1982, 76, 6002–6014.
10. R. N. Schwartz and K. F. Herzfeld, J. Chem. Phys., 1954, 22, 767–773.
11. S. Woutersen, U. Emmerichs, H. K. Nienhuys and H. J. Bakker, Phys. Rev. Lett., 1998, 81, 1106–1109.
12. D. Qin, G. V. Hartland and H. L. Dai, J. Phys. Chem. A, 2000, 104, 10460–10463.
13. G. V. Hartland, D. Qin and H. L. Dai, J. Chem. Phys., 1994, 101, 8554–8563.
14. B. H. Mahan, J. Chem. Phys., 1967, 46, 98–101.
15. W. M. Haynes, CRC Handbook of Chemistry and Physics, 96th edn, 2015.
16. M. P. Grubb, P. M. Coulter, H. J. B. Marroux, B. Hornung, R. S. McMullan, A. J. Orr-Ewing and M. N. R. Ashfold, Nat. Chem., 2016, 8, 1042–1046.
17. A. Delon and R. Jost, J. Chem. Phys., 1991, 95, 5686–5700.
18. P. Hamm and M. T. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, New York, 2011.
19. A. Tokmakoff, B. Sauter and M. D. Fayer, J. Chem. Phys., 1994, 100, 9035–9043.
20. F. R. Ornellas, S. M. Resende, F. B. C. Machado and O. Roberto-Neto, J. Chem. Phys., 2003, 118, 4060–4065.
21. B. M. Toselli, T. L. Walunas and J. R. Barker, J. Chem. Phys., 1990, 92, 4793–4804.
22. G. M. Roberts, H. J. B. Marroux, M. P. Grubb, M. N. R. Ashfold and A. J. Orr-Ewing, J. Phys. Chem. A, 2014, 118, 11211–11225.
23. S. P. Sander, R. R. Friedl, J. P. D. Abbatt, J. R. Barker, J. B. Burkholder, D. M. Golden, C. E. Kolb, M. J. Kurylo, G. K. Moortgat, P. H. Wine, R. E. Huie and V. L. Orkin, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation Number 17, JPL-2010, 2011.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford CT, 2016.

---

Footnotes

† All experimental data are archived in the University of Bristol's Research Data Storage Facility (DOI: 10.5523/bris.2vk036f35m5aq2dnlb79c0wcsh).

‡ Electronic supplementary information (ESI) available: Further discussion of spectral lineshapes, concentration dependence of transient absorption data, theoretical calculations, IR-pump IR-probe spectra, transient absorption spectra including animation of spectra. See DOI: 10.1039/c6sc05234g

---