Modeling of the formation kinetics and size distribution evolution of II–VI quantum dots†
Stefano
Lazzari
 a,
Milad
Abolhasani
a,
Milad
Abolhasani
 ab and
Klavs F.
Jensen
ab and
Klavs F.
Jensen
 *a
*a
aMassachusetts Institute of Technology, Department of Chemical Engineering, 77 Massachusetts Avenue, 02139, Cambridge, MA, USA. E-mail: kfjensen@mit.edu
bDepartment of Chemical and Biomolecular Engineering, North Carolina State University, Raleigh, NC 27695-7905, USA
First published on 13th June 2017
Abstract
A deterministic model based on population balance equations is developed to describe the formation of II–VI semiconductor nanocrystals. After deriving the necessary equations and reviewing the link between model predictions and experimental results, a parametric study is carried out to showcase the model's features. A comparison with literature experimental data shows how the present model can satisfactorily describe average properties of the colloidal semiconductor nanocrystals such as the average diameter or the distribution width. This model represents a first step towards the development of more refined models that would open up the possibility of improved optimization and control of the nanocrystal production process.
1 Introduction
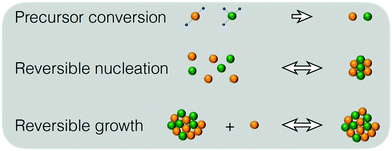
Semiconductor nanocrystals, often referred to as quantum dots (QDs), have received increasing attention from the scientific community in the last few decades because of their unique physicochemical properties.1–3 Their size-dependent optical and electronic properties resulting from quantum confinement make them useful in a wide range of applications, including photovoltaics, LED displays, and bio-imaging.4,5 As a result, the market share of QDs is expected to reach US$ 5 billion in 2020.6 Over the past 3 decades, researchers have developed colloidal synthetic routes for the controlled synthesis of semiconductor nanocrystals.1,7 Nevertheless, a detailed understanding of the nucleation and growth stages of nanocrystals is still missing for optimization and control of QD production processes.1,2,8 Detailed kinetic models and the corresponding kinetic rate constants would be particularly useful.Although QDs of a given average size can be produced with a certain precision, predicting their polydispersity or size distributions is still very challenging.1 No universally accepted model describing the QD formation exists owing to the complex process underlying the QD formation, including a) the decomposition of the so-called precursor molecules, forming free monomers, b) the nucleation of several monomers to form nuclei, and c) the reversible growth of nanoparticles by incorporating free monomers that give rise to a size distribution. This process is further complicated by the role of surface ligands that stabilize the QDs and by ripening phenomena occurring at later stages of the reaction.1,2 Moreover, unexpected high-concentration phenomena affecting the QD size distribution have been recently reported.9 Brauser et al.8 proposed an approach to estimate thermodynamic and kinetic properties relevant to low-temperature synthesis of QDs, further highlighting the need of controlling the QD production process.8 At the same time, the development of a comprehensive model applicable to different stages of the synthesis of QDs ranging from the precursor molecules up to the full nanocrystal size distribution still remains elusive. Without a quantitative comparison between experimental observations (e.g. size distributions and concentrations) and model predictions, little can be done to systematically control product quality.
The first deterministic model attempting to describe the kinetic evolution of the complete nanocrystal size distribution, and not only of average properties, was reported by Rempel et al. in 2009.10 Their model, based on population balance equations (PBEs), accounts for growth and dissociation while combining precursor conversion and nucleation. It was demonstrated that the QD growth process was reaction controlled and not diffusion controlled.10 Recently, the same model has been modified by the deMello group to describe the formation of CdSe QDs.11 In particular, they included a step accounting for the diffusion of monomers towards the QD surface. Notably, the latter step turned out to be always extremely fast, thus shifting their model to a purely reaction-controlled one. Their comparison with experimental data showed an excellent accordance in describing the time evolution of the QD average diameters,11 but no comparisons with experimental distribution widths or shapes were provided.11 Infinite distributions can be constructed with the same average size, but exhibit completely different concentrations, shapes and polydispersities.
Therefore, the present work aims to develop a deterministic model (based on PBEs) to quantitatively describe the time evolution of several properties of the QD size distribution, such as concentration, average diameter and polydispersity. The model is validated against an experimental data set of CdSe QDs, synthesized using a recently developed, well-controlled oscillatory microfluidic reactor.12
2 Kinetic scheme, model equations and rate constants
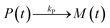
It is currently well understood that the formation of quantum dots is mediated by nucleation and growth mechanisms.1,2 For nucleation to occur, precursor molecules (P) are typically heated up and become monomers (M). Once the concentration of monomers overshoots their solubility in solution (M0), i.e. the supersaturation S = M/M0 > 1, nucleation occurs and the smallest sized QDs are formed. From these nuclei, larger QDs are obtained through a growth mechanism that incorporates free monomers.1 Besides these phenomena, experimental studies report that a dissociation or dissolution step also occurs,13 indicating that the aforementioned growth and nucleation phenomena are reversible processes. Ostwald ripening phenomena are also known to occur, but only at time scales well beyond those of typical reaction times.14 Therefore, Ostwald ripening will not be considered in this model. The implementation of Ostwald ripening in the frame of PBEs has been discussed in the context of ZnO QDs by Segets et al.15 and in the more general perspective of crystallization by Vetter et al.16Here we develop a deterministic model to predict the evolution of the size distribution of QDs. Q(x,t)dx is the number concentration of QDs with sizes of between x and x + Δx at time t. Note that x here is a dimensionless mass, indicating the number of monomers M that constitute the x-sized QDs. It is then possible to write the following kinetic scheme:
 | (1) |
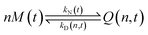 | (2) |
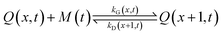 | (3) |
In the above scheme, kN(t) is the time-dependent nucleation rate constant, while kG(x,t) and kD(x,t) are the size- and time-dependent growth and dissociation kinetic constants, respectively. Note that n represents the number of monomers M that constitute the nuclei. In other words, the smallest sized QDs are the nuclei, whose number concentration is represented by Q(n,t). As already assumed by Rempel et al.,10 growth and dissociation phenomena are expected to be dependent upon the size (or the mass) of the involved QDs. A time dependency has been considered in the present case too, as it is known that crystallization rates are a function of the time-dependent free monomer concentration. The precursor to the monomer reaction is assumed to be of first order, with kinetic constant kP, as reported by Liu et al.17 A further model assumption typical of PBE-based models10,11 is that different precursor molecules are treated as the same, generic species P. This simplifying assumption could be relaxed as more information on different precursor reactivities becomes available. A synoptic sketch of the kinetic scheme considered is given in Fig. 1. The corresponding population balance equations, written for a well-mixed, isothermal batch reactor, read:
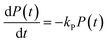 | (4) |
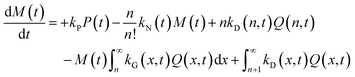 | (5) |
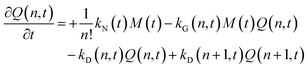 | (6) |
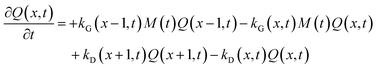 | (7) |
The species initial concentrations are all equal to zero at t = 0, apart from the precursor P, for which P(t = 0) = P0. Note that the prefactor 1/n! in eqn (5) and (6) is necessary to properly count the combination of monomers leading to the formation of nuclei. Additionally, the nucleation rate in eqn (5) is multiplied by n in order to consider the number of monomers lost in a nucleation event. To solve the above reported model (eqn (4)–(7)) the knowledge of kinetic rate constants kN(t), kG(x,t), and kD(x,t) is needed.
Many researchers have been using expressions for kN(t) derived from the classical nucleation theory (CNT).2 Using the CNT would imply using 3 parameters to describe the nucleation, a prefactor, the interfacial surface tension and the monomer solubility. To reduce the number of unknown parameters, we have decided to employ a simple time-dependent expression that reads:
| kN(t) = kN,0e−κNt | (8) |
The latter expression allows one to describe nucleation with 2 parameters only, a prefactor kN,0 and an exponent κN. Assuming a simply decaying exponential for the nucleation rate implies a very fast nucleation rate at the beginning of the reaction. Moreover, this rate decreases with a characteristic time τN = 1/κN. Note that a simple first-order dependence on the monomer concentration has been assumed (cf.eqn (5) and (6)), in agreement with literature expressions.2 As a result, the nucleation rate, rN, reads:
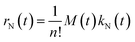 | (9) |
The growth process is known to be a second-order reaction, involving a QD of generic size Q(x,t) and a monomer, M. Moreover, it has been shown to be reaction-limited10 and time-dependent.1,2 It has been further hypothesized that the growth rate depends on the size of the growing QDs.10 Therefore, kG(x,t) should be a function of a time-dependent function, fG(t), and a mass-dependent one, hG(x):
| kG(x,t) = fG(t)hG(x) | (10) |
Following the same reasoning as before, fG(t) has been assumed to be a simply decaying exponential in the form:
| fG(t) = e−κGt | (11) |
As for the size-dependency, we have derived an expression starting from validated kernels employed in colloid science.18 In particular, assuming that the quantum dot Q(x,t) and monomer M are involved in a growing step through a reaction-limited aggregation event, one can write for hG(x):
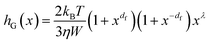 | (12) |
Here kB is the Boltzmann constant, T is the temperature, η is the viscosity of the continuous medium, and W is the Fuchs stability ratio.18 Note that df is the fractal dimension, a measure of the compactness of the colloidal entity19 and λ is typically considered a fitting parameter.20 As QDs are known to be approximately growing as compact spheres, the fractal dimension has been assumed to be df = 3. Employing the df to describe the QD compactness naturally allows extending the current model towards systems where aggregation and growth occur simultaneously, giving rise to fractal structures.21 The exponent λ instead has been said to be related to the number of units present in the outer shell of the colloidal entity22 and therefore has been set to λ = 2/3 given the spherical nature of QDs. The resulting expression for hG(x), lumping the prefactors in the constant kG,0, reads then:
| hG(x) = kG,0(2x2/3 + x1/3 + x) | (13) |
Fig. 2 shows how hG(x) scales with the mass x of the QDs: the larger the QD, the faster the growth process.
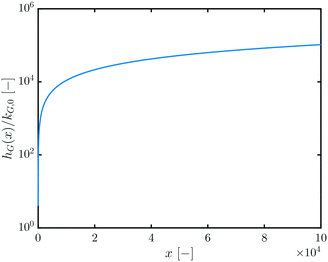 | ||
| Fig. 2 h G(x)/kG,0vs. x. Cf.eqn (13). | ||
Substituting then eqn (11) and (13) in eqn (10), the employed growth rate constant can be calculated as:
| kG(x,t) = kG,0(2x2/3 + x1/3 + x)e−κGt | (14) |
The corresponding total growth rate, rG, reads:
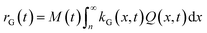 | (15) |
Also, the dissociation rate constant is expected to be size and time dependent:
| kD(x,t) = fD(t)hD(x) | (16) |
The time-dependency has been assumed to be a simple positive exponential in the form:
| fD(t) = kD,0eκDt | (17) |
The underlying assumption in eqn (17) is that along the QD formation process the free monomer in solution will decrease, thus facilitating the release of monomer units from a QD (cf.eqn (3)), allowing for progressively more dissociation to occur. As for the mass dependency, it has been assumed to be in the form:
| hD(x) = xεD | (18) |
| kD(x,t) = kD,0eκDtxεD j > n | (19) |
The exponent εD was set to 2/3 in the work by Rempel et al.10 and subsequently by Maceiczyk et al.,11 arguing that the dissociation is a monomolecular, surface-dependent event. The larger the surface of the QDs, the larger the number of monomers M that detach from the QD surface. At the same time, this assumption does not take into account that smaller QDs are less stable than larger ones, as reported in the literature.23,24 For this reason, the exponent has been left as a further fitting parameter.
To visualize the impact of εD, the function hD(x) (cf.eqn (18)) has been plotted against x for different values of εD in Fig. 3. Fig. 3 shows how for εD = 0 all QDs dissociate the same way, disregardful of their size. For εD > 0, larger QDs tend to dissociate faster than smaller ones, and vice versa for εD < 0. Negative values of εD will therefore lead to a focusing of the distribution, as smaller QDs will become even smaller, releasing monomer in the solution that can be incorporated by larger ones. The same cannot be said for positive values of εD, as growth is assumed to be faster for larger QDs (cf.Fig. 2).
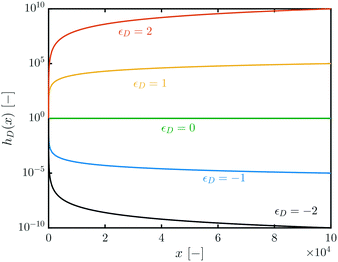 | ||
| Fig. 3 h D(x) vs. x for different values of εD. Cf.eqn (18). | ||
These latter considerations, as well as the general expression for the dissociation rate constant (cf.eqn (19)), are considered to be applicable to all QDs of sizes x > n. The nuclei, Q(n,t), are considered to dissociate with a different pre-factor, given that their dissociation does not correspond to a reversible growth, but to the release of n monomers in solution (cf.eqn (2)). Therefore, the dissociation rate constant of nuclei, kD(n,t), reads:
| kD(n,t) = kD,nuceκDtnεD | (20) |
The corresponding overall dissociation rate, rD(t), is defined as:
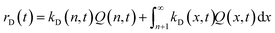 | (21) |
Using the kinetic constants reported in eqn (8), (14), (19) and (20) in the balances (4)–(7), it is possible to follow the time-evolution of the entire QD size distribution. The main differences between this model and the previously published ones by Rempel10 and its modification by Maceiczyk et al.11 are as follows.
1. A nucleation step is explicitly accounted for, distinguishing between precursors (P), monomers (M) and nuclei (Q(n,t)).
2. The rate constants kN(t), kG(x,t), and kD(x,t) are considered to be time-dependent.
3. The mass dependency of the growth rate constant kG(x,t) has been derived from colloid arguments, relating growth to reaction-limited aggregation processes.
4. The mass-dependency of the dissociation rate constant kD(x,t) has been left as a fitting parameter, in the form hD(x) = xε.
Ten model parameters are to be determined for the model (cf.Table 1).
| Reaction | Parameter name |
|---|---|
| Precursor conversion | k P |
| Nucleation | n, kN,0, κN |
| Growth | k G,0, κG |
| Dissociation | k D,0, kD,nuc, κD, εD |
While the number of parameters is large, it should be considered that 5 reactions are being modeled: i) precursor conversion, ii) nucleation, iii) growth, iv) dissociation and v) nuclei dissociation. Of these 5 reactions, the latter 4 are known to be time-dependent. Therefore, the large number of parameters is justified. Notably, many other parameters, such as interfacial tension, ligand equilibria on the QDs, and solvent effects, have been neglected for the sake of simplicity, but will be eventually necessary in a more refined model.
The numerical method used to solve the PBE relies on Gaussian basis functions and has been employed to model several colloid problems.25–28 Details regarding the PBE solution and a full list of the symbols are reported in the ESI† in sections S1 and S5, respectively.
3 Linking experiments and model to the QD size distribution
A crucial step towards the validation of a model is its comparison with experimental data. Therefore, a link between the model predictions and experimental results needs to be established. This section shows how to extract relevant properties of the QD size distribution from the model. Details on how to perform the same task from an experimental perspective are reported in the ESI† (section S2) for the sake of brevity.3.1 Extracting properties from the model
By solving the above reported equation set (4)–(7), one obtains the full mass-based QD size distribution, Q(x,t), at any time t. Being interested in the QD diameter-based size distribution, one needs to switch from one distribution Q(x,t)dx to Q(D,t)dD. Note that Q(D,t)dD represents the concentration of QDs having diameters of between D and D + ΔD, while Q(x,t)dx represents the concentration of QDs having dimensionless masses of between x and x + Δx. Therefore, following the procedure reported by Friedlander,18 one can introduce a given concentration of QDs, dN(t), such that:| dN(t) = Q(x,t)dx = Q(D,t)dD | (22) |
Recalling then that the dimensionless mass x of a cluster and its diameter D are related through:19
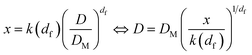 | (23) |
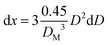 | (24) |
Substituting eqn (24) in eqn (22), and replacing D with its x-based definition (cf.eqn (23)), one gets:
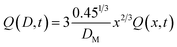 | (25) |
Therefore, after solving the equation set (4)–(7), Q(x,t) and Q(D,t) can be calculated accordingly. Once Q(D,t) is obtained, it is possible to calculate the generic kth moment of the distribution:
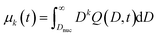 | (26) |
Note that the integration starts at Dnuc, the QD nuclei diameter. It can be estimated that Dnuc = 1.08 nm, knowing that the CdSe nuclei absorption maxima is 348 nm,30 and using the correlation provided by Jasieniak et al.31 that relates absorption maxima and QD sizes. Using the moments of the distribution (cf.eqn (26)), it is possible to define the total concentration of QDs (Ctot,mod(t)), the average diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) mod(t), and the variance of the distribution, σ2D,mod(t):
mod(t), and the variance of the distribution, σ2D,mod(t):
| Ctot,mod(t) = μ0(t) | (27) |
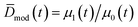 | (28) |
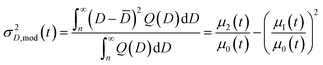 | (29) |
Note that as in previous studies10,11 the size distribution considers only the inhomogeneous broadening caused by varying QD sizes. This is the major factor in the distribution except for nearly monodisperse QDs.
Being now in possession of average properties of the QD size distribution for both model (cf.eqn (25)–(29)) and experiments (cf. ESI† equations S18–S20), it is possible to define the error function minimized during the fitting procedure:
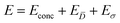 | (30a) |
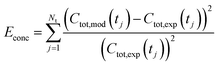 | (30b) |
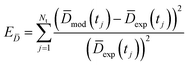 | (30c) |
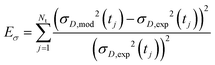 | (30d) |
Notably, using eqn (23), it is possible to establish the size n of the nuclei, therefore reducing the number of parameters to be optimized. In particular, having estimated Dnuc = 1.08 nm, DM = 0.471 nm, df = 3, and k(df = 3), it turns out that n ≈ 6.
4 Results and discussions
Before showing the results of the optimization procedure and elaborating on the performance of the developed model, the model potential is explored through a set of parametric studies.4.1 Parametric studies
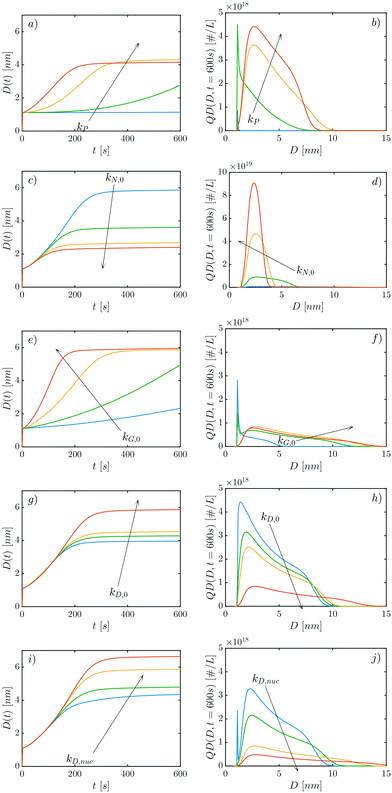
The performed parametric study is aimed at showcasing the model features and the role of the different parameters. After having estimated the nuclei size to be n = 6, there are 9 further parameters to be explored (cf.Table 1), in particular, 5 kinetic rate constants kP, kN,0, kG,0, kD,0, and kD,nuc, 1 exponent characterizing the role of the QDs mass in the dissociation process, εD, and 3 parameters in time-dependent functions, κN, κG, κD.Given the complexity of the model, it is worth exploring the parameters' role in two steps. Initially the values of the parameters κN, κG, κD are set equal to zero, so as to observe the model behavior without considering time-dependent rates. Also, the exponent εD has been kept constant in these first simulations and, in particular, εD = −2. Only in a second step will the role of these parameters be assessed. The properties shown to appreciate the impact of the different parameters are the QD size distribution at a fixed time, QD(D, t = 600 s), and its average size against time, ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) (cf.Fig. 4).
(t) (cf.Fig. 4).
Fig. 4a and b show the impact of kP on the evolution of ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) and Q(D, t = 600 s). For small values of kP, only very small QDs are formed. When increasing the rate of precursor conversion, the following effects are observed: i) the distributions shift to the right, along with their averages, ii) the concentration of QDs increases and iii) the distributions become broader. This trend holds for the first three increases of kP (blue, green and yellow curves), but not for the red curve. A slightly smaller diameter
(t) and Q(D, t = 600 s). For small values of kP, only very small QDs are formed. When increasing the rate of precursor conversion, the following effects are observed: i) the distributions shift to the right, along with their averages, ii) the concentration of QDs increases and iii) the distributions become broader. This trend holds for the first three increases of kP (blue, green and yellow curves), but not for the red curve. A slightly smaller diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) is found at the end of the simulation (cf.Fig. 4a). This difference can be better appreciated when considering the shapes of the yellow and red distributions in Fig. 4b, where a significant shift towards smaller sizes is seen. The reason for this change is reflected by the formation process of QDs (cf.Fig. 1). If more precursor molecules P turn into monomers M, all rates depending on the monomer concentration will increase. Recalling the definitions of rN(t), rG(t) and rD(t) (cf.eqn (9), (15) and (21)), it is evident that both the nucleation and the growth rates increase if more monomer M is available. If more monomer is present, the nucleation rate will be higher and so will the number of available QDs (i.e. the QDs concentration). Moreover, an increased nucleation rate introduces small QDs (of size n = 6) in the system. In contrast, growth will increase the size of all QDs and therefore of the average size. In the case of kP = 10−1 s−1, the growth process stops after about 200 s (cf. red curve in Fig. 4a), implying that no free monomer exists any longer. Hence the monomer is being absorbed by those QDs that nucleated within 200 s of time. In the case of kP = 10−2 s−1 (yellow curves), the average diameter
(t) is found at the end of the simulation (cf.Fig. 4a). This difference can be better appreciated when considering the shapes of the yellow and red distributions in Fig. 4b, where a significant shift towards smaller sizes is seen. The reason for this change is reflected by the formation process of QDs (cf.Fig. 1). If more precursor molecules P turn into monomers M, all rates depending on the monomer concentration will increase. Recalling the definitions of rN(t), rG(t) and rD(t) (cf.eqn (9), (15) and (21)), it is evident that both the nucleation and the growth rates increase if more monomer M is available. If more monomer is present, the nucleation rate will be higher and so will the number of available QDs (i.e. the QDs concentration). Moreover, an increased nucleation rate introduces small QDs (of size n = 6) in the system. In contrast, growth will increase the size of all QDs and therefore of the average size. In the case of kP = 10−1 s−1, the growth process stops after about 200 s (cf. red curve in Fig. 4a), implying that no free monomer exists any longer. Hence the monomer is being absorbed by those QDs that nucleated within 200 s of time. In the case of kP = 10−2 s−1 (yellow curves), the average diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) stops increasing only after 300 s, implying that free monomers exist till that point. This means that QDs may nucleate for a longer time in the case of kP = 10−2 s−1 (yellow curve), as compared to the case of kP = 10−1 s−1 (red curve) As a result, the yellow distribution is more polydispersed and right-shifted than the red one (cf.Fig. 4b).
(t) stops increasing only after 300 s, implying that free monomers exist till that point. This means that QDs may nucleate for a longer time in the case of kP = 10−2 s−1 (yellow curve), as compared to the case of kP = 10−1 s−1 (red curve) As a result, the yellow distribution is more polydispersed and right-shifted than the red one (cf.Fig. 4b).
When the nucleation rate constant kN,0 is increased, more QDs are formed and therefore their average diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) will decrease (cf.Fig. 4c). The corresponding distributions shift to the left (cf.Fig. 4d), exhibiting also a narrowing, as larger quantities of monomer are consumed by nucleation events rather than growth events, limiting the formation of larger sized QDs.
(t) will decrease (cf.Fig. 4c). The corresponding distributions shift to the left (cf.Fig. 4d), exhibiting also a narrowing, as larger quantities of monomer are consumed by nucleation events rather than growth events, limiting the formation of larger sized QDs.
The opposite effect is observed when the growth rate constant kG,0 is increased. The QD distribution shifts to the right and becomes broader (cf.Fig. 4f), while their average diameters ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) increase (cf.Fig. 4e).
increase (cf.Fig. 4e).
Notably, kD,0 and kD,nuc have a comparable effect to that of kG,0, but for very different reasons. When kD,0 and kD,nuc increase, the average QD diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) increases (cf.Fig. 4g and i) and the distributions exhibit a right-shift and become broader (cf.Fig. 4h and j). This result might look counter-intuitive, given that increasing kD,0 and kD,nuc means favoring the reversible growth, penalizing the addition of monomers to QDs towards the formation of larger sized QDs. The latter effect is explained considering that the parameter εD = −2 in all the above simulations. As a result, smaller clusters tend to dissociate faster than larger ones (cf.Fig. 3). The monomer released by the dissociation of smaller clusters is taken up by larger clusters that further increase their size. Overall, this process leads to a right-shift in the distribution.
(t) increases (cf.Fig. 4g and i) and the distributions exhibit a right-shift and become broader (cf.Fig. 4h and j). This result might look counter-intuitive, given that increasing kD,0 and kD,nuc means favoring the reversible growth, penalizing the addition of monomers to QDs towards the formation of larger sized QDs. The latter effect is explained considering that the parameter εD = −2 in all the above simulations. As a result, smaller clusters tend to dissociate faster than larger ones (cf.Fig. 3). The monomer released by the dissociation of smaller clusters is taken up by larger clusters that further increase their size. Overall, this process leads to a right-shift in the distribution.
To further deepen the impact of the remaining parameters, εD, κN, κG and κD, a set of ad hoc simulations have been carried out. These have been reported, for the sake of brevity, in section S3 of the ESI.†
The parametric study (cf.Fig. 4 and Fig. S1 and S2 in the ESI†) showed how intricate a simple kinetic scheme as the one considered in Fig. 1 can be and clarified the relevance of the parameters considered in this model. Notably, very different trends can be reproduced with the present kinetic scheme employed. Besides the growth of QDs through their average diameter, distribution narrowing and broadening, and QD concentration decrease or increase, can also be modeled. In the next section the developed model will be tested against experimental data on CdSe.12
4.2 Case studies
In the present section, model prediction and CdSe experimental data12 are compared. In particular, the data sets corresponding to the CdSe QDs synthesized at 180 °C and 210 °C have been considered. Of the parameters reported in Table 1, the size of the nuclei n was established to be n = 6 (cf. section 3.1). Therefore, 9 parameters need to be determined (cf.Table 1). To fit the parameters, the average properties of the QD size distributions calculated by the model (cf.eqn (27)–(29)) and those obtained experimentally (cf. equations S18–S20 in the ESI†) are compared. In particular, the error function E (cf.eqn (29)) was minimized using the genetic algorithm provided by Matlab.The fitting results are reported in Fig. 5, where the concentration Ctot(t), the average diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t), and the ratio of standard deviation over diameter σD(t)/
(t), and the ratio of standard deviation over diameter σD(t)/![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) are shown in (a), (b) and (c), respectively. Fig. 5d shows instead the full distributions Q(D,t) at t = 600 s at the end of the QD formation process. Note that the standard deviation is defined as:
(t) are shown in (a), (b) and (c), respectively. Fig. 5d shows instead the full distributions Q(D,t) at t = 600 s at the end of the QD formation process. Note that the standard deviation is defined as:
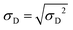 | (31) |
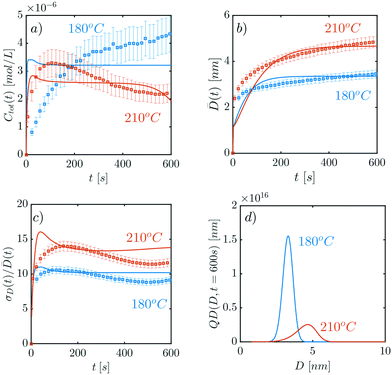 | ||
Fig. 5 (a) Concentration Ctot(t) against time; (b) average QD diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) against time; (c) σD(t)/ (t) against time; (c) σD(t)/![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) against time t; and (d) QD distributions at t = 600 s. Squares are experimental results extracted from Abolhasani et al., and continuous lines are the obtained model fit. Color code: red corresponds to the 210 °C case, blue to the data set at 180 °C. The parameter values employed are reported in the ESI.† (t) against time t; and (d) QD distributions at t = 600 s. Squares are experimental results extracted from Abolhasani et al., and continuous lines are the obtained model fit. Color code: red corresponds to the 210 °C case, blue to the data set at 180 °C. The parameter values employed are reported in the ESI.† | ||
The ratio σD(t)/![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) is considered here instead of the distribution variance, as it is typically employed in the literature, to quantify experimental results.10,12,31
(t) is considered here instead of the distribution variance, as it is typically employed in the literature, to quantify experimental results.10,12,31
Notably, an error bar of 15% has been added to the concentrations' experimental data.31 For diameters and quantities related to standard deviations, an experimental error of 5% has been considered to account for errors on the UV-vis measurements and for the fact that the literature correlations employed31 were obtained in CdSe syntheses using different ligands than in the present case. Notably, this is the first time that a deterministic model based on PBE has been quantitatively compared to several average properties of the QD size distribution. The model initially developed by Rempel et al.10 made only qualitative comparisons with experimental data, as their intent was to prove the reaction-limited nature of the growth process. In the work by Maceiczyk et al.,11 a quantitative comparison with experimental data was performed in terms of the average diameter only, without considering other properties of the QD size distribution.
From Fig. 5 a good agreement between the experimental results and the model is found. The quality of the fit changes significantly according to the selected properties. In particular, the residual error on the concentration fit Ctot(t) is 12.2% for the 210 °C case and 35.5% for the 180 °C case. The model performs better on average diameter and standard deviation over diameter, as can be seen in Fig. 5b and c. The corresponding errors are 7.7% and 5.5% on the diameters ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t), and 11.1% and 8.0% for the standard deviation over diameter, for the 210 °C and 180 °C cases, respectively.
(t), and 11.1% and 8.0% for the standard deviation over diameter, for the 210 °C and 180 °C cases, respectively.
The full details of the parameters fitted against the experimental data can be found in section S4 of the ESI.† It should be stressed though that the exponent εD turned out to be εD = −2. In other words, smaller QDs are more favored in dissociating than larger ones. This allows keeping the broadness of the distribution contained, as proven by the σD(t)/![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) (t) ratio as well as by the full distributions in Fig. 5c and d, respectively.
(t) ratio as well as by the full distributions in Fig. 5c and d, respectively.
The reported fit is overall satisfactory in terms of average diameter and distribution width (cf.Fig. 5b and c). Moreover, the fitted distribution shapes (cf.Fig. 5d) qualitatively match experimental ones from the literature that exhibit a normal shape too.31 On the other hand, the model does not fully represent the QD concentrations (cf.Fig. 5a).
At the same time, the introduced model distinguishes between precursor molecules P, monomers M and nuclei Q(n,t), allowing one to correctly account for the total QD concentration Ctot(t). The latter quantity cannot be correctly described by existing literature models, as no discrimination among the monomers and the nuclei is done.10,11 Despite this improvement and the introduction of other novel features (cf. section 2), a discrepancy between the model prediction and experimental data exists, especially in terms of QD concentration. There are several possible explanations for this discrepancy.
The concentration data are inferred by using only the maximum of the absorption spectrum λ1S, whereas a lot more data are contained in the complete absorption spectrum and hence λ1S offers only a partial view on the full QD distribution.
Moreover, nucleation remains one of the most debated phenomena in the literature.32–34 In the present model the distinction between precursor molecules P, monomers M and QD nuclei Q(n,t) allows a proper definition of the QD concentration, diameter and polydispersity (cf.eqn (27)–(29)). At the same time, nucleation remains an unresolved problem, and the recently proposed two-step nucleation mechanisms still need to be validated in the formation of QDS.33–35 However, this model has not yet been discussed in the frame of QD formation. It is therefore expected that the employed expression kN(t) = kN,0e−κNt can only qualitatively approximate the actual nucleation behavior. Also the nuclei size (n = 6), estimated in this work starting from the first absorption maxima reported by Peng and Peng,30 may be regarded as an approximation, given that very different values were reported in the literature, as discussed by Nguyen et al.36 Notably, these different first absorption maxima values lead to nuclei sizes of between 1 and 3 nm.36 Such large scattering values might be related to the role that ligands play in the growth process. A further point worth noting is that nucleation often occurs at very short time scales, e.g. t < 1 s. Therefore more experimental data points than the ones used in the present paper should be ideally employed. Although obtaining experimental information at these short times is a challenging task, a few examples exist in the literature.37
Ligands are indeed another factor that could explain the mismatch between model and experiments, given that they have not been included in the present model. Ligands are known to have a very significant stabilizing role in the QD formation.1,2,17 In fact, ligands act as surfactants that adsorb on the QD surface, lowering their surface tension, while remaining in a dynamic equilibrium with the ligand molecules in solution. Without being in possession of temperature-dependent solubility and equilibrium data of the ligands, it is not possible to include them in a model describing QD formation. At the same time it is evident that their properties have to play a role in the obtainable size distribution.
A further phenomenon worth mentioning in the context of QD formation is aggregation of QDs. These second-order events have been suggested to play a role in the formation of other types of QDs (i.e. InP QDs).38 At the temperatures at which QDs are typically synthesized, aggregating QDs could sinter completely, preserving their spherical nature even after an aggregation event.18 CdSe could undergo a similar fate and it is clear that including an aggregation event in the proposed kinetic scheme would impact the QD size distribution significantly.
Overall, given the above challenges in the understanding of QD formation, the proposed model can be considered as a starting point towards the development of a more refined description. Compared to existing literature models,10,11 it distinguishes among precursors, monomers and nuclei, allowing for a more accurate description of the growth process. As a result, the model successfully describes average sizes and distribution widths and predicts the correct order of magnitude of QD concentrations while exhibiting distribution shapes comparable to those of experimental ones.
5 Conclusions
In the present work, a deterministic model based on population balance equations has been proposed to describe the formation of II–VI QDs. The model accounts for precursor conversion, reversible nucleation and growth and has been tested against CdSe experimental data after being discussed through parametric studies.As compared to existing models, the current model has four new features: i) it distinguishes among precursor molecules, monomers and nuclei, ii) it accounts for time-dependent kinetic rates, iii) the growth step has been derived employing well-accepted expressions in colloid science and iv) the mass-dependency of the dissociation kinetic rate has been left as a fitting parameter.
The parametric studies performed revealed the complexity of the implemented kinetic scheme, highlighting the model's sensitivity towards certain parameters. It turned out that the time-dependent κN, κG and κD as well as the mass-dependent dissociation exponent εD had a dramatic impact on the predicted QD distribution for relatively small changes in the parameter space.
The model was tested against experimental data, and for the first time 3 average properties of the QD size distribution were taken into account, namely the QD concentration, its average diameter and a measure of the QD distribution width. The fitting results were satisfactory in describing the experimental information on diameter and distribution width as well as distribution shape. Regarding the total concentration of QDs, only the order of magnitude could be satisfactorily predicted, but not the trend.
The discrepancies were ascribed to the lack of quantitative information and understanding of i) QD nucleation kinetics, ii) the role of ligand equlibria, and iii) the presence of aggregation events. Nucleation was explicitly considered in the present model, but using a very simplified kinetics, given that no further information was available in the literature. Ligand equilibria are known to play an essential role in shaping the QD size distribution, but their corresponding temperature-dependent constants are still unavailable. Little evidence is also present in terms of whether or not aggregation phenomena are occurring during the QD formation.
Overall, this model represents a first step towards the development of a more refined model able to describe the formation of QDs and their size distribution. Including ligand binding kinetics would be a logical next step towards quantitative predictions of QD growth.
Acknowledgements
This work was supported by NSF ECCS grant 1449291. S. L. gratefully acknowledges the Swiss National Science Foundation (SNSF) for financial support (grant numbers P2EZP2_159128 and P300P2_167683).References
- J. van Embden, A. S. R. Chesman and J. J. Jasieniak, Chem. Mater., 2015, 27, 2246–2285 CrossRef CAS.
- S. G. Kwon and T. Hyeon, Small, 2011, 7, 2685–2702 CrossRef CAS PubMed.
- A. P. Alivisatos, J. Phys. Chem., 1996, 100, 13226–13239 CrossRef CAS.
- Y. Yin and A. P. Alivisatos, Nature, 2005, 437, 664–670 CrossRef CAS PubMed.
- A. P. Alivisatos, Science, 1996, 271, 933–937 CAS.
- A. M. Research, Quantum Dot Market Analysis, http://www.alliedmarketresearch.com/quantum-dots-market, [Accessed 2017-02-22] Search PubMed.
- T. W. Phillips, I. G. Lignos, R. M. Maceiczyk, A. J. deMello and J. C. deMello, Lab Chip, 2014, 14, 3172–3180 RSC.
- E. M. Brauser, T. D. Hull, J. D. McLennan, J. T. Siy and M. H. Bartl, Chem. Mater., 2016, 28, 3831–3838 CrossRef CAS.
- C. B. Williamson, D. R. Nevers, T. Hanrath and R. D. Robinson, J. Am. Chem. Soc., 2015, 137, 15843–15851 CrossRef CAS PubMed.
- J. Y. Rempel, M. G. Bawendi and K. F. Jensen, J. Am. Chem. Soc., 2009, 131, 4479–4489 CrossRef CAS PubMed.
- R. M. Maceiczyk, L. Bezinge and A. J. deMello, React. Chem. Eng., 2016, 1, 261–271 CAS.
- M. Abolhasani, C. W. Coley, L. Xie, O. Chen, M. G. Bawendi and K. F. Jensen, Chem. Mater., 2015, 27, 6131–6138 CrossRef CAS.
- J. T. Siy and M. H. Bartl, Chem. Mater., 2010, 22, 5973–5982 CrossRef CAS.
- Z. Hens and R. Čapek, Coord. Chem. Rev., 2014, 263, 217–228 CrossRef.
- D. Segets, M. A. Hartig, J. Gradl and W. Peukert, Chem. Eng. Sci., 2012, 70, 4–13 CrossRef CAS.
- T. Vetter, M. Iggland, D. R. Ochsenbein, F. S. Hanseler and M. Mazzotti, Cryst. Growth Des., 2013, 13, 4890–4905 CAS.
- H. Liu, J. S. Owen and A. P. Alivisatos, J. Am. Chem. Soc., 2007, 129, 305–312 CrossRef CAS PubMed.
- S. K. S. K. Friedlander, Smoke, dust, and haze : fundamentals of aerosol dynamics, Oxford University Press, New York, 2nd edn, 2000 Search PubMed.
- S. Lazzari, L. Nicoud, B. Jaquet, M. Lattuada and M. Morbidelli, Adv. Colloid Interface Sci., 2016, 235, 1–13 CrossRef CAS PubMed.
- P. Sandkühler, J. Sefcik, M. Lattuada, H. Wu and M. Morbidelli, AIChE J., 2003, 49, 1542–1555 CrossRef.
- S. Lazzari and M. Lattuada, J. Phys. Chem. B, 2017, 121, 2511–2524 CrossRef CAS PubMed.
- A. Schmitt, G. Odriozola, A. Moncho-Jorda, J. Callejas-Fernandez, R. Martinez-Garcia and R. Hidalgo-Alvarez, Phys. Rev. E, 2000, 62, 8335 CrossRef CAS.
- J. van Embden and P. Mulvaney, Langmuir, 2005, 21, 10226–10233 CrossRef CAS PubMed.
- G. G. Yordanov, C. D. Dushkin and E. Adachi, Colloids Surf., A, 2008, 316, 37–45 CrossRef CAS.
- I. Kryven and P. D. Iedema, Macromol. Theory Simul., 2013, 22, 89–106 CrossRef CAS.
- I. Kryven, S. Lazzari and G. Storti, Macromol. Theory Simul., 2014, 23, 170–181 CrossRef CAS.
- S. Lazzari, B. Jaquet, L. Colonna, G. Storti, M. Lattuada and M. Morbidelli, Langmuir, 2015, 31, 9296–9305 CrossRef CAS PubMed.
- L. Nicoud, S. Lazzari, D. B. Barragan and M. Morbidelli, J. Phys. Chem. B, 2015, 119, 4644–4652 CrossRef CAS PubMed.
- L. Ehrl, M. Soos and M. Lattuada, J. Phys. Chem. B, 2009, 113, 10587–10599 CrossRef CAS PubMed.
- Z. Peng and X. Peng, J. Am. Chem. Soc., 2002, 124, 3343–3353 CrossRef CAS PubMed.
- J. Jasieniak, L. Smith, J. van Embden, P. Mulvaney and M. Califano, J. Phys. Chem. C, 2009, 113, 19468–19474 CAS.
- D. Kashchiev, Nucleation, Butterworth-Heinemann, 2000 Search PubMed.
- F. Ito, Y. Suzuki, J.-i. Fujimori, T. Sagawa, M. Hara, T. Seki, R. Yasukuni and M. L. de la Chapelle, Sci. Rep., 2016, 6, 22918 CrossRef CAS PubMed.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS PubMed.
- P. G. Vekilov, Nat. Mater., 2012, 11, 838–840 CrossRef CAS PubMed.
- K. A. Nguyen, P. N. Day and R. Pachter, J. Phys. Chem. C, 2010, 114, 16197–16209 CAS.
- I. Lignos, S. Stavrakis, A. Kilaj and A. J. deMello, Small, 2015, 11, 4009–4017 CrossRef CAS PubMed.
- J. Baek, P. M. Allen, M. G. Bawendi and K. F. Jensen, Angew. Chem., Int. Ed., 2011, 50, 627–630 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: S1 Numerical method, S2 Link between experiments and QD size distribution, S3 Parametric study, S4 Fitted parameter values, S5 Symbols list. See DOI: 10.1039/c7re00068e |
| This journal is © The Royal Society of Chemistry 2017 |