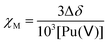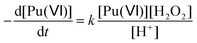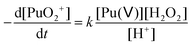DOI:
10.1039/C7QI00389G
(Research Article)
Inorg. Chem. Front., 2018,
5, 100-111
Structural and magnetic susceptibility characterization of Pu(V) aqua ion using sonochemistry as a facile synthesis method†
Received
6th July 2017
, Accepted 13th October 2017
First published on 16th October 2017
Abstract
Since the past few years, Pu(V) has gained much attention due to its potential contribution to the environmental migration of actinides. However, the preparation of concentrated (up to mM) and pure Pu(V) solutions is quite difficult and often hindered by its great instability towards disproportionation, thus limiting the accessibility to physical and chemical property data. This work describes the rapid and facile sonochemical preparation of relatively stable Pu(V) solutions in the millimolar range free from the admixtures of the other oxidation states of plutonium. The mechanism deals with the sonochemical reduction of Pu(VI) in weakly acidic perchloric solutions by using the in situ generated H2O2, where the kinetics can be dramatically enhanced under high frequency ultrasound and an Ar/O2 atmosphere. The quasi-exclusive presence of the Pu(V) aqua ion in solution was evidenced by UV-vis absorption spectroscopy. The prepared solutions were found to be stable for more than one month which allowed the accurate XAFS and NMR investigations of Pu(V). EXAFS spectra revealed the presence of two trans dioxo Pu![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds at 1.81 Å and 4–6 equatorial Pu–Oeq interactions at 2.47 Å characteristic of coordinated water molecules. The exact number of water molecules (N[Oeq(H2O)] = 4) was determined by simulating the EXAFS spectra of the PuO2+ aqua complexes using DFT calculations (geometry and the Debye–Waller factor) and comparing them with experimental signals. For the first time, the magnetic susceptibility of the pentavalent state of plutonium in aqueous solutions was also determined (χM = 16.3 × 10−9 m3 mol−1 at 25 °C) and the related Curie constant was estimated (C = 6.896 × 10−6 m3 K mol−1).
O bonds at 1.81 Å and 4–6 equatorial Pu–Oeq interactions at 2.47 Å characteristic of coordinated water molecules. The exact number of water molecules (N[Oeq(H2O)] = 4) was determined by simulating the EXAFS spectra of the PuO2+ aqua complexes using DFT calculations (geometry and the Debye–Waller factor) and comparing them with experimental signals. For the first time, the magnetic susceptibility of the pentavalent state of plutonium in aqueous solutions was also determined (χM = 16.3 × 10−9 m3 mol−1 at 25 °C) and the related Curie constant was estimated (C = 6.896 × 10−6 m3 K mol−1).
1. Introduction
In acidic aqueous solutions, plutonium exhibits an extraordinary ability to coexist within four oxidation states from +III to +VI. The relative abundance of each oxidation state is highly dependent on the Pu concentration, pH, presence of complexing agents, ionic strength and redox potential.1–3 Tetravalent plutonium, which is the most stable oxidation state in acidic media under an aerobic atmosphere, in combination with trivalent and hexavalent states, has been extensively studied particularly for the development of Pu separation processes.2,3 Investigations devoted to Pu(V) solutions have however been poorly reported in the literature, despite the fact that research studies carried out on the pentavalent state have been more referenced from the 1990s when the behaviour of Pu and its interaction with the environment gained more importance. The subsurface mobility of Pu(V) is indeed predicted to be much higher in comparison with that of the other oxidation states.4–9 However, the pentavalent state of Pu is highly prone to disproportionation even in moderately acidic solutions. As a function of the presence of the other oxidation states in the solutions, several disproportionation mechanisms have been proposed in the literature (reactions ((1)–(2)), the first favoured at very low concentrations of Pu(III)).10,11| | 2PuO2+ + 4H+ ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Pu4+ + PuO22+·2H2O Pu4+ + PuO22+·2H2O | (1) |
| | 3PuO2+ + 4H+ ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Pu3+ + 2PuO22+ + 2H2O Pu3+ + 2PuO22+ + 2H2O | (2) |
Both reactions show strong dependency of Pu(V) disproportionation on the H+ concentration, thus making the preparation of Pu(V) in acid solutions quite tricky, but also confirming the higher stability of Pu(V) in a geochemical context where near neutral conditions dominate.5,6,9 Pu(V) reactivity in addition appears to be strongly dependent on its concentration, the radiolysis, and the presence of other Pu oxidation states due to the closeness of the standard redox potentials of Pu couples. Principally, the reported preparations of Pu(V) solutions deal with electrochemical or separation/extraction methods, and are generally carried out at low concentrations (10−5–10−10 M) and pH >3.9,12,13 Recently, some authors have reported the use of ozone to prepare pure Pu(V) solutions at a relatively low concentration (2 × 10−8 M).14 Bubbling of ozone into a Pu(IV) solution induces its almost total conversion into a mixture composed of Pu(V) and Pu(VI) which then slowly converts to Pu(V), where the kinetics can be improved by increasing the pH in the 3–7 range. Under these conditions, Pu(V) remains stable for more than one month and the solution has the advantage of being quickly prepared without residual oxidants or organic solvents, which can hinder further investigations. The preparation of large volumes and more concentrated solutions of Pu(V) is much more complex and poorly reported in the literature, thus hindering the determination of physical and chemical data from experimental solutions. Cohen et al. nevertheless reported the preparation of a 0.02 M Pu(V) solution by the electrolytic reduction of Pu(VI) at a potential of about 0.54 V (vs. SCE) in 0.2 M HClO4.2,15 Rabideau et al. described the addition of a neutral sodium iodine solution to a plutonyl solution.16 The protocol required carefully selected conditions with a final solution only composed of 25 to 50% of Pu(V).
Probing the magnetic properties of the actinide ions is very important to predict and characterize their interaction with ligands in solution.17,18 To the best of our knowledge, the magnetic susceptibility of the pentavalent state of Pu has never been investigated in aqueous solutions. Nevertheless, we can note that some authors have provided a value in 1944 by means of the Gouy method.10 The studied Pu(V) solution was however not pure and its concentration was changing with time. Otherwise, only a few studies investigated the characterization of the structure of the Pu(V) aqua ion with XAFS (X-ray absorption fine structure) techniques.19–23 Although there is an agreement concerning the presence and distance attributed to the two dioxo bonds, the exact number of water molecules coordinating Pu(V) aqua ions in the equatorial plane still suffer from experimental confirmation.19–23 Such knowledge is highly important to predict the behaviour, complexation, and reactivity of the pentavalent state which is particularly under current focus due to the concern of Pu migration. Generally, a few experimental investigations dedicated to the solvation environment of PuO2+ agree for the predominance of four water molecules in the equatorial plane in non-complexing aqueous media,20–22,24 although the penta-aqua complex has also often been predicted with theoretical calculations to be the most favourable structure.25–27 The interpretation of the results with XAFS techniques however strongly depends on the parameter settings and is often combined with a debatable precision.24,28 More recently, computational studies dedicated to the solvation environment of actinide species concluded that the predominant PuO2+ complex is probably coordinated by four water ligands.29,30
Historically, hydrogen peroxide has been a very important reagent in actinide chemistry and the related industrial processes for purification or separation purposes (U, Pu and Np).2,31–34 Generally, this salt free reagent avoids a large dilution of solutions and generates gaseous by-products without any formation of solution impurities. On the lab scale, H2O2 is often used in nitric media to reduce Pu(VI) to Pu(V) which then disproportionates and allows the generation of stable Pu(IV) solutions in agreement with reactions (1)–(2). Further addition of hydrogen peroxide can lead to the formation of Pu(III) or a mixture of Pu(IV) and Pu(III) depending on the experimental conditions (temperature, acidity, concentration, presence of complexing ligands, etc.). O2/H2O2 (E° = 0.695 V/SHE) or H2O2/H2O (E° = 1.763 V/SHE)35 couples are indeed able to respectively reduce Pu(IV) or oxidize Pu(III) (reactions (3)–(4)). The addition of H2O2 during Pu oxidation state stabilizations is therefore delicate and should be used with parsimony to avoid the mixtures of Pu oxidation states. Under less acidic conditions, studies related to Pu(VI) reduction with H2O2 are really scarce but it is interesting to note that some authors have described the detection of Pu(V) during the whole reduction process into Pu(IV) in 0.5 M HNO3.36
| | 2Pu4+ + H2O2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Pu3+ + O2 + 2H+ 2Pu3+ + O2 + 2H+ | (3) |
| | 2Pu3+ + H2O2 + 2H+ ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Pu4+ + 2H2O 2Pu4+ + 2H2O | (4) |
Sonochemistry has attracted considerable attention as a potentially “reagent-free” route to control the oxidation states of actinide ions during spent nuclear fuel reprocessing, mostly due to the in situ generation of hydrogen peroxide and/or nitrous acid during the sonication of aqueous nitric solutions.37,38 In pure water saturated with noble gases, power ultrasound causes the homolytic splitting of H2O molecules yielding H˙ and OH˙ radicals (reaction (5), “)))” is for a reaction initiated under ultrasound).39–43 These highly reactive species mostly recombine into H2O inside the cavitation bubble,42,43 some OH˙ radicals (roughly 20%)43,44 can nevertheless diffuse to the bubble interface where the temperatures are lower and recombine into hydrogen peroxide (reaction (6)). Molecular hydrogen H2 is formed as a recombination product of H˙ radicals mostly in the gaseous phase of the collapsing bubble (reaction (7)).42,45 Several investigations devoted to the kinetics of H2O2 sonochemical formation have been reported in the literature.46–50 It was shown that the H2O2 formation rate in pure water can be significantly enhanced when increasing the ultrasound frequency or when using a mixture of Ar/O2 as a saturating atmosphere.48,49,51 Experimentations showed that higher yields were observed under an Ar/(20–30 vol%)O2 gas atmosphere and were attributed to the generation of both OH˙ and HO2˙ species as a result of O2 reactivity or dissociation in the cavitation bubbles (reactions (8)–(12)).38,49,52
| | | ˙O˙ + H2O → HO˙ + HO˙ | (12) |
This work can be divided into three distinctive parts focusing on (i) the preparation and study towards the aging of concentrated and relatively stable Pu(V) solutions under ultrasound irradiation at room temperature; (ii) the evidence of the exclusive or quasi-exclusive presence of the pentavalent state in the prepared solutions followed by its structural characterization by XAFS and computational techniques; (iii) the determination of the magnetic susceptibility of Pu(V) by NMR.
2. Experimental
Caution! Pu is an α-emitting element presenting serious health risks. Studies dealing with such an element require a careful handling coupled with appropriate infrastructures and trained workers.
2.1. Materials
Stock solutions were purified in agreement with the previously described procedure.38 Pu isotopic signature consisted of a mixture of 96.90% 239Pu, 2.99% 240Pu, 0.05% 241Pu, and 0.06% 242Pu. Reagents used in this study were all of analytical grade and were purchased from Sigma-Aldrich and VWR. Aqueous solutions were prepared with purified ultrapure water having a resistivity higher than 18.2 MΩ cm at 25 °C. The experiments were performed under pure Ar (purity >99.9%), Ar/O2 (20 vol% of O2) or Ar/CO (10 vol% of CO) atmospheres provided by Air Liquide.
2.2. Pu(VI) preparation
To prepare a Pu(VI) solution, an aliquot of Pu(IV) initially stabilized in nitric acid was evaporated to almost dryness. A concentrated HClO4 aliquot was then added and Pu(IV) was oxidized by heating until fuming perchloric acid followed by evaporation until a wet salt is obtained.5 After dilution in pure water, the obtained orange solution was characterized by UV-vis absorption spectroscopy which showed a complete conversion of the Pu(IV) solution into Pu(VI) in agreement with the literature.2 In general, the as-prepared Pu(VI) solutions exhibit a good stability; however, some Pu(VI) self-irradiation reduction is observed after several weeks of storage. To avoid the formation of the Pu mixture from self-irradiation, the Pu(VI) solution was directly diluted to the appropriate concentration after synthesis and sonicated within a few days following its preparation.
2.3. Sonochemical experiments
The experiments with Pu were performed at the ATALANTE nuclear facility (Marcoule, CEA Research Centre, France) in a glove box under negative pressure. This glove box is equipped with two different sonochemical reactors. The experiments were performed at low frequency ultrasound (20 kHz) with a 1 cm2 titanium horn fitted on top of a 50 mL homemade reactor. Ultrasound was provided by a 750 W generator (Sonics & Materials VCX 750) connected from outside of the glove box.38 High frequency studies (203 kHz) were performed in a 250 mL cylindrical reactor with a 25 cm2 transducer (L3 Communications ELAC Nautik) connected from the bottom of the cell to a 125 W generator situated outside the enclosure (LVG 60 RF-generator). For high frequency experiments, the solution was stirred with mechanical agitation in the meantime (at 240 rpm) to obtain a homogeneous distribution of the acoustic bubbles in the cell.49 The specific absorbed acoustic power equal to 0.34 and 0.13 W mL−1 for 20 and 203 kHz ultrasound, respectively, was obtained by the conventional thermal probe method.39 Both reactors are tight and supplied with several connections dedicated to gas bubbling, temperature control and aliquot sampling. The temperature was maintained at 21 ± 1 °C with a cryostat (Lauda Ecoline RE 210) during ultrasonic treatment and controlled with a thermocouple immersed in the sonicated solutions. Various treated solutions were purged with gas (at a constant flow rate of 100 mL min−1) which started 15 min before ultrasound triggering and was maintained in the solution during the whole experiment. The ratio of polyatomic gas to Ar results from previous investigations which showed the optimized oxidant or reducing conditions with the selected gas mixtures.49,53
2.4. UV-visible spectroscopy
During sonolysis, the aliquots of the solution (2 mL) were sampled at regular time intervals. At a low frequency, aliquots were filtered with 0.2 μm PTFE filters to remove potential Ti particle contamination arising from the horn surface erosion (not required at 203 kHz where Ti erosion does not occur).38,54 Then, samples were analysed by UV–vis absorption spectrophotometry (Shimadzu UV3600 connected to optic fibres or Shimadzu UV3150 directly connected to the glove box) in 1 or 5 cm quartz cells. The concentration of Pu(VI) was followed at 830 nm (ε = 533 cm−1 M−1), while that of Pu(V) was followed at 569 nm (ε = 15 cm−1 M−1). “Peak-valley” differences in absorbance were measured to determine the concentration variations. Due to the spectrophotometer resolution, the narrow Pu(VI) peak at 830 nm was fitted with a Lorentzian function for the concentration calculations. The formation of H2O2 resulting from the homolytic dissociation of sonicated water molecules was measured by mixing the filtered sampled aliquots (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with a 1.2 × 10−2 M TiOSO4 solution (0.330 g of TiOSO4 dissolved in 100 mL of pure water under stirring and previously gently heated in 3.5 mL of 18 M H2SO4) to form a colorimetric complex absorbing at 410 nm (ε = 710 cm−2 M−1).50 An external calibration curve was previously prepared with a H2O2 standard solution.
1) with a 1.2 × 10−2 M TiOSO4 solution (0.330 g of TiOSO4 dissolved in 100 mL of pure water under stirring and previously gently heated in 3.5 mL of 18 M H2SO4) to form a colorimetric complex absorbing at 410 nm (ε = 710 cm−2 M−1).50 An external calibration curve was previously prepared with a H2O2 standard solution.
2.5. XAFS experiments
Pu LIII-edge XAFS measurements were performed at the European Synchrotron (ESRF, Grenoble, France) at the Rossendorf Beamline (BM20, ROBL)55 which is equipped with a collimating and focusing mirror and a water cooled Si(111) double-crystal monochromator in order to reject higher order harmonics and monochromatize the incident white X-rays. The sample spectra were recorded in transmission mode by using Ar/N2 filled ionization chambers, whereas the Ar/N2 ratio was optimized for the measured energy range. The incident photon energy was calibrated in situ by recording after the sample (I1/I2) the first derivative XANES (X-ray Absorption Near Edge Structure) spectrum of a Zr foil defined at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 eV. Experimental spectra were recorded at the Pu LIII edge and the ionization energy (E0) was preliminary defined at the maximum of the white line and varied as a free fit parameter. The energy range investigated for EXAFS (Extended X-ray Absorption Fine Structure) measurements was chosen depending on the Pu content in the samples from 3.3 Å−1 to 12.3 Å−1. EXAFS data analyses were performed with Athena and Artemis software from the ifeffit package56,57 and theoretical scattering phases and amplitude functions were calculated by the ab initio FEFF8.4 code from the hypothetical plutonyl structure.58 All fitting operations were performed in the R-space over individual radial distances: 2 Oyl and several Oeq(H2O) with the corresponding Debye–Weller factors (σ2) for every considered distance in the first coordination shell.
998 eV. Experimental spectra were recorded at the Pu LIII edge and the ionization energy (E0) was preliminary defined at the maximum of the white line and varied as a free fit parameter. The energy range investigated for EXAFS (Extended X-ray Absorption Fine Structure) measurements was chosen depending on the Pu content in the samples from 3.3 Å−1 to 12.3 Å−1. EXAFS data analyses were performed with Athena and Artemis software from the ifeffit package56,57 and theoretical scattering phases and amplitude functions were calculated by the ab initio FEFF8.4 code from the hypothetical plutonyl structure.58 All fitting operations were performed in the R-space over individual radial distances: 2 Oyl and several Oeq(H2O) with the corresponding Debye–Weller factors (σ2) for every considered distance in the first coordination shell.
2.6. Computational methods
Quantum chemical calculations were performed at the DFT level of theory using the B3LYP functional. The Stuttgart small-core relativistic effective core potential (RECP) and the associated basis set were used for the actinide atom.59–61 The 6-311+G(d,p) basis set was employed for other atoms. The DFT calculations were carried out using the Gaussian 09 software package.62 The calculations were carried out in the presence of a continuum solvent model. The geometries of PuO2(H2O)4(H2O)8+ and PuO2(H2O)5(H2O)10+ complexes were optimized and characterized by harmonic frequency analysis as local minima. Several configurations were considered in the calculations corresponding to the different arrangements of water molecules. The results are reported for the lowest energy configuration of each complex.
The ab initio EXAFS spectra were simulated using DFT structural parameters (bond distances and Debye–Waller factors) without any further fitting. Previously, we have shown that it is possible to accurately reproduce the EXAFS experimental spectrum of actinide compounds by using such a methodology.63,64 The EXAFS spectra were simulated with FEFF9 from DFT optimized structures and ab initio Debye–Waller factors for all multiple-scattering paths up to a half-path length of 6 Å. Ab initio Debye–Waller factors were calculated at 300 K for each scattering path from the dynamical matrix extracted from the DFT frequency calculation as implemented in FEFF9.65,66 The amplitude factor S02 was fixed to 0.9 as in the EXAFS fitting procedure for the liquid samples. The geometries and vibrational frequencies of the PuO2+ complex with four and five coordinated water molecules were optimized through DFT calculations and the corresponding thermal Debye–Waller factors were determined from the vibrational frequencies.66
The prerequisite condition to correctly simulate the experimental EXAFS spectra from such calculations is that bond distances are accurately reproduced by the quantum chemical model. For this purpose, we have carried out preliminary calculations on the well characterized uranyl aqua ion. In aqueous solutions, uranyl is known to be predominantly coordinated by five water molecules in the equatorial plane.67 Previous DFT studies on the uranyl ion have shown that the inclusion of an explicit second hydration shell improves the agreement with the experimental data for structural parameters.68,69 In the present work, structural parameters were computed for actinyl complexes with the first and second solvation shell water molecules. Solvent effects beyond the second hydration sphere were taken into account through a continuum model. The bond distances were calculated from DFT (B3LYP) for the UO2(H2O)5(H2O)102+ complex. The predicted U–Oyl and U–Oeq distances are equal to 1.773 Å and 2.445 Å, respectively, which is in close agreement with the experimental values determined from EXAFS in aqueous solutions (the reported values range from 1.76 to 1.78 Å for the U–Oyl distance and from 2.40 to 2.42 Å for the U–Oeq distance).70–73 The good agreement between the experimental and calculated distances (within 0.04 Å) for the uranyl aqua ion made us confident that structural parameters can be correctly reproduced for the PuO2+ ion by using the same approach.
2.7. Magnetic susceptibility
The molar magnetic susceptibility χM was calculated by the chemical shift difference Δδ measured between the 1H NMR signal of working (t-BuOH in) and reference (t-BuOH out) solutions using the Evans method.74 The shift (Δδ = δtBuOH+Pu(v) − δtBuOH) observed on an NMR signal is directly correlated to the magnetic susceptibility χM according to eqn (13). The 1H NMR spectra of Pu(V) solutions were recorded using a 400 MHz Fourier transform spectrometer (Agilent DD2). Measurements were carried out at every 5° step in the 5–50 °C temperature range. For some experiments, and to obtain a higher signal, a Pu(V) solution was concentrated by evaporating the solution at room temperature under Ar bubbling overnight. A careful examination of the UV-vis spectra confirmed the stability of the solution in the concentration range studied. The absence of modification of the spectra in the presence of t-BuOH was also confirmed. The solutions were directly analysed and UV-vis spectra were recorded again to confirm the absence of chemical transformation occurring during NMR analyses.| | 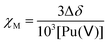 | (13) |
where Δδ represents the chemical shift difference between the reference and the working solution of tert-butanol signals, and χM represents the sample molar magnetic susceptibility (m3 mol−1).
3. Results and discussion
3.1. Pu(VI) sonolysis at high and low frequency ultrasound
The sonication of a 1.2 mM Pu(VI) aqueous solution under 203 kHz ultrasound and an Ar/O2 atmosphere leads to a significant decrease of its concentration which can be followed at 830 nm by UV-vis absorption spectroscopy. The generation of Pu(V) is simultaneously observed with an absorption peak present at 569 nm. The corresponding reduction kinetics is illustrated in Fig. 1a, where the almost total conversion of the initial Pu(VI) into Pu(V) can be observed in less than 3 h of sonication (yield >95%). Interestingly, the amount of residual Pu(VI) is found to decrease again when ultrasound is stopped: as expressed by the corresponding UV-vis spectra shown in Fig. S1 (ESI†), less than 1% of Pu(VI) remains after roughly 2 h of storage. A decrease in the pH of the solution from pH = 3.5 before sonication to pH = 2.8 after 160 min of sonication is also observed. Fig. 1b shows the behaviour of a more concentrated aqueous solution of Pu(VI) (2.3 mM) sonicated at 203 kHz under an Ar/O2 atmosphere. The plotted curves agree with the previous observations reported for a lower concentration although the initial reduction rate is found to be much lower (W0(–PuVI) = 33.6 μmol min−1 against 20.0 μmol min−1 for the 1.2 mM and 2.3 mM solutions, respectively). Furthermore, the reduction of Pu(VI) also continues in the absence of ultrasound (US). The UV-visible spectra of the 2.3 mM Pu solution before and after treatment are shown in Fig. 2 with a 5 cm quartz cuvette in the case of Pu(V) solution which agree with the literature and evidence the high purity of the here-prepared solution.2,10 The narrow peak at 569 nm results from electronic transitions within the 5f shell. The presence of a residual Pu(VI) amount estimated at 2.5 × 10−5 M (less than 1% of the total content) can also be noted. Whatever the Pu concentration, the careful examination of the UV-vis absorption spectra, in combination with the stability of the total Pu(VI) and Pu(V) content in the solution expressed by the green dots as shown in Fig. 1, suggests the absence of other Pu oxidation states in this system, specially Pu(III).
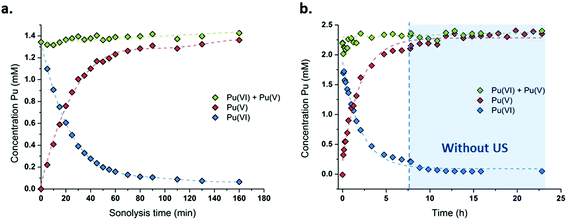 |
| | Fig. 1 Concentration evolution of Pu(VI) and Pu(V) measured at 21 °C under high frequency ultrasound (203 kHz, 0.13 W mL−1, Ar/(20%)O2) for (a) a 1.2 mM solution and (b) a 2.3 mM solution (“⋮” symbolizes ultrasound stop, the green data express the sum of the determined concentrations of Pu(VI) and Pu(V)). | |
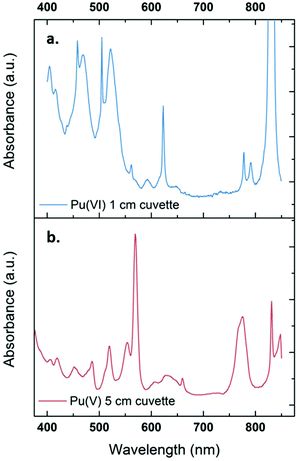 |
| | Fig. 2 UV-vis absorption spectra observed for a 2.3 mM aqueous Pu(VI) solution (a) before and (b) after sonolysis (203 kHz, 0.13 W mL−1, 21 °C, Ar/(20%)O2). The residual content of Pu(VI) in the Pu(V) solution is approximately 1%. The final solution is devoid of other Pu oxidation states or species such as colloids or nitrate complexes. The obtained solution is light pink. | |
Consistent observations were made for similar conditions carried out under a pure Ar atmosphere although the kinetics evidenced a much lower reduction rate for Pu(VI) (Fig. S2, ESI†). It is known that sonication allows the formation of H2O2 that can accumulate in aqueous solutions (reactions (5)–(6)).42,43 Pu(VI) reduction can therefore be explained by the in situ formation of H2O2 resulting from the sonochemical water molecule splitting and the subsequent recombination of the as-formed OH˙ radicals (reaction (14)). Such a behaviour has already been reported during the 20 kHz sonication of aqueous nitric acid solutions of Pu(IV) or Pu(III) in the presence of anti-nitrous reagents.38 The higher accumulation rates observed for Pu(V) under an Ar/O2 atmosphere can be explained by higher H2O2 yields in comparison with pure Ar.50 This phenomenon is explained by the scavenging of H˙ radicals with molecular O2 inside the cavitation bubbles. This reaction avoids the recombination between H˙ and OH˙ radicals and generates hydroperoxyl radicals (HO2˙), which finally enhances H2O2 yields in agreement with reactions (8)–(9).75 H2O2 yields are also promoted by the dissociation of molecular oxygen inside the cavitation bubbles which is known to take place under high frequency ultrasound in agreement with reactions (10)–(12).50 The sonolytic overproduction of H2O2 can therefore enable the continuation of the Pu(VI) reduction process when ultrasound is stopped (Fig. 1b or Fig. S1, ESI†).
| | | 2PuO22+ + H2O2 → 2PuO2+ + O2 + 2H+ | (14) |
According to the literature, the reduction kinetic law for Pu(VI) in the presence of H2O2 is proportional to their respective initial concentrations and inversely proportional to the solution acidity (with k = 0.75 ± 0.1 min−1 at 22 °C (I = 1), eqn (15)).76,77 The preparation of 2.3 mM Pu(VI) solutions by dilution of the stock solution with pure water unavoidably increases the acidity of the sonicated solution in comparison with the 1 mM Pu(VI) solutions, and therefore explains the longer time required to reduce the Pu(VI) amount of the 2.3 mM Pu solution for a similar accumulation rate of H2O2 (Fig. 1a vs. b).
| | 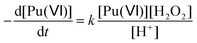 | (15) |
The effect of the ultrasonic frequency on the reduction kinetics was investigated by sonicating Pu(VI) solutions at a low frequency. In agreement with high frequency experiments, the 20 kHz sonolysis of a 1 mM Pu(VI) solution in water (pH = 3.6) under an Ar or Ar/O2 atmosphere leads to its UV-vis absorption decrease at 830 nm and the simultaneous generation of Pu(V) absorbing at 569 nm as shown in Fig. 3 and Fig. S3 and S4 (ESI,† an Ar atmosphere lowers the reduction rate in agreement with 203 kHz experiments).2 The main difference lies in the Pu(VI) reduction rate which was found to be dramatically decreased at 20 kHz whatever the saturating atmosphere. Furthermore, the amount of Pu(VI) remaining after sonication (or one day after sonication) is higher than that observed under high frequency ultrasound (Fig. S3, ESI†). The reduction kinetics differences can be explained by an increase of H2O2 yields at a high frequency in aqueous solutions in comparison with low frequency ultrasound.50 This higher formation rate is related to several phenomena occurring at high frequencies: (i) the increased number of cavitation bubbles,78 (ii) the shortened ultrasound wave periods increasing the bubble surface-to-volume ratio (S/V) and leading to an enhanced rectified diffusion,39,79 and (iii) the higher intrabubble vibronic temperatures providing a higher dissociation degree of O2.49,80 The measured H2O2 rate at a low frequency in pure water saturated with Ar/O2 was found to reach 2.8 ± 0.3 μM min−1, which is much lower than that observed at 203 kHz, i.e. 12.9 ± 1.5 μM min−1. Under pure Ar, the 20 kHz formation rate reaches 1.1 ± 0.1 μM min−1, whereas 2.1 ± 1.5 μM min−1 is measured at a high frequency.50 Whatever the experimental conditions, the sonochemical yields of H2O2 were found to be dramatically reduced in the presence of Pu(VI). For instance, the H2O2 formation rate reached only 0.6 mM at 203 kHz after 140 min of sonolysis, whereas 1.8 mM is usually observed without Pu, thus confirming again its contribution in the reduction process during and a few hours after sonication. Note that the local heat generated at the bubble solution interface (few hundreds of degrees) may also favour an increase in reaction kinetics.54
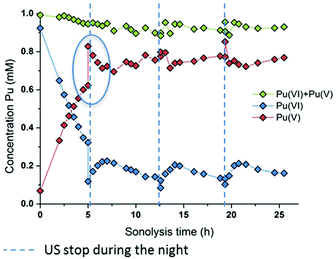 |
| | Fig. 3 Behaviour of a 1 mM Pu(VI) solution under low frequency ultrasound (20 kHz, 0.34 W mL−1, 21 °C, Ar/(20%)O2) as a function of sonolysis time (“⋮” symbolizes ultrasound stop during the night; the green data express the sum of the determined concentrations of Pu(VI) and Pu(V)). A decrease in the pH of the solution from 3.6 to 2.1 after sonication was observed. | |
At 20 kHz, several days were required under an Ar/O2 atmosphere to reduce Pu(VI) solutions as shown in Fig. 3. The plotted measurements indicate that Pu(VI) reduction continues during the night when sonication is stopped (the absence of ultrasound is shown with dashed lines but the measurements acquired during that time are not shown; Fig. 3 only shows the data obtained under sonication). Such observation is related to the overproduction of H2O2 which continues the reduction process without ultrasound in agreement with high frequency experiments. The analyses indicated a H2O2 concentration of about 1.4 mM after 12.5 h of sonication which decreased to 0.6 mM after night. Another striking observation is the increase of the Pu(VI) concentration (with a simultaneous decrease of Pu(V)) when ultrasound is started again. This phenomenon is then followed, after several hours, by a resumption of Pu(VI) reduction, which can be reproduced several times (Fig. 3). This phenomenon was not observed under a pure Ar atmosphere or during the simple bubbling of Ar/O2 into Pu(V) solutions. This phenomenon can therefore be related to the presence of O2 during sonication. In fact, hydroperoxyl radicals that can be produced during sonication in the presence of O2 are very reactive species which can involve complex reactions with Pu ions. Particularly, radiolysis investigations have shown that Pu(V) can be oxidized by hydroperoxyl radicals in agreement with reaction (16).76 We suggest that the sonochemical formation of HO2˙ species may involve two competitive reactions that may interfere with the Pu(VI) reduction process: H2O2 formation versus Pu(V) reoxidation. Once a sufficient amount of H2O2 is produced, Pu(VI) reduction may occur again. Note that under an Ar/(10%)CO atmosphere, which allows the scavenging of OH˙ radicals and prevents H2O2 formation in agreement with reaction (17), Pu(VI) reduction is not observed. This confirms again the proposed mechanism involving H2O2. Furthermore, the pH measured after sonication was found to be about pH = 2.1 (instead of 3.6 before the experiment) which confirms the release of protons during the reduction process (reaction (14)).
| | | PuO2+ + HO2˙ + H+ → PuO22+ + H2O2 | (16) |
Generally, the reported ultrasound procedure for Pu(V) preparation agrees with the conventional chemistry of Pu reported in the literature but allows the control of the kinetics through the in situ generation of active species without the addition of any side chemicals (Fig. S5 and S6, ESI†). It is important to emphasize that under the here-described preparation conditions, Pu(V) solutions are quite concentrated and highly pure. Most of the Pu(VI) is reduced to Pu(V) under high frequency ultrasound in a few hours; the slight sonochemical overproduction of H2O2 allows the reduction of the remaining amount to 1% or less. Whatever the sonication conditions (frequency, atmosphere and concentration), various Pu(VI) solutions never lead to the observation of Pu(III) or Pu(IV), Pu(IV) colloids, brown or red Pu(IV) peroxo complexes, and Pu(IV) green precipitates.2,81
3.2. Stability of the Pu(V) solutions
In the absence of Pu(III) traces in solution, Pu(V) disproportionation has been reported to be strongly dependent on the hydrogen ion concentration (reactions (1)–(2)). Therefore, the stability of the prepared Pu(V) solutions at the laboratory can be explained by their relatively high pH (>2) combined with the moderate Pu concentration of the solutions in agreement with the literature.2,3,36 Under these conditions, the Pu(V) disproportionation rate is very weak. Thermodynamically, Pu(V) can also be reduced by the residual amount of H2O2 present in solution in agreement with the kinetic law shown below (eqn (18)). The rate constant for this reaction was only studied in basic media and was reported to be quite low and reached about 3.59 × 10−9 min−1 against 0.75 min−1 for Pu(VI) reduction with H2O2 and 0.24 M−1 min−1 for Pu(V) disproportionation (at 25 °C, 1 M HClO4).16| | 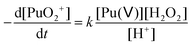 | (18) |
Fig. 4 shows several absorption spectra obtained from 1 mM and 2.3 mM Pu(V) solutions prepared at high frequency ultrasound illustrating their stabilities during storage under an air atmosphere. Note again that some of the freshly prepared solutions contained some traces of Pu(VI) observable on the absorption spectrum because of its high molar attenuation coefficient (ε = 533 cm−1 M−1); but the corresponding concentration represents less than 1% of the Pu content (a few hours after sonication). From the spectroscopic measurements, it follows that Pu(V) solutions prepared under these conditions are stable during approximately one month whatever the saturating gas atmosphere used during sonolysis (Ar or Ar/O2). However, after approximately one month storage, the Pu(VI) concentration slightly increases, while the Pu(V) amount is found to decrease, most probably through disproportionation. Interestingly, this phenomenon is accompanied by the formation of new absorption peaks present at 455 nm and 650 nm (large peak) which are currently under investigation and differ from classical Pu(IV) colloids. Pu colloids can indeed be recognized by the presence of an absorption peak at around 620 nm and a strong absorption in the near UV range attributed to Mie scattering.2,82
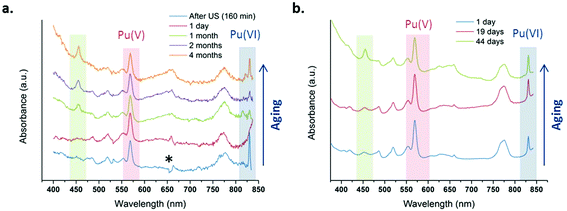 |
| | Fig. 4 UV-vis absorption spectra observed after sonication at 21 °C of a Pu(VI) solution at 203 kHz under an aerobic atmosphere at (a) 1 mM with optic fibers and (b) 2.3 mM without optic fibers. One day after sonication, the final amount of Pu(VI) is <1% of the Pu content (* is an optical artefact due to optic fibers). | |
3.3. Characterization
3.3.1. XAFS experiments.
The relative stability and concentration of the prepared Pu(V) solutions allowed us to investigate the structural properties by XAFS (which were carried out a few days after synthesis). The Pu LIII-edge X-ray absorption near edge structure (XANES) spectrum of a 1 mM Pu(V) solution prepared with ultrasound is shown in Fig. 5a together with the reference XANES spectra of Pu(IV) and Pu(VI) aqua ions. In agreement with the literature,83 the spectrum of the sonochemical Pu(V) exhibits a decreased white line height in comparison with Pu(IV) and Pu(VI). Moreover, the Pu(V) spectrum shows the same “yl” shoulder as that observed for the Pu(VI) reference on its high energy side, which is characteristic of the presence of trans dioxo bounds. Furthermore, the absorption edge of the Pu(V) sample is also found to be shifted to a lower energy when compared with Pu(VI), hence confirming the presence of the pentavalent state in the solution.23,83 A beat node, typical for trans dioxo actinide species, can be observed between 6 and 8.5 Å−1 among the oscillations of the real part of the k3-weighted EXAFS spectra (Fig. 5b, insert). Two large peaks present at 1.38 Å and 1.9 Å (uncorrected for the phase-shift) can be observed in the Fourier transform (FT) of the k3-weighted interval 2 Å−1 < k < 12.3 Å−1 (Fig. 5b), which indicate the presence of two well-defined coordination shells.
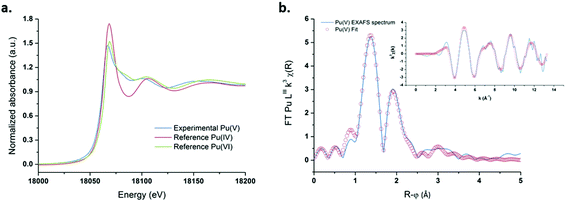 |
| | Fig. 5 (a) XANES spectrum obtained for ultrasound prepared Pu(V) (203 kHz, 20 °C, 0.13 W mL−1) and the reference spectra of pure Pu(VI) and Pu(IV). (b) FT of the experimental k3-weighted EXAFS spectrum of Pu(V) and the theoretical EXAFS spectrum obtained by the shell fit. Insert: Experimental and fitted EXAFS spectra of sonochemical Pu(V). | |
The peak present at R + φ = 1.38 Å corresponds to the scattering contribution of the Pu–Oyl distances, whereas the peak observed in the FT spectra at R + φ = 1.9 Å can be attributed to the scattering contribution of O stemming from coordinated H2O molecules. Theoretical EXAFS simulations confirmed the presence of two oxo moieties at 1.81 Å and 5.3 H2O molecules at 2.47 Å in the equatorial plane. These structural parameters are in line with those generally observed for the pentavalent state of Pu in non-complexing media although a lower coordination number has been reported for the equatorial solvation environment, notably with XAFS (Table 1).21–23,83 In agreement with the work of Ikeda-Ohno et al. dedicated to the complexation behavior of Np ions in aqueous solutions,28 we observed that PuO2+ EXAFS spectra can be simulated with very good fitting residues (R-factor <2%) and appropriate σ2 leading to a coordination number ranging from N[Oeq(H2O)] = 4 to 6. The results are summarized in Fig. S7 (ESI†) and compared with the literature data related to the PuO2+ and NpO2+ first solvation shell in aqueous non-complexing media. As suggested by this figure, the determination of the exact number of water molecules coordinating the ion in the equatorial plane with only the EXAFS technique may suffer from large errors. There appears to be a general consensus in the literature that the coordination environment of Np(V) equal to N[Oeq(H2O)] = 5, whereas the hydration number of PuO2+ is still a matter of discussion.19–21,28,73,84,85 A more relevant approach was therefore considered by simulating an EXAFS signal from PuO2+ complexes generated with 4 or 5 coordinating water molecules in the equatorial plane by DFT calculations with optimized geometries and vibrational frequencies.
Table 1 EXAFS structural parameters calculated from the k3-weighted EXAFS spectra of the sonochemical Pu(V) and its comparison with the literature data. R-factor +1.7% *fixed value, S02 = 0.8. CN: coordination number, R: interatomic distance, σ2: Debye–Waller factor, ΔE0: threshold energy. The standard deviations of the variable parameters estimated by using the IFEFFIT software are given in parentheses56,57
| Atom |
N
|
R (Å) |
σ
2/Å2 |
ΔE0 |
Ref. |
|
N for Pu–Oax is fixed at 2.0.
|
| Oyl |
2.0a |
1.81(1) |
0.002(1) |
2.38(5) |
This work |
| Oeq |
5.3(1.0) |
2.47(2) |
0.009(1) |
2.38(5) |
|
| |
| Oyl |
2.0a |
1.821 (5) |
0.001 |
— |
Panak et al.22 |
| Oeq |
3.8 (4) |
2.48 (1) |
0.005 |
— |
|
| |
| Oyl |
2.0a |
1.81(1) |
0.002 |
— |
Di Giandomenico et al.21 |
| Oeq |
3.3(8) |
2.47(2) |
0.004 |
— |
|
| |
| Oyl |
2.0a |
1.81 |
— |
— |
Conradson et al.23 |
| Oeq |
4 |
2.47 |
— |
— |
|
3.3.2. DFT calculations.
PuO2(H2O)4(H2O)8+ and PuO2(H2O)5(H2O)10+ aqua complexes with respectively four and five inner shell water molecules were considered in the DFT calculations (with optimized geometries and vibrational frequencies) and the corresponding EXAFS spectra were simulated in an attempt to discriminate the solvation shell of the PuO2+ aqua ion. In the complexes, two outer-shell water molecules are hydrogen bonded to each inner shell molecule. Preliminary studies focused on the uranyl aqua ion confirmed that the structural parameters of the aqua ion can be correctly reproduced by such DFT calculations (see the Experimental part). For both plutonyl complexes, the structural parameters are shown in Table 2 and the theoretical EXAFS spectra are compared with the experimental one as shown in Fig. 6. The simulated spectrum of PuO2(H2O)4(H2O)8+ is in very good agreement with the experimental signal, while poor agreement is found for PuO2(H2O)5(H2O)10+. For PuO2(H2O)4(H2O)8+, two well-defined shells attributed to dioxo bonds and Pu–Oeq interactions can be observed in agreement with XAFS experiments. For PuO2(H2O)5(H2O)10+, the second FT peak observed experimentally at R + φ = 1.9 Å is split into two on the FT derived from the calculated spectrum. The calculated Pu–O distances and Debye–Waller factors compare very well with the experimental distances when considering the PuO2+ complex with four inner shell water molecules. The calculated and experimental Pu–Oyl and Pu–Oeq distances lie within 0.02 Å.
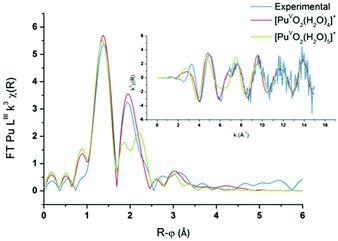 |
| | Fig. 6
Ab initio and experimental Pu LIII-edge k3-weighted EXAFS spectra (inset) and the corresponding Fourier transforms of the Pu(V) aqua ion, and the ab initio spectra of PuO2(H2O)4(H2O)8+ (red) and PuO2(H2O)5(H2O)10+ (green). | |
Table 2 Average values for DFT (B3LYP) structural parameters calculated for PuO2(H2O)4(H2O)8+ and PuO2(H2O)5(H2O)10+ complexes, interatomic distances (R) and Debye–Waller factors (σ2)
| Model |
Atom |
N
|
R (Å) |
σ
2/Å2 |
|
Pu–O distances are split into two groups of distances: 4 Pu–O at 2.54 Å and 1 Pu–O at 2.64 Å.
|
| PuO2(H2O)4(H2O)8+ |
Oyl |
2 |
1.800 |
0.0015 |
| Oeq |
4 |
2.480 |
0.0051 |
| PuO2(H2O)5(H2O)10+ |
Oyl |
2 |
1.801 |
0.0015 |
| Oeq |
5 |
2.561a |
0.0073 |
The calculated Debye–Waller factors are equal to those reported by Panak et al., which is consistent with the good match found between the simulated and experimental EXAFS signal.22 For the PuO2+ complex with five inner shell water molecules, the strong Pu–Oyl bonds remain equal to 1.80 Å and are not altered by the number of coordinating water molecules. By contrast, the value calculated for the Pu–Oeq average bond length is significantly too long by 0.08–0.09 Å to fit with the experimental results. Because of steric crowding in the inner shell, one Pu–Oeq distance is elongated. Accordingly, the calculated Debye–Waller factors are associated with the Pu–Oeq increase since the Pu–Oeq bonds become weaker than in PuO2(H2O)4(H2O)8+. To summarize, the very good agreement found with both the calculated and experimental data for the tetra-aqua PuO2+ complex strongly supports that it is the predominant PuO2+ specie in aqueous non-complexing media.
3.3.3. Magnetic susceptibility.
NMR measurements were performed by using the Evans method in several Pu(V) solutions (Fig. S8, ESI†).74,86 Particularly, the Pu(V) solution was concentrated by dry Ar bubbling overnight (3.8 mM) to provide a better signal intensity for some experiments. Fig. 7 shows the average paramagnetic behaviour of Pu(V) investigated in the 5–50 °C temperature range. To evaluate the accuracy of the measurements, the stability of the solution towards redox transformations during NMR analyses has been followed by UV-visible absorption spectroscopy (Fig. 7, inset) before and after analysis. Before NMR measurements, only traces of Pu(VI) can be noticed in the Pu(V) solution (no other oxidation states or species are observed). Such pollution corresponds to a Pu(VI) concentration of 66 μM which represents less than 1.7% of the total Pu content in the solution. After NMR analyses, the Pu(VI) content is estimated at about 30 μM (0.8% of the total Pu content). The amount of Pu(VI) engaged in the analysed solutions appears nevertheless too low to induce a significant variation of the NMR signal. No other Pu oxidation states or species are observed in these spectra emphasizing the accuracy of the obtained results despite the slight variations observed with the magnetic susceptibility values. It is also important to note that potential traces of hydrogen peroxide resulting from sonication are assumed to not interfere with the NMR signal in agreement with the literature.87
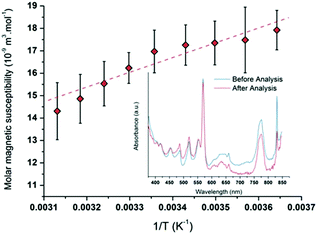 |
| | Fig. 7 Molar magnetic susceptibility as a function of 1/T averaged for different Pu(V) solutions (R2 = 0.96). UV-visible absorption spectra obtained for a 3.8 mM Pu(V) solution before and after NMR experiments showing the absence of modification of the Pu oxidation states excepted a small decrease of the Pu(VI) amount (respectively in blue and red). | |
The plotted molar magnetic susceptibilities (Fig. 7) can be fitted with a linear regression in agreement with a Curie-like law (χ−1 linear with T); the slope of this regression gives a Curie constant of about 6.896 × 10−6 m3 K mol−1. In comparison with the other Pu oxidation states measured in perchloric solutions (Table 3), the experimental value measured at 25 °C for Pu(V) magnetic susceptibility (χM = 16.3 × 10−9 m3 mol−1) is situated between the ones measured for Pu(III) and Pu(IV) (χM = 4.7 × 10−9 and 28.4 × 10−9 m3 mol−1, respectively;18,88 Pu(VI) is much higher).17 Nevertheless, Pu(V) susceptibility is lower than the predicted value for the free ion taking into account the ground state J = 9/2 only (χM about 70 × 10−9 m3 mol−1) and even lower than the one reported for Np(IV) (χM = 48.6 × 10−9 m3 mol−1) which exhibits the same isoelectronic 5f3 configuration.18 The observed difference between Np(IV) and Pu(V) ions supports the current investigations related to the development of theoretical models dedicated to the study of the magnetic susceptibility shifts as a function of the electronic configuration.
Table 3 Comparison of the magnetic susceptibility (χM) of some Pu and Np ions experimentally measured at 25 °C in perchloric media
| Species |
χ
M (10−9 m3 mol−1) |
Ref. |
| Pu(III) |
4.7 |
Autillo et al.88 |
| Pu(IV) |
28.4 |
Autillo et al.18 |
| Pu(V) |
16.3 |
This work |
| Np(IV) |
48.6 |
Autillo et al.18 |
4. Conclusions
This work describes a facile and original sonochemical method for the preparation of Pu(V) solutions free from the admixture of other oxidation states of plutonium. Under the studied conditions, Pu(VI) reduction occurs through the ultrasonically triggered generation of H2O2 in water which can be dramatically enhanced under an Ar/O2 atmosphere and high-frequency ultrasound (203 kHz). Ultrasonic irradiation allows Pu(VI) reduction without the addition of any side chemicals and avoids dilutions often correlated to hydrolysis issues. The prepared Pu solutions are in the millimolar range and are quasi-exclusively composed of Pu(V). Traces of Pu(VI) in the range of the percent can eventually pollute the prepared solutions which were found to be stable for almost one month. Such conditions allowed the solutions to be characterized by XANES and EXAFS spectroscopy which confirmed the presence of the Pu(V) aqua ion in agreement with the literature. The solvation environment of the PuO2+ aqua complex was clarified by simulating EXAFS spectra from optimized PuO2+ structures generated from DFT calculations which evidenced that the tetra-aqua complex [PuVO2(H2O)4(H2O)8]+ dominates in aqueous non-complexing media. For the first time, NMR measurements were enabled for Pu(V) which allowed us to determine its magnetic susceptibility (χM = 16.3 × 10−9 m3 mol−1 at 25 °C) and the Curie constant (C = 6.896 × 10−6 m3 K mol−1). Generally, this work provides an original approach for Pu(V) preparation which contributes to providing new insights regarding its structure and magnetic properties. The preparation of more concentrated Pu(V) solutions is in progress and should improve the accuracy of future investigations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the French CEA/DEN for financial support. Our special thanks to M. Guigue, J. Vermeulen, and J. Maurin for their help in experiments.
References
- S. W. Rabideau and R. J. Kline, J. Phys. Chem., 1958, 62, 617–620 CrossRef CAS.
-
D. Clark, S. Hecker, G. Jarvinen and M. Neu, in The Chemistry of the Actinide and Transactinide Elements, ed. L. Morss, N. Edelstein and J. Fuger, Springer, Netherlands, 2011, ch. 7, pp. 813–1264, DOI:10.1007/978-94-007-0211-0_7.
-
W. Newton
, The kinetics of the oxidation–reduction reactions of uranium, neptunium, plutonium, and americium in solutions, Report TID-26506, Los Alamos Scientific Laboratory, 1975.
- V. Neck, M. Altmaier, A. Seibert, J. I. Yun, C. M. Marquardt and T. Fanghanel, Radiochim. Acta, 2007, 95, 193–207 CrossRef CAS.
- S. Topin and J. Aupiais, J. Environ. Radioact., 2016, 153, 237–244 CrossRef CAS PubMed.
- K. A. Orlandini, W. R. Penrose and D. M. Nelson, Mar. Chem., 1986, 18, 49–57 CrossRef CAS.
- W. R. Penrose, D. N. Metta, J. M. Hylko and L. A. Rinckel, J. Environ. Radioact., 1987, 5, 169–184 CrossRef CAS.
- W. R. Penrose, W. L. Polzer, E. H. Essington, D. M. Nelson and K. A. Orlandini, Environ. Sci. Technol., 1990, 24, 228–234 CrossRef CAS.
- W. L. Keeney-Kennicutt and J. W. Morse, Geochim. Cosmochim. Acta, 1985, 49, 2577–2588 CrossRef CAS.
-
G. T. Seaborg, J. J. Katz and W. M. Manning, The Transuranium Elements: Research Papers, McGraw-Hill Book Co., Inc., New York, 1949 Search PubMed.
- R. E. Connick, J. Am. Chem. Soc., 1949, 71, 1528–1533 CrossRef CAS.
- A. L. Sanchez, J. W. Murray and T. H. Sibley, Geochim. Cosmochim. Acta, 1985, 49, 2297–2307 CrossRef CAS.
- M. P. Neu, D. C. Hoffman, K. E. Roberts, H. Nitsche and R. J. Silva, Radiochim. Acta, 1994, 66–7, 251–258 Search PubMed.
- N. A. Conroy, E. M. Wylie and B. A. Powell, Anal. Chem., 2016, 88, 4196–4199 CrossRef CAS PubMed.
- D. Cohen, J. Inorg. Nucl. Chem., 1961, 18, 207–210 CrossRef CAS.
- S. W. Rabideau, J. Am. Chem. Soc., 1957, 79, 6350–6353 CrossRef CAS.
- T. F. Wall, S. Jan, M. Autillo, K. L. Nash, L. Guerin, C. Le Naour, P. Moisy and C. Berthon, Inorg. Chem., 2014, 53, 2450–2459 CrossRef CAS PubMed.
- M. Autillo, L. Guerin, D. Guillaumont, P. Moisy, H. Bolvin and C. Berthon, Inorg. Chem., 2016, 55, 12149–12157 CrossRef CAS PubMed.
- K. E. Knope and L. Soderholm, Chem. Rev., 2013, 113, 944–994 CrossRef CAS PubMed.
- M. R. Antonio, L. Soderholm, C. W. Williams, J. P. Blaudeau and B. E. Bursten, Radiochim. Acta, 2001, 89, 17–25 CrossRef CAS.
- M. V. Di Giandomenico, C. Le Naour, E. Simoni, D. Guillaumont, P. Moisy, C. Hennig, S. D. Conradson and C. Den Auwer, Radiochim. Acta, 2009, 97, 347–353 CrossRef CAS.
- P. J. Panak, C. H. Booth, D. L. Caulder, J. J. Bucher, D. K. Shuh and H. Nitsche, Radiochim. Acta, 2002, 90, 315–321 CAS.
- S. D. Conradson, K. D. Abney, B. D. Begg, E. D. Brady, D. L. Clark, C. den Auwer, M. Ding, P. K. Dorhout, F. J. Espinosa-Faller, P. L. Gordon, R. G. Haire, N. J. Hess, R. F. Hess, D. W. Keogh, G. H. Lander, A. J. Lupinetti, L. A. Morales, M. P. Neu, P. D. Palmer, P. Paviet-Hartmann, S. D. Reilly, W. H. Runde, C. D. Tait, D. K. Veirs and F. Wastin, Inorg. Chem., 2004, 43, 116–131 CrossRef CAS PubMed.
- S. D. Conradson, Appl. Spectrosc., 1998, 52, 252A–279A CrossRef CAS.
- S. Tsushima and A. Suzuki, J. Mol. Struct. (THEOCHEM), 2000, 529, 21–25 CrossRef CAS.
- A. Y. Garnov, N. N. Krot, A. A. Bessonov and V. P. Perminov, Radiochemistry, 1996, 38, 402–406 CAS.
- P. J. Hay, R. L. Martin and G. Schreckenbach, J. Phys. Chem. A, 2000, 104, 6259–6270 CrossRef CAS.
- A. Ikeda-Ohno, C. Hennig, A. Rossberg, H. Funke, A. C. Scheinost, G. Bernhard and T. Yaita, Inorg. Chem., 2008, 47, 8294–8305 CrossRef CAS PubMed.
- S. O. Odoh, E. J. Bylaska and W. A. de Jong, J. Phys. Chem. A, 2013, 117, 12256–12267 CrossRef CAS PubMed.
- A. E. Clark, A. Samuels, K. Wisuri, S. Landstrom and T. Saul, Inorg. Chem., 2015, 54, 6216–6225 CrossRef CAS PubMed.
- V. S. Koltunov, I. A. Kulikov, N. V. Kermanova and L. K. Nikishova, Sov. Radiochem., 1981, 23, 384–386 Search PubMed.
-
G. A. Fugate and J. D. Navratil, in Separations for the Nuclear Fuel Cycle in the 21st Century, ed. G. J. Lumetta, K. L. Nash, S. B. Clark and J. I. Friese, American Chemical Society, Washington, 2006, vol. 933, pp. 167–181 Search PubMed.
- V. I. Marchenko, K. N. Dvoeglazov and V. I. Volk, Radiochemistry, 2009, 51, 329–344 CrossRef CAS.
-
S. F. Marsh and T. D. Gallegos, Chemical treatment of plutonium with hydrogen peroxide before nitrate anion exchange processing. [Reduction to (IV)], Report LA-10907, 1987.
-
A. J. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, Taylor & Francis, 1985 Search PubMed.
- C. Maillard and J. M. Adnet, Radiochim. Acta, 2001, 89, 485–490 CrossRef CAS.
- S. I. Nikitenko, L. Venault, R. Pflieger, T. Chave, I. Bisel and P. Moisy, Ultrason. Sonochem., 2010, 17, 1033–1040 CrossRef CAS PubMed.
- M. Virot, L. Venault, P. Moisy and S. I. Nikitenko, Dalton Trans., 2015, 44, 2567–2574 RSC.
-
T. J. Mason and J. P. Lorimer, Applied sonochemistry, The uses of power ultrasound in chemistry and processing, Weinheim, 2002 Search PubMed.
- K. Makino, M. M. Mossoba and P. Riesz, J. Am. Chem. Soc., 1982, 104, 3537–3539 CrossRef CAS.
- K. Makino, M. M. Mossoba and P. Riesz, J. Phys. Chem., 1983, 87, 1369–1377 CrossRef CAS.
- E. J. Hart and A. Henglein, J. Phys. Chem., 1985, 89, 4342–4347 CrossRef CAS.
- C. H. Fischer, E. J. Hart and A. Henglein, J. Phys. Chem., 1986, 90, 1954–1956 CrossRef CAS.
- C. H. Fischer, E. J. Hart and A. Henglein, J. Phys. Chem., 1986, 90, 222–224 CrossRef CAS.
- E. L. Mead, R. G. Sutherland and R. E. Verrall, Can. J. Chem., 1976, 54, 1114–1120 CrossRef CAS.
- C. Petrier, A. Jeunet, J. L. Luche and G. Reverdy, J. Am. Chem. Soc., 1992, 114, 3148–3150 CrossRef CAS.
- M. A. Beckett and I. Hua, J. Phys. Chem., 2001, 105, 3796–3802 CrossRef CAS.
- N. M. Navarro, T. Chave, P. Pochon, I. Bisel and S. I. Nikitenko, J. Phys. Chem. B, 2011, 115, 2024–2029 CrossRef CAS PubMed.
- R. Pflieger, T. Chave, G. Vite, L. Jouve and S. I. Nikitenko, Ultrason. Sonochem., 2015, 26, 169–175 CrossRef CAS PubMed.
- E. Dalodière, M. Virot, P. Moisy and S. I. Nikitenko, Ultrason. Sonochem., 2016, 29, 198–204 CrossRef PubMed.
- I. Hua and M. R. Hoffmann, Environ. Sci. Technol., 1997, 31, 2237–2243 CrossRef CAS.
- P. R. Gogate, A. M. Wilhelm and A. B. Pandit, Ultrason. Sonochem., 2003, 10, 325–330 CrossRef CAS PubMed.
- T. Chave, N. M. Navarro, S. Nitsche and S. I. Nikitenko, Chem. – Eur. J., 2012, 18, 3879–3885 CrossRef CAS PubMed.
-
T. J. Mason, Practical sonochemistry: user's guide to applications in chemistry and chemical engineering, E. Horwood, 1991 Search PubMed.
- W. Matz, N. Schell, G. Bernhard, F. Prokert, T. Reich, J. Claussner, W. Oehme, R. Schlenk, S. Dienel, H. Funke, F. Eichhorn, M. Betzl, D. Prohl, U. Strauch, G. Huttig, H. Krug, W. Neumann, V. Brendler, P. Reichel, M. A. Denecke and H. Nitsche, J. Synchrotron Radiat., 1999, 6, 1076–1085 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- B. Ravel and M. Newville, Phys. Scr., 2005, 1007–1010 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- W. Kuchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- X. Y. Cao, M. Dolg and H. Stoll, J. Chem. Phys., 2003, 118, 487–496 CrossRef CAS.
- X. Y. Cao and M. Dolg, J. Mol. Struct. (THEOCHEM), 2004, 673, 203–209 CrossRef CAS.
-
M. J. Frisch, Gaussian 09, Wallingford, CT, 2009 Search PubMed.
- E. Acher, Y. H. Cherkaski, T. Dumas, C. Tamain, D. Guillaumont, N. Boubals, G. Javierre, C. Hennig, P. L. Solari and M. C. Charbonnel, Inorg. Chem., 2016, 55, 5558–5569 CrossRef CAS PubMed.
- E. Acher, T. Dumas, C. Tamain, N. Boubals, P. L. Solari and D. Guillaumont, Dalton Trans., 2017, 46, 3812–3815 RSC.
- J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513 RSC.
- F. D. Vila, V. E. Lindahl and J. J. Rehr, Phys. Rev. B: Condens. Matter, 2012, 85 CrossRef CAS , 024303.
- J. Neuefeind, L. Soderholm and S. Skanthakumar, J. Phys. Chem. A, 2004, 108, 2733–2739 CrossRef CAS.
- B. Siboulet, C. J. Marsden and P. Vitorge, Chem. Phys., 2006, 326, 289–296 CrossRef CAS.
- K. E. Gutowski and D. A. Dixon, J. Phys. Chem. A, 2006, 110, 8840–8856 CrossRef CAS PubMed.
- L. Semon, C. Boehme, I. Billard, C. Hennig, K. Lutzenkirchen, T. Reich, A. Rossberg, I. Rossini and G. Wipff, ChemPhysChem, 2001, 2, 591–598 CrossRef CAS PubMed.
- H. A. Thompson, G. E. Brown and G. A. Parks, Am. Mineral., 1997, 82, 483–496 CAS.
- U. Wahlgren, H. Moll, I. Grenthe, B. Schimmelpfennig, L. Maron, V. Vallet and O. Gropen, J. Phys. Chem. A, 1999, 103, 8257–8264 CrossRef CAS.
- P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and T. Reich, Inorg. Chem., 1997, 36, 4676–4683 CrossRef CAS PubMed.
- D. F. Evans, J. Chem. Soc., 1959, 2003–2005 RSC.
- R. J. Wood, J. Lee and M. J. Bussemaker, Ultrason. Sonochem., 2017, 38, 351–370 CrossRef CAS PubMed.
-
B. Lesigne, PhD thesis, Centre d’études nucléaires de Fontenay-aux-Roses, 1967 Search PubMed.
-
G. A. Fugate and J. D. Navratil, in Acs Sym Ser, American Chemical Society, 2006, vol. 933, ch. 11, pp. 167–181 Search PubMed.
- S. Merouani, H. Ferkous, O. Hamdaoui, Y. Rezgui and M. Guemini, Ultrason. Sonochem., 2015, 22, 51–58 CrossRef CAS PubMed.
- J. Lee, M. Ashokkumar, S. Kentish and F. Grieser, J. Am. Chem. Soc., 2005, 127, 16810–16811 CrossRef CAS PubMed.
- A. A. Ndiaye, R. Pflieger, B. Siboulet, J. Molina, J. F. Dufreche and S. I. Nikitenko, J. Phys. Chem. A, 2012, 116, 4860–4867 CrossRef CAS PubMed.
- R. E. Connick and W. H. Mcvey, J. Am. Chem. Soc., 1949, 71, 1534–1542 CrossRef CAS.
- E. Dalodière, M. Virot, V. Morosini, T. Chave, T. Dumas, C. Hennig, T. Wiss, O. Dieste Blanco, D. K. Shuh, T. Tyliszcak, L. Venault, P. Moisy and S. I. Nikitenko, Sci. Rep., 2017, 7, 43514 CrossRef PubMed.
- S. D. Conradson, I. Al Mahamid, D. L. Clark, N. J. Hess, E. A. Hudson, M. P. Neu, P. D. Palmer, W. H. Runde and C. Drew Tait, Polyhedron, 1998, 17, 599–602 CrossRef CAS.
- J. M. Combes, C. J. Chisholmbrause, G. E. Brown, G. A. Parks, S. D. Conradson, P. G. Eller, I. R. Triay, D. E. Hobart and A. Meijer, Environ. Sci. Technol., 1992, 26, 376–382 CrossRef CAS.
- T. Reich, G. Bernhard, G. Geipel, H. Funke, C. Hennig, A. Rossberg, W. Matz, N. Schell and H. Nitsche, Radiochim. Acta, 2000, 88, 633–637 CrossRef CAS.
- K. De Buysser, G. G. Herman, E. Bruneel, S. Hoste and I. Van Driessche, Chem. Phys., 2005, 315, 286–292 CrossRef CAS.
- M. Autillo, P. Kaden, A. Geist, L. Guerin, P. Moisy and C. Berthon, Phys. Chem. Chem. Phys., 2014, 16, 8608–8614 RSC.
- M. Autillo, L. Guerin, H. Bolvin, P. Moisy and C. Berthon, Phys. Chem. Chem. Phys., 2016, 18, 6515–6525 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7qi00389g |
|
| This journal is © the Partner Organisations 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Thomas
Dumas
*a,
Thomas
Dumas
 b,
Dominique
Guillaumont
b,
Marie-Claire
Illy
b,
Claude
Berthon
b,
Dominique
Guillaumont
b,
Marie-Claire
Illy
b,
Claude
Berthon
 b,
Laëtitia
Guerin
b,
André
Rossberg
c,
Laurent
Venault
b,
Philippe
Moisy
b,
Laëtitia
Guerin
b,
André
Rossberg
c,
Laurent
Venault
b,
Philippe
Moisy
 b and
Sergey I.
Nikitenko
b and
Sergey I.
Nikitenko
 a
a
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds at 1.81 Å and 4–6 equatorial Pu–Oeq interactions at 2.47 Å characteristic of coordinated water molecules. The exact number of water molecules (N[Oeq(H2O)] = 4) was determined by simulating the EXAFS spectra of the PuO2+ aqua complexes using DFT calculations (geometry and the Debye–Waller factor) and comparing them with experimental signals. For the first time, the magnetic susceptibility of the pentavalent state of plutonium in aqueous solutions was also determined (χM = 16.3 × 10−9 m3 mol−1 at 25 °C) and the related Curie constant was estimated (C = 6.896 × 10−6 m3 K mol−1).
O bonds at 1.81 Å and 4–6 equatorial Pu–Oeq interactions at 2.47 Å characteristic of coordinated water molecules. The exact number of water molecules (N[Oeq(H2O)] = 4) was determined by simulating the EXAFS spectra of the PuO2+ aqua complexes using DFT calculations (geometry and the Debye–Waller factor) and comparing them with experimental signals. For the first time, the magnetic susceptibility of the pentavalent state of plutonium in aqueous solutions was also determined (χM = 16.3 × 10−9 m3 mol−1 at 25 °C) and the related Curie constant was estimated (C = 6.896 × 10−6 m3 K mol−1).![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Pu4+ + PuO22+·2H2O
Pu4+ + PuO22+·2H2O![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Pu3+ + 2PuO22+ + 2H2O
Pu3+ + 2PuO22+ + 2H2O![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Pu3+ + O2 + 2H+
2Pu3+ + O2 + 2H+![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) 2Pu4+ + 2H2O
2Pu4+ + 2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with a 1.2 × 10−2 M TiOSO4 solution (0.330 g of TiOSO4 dissolved in 100 mL of pure water under stirring and previously gently heated in 3.5 mL of 18 M H2SO4) to form a colorimetric complex absorbing at 410 nm (ε = 710 cm−2 M−1).50 An external calibration curve was previously prepared with a H2O2 standard solution.
1) with a 1.2 × 10−2 M TiOSO4 solution (0.330 g of TiOSO4 dissolved in 100 mL of pure water under stirring and previously gently heated in 3.5 mL of 18 M H2SO4) to form a colorimetric complex absorbing at 410 nm (ε = 710 cm−2 M−1).50 An external calibration curve was previously prepared with a H2O2 standard solution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 eV. Experimental spectra were recorded at the Pu LIII edge and the ionization energy (E0) was preliminary defined at the maximum of the white line and varied as a free fit parameter. The energy range investigated for EXAFS (Extended X-ray Absorption Fine Structure) measurements was chosen depending on the Pu content in the samples from 3.3 Å−1 to 12.3 Å−1. EXAFS data analyses were performed with Athena and Artemis software from the ifeffit package56,57 and theoretical scattering phases and amplitude functions were calculated by the ab initio FEFF8.4 code from the hypothetical plutonyl structure.58 All fitting operations were performed in the R-space over individual radial distances: 2 Oyl and several Oeq(H2O) with the corresponding Debye–Weller factors (σ2) for every considered distance in the first coordination shell.
998 eV. Experimental spectra were recorded at the Pu LIII edge and the ionization energy (E0) was preliminary defined at the maximum of the white line and varied as a free fit parameter. The energy range investigated for EXAFS (Extended X-ray Absorption Fine Structure) measurements was chosen depending on the Pu content in the samples from 3.3 Å−1 to 12.3 Å−1. EXAFS data analyses were performed with Athena and Artemis software from the ifeffit package56,57 and theoretical scattering phases and amplitude functions were calculated by the ab initio FEFF8.4 code from the hypothetical plutonyl structure.58 All fitting operations were performed in the R-space over individual radial distances: 2 Oyl and several Oeq(H2O) with the corresponding Debye–Weller factors (σ2) for every considered distance in the first coordination shell.