Kinetic enhancement in high-activity enzyme complexes attached to nanoparticles†
Anthony P.
Malanoski
 a,
Joyce C.
Breger
a,
Carl W.
Brown
III
a,
Joyce C.
Breger
a,
Carl W.
Brown
III
 ab,
Jeffrey R.
Deschamps
a,
Kimihiro
Susumu
cd,
Eunkeu
Oh
cd,
George P.
Anderson
a,
Scott A.
Walper
a and
Igor L.
Medintz
ab,
Jeffrey R.
Deschamps
a,
Kimihiro
Susumu
cd,
Eunkeu
Oh
cd,
George P.
Anderson
a,
Scott A.
Walper
a and
Igor L.
Medintz
 *a
*a
aCenter for Bio/Molecular Science and Engineering, Code 6900, U.S. Naval Research Laboratory, Washington, DC 20375, USA. E-mail: Igor.medintz@nrl.navy.mil
bCollege of Science, George Mason University, Fairfax, VA 22030, USA
cOptical Sciences Division, Code 5600, U.S. Naval Research Laboratory, Washington, DC 20375, USA
dSotera Defense Solutions, Inc., Columbia, MD 21046, USA
First published on 25th July 2017
Abstract
Accumulating studies by many groups have found consistent enhancement in a wide variety of enzyme activities when they are displayed around nanoparticles. However, the underlying mechanism(s) that give rise to this phenomenon are still largely unknown. Herein, we develop a detailed reaction scheme that considers many of the various possible interactions between a substrate and a given enzyme–nanoparticle bioconjugate. The properties and some functional predictions that emanate from the reaction scheme were then tested using a model system where the homotetrameric beta-galactosidase enzyme complex was assembled with luminescent semiconductor nanocrystalline quantum dots displayed around its periphery. This type of assembly occurs as the ∼465 kDa enzyme complex is significantly larger than the 4.2 nm diameter green emitting quantum dots utilized. This unique architecture, in conjunction with the fact that this enzyme functions at or near the diffusion limit, provided a unique opportunity to selectively probe certain aspects of enzyme enhancement when attached to a nanoparticle with minimal potential perturbations to the native enzyme structure. Experimental assays were conducted where both free enzymes and quantum dot-decorated enzymes were compared directly in side-by-side samples and included formats where the kinetic processes were challenged with increasing viscosity and competitive inhibitors. The results strongly suggest that it is possible for there to be significant enhancements in an enzyme's catalytic rate or kcat after attachment to a nanoparticle even when it is apparently diffusion limited without requiring any gross changes to the enzyme's structure. A discussion of how this reaction scheme and model can be applied to other systems is provided.
Conceptual insightsWe provide insight into the growing phenomena of enzyme enhancement when displayed at a nanoparticle interface. To accomplish this we develop a de novo model based on the classical Michaelis–Menten formalism to describe the activity of an enzyme in this configuration. Beyond just the enzyme, this model now accounts for many of the interactions between the substrate, product, and nanoparticle. We then utilize the model to make predictions about what type of behavior should be manifested for this configuration and experimentally test the predictions using the unique system of quantum dots displayed around the periphery of the diffusion limited enzyme beta-galactosidase. This is the first example where a model is developed to describe these materials, utilized to predict the activity and then tested. Given the growing importance of cell free synthetic biology, the approach demonstrated here sheds light on how enzymes can be utilized ex vivo and, more importantly, undergo kinetic enhancement when attached to nanoscale scaffolds. |
Introduction
The utilization of enzymes as catalysts ex vivo has become increasingly important for the production of pharmaceuticals and fine chemicals amongst other applications and has recently received considerable attention as a mechanism towards “green” industrial production.1,2 This is primarily because enzymes have evolved over billions of years to catalyse exquisitely complex chemical reactions at moderate temperatures and pressures in benign solutions. For effective utilization of enzymes in this context, methods to enhance their stability and performance in non-native environments, i.e. extracellularly in assays or fermenters, are critically required to increase their useful lifetime and ease of use, and minimize the amount of enzyme required.3,4 The attachment of enzymes to surfaces has been generally found to enhance enzyme stability and facilitate their industrial use but this is very often at a substantial cost in their catalytic activity.5 This is believed to arise from the heterogeneous chemistries very often used for surface attachment which lead to less than optimal enzyme conformations along with restricting enzyme movement; the latter two issues can also combine to inhibit substrate sampling. Moreover, the use of large planar substrates for attachment can lead to sequestration of the localized enzyme environment from the bulk solution by laminar processes.6 Clearly, a greater fundamental understanding of how the attachment of enzymes to surfaces affects their performance would provide opportunities to enhance their performance further.Over the last few years, many research groups, including our own, have observed consistent improvements in Michaelis–Menten (MM) rate parameters after attachment of the enzyme to some type of nanoparticle (NP) material.5,7,8 This has been seen for a wide range of enzymes displaying quite diverse activities and with many different types of nanoparticulate scaffolds. Although many different NP materials are available, within our studies we have primarily utilized luminescent nanocrystalline semiconductor quantum dots (QDs) as a prototypical NP due to the multiple inherent benefits they provide for such assays. Along with brightness for easy tracking and a strong resistance to chemical degradation, QDs have a very low size polydispersity (<10%) and provide access to facile, highly-controllable bioconjugation chemistry.9,10 Assembling QDs with four different enzymes resulted in different degrees of kinetic improvement, which, when analysed in more detail, appeared to possibly arise from different underlying mechanistic causes.11–14 The first enzyme tested, alkaline phosphatase, is an ∼100 kDa dimeric enzyme that is often used in molecular biology as a reporter enzyme since it has a very high rate of activity that approaches diffusion limitations when functioning optimally.13 Displaying alkaline phosphatase on various sizes of QDs demonstrated some marginal improvements in its activity. Here, both the rate of catalytic activity (kcat) and the overall catalytic efficiency (kcat/KM) increased to ca. 25%. The KM (the Michaelis constant and a reflection of the enzyme affinity for the substrate) stayed unchanged, signifying that the enzyme structure remained intact.13 In contrast to these modest improvements, displaying phosphotriesterase (PTE) on the same QDs had a far more dramatic result.11 This ∼75 kDa dimeric enzyme is capable of hydrolysing organophosphate ester molecules having a phosphate center surrounded by 3 O-linked groups such as the insecticide paraoxon and structurally related nerve agents such as sarin and tabun.15,16 The attachment of PTE to QDs resulted in 4-fold increases in the catalytic activity along with 2-fold increases in the efficiency.11 Interestingly, in this case the corresponding KM values appeared to be detrimentally affected and they actually increased in magnitude (a lower affinity). Further experiments established that under the right conditions the off-rate of the product from PTE was the rate-limiting step and the attachment to QDs altered this step in a productive manner leading to the observed enhancements. Similar rates of kcat enhancement over non-QD coordinated activity were also observed for a spontaneously forming recombinant PTE trimer that was expressed as a monomer fused to a collagen helical domain.12 The other NP–enzyme system we studied that also exhibited a large change in the measured kcat from initial rate experiments after QD attachment utilized beta-galactosidase (β-gal).14 This large tetrameric enzyme complex (∼465 kDa, monomer ∼116.3 kDa) is commonly utilized as a reporter enzyme and operates with an extremely high efficiency that under the right conditions can also be diffusion-limited.17 Given the large size of the enzyme, QDs were displayed around the enzyme in assays rather than the previous and converse configuration, see Fig. 1. In these assemblies, enhancements of up to ∼4.5-fold in kcat were observed following QD attachment along with corresponding increases in the KM value (again less affinity). The latter, however, may be explained by the fact that if the system is altered with enhancements to kcat occurring while the system remains diffusion limited, then the value of KM measured in the MM model will have to change (increase) by a corresponding, compensating amount to maintain the same enzyme efficiency or kcat/KM value.18 In this example with its putative maximal enzymatic efficiency already achieved, the enhancement in kcat was postulated to arise from substrate sequestration around the QD complex, which resulted in the appearance of a super-diffusional rate of activity.14
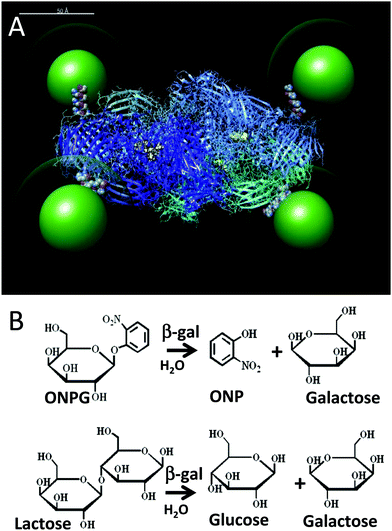 | ||
| Fig. 1 (A) Simulation of the β-gal enzyme (PDB 1DP0) displaying 525 nm green emitting QDs (green) coated with a CL4 ligand (green halo). The CL4 ligand structure is available in the ESI.† The 4 pendent His6 tags from each of the enzyme monomers connect the enzyme to the QDs and are shown in space filling mode at the enzyme periphery. Each of the four tetrameric subunits are shown as ribbons with different colors and each has their active sites highlighted in yellow. The simulation was prepared as described by Brown et al.14 but with appropriate adjustments to the QD size. Scale bar = 50 Å. (B) Top, ONPG reaction that is used to monitor β-gal activity in assays via the ONP absorbance at 420 nm. Bottom, β-gal hydrolysis of lactose into glucose and galactose. | ||
At the time of the initial study, the determination of the rate-limiting step for this enzyme when attached to QDs was not established; however, β-gal is well known to exhibit some types of product inhibition.19–21 In this report, we continue to study this unique QD-β-gal system seeking to further understand what mechanisms give rise to the apparent super-diffusional enhancements. We begin by considering what type of model system could incorporate the observed NP-attached behaviour and then experimentally probe the model with changes in the assay buffer viscosity and addition of product/inhibitor. The resulting analysis suggests that a productive modification to a rate-limiting step might be occurring in the QD assemblies and that the behaviour of other NP–enzyme systems may be consistent with a single model mechanism.
Experimental
Quantum dots
CdSe/ZnS core/shell QDs with an emission maxima centered at ∼525 nm were synthesized and solubilized with a dihydrolipoic acid–zwitterionic compact ligand (CL4) as previously described.22 Such CL4-functionalized QDs demonstrate good biocompatibility, high quantum yields, and long-term stability across a broad pH range. TEM analysis of >100 QDs showed that the 525 nm QDs have a diameter of 4.2 ± 0.5 nm yielding a corresponding hard surface area of ∼55.4 nm2 (see the ESI†).13,23,24β-galactosidase and enzymatic assays
β-gal was recombinantly expressed and prepared as described.14 The 2-nitrophenyl β-D-galactopyranoside substrate (abbreviated as ONPG; O-ortho) was obtained from Sigma Aldrich (St. Louis, MO). Stock solutions of 2 mg mL−1 ONPG in 1× phosphate buffered saline (PBS: 10 mM phosphate buffer, 2.7 mM potassium chloride, and 137 mM sodium chloride, pH 8) were prepared and the β-gal activity was assayed in a similar manner as described previously.14 Experiments were performed side-by-side to compare the activity of the enzyme as assembled on the 525 nm QDs or as freely diffusing in solution. Stock solutions of β-gal (4 nM) or 525 QD-(β-gal)4 (16 nm QD: 4 nm β-gal, respectively) were prepared in 1× PBS or 1× PBS/glycerol and allowed to assemble for at least 30 min. Previous studies have shown that this is sufficient time for the assembly of many enzymes around a QD and that a Poisson distribution of enzyme–QD constructs will result.10,25 Due to β-gal's unique tetrameric QD-coordinating capability, ratios of 4 QDs per enzyme complex were utilized in the experiments and are abbreviated as 525 QD-(β-gal)4. While individual subunits of the tetrameric enzyme can interact with at most a single QD, thereby limiting the maximum ratio to 4 QDs per enzyme, aggregation of multiple enzymes and QD groupings is possible. Although the majority of constructs will form as 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 QD
1 QD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) enzyme, a small fraction may also display lower ratios.10,25 However, the presence of multiple QD
enzyme, a small fraction may also display lower ratios.10,25 However, the presence of multiple QD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) enzyme ratios within a sample does not deleteriously affect the observed assay results and still allows the data to be directly compared to those of free enzyme configurations.26 For the viscosity experiments, the PBS/glycerol solutions correspond to solutions with viscosities (η) ranging from 1 to ∼3 (with the corresponding range of 0 to ∼40% w/w glycerol). For product inhibition studies, stock solutions of lactose ranging in concentration from 0.02 to 200 mM were also prepared in 1× PBS. Lactose was diluted into stock solutions of free β-gal and QD-β-gal assemblies such that the final lactose concentration ranged from 0 to 20 mM while the final β-gal concentration was 4 nM with or without the QD assembly. These solutions were further incubated for three hours at room temperature.
enzyme ratios within a sample does not deleteriously affect the observed assay results and still allows the data to be directly compared to those of free enzyme configurations.26 For the viscosity experiments, the PBS/glycerol solutions correspond to solutions with viscosities (η) ranging from 1 to ∼3 (with the corresponding range of 0 to ∼40% w/w glycerol). For product inhibition studies, stock solutions of lactose ranging in concentration from 0.02 to 200 mM were also prepared in 1× PBS. Lactose was diluted into stock solutions of free β-gal and QD-β-gal assemblies such that the final lactose concentration ranged from 0 to 20 mM while the final β-gal concentration was 4 nM with or without the QD assembly. These solutions were further incubated for three hours at room temperature.
For the assays themselves, 25 μL of the enzyme or the enzyme–QD stock solution at each lactose concentration or glycerol % w/w was pipetted into a 384-well white, clear flat bottom microtiter well plate. Serial dilutions of ONPG ranging in concentration from 40 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μM were also made in 1× PBS or 1× PBS/glycerol in the range of 0–40% w/w. 60 μL of ONPG solution was added to the horizontal rows at each concentration in a 96-well microtiter plate. Utilizing a 12-well multichannel pipette, 25 μL of ONPG was added to each well of the 384-well plate. The final concentration of QDs per well in the assays was kept at 8 nM and the concentration of β-gal was maintained at 2 nM. The final concentration of ONPG in the plate ranged from 20 to 5000 μM and the concentration of lactose ranged from 0 to 10
000 μM were also made in 1× PBS or 1× PBS/glycerol in the range of 0–40% w/w. 60 μL of ONPG solution was added to the horizontal rows at each concentration in a 96-well microtiter plate. Utilizing a 12-well multichannel pipette, 25 μL of ONPG was added to each well of the 384-well plate. The final concentration of QDs per well in the assays was kept at 8 nM and the concentration of β-gal was maintained at 2 nM. The final concentration of ONPG in the plate ranged from 20 to 5000 μM and the concentration of lactose ranged from 0 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μM. The plate was immediately assayed using a Tecan Infinite M1000 plate reader with a kinetic program consisting of shaking the plate for 3–5 s and reading the product absorbance at 420 nm every 20 to 25 seconds for up to 1 hour to generate enzymatic progress curves. The absorbance values were converted into concentrations of ortho-nitrophenol (ONP) utilizing a standard curve. The standard curve was prepared using a 3 mg mL−1 ONPG solution in 1× PBS and exposing it to β-gal overnight at room temperature. The resulting solution was serially diluted in 1× PBS and the absorbance values were measured at 420 nm. All experiments were performed at 25 °C with lactose experiments performed in triplicate and glycerol experiments performed in sextuplet. Linear portions of the progress curves were used to calculate the initial rate at each ONPG concentration.11–14
000 μM. The plate was immediately assayed using a Tecan Infinite M1000 plate reader with a kinetic program consisting of shaking the plate for 3–5 s and reading the product absorbance at 420 nm every 20 to 25 seconds for up to 1 hour to generate enzymatic progress curves. The absorbance values were converted into concentrations of ortho-nitrophenol (ONP) utilizing a standard curve. The standard curve was prepared using a 3 mg mL−1 ONPG solution in 1× PBS and exposing it to β-gal overnight at room temperature. The resulting solution was serially diluted in 1× PBS and the absorbance values were measured at 420 nm. All experiments were performed at 25 °C with lactose experiments performed in triplicate and glycerol experiments performed in sextuplet. Linear portions of the progress curves were used to calculate the initial rate at each ONPG concentration.11–14
Fitting procedures
All initial enzymatic rate versus substrate concentration data were fitted to various models using the nonlinear fitting module in Mathematica. Mathematica was also used to generate the initial rate versus substrate solutions for the full reaction model which included the NP-enhanced pathways under the quasi-steady-state assumption.27Results
Model of nanoparticle-attached enzyme kinetics
Before deriving and presenting a model designed to be applicable to a NP–enzyme system, it is useful to first consider the reaction pathway applicable to the enzyme by itself. The commonly used MM reaction represents the following basic reaction pathway: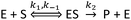 | (1) |
| v = kcat[E][S]/(KM + [S]) | (2) |
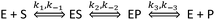 | (3) |
| kcat = k2k3/(k2 + k3) | (4a) |
| KM = k3(k2 + k−1)/(k1(k2 + k3)) | (4b) |
Other pertinent models can be generated for the free enzyme system as well. If only k−2 is assumed to be significantly smaller than k2, then a MM initial rate formulation with an effective kcat and KM can be developed in the case of the product inhibiting catalysis. Assuming this to be the case for competitive product inhibition, then:
| kcat = k2k3/(k2 + k3) | (5a) |
| KM = (k3(k2 + k−1)/(k1(k2 + k3))) (1 + [P]k−3/k3) | (5b) |
| v = kcat[E][S]/(KM(1 + [P]/Kp) + [S]) | (6) |
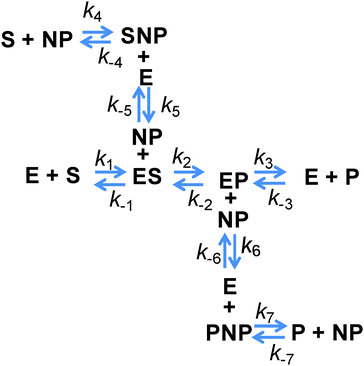
Before considering the addition of new reaction pathways due to the display of an enzyme on a NP, let us consider the possible effects that may manifest on the native enzyme reaction pathways. Direct effects on the enzymes themselves can affect any of the reaction steps; however, the NP attachment schemes used in our group aim to minimize and even remove perturbation of the enzyme structure (see ref. 10, 28 and therein for a detailed discussion of the relevant chemistry). These efforts provide the basis for our working assumption – that the kinetic rates associated with the processes depending on only the enzyme or the enzyme complex are not affected by attachment to NPs. It follows then that the rates of the enzyme–substrate or the enzyme–product disassociation (k−1, k3,) and the conversion of the intermediate complexes (k2, k−2) should also be unchanged after NP attachment, as they are all processes associated with the enzyme or enzyme complex. In contrast, the on-rates (k1, k−3) depend directly on the enzyme and substrate or product and so these rates must always be changed due to the attachment. To better visualize this, consider that these rates can be expressed in terms of an activation energy factor, a steric factor accounting for whether the reactants are in a viable orientation, and a prefactor that accounts for the rate of collision. One frequently used estimate of the enzyme–substrate collision frequency Z is29
| Z = (RT/1500ν) × (1/rE + 1/rS) × (rE + rS) | (7) |
| Z = (RT/1500ν) × (1/(rE + rNP) + 1/rS) × (rE + rS) | (8) |
However, all of the preceding arguments assume that the substrate and the product do not interact with a NP. Yet nearly all NPs are colloids stabilized by a complex architecture of surface ligand molecules, which creates a localized hydration shell and a structured environment whose detailed characteristics are largely unknown.30–32 As NP–substrate or NP–product interactions would have noticeable effects on the observed reaction rates, these additional reaction pathway steps must be considered. To effectively model this system, four additional reaction steps are introduced, as shown in Fig. 2. Here, NP represents an adsorption location on the NP where there can be more than one location/site per NP and the product or substrate may occupy these locations/sites on the NP. We do not explicitly define this as an actual site where the substrate or product may physically adsorb, but rather imply that some type of affinity for the NP surface exists and this may also include a kinetic process that resembles affinity. Moreover, multiple steps may be involved in this process with a slightly different order and as we are unable to discern amongst them mechanistically, we utilize this step to cumulatively represent them. Additional rate constants are also now introduced: k4 and k−4 are the forward and reverse rates of the substrate–NP (SNP) complex forming from S and NP; k5 and k−5 are the forward and reverse rates of the SNP complex interacting with E to form ES and the NP; k6 and k−6 are the forward and reverse rates of the EP complex interacting with a NP to form E and the product–NP (PNP) complex; and k7 and k−7 are the forward and reverse rates of the PNP complex forming P and NP. It is possible to model the cases where only the substrate or the product may interact with the NP by setting the appropriate rate constants to zero. It can be seen from this scheme that the process steps for adsorption and desorption (again, we imply affinity) of both the substrate and the product should be parallel. The interesting feature to consider is that the native enzymatic rates for the direct interaction of the solution phase substrate or the product with the enzyme may actually be irrelevant if the underlying NP scaffold provides a faster mechanism via the on/off-rate of this to the NP surface and then a transfer to the enzyme. It is then possible for the reduction in the native substrate on-rate to be offset by the new pathway introduced. This pathway also suffers from the reduction in diffusion upon attachment of the enzyme and the NP but can offer improvements because the collisional cross-section area of this process is that of the NP which is larger and the rates of these processes can be as fast, or faster, than the rates for the direct substrate–enzyme interactions. When considering the steps associated with the product, both its on and off-rates can potentially be improved by the parallel pathways provided. If the product disassociation from the enzyme is rate limiting as in the case of PTE,11 then in this model it is possible for the measured kcat to increase if the pathway to the NP and then away from it for the product is actually faster.
As a first illustration of this model, consider the MM fitting parameters generated previously for the β-gal system with and without QDs (Fig. 3A).14 The lines represent the fits and the points are generated from a model based on the reaction scheme in Fig. 2 that uses a very large k2 and adjusts the rate constant k3 so that it matches the behaviour of the free enzyme system. The points that follow the higher curve assume an increase to five possible substrate/product adsorption sites on the NP surface instead of the original two. k2 and k3 are the constants from the free enzyme case, k4 and k5 are assumed to be zero, and the rate constants k6 and k7 were adjusted to produce a good fit. Continuing with the initial consideration of the model, we left the rates of substrate interactions with the QDs at zero to simplify the presentation, although it is likely that these rates will be non-zero. If the rates of k6 and k7 are much larger than k4 and k5, the substrate will have a much lower affinity than the product for the QD sites and the behaviour observed would very closely match the behaviour seen when these rates are zero. If k4 and k5 are much larger than k6 and k7, then the substrate will have a much greater affinity than the product for the QD sites, outcompeting the product for the binding sites and potentially blocking the product–NP interaction altogether. In this case, the observed kcat will not be altered from the free enzyme value which is similar to reaction (1); reaction (4) and (5) occur before the effectively irreversible reaction (2) and so the kcat does not depend on them. It should be noted that the KM observed for this case will be much higher than that observed for the previous case. However, if the rates for the product and substrate steps were in an intermediate range, an interesting phenomenon could occur with increasing amounts of initial substrate. At lower amounts of initial substrate, the sites on the QD surface would be free to accept product from the enzyme and a faster EP disassociation pathway than that of the native enzyme would be available. At higher initial substrate concentrations, the QD surface would be occupied by the substrate and the product disassociation pathway would be blocked. Effectively, the initial rate would reach a maximum rate at a certain initial substrate concentration and at higher initial substrate concentrations the rate would approach the original free enzyme rate. The original data set for the β-gal system contains a final data point for many cases that suggests that this could actually be occurring. Unfortunately, the data from which this trend is generated are fairly variable and this is also the highest substrate concentration that could be used within the experimental assay conditions utilized, which cumulatively precludes a full verification of this phenomena. Fig. 3B shows the original experimental data reported along with the original MM fits as solid lines and trial fits as dashed lines using the current model assuming that both the substrate and the product are interacting with the QD. Least squares fitting was not carried out here; rather, the initial parameters were determined from a MM fit and then altered to show the alternate possible fits. These fits used the reaction pathway that includes the QD, as the model itself is over-specified for the number of experimental parameters.
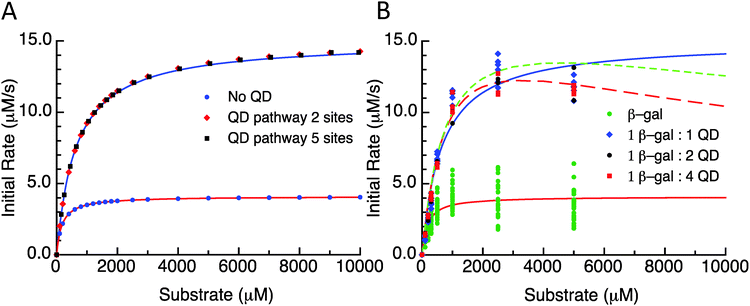 | ||
| Fig. 3 (A) Initial rate versus substrate concentration plot. Lines are fit values to the data from Brown et al.14 Points are the selected substrate concentrations derived using the model. Parameter values are listed in the ESI.† QD pathway sites are meant to reflect the presence of the potential substrate/product binding/adsorption sites on the QD surface. (B) Initial rate versus substrate concentration using the experimental data from Brown et al.14 Free enzymes and 1-, 2-, and 4-QDs per β-gal data are plotted with MM fits as solid lines. Dashed lines are plots of this model with parameters reported in supplemental data. | ||
The number of enzymes attached to the NP surface has so far not been addressed in the model. A higher coverage of the enzyme itself should also reduce the sites available for the product disassociation pathway; so, it is possible that at lower and intermediate coverages of the enzyme, a NP shows an enhanced kcat that then diminishes with a higher coverage of the enzyme. This may actually provide a method to exclude this model from being a candidate to describe the activity of a given experimental NP–enzyme complex. If kcat is enhanced and does not decrease with higher coordination, then the system must be one where the NP–enzyme complex does not depend on the product moving to the NP surface and the enzyme complex must have been directly affected by NP attachment so that its intrinsic rates have been altered.
In the course of developing this model, an expression that can account for enzyme–product inhibition and its potential effect was discussed. Another easily accessible experimental variable to change is the viscosity of the solution. It is, however, much more difficult to predict the effect that this will have on the rates. The on-rates explicitly depend on the diffusion rates which will be altered so that an effect on these should definitely occur, but altering the viscosity of the solution also requires the introduction of an additional material which may have direct interactions with the enzyme or alter the pH of the solution. It is possible for it to directly alter the enzyme conformation potentially affecting the k2 and/or the off-rates of the substrate and the product. It nevertheless remains a useful variable to probe because if the enzyme attached to a NP does not exhibit the same behaviour as the free enzyme, then it still reveals and confirms that the reaction pathway has been altered.
While the actual mechanics and the physical process of substrate and product interactions with the NP have not been explicitly stated, many potential processes could be approximated with the reaction steps listed. If these encompass the new pathways introduced above, then it is possible to state that when an enzyme reaction has a measurably larger kcat following NP attachment this can only be accounted for by either (i) a change in the intrinsic performance of the enzyme or, precluding that, (ii) the enzyme's rate limiting step is the disassociation of the product and the NP provides an alternate pathway for product disassociation that is significantly faster since only this particular change can affect kcat in the requisite way. Furthermore, if the NP bioconjugation chemistries minimally perturb the enzyme activity, as we strive for in all our studies,10,28,33 then there is a high probability that k3 can be rate limiting resulting in faster k6 and k7 rates. Considering all of these points cumulatively, if the activity of an enzyme conjugated NP system is described by this model, then there are several predictions as to what should occur to the various rate constants and observed characteristics in comparison to an enzyme being free in solution including:
(1) if kcat increases by more than a factor of two, then either k2 or k3 are not close in value or both rates increased by large factors;
(2) changes in viscosity should result in different changes in the kcat and KM values from what is observed for the free enzyme;
(3) product inhibition will be different for the NP attached enzyme versus the unattached enzyme;
(4) the NP attached enzyme should not have as strong an observed product inhibition as an unattached enzyme;
(5) higher enzyme to NP ratios should have poorer performance.
Enzymatic assays
To test the validity and, in particular, the predictive power of the model derived above, we again utilize the unique configuration of the β-gal enzyme complex with QDs displayed around its periphery, see Fig. 1.14 The bioconjugation is accomplished by self-assembly as the QDs coordinate to the hexahistidine (His6) sequences which were recombinantly introduced to the termini of the four monomers of the enzyme for purification following expression.10,34 With β-gal being an obligate tetramer, the His6 motifs are fortuitously located at the distal corners of the complex which should also minimize any structural perturbations. The ability of the complex to coordinate up to 4 QDs has been previously verified with TEM analysis.14 Given that a significant assumption in the model is that the enzyme's structure (and hence activity) is not perturbed by QD attachment, we again reiterate that this bioconjugation modality has been utilized by both our group and others with numerous other enzymes and proteins without demonstrating any deleterious effects on activity.10–14,28 The first observation from these experiments confirmed that β-gal activity is indeed significantly increased following QD display. As shown in Table 1, β-gal's kcat value increased at least ∼3.2-fold from 438 to 1416 s−1 with QD attachment. Interestingly, the corresponding KM values changed by almost the exact same factor as β-gal's KM value increased ∼3.3 fold from 81 to 272 μM. This particular set of changes is predicted to occur if the enzyme is already functioning at maximum efficiency. The fact that the kcat/KM of 5.94 and 5.72 μM−1 s−1 estimated for the free enzyme and QD attached configurations, respectively, are nearly equivalent values and also the highest values noted in this study seems to suggest that this is indeed so.| QD:β-gal | Format | η s/ηw (% glyc.) | V max (μM s−1) | k cat (s−1) | K M (μM) | k cat/KM (μM−1 s−1) |
|---|---|---|---|---|---|---|
| Estimated using the MM form. A full list of parameters is available in the ESI. Kp is the estimated product inhibition constant. For the lactose experiments, the data were fit with eqn (6) to derive the parameters. | ||||||
| 0 | Viscosity | 1.0 (0%) | 0.88 ± 0.02 | 438 ± 11 | 81 ± 10 | 5.94 |
| 0 | Viscosity | 1.2 (4.9%) | 1.66 ± 0.05 | 828 ± 26 | 894 ± 83 | 1.02 |
| 0 | Viscosity | 2.9 (40.4%) | 0.76 ± 0.08 | 380 ± 42 | 8183 ± 1310 | 0.05 |
| 4 | Viscosity | 1.0 (0%) | 2.81 ± 0.11 | 1416 ± 56 | 272 ± 45 | 5.72 |
| 4 | Viscosity | 1.2 (4.9%) | 3.04 ± 0.08 | 1520 ± 39 | 950 ± 69 | 1.76 |
| 4 | Viscosity | 2.9 (40.4%) | 0.76 ± 0.07 | 381 ± 37 | 6095 ± 925 | 0.07 |
| QD:β-gal | Format | [Lactose] | V max (μM s−1) | k cat (s−1) | K M (μM) | k cat/KM (μM−1 s−1) | K p (μM) |
|---|---|---|---|---|---|---|---|
| 0 | Product inhibition | (0–10 mM range) | 0.79 ± 0.04 | 395 ± 17 | 93 ± 10 | 4.2 | 62 ± 11 |
| 4 | Product inhibition | (0–10 mM range) | 2.80 ± 0.52 | 1401 ± 26 | 274 ± 22 | 5.1 | 906 ± 130 |
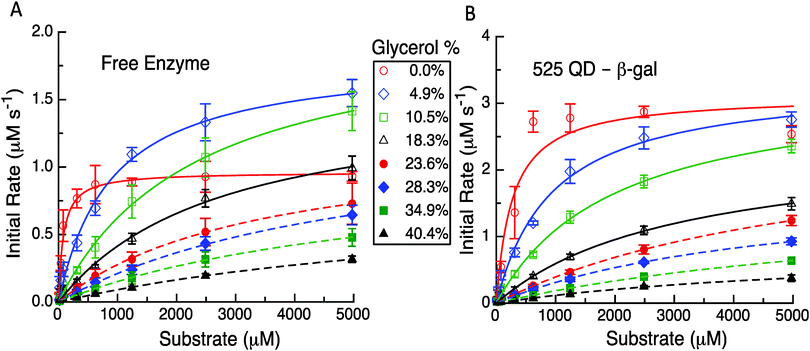
Having established the reproducibility and equivalency to the previous results, we next focused on utilizing different experimental formats to probe the underlying mechanism(s) as related to the model and its predictions. The first experimental format utilized here consisted of performing the initial rate experiments for the free enzyme and QD-enzyme systems with increasing amounts of glycerol added to alter the solution viscosity of the system. In previous studies with PTE, it was found that the dependence of kcat for free PTE and QD-PTE when the viscosity was increased was different.11 The Raushel Lab had previously shown that PTE's rate limiting step was EP dissociation by using an increasing viscosity to challenge this process.16 Attaching PTE to a QD surface alleviated this rate limiting step even in the presence of increasing buffer viscosity, suggesting that this change was the primary contributor to enzymatic enhancement in this case.11 Similar studies were carried out here with β-gal to ascertain if this change was also present and was also contributing to the enhancement in the QD system. The representative results from these studies are highlighted in Fig. 4, Table 1 and the ESI,† Table S1. For freely diffusing β-gal as shown in Fig. 4A, the maximum velocity and kcat initially increase with viscosities of 4.9% and 10.5% w/w of glycerol. Although the maxima observed for these latter two concentrations are greater than those of the no-glycerol control, we note that the slope of the initial rate is far steeper. While it is somewhat speculative to explain this, we note that other enzymes that we have studied in the past have the rate-limiting step altered by changes in viscosity.11 This study later identifies that the removal of the product is rate limiting and we believe that the change in viscosity or some interaction with glycerol is altering this process here as well. Given how large the enzyme is and the fact that it is diffusion limited at low substrate concentrations leads us to consider that the substrate and the product can potentially interact with more of the enzyme surface than just the reaction pocket. This, in effect, serves to stage the substrate and the product and the change in viscosity has improved the movement of the product out of the reaction pocket. The velocities and the corresponding kcat values decrease somewhat monotonically when the viscosity increases from 18.3% up to 40.4% glycerol added in the buffer. Increases in the corresponding KM values are also seen while the overall enzymatic efficiency decreases to nearly 100-fold from 5.94 to 0.05 μM−1 s−1 across the whole viscosity range (ESI,† Table S1).
In contrast to this pattern of an initial increase and then a decrease seen for the free enzyme complex, the QD attached enzyme displayed a pattern of continuous decreases in the initial rates and activity that tracked with the increases in glycerol content of the buffer, see Fig. 4B. The initial changes with the lower amounts of glycerol were relatively small. Due to the overall NP enhancement effect, the maximum velocity and the overall initial rates are still higher for this system. For the QD system, the corresponding KM values compensate for the changes in kcat by increasing up to almost 30-fold from ∼272 μM at 0% glycerol to a maximum of ∼7841 μM at 34.9% glycerol. The efficiency of the QD system drops nearly 80-fold from 5.72 to 0.07 μM−1 s−1 across the whole viscosity range, although some of the intermediary values across the glycerol range are slightly higher and decrease at a slower rate than that of the free enzyme system (ESI,† Table S1). In examining Table 1 and the ESI,† Table S1, we note that the kcat for the two systems remains relatively unaffected over some of the initial changes in glycerol. For example, for the free enzyme at glycerol concentrations of 4.9%, 10.5%, and 18.3%, the average kcat value is ∼828 ± 118 s−1, while for the QD system the average kcat value is ∼1353 ± 183 s−1 over the range of 0% up to 23.6%. At the highest glycerol concentrations, the kcat for the two systems is similar which reflects a much larger loss for the QD system. The fit values for the highest glycerol concentrations for either case are somewhat suspect as all of the experimental data occur before the characteristic bend occurs. Even with nonlinear fitting procedures uncertainty is introduced and thus we cannot make an in-depth conclusion from these latter observed values. Nevertheless, this still does serve as solid evidence that the enzymatic/kinetic pathways are being altered due to QD attachment.
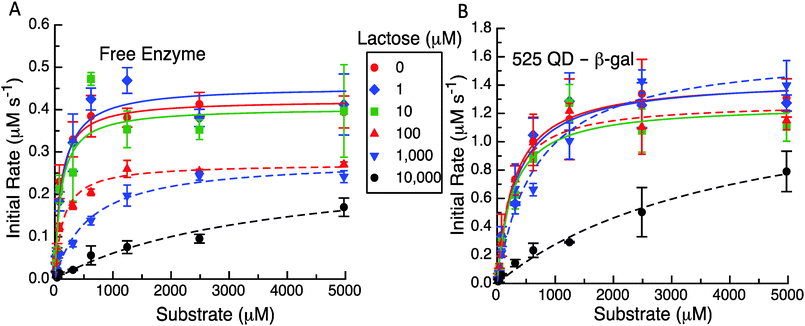
The second experimental format utilized to probe β-gal activity following QD attachment focused on product inhibition. In particular, the enzyme experiences competitive inhibition from the presence somewhat of glucose but especially that of the galactose monosaccharide when present following cleavage of the parent lactose disaccharide when the latter is used as a primary substrate. It is believed that galactose competes with the substrate for the enzyme's active site and typically displays a Ki in the low mM range depending on the enzyme variant used.19–21 The effect of having increasing concentrations of the product (i.e. galactose) present at the beginning of the assays was tested by introducing increasing amounts of lactose to the enzyme or QD enzyme construct and allowing it to react before adding ONPG to track the reaction rates as described in the Experimental section. Given this format, we do not know the actual concentrations of glucose and galactose present but they can be expected to be quite high as the enzyme functions with a high efficiency at or near diffusion limitations.
The representative results from these initial velocity versus substrate assays are presented in Fig. 5, Table 1 and Table S2 (ESI†). As expected in Fig. 5A and B the QD construct starts with an initial rate that is ca. three times that of the free enzyme. It appears that for initial lactose concentrations up to 10 μM, there is not a significant effect on the initial velocities even with the differences between the formats. At higher levels of 100 μM, 1 mM and 10 mM of initial lactose, the maximum velocity reached at higher substrate concentrations for the enzyme only system is reduced (Fig. 5A). For the system with the QDs attached to the enzyme (Fig. 5B), the initial concentrations of up to 1 mM lactose do not appear to inhibit the initial rates nor the maximum initial velocities reached. Only at 10 mM initial lactose does the QD system show a significant drop in activity although this still maintains a higher overall value or rate than the free enzyme with no lactose present. Clearly, the reduction in the maximum velocity with increasing amounts of cleaved lactose products is not as great when the enzyme is tethered to QDs.
The apparent MM parameters for both the free enzyme and the enzyme QD system show relatively minor effects on kcat and KM increasing with the individual amounts of initial lactose (see Table S2, ESI†). For example, the free enzyme kcat has an average value of 362 ± 74 s−1 over the entire range of lactose concentrations, while the KM value increases from 97 to 590 μM (6-fold increase) over the range of 0 up to 1 mM lactose. Only at 10 mM lactose is the enzyme's apparent KM value significantly altered with a >35 fold increase to ∼3548 μM. β-gal efficiency in this assay format decreases ∼50 fold from 4.34 to 0.08 μM−1 s−1 with increasing initial lactose. Similarly, the average kcat value for the QD system does not show much variation at 1420 ± 123 s−1 across the entire lactose range. The corresponding KM values are actually quite consistent from 0 up to 100 μM lactose with an average value of 275 ± 34 μM. Only at 1 and 10 mM initial lactose do the apparent KM values increase to 667 μM (∼2-fold increase) and then to 4126 μM (14-fold increase), respectively. With QD display, the β-gal's kcat/KM decreases to ∼38-fold from 4.96 to 0.34 μM−1 s−1 over the range of lactose tested. This is again not quite as drastic as the changes seen for the free β-gal over the same assay range. We note that all of these data could be fitted to the basic MM form using the competitive inhibition model in eqn (5a). This also yielded kcat and KM values that were in good agreement for no product being present along with having a significantly larger Kp for the QD system (960 μM) as compared to the free enzyme case (62 μM). Clearly, the known product inhibition effect for the free enzyme was significantly lowered when the enzyme was attached to QDs. Overall, this conforms to the model predictions that product dissociation from the enzyme should be significantly modified when the QDs are present and that the inhibition effect should be substantially relieved as well.
Conclusions
In this report, we continue towards trying to understand why enzyme activity is enhanced when attached to a NP surface. For our model system, we again consider the special case of the homotetrameric β-gal enzyme complex as assembled with semiconductor QDs around its periphery. In initial work reporting β-gal enhancement in this QD attached configuration, we did not probe the mechanistic causes of the observed kinetics increases and hypothesized that substrate accumulation and sequestration at the QD-enzyme interface may have been at least partially responsible.14 This was put forth to account for β-gal's diffusion limited activity and is also not out of the realm of possibility as related phenomena have indeed been noted previously in analogous configurations.35–38 Preliminary modeling of this process (data not shown) in conjunction with other related simulations of the enzyme activity when confined on a scaffold suggested that the effect of substrate sequestration on the enzyme in a NP attached configuration would be more transient in nature and not as persistent as we observe in experimental assays.39 The current approach taken was to consider all the possible significant interactions that a substrate could have with a NP–enzyme conjugate and then to construct a simplified model that considers these in the context of the basic MM formalism (Fig. 2). Several basic yet important assumptions were made to utilize this model. Of these, the most important is that the enzyme's structure and its corresponding base catalytic activity are not perturbed by the QD assembly chemistry utilized; this is something that has been worked out through extensive development and testing of the metal-affinity coordination approach utilized and has also been repeatedly confirmed in studies.10,28,40–43The use of activity assays, product inhibition assays, and changes in viscosity clearly established that the β-gal reaction pathways were altered by attachment to QDs. The data were further consistent with a model based on attachment of the QD introducing parallel pathways to introduce the substrate and/or remove the product to/from the enzyme complex site. Critically, this model allowed us to make some testable predictions as to what should manifest once the enzyme is attached to a NP and new pathways are created which facilitate enhanced activity. As confirmed in Fig. 4, changes in the solution viscosity do indeed result in different changes in the kcat and KM values from what is observed for the free enzyme. The data shown in Fig. 5 also confirm that product inhibition was different for the NP attached enzyme versus the unattached enzyme and that the NP attached enzyme did in fact not have as strong an observed product inhibition profile as the unattached enzyme. Interestingly, an almost identical pattern of behaviour was noted for the QD-PTE system when it was challenged with a triethyl phosphate competitive inhibitor.11 In terms of higher enzyme to NP ratios manifesting poorer performance or decreased enhancement, as mentioned, although not perfectly consistent, generalized trends matching this prediction have been noted in almost all of our studies including for the current enzyme configuration as reported in the previous β-gal work.11–14 The remaining prediction – that if kcat increases by more than 2×, then either k2 (ES → EP) and k3 (EP → E + P) are not close in value or both rates increased by large factors – is far harder to ascertain experimentally and the support for this is more by inference. Again, one of the fundamental assumptions of this model is that k2 (essentially kcat) is not changed by NP attachment. Given this, since changes in k1 (E + S → ES) cannot change the enzymes inherent kcat, that leaves only increases in k3, or anything that facilitates this, as the mechanistic cause of the NP-attached enzyme enhancement. We note that this is the same mechanism suggested to cause enhancement within the QD-PTE system.11
But can the k3 (EP → E + P) step be rate-limiting for an enzyme that is already supposedly functioning within a diffusion limited regime? The answer is yes and, moreover, it will become readily apparent in the standard MM assay format when the excess substrate reaches a concentration such that the enzyme is no longer diffusion limited. Under these specific conditions, other kinetic processes that limit the overall catalytic rate will be manifested and can be probed. As to whether the substrate and/or product sequester around the QD-β-gal complex, that is also extremely hard to confirm given the lack of robust metrologies available to probe such localized nanoscale chemical phenomena.31,44 Although we discount its effects as being transient over the lifetime of the measured reaction (vide supra), this point still remains speculative at the current time. Cumulatively, we hypothesize that the unique and still largely undefined nanoscale environment around a NP provides a new pathway or mechanism for alleviating β-gal's rate limiting k3 step when not actively catalysing turnover under diffusion limited conditions. The same mechanism presumably also alleviated the concentration build-up and competitive inhibition of galactose around the enzyme following lactose hydrolysis (Fig. 5). Only at the highest initial concentration of lactose was the QD-β-gal complex unable to fully compensate and remove or otherwise alleviate enough inhibiting galactose as it did at lower concentrations. How all this physically occurs is completely unknown at the present time and still remains to be elucidated. Potential changes in enzyme structure following NP binding are also of interest as they can directly affect the catalytic activity. We work with the assumption that these are minimal given that the underlying chemistry of coordinating the QD to the enzyme monomers distal termini, which are assumed to be flexible as well. In the current example, preliminary circular dichroism spectroscopy of free β-gal along with that assembled to QDs in a complex suggested some changes in the enzymes helicity component, see Fig. S3 (ESI†). However, this result is only preliminary and it is unclear if the changes are even significant; a full analysis is beyond the current scope given the complexity of the underlying system with a solid metallic NP present. Future studies are planned to explore this question.
In terms of other follow-on studies, faster analytical techniques to examine early reaction time kinetics would give more information about individual rate constants. With the individual rate constants resolved, there would be a better chance to see if this model accounts for the observed behaviour in far more detail. If the enhancements occur because of a new pathway that involves movement of the product or the substrate onto the NP surface in some manner, then crowding of the NP surface would remove this pathway or inhibit it so that it did not perform as well. Whether such access to the surface of the NP is critical could be tested by studies where a molecule is used to occupy or block the surface of the NP or alternatively modifications to the NP surface ligand chemistry may similarly serve to alter the reaction pathway(s). Finding appropriate molecules to satisfy these experimental needs and that do not further interfere with the enzyme itself is potentially an issue. The option of changing the NP ligand to accomplish this is also severely constrained, as it must maintain its primary role of preventing aggregation and keeping the NP colloidally stable in solution.
Initial rate fitting to MM expressions is often used not just because it is simple and readily recognized but also because the experiments that can be performed are typically only sufficient to solve for two rate parameters, i.e., kcat and KM. Even the original MM derivation is over-specified with three basic rate constants as in eqn (1) which was then arranged as in eqn (2).45 In interpreting the changes observed in the apparent rate constants for enzyme activity at NP interfaces, we have shown that it is useful to construct alternative models and consider what constraints are placed on the apparent rate constants measured. Importantly, our proposed model for NP–enzyme conjugates demonstrates that large changes in kcat as well as KM are possible without any changes in the intrinsic function of the enzyme. Interestingly, it also suggests that maximizing the ratio of enzymes to NPs may interfere with the mechanism that provides enhancement. Another potential outcome of this work is that attachment of enzymes to NPs actually provides a method to probe the relative importance of the rate steps in the original free enzyme system that normally cannot be separated out or made discrete. The use of an attachment scheme that should not perturb the reactive step but can affect the disassociation of the enzyme and the product also allows useful information to be gained about whether that particular step is rate limiting and is potentially a better estimate of whether their values are close or not to what was assumed. This can then inform decisions on the best method to maximize the performance of the enzyme. Finally, it will be fascinating to see how this model can (or cannot) be applied to other NP–enzyme systems in pursuit of understanding what gives rise to enhancement.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Office of Naval Research, the NRL Nanosciences Institute, and the National Institute of Food and Agriculture, U.S. Department of Agriculture, under award number 11901762 for funding the research.Notes and references
- D. Bezbradica, M. Corovic, S. J. Tanaskovic, N. Lukovic, M. Carevic, A. Milivojevic and Z. Knezevic-Jugovic, Curr. Org. Chem., 2017, 21, 104–138 CrossRef CAS.
- R. A. Sheldon, J. Mol. Catal. A: Chem., 2016, 422, 3–12 CrossRef CAS.
- L. Cao, L. Langen and R. A. Sheldon, Curr. Opin. Biotechnol., 2003, 14, 387–394 CrossRef CAS PubMed.
- J. N. Talbert and J. M. Goddard, Colloids Surf., B, 2012, 93, 8–19 CrossRef CAS PubMed.
- B. J. Johnson, W. R. Algar, A. P. Malanoski, M. G. Ancona and I. L. Medintz, Nano Today, 2014, 9, 102–131 CrossRef CAS.
- D. Q. Li, Colloids Surf., A, 2001, 195, 35–57 CrossRef CAS.
- S. A. Ansari and Q. Husain, Biotechnol. Adv., 2012, 30, 512–523 CrossRef CAS PubMed.
- S. Ding, A. A. Cargill, I. L. Medintz and J. C. Claussen, Curr. Opin. Biotechnol., 2015, 34, 242–250 CrossRef CAS PubMed.
- W. R. Algar, K. Susumu, J. B. Delehanty and I. L. Medintz, Anal. Chem., 2011, 83, 8826–8837 CrossRef CAS PubMed.
- J. B. Blanco-Canosa, M. Wu, K. Susumu, E. Petryayeva, T. L. Jennings, P. E. Dawson, W. R. Algar and I. L. Medintz, Coord. Chem. Rev., 2014, 263, 101–137 CrossRef.
- J. C. Breger, M. G. Ancona, S. A. Walper, E. Oh, K. Susumu, M. H. Stewart, J. R. Deschamps and I. L. Medintz, ACS Nano, 2015, 9, 8491–8503 CrossRef CAS PubMed.
- J. C. Breger, S. A. Walper, E. Oh, K. Susumu, M. H. Stewart, J. R. Deschamps and I. L. Medintz, Chem. Commun., 2015, 51, 6403–6406 RSC.
- J. C. Claussen, A. Malanoski, J. C. Breger, E. Oh, S. A. Walper, K. Susumu, R. Goswami, J. R. Deschamps and I. L. Medintz, J. Phys. Chem. C, 2015, 119, 2208–2221 CAS.
- C. W. Brown, E. Oh, D. A. Hastman, S. A. Walper, K. Susumu, M. H. Stewart, J. R. Deschamps and I. L. Medintz, RSC Adv., 2015, 5, 93089–93094 RSC.
- A. N. Bigley, M. F. Mabanglo, S. P. Harvey and F. M. Raushel, Biochemistry, 2015, 54, 5502–5512 CrossRef CAS PubMed.
- S. R. Caldwell, J. R. Newcomb, K. A. Schlecht and F. M. Raushel, Biochemistry, 1991, 30, 7438–7444 CrossRef CAS PubMed.
- M. M. El-Masry, A. De Maio, P. L. Martelli, R. Casadio, A. B. Moustafa, S. Rossi and D. G. Mita, J. Mol. Catal. B: Enzym., 2001, 16, 175–189 CrossRef CAS.
- A. Cornish-Bowden, Fundamentals of Enzyme Kinetics, Wiley-Blackwell, Weinheim, Germany, 4th edn, 2012 Search PubMed.
- S. A. Ansari and Q. Husain, Food Bioprod. Process., 2012, 90, 351–359 CrossRef CAS.
- S. Erich, B. Kuschel, T. Schwarz, J. Ewert, N. Bohmer, F. Niehaus, J. Eck, S. Lutz-Wahl, T. Stressler and L. Fischer, J. Biotechnol., 2015, 210, 27–37 CrossRef CAS PubMed.
- M. Ladero, M. T. Perez, A. Santos and F. Garcia-Ochoa, Biotechnol. Bioeng., 2003, 81, 241–252 CrossRef CAS PubMed.
- K. Susumu, E. Oh, J. B. Delehanty, J. B. Blanco-Canosa, B. J. Johnson, V. Jain, W. J. Hervey, W. R. Algar, K. Boeneman, P. E. Dawson and I. L. Medintz, J. Am. Chem. Soc., 2011, 133, 9480–9496 CrossRef CAS PubMed.
- E. Oh, F. K. Fatemi, M. Currie, J. B. Delehanty, T. Pons, A. Fragola, S. Leveque-Fort, R. Goswami, K. Susumu, A. L. Huston and I. L. Medintz, Part. Part. Syst. Charact., 2013, 30, 453–466 CrossRef CAS.
- S. A. Diaz, F. Gillanders, K. Susumu, E. Oh, I. L. Medintz and T. M. Jovin, Chem. – Eur. J., 2017, 23, 263–267 CrossRef CAS PubMed.
- T. Pons, I. L. Medintz, X. Wang, D. S. English and H. Mattoussi, J. Am. Chem. Soc., 2006, 128, 15324–15331 CrossRef CAS PubMed.
- M. Wu and W. R. Algar, ACS Appl. Mater. Interfaces, 2015, 7, 2535–2545 CAS.
- W. R. Algar, A. Malonoski, J. R. Deschamps, J. B. Blanco-Canosa, K. Susumu, M. H. Stewart, B. J. Johnson, P. E. Dawson and I. L. Medintz, Nano Lett., 2012, 12, 3793–3802 CrossRef CAS PubMed.
- K. E. Sapsford, W. R. Algar, L. Berti, K. B. Gemmill, B. J. Casey, E. Oh, M. H. Stewart and I. L. Medintz, Chem. Rev., 2013, 113, 1904–2074 CrossRef CAS PubMed.
- K. A. Connors, Chemical Kinetics: The Study of Reaction Rates in Solution, Wiley-VCH, Germany, 1990 Search PubMed.
- M. Zobel, R. B. Neder and S. A. Kimber, Science, 2015, 347, 292–294 CrossRef CAS PubMed.
- C. Pfeiffer, C. Rehbock, D. Huhn, C. Carrillo-Carrion, D. J. de Aberasturi, V. Merk, S. Barcikowski and W. J. Parak, J. R. Soc., Interface, 2014, 11, 20130931 CrossRef PubMed.
- A. M. Dennis, J. B. Delehanty and I. L. Medintz, J. Phys. Chem. Lett., 2016, 7, 2139–2150 CrossRef CAS PubMed.
- I. Medintz, Nat. Mater., 2006, 5, 842 CrossRef CAS PubMed.
- K. E. Sapsford, D. Farrell, S. Sun, A. Rasooly, H. Mattoussi and I. L. Medintz, Sens. Actuators, B, 2009, 139, 13–21 CrossRef CAS.
- A. Harada and K. Kataoka, J. Am. Chem. Soc., 1999, 121, 9241–9242 CrossRef CAS.
- T. Kurinomaru, S. Tomita, Y. Hagihara and K. Shiraki, Langmuir, 2014, 30, 3826–3831 CrossRef CAS PubMed.
- F. Lyu, Y. Zhang, R. N. Zare, J. Ge and Z. Liu, Nano Lett., 2014, 14, 5761–5765 CrossRef CAS PubMed.
- Y. F. Zhang, J. Ge and Z. Liu, ACS Catal., 2015, 5, 4503–4513 CrossRef.
- O. Idan and H. Hess, ACS Nano, 2013, 7, 8658–8665 CrossRef CAS PubMed.
- K. E. Sapsford, T. Pons, I. L. Medintz, S. Higashiya, F. M. Brunel, P. E. Dawson and H. Mattoussi, J. Phys. Chem. C, 2007, 111, 11528–11538 CAS.
- K. Boeneman Gemmill, J. R. Deschamps, J. B. Delehanty, K. Susumu, M. H. Stewart, R. H. Glaven, G. P. Anderson, E. R. Goldman, A. L. Huston and I. L. Medintz, Bioconjugate Chem., 2013, 24, 269–281 CrossRef CAS PubMed.
- A. M. Dennis, D. C. Sotto, B. C. Mei, I. L. Medintz, H. Mattoussi and G. Bao, Bioconjugate Chem., 2010, 21, 1160–1170 CrossRef CAS PubMed.
- I. L. Medintz, T. Pons, K. Susumu, K. Boeneman, A. Dennis, D. Farrell, J. R. Deschamps, J. S. Melinger, G. Bao and H. Mattoussi, J. Phys. Chem. C, 2009, 113, 18552–18561 CAS.
- K. E. Sapsford, K. M. Tyner, B. J. Dair, J. R. Deschamps and I. L. Medintz, Anal. Chem., 2011, 83, 4453–4488 CrossRef CAS PubMed.
- K. A. Johnson and R. S. Goody, Biochemistry, 2011, 50, 8264–8269 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The structure of the CL4 ligand, a representative TEM image of the QDs used and complete listings of the apparent kinetic values in a tabular form. See DOI: 10.1039/c7nh00052a |
| This journal is © The Royal Society of Chemistry 2017 |