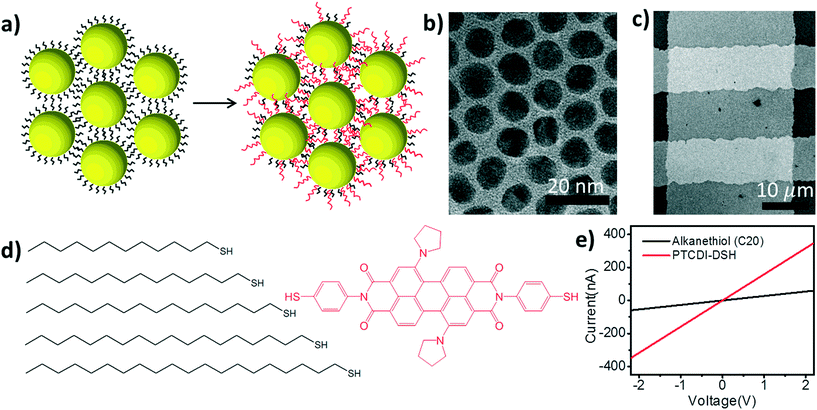
Ligand exchange based molecular doping in 2D hybrid molecule-nanoparticle arrays: length determines exchange efficiency and conductance†
Cliff E.
McCold‡
 a,
Qiang
Fu‡
b,
Sahar
Hihath
a,
Ji-Min
Han
c,
Yaeir
Halfon
d,
Roland
Faller
a,
Qiang
Fu‡
b,
Sahar
Hihath
a,
Ji-Min
Han
c,
Yaeir
Halfon
d,
Roland
Faller
 d,
Klaus
van Benthem
a,
Ling
Zang
c and
Joshua
Hihath
d,
Klaus
van Benthem
a,
Ling
Zang
c and
Joshua
Hihath
 *b
*b
aMaterials Science and Engineering, UC Davis, USA
bElectrical and Computer Engineering, UC Davis, USA. E-mail: jhihath@ucdavis.edu
cMaterials Science and Engineering, University of Utah, USA
dChemical Engineering, UC Davis, USA
First published on 19th July 2017
Abstract
Effective control of ligand exchange is important in the emerging field of nanoparticle-based meta-materials; controlling both the separation and electronic coupling between nanoparticles impacts the electrical, optical, chemical, and thermal properties of these materials. However, methods to evaluate exchange efficiency are generally lacking for solid state devices. In this paper, it is shown that controlling the initial ligand length determines the efficiency of the secondary ligand's substitution into the nanoparticle array. Controlling this ligand exchange efficiency determines the post-exchange conductance in a manner akin to doping in conventional semiconductor systems. For a series of initial ligand lengths the distribution of nanoparticle separations in the array is determined, and the ligand exchange efficiency is extracted using a bond percolation model. Finally, Monte Carlo simulations of charge transport in the arrays agree with the experimental conductance data for each molecular state and support the determination of the corresponding exchange efficiencies. This analysis provides a general framework for maximizing the efficiency of ligand exchange that will benefit the use of nanoparticle films in electronic, optoelectronic, plasmonic, and sensing systems.
Design, System, ApplicationIn this paper, we develop a set of design rules aimed at maximizing the efficiency of interparticle molecular exchange in hybrid molecule-nanoparticle monolayer arrays. Controlling the electronic properties of the ligands that interconnect nanoparticles in these systems is central to the development of nanoparticle-based meta-materials. Also, improving control over the ligand exchange process will allow control over the coupling between the particles, and enable novel optical, plasmonic, electronic, or sensing applications to be developed with greater certainty and reliability. Currently, many of these applications require specific molecular interlinkers that are not compatible with conventional nanoparticle self-assembly processes, so ligand exchange is a necessary and important process step for many applications. Therefore, the development of specific rules designed to control the ligand exchange process will allow this process to be tuned to unique ligands of interest for each application. Furthermore, the design rules and calculation techniques used in this work allow the extraction of ligand exchange efficiency from data readily available to researchers in nanomaterials, and enable exchange efficiency to be a common metric important to the characterization and understanding of the chemical and electronic behavior of nanoparticle arrays. |
The development of nanoparticle-based meta-materials capable of performing unique functions, and possessing unique and tunable electronic, optical, or thermal properties is one of the ultimate goals of nanoscience and nanotechnology. Nanoparticle-based systems have been demonstrated to be useful for biological systems and sensors,1 plasmonic and optoelectronic devices,2,3 and as a model platform for bottom-up electronics.4 Fundamental to the use of nanoparticle-based systems is the necessity to cap the nanoparticles or quantum dots with ligands to protect the high-energy surface states and prevent aggregation.5 These ligands are typically comprised of saturated molecular systems (alkanethiols, oleylamine, citrate, etc.) and as such have large gaps between the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively), and thus prevent strong electronic coupling between particles, which is detrimental for a variety of electronic, optical, and plasmonic functions.6
One typical approach to overcome this issue is to replace the original, large, saturated ligands with very short molecules, which helps maintain the surface stability of the nanoparticles while still improving electronic coupling between them.7 Unfortunately, this method can also cause significant local restructuring due to array volume loss and nanoparticle coalescence. This process can introduce random voids and diminish the long range order within the array,8,9 thus negatively affecting desired charge transport properties.
An alternative approach is to treat the nanoparticle films as a hybrid material where both the nanoparticles and molecules contribute to the electronic properties of the system.10 In this approach the original saturated molecules are replaced (using ligand exchange) with conjugated variants that have smaller HOMO–LUMO energy gaps, and thereby improve the electronic coupling between the nanoparticles.3 Importantly, in these systems the physical separation between the nanoparticles can remain large (>1 nm), thus preventing aggregation, but still result in a large increase in conductance after exchange. Large changes in conductance have been observed using this technique,11 and unique functionalities based on the molecular properties have also been demonstrated.12–14 Despite these successes, in solid state systems it is difficult to determine the degree to which the conjugated molecular system replaces the original ligand and interlinks the nanoparticles, thus limiting the utility of these systems.
In this report we introduce a 2-step ligand exchange strategy aimed at maximizing the exchange efficiency between the initial molecular ligand and the conjugated substitute (Fig. 1). Before the nanoparticles are self-assembled into a monolayer array, their capping ligands are determined during a phase transfer procedure. These initial capping ligands are alkanethiols of varying lengths that establish the steric diameter of the particles. By specifying the length of these alkanethiols while the nanoparticles are still in solution, the behavior of the particles during the interfacial self-assembly process is established.
After the nanoparticles are assembled into a well-ordered 2D array, the array is transferred to the solid substrate for electrical characterization. Subsequently, the saturated, monothiolated ligands are replaced with a secondary ligand: a conjugated perylene tetracarboxylic diimide derivative with pyrroline moieties substituted at the bay positions (PTCDI-DSH, Fig. 1d). By controlling both the initial alkane ligand's length and the ligand exchange process, we are able to tune the conductance of the nanoparticle arrays over a range of ∼7 orders of magnitude. The alkanethiols determine a 6 order of magnitude conductance range, while the secondary PTCDI exchange increases the conductance of the NP array by 1 to 3 orders of magnitude depending on the initial alkanethiol.
The general scheme of the experimental procedure is shown in Fig. 1. Briefly, the process starts by synthesizing a batch of low-dispersion, citrate-capped, Au nanoparticles (∼10.4 ± 0.6 nm diameter) using standard protocols.15 These nanoparticles are then transferred to the organic phase using a ligand-exchange process in ethanol,16 where the citrate is replaced with an alkanethiol ligand of varying lengths (CnH2n+1SH, where n = 12–20). These molecules will be referred to simply by the number of carbons henceforth (i.e. Cn). A drop (∼200 μL) of the resulting nanoparticle solution (∼0.17 mg mL−1) is then deposited on a water surface so that the nanoparticle array can assemble as the organic solvent (chloroform/toluene) evaporates.17,18 Once the assembly is complete, a microcontact printing method is used to transfer the array19 to a pre-fabricated measurement platform with Au electrodes recessed into a Si3N4 layer to create a planar surface (Fig. 1c).20 The conductance of at least 50 of these devices is measured prior to exchanging to the PTCDI-DSH ligand. The exchange to the PTCDI-DSH linker (Fig. 1a) is achieved by immersing the entire system (chip, electrodes, and 2D array) into a saturated ethanol solution overnight (∼18 hours). After exchange, the conductance of the same devices is re-measured to directly determine the effect of the ligand exchange on the conductance of the nanoparticle arrays (Fig. 1d).
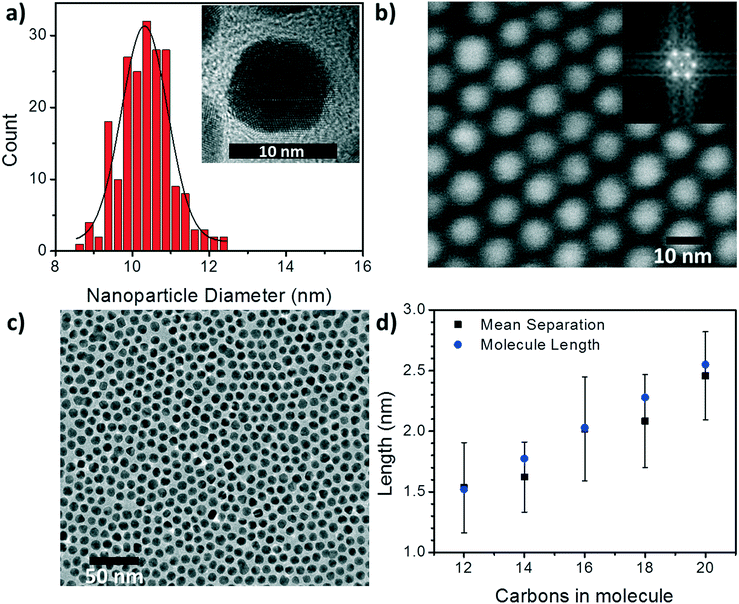
To begin understanding the effect of the various ligands on the charge transport properties of the 2D arrays we start by examining the changes in monolayer morphology that occur with ligand length. By using a combination of scanning electron microscopy (SEM) (Fig. 2b) and transmission electron microscopy (TEM) (Fig. 2c), we are able to examine the film crystallinity, packing, and ordering (inset Fig. 2b), the size and size-dispersion of the nanoparticles in the film (Fig. 2a), and average separation between nanoparticles in the array (Fig. 2d). A histogram of the nanoparticle sizes, as determined from the TEM measurements, is shown in Fig. 2a. From these measurements we are able to determine that the nanoparticles had an average diameter of 10.4 ± 0.6 nm. Furthermore, as the number of carbons in the alkane chain is increased from C12 to C20, the average separation of the nanoparticles in the film increased from 1.53 ± 0.37 nm to 2.46 ± 0.36 nm. As shown in Fig. 2d, these changes in separation are close to, but slightly shorter than, the length of each corresponding ligand. This result implies that the length of the ligand is a determining factor in controlling the separation between neighboring nanoparticles, and that the ligands from adjacent nanoparticles are strongly interdigitated. Further details on TEM and image analysis are available in the supplemental information.
With this understanding of the morphological features of the films, we next turn our attention to the charge transport properties. The devices to be measured were formed by stamping the self-assembled NP monolayers onto patterned substrates using microcontact printing. Because all substrates had planar 10 μm Au electrodes separated by 10 μm s, and all polydimethylsiloxane (PDMS) stamps were patterned to transfer 30 μm wide stripes of NP monolayers, all measured devices were 30 × 10 μm (W × L) and device conductance values are directly comparable.
The conductance was found to range from ∼27 nS in the case of C12 to ∼50 fS in case of C20 (Fig. 3a, black). This large change in the conductance of ∼6 orders of magnitude demonstrates the first step in molecular control over transport properties of these hybrid devices. Because the nanoparticles in each film are of the same size, this large conductance change can only originate from changes in the mobility of the charge carriers in the film, which is determined by the hopping rate from one nanoparticle to another. Because the nanoparticles are separated by saturated alkane chains with relatively long distances (>1.5 nm), the hopping rate will be dominated by the tunneling probability between the nanoparticles.20,21
We can better understand the relative contributions of different variables to the electrical behavior of the films by examining the analytical expressions for conductance in a hopping system
G = Gx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βs)exp(−2EA/kBT) exp(−βs)exp(−2EA/kBT) | (1) |
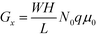 , encompassing geometric and algebraic constants included in the classic conductance equation
, encompassing geometric and algebraic constants included in the classic conductance equation 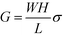 and conductivity σ = nqμ. Here W, H, and L are the width, height, and length of the NP array device, n is the charge carrier concentration, q is the elementary charge, and μ is mobility.22 For eqn (1), we have extracted the temperature-dependent exponent from the charge carrier concentration and the separation- and temperature-dependent exponents from the mobility, leaving the terms N0 and μ0, respectively. See Fig. S1 in ESI† for temperature-dependence of conductance indicating thermally-activated hopping and the measurement of EA.
and conductivity σ = nqμ. Here W, H, and L are the width, height, and length of the NP array device, n is the charge carrier concentration, q is the elementary charge, and μ is mobility.22 For eqn (1), we have extracted the temperature-dependent exponent from the charge carrier concentration and the separation- and temperature-dependent exponents from the mobility, leaving the terms N0 and μ0, respectively. See Fig. S1 in ESI† for temperature-dependence of conductance indicating thermally-activated hopping and the measurement of EA.
By examining eqn (1), we can see the conductance G will be directly proportional to probability of a charge tunneling from one nanoparticle to the next via the exp(−βs) term. This term depends exponentially on the separation (s) between the nanoparticles and a tunneling decay constant β. We also see an Arrhenius-type thermally activated behavior, corresponding to thermally-activated hopping of charge from nanoparticle site to nanoparticle site. Variations in activation energy between the alkanethiol and PTCDI ligands are small and have only minor effect compared to the separation-dependent (temperature-independent) tunneling probabilities.
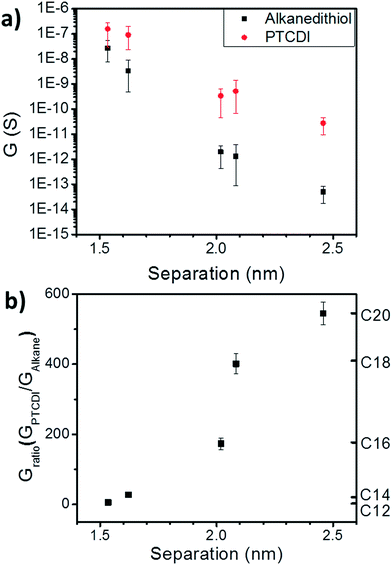
The tunneling decay constant β is determined by the energy barrier for a charge to tunnel between the nanoparticles, and depends on the alignment between the molecular frontier orbitals (HOMO and LUMO) and the chemical potential of the nanoparticles. By plotting the conductance of the nanoparticle arrays vs. the average separation between the nanoparticles in each molecular state (Fig. 3a), we find β = 14.7 nm−1 for the alkanethiols. Many groups have measured β-values for alkanes in a variety of conditions including large-scale self-assembled monolayers,23 nanoscale devices,24,25 and at the single-molecule level.26–29 Although there are some differences in the various systems, generally the β-value is found to be less than 10 nm−1. The large β-value obtained in this case may be a result of several factors: first, it may suggest that there is a significant through-space component to the tunneling pathway since the alkanes are not thiolated on both ends. Alternatively, defects (gauche isomers) in the molecular backbones could cause a decrease in the tunneling probability.28 Additionally, it is possible that the chemical potential of the nanoparticles (and the alignment with the dominant frontier orbital) is significantly different than for bulk electrodes.
Finally, we note that extracting β for a NP-array system relies on an accurate measurement of the interparticle separations. For example, in a nanoparticle array, a molecular junction with separation shorter than the average may increase the conductance locally. A distribution of separations may lead to the existence of “least resistance” current pathways where the average tunneling distance is shorter than the geometrically averaged separation measured by TEM. In this case, a larger β value may result from the conductance vs. separation plot because of the overestimation of the contributing separation. Calculating β from these conductance plots contrasts with conventional molecular conductance experiments where the tunneling distance is directly assumed to be the molecular length, and the other effects noted above are assumed to negligible.
Regardless, by simply measuring this β for the arrays in the alkane case, we are able to compare with the transport properties in the PTCDI state and thus understand the effects of ligand exchange efficiency on the NP array conductance.
Next, we examine the effects of exchange of the alkanethiol linkers to PTCDI-DSH on conductance. As shown in Fig. 3a (red), the conductance of the array always increases upon exchange to the PTCDI, showing the expected increase in transport upon exchange to a molecule with large, delocalized π-orbitals. From Fig. 3a, the tunneling decay constant for PTCDI is found to be 9.9 nm−1. It is expected that a series of NP arrays with sufficiently narrow interparticle separation distributions would have the same conductance if 100% exchange to PTCDI occurred, regardless of the initial molecular state.
Importantly, both the final conductance (Fig. 3a, red) and the conductance ratio (GPTCDI/GAlkane, Fig. 3b) vary depending on the initial alkane. Variations in final conductance indicate that not all nanoparticles are linked by PTCDI-DSH after exchange. The variation in conductance ratio also indicates that the array conductance depends not just on the details of the tunneling probability through the molecular ligand, but upon the probability of a molecule binding in each nanoparticle junction. This means that exchange efficiency depends on the initial molecular state of the array.
Taken together, these observations imply that there will be a maximum exchange ratio that can be obtained when the probability of ligand exchange is maximized. By examining the conductance ratio and the interparticle separation distribution for each molecular state, we can determine the exchange efficiency of PTCDI-DSH binding into the alkane-capped nanoparticle arrays and find the highest exchange efficiency for this system.
We use a bond percolation model to examine our conductance results and determine whether ligand exchange efficiency accurately reflects the change in conductance ratio for each of the ligand states. In this model bonding is defined by a PTCDI molecule successfully linking two nanoparticles. The change in conductance ratio with bonding probability, p, is given in eqn (2):3,30,31
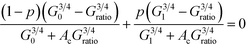 | (2) |
Here G0 is the initial ratio, G1 is the maximum conductance ratio, Gratio is defined as GPTCDI/Galkane for each molecular length, AC is given by Ac = (1 − pc)/pc, and pc is the critical threshold for percolation which determines the percentage of bonds that must be replaced before a percolated pathway exists. For a hexagonally close-packed 2D array, pc = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(π/18) ≈ 0.34.30 From this expression, it is apparent that the critical value to determine is p, the probability of bond replacement.
sin(π/18) ≈ 0.34.30 From this expression, it is apparent that the critical value to determine is p, the probability of bond replacement.
To estimate the probability of bond formation (PTCDI exchange) in this system, we use distribution functions for the separation between nanoparticles extracted from the TEM images described above. For the array in each alkane state, the separations between ∼200 nearest neighbor nanoparticles were measured using ImageJ and the resulting distribution fit with a Gaussian distribution (Fig. 4a). While average interparticle separation increases monotonically from C12 to C20 (Fig. 2d), the dispersion of the Gaussian distribution (Fig. 4a) varies less systematically. To estimate the probability of bond formation, we integrate each of the distributions over the shaded region shown in Fig. 4a (1.70 nm to 2.52 nm). This length range is the range of nanoparticle separations for which PTCDI is likely to substitute into the gap. The range minimum was determined by finding the separation at which the PTCDI-DSH molecule would be at a ∼45° angle with the normal to the nanoparticle surface, and the maximum is the sulfur-to-sulfur length of PTCDI-DSH including a single Au adatom. It is expected that at separations smaller than the minimum, steric hindrance would prevent binding, and separations longer than the molecule cannot be bridged. We also note that these limits are not unique: if slightly different values are used (for example, by including two Au adatoms in the maximum length), it affects the absolute probabilities, but not the validity of fitting with a percolation model. For each Gaussian distribution the total area under the curve is unity for every alkane molecule, as such the area of the integrated region for each distribution generates the probability that a PTCDI-DSH molecule will be able to successfully exchange into a junction in the array. This is the ligand exchange efficiency. These probabilities are extracted from the distribution functions (red circles in Fig. 4b) and the series is fit using eqn (1) with G1 as a fitting parameter. The best fit was found with G1 = 1267, yielding an R2-value of 0.88.
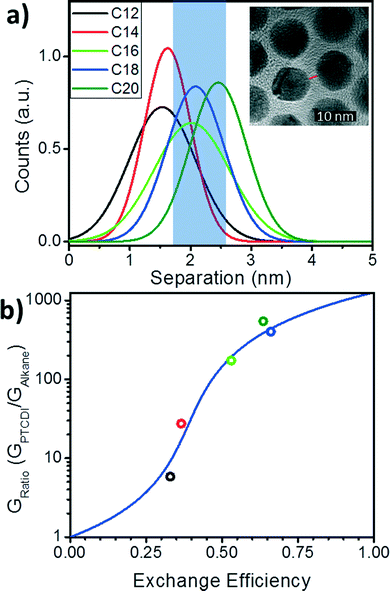 | ||
| Fig. 4 Gaussian distributions of interparticle separations and the bond-percolation model fitting. a) Gaussian distributions of separations of the Au NP arrays before PTCDI exchange. Inset: TEM image defines separation as the shortest interparticle distance taken along the center-to-center line. b) Conductance ratio versus exchange efficiency (circles) and bond percolation model fitting from eqn (2) (blue line). | ||
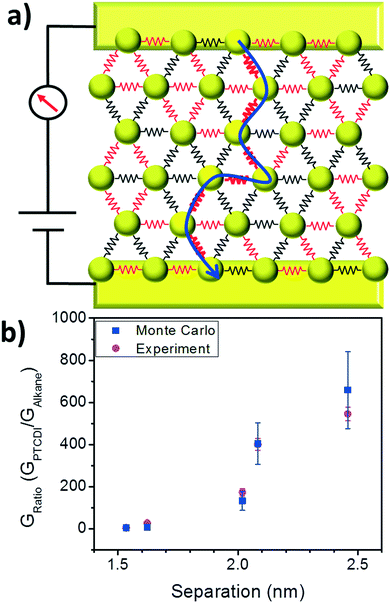
From this analysis we conclude that the increase in conductance from the initial state to the exchanged state depends on the efficiency of ligand exchange, and this process can be understood in terms of a bond percolation model. To provide an additional test of the percolation model, Monte Carlo simulations of hopping based transport were performed using a self-developed Matlab code (see ESI† for details). To perform the simulations, hexagonal arrays of nodes were generated, with each node representing a nanoparticle. Node-to-node separations were generated from the Gaussian distributions of lengths for each of the 5 alkanethiols from TEM images, and the probability of successful hopping between nodes was proportional to exp(−βs)exp(−2EA/kBT), where s is the separation, β is the tunneling decay constant for alkanes,27 and EA is the activation energy. The conductivity in the alkane case for C12, C14, C16, C18, and C20 was simulated by extracting successful hopping probabilities from the transmission of a charge from one side of the array (source electrode) to the opposite side (drain electrode), with a bias applied. This process was repeated for 256 arrays of ∼600 nodes each to generate a statistical representation of the variation of the arrays.
Grids representing nanoparticle monolayers in the PTCDI state were generated by taking alkane-state arrays and simulating a PTCDI exchange. Ligand exchange to PTCDI occurred under the same conditions in the model as in experiment – when interparticle separations fell within the acceptable length range. Fig. 5a depicts a simplified example of the grid configuration. Because the separation distributions in the simulation are identical to the experimental distributions, the exchange efficiencies (or the probability of successful ligand exchange) are the same in simulation and experiment. For each junction, if ligand exchange occurred, then the tunneling probability for that junction increased to match the single molecule transport probability of the PTCDI-DSH derivative.32
Monte Carlo hopping simulations were repeated on grids in the PTCDI state and all other variables (array size, bias voltage, etc.) were kept constant. Simulations were repeated with and without varying activation energies between alkane and PTCDI; in Fig. 5 two activation energies were used (see Fig. S2 in ESI† for simulation results with constant EA). Because the change in the conductance ratio GPTCDI/GAlkane depending on the initial molecular state matches well between Monte Carlo simulations and experiment (Fig. 5b), it supports both the validity of the extracted ligand efficiencies and the use of the bond percolation model.
Understanding how molecular state and the distribution of particle separations affects the change in conductance after ligand exchange allows exchange efficiencies to be extracted for the nanoparticle monolayers in each initial alkane state. Furthermore, by understanding how the ligand exchange efficiency varies with these properties, we are able to distill a set of design rules that will allow one to maximize the ligand exchange efficiency between nanoparticles in molecule/nanoparticle hybrid films. There are two straightforward criteria. First, in the initial state, the average separation between nanoparticles should be as close as possible to the center of the “attachment range” (blue region in Fig. 4a) of the final-state molecule as possible. This requirement can be clearly observed in Fig. 4a by comparing the C18 and C20 cases. Because the C18 and C20 separations are peaked in the middle of this range, the probabilities and exchange ratios are similar and the highest of the molecules examined. Secondly, the distribution of separations should be minimized. Because the range of separations over which the molecules can bind to both nanoparticles is limited, it is necessary to aim for as narrow a distribution as possible. Narrowing this distribution will depend on many factors including the assembly method, the synthesis method for the nanoparticles, the size distribution of the nanoparticles, and uniformity of coverage of the initial-state ligand. Therefore, tuning the separation and minimizing the distribution of these values will allow for maximum exchange and a maximum increase in the conductance for nanoparticle films.
Furthermore, our straightforward technique to calculate exchange efficiency is simple and versatile enough to be used under most conditions when introducing a ligand into an existing nanoparticle-molecule array. We expect that this method would be useful for introducing optical sensing molecules,33 electrochemical molecules,34 and secondary molecules for mechanical purposes.35 This method may also be applicable for the further development of nanoparticle-based transistors36,37 or almost any ligand-exchange process in NP-arrays.38 See ESI† section 7 for further details on the efficiency calculation method.
In conclusion, we have implemented a 2-step ligand exchange protocol that will allow the maximum number of nanoparticles in the film to be coupled with the molecule of interest, and the maximum conductance ratio to be obtained. By first examining the conductance and average separation between nanoparticles in 2D hybrid monolayers as a function of saturated ligand length and then exchanging the ligand to a conjugated – dithiolated linker, we were able to determine that the conductance ratio and exchange probability are both maximized when the average separation between nanoparticles is matched to the length of the exchanged linker and the distribution of separations are minimized. These conclusions yield a general methodology for interlinking nanoparticle systems with ligands with designed properties, and open the door for advancing the development of nanoparticle based electronics, optoelectronics, plasmonics, and sensing applications by using the linkers to improve performance.
Author contributions
Q. F. performed synthesis, ligand exchange, and measurements. C. E. M. facilitated measurements, fabricated substrates, and performed simulations. S. H. and K. v. B. facilitated electron microscopy. Y. H. developed simulation code and R. F. advised simulations. J.-M. H. and L. Z. synthesized the PTCDI molecules. J. H. conceived the experiments. C. E. M., Q. F., and J. H. assembled the manuscript.Notes
The authors declare no competing financial interests.Abbreviations
| NP | Nanoparticle |
| HOMO | Highest occupied molecular orbital |
| LUMO | Lowest unoccupied molecular orbital |
Acknowledgements
The authors would like to acknowledge support from the National Science Foundation 1605338. Y. H. was partially supported by the Chemical Engineering and Materials Science Honors program supported by J. Wasson. S. H. and K. v. B. were supported through a UC Laboratory Fee Grant #12-LR-238313.References
- P. Pandey, S. K. Arya, Z. Matharu, S. P. Singh, M. Datta and B. D. Malhotra, Polythiophene Gold Nanoparticles Composite Film for Application to Glucose Sensor, J. Appl. Polym. Sci., 2008, 110(2), 988–994 CrossRef CAS.
- M. Toma, K. Toma, K. Michioka, Y. Ikezoe, D. Obara, K. Okamoto and K. Tamada, Collective Plasmon Modes Excited on a Silver Nanoparticle 2D Crystalline Sheet, Phys. Chem. Chem. Phys., 2011, 13(16), 7459–7466 RSC.
- J. Liao, S. Blok, S. J. van der Molen, S. Diefenbach, A. W. Holleitner, C. Schönenberger, A. Vladyka and M. Calame, Ordered Nanoparticle Arrays Interconnected by Molecular Linkers: Electronic and Optoelectronic Properties, Chem. Soc. Rev., 2015, 44(44), 999–1014 RSC.
- F. Remacle and R. D. Levine, Quantum Dots as Chemical Building Blocks: Elementary Theoretical Considerations, ChemPhysChem, 2001, 2(1), 20–36 CrossRef CAS PubMed.
- C. Murray, C. R. Kagan and M. Bawendi, Synthesis and Characterization of Monodisperse Nanocrystals and Close-Packed Nanocrystal Assemblies, Annu. Rev. Mater. Sci., 2000, 30(1), 545–610 CrossRef CAS.
- N. J. Tao, Electron Transport in Molecular Junctions, Nat. Nanotechnol., 2006, 1(3), 173–181 CrossRef CAS PubMed.
- A. T. Fafarman, W. K. Koh, B. T. Diroll, D. K. Kim, D. K. Ko, S. J. Oh, X. Ye, V. Doan-Nguyen, M. R. Crump, D. C. Reifsnyder, C. B. Murray and C. R. Kagan, Thiocyanate-Capped Nanocrystal Colloids: Vibrational Reporter of Surface Chemistry and Solution-Based Route to Enhanced Coupling in Nanocrystal Solids, J. Am. Chem. Soc., 2011, 133(39), 15753–15761 CrossRef CAS PubMed.
- J. L. Sample, K. C. Beverly, P. R. Chaudhari, F. Remacle, J. R. Heath and R. D. Levine, Imaging Transport Disorder in Conducting Arrays of Metallic Quantum Dots : An Experimental and Computational Study, Adv. Mater., 2002, 14(2), 124–128 CrossRef CAS.
- F. Remacle, C. P. Collier, G. Markovich, J. R. Heath, U. Banin and R. D. Levine, Networks of Quantum Nanodots: The Role of Disorder in Modifying Electronic and Optical Properties, J. Phys. Chem. B, 1998, 102, 7727–7734 CrossRef CAS.
- D. B. Janes, V. R. Kolagunta, R. G. Osifchin, J. D. Bielefeld, R. P. Andres, J. I. Henderson and C. P. Kubiak, Electronic Conduction through 2D Arrays of Nanometer Diameter Metal Clusters, Superlattices Microstruct., 1995, 18, 275–282 CrossRef CAS.
- J. Liao, L. Bernard, M. Langer, C. Schönenberger and M. Calame, Reversible Formation of Molecular Junctions in 2D Nanoparticle Arrays, Adv. Mater., 2006, 18(18), 2444–2447 CrossRef CAS.
- J. He, X.-M. Lin, H. Chan, L. Vuković, P. Král and H. M. Jaeger, Diffusion and Filtration Properties of Self-Assembled Gold Nanocrystal Membranes, Nano Lett., 2011, 11(6), 2430–2435 CrossRef CAS PubMed.
- P. Kanjanaboos, A. Joshi-Imre, X.-M. Lin and H. M. Jaeger, Strain Patterning and Direct Measurement of Poisson's Ratio in Nanoparticle Monolayer Sheets, Nano Lett., 2011, 11(6), 2567–2571 CrossRef CAS PubMed.
- M. A. Mangold, M. Calame, M. Mayor and A. W. Holleitner, Negative Differential Photoconductance in Gold Nanoparticle Arrays in the Coulomb Blockade Regime, ACS Nano, 2012, 6(5), 4181–4189 CrossRef CAS PubMed.
- G. Tsutsui, S. Huang, H. Sakaue, S. Sshingubara and T. Takahagi, Well-Size-Controlled Colloidal Gold Nanoparticles Dispersed in Organic Solvents, Jpn. J. Appl. Phys., 2001, 40(1), 346–349 CrossRef CAS.
- M. Karg, N. Schelero, C. Oppel, M. Gradzielski, T. Hellweg and R. von Klitzing, Versatile Phase Transfer of Gold Nanoparticles from Aqueous Media to Different Organic Media, Chemistry, 2011, 17(16), 4648–4654 CrossRef CAS PubMed.
- S.-K. Eah, A Very Large Two-Dimensional Superlattice Domain of Monodisperse Gold Nanoparticles by Self-Assembly, J. Mater. Chem., 2011, 21(42), 16866 RSC.
- X. M. Lin, H. M. Jaeger, C. M. Sorensen and K. J. Klabunde, Formation of Long-Range-Ordered Nanocrystal Superlattices on Silicon Nitride Substrates, J. Phys. Chem. B, 2001, 105(17), 3353–3357 CrossRef CAS.
- V. Santhanam and R. P. Andres, Microcontact Printing of Uniform Nanoparticle Arrays, Nano Lett., 2004, 4(1), 41–44 CrossRef CAS.
- C. E. McCold, Q. Fu, J. Y. Howe and J. Hihath, Conductance Based Characterization of Structure and Hopping Site Density in 2D Molecule-Nanoparticle Arrays, Nanoscale, 2015, 7(36), 14937–14945 RSC.
- Y. Liu, M. Gibbs, J. Puthussery, S. Gaik, R. Ihly, H. W. Hillhouse and M. Law, Dependence of Carrier Mobility on Nanocrystal Size and Ligand Length in PbSe Nanocrystal Solids, Nano Lett., 2010, 10(5), 1960–1969 CrossRef CAS PubMed.
- P. Guyot-Sionnest, Electrical Transport in Colloidal Quantum Dot Films, J. Phys. Chem. Lett., 2012, 3(9), 1169–1175 CrossRef CAS PubMed.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Self-Assembled Monolayers of Thiolates on Metals as a Form of Nanotechnology, 2005, vol. 105 Search PubMed.
- W. Wang, T. Lee and M. A. Reed, Elastic and Inelastic Electron Tunneling in Alkane Self-Assembled Monolayers, J. Phys. Chem. B, 2004, 108(48), 18398–18407 CrossRef CAS.
- V. B. Engelkes, J. M. Beebe and C. D. Frisbie, Length-Dependent Transport in Molecular Junctions Based on SAMs of Alkanethiols and Alkanedithiols: Effect of Metal Work Function and Applied Bias on Tunneling Efficiency and Contact Resistance, J. Am. Chem. Soc., 2004, 126(43), 14287–14296 CrossRef CAS PubMed.
- X. Li, J. He, J. Hihath, B. Xu and S. M. Lindsay, Conductance of Single Alkanedithiols : Conduction Mechanism and Effect of Molecule-Electrode Contacts, 2006, no. 24, pp. 2135–2141 Search PubMed.
- H. Rascón-Ramos, J. M. Artés, Y. Li and J. Hihath, Binding Configurations and Intramolecular Strain in Single-Molecule Devices, Nat. Mater., 2015, 14(5), 517–522 CrossRef PubMed.
- C. Li, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, Charge Transport in Single Au|alkanedithiol|Au Junctions: Coordination Geometries and Conformational Degrees of Freedom, J. Am. Chem. Soc., 2008, 130(17), 318–326 CrossRef CAS PubMed.
- X. Li, J. He, J. Hihath, B. Xu, S. M. Lindsay and N. Tao, Conductance of Single Alkanedithiols: Conduction Mechanism and Effect of Molecule-Electrode Contacts, J. Am. Chem. Soc., 2006, 128(6), 2135–2141 CrossRef CAS PubMed.
- B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Springer-Verlag, 1984 Search PubMed.
- J. Wu and D. McLachlan, Percolation Exponents and Thresholds Obtained from the Nearly Ideal Continuum Percolation System Graphite-Boron Nitride, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(3), 1236–1248 CrossRef CAS.
- S. Hosseini, C. Madden, J. Hihath, S. Guo, L. Zang and Z. Li, Single-Molecule Charge Transport and Electrochemical Gating in Redox-Active Perylene Diimide Junctions, J. Phys. Chem. C, 2016, 120(39), 22646–22654 CAS.
- S. van der Molen, J. Liao, T. Kudernac, J. S. Agustsson, L. Bernard, M. Calame, B. J. van Wees, B. L. Feringa and C. Schönenberger, Light-Controlled Conductance Switching of Ordered Metal-Molecule-Metal Devices, Nano Lett., 2009, 9(1), 76–80 CrossRef CAS PubMed.
- J. Liao, J. S. Agustsson, S. Wu, C. Schönenberger, M. Calame, Y. Leroux, M. Mayor, O. Jeannin, Y.-F. Ran, S.-X. Liu and S. Decurtins, Cyclic Conductance Switching in Networks of Redox-Active Molecular Junctions, Nano Lett., 2010, 10(3), 759–764 CrossRef CAS PubMed.
- K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Elastic Membranes of Close-Packed Nanoparticle Arrays, Nat. Mater., 2007, 6(9), 656–660 CrossRef CAS PubMed.
- J.-H. Choi, A. T. Fafarman, S. J. Oh, D.-K. Ko, D. K. Kim, B. T. Diroll, S. Muramoto, J. G. Gillen, C. B. Murray and C. R. Kagan, Bandlike Transport in Strongly Coupled and Doped Quantum Dot Solids: A Route to High-Performance Thin-Film Electronics, Nano Lett., 2012, 12(5), 2631–2638 CrossRef CAS PubMed.
- M. E. Turk, J. H. Choi, S. J. Oh, A. T. Fafarman, B. T. Diroll, C. B. Murray, C. R. Kagan and J. M. Kikkawa, Gate-Induced Carrier Delocalization in Quantum Dot Field Effect Transistors, Nano Lett., 2014, 14(10), 5948–5952 CrossRef CAS PubMed.
- A. Dong, Y. Jiao and D. J. Milliron, Electronically Coupled Nanocrystal Superlattice Films by in Situ Ligand Exchange at the Liquid-Air Interface, ACS Nano, 2013, 7(12), 10978–10984 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Monte Carlo details. See DOI: 10.1039/c7me00033b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |