2D and 3D-printing of self-healing gels: design and extrusion of self-rolling objects†
Milena
Nadgorny
,
Zeyun
Xiao
and
Luke A.
Connal
 *
*
Department of Chemical and Biomolecular Engineering, The University of Melbourne, Parkville, Victoria 3010, Australia. E-mail: luke.connal@unimelb.edu.au
First published on 23rd June 2017
Abstract
In this work, we report the synthesis, characterization and three-dimensional (3D) printing of self-healing gels. The gels are prepared by cross-linking benzaldehyde-functionalized poly(2-hydroxyethyl methacrylate) (PHEMA) with ethylenediamine (EDA) to form dynamic imine bonds. An immediate gelation was observed within seconds, followed by a full maturation, enabling time independent and stable printing. The self-healing gels showed 98% recovery from mechanical damages. To establish a printable window for our well-defined system, and to allow robust printability, we examined a broad number of ink formulations. To tune the rheology towards the formation of soft and extrudable, yet stable and self-supporting materials, we examined self-healing gels with controlled degrees of cross-linking and polymer concentrations. Single-layer patterns and self-healing objects with tunable layer thicknesses and shapes were successfully 3D-printed, with their self-healing capabilities fully retained. After post-printing reinforcement by further imine cross-linking, the swelling properties of these 3D-printed functional structures were employed for the fabrication of self-rolling, dynamic objects. These self-healing “smart” objects could change their shape and axes of folding by sensing their chemical environment.
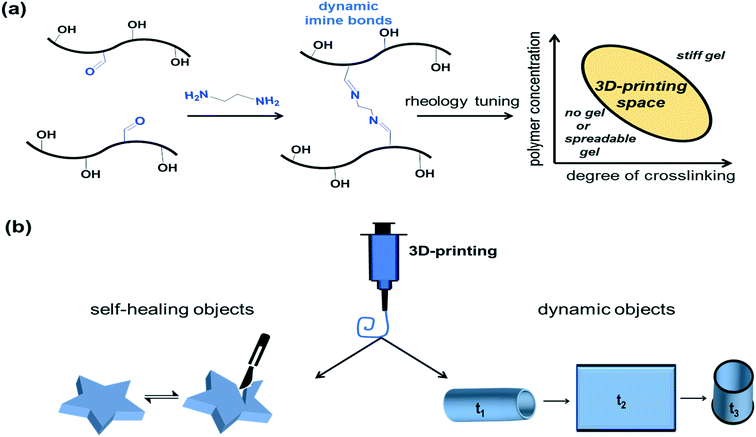
Design, System, ApplicationWe present a methodological approach to design 3D-printable, self-healing gels, covalently cross-linked with small molecules. Our molecular design includes a facile synthesis of polymers, which are employed as a functional platform for preparation of autonomously and rapidly self-healing gels. To make these gels printable, a delicate balance between the ability to flow, and a sufficient rigidity to retain structural fidelity, is required. Therefore, our optimization strategy included a detailed rheological examination of numerous formulations with a precise control of the polymer concentration and degrees of cross-linking. The outcome of this work allowed an efficient mapping of the printability space, and therefore can be implemented as a general approach to formulate and 3D-print covalently cross-linked gels. The utilization of 3D-printing technology to deposit self-healing gels represents a novel approach for a selective application of protective coatings with customable designs, streamlined time and waste. Moreover, the functionality of our gels is not limited to self-healing. These dynamic gels enabled a successful fabrication of “smart” objects, which exhibited environment-dependant swelling, self-assembly and self-rolling properties. 3D-printing of dynamic and self-healing objects represents a proof-of-concept, first of its kind, which holds a promise for a future manufacturing of actuators and soft robots with extended lifespan. |
Introduction
Self-healing materials are capable of recovering from damages and restoring their functionality, just like the natural ability of living creatures to repair their tissues.1 This unique property, offers the ability to extend the lifetime of products, which is usually limited by mechanical failures.2–4 Inspired by nature, scientists are engineering new self-repairing systems and the interest in the field is rapidly growing.5 Autonomously self-healing gels based on hydrogen bonding,2,6,7 and dynamic covalent chemistry approaches1,4,8–12 have been recently reported. These reports concentrate on the development of chemically-tuned performances of self-healing materials. However, very few works discuss the processability of self-healing gels. In order to achieve a desired shape, a gel is usually casted into a mold or applied as a coating.2,13 With the rise of three-dimensional (3D) printing technology, it is now possible to fabricate 3D structures with a customable design. This additive manufacturing technology provides precise control over the shape, dimensions and density of a structure, and allows the streamlining of production costs and time.14–16 Despite the rapid evolution of 3D-printing, the number of functional, 3D-printable inks is still limited, and their development remains a challenge. In particular, 3D-printing of chemically cross-linked gels is not a trivial task, which requires a delicate balance between the flow properties of inks and structural fidelity of printed objects. These properties are dictated by inks rheology, which is a critical factor for inks printability, and therefore must be carefully adjusted.17,18Of particular interest is the 3D-printing of smart materials, which can sense their environment, and change their structure in response to external stimuli.14,19–22 These materials are often employed for fabrication of soft robots, self-evolving structures and actuators.20–24 However, these 3D-printed shape-changing objects are prone to damages, especially due to an extensive and repetitive utilization of their mechanical functions, such as bending or folding. 3D-printing of soft and dynamic objects based on self-healing gels holds a great promise for an advanced design, manufacturing and extended utilization of these functional structures. Herein, we report 3D-printing of self-healing gels prepared from benzaldehyde-functionalized poly(2-hydroxyethyl methacrylate) (PHEMA). Aldehyde groups were cross-linked with a diamine functional small molecule (ethylenediamine, EDA) to form dynamic and reversible imine bonds,25,26 creating gels with fast dynamics of cross-linking, which autonomously self-heal. We investigate the rheological properties of these gels, which can be carefully tuned and controlled by the degree of cross-linking and the concentration of the polymer, making them 3D-printable. After assessing the printing potential of numerous self-healing inks, the optimal formulation was 3D-printed. We employ the dynamic nature of self-healing gels for fabrication of self-rolling structures, which can swell and generate biaxial movements of unfolding and rolling.
Experimental section
Materials
4-Formylbenzoic acid (4FBA, Sigma-Aldrich, 97%), 4-cyano-4[(dodecylsulfanylthiocarbonyl) sulfanyl] pentanoic acid (CTA, Sigma-Aldrich, 97%), diethyl ether (ChemSupply, 99.5%), N,N-dimethylformamide (DMF, VWR, 99.9%), methanol (ChemSupply, 99.8%), DMF anhydrous (VWR, 99.8%), sodium borohydride (Scharlab, 98%), dicyclohexylcarbodiimide (DCC, Alfa Aesar, 99%), 4-(dimethylamino)pyridine (DMAP, Alfa Aesar, 99%), ethylenediamine (EDA, Sigma-Aldrich, >99%) were used as received without further purification.2-Hydroxyethyl methacrylate (HEMA, Sigma-Aldrich, >99%) was purified by basic alumina column to remove the inhibitors. 1,1′-Azobis(cyclohexanecarbonitrile) (ACHN, Sigma-Aldrich, 98%) was recrystallized from ethanol and dried overnight prior to use.
Instrumentation
Size exclusion chromatography (SEC) was performed on the Shimadzu liquid chromatography system with Phenomenex Phenogel columns. DMF with 0.05 mol L−1 LiBr was used as an eluent at 70 °C with a flow rate of 1 mL min−1. Average molecular weights (Mn, Mw) and polydispersity index (Đ) were calculated based on poly(ethylene glycol) calibration standards. Proton nuclear magnetic resonance (1H NMR) analysis was performed on a Varian 400 MHz spectrometer. Rheology study was conducted on a controlled stress rheometer with 40 mm diameter parallel plates geometry (AR-G2, TA Instruments), equipped with a solvent trap. Fourier transform infra-red (FTIR, Varian 7000, ATR mode) was used for infra-red analysis. For 3D-printing, 3D-Bioplotter (Developer Series, EnvisionTec, Germany) was utilized with Bioplotter RP software for file processing. Printing parameters: print head speed 13 mm s−1, piston pressure 0.6 bar, temperature 25 °C, nozzle diameter 0.4 mm, solid infill mode, rectangular (mesh) infill pattern (100%), uniform slicing with a layer thickness of 0.360 mm.Synthesis of PHEMA
HEMA (30.0 g, 231 mmol), 4-cyano-4-[(dodecylsulfanylthiocarbonyl) sulfanyl] pentanoic acid (264.0 mg, 0.654 mmol) and ACHN (31.9 mg, 1.3 × 10−2 mmol) were combined with DMF (30.0 mL) in 250 mL Schlenk tube. After 3 cycles of freeze–pump–thaw the Schlenk tube was sealed under nitrogen, placed in an oil bath, heated to 85 °C, and allowed to react under stirring for 21 h. The reaction was quenched by placing the Schlenk tube into ice. The viscous content of the tube was diluted with DMF and precipitated into diethyl ether twice. The product was filtered, collected and allowed to dry overnight under vacuum.Synthesis of benzaldehyde-functionalized PHEMA (PHEMA0.35-co-P4FBA0.65)
PHEMA (2.0 g, 15.37 mmol), 4FBA (2.31 g, 15.37 mmol), DMAP (0.19 g, 1.54 mmol) and DCC (3.17 g, 15.37 mmol) were separately dissolved in anhydrous DMF. Dissolved PHEMA, 4FBA and DMAP were combined under stirring. DCC was added dropwise to the reaction vessel under rigorous stirring. The reaction lasted for 19 h. After filtration, the liquid was collected and precipitated into methanol. The functionalized polymer (PHEMA0.35-co-P4FBA0.65) was filtered, collected and dried under vacuum.Preparation of self-healing 3D-printable gels
The gel was prepared from PHEMA0.35-co-P4FBA0.65 cross-linked with EDA (molar ratio of aldehyde: EDA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08), optimized polymer concentration was 6.5% (wt/vol). PHEMA0.35-co-P4FBA0.65 (0.4 g) was dissolved in DMF (5.0 mL) until a fully transparent and homogeneous solution was obtained. A stock solution of the cross-linker was prepared by dissolving 57.6 mg EDA in 11.0 mL DMF. An aliquot of the stock solution (1.1 mL) was introduced to the dissolved PHEMA0.35-co-P4FBA0.65 at ambient temperature and immediately vortexed to allow homogenization. Gel formation was verified by a standard inversion test. In a similar manner, self-healing gels with different polymer concentrations and degrees of cross-linking were prepared. General annotation for prepared gels: Gx%_yEDA, where x represents the concentration of PHEMA0.35-co-P4FBA0.65 (wt/vol%) and y represents the molar ratio of EDA to the aldehyde repeating unit.
0.08), optimized polymer concentration was 6.5% (wt/vol). PHEMA0.35-co-P4FBA0.65 (0.4 g) was dissolved in DMF (5.0 mL) until a fully transparent and homogeneous solution was obtained. A stock solution of the cross-linker was prepared by dissolving 57.6 mg EDA in 11.0 mL DMF. An aliquot of the stock solution (1.1 mL) was introduced to the dissolved PHEMA0.35-co-P4FBA0.65 at ambient temperature and immediately vortexed to allow homogenization. Gel formation was verified by a standard inversion test. In a similar manner, self-healing gels with different polymer concentrations and degrees of cross-linking were prepared. General annotation for prepared gels: Gx%_yEDA, where x represents the concentration of PHEMA0.35-co-P4FBA0.65 (wt/vol%) and y represents the molar ratio of EDA to the aldehyde repeating unit.
3D-printing
The gels were loaded into a disposable syringe with the attached nozzle, manually compressed with the lead until a good contact between the lead and the gel was obtained and air bubbles evacuated. The syringe was then loaded into the 3D-Bioplotter. A cycle of purging was performed by applying pneumatic pressure for three seconds, until a filamentous gel strand exited the nozzle. Immediately afterwards, the tip of the nozzle was cleaned with a brush, and the nozzle was automatically calibrated. Optimization of printing parameters (printing speed and pressure) was achieved by examination of alternating speeds and pressures, the combination of which yielded a stable, continuous printing with well-defined gel filaments. 3D-printing could be performed immediately afterwards.Secondary (post-printing) cross-linking
Freshly 3D-printed objects were introduced to the cross-linker solutions of EDA in DMF (2.0 mg mL−1, 1.0 mg mL−1 or 0.7 mg mL−1, as specified) for 20 min. The objects were then removed from the cross-linking solution and allowed to dry.Reduction of the self-healing gel
2 equivalents of sodium borohydride were dissolved in methanol. 3D-printable gel (G6.5%_0.08EDA) was introduced to the sodium borohydride solution and allowed to react overnight. After the reaction, the gel was removed from the reaction vessel, washed with methanol and excess of solvent was gently whipped.Rheology of self-healing gels
Kinetics of gel (G6.5%_0.08EDA) formation was studied by placing the polymer (50.0 mg of PHEMA0.35-co-P4FBA0.65 dissolved in 0.67 mL DMF) on the rheometer plate. Afterwards, 0.1 mL from EDA stock solution (7.0 mg EDA dissolved in 1.0 mL DMF) was directly and evenly introduced to the plate and the changes in dynamic moduli as a function of time were traced at 1% strain, angular frequency of 6.283 rad s−1 and 25 °C. Self-healing properties of the gel were examined by strain ramp up under a constant frequency of 6.283 rad s−1 at 25 °C. The study of dynamic moduli dependence on frequency was performed by conducting a frequency ramp up scanning the region of 0.01 to 1000 rad s−1 under 1% strain at 25 °C. Recovery properties of the gel from high strain deformations were studied by step strain measurements. Oscillatory strains were alternated from 1% to 1000% and vice versa under a constant angular frequency of 6.283 rad s−1 at 25 °C, and the changes in dynamic moduli were examined as a function of time. The % recovery was calculated by formula (1):27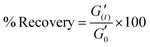 | (1) |
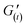 is the elastic modulus of the gel at a defined time (t), and
is the elastic modulus of the gel at a defined time (t), and 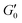 is the elastic modulus of the intact gel monitored at 1% strain. Stress ramp up and viscosity measurements were performed at 25 °C under a constant frequency of 6.283 rad s−1. Overnight stabilized gels were used for self-healing studies.
is the elastic modulus of the intact gel monitored at 1% strain. Stress ramp up and viscosity measurements were performed at 25 °C under a constant frequency of 6.283 rad s−1. Overnight stabilized gels were used for self-healing studies.
Preparation of dynamic objects
The first step of the preparation included 3D-printing of G6.5%_0.08EDA rectangular solids with different dimensions on a glass substrate. While the thickness (z) and the width (w) of the rectangular solids were kept constant (z = 1.0 mm, w = 1.0 cm, respectively), the length (L) of the rectangular solids varied (L = 2.5, 3.5 and 5.0 cm). After a secondary cross-linking with 0.7 mg mL−1 EDA, the structures were allowed to dry in the fume hood for approximately 1 h, which was followed by a gentle detachment of the objects from the glass by a spatula. The objects were kept exposed to air to allow drying.Dynamic self-rolling studies
The 3D-printed objects were submerged into a reservoir of DMF and allowed to self-evolve without any external intervention. Dynamic changes in their shape were monitored (using digital photography) as a function of time.Results and discussion
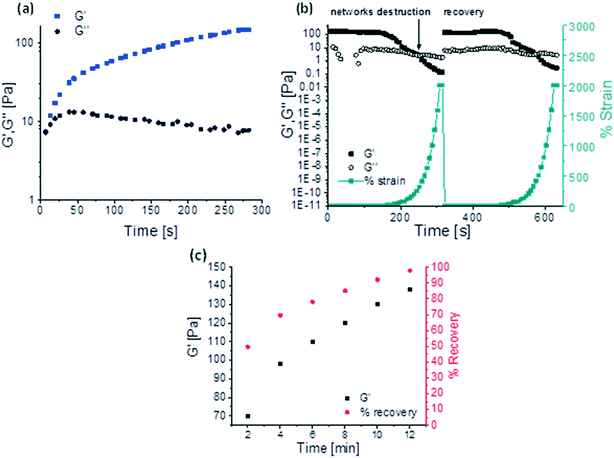
The preparation of 3D-printable chemically cross-linked self-healing gels require a complex, multi-step design, whereby we harness well-defined dynamic covalent chemistry to control the rheology of the inks. We develop a 3D-printable window, which is schematically presented in Fig. 1. The first stage includes the synthesis of self-healing gels. To allow a rapid and autonomous self-healing, imine chemistry has been chosen for current work owing to its dynamic covalent nature and fast reaction kinetics.25 Therefore, in order to develop a functional platform for the formation of imines, benzaldehyde-functionalized polymers were synthesized, which we have recently shown to have versatile functionality and dynamics.28,29 PHEMA was selected as the functional polymer platform owing to its alcohol groups, which allow a facile attachment of benzaldehyde units to the polymer via carbodiimide coupling reaction. To obtain PHEMA with well-defined characteristics (Mn = 31 kDa, Đ = 1.36, yield ∼60%), reversible addition-fragmentation chain transfer (RAFT) polymerization was used according to Scheme S1.† A successful synthesis was supported by 1H NMR and SEC. See Fig. S1† for 1H NMR and Fig. S2† for SEC traces. Functionalization of PHEMA with 1 equivalent of 4FBA resulted in 65% conversion of hydroxyl groups to benzaldehydes (PHEMA0.35-co-P4FBA0.65, 45% yield, Fig. S3†). Benzaldehyde functional handles of PHEMA0.35-co-P4FBA0.65 were employed for the reaction with EDA to form imine bonds. The chemical structure of the gel is illustrated in Fig. S4a.† FTIR spectrum of the gel supports a successful formation of imine cross-links (Fig. S4b†). Gel formation was also evidenced by a standard inversion test, which indicated an immediate sol-to-gel transition. A rapid formation of the gel and its full maturation before printing are important advantages for formulation of printable inks, since they enable robust and time independent printing performances, overcoming the limitations of time dependant printing, by enabling an extended printing window.17 Therefore, a rheological investigation of gelation kinetics was required. The results show an immediate gelation upon introduction of EDA to the polymer, which occurs within approximately 10 s (Fig. 2a). The gelation is indicated by the crossover point of G′ and G′′, which is attributed to the transition from liquid to the solid state, and therefore the dominance of the storage modulus. More importantly, the dynamics of the gel maturation indicate a full stabilization of G′ values after approximately 5 min. G′ values remained unchanged when the same sample was re-examined after a few hours (Fig. S5†). To get further insight into self-healing properties of the gel, rheological examinations were conducted (Fig. 2). Strain sweep shows that at low strains G′ is higher than G′′, indicating the solid nature of the gel. With an increase in the applied strain, G′ values decreased until the network of the gel was destroyed at ∼400% strain. This critical transition occurs as a result of bonds dissociation and can be evidenced by a sharp drop in G′, a simultaneous increase in G′′, and the intersection of both. From this point, the gel exhibits a dominantly fluidic behaviour. With the decrease in strain values back to the linear viscoelastic region, a recovery of the gel occurred, which is a characteristic behaviour of self-healing gels.3 A recovery of ∼97% of the moduli to their initial values occurred immediately (see Fig. 2b for strain sweep results). The gel exhibited frequency dependant behaviour, as can be concluded from the frequency sweep shown in Fig. S6.† In the region of scanned frequencies, G′ was constantly higher than G′′, which indicates that the timescale of the experiment was not sufficient to observe the bulk relaxation of the gel.We further examined the ability of the gel to recover from prolonged exposures to extremely high strains (1000%). When 1000% strain was continuously applied for 2 min, the sample was destroyed and defragmented to multiple pieces. Time dependant recovery is shown in Fig. 2c. The experiments indicate that only 2 min after ceasing the oscillatory stress, the elastic modulus restored 49% of its initial values (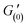 = 141 Pa,
= 141 Pa, 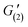 = 70 Pa). G′ values gradually increased with the increase in recovery time (
= 70 Pa). G′ values gradually increased with the increase in recovery time (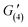 = 98 Pa,
= 98 Pa, 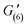 = 110 Pa,
= 110 Pa, 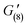 = 120 Pa,
= 120 Pa, 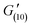 = 130 Pa), until a final recovery of 98% was reached after 12 min (
= 130 Pa), until a final recovery of 98% was reached after 12 min (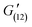 = 138 Pa). The gel could withstand 4 subsequent cycles of defragmentation and recovery. Despite a gradual increase in the time required for self-healing with the increasing number of subsequent cycles, full recovery of the networks could be achieved in all the cases (Fig. S7†). The autonomous, fast and full recovery are significant advantages for self-healing systems. With the increasing degree of cross-linking, full recovery of the gel could be achieved at much shorter times, without any deterioration in % recovery and recovery time with subsequent cycles (Fig. S8†). The imine chemistry allows proving the mechanism of this dynamic covalent bonds driven self-healing gel. The imine bonds can be easily reduced to amines, and hence lose their dynamic properties. When the gel was reduced with sodium borohydride, the self-healing ability of the gel was almost fully lost (Fig. S9a and b†).
= 138 Pa). The gel could withstand 4 subsequent cycles of defragmentation and recovery. Despite a gradual increase in the time required for self-healing with the increasing number of subsequent cycles, full recovery of the networks could be achieved in all the cases (Fig. S7†). The autonomous, fast and full recovery are significant advantages for self-healing systems. With the increasing degree of cross-linking, full recovery of the gel could be achieved at much shorter times, without any deterioration in % recovery and recovery time with subsequent cycles (Fig. S8†). The imine chemistry allows proving the mechanism of this dynamic covalent bonds driven self-healing gel. The imine bonds can be easily reduced to amines, and hence lose their dynamic properties. When the gel was reduced with sodium borohydride, the self-healing ability of the gel was almost fully lost (Fig. S9a and b†).
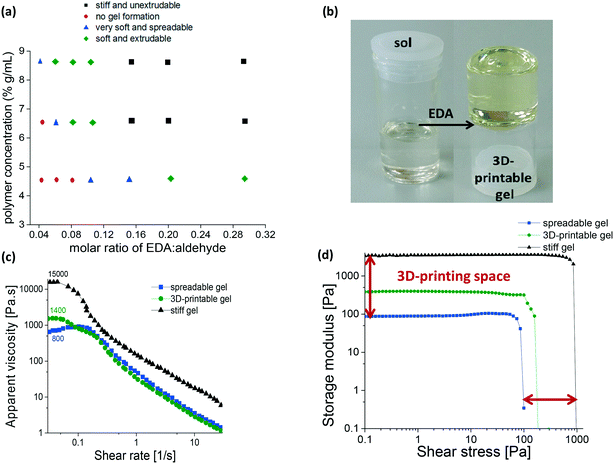
Despite the fact that gels are classified as solids, a manipulation of their chemical composition and precise control over their rheological properties, formulation and cross-linking degrees, have been found efficient in formulating printable inks.17,18 Therefore, in order to map the printability space it is essential to conduct a detailed investigation of the factors which affect the printability of our self-healing system. Printable inks must be extrudable through a nozzle and flow. Contradictory to that, the ability to retain structural integrity after printing is an essential requirement, since failing to do so 3D-printed objects collapse and lose their well-defined architectures.17 To obtain a preliminary assessment of the 3D-printing potential, we examined 21 ink formulations with varying concentrations of PHEMA0.35-co-4FBA0.65 (g mL−1) and different degrees of cross-linking (molar ratios of an aldehyde repeating unit to EDA). In addition to visual assessments, the formulations were manually extruded through a syringe17 with an attached nozzle of 200 and 400 μm diameter (Fig. S10†). During the initial screening process, each formulation was classified according to one of the four categories as following: (a) no gel formation: a formulation did not pass the inversion test and remained in its sol state. (b) Very soft and spreadable: the texture of the gel did not allow a sufficient self-support, essential for the physical stabilization and structural fidelity. (c) Soft and extrudable: these formulations are soft enough to be extruded trough a nozzle and exhibit a good material flow. Their filamentous strands exhibit self-support during a continuous layer-by-layer deposition. These formulations are optimal for 3D-printing. (d) Stiff and unextrudable: stiff gels which resist the applied pressures and are limited in their ability to flow.
The outcome of this qualitative study allows a preliminary assessment of numerous ink formulations and screening of their printing potential (Fig. 3a). This rapid hands-on assessment showed good correlation to formulations printing performances.
For a constant concentration of 4.5% PHEMA0.35-co-P4FBA0.65, no gelation was observed when the molar ratios of an aldehyde repeating unit to EDA were below 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1. Very soft and spreadable gels were obtained when the molar ratios of an aldehyde repeating unit to EDA increased above 1
0.1. Very soft and spreadable gels were obtained when the molar ratios of an aldehyde repeating unit to EDA increased above 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 to a maximum of 1
0.1 to a maximum of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.16. When the molar ratio of an aldehyde repeating unit to EDA increased to 1
0.16. When the molar ratio of an aldehyde repeating unit to EDA increased to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2, a soft and extrudable gel was formed (G4.5%_0.2EDA). The need for an addition of a relatively high amount of EDA to form robust and extrudable gels is attributed to the low polymer concentration (<5.0 wt/vol%). To compensate for the effect of exceedingly high fluidity and low viscosity, a higher cross-linking density is required for the structural stabilization of the networks. When PHEMA0.35-co-P4FBA0.65 concentration increased to 6.5%, a gelation was observed when molar ratios of the aldehyde repeating unit to EDA were higher than 1
0.2, a soft and extrudable gel was formed (G4.5%_0.2EDA). The need for an addition of a relatively high amount of EDA to form robust and extrudable gels is attributed to the low polymer concentration (<5.0 wt/vol%). To compensate for the effect of exceedingly high fluidity and low viscosity, a higher cross-linking density is required for the structural stabilization of the networks. When PHEMA0.35-co-P4FBA0.65 concentration increased to 6.5%, a gelation was observed when molar ratios of the aldehyde repeating unit to EDA were higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04. An optimal formulation for 3D-printing was achieved by using 6.5% PHEMA0.35-co-P4FBA0.65, keeping the molar ratio of the aldehyde repeating unit to EDA at 1
0.04. An optimal formulation for 3D-printing was achieved by using 6.5% PHEMA0.35-co-P4FBA0.65, keeping the molar ratio of the aldehyde repeating unit to EDA at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08 (G6.5%_0.08EDA). The gel is presented in Fig. 3b. Upon the increase in molar ratio of the aldehyde repeating unit to EDA above 1
0.08 (G6.5%_0.08EDA). The gel is presented in Fig. 3b. Upon the increase in molar ratio of the aldehyde repeating unit to EDA above 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, stiff and unextrudable gels were formed, making them unsuitable for 3D-printing. When PHEMA0.35-co-P4FBA0.65 concentration further increased to 8.5%, gel formation was observed for all the examined EDA stoichiometries. 3D-printable formulations were achieved when the molar ratio of the aldehyde repeating unit to EDA was 1
0.1, stiff and unextrudable gels were formed, making them unsuitable for 3D-printing. When PHEMA0.35-co-P4FBA0.65 concentration further increased to 8.5%, gel formation was observed for all the examined EDA stoichiometries. 3D-printable formulations were achieved when the molar ratio of the aldehyde repeating unit to EDA was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06, 1
0.06, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08 and 1
0.08 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 (G8.5%_0.06EDA, G8.5%_0.08EDA and G8.5%_0.1EDA, respectively). As expected, with the increasing concentration of PHEMA0.35-co-P4FBA0.65, a lower degree of cross-linking was required to form extrudable and self-supporting formulations. Interestingly, the gel preparation method affected the gelation process, and as a result impacted the physical properties of prepared gels. To form homogeneous gels, which would allow smooth and continuous printing, PHEMA0.35-co-P4FBA0.65 was dissolved in ∼80% of the required (total) DMF volume. EDA was dissolved in the complementary ∼20% vol. of DMF, and then was introduced to the polymer solution. Direct addition of non-diluted EDA, resulted in an inhomogeneous gelation with local “islands” of gel dispersed inside non-gelated regions of fluid. Application of immediate and prolonged vortex was found inefficient in improving the homogeneity of these gels. The observed effect is attributed to an immediate and localized gelation initiated by EDA. All the categories of gels discussed above are demonstrated in Fig. S11.†
0.1 (G8.5%_0.06EDA, G8.5%_0.08EDA and G8.5%_0.1EDA, respectively). As expected, with the increasing concentration of PHEMA0.35-co-P4FBA0.65, a lower degree of cross-linking was required to form extrudable and self-supporting formulations. Interestingly, the gel preparation method affected the gelation process, and as a result impacted the physical properties of prepared gels. To form homogeneous gels, which would allow smooth and continuous printing, PHEMA0.35-co-P4FBA0.65 was dissolved in ∼80% of the required (total) DMF volume. EDA was dissolved in the complementary ∼20% vol. of DMF, and then was introduced to the polymer solution. Direct addition of non-diluted EDA, resulted in an inhomogeneous gelation with local “islands” of gel dispersed inside non-gelated regions of fluid. Application of immediate and prolonged vortex was found inefficient in improving the homogeneity of these gels. The observed effect is attributed to an immediate and localized gelation initiated by EDA. All the categories of gels discussed above are demonstrated in Fig. S11.†
To be 3D-printable, gels must possess well defined viscoelasticity, which allows flow and deformation when the ink is subjected to extrusion shears.17,18,30–32 Rheological examination of the self-healing gel formulations with various compositions indicates that the gels exhibit shear thinning and shear yielding (Fig. 3c and d). Summary of the rheological parameters of our self-healing formulations is presented in Table 1. Shear yielding and storage modulus are important parameters for the assessment of the inks printability, since they define the stiffness of the gel and the applied pressures required to induce flow through the nozzle. The results indicate differences between the spreadable, 3D-printable, and stiff gels. While the storage moduli of spreadable inks are consistently ∼80 Pa, the storage moduli of 3D-printable gels are higher (∼200–1000 Pa), indicating their increased stiffness, and as a result an improved capability to withstand their own weight without collapsing. Storage moduli of stiff formulations were the highest among the examined gels (∼4000 Pa).
| Formulation | Gel category | [Pa] | Yield stressa [Pa] | Zero shearb viscosity [Pa s] |
|---|---|---|---|---|
| a Values obtained from stress ramp up experiments (mean and standard deviation are presented, N = 3). b Values obtained from the plateau of shear viscosity measurements (mean and standard deviation are presented, N = 2). | ||||
| G 4.5%_0.16EDA | Spreadable | 82 ± 1 | 13 ± 3 | 405 ± 40 |
| G 6.5%_0.06EDA | Spreadable | 84 ± 15 | 39 ± 6 | 801 ± 97 |
| G 8.5%_0.04EDA | Spreadable | 83 ± 5 | 46 ± 14 | 490 ± 56 |
| G 4.5%_0.2EDA | 3D-printable | 867 ± 199 | 266 ± 44 | 5921 ± 638 |
| G 4.5%_0.3EDA | 3D-printable | 1006 ± 360 | 95 ± 45 | 6540 ± 937 |
| G 6.5%_0.08EDA | 3D-printable | 241 ± 140 | 116 ± 62 | 1486 ± 50 |
| G 6.5%_0.1EDA | 3D-printable | 302 ± 56 | 100 ± 15 | 1350 ± 70 |
| G 8.5%_0.06EDA | 3D-printable | 220 ± 39 | 129 ± 11 | 1304 ± 1125 |
| G 8.5%_0.08EDA | 3D-printable | 279 ± 46 | 70 ± 13 | 995 ± 63 |
| G 8.5%_0.1EDA | 3D-printable | 678 ± 236 | 285 ± 148 | 5499 ± 1344 |
| G 6.5%_0.16EDA | Stiff | 3558 ± 383 | 829 ± 186 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 ± 657 335 ± 657 |
| G 8.5%_0.16EDA | Stiff | 4178 ± 1248 | 519 ± 67 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 ± 4171 760 ± 4171 |
All the formulations exhibited shear yielding, with the yield stress of 3D-printable and stiff gels being higher by an order of magnitude than the yield stress of spreadable gels. Although the yield stress of stiff gels and 3D-printable gels is of the same order of magnitude, the shear stresses required for yielding of stiff gels were ∼4–5 times higher.
The examination of apparent viscosity at the low shear region (zero shear viscosity), demonstrates differences of an order of magnitude between spreadable, 3D-printable and stiff gels, providing further evidence for the differences in their physical properties. With the increase in shear rates, all the gels exhibited shear thinning behaviour, reaching similar values at the higher shear region (Fig. 3c).
The viscosity, storage modulus and the yield stress of the examined 3D-printable formulations are in a good agreement with previously reported values for 3D-printable inks.17,32 During the printing process, the gel did not exhibit structural fragmentation and retained its continuous filamentous shape. Based on the rheological studies, the printability space suitable for these self-healing gels could be established. Optimal printing could be achieved in the intermediate region between the stiffest among the spreadable gels (lower limit) and the softest among the stiff gels (upper limit), setting the values of storage modulus, yield stress and zero shear viscosity in the range between 84–3558 Pa, 46–829 Pa, and 801–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 Pa s, respectively (Fig. 3c and d).
335 Pa s, respectively (Fig. 3c and d).
After conducting a detailed rheological characterization and exploring the printability of our imine-based self-healing gels, the optimal ink G6.5%_0.08EDA was employed for 3D-printing. Single layer patterns of micrometric thickness were successfully printed (Fig. 4a). Unlike traditional coating methods, which are time or material-consuming, or allow only a uniform coating on relatively broad surfaces, printing of self-healing gels allows selective deposition of well-defined shapes and patterns with controlled thickness. This is a highly efficient approach towards minimization of materials consumption and selective implementation of self-healing gels on specific regions of interest. Moreover, macroscopic 3D objects of various shapes and dimensions were 3D-printed (Fig. 4b and 5a). The robustness and the self-supporting ability of G6.5%_0.08EDA allowed mounting numerous layers of filamentous ink strands on top of each other without collapsing. The dynamic and reversible nature of imine bonds enabled an immediate recovery of the extruded gel and fusion of its filamentous layers into a monolithic, self-supporting object. In order to reinforce the 3D-printed gel, and to form strong functional objects, secondary (post-printing) cross-linking with EDA was performed. After the secondary cross-linking, 3D-printed objects could be easily lifted from the glass substrate (Fig. 4c and d).
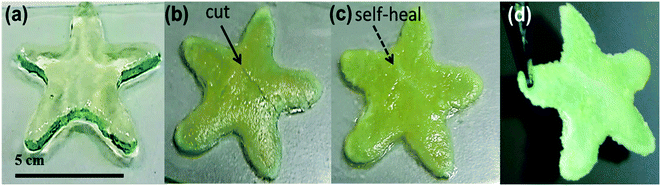
To study the self-healing ability of macroscopic 3D-printed objects, a star shaped structure (5 × 5 × 0.3 cm) was 3D-printed and cross-linked post-printing with EDA (2 mg mL−1). After the secondary cross-linking, a mechanical damage was induced by cutting the object with a scalpel. Immediately after the cutting, the damaged parts were brought to a contact with each other. After ∼30 min of contact, the interfaces self-healed by forming a scar, which bridged the damaged areas. The self-healing process at room temperature occurred autonomously, without any enhancement by external additives. After ∼1 h of self-healing the recovered 3D-printed object could be lifted as a single unit, self-supporting against gravity. The entire process is illustrated in Fig. 5. The presence of solvent is crucial for polymer chains diffusion and bonds exchange across the damaged interface, and therefore can significantly impact the efficiency of self-healing process.2 Owing to the low volatility of DMF and a fast-occurring recovery, no additional solvent was needed to facilitate the self-healing process.
3D-printed G6.5%_0.08EDA was employed for a preparation of self-rolling objects. For that purpose, 3D-printed rectangles were chosen as a simple geometry to demonstrate the proof-of-principle. The initial preparation steps (3D-printing, secondary cross-linking and the detachment of the object from the substrate) were followed by an interesting phenomenon, which took place during the drying process. With the progressive drying, the rectangular object spontaneously re-oriented from its planar sheet shape to a cylindrical, “cigar-like”, rolled shape, as shown in Fig. S12.† This phenomenon is attributed to the accumulation of internal stresses in the structure, generated during the processing of the gel. It is well-known that processing of polymers into thin films or 3D structures generates residual stresses, since polymer chains are forced into their non-equilibrium configuration.33 Moreover, with the evaporation of DMF and a sequent drying, polymer chains become less mobile and more densely packed, which limits their disentanglement and relaxation ability. Driven by strong elastic strains and seeking their minimization, rectangular sheets tend to adopt locally-curved shapes, curved in one direction only (such as cylinders).33 The 3D-printed structure, therefore, equilibrates and self-assembles into its energetically most preferred configuration, a cylindrical rod, shown in Fig. S12e.† When the dry cylinders were submerged into DMF, cylindrical rolls swelled and dynamically self-evolved. Upon introduction of the “cigar-like” cylinder to DMF, the structure gradually unfolded after 6 seconds, and the original, as printed, rectangular structure was restored. The stretching and the sequential unfolding are attributed to the expansion of polymer chains due to solvation. These conformational changes enable the system to reduce its free energy by swelling.24 Immediately after the unfolding was accomplished, the rectangular sheet buckled and rapidly initiated a new rolling cascade. This time, the structure rolled forming a “spiral-like” shape, after ∼20 seconds in DMF. The unfolding and rolling cascade is demonstrated in Fig. 6 and Movie S1.† After accomplishing a single dynamic cycle, the rolled “spiral” would retain its shape and would not further self-evolve. This observation can be attributed to the fact that the structure equilibrated at its energetically stable state.
Self-assembly of rectangular bilayer sheets into cylinders upon swelling is a well-known and broadly studied phenomenon.24,34–36 It was previously shown that the axis of folding, and consequently a final cylindrical shape (“cigar” or “spiral”), can be governed by the geometry of rectangular sheets.24,34,35 Experimental observations supported by numerical simulations indicate that in general, when the aspect ratio (A = L/w) of the rectangle increases, self-folding of a freely floating rectangle into a “spiral” cylinder is usually preferred.33–35 To be able to program and to control the self-rolling by the design of the 3D-printed object, we examined different aspect ratios of the 3D-printed rectangles. In all the cases, when the aspect ratio was bigger than 1.0 (A = 2.5, 3.5 and 5.0), the dry rectangles rolled into a “cigar” shape, while a self-assembly into a “spiral” shape was generated upon solvation in DMF. The diameter of the rolled structures constantly remained 4.0 mm, regardless of the aspect ratios. These results are in agreement with the literature.24 When the aspect ratio was ∼1, random behaviour was observed and no clear conclusion could be made. Therefore, well-controlled self-rolling can be obtained by keeping A > 1. An optimal thickness for preparation of self-rolling objects was 3 to 5 printed layers (1.0–1.8 mm). Owing to the symmetrical printing pattern (100% infill rectangular mesh), printing directionality did not affect the self-rolling behaviour of fabricated objects. Despite the macroscopic size of the 3D-printed objects, the dynamic cycle was rapid and was accomplished within ∼20 s.
Conclusion
In this work, 3D-printing of self-healing gels prepared from benzaldehyde-functionalized PHEMA and EDA were reported. Imine bonds allowed rapid and autonomous self-healing with 98% recovery from induced damages. An accurate tuning of rheological properties by controlling the degree of cross-linking and the concentration of the polymer resulted in successfully formulated 3D-printable inks. A delicate balance between the ability to deform and flow, and a sufficient rigidity required for self-support and structural fidelity, was achieved. As a result, these self-healing gels could be 3D-printed with well-defined shapes, patterns and sizes. The self-healing ability of the 3D-printed objects was demonstrated by rheology and qualitatively shown through the healing of macroscopic cuts. 3D-printed objects exhibited a dynamic response to their chemical environment, which was employed as a principle for fabrication of self-rolling objects. In a dry state, 3D-printed rectangles could spontaneously deform and roll into a well-defined cylindrical “cigar” shape. In DMF, the cylinders stretched by swelling, restored their rectangular shape and further transformed their shape into a “spiral”, by changing their axis of folding. 3D-printing of self-healing gels is a facile approach for a selective deposition of protective coatings, and a fabrication of smart and dynamic objects.Funding sources
This work was supported by the Victorian Endowment for Science Knowledge and Innovation (LAC).Acknowledgements
The authors would like to acknowledge Dr. Mitchell Sesso for his assistance with 3D-Bioplotter and Mr. Matthew Lam for his technical assistance with dynamic experiments.References
- G. Deng, F. Li, H. Yu, F. Liu, C. Liu, W. Sun, H. Jiang and Y. Chen, ACS Macro Lett., 2012, 1, 275–279 CrossRef CAS.
- H. Zhang, H. Xia and Y. Zhao, ACS Macro Lett., 2012, 1, 1233–1236 CrossRef CAS.
- D. L. Taylor and M. in het Panhuis, Adv. Mater., 2016, 28, 9060–9093 CrossRef CAS PubMed.
- S. Mukherjee, M. R. Hill and B. S. Sumerlin, Soft Matter, 2015, 11, 6152–6161 RSC.
- Z. Wei, J. H. Yang, J. Zhou, F. Xu, M. Zrínyi, P. H. Dussault, Y. Osada and Y. M. Chen, Chem. Soc. Rev., 2014, 43, 8114–8131 RSC.
- A. Vidyasagar, K. Handore and K. M. Sureshan, Angew. Chem., Int. Ed., 2011, 50, 8021–8024 CrossRef CAS PubMed.
- D. Zhu, Q. Ye, X. Lu and Q. Lu, Polym. Chem., 2015, 6, 5086–5092 RSC.
- Y. Zhang, L. Tao, S. Li and Y. Wei, Biomacromolecules, 2011, 12, 2894–2901 CrossRef CAS PubMed.
- C. C. Deng, W. L. A. Brooks, K. A. Abboud and B. S. Sumerlin, ACS Macro Lett., 2015, 4, 220–224 CrossRef CAS.
- G. Deng, C. Tang, F. Li, H. Jiang and Y. Chen, Macromolecules, 2010, 43, 1191–1194 CrossRef CAS.
- J. Collins, Z. Xiao, M. Müllner and L. A. Connal, Polym. Chem., 2016, 7, 3812–3826 RSC.
- J. Collins, M. Nadgorny, Z. Xiao and L. A. Connal, Macromol. Rapid Commun., 2017, 38, 1600760 CrossRef PubMed.
- Z. Wei, J. He, T. Liang, H. Oh, J. Athas, Z. Tong, C. Wang and Z. Nie, Polym. Chem., 2013, 4, 4601–4605 RSC.
- M. Nadgorny, Z. Xiao, C. Chen and L. A. Connal, ACS Appl. Mater. Interfaces, 2016, 8, 28946–28954 CAS.
- M. Hofmann, ACS Macro Lett., 2014, 3, 382–386 CrossRef CAS.
- B. C. Gross, J. L. Erkal, S. Y. Lockwood, C. Chen and D. M. Spence, Anal. Chem., 2014, 86, 3240–3253 CrossRef CAS PubMed.
- A. L. Rutz, K. E. Hyland, K. A. E. Jakus, W. R. Burghardt and R. N. Shah, Adv. Mater., 2015, 27, 1607–1614 CrossRef CAS PubMed.
- C. B. Highley, C. B. Rodell and J. A. Burdick, Adv. Mater., 2015, 27, 5075–5079 CrossRef CAS PubMed.
- G. I. Peterson, M. B. Larsen, M. A. Ganter, W. D. Storti and A. J. Boydston, ACS Appl. Mater. Interfaces, 2015, 7, 577–583 CAS.
- Y. Mao, Z. Ding, C. Yuan, S. Ai, M. Isakov, J. Wu, T. Wang, M. L. Dunn and H. J. Qi, Sci. Rep., 2016, 6, 24761–24774 CrossRef PubMed.
- K. Yu, A. Ritchie, Y. Mao, M. L. Dunn and H. J. Qi, Procedia IUTAM, 2015, 12, 193–203 CrossRef.
- S. E. Bakarich, R. Gorkin, M. in het Panhuis and G. Spinks, Macromol. Rapid Commun., 2015, 36, 1211–1217 CrossRef CAS PubMed.
- G. V. Stoychev and L. Ionov, ACS Appl. Mater. Interfaces, 2016, 8, 24281–24294 CAS.
- X. Fan, J. Y. Chung, Y. X. Lim, Z. Li and X. J. Loh, ACS Appl. Mater. Interfaces, 2016, 8, 33351–33370 CAS.
- M. E. Belowich and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 2003–2024 RSC.
- Y. Jin, C. Yu, R. J. Denman and W. Zhang, Chem. Soc. Rev., 2013, 42, 6634–6654 RSC.
- F. Herbst, D. Döhler, P. Michael and W. H. Binder, Macromol. Rapid Commun., 2013, 34, 203–220 CrossRef CAS PubMed.
- E. R. L. Brisson, Z. Xiao, L. Levin, G. V. Franks and L. A. Connal, Polym. Chem., 2016, 7, 1945–1952 RSC.
- E. R. L. Brisson, Z. Xiao, G. V. Franks and L. A. Connal, Biomacromolecules, 2017, 18, 272–280 CrossRef CAS PubMed.
- J. T. Muth, D. M. Vogt, R. L. Truby, Y. Mengüç, D. B. Kolesky, J. R. Wood and J. A. Lewis, Adv. Mater., 2014, 26, 6307–6312 CrossRef CAS PubMed.
- D. M. Kirchmajer, III, R. Gorkin and M. in het Panhuis, J. Mater. Chem. B, 2015, 3, 4105–4117 RSC.
- R. L. Truby and J. A. Lewis, Nature, 2016, 540, 371–378 CrossRef CAS PubMed.
- J. Y. Chung, T. Q. Chastek, M. J. Fasolka, H. W. Ro and C. M. Stafford, ACS Nano, 2009, 3, 844–852 CrossRef CAS PubMed.
- S. Alben, B. Balakrisnan and E. Smela, Nano Lett., 2011, 11, 2280–2285 CrossRef CAS PubMed.
- G. Stoychev, S. Zakharchenko, S. Turcaud, J. W. C. Dunlop and L. Ionov, ACS Nano, 2012, 6, 3925–3934 CrossRef CAS PubMed.
- L. Ionov, Langmuir, 2015, 31, 5015–5024 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis schemes, 1H NMR spectrum, SEC traces, chemical structure of the gel, FTIR spectrum, gels extrusion and rheology and self-assembly of 3D-printed objects. See DOI: 10.1039/c7me00023e |
| This journal is © The Royal Society of Chemistry 2017 |