Chemically coded time-programmed self-assembly

Abstract

Dynamic self-assembly is of great interest in the fields of chemistry, physics and materials science and provides a flexible bottom-up approach to build assemblies at multiscale levels. We propose a method to control the time domain of self-assembling systems in a closed system, from molecular to material level using a driving chemical system: methylene glycol–sulfite pH clock reaction coupled to lactone hydrolysis. The time domain of the transient pH state (alkaline) and the time lag between the initialization of the reaction and the pH change can be efficiently fine-tuned by the initial concentration of the reagents and by the chemical composition of the lactone. The self-assembly of pH-responsive building blocks can be dynamically driven by this kinetic system, in which the time course of the pH change is coded in the system. This approach provides a flexible and autonomous way to control the self-assembly of pH responsive building blocks in closed chemical systems far from their thermodynamic equilibrium.

---

Design, System, Application

Dynamic self-assembly is an important bottom-up technique to design new self-regulating and adaptive materials from building blocks with various sizes. We propose here a robust, facile and autonomous method for driving and controlling the assembly of pH-responsive building blocks with time by combining a pH clock reaction and lactone hydrolysis in a closed system. The method utilizes time scale separation of these chemical processes, which gives rise to the existence of a transient non-equilibrium pH state. pH sensitive building blocks (fatty acid molecules, carboxyl group terminated nanoparticles and amine functionalized polymer chains) follow the driving kinetic system through regulating the interactions between building blocks thus controlling the complexity of the emerging structures. The driving chemical system can be precoded by setting up the initial conditions. In particular, this work provides possible applications for time-programmed drug release and autonomous control of artificial muscle systems.

Introduction

Self-assembly of building blocks on various spatial scales and its dynamic control have gained much interest in the past decades since they are interesting and challenging from a fundamental science point of view and provide new approaches to explore the behavior of self-regulating, dynamic and adaptive systems.^1–6 Recently a new emerging concept has been suggested and utilized to control and regulate the time domain of self-assembling systems. Walther and his co-workers have suggested a robust and facile protocol for time-programmed pH responsive self-assembly.^7–9 The system has two states (at different pH values) and between them there are two kinetic pathways – the first is a fast activation followed by a slow or delayed deactivation step.⁹ This time scale separation of the two processes ensures that one non-equilibrium pH state can transiently exist with time. pH sensitive building blocks follow this time course, and the pH change regulates the interactions between building blocks thus controlling their self-assembly and the complexity of the structures.^10–12

The protocol requires a simultaneous addition of rapid promoters and dormant deactivators to the system. Several systems have been introduced operating from an acidic state back to acidic again through an alkaline state or vice versa. For instance, simultaneous addition of tris(hydroxymethyl)aminomethane hydrochloride (TRIS) buffer (promoter) and a lactone (dormant deactivator) can give rise to the appearance of a transient alkaline pH state.⁹ Upon addition of the TRIS buffer, the pH immediately increases. The presence of the lactone does not interfere with the increase in pH since the rate of hydrolysis of the lactone is pH dependent and practically negligible in an acidic range. Therefore, the pH can rise quickly to alkaline pH and once the system reaches the maximum pH (determined by the concentration of the TRIS buffer), the pH decreases due to the considerably increased hydrolysis rate of the lactone. The lactone as a dormant deactivator produces a deactivating species, H⁺, which decreases the pH back to acidic. The concentration of the promoter, plus the concentration and the chemical composition of the dormant deactivator regulates the lifetime of the transient pH state (in the previous example it is alkaline). Several pH responsive building blocks have been coupled to this system to drive their self-assembly and examples incorporate coil to β-sheet reversible transformation of an oligopeptide, dispersion and aggregation of phenol ligand stabilized gold nanoparticles (AuNPs), and self-assembly of a block copolymer.^7,9,13 This approach and the protocol are flexible and robust and can provide up to a seven-unit change in pH. However, the above described method includes only one control parameter, namely the lifetime of the transient pH state. This can be programmed by varying the initial concentration of the activator (promoter) and that of the dormant deactivator, and by varying their chemical compositions. Moreover, the protocol is non-autonomous since the pH changes immediately upon addition of the activator (promoter). In other words, the pH change occurs due to human intervention, and not because of the intrinsic properties of the system. There is no time lag between the addition of the activator (promoter) and the pH change.

Design and engineering of chemical systems in a fully autonomous chemically coded manner are challenging. Nonlinear chemical dynamics operating under conditions outside equilibrium can offer a possible solution to overcome this issue.^14–17 At the material level, diverse modes of periodic actuation with no external stimuli have been elaborated via coupling nonlinear (oscillatory or even simple clock-type) chemical reactions with physicochemical processes in elastic materials.^2,18–24 Autonomous periodic viscosity changes have been brought about through subsequently building and breaking chemical or physical links between the building blocks.^25–27 In the past few years periodic interconversion of building blocks with time has been successfully realized by using pH oscillators in a continuously stirred-tank reactor.^10,28–31 In a closed system, time-controlled gelation with programmable self-degradation (liquefaction) was designed recently by an enzymatic pH-clock reaction.³²

We show here a strategy to drive and control the self-assembly of building blocks (molecules, nanoparticles (NPs) and macromolecular fibers) in closed and autonomous chemical systems using a combination of a pH clock reaction³³ with slow hydrolysis of lactones.^34,35 In our protocol, there are two independent control parameters (Fig. 1), the time lag between the initialization of the reaction and the fast pH change (t_lag) and the time domain/lifetime of the transient pH state (t_tr), which is defined as the full width at half maximum of the pH–time curve. Both can simply be chemically programmed (precoded) by varying the initial concentrations of reagents of the pH clock reaction and by varying the chemical composition and the concentration of the dormant deactivator.

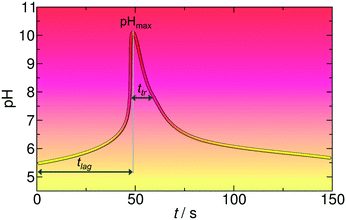Fig. 1 The concept of the time-program of the self-assembly using a combination of a pH clock reaction (MGS) and lactone hydrolysis.

Experimental

Our system consists of the methylene glycol–sulfite (MGS) clock reaction (which is responsible for the fast pH spike due to its autocatalytic nature)³³ coupled to lactone hydrolysis (which slowly decreases the pH back to the acidic range).³⁴ The experiments were carried out in continuously stirred batch reactors (400 rpm) with volumes of 15 or 30 mL. Methylene glycol (MG) stock solution was diluted from 37% formaldehyde solution (Sigma-Aldrich) at least 24 h prior to use. The reagent grade chemicals, sodium sulfite (Sigma-Aldrich), sodium metabisulfite (Sigma-Aldrich), and the lactone, D (+) gluconic acid δ-lactone (GL, Sigma-Aldrich) or δ-valerolactone (VL, Sigma-Aldrich), were dissolved simultaneously in distilled water and freshly prepared in advance of each experiment. The temperature was set to 20 ± 0.5 °C. The pH was monitored using a computer-interfaced combination pH electrode (Mettler Toledo) as a function of time with a resolution of 0.5 s. The initial concentration of methylene glycol was varied between 0.1 M and 0.2 M. The composition of the sulfite/bisulfite buffer solution was [SO₃²⁻]₀ = 0.005 M and [HSO₃⁻]₀ = 0.050 M. The concentrations of the lactones were used in a range of 0.004 M and 0.020 M.

We investigated the self-assembly of three building blocks, namely reversible vesicle–micelle transformation of oleic acid (OA, Sigma-Aldrich), reversible dispersion–aggregation of carboxyl-terminated thiol (mercaptoundecanoic acid, MUA) stabilized AuNPs (average size of 5.6 nm with a standard deviation of 10%), and reversible collapse and rehydration of poly(N-isopropylacrylamide) based network chains with tertiary amine functional groups. In all experiments, all components of the system, sulfite/bisulfite buffer, methylene glycol, lactone and the self-assembling components were simultaneously injected into the batch reactor except the polymer gel filament which was presoaked for at least 1 h in a reacted reaction mixture at ∼pH 7 and then placed in a fresh reaction mixture approximately 30 seconds after mixing.

Cylindrical gel filaments of 1.00 mm initial diameter were synthesized via free-radical crosslinking copolymerization initiated by a Na-sulfite/Na-persulfate redox couple in a 3 : 2 (V/V) tert-butanol–water mixture. The pH-sensitivity of the gel in the neutral to basic pH-region was provided by N-[3-(dimethylamino)propyl]methacrylamide (DMAPrMAAm, Sigma-Aldrich, 99%) (3.00 mol% of total monomers).²⁴ As the pH-window and sharpness of the swelling–shrinking transition is at the same time temperature sensitive, it was necessary to lower the optimum temperature closer to room temperature; therefore, the neutral monomer N-isopropylacrylamide (NIPA, Sigma-Aldrich, 97%) was combined with the more hydrophobic comonomer N-tert butylacrylamide (NTBA, Acros) in a molar ratio 80 : 20. For details of the synthesis refer to our previous works.^20–22 For the dependence of the swelling–shrinking rate and the sharpness of the pH-response on the synthesis parameters (solvent composition, initiator), see the ESI.† The obtained polyNIPA-based gel filaments exhibited the sharpest swollen to shrunken transition at 26 °C, from pH 8.00 to pH 9.25. For the time-programmed transient shrinking–reswelling experiments, the top of the collapsed gel filament was glued to a 100 μL plastic pipette tip using non-dripping cyanoacrylate glue, and then a spherical glass weight (glass bead) was glued to the bottom end of the filament. This glass bead weighed 0.110 g in water (0.170 g in air) and later helped keep the highly swollen gel filament straight in the reaction solution. Time-lapse photographs were taken every 15 s during the time-program. We used a phenol red pH indicator (Sigma-Aldrich, yellow at pH < 6.8, pink at pH > 8.2) to monitor the pH change in the time-program with gel filaments.

Results and discussion

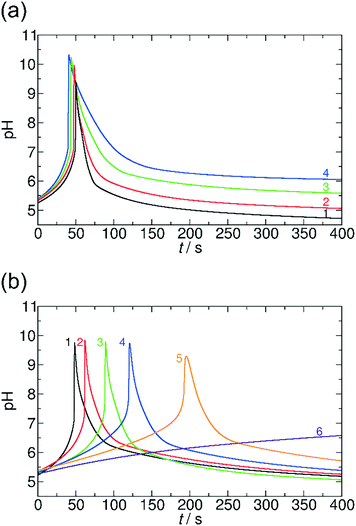
First we focus on the generic features of the coupled kinetic system. Fig. 1 shows a typical kinetic curve for the combination of the MGS pH clock reaction with lactone hydrolysis. All components of the system are added simultaneously to the batch reactor at the initialization of the reaction. At the first stage of the reaction (the induction period), the pH changes slowly due to the buffer capacity of the sulfite/bisulfite system. When all of the buffer is consumed, the pH suddenly increases jumping roughly 5 pH units (second stage). Lactone hydrolysis is pH dependent and its reaction rate is low in acidic, neutral, and slightly alkaline environments. However, when the pH reaches alkaline values the rate of hydrolysis becomes more pronounced, and the hydrolysis product (H⁺, deactivator) slowly decreases the pH back to acidic (third stage). Using a combination of a pH clock reaction with the hydrolysis of a lactone, there are two temporal features that are autonomously coded in the chemical system (Fig. 1): (i) the time lag between the initialization of the reaction and the time when the system reaches the highest pH (t_lag), and (ii) the time domain of the transient pH state (t_tr), which is defined as the full width at half maximum of the pH peak, that is, the duration above this pH. Both can be varied and precoded by varying the initial concentrations of the reactants in the clock reaction and that of the lactone.

Fig. 2 presents a way in which t_tr and t_lag can be finely tuned in the course of the reaction. By increasing the concentration of GL, t_tr decreases due to the enhanced hydrolysis rate (Fig. 2a). However, t_lag (induction period) just slightly changes (within ∼8%). On the other hand, t_lag can be efficiently varied by changing the concentration of methylene glycol (Fig. 2b).

Fig. 2 pH–time curves in the MGS and GL system at different initial concentrations of gluconolactone (a) and methylene glycol (b). Experimental conditions: (a) [CH₂(OH)₂]₀ = 0.2000 M, 1: [GL]₀ = 0.0200 M, 2: [GL]₀ = 0.0100 M, 3: [GL]₀ = 0.0050 M, 4: [GL]₀ = 0.0040 M. (b) [GL]₀ = 0.0100 M, 1: [CH₂(OH)₂]₀ = 0.2000 M, 2: [CH₂(OH)₂]₀ = 0.1750 M, 3: [CH₂(OH)₂]₀ = 0.1500 M, 4: [CH₂(OH)₂]₀ = 0.1250 M, 5: [CH₂(OH)₂]₀ = 0.1125 M, 6: [CH₂(OH)₂]₀ = 0.1000 M. Fixed concentrations: [SO₃²⁻]₀ = 0.0050 M and [HSO₃⁻]₀ = 0.0500 M.

It is noteworthy that the methylene glycol concentration slightly affects both the maximum pH and t_tr. In the extreme case when the concentration of methylene glycol is decreased to 0.1000 M, we could observe no jump in pH; as not all of the buffer is consumed in the reaction due to the low concentration of methylene glycol. It should be noted that if we use a concentrated formaldehyde solution (37%, which would theoretically correspond to 13.43 M methylene glycol), the clock reaction occurs within a few seconds. In the interpretation of this acceleration it has to be taken into account that in such a concentrated solution not all formaldehyde molecules are present in their hydrated form, MG, while the rate determining step in the mechanism is the dehydration of MG. Nevertheless, changing the concentration of one reagent of the clock reaction allows us to vary t_lag from a few seconds up to 200 s.

A similar kinetic behavior can be observed if GL is replaced by VL, but in the latter case the rate of hydrolysis is lower (Fig. 3). The lower rate of hydrolysis results in a considerably longer lasting transient state of high pH (for GL t_tr is between 10.5 s and 39.5 s (Fig. 2a), for VL t_tr varies from 2.4 min to 27.2 min (Fig. 3a)). Additionally, the maximum pH can reach higher values by around half a unit (Fig. 3a) due to the lower hydrolysis rate. Varying the concentration of methylene glycol has a similar effect on t_lag in both cases of VL and GL: the lower is the concentration of methylene glycol, the longer t_lag is obtained (Fig. 3b).

Fig. 3 pH–time curves in the MGS and VL system at different initial concentrations of valerolactone (a) and methylene glycol (b). Experimental conditions: (a) [CH₂(OH)₂]₀ = 0.2000 M, 1: [VL]₀ = 0.0200 M, 2: [VL]₀ = 0.0100 M, 3: [VL]₀ = 0.0050 M, 4: [VL]₀ = 0.0040 M. (b) [VL]₀ = 0.0100 M, 1: [CH₂(OH)₂]₀ = 0.2000 M, 2: [CH₂(OH)₂]₀ = 0.1500 M, 3: [CH₂(OH)₂]₀ = 0.1250 M, 4: [CH₂(OH)₂]₀ = 0.1125 M. Fixed concentrations: [SO₃²⁻]₀ = 0.0050 M and [HSO₃⁻]₀ = 0.0500 M.

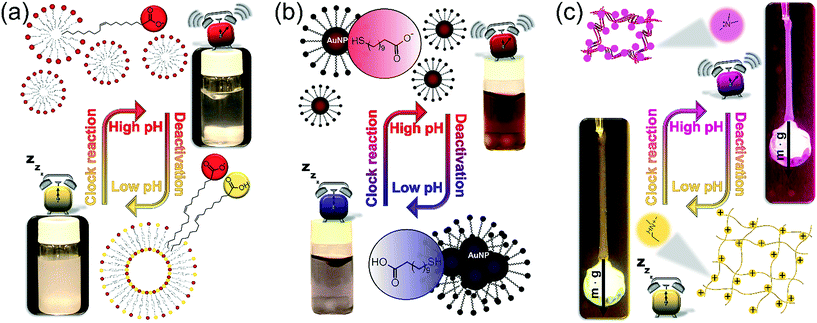
After exploring the main characteristics of the programmed kinetic system, we focus on its application to drive the self-assembly of various building blocks in a time-programmed and precoded manner. We provide three examples with the size of the building blocks changing from molecular to nanoscopic level. In all three cases the self-assembly occurs following a change of electrostatic interactions between the building blocks due to protonation/deprotonation caused by the pH change. To achieve a significant effect on regulating the electrostatic repulsion between building blocks and thus facilitate or repress the self-assembly, the protocol should fulfill one important requirement, namely the pK_a of the building blocks should lie in between the starting pH (pH ∼ 5.5) and the maximum pH (∼10). In our examples this requirement is completely fulfilled since the apparent pK_a of OA in monolayers is ∼8.3,^36,37 the pK_a of MUA was reported between 6 and 8 in the self-assembled monolayer,²⁹ and the polymer network contains tertiary amine functional groups with pK_a ∼ 8.7 (see ESI† Fig. S2). Fig. 4 illustrates the concept of controlling the self-assembly in each of our three examples and shows that the two extreme states of each system at low and high pH, respectively, in between the systems undergo a reversible change. Experimental examples for the complete time-course of these processes are shown in Fig. 5.

Fig. 4 The concept of the time-programmed and precoded self-assembly of fatty acid molecules (oleic acid), AuNPs, and polymer chains in a pH-responsive polyNIPA-based network. Lower and upper photographs show the states of the systems at the starting (low) pH and at the highest pH. (a) Reversible vesicle–micelle transformation of oleic acid molecules (low pH: vesicles – turbid solution, high pH: micelles – transparent solution), (b) reversible dissolution and aggregation of carboxyl terminated AuNPs (low pH: aggregated NPs – blue solution with microscopic aggregates, high pH: free NPs – transparent red solution), (c) volume change (shrinking and swelling) of a hydrogel filament containing tertiary amine functional groups (low pH: swollen, highly elastic state; high pH: shrunken, more rigid state).

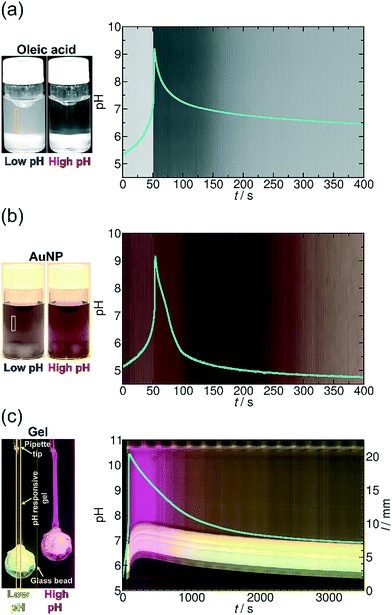Fig. 5 (a) Time evolution of the transparency of the solution and that of the pH (blue line) in the MGS and GL system with oleic acid. [GL]₀ = 0.0100 M, [CH₂(OH)₂]₀ = 0.2000 M, [SO₃²⁻]₀ = 0.0050 M, [HSO₃⁻]₀ = 0.0500 M and [OA] = 0.00125 M (see ESI† Video S1). (b) Time evolution of the color of the solution and that of the pH (blue line) in the MGS and GL system with AuNPs. [GL]₀ = 0.0100 M, [CH₂(OH)₂]₀ = 0.2000 M, [SO₃²⁻]₀ = 0.0050 M, [HSO₃⁻]₀ = 0.0500 M and [COOH@AuNP] = 3.53 × 10⁻⁵ M (see ESI† Video S2). (c) Space–time plot of the gel length and the synchronous pH-change (blue line) in the MGS and VL system. Background color is provided by the phenol red pH-indicator. [Phenol Red]₀ = 0.0145 mM, [VL]₀ = 0.0100 M, [CH₂(OH)₂]₀ = 0.1125 M, [SO₃²⁻]₀ = 0.0050 M, [HSO₃⁻]₀ = 0.0500 M. The diameter of the plastic holder and that of the glass bead were 0.750 mm and 5.00 ± 0.10 mm, respectively. The system was unstirred and the temperature was kept at θ = 25 ± 0.5 °C (see ESI† Video S3). The yellow frames indicate the vertical cut taken to create the space–time plots.

To demonstrate our concept, we first show how to use temporal programming for vesicle–micelle transformation (Fig. 4a). At the start of the experiments (at low pH), the solution in the reactor appears hazy due to light scattering (Tyndall effect) because the fatty acid molecules being under conditions close to their pK_a (where approximately half of the carboxylic groups are ionized) form unilamellar vesicles (spherical bilayers) that have an average diameter of ∼100 nm.³⁸ These vesicles have a bilayer structure and are composed of the protonated and deprotonated (ionized) forms of fatty acid. However, when the clock reaction jumps to pH ∼ 10, the solution turns transparent because 99% of the OA molecules become deprotonated and form spherical micelles having an average diameter of ∼5 nm. When the system returns back to the low-pH state due to deactivation induced by lactone hydrolysis, the micelles revert back to vesicles and an opaque phase appears again (Fig. 4a and 5a, see ESI† Video S1). Here the main driving force for the vesicle–micelle transformation is the changing of the packing parameter³⁹ influenced by the electrostatic interaction (repulsion) between the carboxylate head groups. The vesicles can be considered as a mixture, composed of ionic and noninonic surfactant molecules. In this case the head groups can be densely packed allowing the formation of a supramolecular structure with less curvature (spherical bilayer). When the pH changes from low pH to high pH, more and more carboxylic groups become deprotonated (charged), thus the effective surface area of the head groups increases because of the electrostatic repulsion. The bilayer structure cannot be maintained, and the deprotonated fatty acid molecules develop a thermodynamically more stable, high-curvature supramolecular assembly (spherical micelles).

In the second example (Fig. 4b) we show the temporal control of redispersion and aggregation of NPs in an autonomously programmed way. We use nanoscopic building blocks, namely AuNPs with an average diameter of 5.6 nm (standard deviation: 10%) functionalized with alkane thiolates terminated with carboxyl groups. The MGS + lactone systems control the dissociation of the acidic head groups of the stabilizing groups on the surface of the metal nanoparticles through the pH change in the bulk phase. At the beginning of the time-program, when the system is in the low pH state, the majority of the carboxylic ligands are protonated (uncharged) and the electrostatic repulsion between the NPs is weak. In this case, the interparticle interaction is dominated by van der Waals (vdW) attractions, therefore the NPs aggregate and precipitate. However, when the chemical clock reaches its high pH state, the carboxyl groups – similar to the previous case – are deprotonated. The increased electrostatic interparticle repulsions lead to a resultant potential curve with a sufficiently high potential barrier that keeps the NPs from reaching a distance where the attraction would dominate (Fig. 4b and 5b, see ESI† Video S2). The redispersion manifests itself in a pronounced color change which is due to the surface plasmon resonance (SPR). For smaller aggregates the SPR related light absorption shifts to shorter wavelengths. At the beginning of the timed reaction, the color of the solution of NPs is blue, containing some NP precipitates. At high pH values, when practically all carboxyl groups are negatively charged, the NPs are free and unaggregated, and the color of the Au-sol becomes a distinct red due to SPR. Finally, when the pH returns back to the neutral/acidic range, the attractive vdW interactions overcome the electrostatic repulsion and the resultant potential barrier lowers so that the NPs can cross through it by their translational energy. The NPs lose their stability and they aggregate again, hence the color of the solution changes from red back to blue via purple.

In both previous cases we also investigated the evolution of the transparency/turbidity and the absorbance of the solution for oleic acid and AuNPs, respectively. These two quantities correlate with the stages of the self-assembling processes. The turbidity (grey scale) was derived from the optical images and the absorbance was measured in kinetic mode at 519 nm by using a UV-VIS spectrophotometer. We recorded the pH of the solution in parallel with the measurements. The results clearly show (see ESI† Fig. S3 and S4) that if the pH jumps quickly to alkaline, the transformations (vesicle to micelle and dissolution of NP aggregates) occur simultaneously with the pH change. However, when the pH returns back to the neutral/slightly acidic range, the reconfiguration of the building blocks can be delayed. In particular, it can be vividly seen in the case of NPs. This effect is due to the bistability and hysteresis in the aggregation and dissolution process of charged NPs in the course of the pH change.⁴⁰ Additionally, the dispersion of aggregates or the transformation of a large supramolecular structure (vesicle) to a smaller one (micelle) is a fast process. However, the rearrangement to the compound structure involving more building blocks takes time. In general, the response time of the driven subsystem (in this case, the time scale of the self-assembly) is crucial in time-programmed processes. Thus, the driven building blocks should be able to perform the desired rearrangement within the time domain (time window) of the transient chemical command for “activation”. The more asymmetric the pH-profile in the time-program is (or simply if t_tr is too short), the more care should be taken in choosing the faster process that comes first for a more efficient operation. Accordingly, in our first two examples the quasi instantaneous splitting of a compound structure preceded the more sluggish self-assembly. In our next example, self-assembly in a polymer network is followed by relaxation, where the relaxation process is the slower one.

In the third example (Fig. 4c), contrary to the carboxyl head groups present in the above two types of building blocks, the pH-responsiveness of our gel filament is provided by tertiary amine functional groups. These functions are positively charged when protonated (in acidic and neutral medium), and become electrically neutral (uncharged) when they lose the proton in a sufficiently alkaline medium. When charged, the gel is swollen because of the solvent uptake of the network due to the high driving force for mixing. When uncharged, the solvation of the polyNIPA-based polymer chains by water molecules is thermodynamically not favourable anymore, so the chains aggregate with each other and gradually coil up. This collective rearrangement is accompanied by the expulsion of water and contraction of the whole gel piece, finally leading to the collapse of the network. Rehydration occurs upon protonation of the amine functions, as the pH returns from alkaline in the time-program, followed by the expansion of the polymer chains which manifests macroscopically in reswelling. Therefore, the gel filament can be actuated by an appropriate pH time-program (Fig. 4c, see ESI† Video S3). We show in Fig. 5c that the gel is capable of performing mechanical work (e.g., pulling and releasing a lever) following the imposed time-program. The load (glass bead) on the gel filament is 10–14 times the weight of the swollen gel itself (assuming 0.75 mm diameter and 14 mm length). This load is lifted upon contraction of the gel filament. As the aggregation of the polymer chains is accompanied by an increased stiffness (increase of the elastic modulus) of the gel – and vice versa, the gel is softer when swollen – the load induces an additional elongation (stretching) in the swollen state while this effect is negligible when the network chains are bundled.

To operate according to the time-program, first the signal (here the hydroxide ions) should reach the pH-sensitive sites of the polymer chains in the network. Using thin gel filaments of a diameter of 0.75–1.00 mm, the characteristic time of diffusion of hydroxide ions (assuming D = 9 × 10⁻⁵ cm² s⁻¹) can be estimated for less than a minute from the surface to the core of the gel filament. Then, the shrinking (or the swelling) requires the collective motion of the totality of the polymer chains that constitute the network which is usually two orders of magnitude slower than the diffusion of solvent molecules or solvated ions.^41,42 We managed to considerably enhance the swelling/shrinking kinetics⁴³ by synthesizing the appropriate pH-responsive gel with a macroporous^44,45 network structure that contains channels (for details see ESI† Fig. S1). The MGS and GL pH oscillatory reaction has very sharp, pulse-like periodic switches to the alkaline pH (the lifetime of the alkaline state is short).³⁴ Nevertheless, we succeeded in using this chemical system to achieve measurable contraction and relaxation of the gel. In the time-program with the MGS and VL chemical system in Fig. 5c, t_lag is ca. 1 min long before the jump above pH 10. In this first minute the pH creeps from 5.5 to 7.0 and the load is slowly lifted at a rate of 0.230–0.270 mm min⁻¹. At the same time as the pH-jump, the weight is suddenly lifted by 1.29 mm within 15 s. In the next two minutes, a further lift occurs by 1.26 mm then by 0.41 mm, respectively. The load is in its highest position during the fourth minute after the start. The length of the elongated filament is reduced to 11.0 mm from 14.0 mm, that is, by 22%. The opacity of the gel indicates the phase-separation of the polymer chains of the network from the solution. Surprisingly, reswelling of the gel starts readily when the pH is lowered to 9.5, i.e., 240 s after the peak in pH. The glass bead is lowered to its initial position in 50–60 min. This value agrees with the kinetic measurements on reswelling in a buffer under unloaded conditions (see ESI† Fig. S1). It is a general feature in pNIPA-based gels that reswelling is significantly slower than shrinking, as the rehydration of isopropyl functions (which are responsible for the high volume change) is difficult.⁴⁴ This fact confirms the correctness of our choice for the functional groups in our gel, i.e., amine instead of carboxyl. In this way, we obtained a fast shrinking response (instead of a swelling response) during the activation phase of the time-program letting enough time for the return during the subsequent deactivation, which is inherently the slower process in the MGS + VL time-program. The asymmetry between the rate of shrinking and reswelling appears clearly in the time-program with the MGS + GL chemical system where the pH jump and decrease are symmetric (see ESI† Fig. S5).

Another important aspect in this work is to clarify how the components of the self-assembling system (building blocks) affect the temporal behavior of the original MGS + lactone system. It is inevitable that the building blocks influence the original kinetic system since the pH sensitive groups (carboxyl, amine) consume and produce H⁺ ions upon their protonation/deprotonation. The buffering effect of such coupling is often neglected, and it was not always investigated when autonomous pH oscillators were coupled to pH dependent complexation or precipitation equilibria. Nevertheless, fundamental papers immediately warned of the gradual amplitude decrease till the pH oscillations of the core oscillator diminishes if one tries to increase the concentration of the H⁺-binding functions involved in the coupled equilibrium.^14,46 In periodic gel actuators driven by chemical oscillators, this problem is usually overcome by choosing a large volume ratio between the surrounding oscillatory solution and the driven piece of gel.^2,10,15 The pH-damping effect is crucial if the clock reaction can (or is let to) evolve only inside the responsive gel matrix where the average molar concentration of the H⁺-binding functions is usually quite high.²² The buffering effect of tertiary amine functions on the MGS clock reaction has been investigated.²⁴ The effect of carboxylic functions is known in other pH clock reactions, where the sulfite/bisulfite couple is consumed by an inorganic oxidizing agent (bromate, iodate, or hydrogen peroxide), and the pH drops from neutral to the acid region. Each of these clock variants behaved somewhat individually against buffering from the point of view of, e.g., the upper limit concentration of the H⁺-binding units that would cause the complete damping of the pH.^20–22 So a new reaction has to be experimentally tested with a buffer having a pK_a value similar to the functions of the driven components.

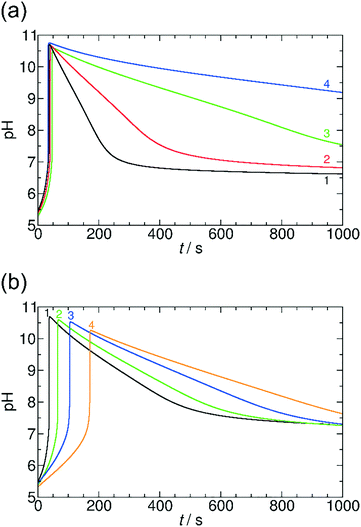
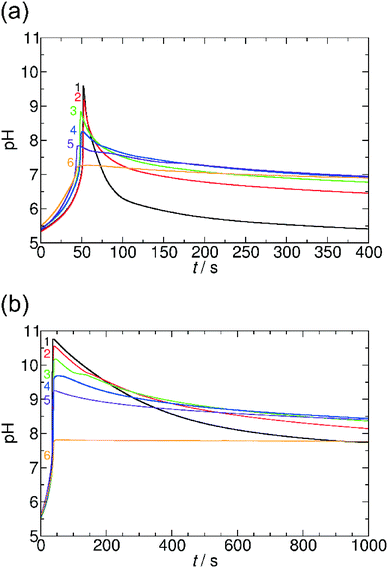
Here, we systematically varied the concentration of OA in the system (between 0 and 0.01 M), thus providing various concentrations of carboxyl groups. When the concentration of OA increases, the pH maximum provided by the coupled clock reaction + lactone hydrolysis system decreases. Additionally, the pH returns back more slowly to the neutral/acidic region, thus the self-assembling component itself affects its lifetime at the transient state (Fig. 6). When the concentration of OA reaches the same order of magnitude as the sulfite concentration, the time-scale separation (delay) between the pH-jump and pH-decrease disappears, and the pH remains at the pH maximum reached after the initial t_lag. Both of these behaviors can be explained and understood by the simple fact that the carboxylate/carboxyl equilibrium provides H⁺ binding capacity. When the pH increases due to the MGS clock reaction, the carboxyl groups are deprotonated and provide extra H⁺ to the system, therefore, the pH maximum decreases. In the stage of lactone hydrolysis, some of the produced H⁺ is consumed by carboxylate groups and the decrease of the pH is delayed. In this way, the carboxylate/carboxyl equilibrium through OA can reversibly affect the characteristics of the driving clock reaction + lactone systems. At extremely high concentration of OA (>0.01 M) there is no significant pH jump due to the buffer capacity of the carboxylate and carboxyl groups. We could observe a similar behavior in the system with AuNPs, as MUA also has carboxylate groups linked to the surface of NPs (see ESI† Fig. S6).

Fig. 6 pH–time curves in the presence of oleic acid in the MGS and GL (a) and MGS and VL (b) systems with the fixed initial concentrations: [CH₂(OH)₂]₀ = 0.20000 M, [SO₃²⁻]₀ = 0.00500 M, [HSO₃⁻]₀ = 0.05000 M, [GL]₀ = 0.01000 M, [VL]₀ = 0.01000 M. 1: [OA]₀ = 0 M, 2: [OA]₀ = 0.00125 M, 3: [OA]₀ = 0.00250 M, 4: [OA]₀ = 0.00500 M, 5: [OA]₀ = 0.00750 M, 6: [OA]₀ = 0.01000 M.

We were able to estimate the concentration of carboxyl groups from the concentration (determined by UV-VIS measurements in terms of gold atoms) and size (determined from TEM measurements) of NPs, and their concentrations were 3 × 10⁻⁵ M and 5 × 10⁻⁴ M.

Fig. 7 summarizes our findings about the change in the pH maxima as a function of carboxylate groups obtained in both systems with GL and VL and using OA and AuNPs. It can be clearly seen that the increasing concentration of carboxylate group causes a decrease in the pH maxima, and this behavior is irrespective of the chemical nature of the carboxyl group whether the group is in fatty acid molecules or attached to the surface of nanoparticles. This finding suggests a quite similar acid strength (pK_a) in the two cases; otherwise the affinity of the building blocks to protons should strongly affect the allowable amount of the given function in the coupled system.²¹

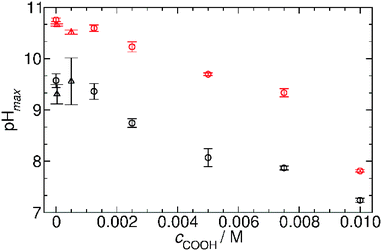Fig. 7 The maximum pH reached by the two chemical systems as a function of carboxyl concentration originating from the different self-assembly driven entities. Black open circles: MGS and GL + oleic acid (experimental conditions as in Fig. 6a); red open circles: MGS and VL + oleic acid (experimental conditions as in Fig. 6b); black open triangles MGS and GL + AuNPs (experimental conditions as in ESI† Fig. S6a); red open triangles: MGS and VL + AuNPs (experimental conditions as in ESI† Fig. S6b).

To support our experimental observation and findings we developed a chemical model based on the MGS + lactone system, for the details see the ESI.† Our results based on numerical simulations are in good agreement with the experimental data. Addition of a carboxylate/carboxyl equilibrium to the MGS + lactone system provides similar trends, namely changing the shapes of the kinetic curves (see ESI† Fig. S7–S9) and the pH maxima (see ESI† Fig. S10).

Conclusions

In summary, we proposed a general concept to drive and control the self-assembly of various chemical entities from molecular to material level, by combining a pH clock reaction and lactone hydrolysis in a closed system. The time scale separation of these two processes (quick pH jump provided by the clock reaction and a slow/delayed decrease of pH by lactone hydrolysis) ensures the existence of a transient alkaline state. This driving chemical system can be used to control and drive autonomously the self-assembly of pH switchable self-assembling components. We used fatty acid molecules, carboxyl group terminated AuNPs and amine functionalized polymer chains in a network to investigate their reversible time-programmed self-assembly. We demonstrated that proper control over the electrostatic interaction between the building blocks can govern and induce reversible transformation of vesicle-to-micelle, dispersion/aggregation of NPs and contraction/reswelling of gel filaments. Our approach differs from the protocol published in ref. 7–9, because our system has two freely adjustable temporal parameters, namely the time lag (t_lag) between the start of the whole process (reaction) and the time when the system reaches the maximum pH state with the existence (t_tr) of the transient pH state. Both control parameters can be “precoded” into the system by setting up the initial concentrations of the pH clock reaction and both the concentration and the chemical composition of the lactone used. In the time course of the process no human intervention is needed to drive and control the self-assembly.

We also highlight that the self-assembling building blocks themselves provide chemical feedback to the driving (master) system by changing the main characteristics of the system (pH maximum, t_tr). The work described here can provide new insight into time-programmed drug release^36,47,48 and artificial muscle^49,50 systems controlled by autonomous stimuli.

Acknowledgements

The authors acknowledge the financial support from the Hungarian Scientific Research Fund (OTKA K104666) and the National Research, Development and Innovation Office of Hungary (TÉT_12_JP-1-2014-0005). J. H. acknowledges financial support from the Hungarian National Research, Development, and Innovation Office (PD105270). H. N., G. H. and I. L. acknowledge support from the Project for Enhancing Research and Education in Polymer and Fiber Science at KIT. H. N. acknowledges funding support from the JSPS KAKENHI Grant Numbers JP15H05410 and JP16K13627, the Ogasawara Foundation, and the Kansai Research Foundation for Technology Promotion.

Notes and references

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418.
2. H. Zhou, X. Ding, Z. Zheng and Y. Peng, Soft Matter, 2013, 9, 4956–4968.
3. A. Grinthal and J. Aizenberg, Chem. Soc. Rev., 2013, 42, 7072–7085.
4. A. Synytska and L. Ionov, Part. Part. Syst. Charact., 2013, 30, 922–930.
5. S. Debnath, S. Roy and R. V. Ulijn, J. Am. Chem. Soc., 2013, 135, 16789–16792.
6. L. Ionov, Adv. Funct. Mater., 2013, 23, 4555–4570.
7. L. Heinen and A. Walther, Soft Matter, 2015, 11, 7857–7866.
8. T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262.
9. T. Heuser, A.-K. Steppert, C. Molano Lopez, B. Zhu and A. Walther, Nano Lett., 2014, 15, 2213–2219.
10. I. Varga, I. Szalai, R. Mészáros and T. Gilányi, J. Phys. Chem. B, 2006, 110, 20297–20301.
11. Y. Bae, S. Fukushima, A. Harada and K. Kataoka, Angew. Chem., 2003, 115, 4788–4791.
12. J. Boekhoven, A. M. Brizard, K. N. Kowlgi, G. J. Koper, R. Eelkema and J. H. van Esch, Angew. Chem., 2010, 122, 4935–4938.
13. A. Aggeli, M. Bell, N. Boden, L. M. Carrick and A. E. Strong, Angew. Chem., Int. Ed., 2003, 42, 5603–5606.
14. K. Kurin-Csörgei, I. R. Epstein and M. Orbán, Nature, 2005, 433, 139–142.
15. M. Orbán, K. Kurin-Csörgei and I. R. Epstein, Acc. Chem. Res., 2015, 48, 593–601.
16. H. W. van Roekel, B. J. Rosier, L. H. Meijer, P. A. Hilbers, A. J. Markvoort, W. T. Huck and T. F. de Greef, Chem. Soc. Rev., 2015, 44, 7465–7483.
17. S. N. Semenov, A. S. Wong, R. M. Van Der Made, S. G. Postma, J. Groen, H. W. Van Roekel, T. F. De Greef and W. T. Huck, Nat. Chem., 2015, 7, 160–165.
18. R. Yoshida, Adv. Mater., 2010, 22, 3463–3483.
19. J. M. Swann and A. J. Ryan, Polym. Int., 2009, 58, 285–289.
20. J. Horváth, J. Phys. Chem. B, 2014, 118, 8891–8900.
21. J. Horváth, Polymer, 2015, 79, 243–254.
22. J. Horváth, Macromol. Symp., 2015, 358, 217–224.
23. Y. S. Kim, R. Tamate, A. M. Akimoto and R. Yoshida, Mater. Horiz., 2017, 4, 38–54.
24. J. Horváth, Chem. Commun., 2017, 53, 4973–4976.
25. T. Ueno, K. Bundo, Y. Akagi, T. Sakai and R. Yoshida, Soft Matter, 2010, 6, 6072–6074.
26. T. Ueki, M. Shibayama and R. Yoshida, Chem. Commun., 2013, 49, 6947–6949.
27. M. Onoda, T. Ueki, M. Shibayama and R. Yoshida, Sci. Rep., 2015, 5, 15792.
28. T. Liedl and F. C. Simmel, Nano Lett., 2005, 5, 1894–1898.
29. I. Lagzi, B. Kowalczyk, D. Wang and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 8616–8619.
30. I. Lagzi, D. Wang, B. Kowalczyk and B. A. Grzybowski, Langmuir, 2010, 26, 13770–13772.
31. H. Nabika, T. Oikawa, K. Iwasaki, K. Murakoshi and K. Unoura, J. Phys. Chem. C, 2012, 116, 6153–6158.
32. E. Jee, T. Bánsági, A. F. Taylor and J. A. Pojman, Angew. Chem., Int. Ed., 2016, 55, 2127–2131.
33. K. Kovács, R. McIlwaine, K. Gannon, A. Taylor and S. Scott, J. Phys. Chem. A, 2005, 109, 283–288.
34. K. Kovács, R. E. McIlwaine, S. K. Scott and A. F. Taylor, J. Phys. Chem. A, 2007, 111, 549–551.
35. K. Kovács, R. E. McIlwaine, S. K. Scott and A. F. Taylor, Phys. Chem. Chem. Phys., 2007, 9, 3711–3716.
36. M. B. Dowling, J.-H. Lee and S. R. Raghavan, Langmuir, 2009, 25, 8519–8525.
37. J. Kanicky and D. Shah, Langmuir, 2003, 19, 2034–2038.
38. K. Morigaki and P. Walde, Curr. Opin. Colloid Interface Sci., 2007, 12, 75–80.
39. J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2011.
40. D. Wang, B. Kowalczyk, I. Lagzi and B. A. Grzybowski, J. Phys. Chem. Lett., 2010, 1, 1459–1462.
41. T. Tanaka, L. O. Hocker and G. B. Benedek, J. Chem. Phys., 1973, 59, 5151–5159.
42. T. Takebe, K. Nawa, S. Suehiro and T. Hashimoto, J. Chem. Phys., 1989, 91, 4360–4368.
43. K.-F. Arndt, F. Krahl, S. Richter and G. Steiner, in Hydrogel Sensors and Actuators, Springer, 2009, pp. 69–136.
44. X. S. Wu, A. S. Hoffman and P. Yager, J. Polym. Sci., Part A: Polym. Chem., 1992, 30, 2121–2129.
45. X.-Z. Zhang, Y.-Y. Yang and T.-S. Chung, Langmuir, 2002, 18, 2538–2542.
46. K. Kurin-Csörgei, I. R. Epstein and M. Orbán, J. Phys. Chem. A, 2006, 110, 7588–7592.
47. P. Gupta, K. Vermani and S. Garg, Drug Discovery Today, 2002, 7, 569–579.
48. Y. Liu, W. Wang, J. Yang, C. Zhou and J. Sun, Asian J. Pharm. Sci., 2013, 8, 159–167.
49. D. Walters, W. Kuhn and H. J. Kuhn, Nature, 1961, 189, 381–383.
50. B. Tondu, R. Emirkhanian, S. Mathé and A. Ricard, Sens. Actuators, A, 2009, 150, 124–130.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis and characterization of the pH-responsive polymer network. Experimental results: effect of gold nanoparticles on the coupled pH clock reaction and lactone system, and the space–time plot of the gel length in the pH clock reaction and D (+) gluconic acid δ-lactone system. Results of the numerical simulations and the reaction mechanism. Movies showing time-programmed self-assembly of fatty acids, gold nanoparticles and pH-responsive polymer filaments. See DOI: 10.1039/c7me00020k

---