Evaluating particle-suspension reactor designs for Z-scheme solar water splitting via transport and kinetic modeling†
Rohini
Bala Chandran
 a,
Sasuke
Breen
b,
Yuanxun
Shao
c,
Shane
Ardo
a,
Sasuke
Breen
b,
Yuanxun
Shao
c,
Shane
Ardo
 *bc and
Adam Z.
Weber
*bc and
Adam Z.
Weber
 *a
*a
aEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: AZWeber@lbl.gov
bDepartment of Chemistry, University of California, Irvine, CA 92697-2025, USA. E-mail: ardo@uci.edu
cDepartment of Chemical Engineering and Materials Science, University of California, Irvine, CA 92697-2025, USA
First published on 22nd September 2017
Abstract
Sunlight-driven water splitting to produce hydrogen and oxygen provides a pathway to store available solar energy in the form of stable, energy-dense chemical bonds. Here we investigate a tandem particle-suspension reactor design for solar water splitting comprising micron-scale photocatalyst particles suspended in an aqueous solution with soluble redox shuttles. A porous separator facilitates redox species transport between the hydrogen and oxygen evolution reaction compartments while averting gas crossover. A two-dimensional, transient model of the reactor is presented to illustrate the coupling between light absorption, interfacial electron-transfer kinetics and species transport, and their combined impacts on overall solar-to-hydrogen conversion efficiency. The volumetric reactivity of the suspended semiconductor particles is dictated by combining the (photo)current–voltage behavior of a photodiode with Butler–Volmer electron-transfer kinetics. For the first time, a quantitative approach to determine the impacts of surface-dependent redox shuttle kinetic parameters on reaction selectivity in a Z-scheme system is established. Model results provide insights on the effects of optical, transport and kinetic properties of the semiconductor particles and the redox shuttles on the overall reactor performance. Solar-to-hydrogen reactor efficiencies predicted with BiVO4 particles for oxygen evolution are at least two times larger than efficiencies achieved with wider band-gap TiO2 particles due to enhanced visible light absorption; hydrogen evolution with SrTiO3:Rh particles was considered for both cases. Superior performance is predicted with proton-coupled electron transfer redox shuttles (para-benzoquinone/hydroquinone and iodide/iodate) that absorb little-to-no visible light, while also facilitating operation at near-neutral pH conditions, as compared to the non-proton-coupled triiodide/iodide and iron(III)/iron(II) redox shuttles. For 1 cm tall reaction compartments, diffusive species transport is fast enough to sustain reactor operation at a 1% solar-to-hydrogen conversion efficiency for both para-benzoquinone/hydroquinone and iodate/iodide redox shuttles with less than 2.2 mg L−1 of each of BiVO4 and SrTiO3:Rh particles in the solution.
Broader contextPairing the most abundant energy resource on our planet, the Sun, with energy storage technologies is essential to overcome the diurnal variations in the availability of sunlight. Taking a leaf from nature's book, artificial photosynthetic devices capture and store sunlight in energy dense fuels by converting water and carbon dioxide to produce hydrogen and other hydrocarbons. For solar hydrogen production, particle-suspension reactor designs comprising suspended photocatalysts in an aqueous electrolyte are projected to be cost-efficient alternatives to the more exhaustively optimized fixed-electrode device architectures. However, there is a lack of a quantitative understanding of the device-scale transport and kinetic processes, and its impacts on the solar-to-hydrogen efficiencies for these designs. An innovative and intrinsically safe reactor design for Z-scheme solar water splitting is proposed. Two reaction compartments with suspended photocatalysts for hydrogen and oxygen production are optically connected in series to more efficiently utilize the incident solar spectrum while facilitating product separation. Soluble redox shuttles relay electrons between these compartments. A computational model is developed to guide device-design and operating conditions to achieve diffusion-sustained, efficient reactor operation. Results reveal the promise of using proton-coupled-electron-transport redox shuttles and the significance of selective surface catalysis to boost efficiency. |
Introduction
Stable, scalable and efficient devices for artificial photosynthesis offer the potential to harness and directly store the Earth's most abundant renewable energy resource in the form of energy-dense chemical bonds, such as those in hydrogen and hydrocarbons derived from carbon dioxide.1–3 These solar fuels are net-carbon-neutral alternatives to fossil fuels (assuming that the carbon is derived from combustion processes or the atmosphere), and enable storage and transport of solar energy for use when and where it is needed. Several solutions are being pursued for solar fuels production including photovoltaic-powered electrochemical devices for water and carbon dioxide splitting,4–7 solar thermochemical cycles,8–10 integrated photoelectrochemical (PEC) devices,11–16 and suspended photocatalyst particles.17–20 Fixed-electrode, wafer-based PEC devices to split water, that consist of photoactive electrodes immersed in an aqueous electrolyte, have been experimentally demonstrated12,21–26 and modeled extensively.27–34 These designs have exhibited solar-to-hydrogen energy-conversion (STH) efficiencies as high as 18%25 at 1 Sun illumination and over 30%26 with concentrated sunlight; however, these demonstrations suffered from stability issues where operational lifetimes were less than one day.12 Recent technoeconomic analyses35–37 make evident the need for fixed-electrode PEC devices to be operated at STH efficiencies greater than 25% to reach price parity with hydrogen produced from fossil fuels. However, the electrode-based devices that were stable for at least one day have exhibited STH efficiencies of at best 2% and they utilized designs that were inherently unsafe due to the generation of an explosive mixture of the H2 and O2 reaction products.20,38,39 Reactor designs based on photocatalyst particle suspensions20 coupled with stable, low-cost and efficient material options are conceived to be cost-competitive with hydrogen produced from fossil sources, even at lower STH efficiencies of ∼10%. The projected low levelized cost of hydrogen generated from particle-suspension reactors combined with the lack of in-depth knowledge for performance optimization of these reactors motivates the present study.Numerous experimental demonstrations pertinent to particle-suspension, Z-scheme reactors with electron transfer mediated by a soluble redox shuttle have been reported,40–50 and a comprehensive review on this topic has been presented by Fabian and colleagues.20 The predominant focus in the aforementioned studies was the identification of semiconductor materials40–48 with enhanced activities for implementing the oxygen evolution reaction (OER) and the hydrogen evolution reaction (HER), development of surface treatment techniques and selection of redox shuttles to suppress undesired interfacial electron-transfer reactions,41,49 and evaluation of the effectiveness of cocatalyst50 and coating materials.51 In prior work, device-scale design and performance dependences on the transport and kinetic processes of the system were not considered. Therefore, from the standpoint of designing particle-suspension reactors, there is a need for a more holistic understanding of the intertwined multiphysics processes of light absorption, species transport in the electrolyte, and heterogeneous surface reactions to maximize the STH efficiency. Moreover, the implications of the kinetic parameters of the redox shuttle on the selectivity towards the desired reactions have not been discussed in the previous studies.
Prior numerical models for solar water and carbon dioxide splitting have mostly been developed to guide the design of the fixed-electrode PEC devices.27–34 Jaini and Fuller52 evaluated mass-transfer correlations for gas-induced convective mixing in a dual-bed, particle-suspension reactor and determined the steady-state redox shuttle concentration profiles assuming spatially homogenous reaction rates. However, the effects of optical absorption by the particles and the influence of interfacial electron-transfer kinetics on the species mass transport were absent from that study. For applications of water treatment with colloidal suspensions of TiO2, volumetric light absorption and scattering properties of the suspension,53–55 mass-transport limitations56 and radiative transport57 have been evaluated using numerical and experimental techniques. However, the target chemical reactions for water treatment are inherently different from water splitting, primarily because the overall reactions are often thermodynamically favorable, and tandem photosystems with soluble redox shuttles have not been considered for these applications.
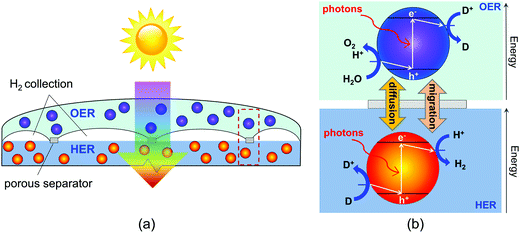
In this paper, we report on the development of a transient, two-dimensional numerical model of a vertically stacked, Z-scheme particle-suspension reactor for sunlight-driven water splitting. This design (Fig. 1) includes two important advances from prior conceptual designs for dual-bed Z-scheme reactors. The vertical arrangement of the reaction compartments facilitates tandem light absorption, which results in increased theoretical maximum STH efficiencies. By stacking the compartments, this design can afford mass transport over the smallest possible distances, therefore enabling sustained (effectively indefinite) reactor operation in the absence of convection. A notable advantage of the proposed Z-scheme reactor design is the opportunity to evolve H2 and O2 in separate physical locations, thus preventing formation of an explosive mixture of gases. The model developed accounts for diurnal variations in the incident solar irradiation and couples the effects of optical absorption in the aqueous suspension, power supply of an ideal photodiode, reversible interfacial reaction kinetics, and species mass transport. By varying reactor height and concentrations of the semiconductor particles and the redox shuttle species the model is used to evaluate transient reactor performance and identifies STH efficiencies that maintain sustained reactor operation.
Particle-suspension reactor
Our study specifically considers a tandem particle-suspension reactor for solar water splitting that relies on a two-step Z-scheme mechanism58 and a reversible redox shuttle dissolved in an aqueous electrolyte (Fig. 1). In a Z-scheme mechanism, the thermodynamic energy requirement for water splitting (WS) is attained using two photosystems (L1 and L2), similar to natural photosynthesis. Absorption of solar photons by a particle results in both an anodic (OER or Rox) and a cathodic (HER or Rred) half-reaction being driven at distinct semiconductor–electrocatalyst–electrolyte interfaces. Fig. 1 shows OER and Rred in the top compartment, and HER and Rox in the bottom compartment, but the locations of these reactions is a design variable and the choice of the redox shuttle determines which reactions should optimally be driven in the top and bottom compartments. Electrocatalysts deposited on semiconductor surfaces are commonly referred to as cocatalysts in the pertinent literature,20 and we adopt this terminology in the rest of this paper. As shown in Fig. 1, in the top compartment, light absorption generates holes that oxidize water to O2 (OER) and electrons that reduce the oxidized state of the redox shuttle, D+ → D (Rred). In the bottom compartment, light absorption generates electrons that reduce protons to H2 (HER), while simultaneously the photo-generated holes regenerate the oxidized state of the redox shuttle, D → D+ (Rox). Cocatalysts deposited on these particles reduce overpotentials for the desired redox reactions and potentially also improve the product selectivity for the desired pair of surface reactions (OER and Rred; HER and Rox) by influencing the charge-separation and electron transfer mechanisms. Intrinsic separation of product gases makes this design safe, and reduces Faradaic losses and explosion hazards that can occur due to reactions between product gases.| Oxygen evolution reaction (OER) particles |
|
|||||
| H2O + 2h+ → 2H+ + ½O2 (OER) | 2D+ + 2e− → 2D (Rred) | |||||
| Hydrogen evolution reaction (HER) particles |
|
|||||
| 2D + 2h+ → 2D+ (Rox) | 2H+ + 2e− → H2 (HER) | |||||
| Net | H2O + 4hν → H2 + ½O2 | (WS) | ||||
The ability of a particle-suspension reactor to attain large STH efficiencies and demonstrate sustainable operation relies in part on effective mass transport of the redox shuttle (D+/D) and protons, or hydroxides under alkaline conditions, between the physical locations of the OER and the HER particles.20 In the proposed reactor design, the characteristic lengthscale for diffusive mass transport and incident light absorption is the reaction compartment height. To maximize the rate of photon absorption and minimize energy losses associated with large concentration gradients, the reactor compartment height therefore needs to be optimized. The mass-transport lengthscales considered here are on the order of centimeters, in contrast to the lengthscales on the order of meters that were considered for horizontally-adjacent dual-bed designs.35,36
After surveying the semiconductor materials, dopants, cocatalysts, and redox shuttles reported in the literature,20 we selected semiconductor materials with demonstrated stability as aqueous suspensions, appropriate band energies to drive the desired reactions, and availability of published data on optical properties. Two options were investigated: Option I, which benefited from use of semiconductor particles with complementary bandgaps (Ebg), and Option II, which did not (Table 1). For Option I, the OER material was TiO2 (Ebg = 3.1 eV,59 average value of its two most common crystal structures) and for Option II the OER material was BiVO4 (Ebg = 2.5 eV),20,60 both materials with high reported activities for the light-driven OER in Z-scheme designs.41,49,50,61 The HER material for both these options was SrTiO3:Rh (rhodium-doped SrTiO3), with a lowest-energy absorption onset of 2.5 eV, due to excitation from a Rh3+ defect band to the SrTiO3 conduction band,63 and one-of-the-best reported activities for the light-driven HER in Z-scheme designs.45,48,51Table 1 shows the band gaps of the selected photocatalysts, which have suitable band-edge positions for the valence and conduction bands (denoted by Evb and Ecb in Table 2) relative to the desired redox reaction potentials. To mediate charge transport across the solutions, various demonstrated redox shuttles were analyzed (I3−/I−, IO3−/I−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20,41,42,49 and Fe3+/Fe2+
20,41,42,49 and Fe3+/Fe2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48,50,68) as well as an organic redox couple, p-benzoquinone/hydroquinone (Q/QH2), which has been used in state-of-the-art aqueous redox flow batteries and can undergo proton-coupled electron transfer redox chemistry.69–71Table 1 shows the pH conditions required for each redox shuttle to maintain it as the dominant species in solution. Acidic conditions (pH < 4) are required for the I3−/I− and the Fe3+/Fe2+ redox shuttles; for the Fe3+/Fe2+ redox shuttle, a one-electron-transfer reaction was analyzed. By coupling the proton-coupled electron transfer reactions for Q/QH2 with the inherently proton-coupled-electron-transfer OER or HER the overall reactions in each compartment exhibit pH independent thermodynamic potentials,
48,50,68) as well as an organic redox couple, p-benzoquinone/hydroquinone (Q/QH2), which has been used in state-of-the-art aqueous redox flow batteries and can undergo proton-coupled electron transfer redox chemistry.69–71Table 1 shows the pH conditions required for each redox shuttle to maintain it as the dominant species in solution. Acidic conditions (pH < 4) are required for the I3−/I− and the Fe3+/Fe2+ redox shuttles; for the Fe3+/Fe2+ redox shuttle, a one-electron-transfer reaction was analyzed. By coupling the proton-coupled electron transfer reactions for Q/QH2 with the inherently proton-coupled-electron-transfer OER or HER the overall reactions in each compartment exhibit pH independent thermodynamic potentials,
| H2O + Q → QH2 + ½O2 E0 = 0.53 V |
| QH2 → H2 + Q E0 = 0.7 V |
| Category | Parameter (unit) | Values | |
|---|---|---|---|
| Geometric and porous separator parameters | t sep (mm) | 1 | |
| w unit (cm) | 1 | ||
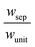
|
0.8 | ||
| ε sep | 0.26 | ||
| Semiconductor particles | j rr (A m−2) | TiO2 and BiVO4 | 10−18 |
| SrTiO3:Rh | 10−15 | ||
| E vb (V vs. NHE)20,59,62,63,65 | TiO2 | 2.7 | |
| BiVO4 | 2.3 | ||
| SrTiO3:Rh | 1.5 | ||
| E cb (V vs. NHE)20,59,62,63,65 | TiO2 | −0.4 | |
| BiVO4 | −0.2 | ||
| SrTiO3:Rh | −1 | ||
| ρ p (g cm−3) | TiO2 | 4.23 | |
| BiVO4 | 6.95 | ||
| SrTiO3:Rh | 4.81 | ||
| γ d | 1 | ||
| d p (nm) | 100 | ||
| Redox shuttles and electrolytes | D i 70,78 (10−9 m2 s−1) | I−, I3−, IO3− | 2, 1, 1 |
| Fe3+, Fe2+ | 0.8, 0.8 | ||
| Q, QH2 | 0.6, 0.74 | ||
| H+ | 9.3 | ||
| K+, Cl− | 2 | ||
| Aqueous solubility (M)79 | KI, KIO3 | 8.92, 0.43 | |
| FeCl3, FeCl2 | 5.7, 5.2 | ||
| Q, QH2 | 0.1, 0.5 | ||
| E 0 (V vs. NHE)80 | I3−/I−; IO3−/I− | 0.536; 1.085 | |
| Fe3+/Fe2+ | 0.771 | ||
| Q/QH2 | 0.7 | ||
| Kinetic parameters | j 0,OER (A m−2) | OER27,72,73 | 10−3 |
| α a,OER, αc,OER | 1, 0.1 | ||
| j 0,HER (A m−2) | HER27,74,75 | 10 | |
| α a,HER, αc,HER | 2.56, 2.56 | ||
| f cat | 0.5 | ||
The IO3−/I− redox shuttle also exhibits proton-coupled electron-transfer reactions (six proton, six electron-transfer reactions) for neutral to alkaline pH conditions.41
The interfacial reaction kinetics for the OER and the HER were modeled by considering the electron-transfer properties of state-of-the-art electrocatalysts, RuO2 for OER27,72,73 and Pt for HER,27,74,75 even though in practice these cocatalysts are not always used.20 The choice of the photocatalyst and the cocatalyst (if present) will impact the overpotentials for each redox reaction and determine the reaction selectivity. Therefore, the impacts of the redox shuttle kinetic parameters (exchange current density, j0,sh, and charge transfer coefficients, αa,sh, αc,sh) were examined in addition to the baseline simulations that assumed ideal selective catalysis with facile redox chemistry.
For each of these cases, the developed model was used to evaluate the effects of the reaction compartment heights (1 to 10 cm), and the concentrations of the semiconductor particles (10−6 to 1 g L−1) and the redox shuttles (10−4 to 5 M) on achieving sustained reactor operation, aided by only diffusive species transport, for a baseline STH efficiency of 1%. This modest efficiency target is set to evaluate the theoretical feasibility of the reactor design. Pathways to achieve higher STH efficiencies with the proposed design are also reported.
Theoretical
Modeling domain and assumptions
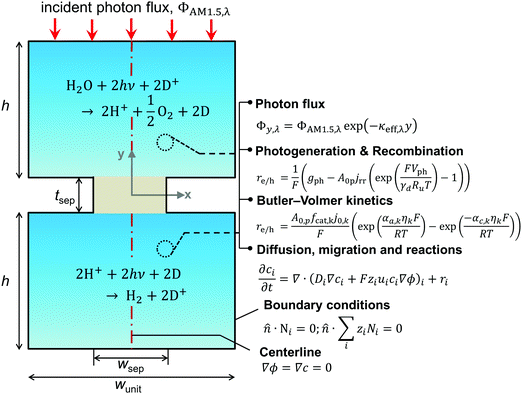
A transient, two-dimensional, continuum transport model was developed to simulate light absorption and mass transport in the reactor. Fig. 2 depicts the numerical modeling domain with the key governing equations used to model the coupled physical processes and the applied boundary conditions. Table 2 presents the baseline case modeling parameters. The domain comprises the two reaction compartments and a porous separator, and exploits centerline symmetry to reduce the computational expense. The aqueous suspension is assumed to contain a spatially homogeneous and continuous distribution of particles that remain completely soluble. Individual photocatalyst particles are not explicitly modeled and instead are treated as point locations that collectively exhibit diode current–voltage behavior (explained in the subsection on Conversion of light to power). The continuum transport equations formulated are hence applied for an “effective” medium comprising the suspended particles and the aqueous electrolyte. For colloidal suspensions with solid/particle volume fractions less than 0.006, the effective medium and independent light scattering are valid approximations.76 These volume fractions translate to particle concentrations less than 20 g L−1, 40 g L−1, and 30 g L−1 based on the bulk densities of TiO2, BiVO4, and SrTiO3:Rh, respectively (listed in Table 2), and we consider concentrations below 1 g L−1 for the model simulations. Therefore, treating the suspension as an effective medium is a reasonable approximation.A nominal particle diameter, dp, of 100 nm was used based on a reported powder-to-agglomerate size range of 10–1000 nm77 for the OER and the HER semiconductor particles. The particle size does not directly enter the analysis since the model treats the particles as point locations and thus assumes that the rates of charge-carrier transport (diffusion and migration) within the particle are much faster than the reaction rates and device-scale diffusive rates of species transport. This assumption is reasonable because the particle sizes considered here are much smaller relative to the device dimensions (dp ∼ 100 nm vs. h = 1–10 cm). The choice of the particle size was rather inconsequential because modeling results for reaction rates and STH efficiencies were found to be insensitive to the value of dp. This insensitivity is a consequence of the model treating the particles as point locations and the particle size only implicitly enters the analysis as a scale factor for the specific surface area, A0p (as will be shown in eqn (4a) and (6)).
Porous separator
The porous separator dimensions (tsep, wsep) and porosity, εsep, are selected to restrict diffusive gas crossover losses to less than 2%, a value that results in H2 and O2 streams with purity that is large enough to prevent formation of explosive mixtures.28 The conditions for this safe operation were determined by applying a one-dimensional Fickian diffusion model assuming saturated dissolved gas concentrations (1.23 mM for H2 and 0.78 mM for O2). For a separator thickness (tsep) of 1 mm, the following constraint,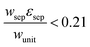 , arises to minimize gas crossover. More details about this calculation are provided in the ESI.† For the baseline case, the ratio of the separator width to the unit cell width,
, arises to minimize gas crossover. More details about this calculation are provided in the ESI.† For the baseline case, the ratio of the separator width to the unit cell width, 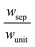 , is arbitrarily chosen to be 0.8, yielding a required separator porosity, εsep < 0.26.
, is arbitrarily chosen to be 0.8, yielding a required separator porosity, εsep < 0.26.
Conversion of light to power
The spatial profile of light intensity in the compartments depends on the effective optical properties (absorption and scattering) and can be approximated by the Beer–Bouguer–Lambert law for solutions with negligible scattering and radiative emission. Negligible radiative emission is a reasonable assumption at low operating temperatures, whereas scattering effects can be neglected only when particle/aggregate sizes are small (typically less than 10 nm) relative to the incident wavelengths of sunlight. For larger particles/aggregates, both absorption and scattering effects have to be taken into consideration to obtain the spatial distribution of photon fluxes,53,76 and therefore the reaction rates. However, in the absence of literature data to correlate the particle size-optical property dependencies and the added complexities to solve the full radiative transport equation, we applied Beer's law (eqn (1)) to evaluate the spatial profile of photon flux Φ along the height of the reactor,Φy,λ = ΦAM1.5,λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−κeff,λy) exp(−κeff,λy) | (1) |
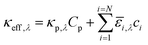 | (2) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) i and ci are the molar absorption coefficient and concentration of the ith species in the electrolyte, including water.83 Fig. S1 (ESI†) depicts the absorption coefficients of the various semiconductor particles48,77,84 and redox shuttles85–87 considered. Optical attenuation of incident light by the cocatalysts and the porous separator are neglected. This is a reasonable assumption because shading effects due to the cocatalysts are anticipated to be small in particle-suspension reactor designs. Moreover, cocatalysts are often used at far less than submonolayer coverages and are likely present in discontinuous patches on the particles, and polymer materials suitable for the porous separator exhibit negligibly low absorbance values in the near ultraviolet-visible region of the electromagnetic spectrum (see Fig. S2, ESI†). Values for ΦAM1.5,λ and κeff,λ can also be used to calculate the photon-flux weighted absorption cross-section of the particle,
i and ci are the molar absorption coefficient and concentration of the ith species in the electrolyte, including water.83 Fig. S1 (ESI†) depicts the absorption coefficients of the various semiconductor particles48,77,84 and redox shuttles85–87 considered. Optical attenuation of incident light by the cocatalysts and the porous separator are neglected. This is a reasonable assumption because shading effects due to the cocatalysts are anticipated to be small in particle-suspension reactor designs. Moreover, cocatalysts are often used at far less than submonolayer coverages and are likely present in discontinuous patches on the particles, and polymer materials suitable for the porous separator exhibit negligibly low absorbance values in the near ultraviolet-visible region of the electromagnetic spectrum (see Fig. S2, ESI†). Values for ΦAM1.5,λ and κeff,λ can also be used to calculate the photon-flux weighted absorption cross-section of the particle, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) p, and the optical thickness, τp (eqn (3)). Optical thickness is a critical dimensionless parameter that is linearly dependent on the particle concentration, absorption cross-section of the particles, and optical path length, h. It is a dimensionless indicator of the amount of sunlight absorbed by the semiconductor particles. The photon-flux weighted absorption cross-section of the particle,
p, and the optical thickness, τp (eqn (3)). Optical thickness is a critical dimensionless parameter that is linearly dependent on the particle concentration, absorption cross-section of the particles, and optical path length, h. It is a dimensionless indicator of the amount of sunlight absorbed by the semiconductor particles. The photon-flux weighted absorption cross-section of the particle, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) p, is used to determine the particle optical thickness, due to wavelength dependent optical properties.
p, is used to determine the particle optical thickness, due to wavelength dependent optical properties.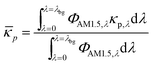 | (3a) |
τp = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) pCph pCph | (3b) |
Larger optical thicknesses result in increased sunlight absorption, which can be obtained by increasing the particle concentration and/or absorption properties of the material and/or optical path length. For simplicity, this weighted optical thickness is termed solely the “optical thickness” throughout the text. We chose this value over the photon-flux-weighted, spectrally-averaged percent of light absorbed (absorptance) because optical thickness is linear in both concentration of particles and reactor height, allowing for a more conceptual interpretation of the values. For reference, using 1 g L−1 of the suspended particles and h = 1 cm, the particle optical thicknesses are 54.5, 18.2 and 16.5 for TiO2, BiVO4 and SrTiO3:Rh, respectively.
The ideal photodiode equation has been used in prior modeling of fixed-electrode PEC devices to describe the (photo)current–voltage behavior of rectifying semiconductor–electrolyte junctions.29,33,88,89 While the photodiode equation may not be appropriate to describe the behavior of individual semiconductor particles whose photon absorption rate is low, we expect that the photodiode equation is appropriate to describe an ensemble of semiconductor particles in a suspension.90 In this approach, physical processes within individual particles, such as charge-carrier transport by diffusion and migration, and specific recombination pathways, are not considered, but instead represented by the reverse saturation current density (jrr in eqn (4a)) for the ensemble of particles. The magnitude of the reverse saturation current density will depend on many factors including the recombination rates and mechanisms that influence charge-carrier lifetimes, optical material properties, dopant densities, surface states, etc. The photodiode equation therefore presents a tractable method to capture the underlying physics of converting the flux of incident photons to an interfacial flux of charge-carriers.
Particle-suspension reactors effectively perform volumetric reactivity as compared to interfacial, areal reactivity in the fixed-electrode, wafer-based PEC geometries. Therefore, the flux of charge carriers transported across the semiconductor–electrolyte interface89 was recast as a volumetric rate, re/h, to obtain the volumetric version of the ideal photodiode equation,
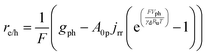 | (4a) |
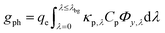 | (4b) |
The first term in eqn (4a), gph, is the volumetric absorption rate of the incident photons by the particles in the suspension; only photons with energies greater than the semiconductor absorption onset (oftentimes the bandgap) are considered to be absorbed. The second term is the volumetric recombination rate in the absence of illumination with an exponential dependence on the voltage, Vph, and influenced by the surface-specific, reverse saturation current density, the diode quality factor, γd, the operating temperature, T = 298.15 K, and the specific surface area of the semiconductor particles, 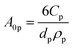 , where ρp is the bulk density of the semiconductor particle. The reverse saturation current densities modeled for the semiconductor particles influences the open-circuit potentials, with smaller values for jrr increasing the open-circuit potential and improving the reaction rates by decreasing the recombination rates of the charge-carriers produced. Reverse saturation current densities have not been reported for semiconductors in the particle form factor. Therefore, baseline values (Table 2) were selected from experimentally measured open-circuit potentials for BiVO4 electrodes affecting OER. For SrTiO3:Rh particles, the baseline reverse saturation current density was chosen to be several orders of magnitude larger than the detailed balance, Shockley–Queisser limit while also being small enough to yield desired rates of product formation. For comparison, based on the material bandgaps the Shockley–Queisser limits, for TiO2, BiVO4, and SrTiO3:Rh are on the order of 10−45, 10−35 and 10−35 A m−2, respectively at 298.15 K. Furthermore, the sensitivity of model results to the choice of jrr for the OER and the HER particles was evaluated and the results are shown in Fig. S8 (ESI†). These results indicate that reaction rates expected for reverse saturation current densities dictated by the Shockley–Queisser limit are predicted to be nearly equal to the baseline reaction rates (although the photovoltages are drastically different), suggesting that increasing the sunlight-driven power production of the semiconductor particles, by further decreasing the reverse saturation current densities toward the Shockley–Queisser limits, will not substantially alter the rate of H2 evolution.
, where ρp is the bulk density of the semiconductor particle. The reverse saturation current densities modeled for the semiconductor particles influences the open-circuit potentials, with smaller values for jrr increasing the open-circuit potential and improving the reaction rates by decreasing the recombination rates of the charge-carriers produced. Reverse saturation current densities have not been reported for semiconductors in the particle form factor. Therefore, baseline values (Table 2) were selected from experimentally measured open-circuit potentials for BiVO4 electrodes affecting OER. For SrTiO3:Rh particles, the baseline reverse saturation current density was chosen to be several orders of magnitude larger than the detailed balance, Shockley–Queisser limit while also being small enough to yield desired rates of product formation. For comparison, based on the material bandgaps the Shockley–Queisser limits, for TiO2, BiVO4, and SrTiO3:Rh are on the order of 10−45, 10−35 and 10−35 A m−2, respectively at 298.15 K. Furthermore, the sensitivity of model results to the choice of jrr for the OER and the HER particles was evaluated and the results are shown in Fig. S8 (ESI†). These results indicate that reaction rates expected for reverse saturation current densities dictated by the Shockley–Queisser limit are predicted to be nearly equal to the baseline reaction rates (although the photovoltages are drastically different), suggesting that increasing the sunlight-driven power production of the semiconductor particles, by further decreasing the reverse saturation current densities toward the Shockley–Queisser limits, will not substantially alter the rate of H2 evolution.
Interfacial reaction kinetics
On the surface of the semiconductor particles at least one pair of redox half-reactions occurs. One of the factors that influences the reaction rate is the photovoltage (Vph), which is equal to the sum of the surface overpotentials for the two redox reactions and the species-concentration-dependent thermodynamic equilibrium potential (Nernstian potential), U, for the net reaction on the semiconductor particle surface (L1 or L2)| Vph = UL1/L2 + |ηOER/HER| + |ηRred/Rox| | (5) |
The baseline case assumed complete selectivity toward the desired reactions, i.e. L1 and L2 (Fig. 1(b)). The flux of electrons/holes across the cocatalyst surface area for the kth reaction (k = OER, HER, Rrd, and Rox) is
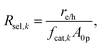 | (6) |
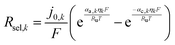 | (7) |
Selective catalysis is crucial to achieve large STH efficiencies in particle-suspension reactors, however, in reality each particle is wetted by electrolyte that contains at least four chemical species that can partake in redox chemistry at the particle surface, and a quanta of separated charge could be lost due to recombination to undesired “back-reactions” with two of the species. Note that only particle-mediated surface reactions were considered in this analysis for non-baseline cases, and the homogeneous chemical reactions of the species in the electrolyte were neglected. For example, on the surface of the HER particles the undesired reactions are the dissolved H2 oxidation reaction (HOR) by holes in the valence band and/or reduction of the oxidized form of the redox shuttle, D+ → D (Rred), by electrons in the conduction band. These reactions occur simultaneously with the desired surface reactions of HER by electrons in the conduction band and oxidation of the reduced form of the redox shuttle, D → D+ (Rox), by holes in the valence band. The overpotentials for these competing reactions on the HER semiconductor particles can be related to the photovoltage in eqn (5) as,
| |ηRred/HOR| = Vph − |ηRox/HER| | (8) |
Butler–Volmer kinetics, as shown in eqn (7), was applied to obtain the rate of competing back-reactions as a function of the respective overpotentials in eqn (8). The effective reaction rate, Reff, was expressed as the difference of the rate of selective catalysis, Rsel, and the competitive back reactions, Rback. When the back-reaction rates were predicted to be larger than the rates of the desired reactions, particle shunting occurs with unity yield, and the effective reaction rate is zero.
| Reff,j = Rsel,j − Rback,i | (9) |
For the OER particles j = OER/Rred, i = ORR, Rox and likewise, for the HER particles, j = HER/Rox; i = HOR, Rred.
Species transport
For dilute solutions, the Nernst–Planck equation78 dictates the migration and diffusion species fluxes (convective fluxes are not considered here as a worse-case stationary system is assumed),| Ni = −ziuiFci∇ϕ − Di∇ci | (10) |
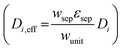 was used.
was used.
Overall mass conservation,
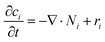 | (11) |
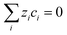 | (12) |
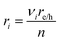 | (13) |
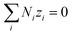 | (14) |
Combining eqn (10) and (14), electrostatic potential gradient in the bulk solution can be related to the diffusion fluxes of ionic species,
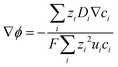 | (15) |
Metrics
The projected areal rate of charge-carrier production, Ra, is obtained by spatially integrating the volumetric rate (eqn (13)) in the respective reaction compartment over the two-dimensional reaction compartment surface area, A, and averaging the integrated value over the reaction compartment height,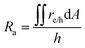 | (16) |
This areal reaction rate is reported here instead of a current density, because, unlike fixed-electrode PEC reactors, particle-suspension designs do not result in a net ionic/electronic current that spans the entire length of the reactor necessitating ion migration and the associated ohmic potential drops. The areal H2 production rate (RH2,a) is half of the areal rate of charge-carrier production, 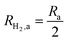 , based on the reaction stoichiometry (eqn (L1) and (L2)). From the areal H2 production rate, the peak and day-averaged STH efficiencies are,
, based on the reaction stoichiometry (eqn (L1) and (L2)). From the areal H2 production rate, the peak and day-averaged STH efficiencies are,
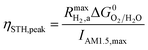 | (17) |
 | (18) |
For the particle-suspension design, potential/energy losses arises due to a change in the concentrations of the reaction species between the two compartments and contributes to spatially variant reaction potentials. This mass-transfer-related potential loss or overpotential, Δϕmt, between two locations in the particle-suspension designs, one in the OER compartment and one in the HER compartment, has contributions from pH gradients, ΔϕpH, and the concentration gradient of the redox shuttle species, ΔϕD+/D,
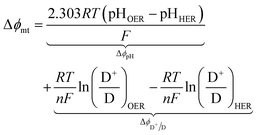 | (19) |
The species concentrations in eqn (19) are computed as volume-averaged values in the OER and the HER compartments. Ohmic potential losses between the reaction compartments are not present due to the lack of an externally applied field/current density to drive ion transport.
Solution procedure
The coupled governing equations (eqn (1), (2) and (4a)–(13)) were solved on the two-dimensional numerical domain with the appropriate boundary conditions (Fig. 2) using the finite element method on a mapped mesh with a maximum of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements. The discretized equations were solved using COMSOL Multiphysics92 with quadratic element discretization and a time-dependent direct linear solver (PARADISO). Implicit and adaptive time stepping, with a maximum time-step of 600 s, was employed to attain a relative tolerance of 10−4 for all the scaled variables. Mesh independence was verified by doubling the mesh size, which yielded a maximum change of 1% in the spatially-averaged species concentrations and the sink-term/source-term computed in eqn (11). Zero current density and zero species flux boundary conditions were applied on the external boundaries and symmetry boundary conditions were imposed at the vertical centerline (Fig. 2). All the simulations were performed on a dual core Intel Xeon X5660 processor (2.8 GHz, 24 GB), and the model developed is robust enough to tackle the various semiconductor particles, redox shuttles and reaction compartment heights investigated in this study. For the largest reaction compartments (10 cm tall) the transient simulations take approximately 8 hours of wall clock time to attain steady-periodic conditions. The procedure adopted for the quasi-steady simulations and determination of initial values of the solution variables for the transient simulations is detailed below.
000 elements. The discretized equations were solved using COMSOL Multiphysics92 with quadratic element discretization and a time-dependent direct linear solver (PARADISO). Implicit and adaptive time stepping, with a maximum time-step of 600 s, was employed to attain a relative tolerance of 10−4 for all the scaled variables. Mesh independence was verified by doubling the mesh size, which yielded a maximum change of 1% in the spatially-averaged species concentrations and the sink-term/source-term computed in eqn (11). Zero current density and zero species flux boundary conditions were applied on the external boundaries and symmetry boundary conditions were imposed at the vertical centerline (Fig. 2). All the simulations were performed on a dual core Intel Xeon X5660 processor (2.8 GHz, 24 GB), and the model developed is robust enough to tackle the various semiconductor particles, redox shuttles and reaction compartment heights investigated in this study. For the largest reaction compartments (10 cm tall) the transient simulations take approximately 8 hours of wall clock time to attain steady-periodic conditions. The procedure adopted for the quasi-steady simulations and determination of initial values of the solution variables for the transient simulations is detailed below.
Model simulations
Quasi-steady simulations were performed to evaluate the impacts of the semiconductor and the electrolyte optical properties on the reactor performance in the absence of any mass transport limitations. These simulations used simplified model conditions of peak incident photon flux (i.e. solar noon) and time-invariant and position-invariant concentrations of the electrolyte species, and only eqn (4a)–(7) are solved along the height of the reactor. The thermodynamic potentials for effecting reactions (L1) and (L2) for the various redox species considered are fixed at the respective standard-state values indicated in Table 2. For all these simulations, only the concentrations of the most strongly sunlight-absorbing redox species (i.e. I3−, Fe3+, Q and QH2) were varied. The concentrations of the other redox species (I−, IO3−, and Fe2+), which absorb little light at λ > 280 nm, were set to values required to maintain the respective E0 values (listed in Table 2) because the areal reaction rates were not affected by changes to the concentrations of these redox species. Moreover, reaction kinetics is not affected by the concentration of these redox species for the baseline cases that assumed selective surface catalysis, because the OER and the HER are rate limiting. For all the quasi-steady simulations, the proton concentration, cH+, was fixed at 1 M. For the Q/QH2 redox shuttle, equal concentrations of Q and QH2 were assumed, with a maximum concentration of 0.5 M, which is the aqueous solubility of QH2.70For the transient simulations, transport, production and consumption of the various species (eqn (8)–(13)) in the reactor were considered in addition to the volumetric charge-carrier generation rate (eqn (4a)–(7)) in the presence of diurnal illumination cycles. The spatial and temporal variations of the electrolyte species concentrations and their influence on light absorption, Nernst reaction potential and reaction kinetics are all inherently accounted for in these simulations. For these simulations, at t = 0 s, the variables re/h, Rsel,k, ηOER/HER and ϕ were initialized to 0 and the photovoltage, Vph, was set equal to the position-dependent open-circuit potential (from eqn (4a)). The concentrations of electrolyte species required to sustain reactor operation at desired STH efficiencies (D+, D, H+, OH−) were evaluated iteratively from the model results. Guess values for these initial concentrations were obtained by solving the transient species transport equations, eqn (10)–(12), with spatially homogeneous reaction rates that were consistent with a 1% STH efficiency at peak solar insolation; the day/night illumination profiles were superimposed on these rates.
Results and discussion
The influence of the optical properties of the semiconductor materials and the redox couples on the reactor performance was first evaluated under quasi-steady conditions and in the absence of any mass transport limitations. Transient reactor performance as well as the impacts of competitive back reactions is then discussed.Effects of optical properties
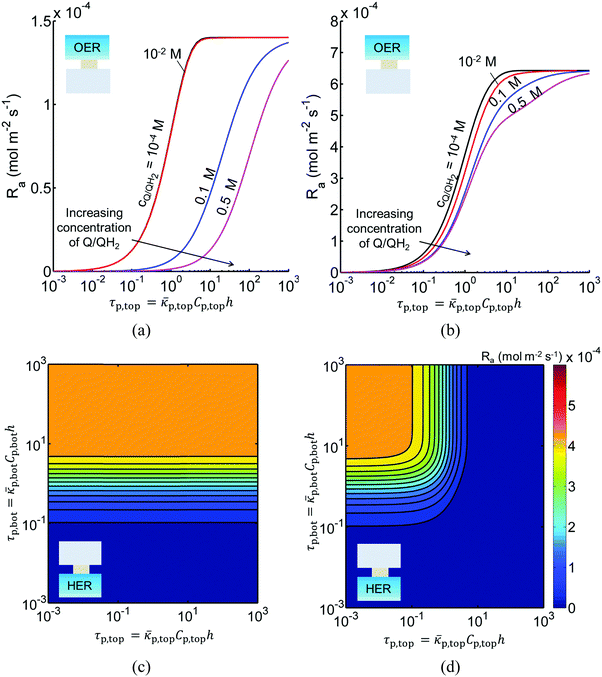
Fig. 3 shows the impact of competitive light absorption by the redox shuttle for fixed semiconductor particle concentrations of 1 g L−1, with and without tandem light absorption. For both the tandem (Option I) and the same-bandgap cases (Option II), the areal reaction rate decreased exponentially with redox shuttle concentration (Fig. 3) due to competitive light absorption. Incorporation of triiodide ions led to the lowest predicted reaction rates in the top and bottom compartments, because I3− exhibits the strongest visible light absorption (Fig. S1, ESI†). The rates were slightly larger for Fe3+/Fe2+ and even larger for the organic redox couple because these species absorb very little visible light. Option I achieved baseline STH efficiencies in the absence of mass transport limitations when using redox shuttles that contain <2 mM I3− or <5 mM Fe3+, constraints that arise due to competitive absorption of sunlight. It was determined that, for all redox shuttles considered, the rates in the top OER compartment are larger for Option II (Fig. 3(b)) relative to Option I (Fig. 3(a)). This effect is because BiVO4 absorbs more sunlight than the wide-bandgap TiO2. However, this improvement in light absorption comes at the expense of the reaction rates in the bottom compartment, which are larger for Option I than Option II owing to improved visible-light transmission to the bottom HER compartment when TiO2 is used in place of BiVO4. The consequence is that the reaction rates for Option II in the bottom compartment are negligibly low even for the smallest redox shuttle concentration (10−4 M) considered (Fig. 3(b)). This result suggests that the BiVO4 particle concentration and/or pathlength for light absorption have to be further optimized to achieve the baseline STH efficiency of 1% for Option II.In addition to the type and redox shuttle concentrations, the reaction rates are influenced by the optical thicknesses of the semiconductor particles (eqn (3)). Optical thickness linearly depends on the particle concentration (Cp), absorption cross-section (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) p) of the particles, and reaction compartment height (h). Fig. 4 illustrates the effects of optical thicknesses on the reaction rates in the top and bottom reaction compartments at various concentrations of Q/QH2 with and without tandem light absorption. The rates in the top compartment are only dependent on the optical thickness of the top compartment, τp,top (Fig. 4(a and b)), whereas the rates in the bottom compartment are dependent on the optical thicknesses in both the top and bottom compartments (Fig. 4(c and d)). In both options considered, the reaction rate in the top OER compartment increased asymptotically with optical thickness until a rate of 1.4 × 10−4 mol m−2 s−1 for Option I (Fig. 4(a)), and 6.4 × 10−4 mol m−2 s−1 for Option II (Fig. 4(b)), values that are dictated primarily by the band gap and spectral absorptivities of the particles. Supported by the data in Fig. 3, reaction rates decrease as the concentrations of the redox shuttle increase due to competitive light absorption. The reaction rates in the bottom reaction compartment are shown in Fig. 4(c and d) for the largest redox shuttle concentration considered, 0.5 M. Results for the other concentrations of Q/QH2 show qualitatively similar trends and are presented in Fig. S3 (ESI†). In both options, the reaction rates increased as the optical thickness of the SrTiO3:Rh particles, τp,bot, increased, to a maximum value of about 4.5 × 10−4 mol m−2 s−1. For Option I (Fig. 4(c)), the rates were largely insensitive to the TiO2 particle optical thickness owing to its transmission of light beyond 400 nm, which can be absorbed by SrTiO3:Rh. For Option II, where the particles have similar absorption onsets, a “pseudo-tandem” effect is obtained by modulating the relative optical thicknesses of the top and bottom compartments. If the optical thickness of the top compartment particles is small, τtop,p < 0.01, reaction rates in the bottom compartment are as large as those obtained for the true tandem condition with Option I. These results clearly indicate that the semiconductor particle optical thicknesses have to be optimized to maximize the reaction rates for the OER and the HER in the two compartments. The optimal values are strongly influenced by not only choice of the semiconductor particles in the two reaction compartments, but also the type and concentration of the redox shuttle species considered.
p) of the particles, and reaction compartment height (h). Fig. 4 illustrates the effects of optical thicknesses on the reaction rates in the top and bottom reaction compartments at various concentrations of Q/QH2 with and without tandem light absorption. The rates in the top compartment are only dependent on the optical thickness of the top compartment, τp,top (Fig. 4(a and b)), whereas the rates in the bottom compartment are dependent on the optical thicknesses in both the top and bottom compartments (Fig. 4(c and d)). In both options considered, the reaction rate in the top OER compartment increased asymptotically with optical thickness until a rate of 1.4 × 10−4 mol m−2 s−1 for Option I (Fig. 4(a)), and 6.4 × 10−4 mol m−2 s−1 for Option II (Fig. 4(b)), values that are dictated primarily by the band gap and spectral absorptivities of the particles. Supported by the data in Fig. 3, reaction rates decrease as the concentrations of the redox shuttle increase due to competitive light absorption. The reaction rates in the bottom reaction compartment are shown in Fig. 4(c and d) for the largest redox shuttle concentration considered, 0.5 M. Results for the other concentrations of Q/QH2 show qualitatively similar trends and are presented in Fig. S3 (ESI†). In both options, the reaction rates increased as the optical thickness of the SrTiO3:Rh particles, τp,bot, increased, to a maximum value of about 4.5 × 10−4 mol m−2 s−1. For Option I (Fig. 4(c)), the rates were largely insensitive to the TiO2 particle optical thickness owing to its transmission of light beyond 400 nm, which can be absorbed by SrTiO3:Rh. For Option II, where the particles have similar absorption onsets, a “pseudo-tandem” effect is obtained by modulating the relative optical thicknesses of the top and bottom compartments. If the optical thickness of the top compartment particles is small, τtop,p < 0.01, reaction rates in the bottom compartment are as large as those obtained for the true tandem condition with Option I. These results clearly indicate that the semiconductor particle optical thicknesses have to be optimized to maximize the reaction rates for the OER and the HER in the two compartments. The optimal values are strongly influenced by not only choice of the semiconductor particles in the two reaction compartments, but also the type and concentration of the redox shuttle species considered.
Sustained reactor operation requires equal rates of production and consumption of the redox shuttle species in the two reaction compartments. In Option I, the maximum attainable STH efficiency with sustained operation is limited to ∼1.7% because the maximum reaction rate for TiO2 is three times slower than SrTiO3:Rh, 1.4 × 10−4 mol m−2 s−1versus 4.5 × 10−4 mol m−2 s−1 (Fig. 4(a and b)). Table 3 presents the particle optical thickness combinations required to attain the specified STH efficiency with sustained reactor operation for each option of the OER particles and each redox shuttle, and assuming rapid mixing that affords fixed redox shuttle concentrations at all spatial locations in the reactor. These results reinforce the negative impacts of competitive light absorption, necessitating rather low concentrations of the I3−/I− and Fe3+/Fe2+ redox shuttles (<5 mM) to possibly attain the baseline STH efficiency of 1%. These concentrations are prohibitively low, because as discussed next, when mass transport is included in the model, the rate of diffusive species transport is unable to keep up with the rates of redox species consumption/production consistent with a 1% STH efficiency, leading to local depletion of the reactants. For Option II and the quinone redox shuttle, STH efficiencies up to 3% are feasible even with 0.5 M of Q/QH2, the solubility limit. For lower concentrations of Q/QH2 (<10−3 M), the largest attainable STH efficiency is 3.8% for sustained reactor operation. For the I−/IO3− redox shuttle, which also undergoes proton-coupled electron-transfer, the STH efficiencies are not affected by the redox shuttle concentrations because of their negligible sunlight absorption. However, compared to Q/QH2, a higher photovoltage (>1.085 V) is required in the HER light absorbers due to the more positive standard-state potential of the I−/IO3− redox shuttle. This large photovoltage requirement can only be obtained when a smaller reverse saturation current density, jrr, of 10−20 A m−2 is utilized for the SrTiO3:Rh particles in place of the baseline value of 10−15 A m−2. In that case, the maximum attainable STH efficiency for the I−/IO3− redox shuttle is 3.8%, the same maximum value obtained for the Q/QH2 redox shuttle.
| Redox shuttle: I/I3−; UL1 = −0.694 V and UL2 = −0.536 V vs. NHE | ||||||
|---|---|---|---|---|---|---|
| Option I | Option II | |||||
| c A/A− (M) | η STH,peak = 1% | η STH,peak = 1% | η STH,peak = 2% | |||
| τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | |
| 10−4 | 3.162 | 0.316 | 0.178 | 0.316 | 0.562 | 1.778 |
| 10−3 | 31.62 | 1.77 | 0.562 | 3.16 | 1 | N/A |
| 0.1 | N/A | N/A | 17.78 | N/A | 56.23 | N/A |
| 1 | N/A | N/A | 177.82 | N/A | 562.3 | N/A |
| Redox shuttle: Fe2+/Fe3+; UL1 = −0.459 V and UL2 = −0.771 V vs. NHE | ||||||
|---|---|---|---|---|---|---|
| Option I | Option II | |||||
| c A/A− (M) | η STH,peak = 1% | η STH,peak = 1% | η STH,peak = 2% | |||
| τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | |
| 10−4 | 1 | 0.316 | 0.178 | 0.178 | 0.316 | 0.562 |
| 10−3 | 3.162 | 1.77 | 0.178 | 0.562 | 0.562 | 1.778 |
| 0.1 | 316.2 | N/A | 17.78 | N/A | 56.23 | N/A |
| 1 | N/A | N/A | 177.82 | N/A | 562.3 | N/A |
| Redox shuttle: Q/QH2; UL1 = −0.53 V and UL2 = −0.7 V vs. NHE | ||||||||
|---|---|---|---|---|---|---|---|---|
| Option I | Option II | |||||||
| c A/A− (M) | η STH,peak = 1% | η STH,peak = 1% | η STH,peak = 3% | η STH,peak = 3.8% | ||||
| τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | |
| 10−4 | 0.83 | 0.186 | 0.128 | 0.155 | 0.47 | 1 | 0.77 | 6.46 |
| 10−3 | 1 | 0.186 | 0.155 | 0.155 | 0.57 | 1.2 | 0.82 | 9.4 |
| 0.1 | 28.8 | 0.225 | 0.27 | 0.326 | 1 | 5.36 | 1.75 | N/A |
| 0.5 | 128.27 | 0.225 | 0.27 | 0.393 | 1 | 5.36 | 2.1 | N/A |
|
Redox shuttle: I−/IO3−; UL1 = −0.145 V and UL2 = −1.085 V vs. NHE
j rr,OER = 10−18 A m−2, jrr,HER = 10−20 A m−2 |
||||||||
|---|---|---|---|---|---|---|---|---|
| Option I | Option II | |||||||
| η STH,peak = 1% | η STH,peak = 1% | η STH,peak = 3% | η STH,peak = 3.8% | |||||
| τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | τ p,top | τ p,bot | |
| 0.91 | 0.215 | 0.142 | 0.17 | 0.55 | 1.53 | 0.72 | 7.1 | |
Effect of species transport
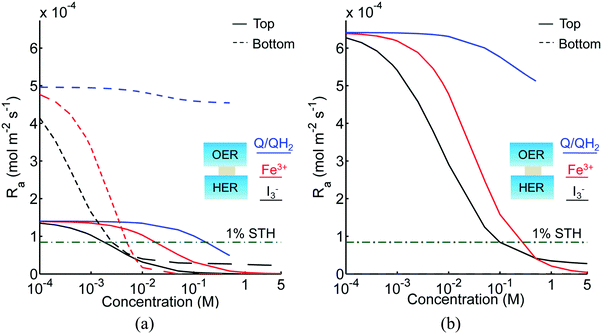
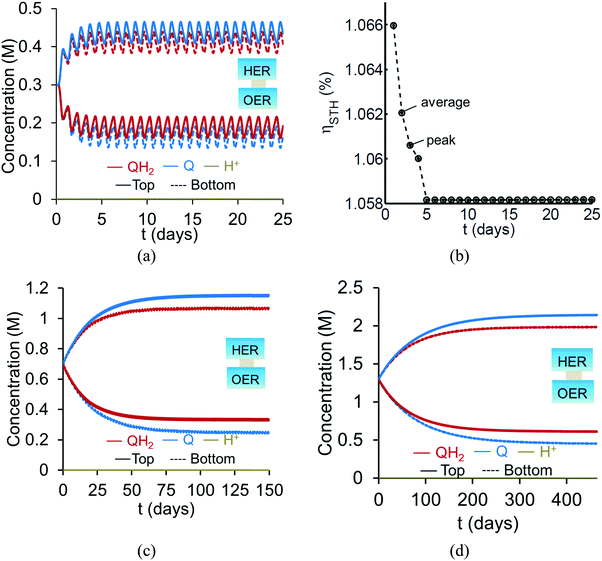
Based on the model predictions that indicate that Option II has larger theoretically achievable efficiencies (Table 3), this option was chosen for further investigation to evaluate the effects of coupled light absorption, species transport, and reaction kinetics. Transient reactor performance is shown in Fig. 5 for the Q/QH2 redox shuttle, which is projected to attain larger than baseline STH efficiencies for all redox species concentrations considered. The locations of the redox chemistries are opposite of that shown in Fig. 1, with HER/Rox in the top compartment and OER/Rred in the bottom compartment. The optical properties of Q/QH2 are less detrimental in this modified configuration, suggesting that this arrangement could be more efficient with this redox shuttle. The data indicate that a steady-periodic state of reactor operation is attained after about 5 days, 125 days, and 500 days for 1 cm, 5 cm, and 10 cm tall reaction compartments, respectively. Fig. 5(b) illustrates that the peak and day-averaged STH efficiencies are ∼1.06%, which remains constant beyond five days of reactor operation. Stable steady-periodic operation is also observed for the 5 cm and 10 cm tall compartments, as shown in Fig. 5(b and c), and for operation at the same baseline STH efficiency of ∼1%. For each of these conditions, the areal reaction rates (not shown) in the two compartments are very similar during steady-periodic reactor operation. The time taken to attain steady-periodic conditions is computed as the time after which the percentage changes in species concentrations (spatially-averaged concentrations in each reaction compartment) are less than 0.1% from the concentrations predicted in the previous illumination cycle and when the STH efficiency remains constant (as shown in Fig. 5(b)). In comparison, an order-of-magnitude estimate for the diffusion timescales, tdiff ∼ h2/Di, are 2 days, 50 days and 250 days for respective reaction compartment heights of 1 cm, 5 cm and 10 cm, and computed using the diffusivity of para-benzoquinone (slowest diffusing species in the suspension). Model predictions align with the expectation that steady-state conditions will prevail for timescales larger than the diffusion timescales, and in this case, tsteady ∼ 2.5tdiff. The fact that the predicted time to attain the steady-periodic state is approximately proportional to the square of the compartment height (tsteady ∝ h2), is indicative of a diffusion controlled process. Without day-and-night variations in the incident sunlight, local depletion of the redox species (Q) occurs within a day of reactor operation for the 1 cm tall reaction compartments (Fig. S4, ESI†). Therefore, much larger initial redox species concentrations (0.65 M versus 0.3 M for h = 1 cm) are required to attain steady-state conditions for this situation. Irrespective of the pH, the concentration of protons is time-invariant and position-invariant because it was assumed that the Q/QH2 redox shuttle underwent proton-coupled electron transfer with unity yield in these simulations. Therefore, any pH (pH = 7 in Fig. 5) is sustainable using this reactor design, provided that the redox shuttle undergoes rapid proton-coupled electron transfer. At a fixed STH efficiency, the volumetric reaction rate varies inversely with the reaction compartment height, whereas the rate of diffusive species transport decreases proportional to the square of the height. Therefore, to maintain steady and sustained reactor operation, at roughly 1% STH efficiency, the minimum initial concentrations of the redox shuttle increases nearly linearly with the reaction compartment height (csteady ∝ h). Slight deviations from linearity occur due to the spatial location and concentration dependence of the reaction rates, and the minor differences in the STH efficiencies obtained with the different heights of the reaction compartments. Overall, these scaling relationships underscore the dominance of diffusion as a mode of species transport in the solution compared to migration. For the neutral Q/QH2 redox shuttle, results in Fig. 5 demonstrate species mixing entirely controlled by diffusion (in the absence of any forced/natural convection). This result is because with spatially invariant proton concentrations, the net diffusive flux of any charged species is zero, i.e. the numerator in eqn (15) is zero. In the absence of an externally applied field or current density, the driving force for ion migration is essentially zero.For all the reaction compartment heights considered, the potential losses associated with pH gradients are zero with the quinone redox shuttles because the proton concentrations in the solution are spatio-temporally invariant. The mass-transfer overpotential (eqn (19)) due to the redox species concentration gradients attains a maximum of 28 mV, 33 mV, and 35 mV during steady-periodic reactor operation for the 1 cm, 5 cm, and 10 cm tall reactors.
For reaction compartment heights greater than 5 cm the predicted concentration profiles in Fig. 5 suggest that sustained reactor operation, is limited by the aqueous solubility of Q and QH2. Even for h = 1 cm, the required concentration of Q for sustained reactor operation is larger than its aqueous solubility limit of 0.1 M. While aqueous solubility can be improved through introduction of sulfonate groups on the redox shuttle molecules,70 these large groups also reduce species diffusivities and therefore, optimization of these tradeoffs is required. Therefore, one solution to enable sustained reactor operation via diffusive species transport with reasonable concentrations of these redox shuttles, is to reduce the reaction compartment heights to the sub-centimeter length scales with concomitant increase in the semiconductor particle concentration to maintain the same reaction rates.
Profiles along the reactor height are informative when visualizing the conditions present under steady-periodic operation. Therefore, depicted in Fig. 6 are the following parameter profiles at solar noon for h = 1 cm: redox shuttle concentrations, volumetric reaction rates, photovoltages, and reaction overpotentials. The concentration profiles (Fig. 6(a)) are reflected about the center of the reactor (x = 0, y = 0) with equal rates of production and consumption of the redox shuttle in the two compartments during steady-periodic operation. The spatial profiles of the volumetric reaction rates, photovoltage, and overpotentials (Fig. 6(b–d)) follow the trend of the absorbed photon flux and therefore, decrease along the reactor height. The relatively more linear spatial profiles of the volumetric reaction rate in the bottom compartment in comparison to the top compartment are due to the differences in the optical properties of the semiconductor materials and the increased light attenuation by the electrolyte along the reactor height. The average photovoltage produced by the photocatalysts that drive Rox/HER is 0.734 V, while the photovoltage is ∼100 mV larger at 0.824 V for the photocatalyst particles that implement OER/Rred, which is in part required to supply the larger overpotentials for the OER (Fig. 6(d)).
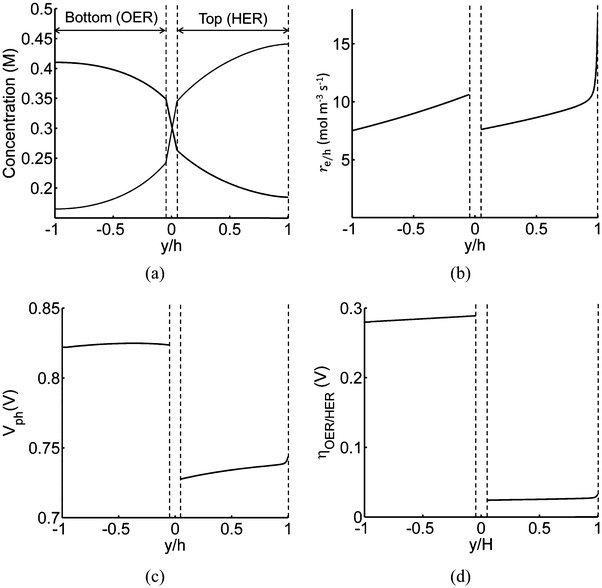 | ||
| Fig. 6 Spatial profiles along the reactor centerline at x = 0 (see Fig. 2) during steady-periodic operation at solar noon with 1.53 × 10−3 g L−1 of SrTiO3:Rh (top, HER) and 2.12 × 10−3 g L−1 of BiVO4 (bottom, OER) particles: (a) redox shuttle concentrations, (b) volumetric rates of charge-carrier production, re/h, (c) photovoltage, Vph, and (d) reaction overpotentials, ηOER/HER. | ||
In addition to the Q/QH2 redox shuttle, transient reactor performance was also evaluated for the IO3−/I− redox shuttle (Fig. S5, ESI†), which is also predicted to achieve baseline and up to 3.8% STH efficiency like the quinone redox shuttles (Table 3). With exceptions of the requirements of larger photovoltages from the HER semiconductor particles than with the Q/QH2 redox shuttle and the need for more alkaline conditions to favor conversion of I− to IO3− instead of strongly-visible-light-absorbing I3−, the results using this redox shuttle are promising. Sustained reactor operation at a 1% STH efficiency is achieved with redox shuttle concentrations well below their solubility limits even for 10 cm tall reactor compartments (see Fig. S5, ESI†), and Fig. S6 (ESI†) shows that diffusion-driven species transport is able to sustain reactor operation at 3.8% STH efficiency with 1 cm tall reaction compartments for the IO3−/I− redox shuttle. The mass-transfer overpotential due to the redox species concentration gradients has a maximum of 11 mV for the 10 cm tall reaction compartments during steady-periodic operation.
For the strongly-visible-light-absorbing I3−/I− and Fe3+/Fe2+ redox shuttles, because concentrations less than 5 mM are required to minimize the impacts of competitive light absorption, diffusion distances less than 0.01 cm are needed to sustain the reaction rates corresponding to the baseline STH efficiency of 1%. However, this short distance implies that impractically large semiconductor particle concentrations, i.e. >10 g L−1, are required to achieve the required optical thicknesses reported in Table 3. Moreover, reactor heights on the sub-mm lengthscale will be extremely challenging to fabricate and to prevent bubble occlusion. For taller reaction compartments, h > 0.01 cm, the diffusion-sustained STH efficiencies are restricted to less than 0.2% due to competitive light absorption by I3− and Fe3+ redox species, as suggested by Fig. S7 (ESI†). Because these redox shuttles are not modeled to undergo proton-coupled electron-transfer, spatial gradients in pH and the redox shuttle species concentration gradients result in mass-transfer-related overpotentials. However, at low STH efficiencies of 0.2%, these overpotentials are less than 1 mV. These results indicate that reactor heights on the lengthscales of centimeters are best to achieve the 1% baseline STH efficiency for the I3−/I− and Fe3+/Fe2+, provided that some form of active species mixing is possible.
Effects of competitive surface reactions
The above analysis assumed perfectly selective reactions without considering the overpotentials for the undesired back reactions. Fig. 7 shows the impacts of the redox shuttle kinetic parameters for Q/QH2 on the competing back reactions of redox chemistry with the redox shuttle species. The effective reaction rates (Reff, eqn (9)) for HER/Rox and OER/Rred are normalized with the baseline rates obtained in Fig. 6, which assumed selective surface catalysis. The overpotential for oxidation of liberated H2 by holes in the valence band for the HER particles is large (>1.23 V), and the models predict very rapid hydrogen oxidation, so much so that in the absence of active removal of H2 or asymmetric charge transfer coefficients for the HER there is no net desired H2 formation (data not shown). For all exchange current densities investigated for the redox shuttle, symmetric charge-transfer coefficients (αa,sh = αc,sh = 0.5) resulted in net rates that were zero. Fig. 7(a) suggests that for asymmetric charge-transfer coefficients there is an optimum redox shuttle exchange current density to maximize the resultant surface reaction rate in the presence of back reactions of the redox shuttle, in this case, the reduction of Q. The contending effects are that an increase in the exchange current density reduces the overpotential for the oxidation (QH2 to Q) and thereby, intensifies the driving force for the reduction reaction, which acts as a recombination pathway shunt. For smaller exchange current densities, the overpotential increases for the oxidation reaction, and shifts the photovoltage closer to the open-circuit potential of the photodiode, which diminishes the reaction rate. With increase in the anodic charge transfer coefficient, αa,sh, the oxidation of QH2 is favored more than the reduction of Q, and therefore the resultant reaction rates increase. The highest predicted rate for the case of αa,sh = 0.9 with the selected concentration ratio is at least 15% smaller than the baseline reaction rate without competing surface reactions.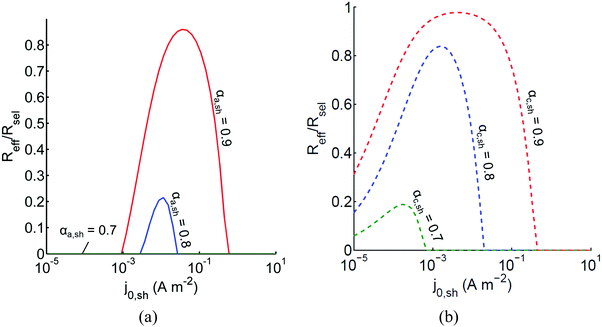 | ||
Fig. 7 Effective redox shuttle reaction rates, Reff, normalized to the baseline reaction rate, Rsel,k, that assumed selective catalysis, as a function of kinetic parameters (j0,sh, αa,sh and αc,sh = 1 − αa,sh) for h = 1 cm with the Q/QH2 redox shuttle at concentration ratios that are consistent with the steady-periodic results from Fig. 5 (i.e.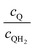 equals 2.56 and 0.44 in the HER (top) and the OER (bottom) compartments respectively) for (a) SrTiO3:Rh (top, HER) and (b) BiVO4 (bottom, OER) particles. equals 2.56 and 0.44 in the HER (top) and the OER (bottom) compartments respectively) for (a) SrTiO3:Rh (top, HER) and (b) BiVO4 (bottom, OER) particles. | ||
Oxygen reduction using the OER particles is much more challenging than H2 oxidation using the HER particles owing to the relatively low cathodic transfer coefficient to effect the oxygen reduction reaction (αc,OER = 0.1 compared to αa,OER = 127,72,73). The resultant reaction rates change by less than 3% when back reactions with dissolved O2 are taken into account, and therefore, those results are indistinguishable from the results shown in Fig. 7(b). Similar to the HER particles, symmetric charge transfer coefficients result in no net desired reactions and an optimum exchange current density arises due to the tradeoffs in decreasing the overpotential of the desired reaction (Rred in this case) for larger values of j0,sh and operating near the open-circuit potential of the modeled photodiode when the exchange current density is low. The optimum exchange current densities are in general lower compared to those of the HER particles for all cases considered, and the highest reaction rate for the case of αc,sh = 0.9 is only 2% lower than the baseline reaction rate. These contrasting effects are due to the relatively larger open-circuit photovoltage modeled for the BiVO4 particles than in the SrTiO3:Rh particles of 1.06 V versus 0.88 V, respectively. Fig. 7 is suggestive that redox shuttles with asymmetric charge-transfer coefficients and small exchange current densities (typically <1 A m−2) are likely to result in larger STH efficiencies.
Fig. 8 shows the variations in the effective OER/Rred and HER/Rox reaction rates normalized to the baseline reaction rates as the ratio of the concentrations of the oxidized and reduced forms of the redox shuttle, 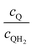 , changes from 0.1 to 10. The concentration ratio affects the driving force for the redox shuttle reactions via the Nernst equation such that larger driving forces result in faster reactions. The optimum exchange current density decreases as the concentration ratio is modified such that it favors the desired reactions by reducing the reaction overpotentials (decreased/increased redox shuttle concentration ratio for the HER/OER particles, respectively).
, changes from 0.1 to 10. The concentration ratio affects the driving force for the redox shuttle reactions via the Nernst equation such that larger driving forces result in faster reactions. The optimum exchange current density decreases as the concentration ratio is modified such that it favors the desired reactions by reducing the reaction overpotentials (decreased/increased redox shuttle concentration ratio for the HER/OER particles, respectively).
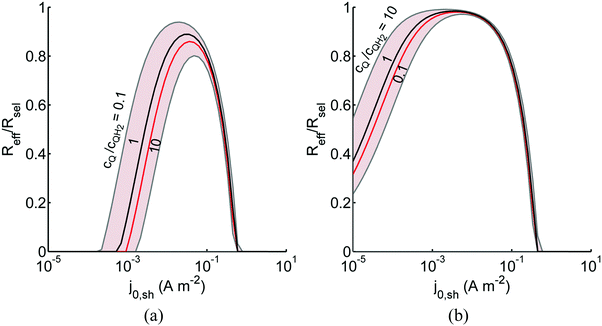 | ||
Fig. 8 Effective redox shuttle reaction rates normalized to the baseline reaction rate, Rsel,k, that assumed selective catalysis as a function of the exchange current density (j0,sh) and the concentration ratio of the Q/QH2 redox shuttle (cQ/cQH2) for h = 1 cm with (a) SrTiO3:Rh (top, HER), αa,sh, αc,sh = 0.9, 0.1, and (b) BiVO4 (bottom, OER), αa,sh, αc,sh = 0.1, 0.9 particles. The solid red line corresponds to values of 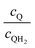 consistent with steady-periodic results in Fig. 5 with (a) consistent with steady-periodic results in Fig. 5 with (a) 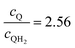 and (b) and (b) 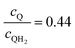 . . | ||
Comparison with fixed-electrode PEC designs
An important aspect of the particle-suspension reactor is that local currents between sites of anodic (holes) and cathodic (electrons) reactions are very small, even for efficient designs that generate O2 and H2 at a rate consistent with the benchmark current density for an efficient solar water splitting device of 20 mA cm−2. This is because these reaction rates are distributed over the height of the compartment such that on average the rates are consistent with a current density of 20/n mA cm−2, for a reactor with n particles in the optical pathlength to attain the benchmark current density. For the particles modeled in this study the current densities were at most 20 μA cm−2 particle−1, which results in a reaction rate expressed as an effective volumetric current density of 250 attoA per particle. These calculations assumed 1 cm tall reaction compartments, a maximum particle concentration of 5 g L−1 and dp = 100 nm. One benefit of the small local currents present in particle-suspension reactors is that it results in negligibly low ohmic potential losses in the solution. For a single semiconductor particle with radius of 100 nm to at most several microns, the ohmic potential drop due to migration of ions between the sites of anodic and cathodic reactions is expected to be negligibly small (<1 mV), even when using water with little-to-no supporting electrolyte and redox shuttles.20 However, ionic migration over the small lengthscales of individual particles makes separation of the anodic and cathodic reactions on their surfaces nearly impossible, meaning that incorporation of a membrane between those sites becomes challenging. Therefore, highly selective particle reactivity, as shown in Fig. 7, is required to achieve large efficiencies. This is in contrast to the fixed-electrode PEC designs where membrane separators are common and the device dimensions, including species transport lengthscales and operating conditions, must be carefully optimized to minimize the ohmic potential drop and the overall solution transport losses, often to a target value of less than 100 mV.28,31Another benefit of the small local currents present in efficient particle-suspension reactors is that near-neutral pH conditions can be used, yet, little-to-no variation in the local pH is generated during operation on the surface of an individual particle. Changes in local pH are detrimental to device efficiency because they result in potential losses, as described in eqn (19). This is in stark contrast to the fixed-electrode designs that are incorporated with membranes, where local pH gradients are much more likely to be generated, especially at near-neutral pH conditions. Even for pH 1 electrolytes the pH gradient potential loss is roughly 70 mV for a fixed-electrode PEC device operating at a 10% STH efficiency.31
Even in the absence of a local pH gradient on the particle surface, there are potential losses due to pH gradients between the OER compartment and the HER compartment in the particle-suspension reactor designs. These losses are anticipated to be similar in magnitude to those observed in fixed-electrode designs. An approximately 60 mV pH gradient loss was evaluated for a hypothetical simulation case operating at 10% STH efficiency and using the I3−/I− redox shuttle. The pH losses are however nearly zero for redox shuttles that undergo rapid proton-coupled electron-transfer. Also, in the particle-suspension reactor designs, additional potential losses occur due to redox shuttle concentration gradients, the magnitude of which depends greatly on the diffusion lengthscales in the absence of active mixing. Shorter compartment heights facilitate rapid mass transport and decrease this loss, but require a concomitant increase in the concentrations of semiconductor particles to maintain the same performance. These losses are not present in fixed-electrode PEC designs.
A related aspect to the small local currents is that particle-suspension reactors facilitate volumetric, three-dimensional reactivity in comparison to the fixed-electrode, wafer-based PEC device designs that drive areal, interfacial activity. In the suspension reactors, the overall reaction rates are distributed throughout the active semiconductor particle surface sites, behavior that is similar to mesoporous electrodes93,94 and microwire/nanowire array designs.95–97 This redistribution of the charge carriers and reaction sites reduces the charge-carrier flux to the surface and lowers the reaction overpotentials at any point location. Similar to other micro-structured and nano-structured PEC designs, the high specific-surface areas of the suspended semiconductor particles can enhance the redox-active surface area per unit sunlight collection area compared to the fixed electrode devices and increase efficiency and scalability, assuming that recombination rates are not limited by surface processes. If surface or near-surface sites facilitate recombination, then the benefit of low electrocatalytic rates is at least in part negated by lower observed photovoltages.98 Finally, particle-suspension reactors can tolerate particle failure (e.g., due to corrosion), because it may not impact other particles to cause a catastrophic failure in the entire device. This is not the case in many fixed-electrode designs where impurities or surface oxides introduce detrimental recombination centers, even at very low concentrations, which then affect the efficacy of charge carriers over a much larger area than just the size (cross-section) of the recombination center.
Conclusion
For the first time, the combined effects of device design, and choice and concentrations of semiconductor particles and redox shuttles were numerically evaluated to understand their effects on the overall performance of a vertically stacked, particle-suspension reactor with soluble redox shuttles implementing Z-scheme solar water splitting. The feature that distinguishes the proposed reactor design from prior work is that the compartments effecting the OER and the HER were optically in series, which facilitated tandem light absorption and larger possible STH efficiencies. A transient, two-dimensional reactor model was developed to identify the reaction compartment heights and the operating conditions to achieve sustained reactor operation at 1% STH, facilitated by only diffusion. The volumetric rates of H2 and O2 generation in the reaction compartments were evaluated by coupling the photodiode (photo)current–voltage relationship with Butler–Volmer electron transfer kinetics, and taking into account volumetric light absorption and recombination effects in the suspension. The two materials options that were considered for the OER semiconductor particles were TiO2 and BiVO4, while SrTiO3:Rh was the HER semiconductor particle for all cases. The redox shuttles investigated included I3−/I−, Fe3+/Fe2+, IO3−/I−, and Q/QH2, with the last two modeled as proton-coupled electron transfer redox reactions.The optical thickness of the semiconductor particles, which is proportional to particle concentration and absorption cross-section, and reaction compartment height, emerges as an important dimensionless parameter, and was optimized specific to the redox shuttle considered to attain the desired STH efficiency. Results illustrated that amongst the redox shuttles considered, Q/QH2 and IO3−/I− are more promising than I3−/I− and Fe3+/Fe2+ owing to substantial visible light absorption by I3− and Fe3+ redox species. Competitive light absorption by the I3− and Fe3+ redox species restricts their concentrations to 5 mM, to attain 1% STH efficiency, requiring small reaction compartment heights and subsequently unrealistically high particle concentrations. OER semiconducting particles consisting of BiVO4 outperformed those consisting of TiO2, and were projected to achieve STH efficiencies of 3.8% and 1.7% respectively with the Q/QH2 and IO3−/I− redox shuttles. Species transport is dominated by diffusion over migration for all the reaction compartment heights considered, and purely diffusion driven for the neutral, proton-coupled-electron-transfer quinone redox shuttles. The baseline STH efficiency and steady-periodic reactor operation was attained within the first five days of operation for 1 cm tall reaction compartments with 2.12/1.53 mg L−1 of BiVO4/SrTiO3:Rh particles for the Q/QH2 redox shuttles. Because of the drawback of a low aqueous solubility for p-benzoquinone, the quinone redox shuttle is not anticipated to sustain larger STH efficiencies. On the other hand, the IO3−/I− redox shuttles achieved sustainable baseline STH efficiency while maintaining concentrations below their solubility limits even for 10 cm tall reaction compartments. These model predictions assumed that the HER particles generated photovoltages larger than 1.04 V, which poses both challenges and great opportunities for continued research into these HER semiconducting materials. For both these proton-coupled electron transfer redox shuttles potential losses due to pH gradients are absent, and the species concentration gradients yield a maximum mass-transfer overpotential of 35 mV and 11 mV with the Q/QH2 and IO3−/I− redox shuttles for 10 cm tall reaction compartments.
In the particle-suspension reactor designs, a fixed areal reaction rate or current density of H2 generation is divided into much smaller localized anodic and cathodic reaction rates (current densities) as compared to the fixed-electrode counterparts, which results in negligible ohmic/migration potential losses. However, this attribute also poses challenges for placement of membranes between the reaction sites, making selective surface catalysis a crucial requirement for improving the efficiency of these reactor designs. Facile/reversible redox shuttles with symmetric charge transfer coefficients and large exchange current densities lead to large rates for shunting reactions. Asymmetric charge transfer coefficients and optimal exchange current densities for the redox shuttle are required to suppress these undesired back reactions.
In summary, the proposed reactor design is projected to sustain at least a 1% STH efficiency with BiVO4 and SrTiO3:Rh photocatalyst particles, aided by diffusive transport of Q/QH2 and IO3−/I− redox shuttles; the latter redox shuttle exhibits promise of achieving STH efficiencies up to 3.8%. While the model was applied to consider specific photocatalyst materials and redox shuttles, the model formulation is general and can be widely applied for any material and redox shuttle of interest. The effects of particle size and detailed particle-scale photophysics, and natural convection induced species mixing on the overall reactor performance were not considered in this study, but we anticipate that they will be influential parameters to be considered in future work.
Conflicts of interest
There are no conflicts of interest to declare for the work presented in this manuscript.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Incubator Program under Award No. DE-EE0006963 and Lawrence Berkeley National Laboratory under Contract No. DE-AC02-05CH11231. We cordially thank Dr Chengxiang Xiang at the Joint Center for Artificial Photosynthesis at the California Institute of Technology for providing critical insights and suggestions towards the model development. The authors also acknowledge inputs from colleagues at University of California, Irvine—Dr Houman Yaghoubi for providing current–voltage data for BiVO4 electrodes, and Mr William Gaieck and Mr Kevin Tkacz for obtaining spectroscopic measurements on the redox shuttles and the porous separators.References
- M. Grätzel, Photoelectrochemical cells, Nature, 2001, 414, 338–344, DOI:10.1038/35104607.
- N. S. Lewis and D. G. Nocera, Powering the planet: Chemical challenges in solar energy utilization, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735, DOI:10.1073/pnas.0603395103.
- N. S. Lewis, Research opportunities to advance solar energy utilization, Science, 2016, 351, aad1920, DOI:10.1126/science.aad1920.
- T. J. Jacobsson, V. Fjällström, M. Edoff and T. Edvinsson, Sustainable solar hydrogen production: from photoelectrochemical cells to PV-electrolyzers and back again, Energy Environ. Sci., 2014, 7, 2056, 10.1039/c4ee00754a.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, A comprehensive review on PEM water electrolysis, Int. J. Hydrogen Energy, 2013, 38, 4901–4934, DOI:10.1016/j.ijhydene.2013.01.151.
- M. Schreier, L. Curvat, F. Giordano, L. Steier, A. Abate and S. M. Zakeeruddin, et al., Efficient photosynthesis of carbon monoxide from CO2 using perovskite photovoltaics, Nat. Commun., 2015, 6, 7326, DOI:10.1038/ncomms8326.
- J. H. Montoya, L. C. Seitz, P. Chakthranont, A. Vojvodic, T. F. Jaramillo and J. K. Nørskov, Materials for solar fuels and chemicals, Nat. Mater., 2016, 16, 70–81, DOI:10.1038/nmat4778.
- C. Graves, S. D. Ebbesen, M. Mogensen and K. S. Lackner, Sustainable hydrocarbon fuels by recycling CO2 and H2O with renewable or nuclear energy, Renewable Sustainable Energy Rev., 2011, 15, 1–23, DOI:10.1016/j.rser.2010.07.014.
- C. L. Muhich, B. D. Ehrhart, I. Al-Shankiti, B. J. Ward, C. B. Musgrave and A. W. Weimer, A review and perspective of efficient hydrogen generation via solar thermal water splitting, Wiley Interdiscip. Rev.: Energy Environ., 2016, 5 DOI:10.1002/wene.174.
- B. J. Hathaway, R. Bala Chandran, A. C. Gladen, T. R. Chase and J. H. Davidson, Demonstration of a Solar Reactor for Carbon Dioxide Splitting via the Isothermal Ceria Redox Cycle and Practical Implications, Energy Fuels, 2016, 30, 6654–6661, DOI:10.1021/acs.energyfuels.6b01265.
- J. R. Bolton, Solar photoproduction of hydrogen: A review, Sol. Energy, 1996, 57, 37–50, DOI:10.1016/0038-092X(96)00032-1.
- J. W. Ager III, M. Shaner, K. Walczak, I. D. Sharp and S. Ardo, Experimental Demonstrations of Spontaneous, Solar-Driven Photoelectrochemical Water Splitting, Energy Environ. Sci., 2015, 8, 2811–2824, 10.1039/C5EE00457H.
- R. L. House, N. Y. M. Iha, R. L. Coppo, L. Alibabaei, B. D. Sherman and P. Kang, et al., Artificial photosynthesis: Where are we now? Where can we go?, J. Photochem. Photobiol., C, 2015, 25, 32–45, DOI:10.1016/j.jphotochemrev.2015.08.002.
- M. A. Modestino and S. Haussener, An Integrated Device View on Photo-Electrochemical Solar-Hydrogen Generation, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 13–34, DOI:10.1146/annurev-chembioeng-061114-123357.
- C. Xiang, A. Z. Weber, S. Ardo, A. Berger, Y. Chen and R. Coridan, et al., Modeling, Simulation, and Implementation of Solar-Driven Water-Splitting Devices, Angew. Chem., Int. Ed., 2016, 55, 12974–12988, DOI:10.1002/anie.201510463.
- A. Fujishima and K. Honda, Electrochemical Photolysis of Water at a Semiconductor Electrode, Nature, 1972, 238, 37–38, DOI:10.1038/238037a0.
- K. Maeda, K. Teramura, D. Lu, T. Takata, N. Saito and Y. Inoue, et al., Photocatalyst releasing hydrogen from water, Nature, 2006, 440, 295, DOI:10.1038/440295a.
- K. Maeda and K. Domen, Photocatalytic Water Splitting: Recent Progress and Future Challenges, J. Phys. Chem. Lett., 2010, 1, 2655–2661, DOI:10.1021/jz1007966.
- F. E. Osterloh, Boosting the Efficiency of Suspended Photocatalysts for Overall Water Splitting, J. Phys. Chem. Lett., 2014, 5, 2510–2511, DOI:10.1021/jz501342j.
- D. M. Fabian, S. Hu, N. Singh, F. A. Houle, T. Hisatomi and K. Domen, et al., Particle suspension reactors and materials for solar-driven water splitting, Energy Environ. Sci., 2015, 8, 2825–2850, 10.1039/C5EE01434D.
- O. Khaselev, High-efficiency integrated multijunction photovoltaic/electrolysis systems for hydrogen production, Int. J. Hydrogen Energy, 2001, 26, 127–132, DOI:10.1016/S0360-3199(00)00039-2.
- S. Y. Reece, J. A. Hamel, K. Sung, T. D. Jarvi, A. J. Esswein and J. J. H. Pijpers, et al., Wireless Solar Water Splitting Using Silicon-Based Semiconductors and Earth-Abundant Catalysts, Science, 2011, 334, 645–648, DOI:10.1126/science.1209816.
- K. Walczak, Y. Chen, C. Karp, J. W. Beeman, M. Shaner and J. Spurgeon, et al., Modeling, Simulation, and Fabrication of a Fully Integrated, Acid-stable, Scalable Solar-Driven Water-Splitting System, ChemSusChem, 2015, 8, 544–551, DOI:10.1002/cssc.201402896.
- M. A. Modestino, K. A. Walczak, A. Berger, C. M. Evans, S. Haussener and C. Koval, et al., Robust production of purified H 2 in a stable, self-regulating, and continuously operating solar fuel generator, Energy Environ. Sci., 2014, 7, 297–301, 10.1039/C3EE43214A.
- S. Licht, B. Wang, S. Mukerji, T. Soga, M. Umeno and H. Tributsch, Over 18% solar energy conversion to generation of hydrogen fuel; theory and experiment for efficient solar water splitting, Int. J. Hydrogen Energy, 2001, 26, 653–659, DOI:10.1016/S0360-3199(00)00133-6.
- J. Jia, L. C. Seitz, J. D. Benck, Y. Huo, Y. Chen and J. W. D. Ng, et al., Solar water splitting by photovoltaic-electrolysis with a solar-to-hydrogen efficiency over 30%, Nat. Commun., 2016, 7, 13237, DOI:10.1038/ncomms13237.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, An analysis of the optimal band gaps of light absorbers in integrated tandem photoelectrochemical water-splitting systems, Energy Environ. Sci., 2013, 6, 2984, 10.1039/c3ee40453f.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Modeling, simulation, and design criteria for photoelectrochemical water-splitting systems, Energy Environ. Sci., 2012, 5, 9922, 10.1039/c2ee23187e.
- S. Haussener, S. Hu, C. Xiang, A. Z. Weber and N. S. Lewis, Simulations of the irradiation and temperature dependence of the efficiency of tandem photoelectrochemical water-splitting systems, Energy Environ. Sci., 2013, 6, 3605, 10.1039/c3ee41302k.
- C. Xiang, Y. Chen and N. S. Lewis, Modeling an integrated photoelectrolysis system sustained by water vapor, Energy Environ. Sci., 2013, 6, 3713, 10.1039/c3ee42143k.
- M. R. Singh, K. Papadantonakis, C. Xiang and N. S. Lewis, An electrochemical engineering assessment of the operational conditions and constraints for solar-driven water-splitting systems at near-neutral pH, Energy Environ. Sci., 2015, 8, 2760–2767, 10.1039/C5EE01721A.
- J. C. Stevens and A. Z. Weber, A Computational Study of Optically Concentrating, Solar-Fuels Generators from Annual Thermal- and Fuel-Production Efficiency Perspectives, J. Electrochem. Soc., 2016, 163, H475–H484, DOI:10.1149/2.0121607jes.
- Y. Surendranath, D. K. Bediako and D. G. Nocera, Interplay of oxygen-evolution kinetics and photovoltaic power curves on the construction of artificial leaves, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15617–15621, DOI:10.1073/pnas.1118341109.
- S. Tembhurne and S. Haussener, Integrated Photo-Electrochemical Solar Fuel Generators under Concentrated Irradiation, J. Electrochem. Soc., 2016, 163, H988–H998, DOI:10.1149/2.0311610jes.
- B. D. James, G. N. Baum, J. Perez and K. N. Baum, Technoeconomic Analysis of Photoelectrochemical (PEC) Hydrogen Production, Virginia, 2009, http://energy.gov/eere/fuelcells/downloads/technoeconomic-analysis-photoelectrochemical-pec-hydrogen-production.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen and T. G. Deutsch, et al., Technical and economic feasibility of centralized facilities for solar hydrogen production via photocatalysis and photoelectrochemistry, Energy Environ. Sci., 2013, 6, 1983, 10.1039/c3ee40831k.
- M. R. Shaner, H. A. Atwater, N. S. Lewis and E. W. McFarland, A comparative technoeconomic analysis of renewable hydrogen production using solar energy, Energy Environ. Sci., 2016, 9, 2354–2371, 10.1039/C5EE02573G.
- Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome, M. Zhong and C. Wang, et al., Scalable water splitting on particulate photocatalyst sheets with a solar-to-hydrogen energy conversion efficiency exceeding 1%, Nat. Mater., 2016, 15, 611–615, DOI:10.1038/nmat4589.
- Q. Wang, T. Hisatomi, Y. Suzuki, Z. Pan, J. Seo and M. Katayama, et al., Particulate Photocatalyst Sheets Based on Carbon Conductor Layer for Efficient Z-Scheme Pure-Water Splitting at Ambient Pressure, J. Am. Chem. Soc., 2017, 139, 1675–1683, DOI:10.1021/jacs.6b12164.
- K. Sayama, K. Mukasa, R. Abe, Y. Abe and H. Arakawa, Stoichiometric water splitting into H2 and O2 using a mixture of two different photocatalysts and an IO3−/I− shuttle redox mediator under visible light irradiation, Chem. Commun., 2001, 2416–2417, 10.1039/b107673f.
- Y. Miseki, S. Fujiyoshi, T. Gunji and K. Sayama, Photocatalytic water splitting under visible light utilizing I3−/I− and IO3−/I− redox mediators by Z-scheme system using surface treated PtOx/WO3 as O2 evolution photocatalyst, Catal. Sci. Technol., 2013, 3, 1750, 10.1039/c3cy00055a.
- R. Abe, T. Takata, H. Sugihara and K. Domen, Photocatalytic overall water splitting under visible light by TaON and WO3 with an IO3−/I− shuttle redox mediator, Chem. Commun., 2005, 3829–3831, 10.1039/b505646b.
- K. Maeda, M. Higashi, D. Lu, R. Abe and K. Domen, Efficient nonsacrificial water splitting through two-step photoexcitation by visible light using a modified oxynitride as a hydrogen evolution photocatalyst, J. Am. Chem. Soc., 2010, 132, 5858–5868, DOI:10.1021/ja1009025.
- S.-C. Yu, C.-W. Huang, C.-H. Liao, J. C. S. Wu, S.-T. Chang and K.-H. Chen, A novel membrane reactor for separating hydrogen and oxygen in photocatalytic water splitting, J. Membr. Sci., 2011, 382, 291–299, DOI:10.1016/j.memsci.2011.08.022.
- C.-C. Lo, C.-W. Huang, C.-H. Liao and J. C. S. Wu, Novel twin reactor for separate evolution of hydrogen and oxygen in photocatalytic water splitting, Int. J. Hydrogen Energy, 2010, 35, 1523–1529, DOI:10.1016/j.ijhydene.2009.12.032.
- K. Maeda, Rhodium-Doped Barium Titanate Perovskite as a Stable p-Type Semiconductor Photocatalyst for Hydrogen Evolution under Visible Light, ACS Appl. Mater. Interfaces, 2014, 6, 2167–2173, DOI:10.1021/am405293e.
- H. Suzuki, O. Tomita, M. Higashi and R. Abe, Two-step photocatalytic water splitting into H2 and O2 using layered metal oxide KCa2Nb3O10 and its derivatives as O2-evolving photocatalysts with IO3−/I− or Fe3+/Fe2+ redox mediator, Catal. Sci. Technol., 2015, 5, 2640–2648, 10.1039/C5CY00128E.
- H. Kato, Y. Sasaki, N. Shirakura and A. Kudo, Synthesis of highly active rhodium-doped SrTiO3 powders in Z-scheme systems for visible-light-driven photocatalytic overall water splitting, J. Mater. Chem. A, 2013, 1, 12327, 10.1039/c3ta12803b.
- R. Abe, K. Sayama and H. Arakawa, Significant effect of iodide addition on water splitting into H2 and O2 over Pt-loaded TiO2 photocatalyst: suppression of backward reaction, Chem. Phys. Lett., 2003, 371, 360–364, DOI:10.1016/S0009-2614(03)00252-5.
- Y. Sasaki, A. Iwase, H. Kato and A. Kudo, The effect of co-catalyst for Z-scheme photocatalysis systems with an Fe3+/Fe2+ electron mediator on overall water splitting under visible light irradiation, J. Catal., 2008, 259, 133–137, DOI:10.1016/j.jcat.2008.07.017.
- Q. Wang, T. Hisatomi, S. S. K. Ma, Y. Li and K. Domen, Core/Shell Structured La- and Rh-Codoped SrTiO3 as a Hydrogen Evolution Photocatalyst in Z-Scheme Overall Water Splitting under Visible Light Irradiation, Chem. Mater., 2014, 26, 4144–4150, DOI:10.1021/cm5011983.
- R. R. Jaini and T. F. Fuller, Overcoming mass-transfer limitations in the Dual Bed Colloidal Suspension Reactor, Int. J. Hydrogen Energy, 2014, 39, 2462–2471, DOI:10.1016/j.ijhydene.2013.12.018.
- R. J. Brandi, O. M. Alfano and A. E. Cassano, Evaluation of Radiation Absorption in Slurry Photocatalytic Reactors. 1. Assessment of Methods in Use and New Proposal, Environ. Sci. Technol., 2000, 34, 2623–2630, DOI:10.1021/es9909428.
- A. Busciglio, O. M. Alfano, F. Scargiali and A. Brucato, A probabilistic approach to radiant field modeling in dense particulate systems, Chem. Eng. Sci., 2015, 142, 79–88, DOI:10.1016/j.ces.2015.11.025.
- M. L. Satuf, R. J. Brandi, A. E. Cassano and O. M. Alfano, Experimental Method to Evaluate the Optical Properties of Aqueous Titanium Dioxide Suspensions, Ind. Eng. Chem. Res., 2005, 44, 6643–6649, DOI:10.1021/ie050365y.
- M. de los M. Ballari, R. Brandi, O. Alfano and A. Cassano, Mass transfer limitations in photocatalytic reactors employing titanium dioxide suspensions: II. External and internal particle constrains for the reaction, Chem. Eng. J., 2008, 136, 242–255, DOI:10.1016/j.cej.2007.03.031.
- A. E. Cassano and O. M. Alfano, Reaction engineering of suspended solid heterogeneous photocatalytic reactors, Catal. Today, 2000, 58, 167–197, DOI:10.1016/S0920-5861(00)00251-0.
- H. Li, W. Tu, Y. Zhou and Z. Zou, Z-Scheme Photocatalytic Systems for Promoting Photocatalytic Performance: Recent Progress and Future Challenges, Adv. Sci., 2016, 1500389, DOI:10.1002/advs.201500389.
- R. M. Navarro, F. del Valle, J. A. Villoria de la Mano, M. C. Álvarez-Galván and J. L. G. Fierro, Advances in Chemical Engineering – Photocatalytic Technologies, Elsevier, 2009 DOI:10.1016/S0065-2377(09)00404-9.
- Y. Xu and M. A. A. Schoonen, The absolute energy positions of conduction and valence bands of selected semiconducting minerals, Am. Mineral., 2000, 85, 543–556, DOI:10.2138/am-2000-0416.
- Y. Park, K. J. McDonald and K.-S. Choi, Progress in bismuth vanadate photoanodes for use in solar water oxidation, Chem. Soc. Rev., 2013, 42, 2321–2337, 10.1039/C2CS35260E.
- S. Xie, Q. Zhang, G. Liu and Y. Wang, Photocatalytic and photoelectrocatalytic reduction of CO2 using heterogeneous catalysts with controlled nanostructures, Chem. Commun., 2016, 52, 35–59, 10.1039/C5CC07613G.
- R. Asai, H. Nemoto, Q. Jia, K. Saito, A. Iwase and A. Kudo, A visible light responsive rhodium and antimony-codoped SrTiO3 powdered photocatalyst loaded with an IrO2 cocatalyst for solar water splitting, Chem. Commun., 2014, 50, 2543, 10.1039/c3cc49279f.
- S. Kawasaki, K. Akagi, K. Nakatsuji, S. Yamamoto, I. Matsuda and Y. Harada, et al., Elucidation of Rh-Induced In-Gap States of Rh:SrTiO3 Visible-Light-Driven Photocatalyst by Soft X-ray Spectroscopy and First-Principles Calculations, J. Phys. Chem. C, 2012, 116, 24445–24448, DOI:10.1021/jp3082529.
- B. Modak and S. K. Ghosh, Enhancement of Visible Light Photocatalytic Activity of SrTiO3: A Hybrid Density Functional Study, J. Phys. Chem. C, 2015, 119, 23503–23514, DOI:10.1021/acs.jpcc.5b06667.
- D. Perrin, Dissociation constants of organic bases in aqueous solution, Butterworths, London, 1972, http://www.worldcat.org/title/dissociation-constants-of-organic-bases-in-aqueous-solution/oclc/878462380?referer=null&ht=edition, accessed July 27, 2017 Search PubMed.
- E. P. Serjeant and B. Dempsey, Ionisation constants of organic acids in aqueous solution, Pergamon Press, Oxford; New York, 1979, http://www.worldcat.org/title/ionisation-constants-of-organic-acids-in-aqueous-solution/oclc/4494248, accessed July 27, 2017 Search PubMed.
- Y. Miseki, H. Kusama, H. Sugihara and K. Sayama, Cs-Modified WO3 Photocatalyst Showing Efficient Solar Energy Conversion for O 2 Production and Fe(III) Ion Reduction under Visible Light, J. Phys. Chem. Lett., 2010, 1, 1196–1200, DOI:10.1021/jz100233w.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt and C. J. Galvin, et al., A metal-free organic–inorganic aqueous flow battery, Nature, 2014, 505, 195–198, DOI:10.1038/nature12909.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. K. Surya Prakash and S. R. Narayanan, An Inexpensive Aqueous Flow Battery for Large-Scale Electrical Energy Storage Based on Water-Soluble Organic Redox Couples, J. Electrochem. Soc., 2014, 161, A1371–A1380, DOI:10.1149/2.1001409jes.
- K. Lin, Q. Chen, M. R. Gerhardt, L. Tong, S. B. Kim and L. Eisenach, et al., Alkaline quinone flow battery, Science, 2015, 349, 1529–1532 CrossRef CAS PubMed.
- G. Lodi, E. Sivieri, A. De Battisti and S. Trasatti, Ruthenium dioxide-based film electrodes, J. Appl. Electrochem., 1978, 8, 135–143, DOI:10.1007/BF00617671.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135, 16977–16987, DOI:10.1021/ja407115p.
- S. Trasatti, Work function, electronegativity, and electrochemical behaviour of metals, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184, DOI:10.1016/S0022-0728(72)80485-6.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. Chatman, J. C. Peters and T. F. Jaramillo, Benchmarking HER and OER Electrocatalysts for Solar Water Splitting Devices, J. Am. Chem. Soc., 2015, 137, 4347–4357, DOI:10.1021/ja510442p.
- M. F. Modest, The Radiative Transfer Equation in Participating Media(RTE), Radiat. Heat Transf., Second, Academic Press, 2003, pp. 279–302 Search PubMed.
- M. I. Cabrera, O. M. Alfano and A. E. Cassano, Absorption and Scattering Coefficients of Titanium Dioxide Particulate Suspensions in Water, J. Phys. Chem., 1996, 100, 20043–20050, DOI:10.1021/jp962095q.
- J. Newman and K. E. Thomas-Alyea, Infinitely Dilute Solutions, Electrochemical Systems, John Wiley & Sons, Inc., Hoboken, NJ, USA, 3rd edn, 2004, pp. 271–289 Search PubMed.
- W. M. Haynes, Thermochemistry, Electrochemistry and Solution Chemistry, CRC Handbook of Chemistry and Physics, CRC Press, Baca Raton, 95th edn, 2014, pp. 154–190 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods Fundamentals and Applications, John Wiley & Sons, Inc., 2001 Search PubMed.
- ASTM, Reference Solar Spectral Irradiance: Air Mass 1.5, http://rredc.nrel.gov/solar/spectra/am1.5/.
- NREL, National Solar Radiation Data Base, 1991–2005 Update: Typical Meteorological Year 3, http://rredc.nrel.gov/solar/old_data/nsrdb/1991-2005/tmy3/.
- G. M. Hale and M. R. Querry, Optical Constants of Water in the 200 nm to 200 μm Wavelength Region, Appl. Opt., 1973, 12, 555, DOI:10.1364/AO.12.000555.
- V. Sivakumar, R. Suresh, K. Giribabu and V. Narayanan, BiVO4 nanoparticles: Preparation, characterization and photocatalytic activity, Cogent Chem., 2015, 1, 1074647, DOI:10.1080/23312009.2015.1074647.
- R. O. Rahn, M. I. Stefan, J. R. Bolton, E. Goren, P.-S. Shaw and K. R. Lykke, Quantum yield of the iodide-iodate chemical actinometer: dependence on wavelength and concentrations, Photochem. Photobiol., 2003, 78, 146–152 CrossRef CAS PubMed , http://www.ncbi.nlm.nih.gov/pubmed/12945582, accessed June 29, 2016.
- M. Huwiler and H. Kohler, Pseudo-catalytic degradation of hydrogen peroxide in the lactoperoxidase/H2O2/iodide system, Eur. J. Biochem., 1984, 141, 69–74, DOI:10.1111/j.1432-1033.1984.tb08158.x.
- V. Talrose, A. N. Yermakov, A. A. Usov, A. A. Goncharova, A. N. Leskin and N. A. Messineva, et al., in UV/Visible Spectra, ed. P. J. Linstrom and W. G. Mallard, NIST Chem. WebBook, NIST Stand. Ref. Database Number 69, Gaithersburg, http://webbook.nist.gov, accessed June 2017 Search PubMed.
- M. R. Shaner, K. T. Fountaine and H.-J. Lewerenz, Current-voltage characteristics of coupled photodiode-electrocatalyst devices, Appl. Phys. Lett., 2013, 103, 143905, DOI:10.1063/1.4822179.
- M. X. Tan, P. E. Laibinis, S. T. Nguyen, J. M. Kesselman, C. E. Stanton and N. S. Lewis, in Principles and Applications of Semiconductor Photoelectrochemistry, ed. K. D. Karlin, Prog. Inorg. Chem., John Wiley & Sons, Inc., Hoboken, 1984, vol. 41, pp. 21–144 DOI:10.1002/9780470166420.ch2.
- T. Markvart and P. T. Landsberg, Thermodynamics and reciprocity of solar energy conversion, Phys. E, 2002, 14, 71–77, DOI:10.1016/S1386-9477(02)00352-1.
- J. Newman and K. E. Thomas-Alyea, Electrode Kinetics, Electrochem. Syst., John Wiley & Sons, Inc., Hoboken, NJ, USA, 3rd edn, 2004, pp. 203–230 Search PubMed.
- Comsol Inc., Comsol Multiphysics 5.2, 2015.
- M. Grätzel, U. Bach, D. Lupo, P. Comte, J. E. Moser and F. Weissörtel, et al., Solid-state dye-sensitized mesoporous TiO2 solar cells with high photon-to-electron conversion efficiencies, Nature, 1998, 395, 583–585, DOI:10.1038/26936.
- A. Kay, I. Cesar and M. Grätzel, New Benchmark for Water Photooxidation by Nanostructured α-Fe2O3 Films, J. Am. Chem. Soc., 2006, 128, 15714–15721, DOI:10.1021/ja064380l.
- J. M. Spurgeon, M. G. Walter, J. Zhou, P. A. Kohl, N. S. Lewis and E. L. Warren, et al., Electrical conductivity, ionic conductivity, optical absorption, and gas separation properties of ionically conductive polymer membranes embedded with Si microwire arrays, Energy Environ. Sci., 2011, 4, 1772, 10.1039/c1ee01028j.
- E. L. Warren, S. W. Boettcher, M. G. Walter, H. A. Atwater and N. S. Lewis, pH-Independent, 520 mV Open-Circuit Voltages of Si/Methyl Viologen2+/+ Contacts Through Use of Radial n+ p-Si Junction Microwire Array Photoelectrodes, J. Phys. Chem. C, 2011, 115, 594–598, DOI:10.1021/jp109147p.
- C. Liu, J. Tang, H. M. Chen, B. Liu, P. Yang and A. Fully, Integrated Nanosystem of Semiconductor Nanowires for Direct Solar Water Splitting, Nano Lett., 2013, 13, 2989–2992, DOI:10.1021/nl401615t.
- D. V. Esposito, Y. Lee, H. Yoon, P. M. Haney, N. Y. Labrador and T. P. Moffat, et al., Deconvoluting the influences of 3D structure on the performance of photoelectrodes for solar-driven water splitting, Sustain, Energy Fuels, 2017, 1, 154–173, 10.1039/C6SE00073H.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee01360d |
| This journal is © The Royal Society of Chemistry 2018 |