DOI:
10.1039/C7DT01747B
(Paper)
Dalton Trans., 2017,
46, 8992-9009
CrIII as an alternative to RuII in metallo-supramolecular chemistry†
Received
12th May 2017
, Accepted 8th June 2017
First published on 27th June 2017
Abstract
Compared to divalent ruthenium coordination complexes, which are widely exploited as parts of multi-component photonic devices, optically active trivalent chromium complexes are under-represented in multi-metallic supramolecular architectures performing energy conversion mainly because of the tricky preparation of stable heteroleptic CrIII building blocks. We herein propose some improvements with the synthesis of a novel family of kinetically inert heteroleptic bis-terdentate mononuclear complexes, which can be incorporated into dinuclear rod-like dyads as a proof-of-concept. The mechanism and magnitude of intermetallic Cr⋯Cr communication have been unraveled by a combination of magnetic, photophysical and thermodynamic investigations. Alternated aromatic/alkyne connectors provided by Sonogashira coupling reactions emerge as the most efficient wires for long-distance communication between two chromium centres bridged by Janus-type back-to-back bis-terdentate receptors.
Introduction
Since the discovery of chromium by Louis Nicolas Vauquelin in 1798, chromium derivatives, particularly in their most stable oxidation state CrIII, have been widely studied for their catalytic,1–3 hole transfer ability in photo-cathodic solar cells,4,5 magnetic,6–12 and optical properties.13–15 The latter aspect culminated with the building of the first laser in 1960,16 which exploited the stimulated emission of electromagnetic radiation from the CrIII-centred excited levels found in ruby. Despite its appealing electronic properties, CrIII has been scarcely introduced into polymetallic supramolecular architectures working as photonic devices,17,18 whereas hundreds, if not thousands of sophisticated structures built with luminescent divalent ruthenium complexes have been designed and tested so far.19–24 The main reason for this sidelining can be found in the CrIII coordination chemistry, which somehow mirrors that of trivalent cobalt with the formation of kinetically inert complexes as exemplified by the very small rate constants found for ligand exchange (e.g., kH2O = 2.4 × 10−6 s−1 for [Cr(H2O)6]3+)25 and for hydrolysis (e.g., khydrolysis = 3.5 × 10−4 s−1 for cis-[Cr(ethylenediamine)2Cl2]+ under acidic conditions).26 Consequently, CrIII cannot be part of sophisticated multi-component self-assembly processes, in which structural self-healing under thermodynamic control is crucial.27 Some rare (but remarkable) exceptions arose with (i) the serendipitous crystallization by Winpenny and coworkers of poly-chromium wheels at high temperatures (210 °C to 400 °C) using thermally resistant ligands28–30 and (ii) the use of preformed chromium complexes working as inert partners for the preparation of hydroxo,31 oxalato,32,33–36 and cyano bridged architectures.7,9,37 In this context, post-modifications were recently shown to open novel pathways for the stepwise building of multi-metallic assemblies including inert ruthenium–polypyridine complexes38–40 or platinum–salen derivatives,41,42 but the manipulation of related CrIII–polypyridine entities remains scarce and elusive.43–45 Moreover, recent demonstration that [Cr(2,2′:6′,2′′-terpyridine)2]3+ (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cr(tpy)2]3+) complexes rapidly dissociate under slightly alkaline conditions,46 a trend which confirms a previous observation reported for [Cr(2,2′-bipyridine)3]3+ (
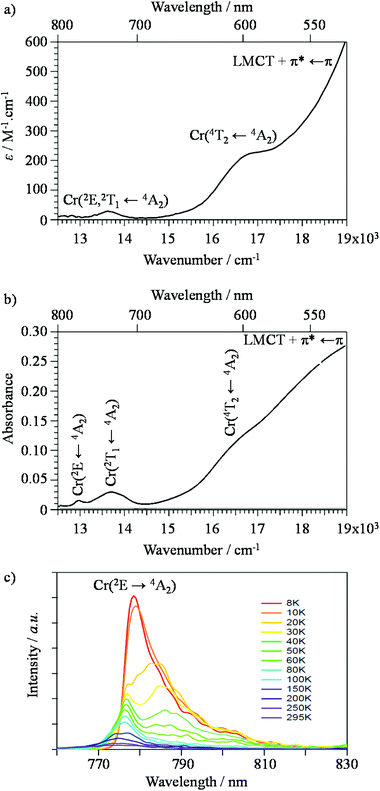
[Cr(tpy)2]3+) complexes rapidly dissociate under slightly alkaline conditions,46 a trend which confirms a previous observation reported for [Cr(2,2′-bipyridine)3]3+ (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cr(bpy)3]3+),47 prevents post-treatment of these complexes for the design of organized polynuclear assemblies. To the best of our knowledge, trivalent chromium has thus never been used as a partner for thermodynamic multi-component self-assembly processes occurring in solution, but its labile divalent precursor CrII was shown to successfully promote the synthesis of heterometallic d–f triple-stranded helicates under thermodynamic control.48,49 Subsequent air oxidation led to inert luminescent CrIII sensitizers, which induced unprecedented lanthanide-centred molecular energy-transfer upconversion.50–53 Last but not least, the characterization of CrIII complexes in solution is severely hampered by the broad and poorly interpretable NMR signals produced by the long electronic relaxation times (about 0.5 ns) of their zero-field split Cr(4A2) ground state.54 This drawback is overcome for diamagnetic RuII complexes, which were thus selected for building well-defined photoactive polynuclear architectures useful for water splitting,55 light-harvesting and energy conversion.56–58 Nevertheless, while trivalent chromium exhibits some shortcomings compared to divalent ruthenium, its photophysical properties in pseudo-octahedral complexes offer some unparalleled attractiveness since the visible window is dominated by a single spin-allowed absorption band corresponding to the Cr(4T2 ← 4A2) transition, the energy of which can be easily tuned by the ligand-field parameter Δ, whereas the near-infrared window is governed by efficient long-lived Cr(2E ← 4A2) phosphorescence, the energy of which is controlled by the nephelauxetic effect tuned by the Racah parameters B and C (Fig. 1).13,59,60 It is thus trivial to switch from low-energy absorption combined with high-energy phosphorescence found in CrO6 chromophores (small values of Δ and large values of B) toward the opposite situation found in CrN6 chromophores.13 Furthermore, the almost spin-only behavior combined with negligible zero-field splitting parameters measured for the degenerate paramagnetic Cr(4A2) ground state (for instance D = 0.03 cm−1 for [(tpy)CrCl3])61 offers a simple approach for unravelling electronic intermetallic communications via the estimation of the isotropic exchange coupling constant operating between chromium centres.10,12,62
[Cr(bpy)3]3+),47 prevents post-treatment of these complexes for the design of organized polynuclear assemblies. To the best of our knowledge, trivalent chromium has thus never been used as a partner for thermodynamic multi-component self-assembly processes occurring in solution, but its labile divalent precursor CrII was shown to successfully promote the synthesis of heterometallic d–f triple-stranded helicates under thermodynamic control.48,49 Subsequent air oxidation led to inert luminescent CrIII sensitizers, which induced unprecedented lanthanide-centred molecular energy-transfer upconversion.50–53 Last but not least, the characterization of CrIII complexes in solution is severely hampered by the broad and poorly interpretable NMR signals produced by the long electronic relaxation times (about 0.5 ns) of their zero-field split Cr(4A2) ground state.54 This drawback is overcome for diamagnetic RuII complexes, which were thus selected for building well-defined photoactive polynuclear architectures useful for water splitting,55 light-harvesting and energy conversion.56–58 Nevertheless, while trivalent chromium exhibits some shortcomings compared to divalent ruthenium, its photophysical properties in pseudo-octahedral complexes offer some unparalleled attractiveness since the visible window is dominated by a single spin-allowed absorption band corresponding to the Cr(4T2 ← 4A2) transition, the energy of which can be easily tuned by the ligand-field parameter Δ, whereas the near-infrared window is governed by efficient long-lived Cr(2E ← 4A2) phosphorescence, the energy of which is controlled by the nephelauxetic effect tuned by the Racah parameters B and C (Fig. 1).13,59,60 It is thus trivial to switch from low-energy absorption combined with high-energy phosphorescence found in CrO6 chromophores (small values of Δ and large values of B) toward the opposite situation found in CrN6 chromophores.13 Furthermore, the almost spin-only behavior combined with negligible zero-field splitting parameters measured for the degenerate paramagnetic Cr(4A2) ground state (for instance D = 0.03 cm−1 for [(tpy)CrCl3])61 offers a simple approach for unravelling electronic intermetallic communications via the estimation of the isotropic exchange coupling constant operating between chromium centres.10,12,62
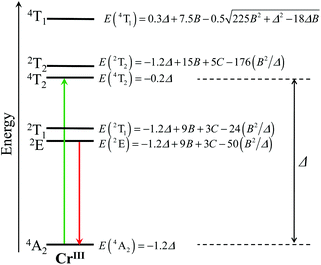 |
| | Fig. 1 Low-energy part of the energy level diagram for an octahedral CrIII sensitizer showing the energy levels modeled in terms of the ligand field strength Δ and the Racah parameters B and C.59,60 The upward green arrow stands for the lowest-energy spin-allowed absorption transition, while the downward red arrow refers to the lowest-energy phosphorescence. | |
In diamagnetic polynuclear RuII architectures, for which the Creutz–Taube complex is the archetype (Fig. 2a),63 the magnitude of the intermetallic interaction is deduced from the envelope of the intervalence electronic absorption bands occurring in mixed valence RuII–RuIII dimers.64–68 When applied to back-to-back bis-terpyridine bridging ligands L in [(tpy)Ru(L)Ru(tpy)]5+ (Fig. 2b), the associated theories successfully rationalized the exponential decrease of the electronic interaction parameter with increasing intermetallic separations69–71 and the magnification of both through-bond electron transfer (Fig. 2c)72,73 and energy transfer (Fig. 2d)74–78 for short electron-rich aromatic bridges. Unfortunately, one-electron reductions of [Cr(bpy)3]3+ and [Cr(tpy)2]3+ occur on the bound ligands79,80 and no related approach can be envisioned for unravelling intermetallic coupling in analogous polypyridine CrIII complexes.
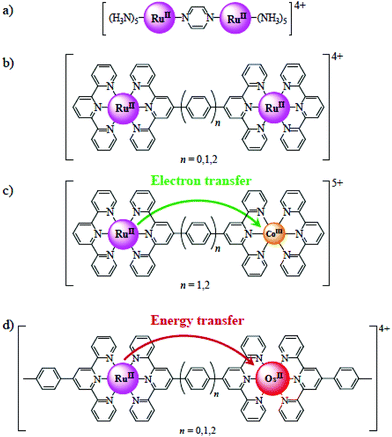 |
| | Fig. 2 (a) Creutz–Taube complex, (b) [(tpy)Ru(L)Ru(tpy)]m+ complexes,69–71 (c) [(tpy)RuII(L)CoIII(tpy)]5+ complexes displaying directional electron transfer,72,73 (d) [(tpy)RuII(L)OsII(tpy)]4+ complexes displaying directional energy transfer.74,75 | |
Altogether, the magnetic and photophysical properties of RuII polypyridine and CrIII polypyridine complexes are complementary, with each series displaying specific advantages and shortcomings, but the paramagnetism associated with the three unpaired electrons in CrIII opens additional perspectives. However, the lack of easy accessible synthetic procedures for the preparation and characterization of pure heteroleptic polynuclear chromium complexes has up to now prevented CrIII polypyridines from being used as active building blocks in (supra)molecular optical devices. Recently, Barker et al.,81 Isaacs et al.82 and Housecroft and Constable et al.46,83,84 tried to find a remedy for this frustrating limitation with the systematic exploration of the stability and lability of mononuclear six-coordinate bis-terimine83,84 and ter-bisimine46,81,82 CrIII complexes. Building on the identification of labile CrIII–O(triflate) bonds and their easy formation from Cr–Cl bonds, we herein propose to extend this procedure for the synthesis of a series of novel back-to-back dinuclear [X3CrIII(L)CrIIIX3] complexes (Scheme 1, X3 = Cl3 or X3 = tpy), which are reminiscent of the well-known RuII dyads. We also plan to unravel the intermetallic electronic communication with the help of magnetic measurements (isotropic superexchange coupling constants), photophysical studies (ligand-field and Racah parameters and intermetallic energy transfer rate constants) and thermodynamic considerations (cooperative binding of labile Er3+ as a model for Cr3+).
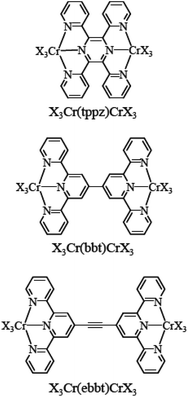 |
| | Scheme 1 Structures and nomenclature of the investigated dinuclear chromium complexes. tppz = 2,3,5,6-tetra-2-pyridinylpyrazine, bbt = 4,4′′′-bis(2,2′:6′,2′′-terpyridine), and ebbt = 4,4′′′-(ethynyl)-bis(2,2′:6′,2′′-terpyridine). X3 stands for Cl3 or 2,2′:6′,2′′-terpyridine. | |
Results and discussion
Synthesis and characterization of homoleptic and heteroleptic mononuclear [CrLCl3], [CrL2](PF6)3 (L = tpy, ebzpy, tppz) and dinuclear [Cl3Cr(L)CrCl3], [(tpy)Cr(L)Cr(tpy)](PF6)6 (L = tppz, bbt, ebbt) complexes
As a first step toward this goal, we used GaIII as a trivalent labile diamagnetic model cation for CrIII for the straightforward formation of a homoleptic [Ga(tpy)2]3+ cation (Table S1, ESI†), which displayed the expected well-resolved D2d-symmetrical 1H NMR spectrum (6 signals observed for 22 available aromatic protons, Fig. S1, ESI†). The downfield shifts of the aromatic signal (Δδ = −1.01 ppm) observed for the hydrogen nuclei located at the ortho-positions of the nitrogen atoms of the distal pyridine rings are diagnostic for an orthogonal arrangement of the two planar tridentate terpyridine ligands around the central cation as found in [Fe(tpy)2]2+ (Δδ = −1.64 ppm), [Ru(tpy)2]2+ (Δδ = −1.37 ppm) and [Os(tpy)2]2+ (Δδ = −1.43 ppm).85 The crystal structure of [Ga(tpy)2](PF6)3·2CH3CN (1, Fig. 3 left, Fig. S2 and Tables S2, S4 and S5†) confirmed this statement with an interplanar angle of 88.5° between the two tridentate N3 chelates. Combined with the pincer effect brought by the two-fused 5-membered chelate rings in the terpyridine moieties (Ndistal–Cr–Ndistal = 156.6(1)° instead of 180° expected for octahedral geometry, see Fig. 3), the diamagnetic GaN6 core adopts the expected compact and slightly distorted pseudo-octahedral geometry previously reported for other [M(tpy)2]z+ (z = 2, 3) complexes.86,87 No specific close-packing interactions due to significant π–π aromatic interactions compatible with ‘terpyridine embrace’ supramolecular patterns87 could be identified (the closest inter-aromatic distance amounts to 4.5 Å, far beyond the accepted cutoff of 3.8 Å for π-stacking interactions; Fig. S3†).88,89 We however note that [Ga(tpy)2](PF6)3·2CH3CN (1) crystallizes in the chiral P212121 space group, the origin of which probably arises from packing effects since [Ga(tpy)2]3+ cations are essentially achiral. In order to overcome the complications produced by the kinetic inertness of CrIII salts, the related homoleptic complex [Cr(tpy)2]3+ is obtained by the reaction of the reduced labile precursor Cr(CF3SO3)2·H2O48 with 2,2′:6′,2′′-terpyridine (tpy), or with its extended analogue 2,6-bis(1-ethyl-benzimidazol-2-yl)pyridine (ebzpy),90 to give saturated six-coordinated CrII complexes.80 Subsequent air oxidation (outer sphere mechanism)48 provides [Cr(tpy)2](PF6)3·2.5CH3CN (2, Fig. S4 and Tables S2, S6 and S7, ESI†) and [Cr(ebzpy)2](PF6)3·5.5CH3CN (3, Fig. S5 and Tables S3, S8–S11, ESI†) in 70–80% yields after metathesis with PF6− (Fig. 3). The molecular structures of the CrN6 (2 and 3) and GaN6 (1) moieties are almost superimposable and closely match that previously reported for [Cr(tpy)2](ClO4)3·H2O.91,92 Again, intermolecular packing interactions are very limited for these chromium complexes (Fig. S6 and S7, ESI†), a trend assigned to the combination of (i) the considerable inter-cation repulsions and (ii) the delicate accommodation of three counter-anions per cationic complex in the crystal structures.46 We would like to stress here that the crystal structure of 2, monitored at 180 K in this work, is identical to that previously deposited for 2{[Cr(tpy)2](PF6)3}·5CH3CN recorded at 123 K,46 an observation which confirms the robustness of the packing process despite the lack of identifiable strong intermolecular interactions in the crystal structures of these [Cr(tpy)2]X2 complexes.
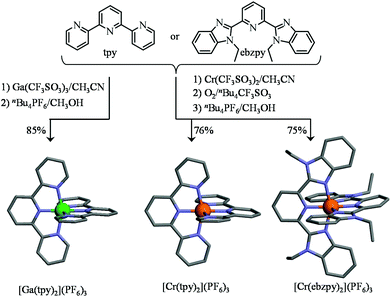 |
| | Fig. 3 Synthesis of the homoleptic tricationic [Ga(tpy)2]3+ [Cr(tpy)2]3+ and [Cr(ebzpy)2]3+ complexes. The molecular structures of the cations are those found in the crystal structures of [Ga(tpy)2](PF6)3·2CH3CN (1), [Cr(tpy)2](PF6)3·2.5CH3CN (2) and [Cr(ebzpy)2](PF6)3·5.5CH3CN (3). The hydrogen atoms have been omitted for clarity. Color code: C = grey, N = blue, Cr = orange, Ga = green. | |
Since no high-resolution NMR signals could be recorded for the slow-relaxing CrIII complexes, their magnetic characterization in solution is restricted to the measurement of the effective magnetic moments in acetonitrile for [Cr(tpy)2](PF6)3 (μeff = 4.4(4) BM) and [Cr(ebzpy)2](PF6)3 (μeff = 4.2(4) BM), which only slightly deviate from the spin-only value (μeff = 3.88 BM). Unfortunately, we were not able to record satisfying ESI-MS spectra for these mononuclear triply-charged complexes in solution, probably because of partial dissociation occurring during the vaporization process.46
Higher structural complexity requires the rational synthesis of heteroleptic bis-terdentate CrN6 chromophores following the strategy originally proposed by Barker et al. for bidentate phenanthroline ligands81 and adapted for tridentate terpyridines by Housecroft and Constable and coworkers (Fig. 4).46,84 Beyond [Cr(tpy)Cl3], the structure of which was previously reported (Fig. 4 top centre),61,93 we confirm that the three weakly bound THF molecules in CrCl3(THF)3 can be displaced by closely related tridentate ligands94 to give [Cr(ebzpy)Cl3]·DMF (5, Tables S12–S14 and Fig. S8 and S9†) and [Cr(tppz)Cl3]·2DMF (6, Tables S12, S15, and S16 and Fig. S8 and S9†).95 The three CrN3 chelate units are almost superimposable showing similar bond distances (Cr–N = 2.05(3) Å) and bond angles (average pincer angle Ndistal–Cr–Ndistal = 156.5(5)°). The crystal structure of [Cr(tppz)Cl3] (6) reveals specific geometric distortions at the metal centre caused by the repulsion of the hydrogen atoms at the 3-position of the bound pyridine rings with the two unbound pyridine units. The result is a twisting of the bound part of the tppz ligand, in which the dihedral angles between the pyridine and pyrazine rings amount to 19.46°. The reaction of [Cr(L)Cl3] with concentrated trifluoromethanesulfonic acid (CF3SO3H) displaces the three chloride anions to give [Cr(L)(CF3SO3)3] (L = tpy, ttpz, Table S1†). The slightly more basic ebzpy ligand (compared with tpy and ttpz) did not resist protonation and only [H2ebzpy](CF3SO3)2 could be isolated (10, Fig. S10 and Tables S17 and S18†). Subsequent mixing of [Cr(L)(CF3SO3)3] with a second tridentate ligand L′ either restores the homoleptic complexes (L′ = L) or provides (L′ ≠ L) the heteroleptic complexes [Cr(tpy)(ebzpy)](PF6)3 (7, Fig. S11 and Tables S17, S19 and S20†) and [Cr(tpy)(tppz)](PF6)3 (8, Fig. S12 and Tables S21–S25†) in fair to good yields (Fig. 4 bottom). Their molecular structures show CrN6 units almost superimposable with those found in the homoleptic model cations [Cr(tpy)2]3+ and [Cr(ebzpy)2]3+. Again, no remarkable intermolecular π-stacking interactions could be highlighted (Fig. S13 and S14†) and the structural distortion produced by steric congestion with the non-coordinated pyridine rings in the tppz ligand is retained in [Cr(tpy)(tppz)]3+ (the average dihedral angle between the pyridine and pyrazine rings in the tridentate bound unit amounts to 19(4)°).
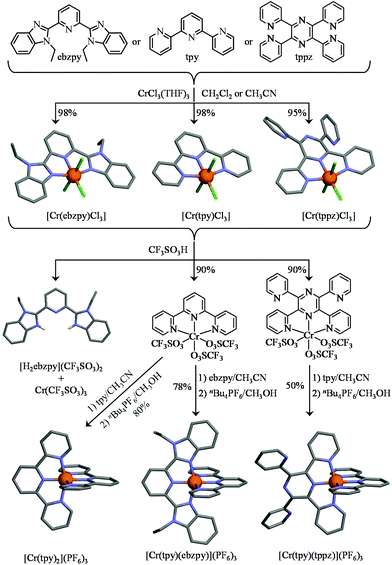 |
| | Fig. 4 Synthesis of the heteroleptic mononuclear chromium complexes. The molecular structures are those found in the crystal structures of [Cr(ebzpy)Cl3]·DMF (5), [Cr(tpy)Cl3]·(CH3)2SO,93 [Cr(tppz)Cl3]·2DMF (6) [Cr(tpy)2](PF6)3·2.5CH3CN (2), [Cr(tpy)(ebzpy)](PF6)3·2CH3CN (7), [Cr(tpy)(tppz)](PF6)3·3CH3CN (8) and [H2(ebzpy)](CF3SO3)2 (10). The hydrogen atoms have been omitted for clarity. Color code: C = grey, N = blue, Cr = orange, Cl = green, H = yellow. | |
With this strategy at hand, the synthesis of a series of six rod-like heteroleptic dinuclear CrIII complexes with three different bridging ligands (tppz, bbt, and ebbt) and two types of capping entities (Cl3 or tpy) can be envisioned. Firstly, the reaction of an excess of CrCl3·6H2O with the appropriate bridging ligand95 quantitatively yields [Cr2Cl6(tppz)] and [Cr2Cl6(bbt)], while [Cr2Cl6(ebbt)] is obtained with more difficulties because of the low solubility of the free ligand in common organic solvents (left part of Fig. 5 and Table S1†). Alternatively, stoichiometric reactions between the bridging ligand (1 eq.) and labile [Cr(tpy)(CF3SO3)3] (2 eq.) lead to the targeted dinuclear complexes [Cr2(tpy)2(bbt)](PF6)6 and [Cr2(tpy)2(ebbt)](PF6)6, but we were unable to connect two triply charged [Cr(tpy)]3+ cations at the termini of the shorter tppz ligand (Fig. 5). The crystal structure of [Cr2Cl6(tppz)]·3C5H9NO (11, Fig. S15 and Tables S26–S28†), with its intermetallic distance 6.662(3) Å and interplanar angle of 25.5° between the two chelate N3 planes, completes a collection of similar rod-like dyads reported for [Ru2Cl6(tppz)]− (RuII⋯RuIII = 6.504 Å, interplanar angle = 26.38°),96 [Ru2(CH3CN)6(tppz)] (RuII⋯RuII = 6.56 Å, interplanar angle = 27.08°)97 and for other [M2X6(tppz)] binuclear complexes.98–102 The crystal structures involving the extended bbt bridging ligands [Cr2Cl6(bbt)] (12, Fig. S16 and Tables S26, S29 and S30†) and [Cr2(tpy)2(bbt)](PF6)6·8CH3CN·(CH3CH2)2O (13, Fig. S17 and Tables S31–S33†) have surprisingly no precedent for analogous ruthenium complexes despite the intense activity dedicated to these specific supramolecular architectures.19–24,69 The intermetallic separation is fixed to ca. 10.9 Å by the back-to-back bis(terpyridine) spacer (Fig. 5). The dihedral angle within the bridging 4,4′-bipyridine motif amounts to 36.5(4)° in [Cr2Cl6(bbt)] and to 83.0(1)° in [Cr2(tpy)2(bbt)](PF6)6. While the smaller angle matches the theoretically computed interplanar angle of 35–40°, which simultaneously minimizes the torsion energy and optimizes orbital overlap in 4,4′-bipyridine,103–105 the almost orthogonal arrangement of the two central pyridine rings found in [Cr2(tpy)2(bbt)](PF6)6 is unique for this spacer since the largest value reported so far reached 61(1)° for a dinuclear copper(II) complex.106 Four PF6− counter-anions are located between the two CrN6 units of the dinuclear complex. They are involved in twelve Caromatic–H⋯F–P hydrogen bonds (2.4 Å to 2.6 Å),107,108 which significantly stabilize the orthogonal arrangement of the central back-to-back bis(terpyridine) spacer (Fig. S18†). The crystal structure of [Cr2(tpy)2(ebbt)](PF6)6·10CH3CN (14, Fig. S19 and Tables S31, S34 and S35†) obviously displays not only the longest intramolecular Cr⋯Cr distance (13.4669(6) Å, Fig. 5), but also the smallest dihedral angle between the two quasi-planar terpyridine units connected by the alkyne bridge (0.1(3)°). To the best of our knowledge, no molecular structure has been previously reported with this extended ebbt ligand.109 We are now in a position to investigate the nature and magnitude of intramolecular intermetallic interactions operating between pseudo-octahedral CrIII metallic cations incorporated into rod-like heteroleptic dyads possessing variable lengths.
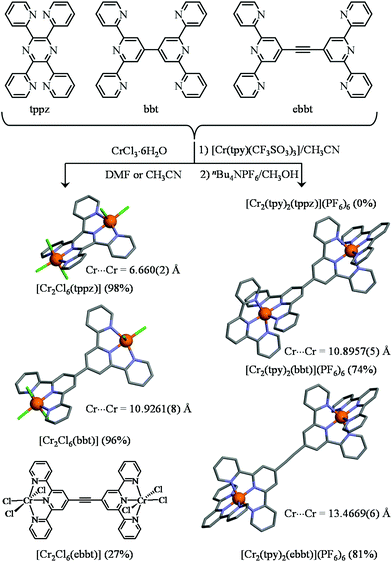 |
| | Fig. 5 Synthesis of the heteroleptic dinuclear chromium complexes. The molecular structures are those found in the crystal structures of [Cr2Cl6(tppz)]·3C5H9NO (11), [Cr2Cl6(bbt)] (12), [Cr2(tpy)2(bbt)](PF6)6·8CH3CN·(CH3CH2)2O (13) and [Cr2(tpy)2(ebbt)](PF6)6·10CH3CN (14). The hydrogen atoms have been omitted for clarity. Color code: C = grey, N = blue, Cr = orange, Cl = green. | |
Unravelling intermetallic communication in dinuclear [Cl3Cr(L)CrCl3], [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt): magnetic evidence
Two trivalent CrIII centres connected by short oxide bridges usually display strong anti-ferromagnetic interaction (Jex < 0) operating between the two S = 3/2 spin carriers via a superexchange mechanism.62 Application of the van Vleck equation to a coupled CrIII pair obeying the Heisenberg–Dirac–van Vleck spin Hamiltonian ĤHDVV = −JexŜAŜB (ŜA and ŜB are the spin operators localized on each metallic centre and Jex is the phenomenological magnetic exchange coupling constant) provides a contribution to the paramagnetic susceptibility χdimerpara expressed in eqn (1), where g is the Landé factor, NA = 6.022 × 1023 mol−1 is Avogadro's number, μB = 9.274 × 10−24 J T−1 is the Bohr magneton and kB = 1.3806 × 10−23 J K−1 is the Boltzmann constant.62| | 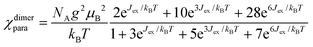 | (1) |
Compared with |Jex| values expected in the 1–10 cm−1 range for the [X3Cr(L)CrX3] dyads, the weak contribution of the zero-field splitting (D = 0.03 cm−1 for [Cr(tpy)Cl3], D = 0.2 cm−1 for [Cr(tpy)2]3+)12,61,80 can be neglected and the magnetic susceptibilities recorded in the 2–300 K range for the five dimeric complexes (Fig. 6 plotted as χT vs. T) could be satisfyingly fitted to eqn (2), where χdimerpara is given in eqn (1), χdimerdia is the diamagnetic susceptibility of the dimer calculated by means of Pascal's constant110 and χdimerTIP is the temperature-independent paramagnetic contribution of the dimer (Table S36†).
| | | χdimertot = χdimerpara + χdimerdia + χdimerTIP | (2) |
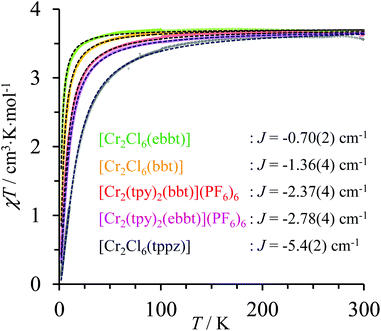 |
| | Fig. 6 Dependence of χdimertotT on the applied temperature (2–300 K) for the dinuclear CrIII complexes showing the experimental data (colored crosses) and non-linear least-square fits with eqn (2) (black dotted traces). | |
For temperatures larger than 150 K, the magnetic susceptibilities of all dinuclear complexes converge to a common constant value of 3.55 ≤ χT ≤ 3.67 cm3 mol−1, which is close to χT = 3.75 cm3 mol−1 calculated for two independent spin-only CrIII centres (S = 3/2). At low temperature, the χT versus T curves abruptly decrease, which is diagnostic for weak intramolecular anti-ferromagnetic interactions, the magnitude of which can be estimated by the exchange constants −5.4 ≤ Jex≤ −0.7 cm−1 collected in Fig. 6 (Table S36†). The Jex values found for pairs of coupled CrN3Cl3 units in dinuclear [Cl3Cr(L)CrCl3] dyads (orange, green and black traces in Fig. 6) show the expected reduction of the efficiency of the anti-ferromagnetic superexchange pathway with the increasing length of the molecular bridge separating the paramagnetic CrIII centres (Jtppzex < Jbbtex < Jebbtex). Switching from CrCl3N3 to CrN6 coordination spheres in going from [Cl3Cr(bbt)CrCl3] (Jex = −1.36 cm−1, orange trace) to [(tpy)Cr(bbt)Cr(tpy)]6+ (Jex = −2.37 cm−1, red trace) is accompanied by an almost doubling of the magnitude of the anti-ferromagnetic exchange interactions for a fixed intermetallic distance of 10.9 Å (Fig. 5 and Table S36†). This trend is particularly counter-intuitive since the largest anti-ferromagnetic communication is found for [(tpy)Cr(bbt)Cr(tpy)]6+, in which the dihedral angle between the connected pyridine rings of the 4,4′-bipyridine bridge is close to 90° thus minimizing π-orbital overlap.111,112 We however note that related trends, previously observed for oxo bridged CrIII binuclear complexes, could be assigned to the relative energies of the natural magnetic orbitals (t2g for a pseudo-octahedral CrIII complex) with respect to that of the HOMO orbital of the bridging ligand.113 Applying this reasoning to the replacement of three anionic π-donor chloride ligands in [Cl3Cr(bbt)CrCl3] with three π-acceptor heterocyclic nitrogen atoms in the capping terpyridine units in [(tpy)Cr(bbt)Cr(tpy)]6+ is expected to decrease the energy of the Cr-centred pseudo-t2g magnetic orbitals, thus favoring their mixing with the occupied molecular orbitals of the back-to-back bis(terpyridine) bridge. A thorough theoretical approach dealing with FeIII–CuII complexes recently confirmed the prospective dependence of the exchange interaction constant with the nature of the ligand field.114 Finally, the a priori surprising increase of the anti-ferromagnetic interaction accompanying the 24% increase of the intermetallic distance on going from [(tpy)Cr(bbt)Cr(tpy)]6+ (Cr⋯Cr = 10.9 Å, Jex = −2.37 cm−1, red trace) to [(tpy)Cr(ebbt)Cr(tpy)]6+ (Cr⋯Cr = 13.5 Å, Jex = −2.78 cm−1, violet trace) can be assigned to the beneficial effect of the bridging alkyne unit, which reduces the dihedral angle between the connected pyridine rings from 83.2(3)° in the bbt spacer to 0.1(3)° in the ebbt analogue and thus favors the overlap integral leading to detectable intramolecular anti-ferromagnetic interactions on the nanometric scale.
Unravelling intermetallic communication in dinuclear [Cl3Cr(L)CrCl3], [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt): optical evidence
The experimental energies of the CrIII-centred excited states (with respect to that of the Cr(4A2) ground state) are deduced from the combination of the absorption (Fig. 7a and b and Appendix 1 in the ESI†) and emission (Fig. 7c and Appendix 2 in the ESI†) spectra recorded for the dinuclear complexes in solution and in the solid state (Table 1 columns 7–9). At first sight, the energy of these levels can be roughly modeled by using the diagonal elements of the Tanabe–Sugano matrices assuming a pseudo-octahedral geometry for the CrN3Cl3 and CrN6 chromophores found in [Cl3Cr(L)CrCl3] (L = tppz, bbt, ebbt) and [(tpy)Cr(L)Cr(tpy)](PF6)6 (L = bbt, ebbt).115 However, this level of approximation implies that the Cr(2E) and Cr(2T1) states are degenerate, which is clearly not the case in these dimeric complexes (Fig. 7 and Table 1).
 |
| | Fig. 7 Absorption spectra recorded for [(tpy)Cr(bbt)Cr(tpy)](PF6)6 (a) in acetonitrile solution (2.5 × 10−5 mol dm−3, 295 K) and (b) in the solid state. (c) Corresponding solid state emission spectra collected at variable temperatures (λexc = 400 nm). | |
Table 1 Ligand-field energy Δ and Racah parameters (B and C) deduced with eqn (3), (4) and (6) by using the experimental energy of the excited Cr(2E), Cr(2T1) and Cr(4T2) levels observed for the dinuclear [Cl3Cr(L)CrCl3] and [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt) and for their mononuclear analogues [Cr(L)Cl3] (L = tppz, tpy) and [Cr(tpy)2](PF6)3
| Compound |
Δ/cm−1 |
B/cm−1 |
C/cm−1 |
Δ/B |
C/B |
E/cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
2E |
2T1 |
4T2 |
2T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
4T1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|
Energies are given with respect to that of the ground Cr(4A2) level.
Computed with eqn (7).
Computed with eqn (8).
The Cr(2T1 ← 4A2) transition could not be unambiguously assigned and the associated Racah parameters were calculated assuming C = 4B. The energy of the Cr(2T1) level was computed using eqn (4).
|
| [Cr2Cl6(tppz)] |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
708 |
2564 |
23 |
3.6 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 316 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 927 927
|
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 893 893
|
| [Cr2Cl6(bbt)] |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393 393 |
648 |
2785 |
25 |
4.3 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903 903 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 569 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393 393 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 134 134
|
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
| [Cr2Cl6(ebbt)] |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
604 |
2863 |
27 |
4.7 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 495 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 482 482
|
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 671 671
|
| [Cr2(tpy)2(bbt)](PF6)6 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
720 |
2636 |
23 |
3.7 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 837 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 643 643 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 524 524
|
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 782 782
|
| [Cr2(tpy)2(ebbt)](PF6)6 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
668 |
2672 |
25 |
4d |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 674 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 379d 379d |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 614 614
|
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 132 132
|
| [Cr(tppz)Cl3] |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
693 |
2770 |
24 |
4d |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089 089 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 846d 846d |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 117 117
|
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 312 312
|
| [Cr(tpy)Cl3] |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
697 |
2786 |
24 |
4d |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 175 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931d 931d |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694 694 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 265 265
|
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 585 585
|
| [Cr(tpy)2](PF6)3 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
675 |
2698 |
28 |
4d |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 953 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584d 584d |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 340 340
|
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 663 663
|
The additional consideration of configuration interaction between the states of the same multiplicity and symmetry, but from different strong field configurations led Jorgensen59 to introduce second-order corrections αB2/Δ in eqn (3)–(5), which are derived from the off-diagonal elements of the Tanabe–Sugano matrices.
| | | E(2T1) = 9B + 3C − 24(B2/Δ) | (4) |
| | | E(2E) = 9B + 3C − 90(B2/Δ) | (5) |
Although Jorgensen59 fixed C/B = 4 for deriving eqn (3)–(5), there is no obvious reason for this assumption and a systematic and detailed ligand-field analysis of electronic spectra recorded for CrIII compounds revealed that 3 ≤ C/B ≤ 8.115 In his seminal textbook,60 Lever replaced eqn (5) with eqn (6).
| | | E(2E) = 9B + 3C − 50(B2/Δ) | (6) |
This transforms the modelling of the E(2T1) − E(2E) energy gap, for which Jorgensen's approach predicts 66B2/Δ (eqn (5)), to only 26B2/Δ (eqn (6)). Compared with the theoretical set of exact energies computed by Ferguson by means of full Eisenstein's matrices with B = 680 cm−1 and C = 2720 cm−1 (C/B = 4.0),116,117 the exact computed E(2T1) − E(2E) energy gap amounts to 630 cm−1 for Δ = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 cm−1 in fair to good agreement with the prediction of the second-order correction 26B2/Δ = 603 cm−1 (eqn (6)), but rather far from 1531 cm−1 obtained with eqn (5). We conclude that only a complete ligand-field treatment is capable of extracting reliable Racah parameters B and C for CrIII complexes,119 but eqn (6) seems superior to eqn (5) when a rough modeling of the energy of the lowest spin–flip 2E excited state is foreseen. We therefore used eqn (3), (4) and (6) for estimating the ligand-field strength Δ and the Racah parameters B and C for each dimeric and monomeric complex (Table 1 and Fig. 8, Table S37 and Fig. S20 in the ESI†) together with eqn (7) and (8) for predicting the energy of the missing Cr(2T2) and Cr(4T1) levels.
940 cm−1 in fair to good agreement with the prediction of the second-order correction 26B2/Δ = 603 cm−1 (eqn (6)), but rather far from 1531 cm−1 obtained with eqn (5). We conclude that only a complete ligand-field treatment is capable of extracting reliable Racah parameters B and C for CrIII complexes,119 but eqn (6) seems superior to eqn (5) when a rough modeling of the energy of the lowest spin–flip 2E excited state is foreseen. We therefore used eqn (3), (4) and (6) for estimating the ligand-field strength Δ and the Racah parameters B and C for each dimeric and monomeric complex (Table 1 and Fig. 8, Table S37 and Fig. S20 in the ESI†) together with eqn (7) and (8) for predicting the energy of the missing Cr(2T2) and Cr(4T1) levels.
| | | E(2T2) = 15B + 5C − 176(B2/Δ) | (7) |
| | 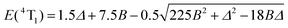 | (8) |
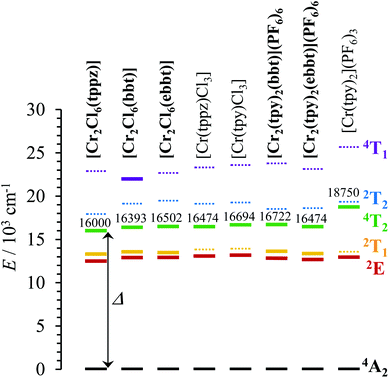 |
| | Fig. 8 Low-energy part of the energy level diagrams obtained for the dinuclear [Cl3Cr(L)CrCl3] and [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt, bold font) and for their mononuclear analogues [Cr(L)Cl3] (L = tppz, tpy) and [Cr(tpy)2](PF6)3 (normal font). The ligand-field Δ parameter is highlighted. Full traces are used for experimentally observed excited levels, whereas dotted traces correspond to calculated levels. | |
In agreement with both the spectrochemical and the nephelauxetic series,118 the ligand-field parameters in mononuclear complexes increase on going from CrN3Cl3 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ≤ Δ ≤ 17
300 ≤ Δ ≤ 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) to CrN6 (18
000 cm−1) to CrN6 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 ≤ Δ ≤ 19
750 ≤ Δ ≤ 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 cm−1), whereas the Racah parameters B = 682(19) cm−1 are comparable for both types of chromophores. A narrow distribution of these complexes around Δ/B ≈ 25 results in the d3 Tanabe–Sugano diagram (Fig. S21†). The latter Δ/B values are significantly smaller than Δ/B = 31.2 reported for the well-known [Cr(bpy)3](PF6)3 complex (Δ = 23
120 cm−1), whereas the Racah parameters B = 682(19) cm−1 are comparable for both types of chromophores. A narrow distribution of these complexes around Δ/B ≈ 25 results in the d3 Tanabe–Sugano diagram (Fig. S21†). The latter Δ/B values are significantly smaller than Δ/B = 31.2 reported for the well-known [Cr(bpy)3](PF6)3 complex (Δ = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1, B = 730 cm−1 and C = 2730 cm−1, C/B = 3.7)119 because the pincer effect produced by 5-membered chelate rings operates four times in [Cr(L)2]3+ (L = tpy, ebzpy) and only three times in [Cr(bpy)3]3+. This deleterious effect is not a fatality for tridentate ligands and it can be overcome by the use of six-membered chelate rings as found in [Cr(ddpd)Cl3] (15) (Fig. S22 and S23 and Tables S38–S40 in the ESI†) and in [Cr(ddpd)2](BF4)3 complexes (ddpd = N,N′-dimethyl-N,N′′-dipyridin-2-ylpyridine-2,6-diamine).120 The larger Ndistal–Cr–Ndistal angle of 172.0(9)° observed in [Cr(ddpd)2]3+ (compared with 156.5(5)° in [Cr(tpy)2]3+) indeed restores a large ligand field strength in bis-terdentate pseudo-octahedral complexes (Δ = 22
400 cm−1, B = 730 cm−1 and C = 2730 cm−1, C/B = 3.7)119 because the pincer effect produced by 5-membered chelate rings operates four times in [Cr(L)2]3+ (L = tpy, ebzpy) and only three times in [Cr(bpy)3]3+. This deleterious effect is not a fatality for tridentate ligands and it can be overcome by the use of six-membered chelate rings as found in [Cr(ddpd)Cl3] (15) (Fig. S22 and S23 and Tables S38–S40 in the ESI†) and in [Cr(ddpd)2](BF4)3 complexes (ddpd = N,N′-dimethyl-N,N′′-dipyridin-2-ylpyridine-2,6-diamine).120 The larger Ndistal–Cr–Ndistal angle of 172.0(9)° observed in [Cr(ddpd)2]3+ (compared with 156.5(5)° in [Cr(tpy)2]3+) indeed restores a large ligand field strength in bis-terdentate pseudo-octahedral complexes (Δ = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1, Table S37†). Focusing now on the through-bridge effect produced by the connection of a second neutral CrCl3 unit which transforms [Cr(tppz)Cl3] into its dinuclear [Cl3Cr(tppz)CrCl3] analogue (Cr⋯Cr = 6.66 Å), we observe that Δ decreases by almost 500 cm−1 (Fig. 8). This effect can be taken as an assessment of the mutual polarization (i.e. electronic communication) produced by the two CrIII centres connected to the bridging back-to-back bis-terdentate ligand. Taking now [Cr(tpy)Cl3] as the mononuclear reference, the same trend is monitored for [Cl3Cr(bbt)CrCl3] (Δ decreases by 300 cm−1 for Cr⋯Cr = 10.93 Å) and [Cl3Cr(ebbt)CrCl3] (Δ decreases by 200 cm−1 for Cr⋯Cr ≥ 13 Å), but with an expected attenuation for longer intermetallic distances. For the charged [CrN6]3+ chromophore found in the mononuclear [Cr(tpy)2]3+ reference complex (Δ = 18
990 cm−1, Table S37†). Focusing now on the through-bridge effect produced by the connection of a second neutral CrCl3 unit which transforms [Cr(tppz)Cl3] into its dinuclear [Cl3Cr(tppz)CrCl3] analogue (Cr⋯Cr = 6.66 Å), we observe that Δ decreases by almost 500 cm−1 (Fig. 8). This effect can be taken as an assessment of the mutual polarization (i.e. electronic communication) produced by the two CrIII centres connected to the bridging back-to-back bis-terdentate ligand. Taking now [Cr(tpy)Cl3] as the mononuclear reference, the same trend is monitored for [Cl3Cr(bbt)CrCl3] (Δ decreases by 300 cm−1 for Cr⋯Cr = 10.93 Å) and [Cl3Cr(ebbt)CrCl3] (Δ decreases by 200 cm−1 for Cr⋯Cr ≥ 13 Å), but with an expected attenuation for longer intermetallic distances. For the charged [CrN6]3+ chromophore found in the mononuclear [Cr(tpy)2]3+ reference complex (Δ = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, Table 1), the latter effect is drastically amplified leading to a ca. 2000 cm−1 reduction of the ligand-field parameter Δ in the related charged dinuclear complexes [(tpy)Cr(L)Cr(tpy)]6+ (L = bbt, ebbt, Fig. 8 and Table 1). The considerable reduction of Δ recorded for the longest ebbt bridging ligand in [(tpy)Cr(ebbt)Cr(tpy)]6+ combined with the operation of the largest nephelauxetic dispersion (i.e. the minimum B Racah parameter, Table 1) confirms that an alternation of alkyne/aromatic groups is particularly adapted for the design of electronic wires between CrIII centres, a result in line with the exceptional delocalization of the electronic density from the metal centres reported for analogous rod-like Ru(II)/Os(II) dyads.121–123 Intermetallic communication can be alternatively probed by time-resolved emission spectroscopy performed on powder samples of the dinuclear complexes at cryogenic temperatures. The Cr(2E → 4A2) phosphorescence signals showed double exponential decays for all complexes except for the unsolvated centrosymmetrical [Cr2Cl6(bbt)] complex, for which the kinetic decay trace is mono-exponential (Table 2 and Fig. A2-9–A2-13 in Appendix 2†).
750 cm−1, Table 1), the latter effect is drastically amplified leading to a ca. 2000 cm−1 reduction of the ligand-field parameter Δ in the related charged dinuclear complexes [(tpy)Cr(L)Cr(tpy)]6+ (L = bbt, ebbt, Fig. 8 and Table 1). The considerable reduction of Δ recorded for the longest ebbt bridging ligand in [(tpy)Cr(ebbt)Cr(tpy)]6+ combined with the operation of the largest nephelauxetic dispersion (i.e. the minimum B Racah parameter, Table 1) confirms that an alternation of alkyne/aromatic groups is particularly adapted for the design of electronic wires between CrIII centres, a result in line with the exceptional delocalization of the electronic density from the metal centres reported for analogous rod-like Ru(II)/Os(II) dyads.121–123 Intermetallic communication can be alternatively probed by time-resolved emission spectroscopy performed on powder samples of the dinuclear complexes at cryogenic temperatures. The Cr(2E → 4A2) phosphorescence signals showed double exponential decays for all complexes except for the unsolvated centrosymmetrical [Cr2Cl6(bbt)] complex, for which the kinetic decay trace is mono-exponential (Table 2 and Fig. A2-9–A2-13 in Appendix 2†).
Table 2 Experimental lifetimes found for the dinuclear [Cl3Cr(L)CrCl3] and [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt) and intermetallic energy transfer rate constants WD→A estimated with eqn (9)
| Complex |
T/K |
τ
1/μs |
τ
2/μs |
W
D→A/s−1 |
Cr⋯Cra/Å |
|
Intermetallic distance measured in the crystal structures.
Mono-exponential decay.
|
| [Cr2Cl6(tppz)] |
5 |
3.6(1) |
0.9(1) |
8(2) × 105 |
6.660(2) |
| [Cr2Cl6(bbt)] |
5 |
21(1)b |
— |
— |
10.9261(8) |
| [Cr2Cl6(ebbt)] |
3.5 |
3.6(1) |
0.4(1) |
2.2(4) × 106 |
— |
| [Cr2(tpy)2(bbt)](CF3SO3)6 |
5 |
40.3(1) |
2.3(1) |
4.1(8) × 105 |
10.8957(5) |
| [Cr2(tpy)2(ebbt)](PF6)6 |
3.5 |
0.24(1) |
0.04(1) |
2.1(4) × 107 |
13.4669(6) |
Since (i) mono-exponential decay traces in the millisecond range are systematically recorded for the Cr(2E) phosphorescence occurring in related mononuclear chromium complexes (0.24 ≤ τCr(2E) ≤ 1.37 ms at 3 K, Table S37 and Table A2 I Appendix 2†) and (ii) the fast components of the multi-exponential Cr(2E → 4A2) decay traces account for less than 20% of total intensities in the dinuclear complexes, we assume that the powder samples of [Cl3Cr(L)CrCl3] (L = tppz, ebbt) and [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = bbt, ebbt) possess two non-equivalent chromium sites as found in the crystal structures of [Cr2Cl6(tppz)]·3C5H9NO (11) and [Cr2(tpy)2(bbt)](PF6)6·8CH3CN·(CH3CH2)2O (13). The energies of the two Cr(2E) levels, referred to as D = donor and A = acceptor in the dinuclear complexes, are therefore slightly different and compatible with the operation of intramolecular intermetallic energy transfers characterized by their first-order rate constants WD→A and WA→D (Fig. 9a). This model was previously postulated by Castelli and Forster for rationalizing the multi-exponential decay observed in solid samples of [Cr(urea)6]3+ chromophores.124 It is further supported by the time-resolved luminescence spectra recorded for [(tpy)Cr(bbt)Cr(tpy)]X6 (X = PF6 in Fig. 7c and X = CF3SO3 in Fig. A2-13 in Appendix 2†), which show a faster decay of the high energy part of the emission band (corresponding to the lifetime of CrD(2E)) followed by a longer decay for the low energy part (corresponding to the lifetime of CrA(2E)).
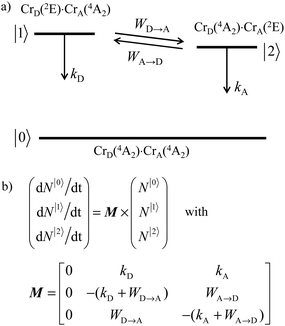 |
| | Fig. 9 (a) Energy level diagram and (b) kinetic matrix equations for the relaxation of the Cr(2E) excited levels occurring in a dinuclear chromium complex with non-equivalent metallic sites (CrD·CrA). kA and kD are the first-order de-excitation rate constants (sum of radiative and non-radiative processes), whereas WD→A and WA→D are the intramolecular energy transfer rate constants. | |
Although the time evolution of the population densities of the three states (N|i〉, i = 0, 1, 2) can be obtained by numerically solving the matrix kinetic equation shown in Fig. 9b with the help of projection operators and Lagrange–Sylvester formula,125 reasonable approximations assume that (i) the back energy transfer is negligible (WA→D ≈ 0) for time-resolved measurements performed below 5 K, (ii) the long-lived component τ1 of the bi-exponential decay kinetic trace (Table 2, column 3) reflects the sum of radiative and non-radiative relaxation rate constants of the acceptor (kA ≈ (τ1)−1 in Fig. 9) and (iii) τ1 can also be taken as an acceptable estimation for the relaxation rate constant of the donor in the absence of acceptor (kD ≈ kA ≈ (τ1)−1 in Fig. 9). With this in mind, the short-lived component τ2 observed in the dinuclear complexes (Table 2, column 4) stands for the sum of the relaxation pathways affecting CrD(2E) (eqn (9) left), from which the intramolecular intermetallic energy transfer rate constants WD→A can be easily deduced (eqn (9) and Table 2 column 5).
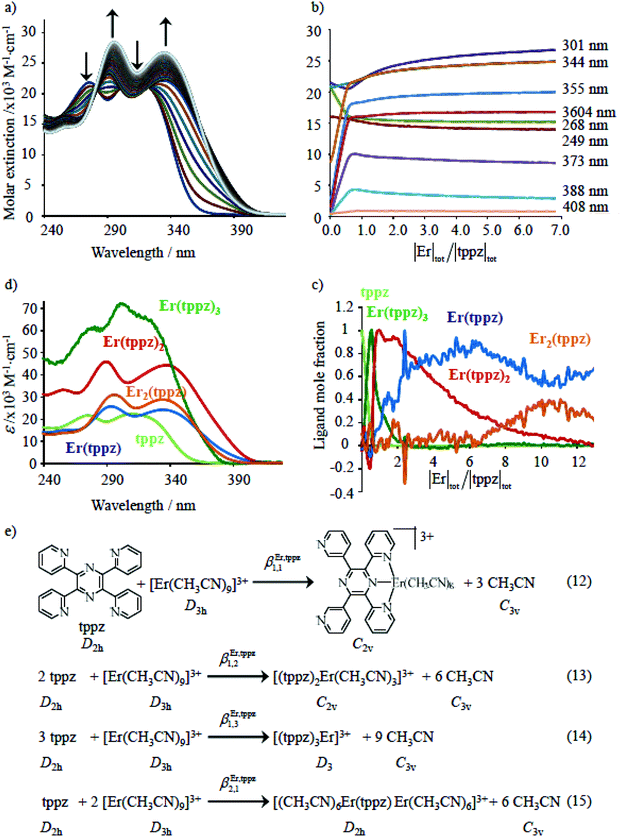
| | 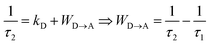 | (9) |
The first striking results concern the rather short characteristic lifetimes 0.2 ≤ τ1 ≤ 40 μs measured for the Cr(2E) levels in the dinuclear complexes in the absence of energy transfer (τ1 = (kA)−1 ≈ (kD)−1, Table 2, column 3). The reduction by one to two orders of magnitude compared with related data recorded for the mononuclear analogues under the same experimental conditions (solid state, cryogenic temperatures, Table S37†) are reminiscent of the well-documented4,127 effect of the reduction in ligand-field strength on the relaxation pathways affecting the Cr(2E) level. For a given chromophore (CrN3Cl3 in [Cl3Cr(L)CrCl3] or CrN6 in [(tpy)Cr(L)Cr(tpy)](PF6)6), we additionally detect a surprising counter-intuitive increase of the intermetallic energy transfer rate constant for larger intramolecular Cr⋯Cr distances (Table 2). According to the Fermi's golden rule summarized in eqn (10), the rate of resonant intermetallic energy transfer depends on (i) the spectral overlap integral ΩDA between the absorption spectrum of the acceptor A, and the emission spectrum of the donor D and (ii) the perturbation operator Hp usually modelling the magnitude of through-space (multipolar electrostatic) and/or through-bond (double electronic exchange) communication.75,126
| | | WD→A ∝ (2π/ħ)|〈DA*|Hp|D*A〉|2ΩDA | (10) |
Since the energies of the narrow and weakly Stokes-shifted spin–flip Cr(2E ↔ 4A2) transitions do not significantly depend on the ligand-field strength, the 810–1080 cm−1 spectral widths measured for the Cr(2E → 4A2) phosphorescence band in the dinuclear complexes (Fig. A2-4 to A2-8 in Appendix 2†) are compatible with non-negligible and comparable spectral overlap integrals ΩDA along the complete series. We therefore assign the unusually large energy transfer rate constants operating in the longest rod-like dyads [Cl3Cr(ebbt)CrCl3] (WD→A = 2.2(4) × 106 s−1) and [(tpy)Cr(ebbt)Cr(tpy)]6+ (WD→A = 2.1(4) × 107 s−1) to the exceptional through-bond conducting character of alkyne-containing bridges doped with aromatic rings,121,122 a trend in line with magnetic data (see the previous section). For unsolvated crystals of [Cr2Cl6(bbt)] (12), the center of symmetry found in the crystal structure is maintained in the powder sample and a mono-exponential decay is observed (Table 2, entry 2), in agreement with the kinetic model for which kA = kD and WD→A = WA→D.128
Unravelling intermetallic communication in dinuclear [Cl3Cr(L)CrCl3], [(tpy)Cr(L)Cr(tpy)](PF6)6 complexes (L = tppz, bbt, ebbt): thermodynamic evidence
The failure to isolate the dinuclear [(tpy)Cr(tppz)Cr(tpy)](PF6)6 complex from the reaction of [(tpy)Cr(CF3SO3)3] with tppz (Fig. 5) suggests the operation of a strong anti-cooperative protocol for the successive binding of two [Cr(tpy)]3+ to the bridging tppz ligand. The spectrophotometric titrations of [(tpy)Cr(tppz)]3+ with Er3+ in acetonitrile (Er3+ stands for a labile and non-hydrolyzable substitute of [Cr(tpy)]3+) confirms the lack of affinity of the available tridentate site of tppz in [(tpy)Cr(tppz)]3+ for a second trivalent cation (βCr(tppz),Er11 ≪ 50 in equilibrium (11), Fig. 10).129 A quantitative assessment of the searched cooperative factors can be approached by the spectrophotometric titrations of the bridging ligand tppz (or bbt) with Er(CF3SO3)3 in acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform = 65
chloroform = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 (Fig. 11). The resulting changes in the absorption spectra are characterized by smooth end points occurring at Eu
35 (Fig. 11). The resulting changes in the absorption spectra are characterized by smooth end points occurring at Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, Eu
3, Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, Eu
2, Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and Eu
3 and Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
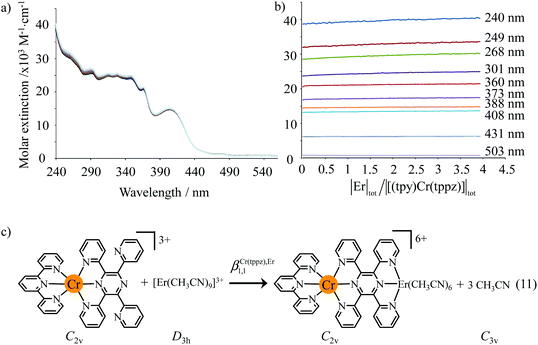
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 11a and b for L = tppz and Fig. S24a for L = bbt in the ESI†). Factor analysis (Fig. 11c and Fig. S24c†)130 followed by non-linear least square fits131 to equilibria (12)–(15) (Fig. 11e) provide satisfying re-constructed individual absorption spectra (Fig. 11d and Fig. S24d†) together with macroscopic formation constants gathered in Table 3 (entries 1–4).
1 (Fig. 11a and b for L = tppz and Fig. S24a for L = bbt in the ESI†). Factor analysis (Fig. 11c and Fig. S24c†)130 followed by non-linear least square fits131 to equilibria (12)–(15) (Fig. 11e) provide satisfying re-constructed individual absorption spectra (Fig. 11d and Fig. S24d†) together with macroscopic formation constants gathered in Table 3 (entries 1–4).
 |
| | Fig. 10 (a) Variation of absorption spectra, (b) corresponding variation of molar extinctions and (c) proposed modeling (βCr(tppz),Er1,1 ≪ 50) for the titration of [(tpy)Cr(tppz)]3+ (2 × 10−4 M) with Er(CF3SO3)3 in acetonitrile (298 K). | |
 |
| | Fig. 11 (a) Variation of absorption spectra and (b) corresponding variation of observed molar extinctions at different wavelengths observed for the spectrophotometric titration of tppz with Er(CF3SO3)3 (total ligand concentration: 8 × 10−5 mol dm−3 in CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHCl3 = 65 CHCl3 = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35, 298 K). (c) Evolving factor analysis using five absorbing eigenvectors,130 (d) re-constructed individual electronic absorption spectra131 and (e) proposed thermodynamic model. 35, 298 K). (c) Evolving factor analysis using five absorbing eigenvectors,130 (d) re-constructed individual electronic absorption spectra131 and (e) proposed thermodynamic model. | |
Table 3 Experimental stability constants (log(βEr,Lm,n)) and microscopic thermodynamic parameters fitted with eqn (17)–(20) for the reaction of tppz or bbt with Er(CF3SO3)3 in acetonitrile/chloroform (65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35) at 298 K
35) at 298 K
| Ligand |
tppz |
bbt |
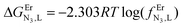 .
ΔEL,LEr = −2.303RT .
ΔEL,LEr = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(uL,LEr).
ΔEEr,ErL = −2.303·RT log(uL,LEr).
ΔEEr,ErL = −2.303·RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(uEr,ErL).
Agreement factor log(uEr,ErL).
Agreement factor 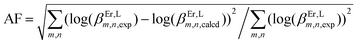 . .
|
| log(βEr,L1,1) |
6.42(2) |
8.19(16) |
| log(βEr,L1,2) |
12.03(3) |
13.76(32) |
| log(βEr,L1,3) |
15.89(4) |
18.16(50) |
| log(βEr,L2,1) |
9.80(3) |
13.63(16) |
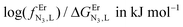 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
5.5(4)/−32(2) |
6.9(4)/−40(2) |
log(L,LEr)/ΔEL,LEr in kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−0.9(5)/5(3) |
−1.6(5)/9(2) |
log(uEr,ErL)/ΔEEr,ErL in kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
−3.1(9)/18(5) |
−2.1(9)/12(5) |
| AFd |
1.23 × 10−2 |
9.46 × 10−3 |
Monitoring these titrations using light-scattering techniques did not reveal any sign of aggregation due to the formation of two-dimensional and three-dimensional polymers as postulated by Long and coworkers for related reactions involving a back-to-back bis-terdentate ligand and Eu(NO3)3.132 Application of the site binding model (eqn (16))133 to equilibria (12)–(15) leads to eqn (17)–(20), which model the complete complexation process with only four parameters. (1) ωEr,Lm,n stands for pure entropic contribution to the complexation reaction brought by the change in the rotational entropy when the reactants are transformed into products (Appendix 3 in the ESI†).134 (2) 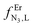 represents the intrinsic affinity of Er3+ for the tridentate binding unit of the bridging ligand (including desolvation processes). (3) uL,LEr = exp(−ΔEL,LEr/RT), respectively (4) uEr,ErL = exp(−ΔEEr,ErL/RT) are the cooperative effects, in terms of Boltzmann factors, which accompany the successive binding of ligands to the same metallic centre (uL,LEr), respectively, the successive binding of metals to the same bridging ligand (uEr,ErL). Multi-linear least-square fits of eqn (17)–(20) to the experimental stability constants provided the thermodynamic descriptors collected in Table 3 (entries 5–7).
represents the intrinsic affinity of Er3+ for the tridentate binding unit of the bridging ligand (including desolvation processes). (3) uL,LEr = exp(−ΔEL,LEr/RT), respectively (4) uEr,ErL = exp(−ΔEEr,ErL/RT) are the cooperative effects, in terms of Boltzmann factors, which accompany the successive binding of ligands to the same metallic centre (uL,LEr), respectively, the successive binding of metals to the same bridging ligand (uEr,ErL). Multi-linear least-square fits of eqn (17)–(20) to the experimental stability constants provided the thermodynamic descriptors collected in Table 3 (entries 5–7).
| | 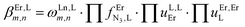 | (16) |
| | 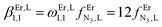 | (17) |
| | 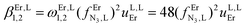 | (18) |
| | 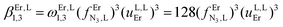 | (19) |
| | 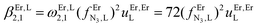 | (20) |
The intrinsic affinity of the tridentate N3 binding units for the entering trivalent Er3+ cation in the bridging bbt ligand 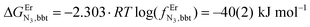 perfectly matches the one previously reported for the monomeric precursor terpyridine (tpy) ligand under similar conditions (acetonitrile, 298 K).135 This implies that, beyond an obvious statistical factor of 2, the connection of a second tridentate binding unit in the back of the original terpyridine units to give bbt has little effect on the binding properties of the tridentate N3 site taken separately. As expected, the successive binding of several tridentate N3 units to the same trivalent Er3+ centre is accompanied by some minor anti-cooperative processes (ΔEL,LEr = 9(2) kJ mol−1 for bbt and 6(2) kJ mol−1 for tpy) resulting from the stepwise neutralization of the positive metallic charge by an increasing number of bound nitrogen donors.135 With this in mind, it appears logical that the much less basic bridging pyrazine ring found in tppz (pKa = 0.37),136 compared with the 4,4′-bipyridine bridge in bbt (pKa = 4.8),137 leads to both a reduced affinity for Er3+
perfectly matches the one previously reported for the monomeric precursor terpyridine (tpy) ligand under similar conditions (acetonitrile, 298 K).135 This implies that, beyond an obvious statistical factor of 2, the connection of a second tridentate binding unit in the back of the original terpyridine units to give bbt has little effect on the binding properties of the tridentate N3 site taken separately. As expected, the successive binding of several tridentate N3 units to the same trivalent Er3+ centre is accompanied by some minor anti-cooperative processes (ΔEL,LEr = 9(2) kJ mol−1 for bbt and 6(2) kJ mol−1 for tpy) resulting from the stepwise neutralization of the positive metallic charge by an increasing number of bound nitrogen donors.135 With this in mind, it appears logical that the much less basic bridging pyrazine ring found in tppz (pKa = 0.37),136 compared with the 4,4′-bipyridine bridge in bbt (pKa = 4.8),137 leads to both a reduced affinity for Er3+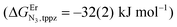 and a smaller ligand–ligand interaction (ΔEtppz,tppzEr = 5(3) kJ mol−1). However, the most noteworthy thermodynamic result concerns the considerable anti-cooperative mechanism accompanying the successive fixation of two Er3+ cations onto the bridging ligand, which are diagnostic for the operation of intermetallic electrostatic communication on the nanometric scale in these polyaromatic dyads. The large value ΔEEr,Ertppz = 18(5) kJ mol−1 found for the short-bridging tppz ligand combined with its limited intrinsic affinity
and a smaller ligand–ligand interaction (ΔEtppz,tppzEr = 5(3) kJ mol−1). However, the most noteworthy thermodynamic result concerns the considerable anti-cooperative mechanism accompanying the successive fixation of two Er3+ cations onto the bridging ligand, which are diagnostic for the operation of intermetallic electrostatic communication on the nanometric scale in these polyaromatic dyads. The large value ΔEEr,Ertppz = 18(5) kJ mol−1 found for the short-bridging tppz ligand combined with its limited intrinsic affinity 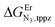 explains the difficulties in isolating dinuclear [X3Cr(tppz)CrX3] complexes. The smaller anti-cooperative effect observed for bbt (ΔEEr,Erbbt = 12(5) kJ mol−1) restores sufficient affinity for the formation of dinuclear [X3Cr(bbt)CrX3] complexes.
explains the difficulties in isolating dinuclear [X3Cr(tppz)CrX3] complexes. The smaller anti-cooperative effect observed for bbt (ΔEEr,Erbbt = 12(5) kJ mol−1) restores sufficient affinity for the formation of dinuclear [X3Cr(bbt)CrX3] complexes.
Conclusion
The synthetic method developed by Housecroft and Constable46 for the preparation of a semi-labile [(tpy)Cr(O3SCF3)3] precursor can be successfully applied for [(tppz)Cr(O3SCF3)3], but failed for the slightly more basic bis-benzimidazole derivative ebzpy, which is decomplexed from CrIII in trifluoromethanesulfonic acid. A subsequent reaction of [(L)Cr(O3SCF3)3] (L = tpy, tppz) with a second tridentate binding unit L′ leads to the targeted heteroleptic mononuclear [(L)Cr(L′)]3+ complexes, a procedure which can be extended for the preparation of unprecedented dinuclear rod-like [(tpy)Cr(L′)Cr(tpy)]6+ dyads when [(tpy)Cr(O3SCF3)3] is reacted with the Janus-type bis-terdentate receptors L′ = bbt or ebbt. In other words, [(tpy)Cr(O3SCF3)3] can be considered as an analogue of [(tpy)Ru(DMSO)Cl2]138 for the introduction of [(tpy)M]z+ fragments into (supra)molecular architectures, thus opening large avenues for the selective introduction of trivalent [CrN6]3+ chromophores in linear dyads and triads, and in di- and tridimensional networks similar to those designed with RuII.19–24 While the assessment of the degree of communication between RuII centres requires partial reduction to get mixed-valence systems, the paramagnetic and spin-only character of CrIII centres offers a straightforward access to this parameter with the simple determination of the isotropic magnetic coupling constants. For the [Cl3Cr(L)CrCl3] and [(tpy)Cr(L)Cr(tpy)]6+ dyads investigated here as proof-of-concept, the distance dependence of the magnetic communication reveals subtle modulations due to ligand-field effects and orbital overlap, which are optimized when two CrN6 chromophores are connected through an alkyne bridge in [(tpy)Cr(ebbt)Cr(tpy)]6+. Again, compared with RuII (strong-field low-spin d6 electronic configuration), the photophysical properties of CrIII (d3 electronic configuration) are better suited for unravelling intermetallic communication via the straightforward determination of ligand-field and Racah parameters, which are difficult to address in analogous ruthenium complexes. Moreover, minor non-equivalence of the CrIII coordination sites is accompanied by efficient intramolecular intermetallic energy transfer processes, the rate constants of which can be exploited for estimating the efficiency of intermetallic interactions. Finally, our fear that the successive connection of two triply-charged CrIII-type cations (instead of two divalent RuII-type cations) to a Janus-type bridging ligand may be hindered by a strong (electrostatic) anti-cooperative contribution seems only justified for the smallest pyrazine bridge in tppz. For the longer distance found in bbt, the anti-cooperative factor estimated with Er3+ taken as a trivalent model cation is reduced to such an extent that successive metallic complexation processes become accessible as demonstrated by the isolation of [Cr2(tpy)2(bbt)](PF6)6 and [Cr2(tpy)2(ebbt)](PF6)6 in fair to good yields.
Experimental section
Solvents and starting materials
2,2′:6′,2′′-Terpyridine (tpy) and the Janus-type bridging ligand tetra-2-pyridinylpyrazine (tppz) are commercially available. 2,6-Bis(1-ethyl-1H-benzo[d]imidazol-2-yl) pyridine (ebzpy),90N,N′-dimethyl-N,N′′-dipyridin-2-ylpyridine-2,6-diamine (ddpd)120 and 6′,6′′-di(pyridin-2-yl)-2,2′:4′,4′′:2′′,2′′′-quaterpyridine (bbt)139 were synthesized according to the published procedures. The synthesis of 4′,4′′′′-(ethynyl)bis(2,2′:6′,2′′-terpyridine) (ebbt) was adapted from the literature (Appendix 4†).109 Reagent grade acetonitrile (ACN) and chloroform were distilled from CaH2 when needed. All other chemicals were purchased from commercial suppliers and used without further purification. Silica-gel plates (Merck, 60 F254) were used for thin-layer chromatography. Preparative column chromatography was performed using either neutral alumina gel from Fluka (Typ 507 C) 100–125 mesh or SiliaFlash® silica gel P60 (0.04–0.063 mm).
Synthesis of gallium and chromium complexes
All complexes were characterized by IR spectroscopy (Tables S41–S44†) and gave satisfying elemental analyses (Table S1†).
[Ga(tpy)2](PF6)3.
A solution of Ga(CF3SO3)3 (60.5 mg, 0.117 mmol, 1 eq.) in degassed acetonitrile was added into a solution of terpyridine (54.8 mg, 0.235 mmol, 2.01 eq.) in distilled acetonitrile (20 mL). The color of the mixture immediately turned yellow. After being stirred at 50 °C overnight, acetonitrile was evaporated and the resulting solid was re-solubilized in methanol (5–8 mL). A solution of saturated (n-Bu)4NPF6 (2.5 mL, C = 90–100 mg mL−1) was added and the resulting pale yellow precipitate was filtered, washed with dichloromethane (2 × 5 mL) and diethyl ether (2 × 5 mL) and dried under vacuum to obtain [Ga(tpy)2](PF6)3 as a yellow powder (98 mg, 0.101 mmol, yield 86%). Slow diffusion of diethyl ether into a solution of the complex in acetonitrile gave pale yellow single crystals of [Ga(tpy)2](PF6)3·2CH3CN (1) suitable for X-ray diffraction studies. 1H NMR of [Ga(tpy)2](PF6)3 (CD3CN, 400 MHz, δ/ppm): 9.10 (6H, m), 8.80 (4H, d, 3J = 8 Hz), 8.43 (4H, td, 3J = 8 Hz, 4J = 0.8 Hz), 7.74 (4H, d, 3J = 8 Hz), 7.63 (4H, t, 3J = 8 Hz). ESI-MS (CH3CN) m/z: 825.8 ([Ga(tpy)2(PF6)2]+), 339.8 ([Ga(tpy)2(PF6)]2+) and 178.7 ([Ga(tpy)2]3+).
[Cr(tpy)2](PF6)3.
In a glovebox, a solution of Cr(CF3SO3)2·H2O (166 mg, 0.450 mmol, 1 eq.)48 in degassed acetonitrile was added into a solution of terpyridine (209 mg, 0.895 mmol, 1.99 eq.) in degassed acetonitrile (20 mL). The color of the mixture immediately turned deep dark green. After being stirred at 45 °C for 4 hours, a solution of (n-Bu)4NCF3SO3 (177 mg, 0.450 mmol, 1 eq.) in degassed acetonitrile (2 mL) was added. The Schlenk tube was transferred into the lab and Cr(II) was oxidized by bubbling dioxygen. The colour changed to red-orange. After being stirred for 1 hour at RT, acetonitrile was evaporated and the resulting solid was solubilized in hot methanol (20 mL). A solution of saturated (n-Bu)4NPF6 in methanol (4 mL, C = 100 mg ml−1) was added into the solution in order to precipitate a red-orange complex, which was filtered, washed with dichloromethane (3 × 15 mL) and diethyl ether (3 × 10 mL) and dried under vacuum to obtain a red-orange powder [Cr(tpy)2](PF6)3 (326 mg, 0.342 mmol, yield 76%). Slow diffusion of diethyl ether into a solution of the complex in acetonitrile gave red-orange single crystals of [Cr(tpy)2](PF6)3·2.5CH3CN (2) suitable for X-ray diffraction studies.
[Cr(ebzpy)2](PF6)3.
In a glovebox, a sky blue solution of Cr(CF3SO3)2·H2O (155 mg, 0.420 mmol, 1 eq.)48 in degassed acetonitrile was introduced into a 50 mL Schlenk tube containing a solution of 2,6-bis(1-ethyl-1H-benzo[d]imidazol-2-yl)pyridine (ebzpy, 307 mg, 0.835 mmol, 1.99 eq.) in degassed acetonitrile (20 mL). The blue color of the Cr(II) solution turned immediately dark green. After being stirred at 45 °C for 4 hours, a solution of (n-Bu)4NCF3SO3 (165 mg, 0.420 mmol, 1 eq.) in degassed acetonitrile (2 mL) was added. The Schlenk tube was transferred into the lab and the Cr(II) was oxidized by bubbling dioxygen. The colour of the solution changed to red-orange to give [Cr(ebzpy)2](CF3SO3)3. The red-orange acetonitrile solution of [Cr(ebzpy)2](CF3SO3)3 was evaporated and the resulting solid was solubilized in hot methanol (20 mL). Anion metathesis was performed by adding 4 mL of a saturated solution of (n-Bu)4NPF6 in methanol (100 mg mL−1). The red-orange precipitate was filtered, washed with dichloromethane (3 × 15 mL) and diethyl ether (3 × 10 mL) and dried under vacuum to give [Cr(ebzpy)2](PF6)3 as a red-orange powder (385 mg, 0.315 mmol, yield 75%). Slow diffusion of diethyl ether into a solution of the complex in acetonitrile gave red-orange single crystals of [Cr(ebzpy)2](PF6)3·5.5CH3CN (3) suitable for X-ray diffraction studies. Slow diffusion of diethyl ether into a solution of the intermediate [Cr(ebzpy)2](CF3SO3)3 complex in acetonitrile gave red-orange single crystals of [Cr(ebzpy)2](CF3SO3)3·2CH3CN (4) suitable for X-ray diffraction studies as well.
[Cr(ebzpy)Cl3].
A solution of 2,6-bis(1-ethyl-1H-benzo[d]imidazol-2-yl)pyridine (182 mg, 0.495 mmol, 1.01 eq.) in dry dichloromethane (5 mL) was dropwise added into a solution of [CrCl3(THF)3] (184 mg, 0.490 mmol, 1 eq.) in dry dichloromethane (30 mL). The color of the mixture changed from purple to green. After being stirred at room temperature for 24 hours, the mixture was filtered and the solid was washed with dichloromethane (3 × 15 mL) and diethyl ether (3 × 10 mL), and dried under vacuum to give [Cr(ebzpy)]Cl3 (253 mg, 0.47 mmol, yield 98%). Slow diffusion of diethyl ether into a solution of a complex in DMF gave dark green single crystals of [Cr(ebzpy)Cl3]·DMF (5) suitable for X-ray diffraction studies. The complex was characterized by elemental analysis (Table S1†).
[Cr(tppz)Cl3].
Tetra-2-pyridinylpyrazine (tppz) (170 mg, 0.438 mmol, 2 eq.) was suspended in a distilled mixture of acetonitrile and ethanol (25 mL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 mL) and heated under reflux. A solution of [CrCl3(THF)3] in acetonitrile (82 mg, 0.219 mmol, 1 eq.) was added dropwise to the tppz solution mixture, the colour of which immediately turned from purple to green. After being stirred and refluxed for 24 hours under an inert N2 atmosphere, the insoluble product was filtered (micro-filtering), then washed with a hot solution of acetonitrile and ethanol (1
25 mL) and heated under reflux. A solution of [CrCl3(THF)3] in acetonitrile (82 mg, 0.219 mmol, 1 eq.) was added dropwise to the tppz solution mixture, the colour of which immediately turned from purple to green. After being stirred and refluxed for 24 hours under an inert N2 atmosphere, the insoluble product was filtered (micro-filtering), then washed with a hot solution of acetonitrile and ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for removing the excess ligand. The resulting solid was washed with diethyl ether (3 × 7 mL) and dried under vacuum to give Cr(tppz)Cl3 (114 mg, 0.208 mmol, yield 95%). Slow diffusion of diethyl ether into a solution of the complex in DMF gave dark green single crystals of [Cr(tppz)Cl3]·2DMF (6) suitable for X-ray diffraction studies.
1) for removing the excess ligand. The resulting solid was washed with diethyl ether (3 × 7 mL) and dried under vacuum to give Cr(tppz)Cl3 (114 mg, 0.208 mmol, yield 95%). Slow diffusion of diethyl ether into a solution of the complex in DMF gave dark green single crystals of [Cr(tppz)Cl3]·2DMF (6) suitable for X-ray diffraction studies.
Cr(tppz)(SO3CF3)3.
Cr(tppz)Cl3 (140 mg, 0.256 mmol, 1 eq.) and triflic acid (300 μL, 3.4 mmol, 13 eq.) were loaded into a 50 mL Schlenk tube under a N2 atmosphere. The green colour of the complex turned to dark red immediately together with gas escape of HCl (confirmed by precipitation of AgCl when bubbling into an aqueous solution of AgNO3). After being stirred at room temperature for 3 hours, the dark red complex of Cr(tppz)(CF3SO3)3 was precipitated by the addition of 25 mL of diethyl ether. The complex was filtered, washed with diethyl ether (3 × 6 mL) and dried under vacuum to give Cr(tppz)(CF3SO3)3 (204 mg, 0.230 mmol, yield 90%).
[Cr(ebzpy)(tpy)](PF6)3.
A dark red solution of [Cr(tpy)(CF3SO3)3] (168 mg, 0.230 mmol, 1 eq.) in distilled acetonitrile was loaded into a 50 mL Schlenk tube under an inert N2 atmosphere. A solution of 2,6-bis(1-ethyl-1H-benzo[d]imidazol-2-yl) pyridine (85 mg, 0.230 mmol, 1 eq.) in acetonitrile (8–10 mL) was added to the Schlenk tube. The mixture was refluxed under N2 for 3 hours, then the solution was evaporated to dryness and the residual solid solubilized in distilled acetonitrile (3 mL). Slow diffusion of diethyl ether into the concentrated solution of the complex in acetonitrile gave [Cr(tpy)(ebzpy)](CF3SO3)3 as red crystals (126 mg, 0.115 mmol, yield 50%). [Cr(tpy)(ebzpy)](CF3SO3)3 was solubilized in MeOH, then anion metathesis was initiated by adding 4 mL of a saturated solution of tetrabutylammonium hexafluorophosphate [(n-Bu)4NPF6] in methanol (100 mg mL−1). The resulting red-orange precipitate was filtered, washed with diethyl ether and dried under vacuum to give [Cr(tpy)(ebzpy)](PF6)3. Slow diffusion of diethyl ether in a concentrated solution of the complex in acetonitrile (3 ml) produced red single crystals of [Cr(tpy)(ebzpy)](PF6)3·2CH3CN (7) suitable for X-ray diffraction studies.
[Cr(tppz)(tpy)](PF6)3.
A solution of Cr(tppz)(CF3SO3)3 (177.5 mg, 0.2 mmol, 1 eq.) in distilled acetonitrile was dropwise added into a concentrated solution of terpyridine in acetonitrile (58 mg, 0.25 mmol in 8 mL). The solution became warm during the addition and was then refluxed for 3 hours. The resulting mixture was cooled, filtered and the remaining dark-red solution was evaporated to dryness. Slow diffusion of diethyl ether into a concentrated solution of the complex in acetonitrile (3 ml) produced yellow single crystals of [Cr(tppz)(tpy)](CF3SO3)3 suitable for X-ray diffraction studies in approximately 40–50% yields. [Cr(tppz)(tpy)](CF3SO3)3 was solubilized in MeOH, then anion metathesis was initiated by adding 4 mL of a saturated solution of tetrabutylammonium hexafluorophosphate [(n-Bu)4NPF6] in methanol (100 mg mL−1). The resulting red-orange precipitate was filtered, washed with diethyl ether and dried under vacuum to give [Cr(tppz)(tpy)](PF6)3 (104 mg, 0.094 mmol, yield 47%). Slow diffusion of diethyl ether in a concentrated solution of the complex in acetonitrile (3 ml) produced red single crystals of [Cr(tpy)(tppz)](PF6)3·3CH3CN (8) suitable for X-ray diffraction studies.
[Cr2Cl6(tppz)].
Tetra-2-pyridinylpyrazine (220 mg, 0.566 mmol, 1 eq.), CrCl3, 6H2O (440 mg, 1.65 mmol, 2.9 eq.), and EtOH (12 mL) were introduced into a round bottom flask. After complete dissolution of CrCl3, acetonitrile (24 mL) was added to the resulting green solution, and the mixture was refluxed for 24 hours. The brown greenish precipitate was filtered off, washed with boiling EtOH (4 times), and dried with diethylether to give [Cr2Cl6(tppz)] as a brown greenish solid (390 mg, 0.555 mmol, yield 98%). Slow diffusion of diethylether in a concentrated solution of the [Cr2Cl6(tppz)] complex in N-methyl-2-pyrrolidone (NMP) provided green crystals of [Cr2Cl6(tppz)]·3C5H9NO (11) suitable for X-ray diffraction studies.
[Cr2Cl6(bbt)].
6′,6′′-Bis(2-pyridyl)-2,2′:4′,4:2′′,2′′′-quaterpyridine (bbt, 50 mg, 0.108 mmol, 1 eq.), CrCl3, 6H2O (86 mg, 0.323 mmol, 3 eq.), and DMF (10 mL) were introduced into a round bottom flask. The mixture was stirred at 90 °C for 64 hours. The green precipitate was filtered on a PTFE membrane, washed with EtOH, and dried with diethylether to give Cr2Cl6(bbt)·H2O (83 mg, 0.089 mmol, yield 96%) as a green solid. Slow diffusion of diethylether in a saturated solution of the [Cr2Cl6(bbt)] complex in N-methyl-2-pyrrolidone (NMP) provided green crystals of [Cr2Cl6(bbt)] (12) suitable for X-ray diffraction studies.
[Cr2Cl6(ebbt)].
4′,4′′′′-(Ethynyl)bis(2,2′:6′,2′′-terpyridine) (ebbt, 74 mg, 0.151 mmol, 1 eq.), CrCl3, 6H2O (121 mg, 0.454 mmol, 3 eq.), and DMF (20 mL) were introduced into a round bottom flask. The mixture was stirred at 90 °C for 64 hours. The green precipitate was filtered on a PTFE membrane, washed with EtOH, and dried with diethylether to give [Cr2Cl6(ebbt)]·2H2O as a green solid (34 mg, 0.041 mmol, yield 27%). Due to the very low solubility of this complex in common organic solvents, we were not able to obtain crystals suitable for X-ray diffraction studies.
[Cr2(tpy)2(bbt)](PF6)6.
6′,6′′-Bis(2-pyridyl)-2,2′:4′,4:2′′,2′′′-quaterpyridine (bbt) (30 mg, 0.065 mmol, 1 eq.), and distillated CHCl3 (12 mL) were introduced into a Schlenk tube under argon. After complete ligand dissolution, a solution of [Cr(tpy)(SO3CF3)3] (109 mg, 0.148 mmol, 2.3 eq.)46 dissolved in distilled acetonitrile (4 mL) was added. The mixture was stirred at 70 °C for 15 hours. The orange precipitate was filtered, washed with dichloromethane, and dried with diethylether. The orange solid so obtained was recrystallized from EtOH and dried with diethylether to give [Cr2(tpy)2(bbt)](SO3CF3)3 (92 mg, 0.048 mmol, yield 74%) as an orange solid. [Cr2(tpy)2(bbt)](SO3CF3)3 was dissolved in MeOH, and a saturated solution of TBAPF6 in MeOH was slowly added until complete precipitation of the yellow compound. The precipitate was filtered, washed with a few drops of MeOH, and dried with diethylether, to provide [Cr2(tpy)2(bbt)](PF6)6 as a yellow solid. Slow diffusion of diethylether into a solution of [Cr2(tpy)2(bbt)](PF6)6 in acetonitrile provided orange crystals of [Cr2(tpy)2(bbt)](PF6)6·8CH3CN·(CH3CH2)2O (13) suitable for X-ray diffraction studies. ESI-MS m/z: [Cr2(tpy)2(bbt); 5SO3CF3]+ calc: 1779.0, found: 1780.3; [Cr2(tpy)2(bbt); 4SO3CF3]2+ calc: 815.0, found: 814.3; [Cr2(tpy)2(bbt); 3SO3CF3]3+ calc: 493.7, found: 493.6.
[Cr2(tpy)2(ebbt)](PF6)6.
4′,4′′′′-(Ethynyl)bis(2,2′:6′,2′′-terpyridine) (ebbt, 40 mg, 0.082 mmol, 1 eq.), and distillated CHCl3 (15 mL) were introduced into a Schlenk tube under argon. After complete ligand dissolution, a solution of [Cr(tpy)(SO3CF3)3] (180 mg, 0.246 mmol, 3 eq.) dissolved in distilled acetonitrile (5 mL) was added. The mixture was stirred at 70 °C for 15 hours. The orange precipitate was filtered, washed with dichloromethane and dried with diethylether. The resulting orange solid was recrystallized from EtOH and dried with diethylether to give [Cr2(tpy)2(ebbt)](SO3CF3)6 (130 mg, 0.066 mmol, yield 81%) as an orange solid. [Cr2(tpy)2(ebbt)](SO3CF3)6 was dissolved in MeOH, and a saturated solution of TBAPF6 in MeOH was slowly added until complete precipitation of the yellow compound. The precipitate was filtered, washed with a few drops of MeOH, and dried with diethylether to give [Cr2(tpy)2(ebbt)](PF6)6 as a yellow solid. Slow diffusion of diethylether into a solution of the [Cr2(tpy)2(ebbt)](PF6)6 complex in acetonitrile provided orange crystals of [Cr2(tpy)2(ebbt)](PF6)6·10CH3CN (14) suitable for X-ray diffraction studies. ESI-MS m/z: [Cr2(tpy)2(ebbt); 5SO3CF3]+ calc: 1803.0, found: 1803.4; [Cr2(tpy)2(ebbt); 4SO3CF3]2+ calc: 827.0, found: 827.8; [Cr2(tpy)2(ebbt); 3SO3CF3]3+ calc: 501.7, found: 502.3; [Cr2(tpy)2(ebbt); 2SO3CF3]4+ calc: 339.0, found: 339.7; [Cr2(tpy)2(ebbt); 1SO3CF3]5+ calc: 241.4, found: 241.8; [Cr2(tpy)2(ebbt)]6+ calc: 176.4, found: 176.9.
[CrCl3(ddpd)].
N,N′-Dimethyl-N,N′-dipyridin-2-ylpyridine-2,6-diamine (ddpd) (80 mg, 0.274 mmol, 1 eq.), CrCl3, 6H2O (95 mg, 0.357 mmol, 1.3 eq.), and EtOH (20 mL) were introduced into a round bottom flask. After refluxing for 15 hours, a green precipitate formed was filtered and dried with diethylether to give [CrCl3(ddpd)] (75 mg, 0.167 mmol, yield 61%) as a green solid. Slow diffusion of diethylether into a concentrated solution of [CrCl3(ddpd)] in DMF provided green crystals of [CrCl3(ddpd)] (15) suitable for X-ray diffraction studies.
Spectroscopic and analytical measurements
1H and 13C NMR spectra were recorded on a Bruker Avance 400 MHz spectrometer equipped with a variable temperature unit. Chemical shifts are given in ppm with respect to tetramethylsilane Si(CH3)4. Pneumatically-assisted electrospray (ESI) mass spectra were recorded from 10−4 M solutions on an Applied Biosystems API 150EX LC/MS System equipped with a Turbo Ionspray source®. Elemental analyses were performed by K. L. Buchwalder from the Microchemical Laboratory of the University of Geneva. Spectrophotometric titrations were performed with a J&M diode array spectrometer (Tidas series) connected to an external computer. In a typical experiment, 50 cm3 of ligand in acetonitrile![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform (65
chloroform (65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35) (8 × 10−5 mol dm−3) were titrated at 298 K with a solution of Er(CF3SO3)3 (2 × 10−3 mol dm−3) in the same solvent under an inert atmosphere. After each addition of 0.10 mL, the absorbance was recorded using a Hellma optrode (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis130 and with the SPECFIT program.131 Absorption spectra in solution were recorded using a Cary 5000 Varian spectrometer (quartz cell path length 1 mm, 200–800 nm domain). Absorption spectra in the solid state were recorded on a Lambda 900 PerkinElmer spectrometer equipped with an integration sphere (background recorded on MgO). Emission spectra were recorded upon excitation at 400 nm from powder samples at various temperatures from 3 K to 295 K with a Fluorolog 3-22 (Horiba Jobin–Yvon), equipped with a peltier-cooled photo multiplier tube (Hamamatsu R2658P), and corrected for the spectral response of the system. Excitation at 355 nm was obtained with the third harmonic of a pulsed Nd:YAG laser (Quantel Brilliant). The emitted light was collected with a telescope and focused onto a light-guide with a fibre bundle connected to a monochromator (Spex 270 M). Full spectra were recorded with a CCD (Spex Spectrum One), decay curves with a photomultiplier (Hamamatsu R928) and a digital oscilloscope (Tektronix TDS540B) or a multichannel scaler (Stanford Research SR430). For the latter the spectral bandwidth of the monochromator was set to 20 nm, thus giving the decay of the integral signal. Low temperatures were achieved with a closed cycle cryosystem (Janis, SHI-950) with the sample sitting in exchange gas for efficient cooling. Microcrystalline samples were mounted on copper plates with rubber cement. The copper plates were attached to the sample holder. Magnetization was measured using a Quantum Design VSM system (Department of Quantum Matter Physics, University of Geneva) in the range of 2–300 K. Solid samples of Cr2Cl6(tppz) (15.8 mg), Cr2Cl6(bbt) (16.0 mg), Cr2Cl6(ebbt) (4.7 mg), [Cr2(tpy)2(bbt)](PF6)6 (8.1 mg) and [Cr2(tpy)2(ebbt)](PF6)6 (14.9 mg) were immobilized in capsules, which were locked in a straw. The samples were introduced in the SQUID under an inert atmosphere of helium.
35) (8 × 10−5 mol dm−3) were titrated at 298 K with a solution of Er(CF3SO3)3 (2 × 10−3 mol dm−3) in the same solvent under an inert atmosphere. After each addition of 0.10 mL, the absorbance was recorded using a Hellma optrode (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis130 and with the SPECFIT program.131 Absorption spectra in solution were recorded using a Cary 5000 Varian spectrometer (quartz cell path length 1 mm, 200–800 nm domain). Absorption spectra in the solid state were recorded on a Lambda 900 PerkinElmer spectrometer equipped with an integration sphere (background recorded on MgO). Emission spectra were recorded upon excitation at 400 nm from powder samples at various temperatures from 3 K to 295 K with a Fluorolog 3-22 (Horiba Jobin–Yvon), equipped with a peltier-cooled photo multiplier tube (Hamamatsu R2658P), and corrected for the spectral response of the system. Excitation at 355 nm was obtained with the third harmonic of a pulsed Nd:YAG laser (Quantel Brilliant). The emitted light was collected with a telescope and focused onto a light-guide with a fibre bundle connected to a monochromator (Spex 270 M). Full spectra were recorded with a CCD (Spex Spectrum One), decay curves with a photomultiplier (Hamamatsu R928) and a digital oscilloscope (Tektronix TDS540B) or a multichannel scaler (Stanford Research SR430). For the latter the spectral bandwidth of the monochromator was set to 20 nm, thus giving the decay of the integral signal. Low temperatures were achieved with a closed cycle cryosystem (Janis, SHI-950) with the sample sitting in exchange gas for efficient cooling. Microcrystalline samples were mounted on copper plates with rubber cement. The copper plates were attached to the sample holder. Magnetization was measured using a Quantum Design VSM system (Department of Quantum Matter Physics, University of Geneva) in the range of 2–300 K. Solid samples of Cr2Cl6(tppz) (15.8 mg), Cr2Cl6(bbt) (16.0 mg), Cr2Cl6(ebbt) (4.7 mg), [Cr2(tpy)2(bbt)](PF6)6 (8.1 mg) and [Cr2(tpy)2(ebbt)](PF6)6 (14.9 mg) were immobilized in capsules, which were locked in a straw. The samples were introduced in the SQUID under an inert atmosphere of helium.
X-Ray crystallography
A summary of crystal data, intensity measurements and structure refinements for compounds (1) to (15) is collected in Tables S2, S3, S12, S17, S21, S26, S31 and S38 (ESI†). The crystals were mounted on MiTeGen raptor cryoloops with protection oil. X-ray data collections were performed with an Agilent SuperNova Dual diffractometer equipped with a CCD Atlas detector (Cu[Kα] radiation). The structures were solved by using direct methods.140 Full-matrix least-square refinements on F2 were performed with SHELX97.141
Specific refinement details. [Cr(ebzpy)2](CF3SO3)3·2CH3CN (4): One triflate (of the 3 which are required for electroneutrality) and 0.5 CH3CN molecules were extremely disordered. Because of the lack of well-defined features in the electron density map, several attempts to model this disorder didn't give satisfactory refinement. We thus performed SQUEEZE after exclusion of these disordered molecules (using Platon)142 and found 8 voids of 123 Å3 containing 75 electrons (corresponding to one CF3SO3) and 4 voids of 71 Å3 containing 20 electrons (leading to 0.5 CH3CN per formula unit).
[Cr2Cl6(tppz)]·3C5H9NO (11): The crystal was twinned. The twinned operation was a two-fold rotation along the c axis producing apparent Laue symmetry 6/m. The twin law [−1 0 0; 0 −1 0; 0 0 1] was applied in SHELXL,141 including racemic twinning (four components). The twin fraction was 0.405(5) and the corresponding racemic twinning fractions were close to zero. Reflections hk2l were weak. There was almost translational symmetry with vector c/2. Indeed, the structure could be solved and refined in the smaller unit-cell with one complex and three solvent molecules, one of them disordered over two positions. The packing of this molecule produced the superstructure.
[Cr2Cl6(bbt)] (12): A very large hole (around 1700 Å3) was present in the structure. The squeeze/bypass procedure as implemented in Platon142 was used to take care of the disordered solvent present in this hole (which could not be modelled otherwise). Around 505 electrons were found in each hole, which corresponded to about 4 acetone molecules per formula unit (Z = 4). These molecules were not added to the formula so that the density and absorption coefficients were somehow underestimated. R factors before squeezing: R1 0.0788 and wR2 0.22756 (all data).
CCDC 1542315–1542329† contain the supplementary crystallographic data.
Acknowledgements
Financial support from the Swiss National Science Foundation is gratefully acknowledged.
References
- M. P. McDaniel, Adv. Catal., 1985, 33, 47–98 CAS.
- S. E. Schaus, J. Brånalt and E. N. Jacobsen, J. Org. Chem., 1998, 63, 403–405 CrossRef CAS.
- A. G. Dossetter, T. F. Jamison and E. N. Jacobsen, Angew. Chem., Int. Ed., 1999, 38, 2398–2400 CrossRef CAS PubMed.
- A. M. McDaniel, H.-W. Tseng, N. H. Damrauer and M. P. Shores, Inorg. Chem., 2010, 49, 7981–7991 CrossRef CAS PubMed.
- A. M. McDaniels, H.-W. Tseng, E. A. Hill, N. H. Damrauer, A. K. Rappé and M. P. Shores, Inorg. Chem., 2013, 52, 1368–1378 CrossRef PubMed.
- T. Mallah, S. Thiébaut, M. Verdaguer and P. Veillet, Science, 1993, 262, 1554–1557 CAS.
- V. Gadet, T. Mallah, I. Castro, M. Verdaguer and P. Veillet, J. Am. Chem. Soc., 1992, 114, 9213–9214 CrossRef CAS.
- R. L. Carlin and R. Burriel, Phys. Rev. B: Condens. Matter, 1983, 27, 3012–3017 CrossRef CAS.
- M. Verdaguer, A. Bleuzen, V. Marvaud, J. Vaissermann, M. Seuleiman, C. Desplanches, A. Scuiller, C. Train, R. Garde, G. Gelly, C. Lomenech, I. Rosenman, P. Veillet, C. Cartier and F. Villain, Coord. Chem. Rev., 1999, 190–192, 1023–1047 CrossRef CAS.
- O. Kahn and B. Briat, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 268–281 RSC.
- W. Liu, J. H. Christian, R. Al-Oweini, B. S. Bassil, J. van Tol, M. Atanasov, F. Neese, N. S. Dalal and U. Kortz, Inorg. Chem., 2014, 53, 9274–9283 CrossRef CAS PubMed.
- N. Novosel, D. Žilić, D. Pajić, M. Jurić, B. Perić, K. Zadro, B. Rakvin and P. Planinić, Solid State Sci., 2008, 10, 1387–1394 CrossRef CAS.
- L. S. Forster, Chem. Rev., 1990, 90, 331–353 CrossRef CAS.
- M. A. Jamieson, N. Serpone and M. Z. Hoffman, Coord. Chem. Rev., 1981, 39, 121–179 CrossRef CAS.
- A. D. Kirk, Coord. Chem. Rev., 1981, 39, 225–263 CrossRef CAS.
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef.
- F.-F. Chen, Z.-Q. Chen, Z.-Q. Bian and C.-H. Huang, Coord. Chem. Rev., 2010, 254, 991–1010 CrossRef CAS.
- L. Aboshyan-Sorgho, M. Cantuel, S. Petoud, A. Hauser and C. Piguet, Coord. Chem. Rev., 2012, 256, 1644–1663 CrossRef CAS.
- T. J. Meyer, Pure Appl. Chem., 1986, 58, 1193–1206 CrossRef CAS.
- V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759–833 CrossRef CAS PubMed.
- V. Balzani, G. Bergamini, F. Marchioni and P. Ceroni, Coord. Chem. Rev., 2006, 250, 1254–1266 CrossRef CAS.
- F. R. Keene, Dalton Trans., 2011, 40, 2405–2418 RSC.
- A. K. Pal and G. S. Hanan, Chem. Soc. Rev., 2014, 43, 6184–6197 RSC.
- A. Winter and U. S. Schubert, Chem. Soc. Rev., 2016, 45, 5311–5357 RSC.
- L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923–1960 CrossRef CAS PubMed.
- R. G. Pearson, R. A. Munson and F. Basolo, J. Am. Chem. Soc., 1958, 80, 504 CrossRef CAS.
- C.-A. Palma, M. Cecchini and P. Samori, Chem. Soc. Rev., 2012, 41, 3713–3730 RSC.
- M. Murrie, S. Parsons, R. E. P. Winpenny, I. M. Atkinson and C. Benelli, Chem. Commun., 1999, 285–286 RSC.
- E. J. L. McInnes, S. Piligkos, G. A. Timco and R. E. P. Winpenny, Coord. Chem. Rev., 2005, 249, 2577–2590 CrossRef CAS.
- G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem. Soc. Rev., 2013, 42, 1796–1806 RSC.
- J. Springborg, Adv. Inorg. Chem., 1988, 32, 55–169 CrossRef CAS.
- G. Marinescu, M. Andruh, F. Lloret and M. Julve, Coord. Chem. Rev., 2011, 255, 161–185 CrossRef CAS.
- S. Decurtins, M. Gross, H. W. Schmalle and S. Ferlay, Inorg. Chem., 1998, 37, 2443–2448 CrossRef CAS.
- R. Sieber, S. Decurtins, H. Stoeckli-Evans, C. Wilson, D. Yufit, J. A. K. Howard, S. C. Capelli and A. Hauser, Chem. – Eur. J., 2000, 6, 361–368 CrossRef CAS.
- M. E. von Arx, E. Burattini, A. Hauser, L. van Pietserson, R. Pellaux and S. Decurtins, J. Phys. Chem. A, 2000, 104, 883–893 CrossRef CAS.
- M. A. Subhan, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 2001, 492–497 RSC.
- H.-Z. Kou, B. C. Zhou, S. Gao and R.-J. Wang, Angew. Chem., Int. Ed., 2003, 42, 3288–3291 CrossRef CAS PubMed.
- Y. Li, Z. Jiang, M. Wang, J. Yuan, D. Liu, X. Yang, M. Chen, J. Yan, X. Li and P. Wang, J. Am. Chem. Soc., 2016, 138, 10041–10046 CrossRef CAS PubMed.
- D. Liu, Z. Jiang, M. Wang, X. Yang, H. Liu, M. Chen, C. N. Moorefield, G. R. Newkome, X. Li and P. Wang, Chem. Commun., 2016, 52, 9773–9776 RSC.
- H. Iranmanesh, K. S. A. Arachchige, M. Bhadhade, W. A. Donald, J. Y. Liew, K. T.-C. Liu, E. T. Luis, E. G. Moore, J. R. Price, H. G. Yan, J.-X. Yang and J. E. Beves, Inorg. Chem., 2016, 55, 12737–12751 CrossRef CAS PubMed.
- B. Doistau, A. Tron, S. A. Denisov, G. Jonusauskas, N. D. McClenaghan, G. Gontard, V. Marvaud, B. Hasenknopf and G. Vives, Chem. – Eur. J., 2014, 20, 15799–15807 CrossRef CAS PubMed.
- B. Doistau, J.-L. Cantin, L.-M. Chamoreau, V. Marvaud, B. Hasenknopf and G. Vives, Chem. Commun., 2015, 51, 12916–12919 RSC.
- R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918 CrossRef CAS PubMed.
- M. Wang, K. Wang, C. Wang, M. Huang, X.-Q. Hao, M.-Z. Shen, G.-Q. Shi, Z. Zhang, B. Song, A. Cisneros, M.-P. Song, B. Xu and X. Li, J. Am. Chem. Soc., 2016, 138, 9258–9268 CrossRef CAS PubMed.
- E. C. Constable and A. M. W. Cargill-Thompson, J. Chem. Soc., Dalton Trans., 1995, 1615–1627 RSC.
- E. C. Constable, C. E. Housecroft, M. Neuburger, J. Schönle and J. A. Zampese, Dalton Trans., 2014, 43, 7227–7235 RSC.
- M. Maestri, F. Bolletta, N. Serpone, L. Moggi and V. Balzani, Inorg. Chem., 1976, 15, 2048–2051 CrossRef CAS.
- M. Cantuel, G. Bernardinelli, D. Imbert, J.-C. G. Bunzli, G. Hopfgartner and C. Piguet, J. Chem. Soc., Dalton Trans., 2002, 1929–1940 RSC.
- M. Cantuel, F. Gumy, J.-C. G. Bunzli and C. Piguet, Dalton Trans., 2006, 2647–2660 RSC.
- L. Aboshyan-Sorgho, C. Besnard, P. Pattison, K. R. Kittilstved, A. Aebischer, J.-C. G. Bünzli, A. Hauser and C. Piguet, Angew. Chem., Int. Ed., 2011, 50, 4108–4112 CrossRef CAS PubMed.
- Y. Suffren, D. Zare, S. V. Eliseeva, L. Guénée, H. Nozary, T. Lathion, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, J. Phys. Chem. C, 2013, 117, 26957–26963 CAS.
- D. Zare, Y. Suffren, L. Guénée, S. V. Eliseeva, H. Nozary, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, Dalton Trans., 2015, 44, 2529–2540 RSC.
- Y. Suffren, B. Golesorkhi, D. Zare, L. Guénée, H. Nozary, S. V. Eliseeva, S. Petoud, A. Hauser and C. Piguet, Inorg. Chem., 2016, 55, 9964–9972 CrossRef CAS PubMed.
- I. Bertini, P. Turano and A. J. Vila, Chem. Rev., 1993, 93, 2833–2932 CrossRef CAS.
- E. Rousset, D. Chartrand, I. Ciofini, V. Marvaud and G. S. Hanan, Chem. Commun., 2015, 51, 9261–9264 RSC.
- V. Balzani, A. Credi and M. Venturi, ChemSusChem, 2008, 1, 26–58 CrossRef CAS PubMed.
- M. Schulze, V. Kunz, P. D. Frischmann and F. Würthner, Nat. Chem., 2016, 8, 576–583 CrossRef CAS PubMed.
- J. P. Collin, S. Guillerez, J. P. Sauvage, F. Barigelletti, L. De Cola, L. Flamigni and V. Balzani, Inorg. Chem., 1991, 30, 4230–4238 CrossRef CAS.
- C. K. Jorgensen, Adv. Chem. Phys., 1963, 5, 33–146 CrossRef CAS.
-
A. B. P. Lever, Inorganic Electronic Spectroscopy, Elsevier, Amsterdam, Oxford, New York, Tokyo, 2nd edn, 1984, p. 126 Search PubMed.
- S. K. Padhi, D. Saha, R. Sahu, J. Subramanian and V. Manivannan, Polyhedron, 2008, 27, 1714–1720 CrossRef CAS.
- T. J. Morsing, S. P. A. Sauer, H. Weihe, J. Bendix and A. Døssing, Inorg. Chim. Acta, 2013, 396, 72–77 CrossRef CAS.
- C. Creutz and H. Taube, J. Am. Chem. Soc., 1969, 91, 3988–3989 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- A. Heckmann and C. Lambert, Angew. Chem., Int. Ed., 2012, 51, 326–392 CrossRef CAS PubMed.
-
M. B. Robin and P. Day, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1968, vol. 10, pp. 247–422 Search PubMed.
- P. Day, N. S. Hush and R. J. H. Clarck, Philos. Trans. R. Soc., A, 2008, 366, 5–14 CrossRef CAS PubMed.
- J. P. Sauvage, J. P. Collin, J. C. Chambron, S. Guillerez, C. Coudret, V. Balzani, F. Barigelletti, L. De Cola and L. Flamigni, Chem. Rev., 1994, 94, 993–1019 CrossRef CAS.
- H. Ozawa, M. Baghernejad, O. A. Al-Owaedi, V. Kaliginedi, T. Nagashima, J. Ferrer, T. Wandlowski, V. M. García-Suárez, P. Broekmann, C. J. Lambert and M.-A. Haga, Chem. – Eur. J., 2016, 22, 12732–12740 CrossRef CAS PubMed.
- J.-P. Collin, P. Laine, J.-P. Launay, J.-P. Sauvage and A. Sour, J. Chem. Soc., Chem. Commun., 1993, 434–435 RSC.
- H. Torieda, K. Nozaki, A. Yoshimura and T. Ohno, J. Phys. Chem. A, 2004, 108, 4819–4829 CrossRef CAS.
- H. Torieda, A. Yoshimura, K. Nozaki, S. Sakai and T. Ohno, J. Phys. Chem. A, 2002, 106, 11034–11044 CrossRef CAS.
- B. Schlicke, P. Belser, L. De Cola, E. Sabbioni and V. Balzani, J. Am. Chem. Soc., 1999, 121, 4207–4214 CrossRef CAS.
- F. Barigelletti, L. Flamigni, V. Balzani, J.-P. Collin, J.-P. Sauvage, A. Sour, E. C. Constable and A. M. W. Cargill-Thompson, J. Am. Chem. Soc., 1994, 116, 7692–7699 CrossRef CAS.
- M. Bar, D. Maity, S. Das and S. Baitalik, Dalton Trans., 2016, 45, 17241–17253 RSC.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- S. S. Skourtis, C. Liu, P. Antoniou, A. M. Virshup and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8115–8120 CrossRef CAS PubMed.
- C. C. Scarborough, S. Sproules, T. Weyhermueller, S. DeBeer and K. Wieghardt, Inorg. Chem., 2011, 50, 12446–12462 CrossRef CAS PubMed.
- C. C. Scarborough, K. M. Lancaster, S. DeBeer, T. Weyhermüller, S. Sproules and K. Wieghardt, Inorg. Chem., 2012, 51, 3718–3732 CrossRef CAS PubMed.
- K. D. Barker, K. A. Barnett, S. M. Connell, J. W. Glaeser, A. J. Wallace, J. Wildsmith, B. J. Herbert, J. F. Wheeler and N. A. P. Kane-Maguire, Inorg. Chim. Acta, 2001, 316, 41–49 CrossRef CAS.
- M. Isaacs, A. G. Sykes and S. Ronco, Inorg. Chim. Acta, 2006, 359, 3847–3854 CrossRef CAS.
- J. Schönle, E. C. Constable, C. E. Housecroft and M. Neuburger, Inorg. Chem. Commun., 2015, 53, 80–83 CrossRef.
- J. Schönle, E. C. Constable, C. E. Housecroft, A. Prescimone and J. A. Zampese, Polyhedron, 2015, 89, 182–188 CrossRef.
- L. Pazderski, T. Pawlak, J. Sitkowski, L. Kozerski and E. Szlyk, Magn. Reson. Chem., 2011, 49, 237–241 CrossRef CAS PubMed.
- E. C. Constable, Adv. Inorg. Chem. Radiochem., 1986, 30, 69–121 CAS.
- M. L. Scudder, H. A. Goodwin and I. G. Dance, New J. Chem., 1999, 23, 695–705 RSC.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed.
- R. Zhao and R.-Q. Zhang, Phys. Chem. Chem. Phys., 2016, 18, 15452–25457 Search PubMed.
- C. Piguet, J.-C. G. Bünzli, G. Bernardinelli and A. F. Williams, Inorg. Chem., 1993, 32, 4139–4149 CrossRef CAS.
- W. A. Wickramasinghe, P. H. Bird, M. A. Jamieson and N. Serpone, J. Chem. Soc., Chem. Commun., 1979, 1979, 798–800 RSC.
- W. A. Wickramasinghe, P. H. Bird and N. Serpone, Inorg. Chem., 1982, 21, 2694–2698 CrossRef CAS.
- N. Cloete, H. G. Visser and A. Roodt, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, m45–m47 CAS.
- W. Zhang, W.-H. Sun, S. Zhang, J. Hou, K. Wedeking, S. Schultz, R. Fröhlich and H. Song, Organometallics, 2006, 25, 1961–1969 CrossRef CAS.
- R. S. Bitzer, C. A. L. Filgueiras, J. G. S. Lopes, P. S. Santos and M. H. Herbst, Transition Met. Chem., 2005, 30, 636–642 CrossRef CAS.
- R. C. Rocha, F. N. Rein, H. Jude, A. P. Shreve, J. J. Concepcion and T. J. Meyer, Angew. Chem., Int. Ed., 2008, 47, 503–506 CrossRef CAS PubMed.
- B. A. Albani, B. Pena, S. Saha, J. K. White, A. M. Schaeffer, K. R. Dunbar and C. Turro, Chem. Commun., 2015, 51, 16522–16525 RSC.
- R. Davidson, J.-H. Liang, D. Costa Milan, B.-W. Mao, R. J. Nichols, S. J. Higgins, D. S. Yufit, A. Beeby and P. J. Low, Inorg. Chem., 2015, 54, 5487–5494 CrossRef CAS PubMed.
- M. Graf, H. Stoeckli-Evans, A. Escuer and R. Vicente, Inorg. Chim. Acta, 1997, 257, 89–97 CrossRef CAS.
- T. Nagashima, T. Nakabayashi, T. Suzuki, K. Kanaizuka, H. Ozawa, Y.-W. Zhong, S. Masaoka, K. Sakai and M.-A. Haga, Organometallics, 2014, 33, 4893–4904 CrossRef CAS.
- C.-J. Yao, Y.-W. Zhong and J. Yao, Inorg. Chem., 2013, 52, 4040–4045 CrossRef CAS PubMed.
- N. Yoshikawa, S. Yamabe, N. Kanehisa, T. Inoue, H. Takashima and K. Tsukahara, J. Phys. Org. Chem., 2011, 24, 1110–1118 CrossRef CAS.
- Á. J. Pérez-Jiménez, J. C. Sancho-García and J. M. Pérez-Jordá, J. Chem. Phys., 2005, 123, 134309 CrossRef PubMed.
- M. P. Johansson and J. Olsen, J. Chem. Theor. Comput., 2008, 4, 1460–1471 CrossRef CAS PubMed.
- W. Ouellette, B.-K. Koo, E. Burkholder, V. Golub, C. J. O'Connor and J. Zubieta, Dalton Trans., 2004, 1527–1538 RSC.
- S. Jones, J. M. Vargas, S. Pellizzeri, C. J. O'Connor and J. Zubieta, Inorg. Chim. Acta, 2013, 395, 44–57 CrossRef CAS.
- S. Dev, S. Maheshwari and A. R. Choudhury, RSC Adv., 2015, 5, 26932–26940 RSC.
- E. Kryachko and S. Scheiner, J. Phys. Chem. A, 2004, 108, 2527–2535 CrossRef CAS.
- V. Grosshenny, F. M. Romero and R. Ziessel, J. Org. Chem., 1997, 62, 1491–1500 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
-
J.-P. Launay and M. Verdaguer, Electrons in Molecules from Basic Principles to Molecular Electronics, Oxford University Press, Oxford, 2014 Search PubMed.
-
O. Kahn, Molecular Magnetism, VCH Publishers, Weinheim, 1993, pp. 150–164 Search PubMed.
- Q. Ren and Z. Chen, J. Mol. Struct. (THEOCHEM), 2005, 719, 159–168 CrossRef CAS.
- M. Atanasov, P. Comba and C. A. Daul, Inorg. Chem., 2008, 47, 2449–2463 CrossRef CAS PubMed.
- H. Witzke, Theor. Chim. Acta, 1971, 20, 171–185 CrossRef CAS.
- D. L. Wood, J. Ferguson, K. Knox and J. F. Dillon, J. Chem. Phys., 1963, 39, 890–898 CrossRef CAS.
- J. Ferguson, Prog. Inorg. Chem., 1970, 12, 159–293 CAS.
-
C. K. Jorgensen, Modern Aspects of Ligand Field Theory, North Holland Publishing Company, Amsterdam, 1971, ch. 23 and 26 Search PubMed.
- A. Hauser, M. Maeder, W. T. Robinson, R. Murugesan and J. Ferguson, Inorg. Chem., 1987, 26, 1331–1338 CrossRef CAS.
- S. Otto, M. Grabolle, C. Förster, C. Kreitner, U. Resch-Genger and K. Heinze, Angew. Chem., Int. Ed., 2015, 54, 11572–11576 CrossRef CAS PubMed.
- A. Harriman, A. Khatyr, R. Ziessel and A. C. Benniston, Angew. Chem., Int. Ed., 2000, 39, 4287–4290 CrossRef CAS.
- A. C. Benniston, G. Chapman, A. Harriman, M. Mehrabi and C. A. Sams, Inorg. Chem., 2004, 43, 4227–4233 CrossRef CAS PubMed.
- T. V. Duncan, K. Song, S.-T. Hung, I. Miloradovic, A. Nayak, A. Persoons, T. Verbiest, M. J. Therien and K. Clays, Angew. Chem., Int. Ed., 2008, 47, 2978–2981 CrossRef CAS PubMed.
- F. Castelli and L. S. Forster, J. Am. Chem. Soc., 1975, 97, 6306–6309 CrossRef CAS.
-
M. E. Starzak, in Mathematical Methods in Chemistry and Physics, Plenum Press, New York, 1989, pp. 289–357 Search PubMed.
-
B. Henderson and G. F. Imbusch, Optical Spectroscopy of Inorganic Solids, Clarendon Press, Oxford, 1989 Search PubMed.
- Y. Shen, T. Riedener and K. L. Bray, Phys. Rev. B: Condens. Matter, 2000, 61, 11460–11471 CrossRef CAS.
- A. Zaïm, S. V. Eliseeva, L. Guénée, H. Nozary, S. Petoud and C. Piguet, Chem. – Eur. J., 2014, 20, 12172–12182 CrossRef PubMed.
- J. Yuasa and S. Fukuzumi, J. Am. Chem. Soc., 2008, 130, 566–575 CrossRef CAS PubMed.
-
(a)
E. R. Malinowski and D. G. Howery, Factor Analysis in Chemistry, Wiley, New York, Chichester, 1980 Search PubMed;
(b) H. Gampp, M. Maeder, C. J. Meyer and A. Zuberbühler, Talanta, 1986, 33, 943–951 CrossRef CAS PubMed;
(c) B. R. Hall, L. E. Manck, I. S. Tidmarsh, A. Stephenson, B. F. Taylor, E. J. Blaikie, D. A. Vander Griend and M. D. Ward, Dalton Trans., 2011, 40, 12132–12145 RSC.
-
(a) H. Gampp, M. Maeder, C. J. Meyer and A. Zuberbühler, Talanta, 1985, 32, 1133–1139 CrossRef CAS PubMed;
(b)
M. Maeder and P. King, Analysis of Chemical Processes, Determination of the Reaction Mechanism and Fitting of Equilibrium and Rate Constants, in Chemometrics in Practical Applications, ed. K. Varmuza, InTech, 2012, ISBN: 978-953-51-0438-4, DOI:10.5772/31896;
(c) Specfit/32 from ReactLab Equilibria: http://jplusconsulting.com/products/reactlab-equilibria/.
- A. Duerrbeck, S. Gorelik, J. Hobley, J. Wu, A. Hor and N. Long, Chem. Commun., 2015, 51, 8656–8659 RSC.
- C. Piguet, Chem. Commun., 2010, 46, 6209–6231 RSC.
- G. Ercolani, C. Piguet, M. Borkovec and J. Hamacek, J. Phys. Chem. B, 2007, 111, 12195–12203 CrossRef CAS PubMed.
- A. Escande, L. Guénée, K.-L. Buchwalder and C. Piguet, Inorg. Chem., 2009, 48, 1132–1147 CrossRef CAS PubMed.
- A. Albert and J. N. Phillips, J. Chem. Soc., 1956, 1294–1304 RSC.
- A. W.-H. Mau, J. H. Overbeek, J. W. Loder and W. H. F. Sasse, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 869–876 RSC.
- V. Grosshenny and R. Ziessel, J. Organomet. Chem., 1993, 453, C19–C22 CrossRef CAS.
-
(a) E. C. Constable and M. D. Ward, J. Chem. Soc., Dalton Trans., 1990, 1405–1409 RSC;
(b) E. C. Constable and A. M. W. C. Thompson, J. Chem. Soc., Dalton Trans., 1992, 3467–3475 RSC.
-
(a) SHELXS97 G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed;
(b) SIR97 A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119 CrossRef CAS;
(c) SIR92: A. Altomare, G. Cascarano, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 1993, 26, 343–350 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 CrossRef PubMed.
- P. van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 194–201 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1542315–1542329. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt01747b |
| ‡ These authors contributed equally to this research work. |
|
| This journal is © The Royal Society of Chemistry 2017 |
 Open Access Article
Open Access Article *a
*a
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cr(tpy)2]3+) complexes rapidly dissociate under slightly alkaline conditions,46 a trend which confirms a previous observation reported for [Cr(2,2′-bipyridine)3]3+ (
[Cr(tpy)2]3+) complexes rapidly dissociate under slightly alkaline conditions,46 a trend which confirms a previous observation reported for [Cr(2,2′-bipyridine)3]3+ (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [Cr(bpy)3]3+),47 prevents post-treatment of these complexes for the design of organized polynuclear assemblies. To the best of our knowledge, trivalent chromium has thus never been used as a partner for thermodynamic multi-component self-assembly processes occurring in solution, but its labile divalent precursor CrII was shown to successfully promote the synthesis of heterometallic d–f triple-stranded helicates under thermodynamic control.48,49 Subsequent air oxidation led to inert luminescent CrIII sensitizers, which induced unprecedented lanthanide-centred molecular energy-transfer upconversion.50–53 Last but not least, the characterization of CrIII complexes in solution is severely hampered by the broad and poorly interpretable NMR signals produced by the long electronic relaxation times (about 0.5 ns) of their zero-field split Cr(4A2) ground state.54 This drawback is overcome for diamagnetic RuII complexes, which were thus selected for building well-defined photoactive polynuclear architectures useful for water splitting,55 light-harvesting and energy conversion.56–58 Nevertheless, while trivalent chromium exhibits some shortcomings compared to divalent ruthenium, its photophysical properties in pseudo-octahedral complexes offer some unparalleled attractiveness since the visible window is dominated by a single spin-allowed absorption band corresponding to the Cr(4T2 ← 4A2) transition, the energy of which can be easily tuned by the ligand-field parameter Δ, whereas the near-infrared window is governed by efficient long-lived Cr(2E ← 4A2) phosphorescence, the energy of which is controlled by the nephelauxetic effect tuned by the Racah parameters B and C (Fig. 1).13,59,60 It is thus trivial to switch from low-energy absorption combined with high-energy phosphorescence found in CrO6 chromophores (small values of Δ and large values of B) toward the opposite situation found in CrN6 chromophores.13 Furthermore, the almost spin-only behavior combined with negligible zero-field splitting parameters measured for the degenerate paramagnetic Cr(4A2) ground state (for instance D = 0.03 cm−1 for [(tpy)CrCl3])61 offers a simple approach for unravelling electronic intermetallic communications via the estimation of the isotropic exchange coupling constant operating between chromium centres.10,12,62
[Cr(bpy)3]3+),47 prevents post-treatment of these complexes for the design of organized polynuclear assemblies. To the best of our knowledge, trivalent chromium has thus never been used as a partner for thermodynamic multi-component self-assembly processes occurring in solution, but its labile divalent precursor CrII was shown to successfully promote the synthesis of heterometallic d–f triple-stranded helicates under thermodynamic control.48,49 Subsequent air oxidation led to inert luminescent CrIII sensitizers, which induced unprecedented lanthanide-centred molecular energy-transfer upconversion.50–53 Last but not least, the characterization of CrIII complexes in solution is severely hampered by the broad and poorly interpretable NMR signals produced by the long electronic relaxation times (about 0.5 ns) of their zero-field split Cr(4A2) ground state.54 This drawback is overcome for diamagnetic RuII complexes, which were thus selected for building well-defined photoactive polynuclear architectures useful for water splitting,55 light-harvesting and energy conversion.56–58 Nevertheless, while trivalent chromium exhibits some shortcomings compared to divalent ruthenium, its photophysical properties in pseudo-octahedral complexes offer some unparalleled attractiveness since the visible window is dominated by a single spin-allowed absorption band corresponding to the Cr(4T2 ← 4A2) transition, the energy of which can be easily tuned by the ligand-field parameter Δ, whereas the near-infrared window is governed by efficient long-lived Cr(2E ← 4A2) phosphorescence, the energy of which is controlled by the nephelauxetic effect tuned by the Racah parameters B and C (Fig. 1).13,59,60 It is thus trivial to switch from low-energy absorption combined with high-energy phosphorescence found in CrO6 chromophores (small values of Δ and large values of B) toward the opposite situation found in CrN6 chromophores.13 Furthermore, the almost spin-only behavior combined with negligible zero-field splitting parameters measured for the degenerate paramagnetic Cr(4A2) ground state (for instance D = 0.03 cm−1 for [(tpy)CrCl3])61 offers a simple approach for unravelling electronic intermetallic communications via the estimation of the isotropic exchange coupling constant operating between chromium centres.10,12,62



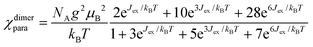

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316
316![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 927
927
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 893
893
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393
393![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903
903![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569
569![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393
393![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 134
134
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980
980![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502
502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920
920![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495
495![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502
502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 482
482
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 671
671
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722
722![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837
837![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 643
643![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722
722![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 524
524
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 782
782
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674
674![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 379d
379d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 614
614
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 132
132
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089
089![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 846d
846d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 117
117
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 312
312
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694
694![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175
175![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931d
931d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 694
694![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 265
265
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 585
585
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953
953![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584d
584d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 340
340
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 663
663
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 cm−1 in fair to good agreement with the prediction of the second-order correction 26B2/Δ = 603 cm−1 (eqn (6)), but rather far from 1531 cm−1 obtained with eqn (5). We conclude that only a complete ligand-field treatment is capable of extracting reliable Racah parameters B and C for CrIII complexes,119 but eqn (6) seems superior to eqn (5) when a rough modeling of the energy of the lowest spin–flip 2E excited state is foreseen. We therefore used eqn (3), (4) and (6) for estimating the ligand-field strength Δ and the Racah parameters B and C for each dimeric and monomeric complex (Table 1 and Fig. 8, Table S37 and Fig. S20 in the ESI†) together with eqn (7) and (8) for predicting the energy of the missing Cr(2T2) and Cr(4T1) levels.
940 cm−1 in fair to good agreement with the prediction of the second-order correction 26B2/Δ = 603 cm−1 (eqn (6)), but rather far from 1531 cm−1 obtained with eqn (5). We conclude that only a complete ligand-field treatment is capable of extracting reliable Racah parameters B and C for CrIII complexes,119 but eqn (6) seems superior to eqn (5) when a rough modeling of the energy of the lowest spin–flip 2E excited state is foreseen. We therefore used eqn (3), (4) and (6) for estimating the ligand-field strength Δ and the Racah parameters B and C for each dimeric and monomeric complex (Table 1 and Fig. 8, Table S37 and Fig. S20 in the ESI†) together with eqn (7) and (8) for predicting the energy of the missing Cr(2T2) and Cr(4T1) levels.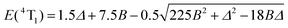
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ≤ Δ ≤ 17
300 ≤ Δ ≤ 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) to CrN6 (18
000 cm−1) to CrN6 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 ≤ Δ ≤ 19
750 ≤ Δ ≤ 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 cm−1), whereas the Racah parameters B = 682(19) cm−1 are comparable for both types of chromophores. A narrow distribution of these complexes around Δ/B ≈ 25 results in the d3 Tanabe–Sugano diagram (Fig. S21†). The latter Δ/B values are significantly smaller than Δ/B = 31.2 reported for the well-known [Cr(bpy)3](PF6)3 complex (Δ = 23
120 cm−1), whereas the Racah parameters B = 682(19) cm−1 are comparable for both types of chromophores. A narrow distribution of these complexes around Δ/B ≈ 25 results in the d3 Tanabe–Sugano diagram (Fig. S21†). The latter Δ/B values are significantly smaller than Δ/B = 31.2 reported for the well-known [Cr(bpy)3](PF6)3 complex (Δ = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1, B = 730 cm−1 and C = 2730 cm−1, C/B = 3.7)119 because the pincer effect produced by 5-membered chelate rings operates four times in [Cr(L)2]3+ (L = tpy, ebzpy) and only three times in [Cr(bpy)3]3+. This deleterious effect is not a fatality for tridentate ligands and it can be overcome by the use of six-membered chelate rings as found in [Cr(ddpd)Cl3] (15) (Fig. S22 and S23 and Tables S38–S40 in the ESI†) and in [Cr(ddpd)2](BF4)3 complexes (ddpd = N,N′-dimethyl-N,N′′-dipyridin-2-ylpyridine-2,6-diamine).120 The larger Ndistal–Cr–Ndistal angle of 172.0(9)° observed in [Cr(ddpd)2]3+ (compared with 156.5(5)° in [Cr(tpy)2]3+) indeed restores a large ligand field strength in bis-terdentate pseudo-octahedral complexes (Δ = 22
400 cm−1, B = 730 cm−1 and C = 2730 cm−1, C/B = 3.7)119 because the pincer effect produced by 5-membered chelate rings operates four times in [Cr(L)2]3+ (L = tpy, ebzpy) and only three times in [Cr(bpy)3]3+. This deleterious effect is not a fatality for tridentate ligands and it can be overcome by the use of six-membered chelate rings as found in [Cr(ddpd)Cl3] (15) (Fig. S22 and S23 and Tables S38–S40 in the ESI†) and in [Cr(ddpd)2](BF4)3 complexes (ddpd = N,N′-dimethyl-N,N′′-dipyridin-2-ylpyridine-2,6-diamine).120 The larger Ndistal–Cr–Ndistal angle of 172.0(9)° observed in [Cr(ddpd)2]3+ (compared with 156.5(5)° in [Cr(tpy)2]3+) indeed restores a large ligand field strength in bis-terdentate pseudo-octahedral complexes (Δ = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1, Table S37†). Focusing now on the through-bridge effect produced by the connection of a second neutral CrCl3 unit which transforms [Cr(tppz)Cl3] into its dinuclear [Cl3Cr(tppz)CrCl3] analogue (Cr⋯Cr = 6.66 Å), we observe that Δ decreases by almost 500 cm−1 (Fig. 8). This effect can be taken as an assessment of the mutual polarization (i.e. electronic communication) produced by the two CrIII centres connected to the bridging back-to-back bis-terdentate ligand. Taking now [Cr(tpy)Cl3] as the mononuclear reference, the same trend is monitored for [Cl3Cr(bbt)CrCl3] (Δ decreases by 300 cm−1 for Cr⋯Cr = 10.93 Å) and [Cl3Cr(ebbt)CrCl3] (Δ decreases by 200 cm−1 for Cr⋯Cr ≥ 13 Å), but with an expected attenuation for longer intermetallic distances. For the charged [CrN6]3+ chromophore found in the mononuclear [Cr(tpy)2]3+ reference complex (Δ = 18
990 cm−1, Table S37†). Focusing now on the through-bridge effect produced by the connection of a second neutral CrCl3 unit which transforms [Cr(tppz)Cl3] into its dinuclear [Cl3Cr(tppz)CrCl3] analogue (Cr⋯Cr = 6.66 Å), we observe that Δ decreases by almost 500 cm−1 (Fig. 8). This effect can be taken as an assessment of the mutual polarization (i.e. electronic communication) produced by the two CrIII centres connected to the bridging back-to-back bis-terdentate ligand. Taking now [Cr(tpy)Cl3] as the mononuclear reference, the same trend is monitored for [Cl3Cr(bbt)CrCl3] (Δ decreases by 300 cm−1 for Cr⋯Cr = 10.93 Å) and [Cl3Cr(ebbt)CrCl3] (Δ decreases by 200 cm−1 for Cr⋯Cr ≥ 13 Å), but with an expected attenuation for longer intermetallic distances. For the charged [CrN6]3+ chromophore found in the mononuclear [Cr(tpy)2]3+ reference complex (Δ = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, Table 1), the latter effect is drastically amplified leading to a ca. 2000 cm−1 reduction of the ligand-field parameter Δ in the related charged dinuclear complexes [(tpy)Cr(L)Cr(tpy)]6+ (L = bbt, ebbt, Fig. 8 and Table 1). The considerable reduction of Δ recorded for the longest ebbt bridging ligand in [(tpy)Cr(ebbt)Cr(tpy)]6+ combined with the operation of the largest nephelauxetic dispersion (i.e. the minimum B Racah parameter, Table 1) confirms that an alternation of alkyne/aromatic groups is particularly adapted for the design of electronic wires between CrIII centres, a result in line with the exceptional delocalization of the electronic density from the metal centres reported for analogous rod-like Ru(II)/Os(II) dyads.121–123 Intermetallic communication can be alternatively probed by time-resolved emission spectroscopy performed on powder samples of the dinuclear complexes at cryogenic temperatures. The Cr(2E → 4A2) phosphorescence signals showed double exponential decays for all complexes except for the unsolvated centrosymmetrical [Cr2Cl6(bbt)] complex, for which the kinetic decay trace is mono-exponential (Table 2 and Fig. A2-9–A2-13 in Appendix 2†).
750 cm−1, Table 1), the latter effect is drastically amplified leading to a ca. 2000 cm−1 reduction of the ligand-field parameter Δ in the related charged dinuclear complexes [(tpy)Cr(L)Cr(tpy)]6+ (L = bbt, ebbt, Fig. 8 and Table 1). The considerable reduction of Δ recorded for the longest ebbt bridging ligand in [(tpy)Cr(ebbt)Cr(tpy)]6+ combined with the operation of the largest nephelauxetic dispersion (i.e. the minimum B Racah parameter, Table 1) confirms that an alternation of alkyne/aromatic groups is particularly adapted for the design of electronic wires between CrIII centres, a result in line with the exceptional delocalization of the electronic density from the metal centres reported for analogous rod-like Ru(II)/Os(II) dyads.121–123 Intermetallic communication can be alternatively probed by time-resolved emission spectroscopy performed on powder samples of the dinuclear complexes at cryogenic temperatures. The Cr(2E → 4A2) phosphorescence signals showed double exponential decays for all complexes except for the unsolvated centrosymmetrical [Cr2Cl6(bbt)] complex, for which the kinetic decay trace is mono-exponential (Table 2 and Fig. A2-9–A2-13 in Appendix 2†).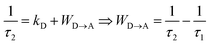
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform = 65
chloroform = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 (Fig. 11). The resulting changes in the absorption spectra are characterized by smooth end points occurring at Eu
35 (Fig. 11). The resulting changes in the absorption spectra are characterized by smooth end points occurring at Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, Eu
3, Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, Eu
2, Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and Eu
3 and Eu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 1
L = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 11a and b for L = tppz and Fig. S24a for L = bbt in the ESI†). Factor analysis (Fig. 11c and Fig. S24c†)130 followed by non-linear least square fits131 to equilibria (12)–(15) (Fig. 11e) provide satisfying re-constructed individual absorption spectra (Fig. 11d and Fig. S24d†) together with macroscopic formation constants gathered in Table 3 (entries 1–4).
1 (Fig. 11a and b for L = tppz and Fig. S24a for L = bbt in the ESI†). Factor analysis (Fig. 11c and Fig. S24c†)130 followed by non-linear least square fits131 to equilibria (12)–(15) (Fig. 11e) provide satisfying re-constructed individual absorption spectra (Fig. 11d and Fig. S24d†) together with macroscopic formation constants gathered in Table 3 (entries 1–4).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHCl3 = 65
CHCl3 = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35, 298 K). (c) Evolving factor analysis using five absorbing eigenvectors,130 (d) re-constructed individual electronic absorption spectra131 and (e) proposed thermodynamic model.
35, 298 K). (c) Evolving factor analysis using five absorbing eigenvectors,130 (d) re-constructed individual electronic absorption spectra131 and (e) proposed thermodynamic model.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35) at 298 K
35) at 298 K
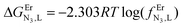 .
b ΔEL,LEr = −2.303RT
.
b ΔEL,LEr = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(uL,LEr).
c ΔEEr,ErL = −2.303·RT
log(uL,LEr).
c ΔEEr,ErL = −2.303·RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(uEr,ErL).
d Agreement factor
log(uEr,ErL).
d Agreement factor 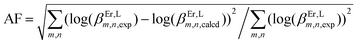 .
.
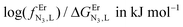
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c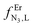 represents the intrinsic affinity of Er3+ for the tridentate binding unit of the bridging ligand (including desolvation processes). (3) uL,LEr = exp(−ΔEL,LEr/RT), respectively (4) uEr,ErL = exp(−ΔEEr,ErL/RT) are the cooperative effects, in terms of Boltzmann factors, which accompany the successive binding of ligands to the same metallic centre (uL,LEr), respectively, the successive binding of metals to the same bridging ligand (uEr,ErL). Multi-linear least-square fits of eqn (17)–(20) to the experimental stability constants provided the thermodynamic descriptors collected in Table 3 (entries 5–7).
represents the intrinsic affinity of Er3+ for the tridentate binding unit of the bridging ligand (including desolvation processes). (3) uL,LEr = exp(−ΔEL,LEr/RT), respectively (4) uEr,ErL = exp(−ΔEEr,ErL/RT) are the cooperative effects, in terms of Boltzmann factors, which accompany the successive binding of ligands to the same metallic centre (uL,LEr), respectively, the successive binding of metals to the same bridging ligand (uEr,ErL). Multi-linear least-square fits of eqn (17)–(20) to the experimental stability constants provided the thermodynamic descriptors collected in Table 3 (entries 5–7).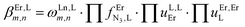
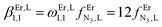
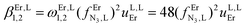
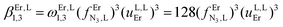
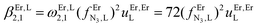
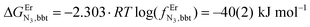 perfectly matches the one previously reported for the monomeric precursor terpyridine (tpy) ligand under similar conditions (acetonitrile, 298 K).135 This implies that, beyond an obvious statistical factor of 2, the connection of a second tridentate binding unit in the back of the original terpyridine units to give bbt has little effect on the binding properties of the tridentate N3 site taken separately. As expected, the successive binding of several tridentate N3 units to the same trivalent Er3+ centre is accompanied by some minor anti-cooperative processes (ΔEL,LEr = 9(2) kJ mol−1 for bbt and 6(2) kJ mol−1 for tpy) resulting from the stepwise neutralization of the positive metallic charge by an increasing number of bound nitrogen donors.135 With this in mind, it appears logical that the much less basic bridging pyrazine ring found in tppz (pKa = 0.37),136 compared with the 4,4′-bipyridine bridge in bbt (pKa = 4.8),137 leads to both a reduced affinity for Er3+
perfectly matches the one previously reported for the monomeric precursor terpyridine (tpy) ligand under similar conditions (acetonitrile, 298 K).135 This implies that, beyond an obvious statistical factor of 2, the connection of a second tridentate binding unit in the back of the original terpyridine units to give bbt has little effect on the binding properties of the tridentate N3 site taken separately. As expected, the successive binding of several tridentate N3 units to the same trivalent Er3+ centre is accompanied by some minor anti-cooperative processes (ΔEL,LEr = 9(2) kJ mol−1 for bbt and 6(2) kJ mol−1 for tpy) resulting from the stepwise neutralization of the positive metallic charge by an increasing number of bound nitrogen donors.135 With this in mind, it appears logical that the much less basic bridging pyrazine ring found in tppz (pKa = 0.37),136 compared with the 4,4′-bipyridine bridge in bbt (pKa = 4.8),137 leads to both a reduced affinity for Er3+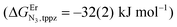 and a smaller ligand–ligand interaction (ΔEtppz,tppzEr = 5(3) kJ mol−1). However, the most noteworthy thermodynamic result concerns the considerable anti-cooperative mechanism accompanying the successive fixation of two Er3+ cations onto the bridging ligand, which are diagnostic for the operation of intermetallic electrostatic communication on the nanometric scale in these polyaromatic dyads. The large value ΔEEr,Ertppz = 18(5) kJ mol−1 found for the short-bridging tppz ligand combined with its limited intrinsic affinity
and a smaller ligand–ligand interaction (ΔEtppz,tppzEr = 5(3) kJ mol−1). However, the most noteworthy thermodynamic result concerns the considerable anti-cooperative mechanism accompanying the successive fixation of two Er3+ cations onto the bridging ligand, which are diagnostic for the operation of intermetallic electrostatic communication on the nanometric scale in these polyaromatic dyads. The large value ΔEEr,Ertppz = 18(5) kJ mol−1 found for the short-bridging tppz ligand combined with its limited intrinsic affinity 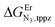 explains the difficulties in isolating dinuclear [X3Cr(tppz)CrX3] complexes. The smaller anti-cooperative effect observed for bbt (ΔEEr,Erbbt = 12(5) kJ mol−1) restores sufficient affinity for the formation of dinuclear [X3Cr(bbt)CrX3] complexes.
explains the difficulties in isolating dinuclear [X3Cr(tppz)CrX3] complexes. The smaller anti-cooperative effect observed for bbt (ΔEEr,Erbbt = 12(5) kJ mol−1) restores sufficient affinity for the formation of dinuclear [X3Cr(bbt)CrX3] complexes.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 mL) and heated under reflux. A solution of [CrCl3(THF)3] in acetonitrile (82 mg, 0.219 mmol, 1 eq.) was added dropwise to the tppz solution mixture, the colour of which immediately turned from purple to green. After being stirred and refluxed for 24 hours under an inert N2 atmosphere, the insoluble product was filtered (micro-filtering), then washed with a hot solution of acetonitrile and ethanol (1
25 mL) and heated under reflux. A solution of [CrCl3(THF)3] in acetonitrile (82 mg, 0.219 mmol, 1 eq.) was added dropwise to the tppz solution mixture, the colour of which immediately turned from purple to green. After being stirred and refluxed for 24 hours under an inert N2 atmosphere, the insoluble product was filtered (micro-filtering), then washed with a hot solution of acetonitrile and ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for removing the excess ligand. The resulting solid was washed with diethyl ether (3 × 7 mL) and dried under vacuum to give Cr(tppz)Cl3 (114 mg, 0.208 mmol, yield 95%). Slow diffusion of diethyl ether into a solution of the complex in DMF gave dark green single crystals of [Cr(tppz)Cl3]·2DMF (6) suitable for X-ray diffraction studies.
1) for removing the excess ligand. The resulting solid was washed with diethyl ether (3 × 7 mL) and dried under vacuum to give Cr(tppz)Cl3 (114 mg, 0.208 mmol, yield 95%). Slow diffusion of diethyl ether into a solution of the complex in DMF gave dark green single crystals of [Cr(tppz)Cl3]·2DMF (6) suitable for X-ray diffraction studies.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform (65
chloroform (65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35) (8 × 10−5 mol dm−3) were titrated at 298 K with a solution of Er(CF3SO3)3 (2 × 10−3 mol dm−3) in the same solvent under an inert atmosphere. After each addition of 0.10 mL, the absorbance was recorded using a Hellma optrode (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis130 and with the SPECFIT program.131 Absorption spectra in solution were recorded using a Cary 5000 Varian spectrometer (quartz cell path length 1 mm, 200–800 nm domain). Absorption spectra in the solid state were recorded on a Lambda 900 PerkinElmer spectrometer equipped with an integration sphere (background recorded on MgO). Emission spectra were recorded upon excitation at 400 nm from powder samples at various temperatures from 3 K to 295 K with a Fluorolog 3-22 (Horiba Jobin–Yvon), equipped with a peltier-cooled photo multiplier tube (Hamamatsu R2658P), and corrected for the spectral response of the system. Excitation at 355 nm was obtained with the third harmonic of a pulsed Nd:YAG laser (Quantel Brilliant). The emitted light was collected with a telescope and focused onto a light-guide with a fibre bundle connected to a monochromator (Spex 270 M). Full spectra were recorded with a CCD (Spex Spectrum One), decay curves with a photomultiplier (Hamamatsu R928) and a digital oscilloscope (Tektronix TDS540B) or a multichannel scaler (Stanford Research SR430). For the latter the spectral bandwidth of the monochromator was set to 20 nm, thus giving the decay of the integral signal. Low temperatures were achieved with a closed cycle cryosystem (Janis, SHI-950) with the sample sitting in exchange gas for efficient cooling. Microcrystalline samples were mounted on copper plates with rubber cement. The copper plates were attached to the sample holder. Magnetization was measured using a Quantum Design VSM system (Department of Quantum Matter Physics, University of Geneva) in the range of 2–300 K. Solid samples of Cr2Cl6(tppz) (15.8 mg), Cr2Cl6(bbt) (16.0 mg), Cr2Cl6(ebbt) (4.7 mg), [Cr2(tpy)2(bbt)](PF6)6 (8.1 mg) and [Cr2(tpy)2(ebbt)](PF6)6 (14.9 mg) were immobilized in capsules, which were locked in a straw. The samples were introduced in the SQUID under an inert atmosphere of helium.
35) (8 × 10−5 mol dm−3) were titrated at 298 K with a solution of Er(CF3SO3)3 (2 × 10−3 mol dm−3) in the same solvent under an inert atmosphere. After each addition of 0.10 mL, the absorbance was recorded using a Hellma optrode (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis130 and with the SPECFIT program.131 Absorption spectra in solution were recorded using a Cary 5000 Varian spectrometer (quartz cell path length 1 mm, 200–800 nm domain). Absorption spectra in the solid state were recorded on a Lambda 900 PerkinElmer spectrometer equipped with an integration sphere (background recorded on MgO). Emission spectra were recorded upon excitation at 400 nm from powder samples at various temperatures from 3 K to 295 K with a Fluorolog 3-22 (Horiba Jobin–Yvon), equipped with a peltier-cooled photo multiplier tube (Hamamatsu R2658P), and corrected for the spectral response of the system. Excitation at 355 nm was obtained with the third harmonic of a pulsed Nd:YAG laser (Quantel Brilliant). The emitted light was collected with a telescope and focused onto a light-guide with a fibre bundle connected to a monochromator (Spex 270 M). Full spectra were recorded with a CCD (Spex Spectrum One), decay curves with a photomultiplier (Hamamatsu R928) and a digital oscilloscope (Tektronix TDS540B) or a multichannel scaler (Stanford Research SR430). For the latter the spectral bandwidth of the monochromator was set to 20 nm, thus giving the decay of the integral signal. Low temperatures were achieved with a closed cycle cryosystem (Janis, SHI-950) with the sample sitting in exchange gas for efficient cooling. Microcrystalline samples were mounted on copper plates with rubber cement. The copper plates were attached to the sample holder. Magnetization was measured using a Quantum Design VSM system (Department of Quantum Matter Physics, University of Geneva) in the range of 2–300 K. Solid samples of Cr2Cl6(tppz) (15.8 mg), Cr2Cl6(bbt) (16.0 mg), Cr2Cl6(ebbt) (4.7 mg), [Cr2(tpy)2(bbt)](PF6)6 (8.1 mg) and [Cr2(tpy)2(ebbt)](PF6)6 (14.9 mg) were immobilized in capsules, which were locked in a straw. The samples were introduced in the SQUID under an inert atmosphere of helium.







