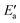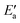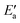Open Access Article
Open Access ArticleCarboxylic acid formation by hydroxyl insertion into acyl moieties on late transition metals†
Benjamin W. J.
Chen‡
 a,
Alexander
Genest
a,
Alexander
Genest
 a,
Adrian
Hühn
a and
Notker
Rösch
a,
Adrian
Hühn
a and
Notker
Rösch
 *ab
*ab
aInstitute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, #16–16 Connexis, Singapore 138632, Singapore
bDepartment Chemie and Catalysis Research Center, Technische Universität München, 85747 Garching, Germany. E-mail: roesch@mytum.de
First published on 14th July 2017
Abstract
Aqueous phase reforming of alcohols over Pt has been discussed to operate along two pathways, decarbonylation and decarboxylation. To gain a better understanding of the activity of various catalysts for decarboxylation, we examined computationally a key step of this mechanism on the 12 transition metals of groups 8 to 11, namely the formation of a carboxylic acid intermediate via metal-mediated insertion of OH into an acyl group. The trend of the calculated barriers of OH insertion parallels the oxophilicity of the metals. A separation of the reaction into two formal steps isolates OH activation as a major contribution to the barrier and, not unexpectedly, indicates a strong dependence on the OH adsorption energy. A decomposition analysis of the activation energy reveals that weaker OH adsorption also correlates with the interaction energy between the adsorbed fragments in the transition state, thus indirectly lowering the barrier for OH insertion. Metals in the bottom right-hand corner of the transition metal block studied –Pt, Au, and Ag– bind OH relatively weakly, hence feature a high OH insertion activity. We applied these findings to rationalize various experimental results and suggest catalysts for decarboxylation.
Introduction
Biomass is a cheap and renewable source of carbon that can be converted into a variety of fuels and chemicals.1–5 Biomass-derived alcohols are a promising feedstock6–9 which, by tuning of the reaction conditions, can be reformed into either H2 or alkanes, thus serving as an important sustainable source of energy carriers.6,10 Alternatively, biomass-derived alcohols may be selectively functionalized for further processing into fine chemicals. One example is the selective oxidation of glycerol, a byproduct of biodiesel production, into glyceric and glycolic acids.11Aqueous phase reforming (APR)3,7,12,13 has emerged as an important method for processing biomass. It is preferred over steam reforming14,15 for the lower temperatures involved, because the reaction mixture does not need to be vaporized, resulting in notable energy savings. Dumesic and coworkers reported the first use of Pt/Al2O3 catalysts in producing H2 by APR of biomass-derived hydrocarbons.6 Since then, many bimetallic catalysts based on Pt and Pd have been developed, e.g., PtRe,16,17 PtNi,18 and PdFe.18 RANEY®-NiSn has emerged as a cheaper alternative that still retains the activity of the precious metal catalysts.8
Wawrzetz et al. experimentally probed the reaction network of the APR of glycerol and propanol on Pt/Al2O3, where carboxylic acids were observed as intermediates.19 In a follow-up computational catalysis study, chain shortening was discussed as proceeding via two pathways, one where CO2 is produced from carboxylic acid intermediates, and another where CO is released from aldehydes.20,21 DFT model studies on 1-propanol suggested20–22 that multiple dehydrogenation steps of the alcohol first produce acyl species adsorbed on the metal surface. Along the decarbonylation pathway (DCN), the acyl species is directly transformed producing an alkane and CO upon C–C bond scission. Alternatively, an OH group on the metal surface inserts into the acyl group, forming a carboxylic acid.19 This is the key step which we wish to study; we shall refer to this process as the insertion reaction. Subsequently, the acid is dehydrogenated and then undergoes C–C bond scission to produce directly CO2 and an alkane,20 completing the decarboxylation pathway (DCX).
It is difficult to determine experimentally how large a role DCX plays in the APR of alcohols on Pt, as the water gas shift reaction (WGS) easily catalyzes the interconversion of CO into CO2 under the reaction conditions.23 DFT results20,21 indicate that for 1-propanol, DCN and DCX could be competitive on Pt(211) steps. Heyden and coworkers used microkinetic models to study the reforming of propanoic acid itself on Pd(111); they also concluded that DCX and DCN are highly competitive and found that the major pathway depends on the choice of the solvent.24,25 On the other hand, Lobo et al., having conducted experiments where 1-propanol was reformed over various supported Pt catalysts, suggested that DCX is the major contributor to CO2 and alkane production.23 A DFT study on methanol steam reforming on PdZn(111) also showed that inserting OH into formaldehyde is much easier than cleaving the C–H bond of formaldehyde, thus supporting DCX as the main pathway in this similar chemistry.26
The observation of carboxylic acids as products from reactions of alcohols can also be a revealing sign of contributions from the DCX pathway. Nozawa et al. noticed an accumulation of acetic acid during the reforming of ethanol on Ru, Pt, and Ir nanoparticles supported on TiO2, showing that DCX cannot be ruled out on these metals.27 Additionally, experiments on the oxidation of 1-octanol to octanoic acid over Pt showed that using a mixture of water and dioxane as the solvent greatly enhanced reaction rates as compared to using pure dioxane, providing circumstantial evidence that DCX is promoted over DCN in aqueous environments such as those found in APR.28
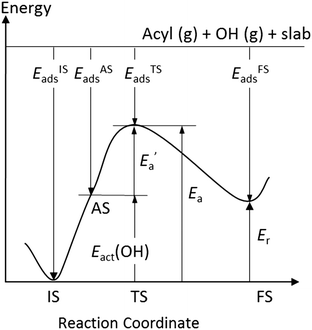
From this non-exhaustive review of the literature, we can see that selectivity towards either DCX or DCN is thus likely to be strongly dependent on the reaction conditions as well as the identity of the substrate. After this literature overview, which suggests that DCX plays a role in the APR on Pt, we aim at assessing the importance of DCX on transition metals of groups 8 to 11. We chose to study the OH insertion reaction as it is a necessary step for DCX to occur, hence a high barrier of this reaction will exclude the whole DCX pathway. The OH insertion is formally an association of two radical fragments, both adsorbed on a metal surface, to form a carboxylic acid, the intermediate characteristic of the DCX pathway:
| OH* + RCO** → RCOOH* + ** | (1) |
Here, the symbol * denotes a surface site. Scope and utility of this reaction are not limited to reforming; as examples, the aerobic oxidation of alcohols to carboxylic acids,28–31 as well as the electrooxidation of methanol,32,33 are also thought to involve a similar OH insertion step.
We studied the insertion reaction on model close-packed surfaces of the 12 transition metals of groups 8 to 11. In the following, we will focus on characterizing the transition state (TS) structures involved, as well as on understanding the physical origins of the barrier. Brønsted–Evans–Polanyi (BEP-type) relations lend support to the conceptually useful tool of splitting the reaction into two formal steps. An energy decomposition analysis of the activation energies reveals how the activation barriers correlate with OH and acyl adsorption energies. We will end with a discussion of related experimental results on OH insertion and APR, suggesting which of the two pathways, DCX and DCN, would be favored on what kinds of catalysts.
Results
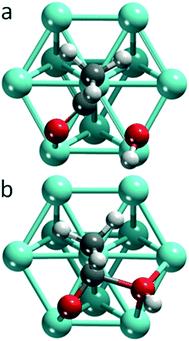
On all 12 transition metals examined, we determined the equilibrium structures of an adsorbed hydroxyl (OH), the adsorption complexes of acyl fragments (RCO) and the corresponding carboxylic acids (RCOOH), as well as the TS structures of OH insertion. We focused on acetic acid and acetyl, R = CH3. Sketches of the TS geometries are provided as Fig. S1 and S2 of the ESI.† Replacing acetyl by propionyl on Pt, Pd and Ru, affected neither the geometry of the TS nor the activation barrier in a substantial fashion. We will label the atoms of the carbonyl group of the acyl moiety as C1 and O1, while we will refer to the oxygen center of the hydroxyl group as O2, see Fig. S3 of the ESI.†Structure changes and orbital interactions driving OH insertion
Among the systems studied, two main types of TSs can be differentiated by the position of the hydroxyl moiety in the TS (Fig. 1): OH near a top (top TS) or a bridge site (bridge TS). In both cases, the acetyl group adopts similar di-σ binding configurations, with the atoms of the carbonyl moieties bonded on top of adjacent metal centers. The M–C1 bond lengths vary in the range of 196–233 pm, and the M–O2 bond distances in the range of 193–214 pm, depending on the metal and coordination mode.Fig. 2 provides an overview of the types of TSs isolated and the barriers corresponding to the lowest lying TS for each metal. Top TSs were determined on all metals except Ag and Au, while bridge TSs were located on the four 3d metals Fe, Co, Ni, and Cu, as well as on Au and Ag (Table 1). When both types of barriers were identified for a given metal, their heights varied by 8 kJ mol−1 at most, which is small compared to the variation between barriers for different metals. In the TS structures, the C1–O2H distances range from 190–220 pm for top TSs, and are ∼30 pm shorter, 170–180 pm, for bridge TSs. The C1–O2H bond length of the final state, FS, where the carboxylic acid is bonded through the carbonyl O1 on a top site, is ∼130 pm. We thus observe that the C1–O2H distance in the TS is notably longer than the corresponding bond in the FS. This points to an “early” TS for OH insertion, where the metal–acyl bonding in the TS is similar to that in the IS. A list of the C1–O2H distances in the TS, as well as the calculated energy barriers and other pertinent energy information has been collected in Table 1.
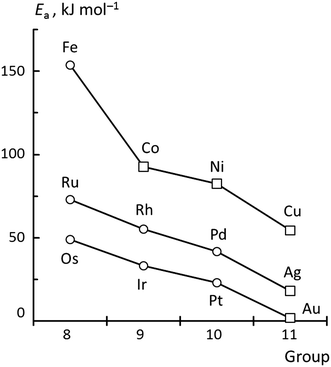 | ||
| Fig. 2 Activation energies of the most favorable TS structures for the metals under study. Circles and squares denote top and bridge TS, respectively. The lines are a guide for the eye. | ||
| M | TS | E a | E act(OH) | E r | E reva | E prp(OH) | E prp(RCO) | E prp(M) | E TSint | E ISads | E ASads | E TSads | E FSads | C–OHb | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
a Reported energy quantities: Ea – activation barrier of OH insertion into acyl RCO, Eact(OH) – energy to promote OH to the activated state AS, 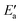 – reduced barrier, after OH activation, Er – reaction energy of OH insertion, Ereva – barrier of RCO–OH dissociation, Eprp(X) – preparation energies of the system components X = OH, RCO, and metal slab M, in the energy decomposition analysis, ETSint – corresponding interaction energy in the TS, eqn (13), Eads – adsorption energies of all surface species in the initial state IS, the activated state AS, the transition state TS, and the final state FS.
b C–OH bond length in the TS.
c Propionyl used as the acyl group instead of acetyl. – reduced barrier, after OH activation, Er – reaction energy of OH insertion, Ereva – barrier of RCO–OH dissociation, Eprp(X) – preparation energies of the system components X = OH, RCO, and metal slab M, in the energy decomposition analysis, ETSint – corresponding interaction energy in the TS, eqn (13), Eads – adsorption energies of all surface species in the initial state IS, the activated state AS, the transition state TS, and the final state FS.
b C–OH bond length in the TS.
c Propionyl used as the acyl group instead of acetyl.
|
||||||||||||||||
| 3d | Fe | Bridge | 159.3 | 25.2 | 134.0 | 125.8 | 33.5 | 49.9 | 93.9 | 13.7 | 29.1 | −649.1 | −632.8 | −489.8 | −523.3 | 168.8 |
| Top | 153.7 | 71.2 | 82.5 | 125.8 | 27.9 | 85.3 | 50.6 | 12.1 | 29.8 | −649.1 | −577.9 | −495.4 | −523.3 | 194.5 | ||
| Co | Bridge | 92.6 | 19.8 | 72.8 | 2.9 | 89.7 | 56.2 | 45.6 | 13.8 | 4.6 | −515.1 | −495.3 | −422.5 | −512.2 | 171.2 | |
| Top | 95.2 | 60.5 | 34.7 | 2.9 | 92.3 | 73.7 | 26.8 | 9.8 | 4.4 | −515.1 | −454.5 | −419.9 | −512.2 | 199.3 | ||
| Ni | Bridge | 82.3 | 14.2 | 68.1 | −11.2 | 93.5 | 54.9 | 42.2 | 13.5 | −1.3 | −504.3 | −490.1 | −422.0 | −515.5 | 175.7 | |
| Top | 83.4 | 60.1 | 23.4 | −11.2 | 94.6 | 72.4 | 23.7 | 13.1 | 0.5 | −504.3 | −444.2 | −420.9 | −515.5 | 210.6 | ||
| Cu | Bridge | 54.4 | 14.8 | 39.6 | −86.4 | 140.8 | 43.7 | 30.2 | 11.7 | −7.9 | −409.6 | −394.9 | −355.2 | −496.0 | 180.2 | |
| Top | 62.6 | 57.6 | 5.0 | −86.4 | 149.0 | 64.8 | 14.4 | 10.8 | −5.8 | −409.6 | −352.0 | −347.0 | −496.0 | 217.3 | ||
| 4d | Ru | Top | 72.7 | 36.1 | 36.6 | 19.4 | 53.3 | 50.2 | 31.9 | 8.1 | −1.4 | −552.6 | −516.5 | −480.0 | −533.2 | 192.7 |
| Topc | 73.7 | 36.1 | 37.6 | 23.0 | 50.7 | 52.4 | 38.1 | 8.4 | −8.4 | −551.0 | −514.9 | −477.2 | −527.9 | 187.8 | ||
| Rh | Top | 55.1 | 31.2 | 23.9 | −13.3 | 68.4 | 50.6 | 28.8 | 16.0 | −8.3 | −510.9 | −479.7 | −455.8 | −524.1 | 198.8 | |
| Pd | Top | 41.8 | 24.2 | 17.7 | −67.6 | 109.4 | 34.9 | 25.3 | 8.4 | −9.9 | −448.3 | −424.1 | −406.4 | −515.8 | 216.8 | |
| Topc | 35.3 | 24.2 | 11.1 | −72.4 | 107.7 | 36.1 | 23.2 | 9.5 | −14.5 | −443.2 | −419.0 | −407.9 | −515.6 | 211.4 | ||
| Ag | Bridge | 18.1 | 14.1 | 4.0 | −173.1 | 191.2 | 17.4 | 13.1 | 7.1 | −5.4 | −318.0 | −304.0 | −300.0 | −491.1 | 214.1 | |
| 5d | Os | Top | 48.9 | 11.1 | 37.8 | 11.2 | 37.7 | 37.5 | 42.7 | 13.4 | −17.9 | −544.9 | −533.8 | −496.1 | −533.8 | 187.2 |
| Ir | Top | 33.0 | 6.3 | 26.7 | −23.1 | 56.1 | 38.0 | 45.4 | 18.7 | −31.6 | −500.5 | −494.2 | −467.5 | −523.6 | 186.0 | |
| Pt | Top | 23.2 | 2.0 | 21.1 | −65.7 | 88.9 | 29.0 | 37.3 | 15.0 | −28.1 | −450.3 | −448.3 | −427.1 | −516.0 | 196.0 | |
| Topc | 23.6 | 2.0 | 21.6 | −65.9 | 89.5 | 27.3 | 41.8 | 14.7 | −30.8 | −449.1 | −447.1 | −425.5 | −515.0 | 192.5 | ||
| Au | Bridge | 5.9 | 0.0 | 5.9 | −197.3 | 203.2 | 16.2 | 27.6 | 15.5 | −22.5 | −290.6 | −290.6 | −284.8 | −487.9 | 211.1 | |
An isolated OH moiety usually is adsorbed at either a three-fold hollow site (on all 3d metals studied, Ru, and Ag) or at a bridge site (on the remaining 4d metals, and all 5d metals). If OH prefers a three-fold hollow site at equilibrium, it moves to a bridge or top site in the TS, Fig. S4 of the ESI.† In contrast, if OH prefers a bridge site at equilibrium, it shifts to a top site in the TS. Thus, OH always has a lower metal coordination in the TS than in the IS, except on Au where OH stays at its preferred bridge site up to the TS. The OH group almost always migrates significantly from its equilibrium position to its location in the TS, e.g., 127 pm on Pt(111), while the acyl group shifts notably less from its preferred di-σ bonding configuration (as measured by the C1 center), e.g., 36 pm on Pt(111). The OH displacement depends notably on the metal. For top TSs, it falls in the range of 118–161 pm. Yet, for bridge TSs such as Ni, Cu, and Ag, where OH shifts from a hollow to a bridge site, the displacement is much shorter, about 66 pm. The acyl moiety migrates substantially less, 12–53 pm, with the exception of Pd where we determined a migration by 113 pm.
The much larger shift of OH provides a first hint that this moiety is crucially involved in the formation of the TS. This is even more noteworthy considering that OH binds much more strongly than the acyl moiety on most metals except for Pt, where OH and acyl bind almost equally strongly (Table S1 of the ESI†). A shift in adsorption site from hollow to bridge position of a (bare) oxygen atom in preparation for a transition state of O insertion into CO on a Rh(111) surface has previously been rationalized as a way to “free” the py orbital of the O atom to form the new C–O bond.34,35 In its equilibrium structure, the oxygen atom of OH extends one bond to the H atom and the remaining valence p orbitals are involved in forming M–O2H bonds. Assuming the situation to be sufficiently analogous to O insertion into a CO adsorbate on Rh(111),34,35 we thus expect the number of M–O2H interactions to be reduced during OH insertion. Invoking the principle of bond conservation leads to the same conclusion, namely that the formation of a new C1–O2 bond entails a weakening of the existing M–C1 and M–O2 bonds.
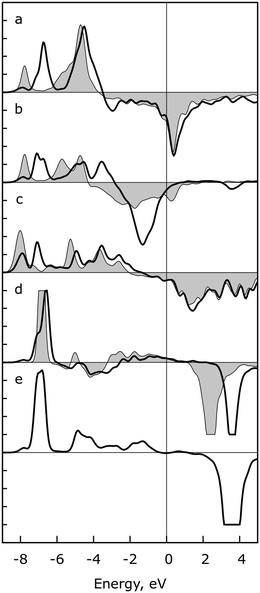
To elucidate the key orbital interactions in these TS structures, and to confirm the qualitative ideas of bonding we raised in the previous paragraph, a crystal orbital overlap population (COOP) analysis of several binding atom pairs was carried out. We used the example of OH insertion into acetyl on Pt(111) (Fig. 3); see the section “Computational”. To ensure comparability of differently oriented atom pairs, we are treating two types of interactions: (i) the σ-component along the axis between these two atoms (d–pσ), and (ii) the sum of the two π-contributions (d–p⊥) relative to this axis.36 All energies here and in the following discussion are relative to the Fermi energy εF (Fig. 3).
In the COOP of the Pt–O2 bond of the separated OH fragment, the peak in the d–pσ component near −8 eV is slightly shifted, to about −6.5 eV, in the TS, while the peak at −4.5 eV in the IS remains at this energy, Fig. 3a. Peaks of the d–p⊥ component of the Pt–O2 spectrum are shifted to higher energies in the TS, by ∼0.5 eV, and a large antibonding signal at ∼−1.5 eV appears, Fig. 3b. We interpret the peak at −4.5 eV and −5.7 eV as a π-type interaction of oxygen with the examined Pt atom at the bridge site, in line with a previous study for OH adsorption on Ag and Ru.37 The destabilization of the p orbital from IS to TS is analogous to the one observed for OC–O formation on Rh(111).34,35 We measured only a small shortening, by ∼10 pm, of the Pt–O2 bond, despite the transition from bridge to top coordination on going from the IS to the TS. In the COOP spectra for the Pt–C1 atom pair, one observes only a tiny shift to smaller binding energies in both components of the spectra, Fig. 3c and d, reflecting the much smaller structure rearrangement of the acyl moiety between IS and TS. In the COOP projected on C1 and O2 in the TS structure (Fig. 3e), one clearly identifies a bonding peak at about −7 eV, representing the C1–O2 bond to be formed by OH insertion; see the formation of the OC–O bond on Rh(111).34,35
Analysis of the reaction barrier
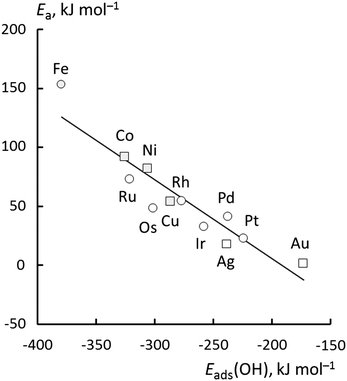
Now, we turn to an analysis of the reaction barrier Ea associated with hydroxyl insertion (Fig. 2). The Ea values decrease across the periods and down the groups, spanning a wide range, from 159 kJ mol−1 on Fe to just 2 kJ mol−1 on Au. When plotted against the adsorption energy Eads(OH/M) of the OH group at its preferred adsorption site, a fairly good linear correlation results (Fig. 4), whereas a similar analysis with the acyl adsorption energies does not produce any trend. This is a clear hint at the much stronger influence of Eads(OH/M) on the energy of the transition state, compared to Eads(acyl/M). The strongly decreasing values of Ea with Eads(OH/M) are consistent with the notion that a weaker metal–OH bond will facilitate OH insertion. To corroborate this argument, we searched for linear energy relationships in the spirit of a BEP-type analysis.38,39In line with our previous analysis which showed the need for OH to be activated onto less coordinated sites (except for the reaction on Au) we formally split the activation into two steps (Fig. 5). In the first step, OH is activated to a top or a bridge site, depending on the structure of the TS. In this way, an activated precursor state AS is created by expenditure of an OH activation energy, Eact(OH). This energy can be determined without detailed knowledge of the TS. In the second step, the acyl moiety is (formally) added to complete the TS structure. This latter step requires the recombination activation energy 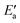 to yield Ea = Eact(OH) +
to yield Ea = Eact(OH) + 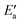 (Fig. 5).
(Fig. 5).
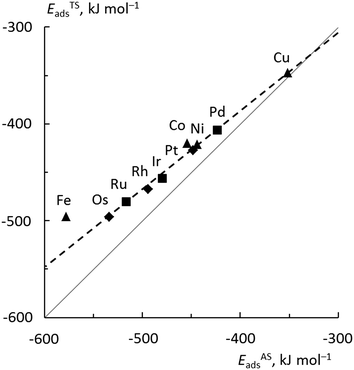
In Fig. 6, the values of ETSads for all top TSs are plotted against EASads = EISads + Eact(OH), eqn (4). (Note that in Fig. 6, the addition of Eact(OH) corresponds to a shift of all points to the right). One now obtains a good fit with a low mean average error (MAE) of 5 kJ mol−1. A least-squares fit addressing only the bridge TSs also yields a good MAE of 4 kJ mol−1 (Fig. S5 of the ESI†). The result for Fe, the only material where we examined a more open surface, is the only outlier in this analysis and was not included in the linear fits. A similar effect of the surface structure on scaling relations has previously been reported.42
The slopes of the regression lines are 0.81 for top TSs and 0.67 for bridge TSs, indicating that the bridge TSs are less similar to the corresponding ASs, exhibiting a somewhat “later” character than the top TSs. This is consistent with the shorter C–OH bonds, by ∼30 pm, determined for bridge TSs as compared to those for top TSs; see above.
The value of the recombination activation energy 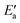 can be read off in Fig. 6 as the vertical distance of the data points from the bisecting line. Thus, the BEP relation admits one to predict
can be read off in Fig. 6 as the vertical distance of the data points from the bisecting line. Thus, the BEP relation admits one to predict 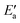 to reasonable accuracy. Thus, together with the calculated value of Eact(OH), the total activation energy Ea can be estimated without explicitly locating the TS structure.
to reasonable accuracy. Thus, together with the calculated value of Eact(OH), the total activation energy Ea can be estimated without explicitly locating the TS structure.
One obtains another useful view on the two-step analysis by comparing the contributions across all metals studied (Fig. 7a). Obviously, the values of Eact(OH) span a much larger range, 0–70 kJ mol−1, compared to those of 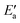 , 0–40 kJ mol−1 (with the exception of Fe). As can be expected, Eact(OH) for any type of TS is largest for the oxophilic 3d metals Fe, Co, Ni, Cu and smallest for the 5d noble metals such as Pt and Au. Interestingly, while there are large variations in Eact(OH) when going down the columns of the periodic table, this quantity remains relatively constant along each row. In contrast, the
, 0–40 kJ mol−1 (with the exception of Fe). As can be expected, Eact(OH) for any type of TS is largest for the oxophilic 3d metals Fe, Co, Ni, Cu and smallest for the 5d noble metals such as Pt and Au. Interestingly, while there are large variations in Eact(OH) when going down the columns of the periodic table, this quantity remains relatively constant along each row. In contrast, the 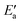 values drop across each row, upon going to the right in the periodic table, and they do so in a rather similar fashion. However, going down the rows, the
values drop across each row, upon going to the right in the periodic table, and they do so in a rather similar fashion. However, going down the rows, the 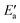 values remain rather constant within each group, again with the exception of Fe. Therefore, the contributions from Eact(OH) dominate the total barriers Ea of the 3d metals, they are surprisingly similar in values and trends for the 4d metals, but they are rather negligible for the 5d metals compared to
values remain rather constant within each group, again with the exception of Fe. Therefore, the contributions from Eact(OH) dominate the total barriers Ea of the 3d metals, they are surprisingly similar in values and trends for the 4d metals, but they are rather negligible for the 5d metals compared to 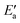 (Fig. 7a). In summary, one thus obtains the lowest barriers Ea on the bottom-right hand metals Pt, Ag and Au. A similar analysis for bridge vs. top TSs on 3d metals is shown as Fig. S5 of the ESI.†
(Fig. 7a). In summary, one thus obtains the lowest barriers Ea on the bottom-right hand metals Pt, Ag and Au. A similar analysis for bridge vs. top TSs on 3d metals is shown as Fig. S5 of the ESI.†
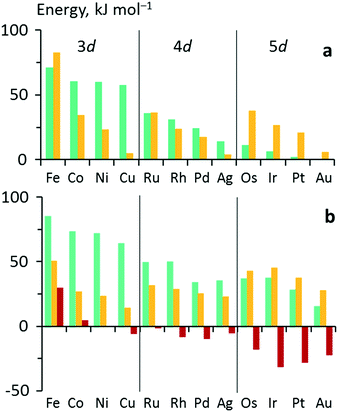 | ||
Fig. 7 Energy analyses of the activation energy Ea. (a) Breakdown according to the two-step mechanism: Ea = Eact(OH) + 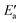 for top TSs (bridge TSs for Au and Ag). Color coding: green – Eact(OH), yellow – for top TSs (bridge TSs for Au and Ag). Color coding: green – Eact(OH), yellow – 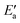 . (b) Breakdown according to preparation energies for the various parts of the adsorption system, eqn (13): Ea = Eprp(OH) + Eprp(RCO) − Eprp(M) + ETSint. Color coding: green – Eprp(OH), yellow – Eprp(RCO), red – ETSint. . (b) Breakdown according to preparation energies for the various parts of the adsorption system, eqn (13): Ea = Eprp(OH) + Eprp(RCO) − Eprp(M) + ETSint. Color coding: green – Eprp(OH), yellow – Eprp(RCO), red – ETSint. | ||
This analysis seems to contradict the view that OH activation is the main component of the barrier, as 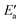 is much larger than Eact(OH) for the 5d metals. However, we note that additional energy will be required for OH to move from its geometry in the AS to its geometry in TS; this energy is captured in
is much larger than Eact(OH) for the 5d metals. However, we note that additional energy will be required for OH to move from its geometry in the AS to its geometry in TS; this energy is captured in 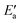 . To obtain a fuller representation of how much energy is required to activate OH to the TS, we have conducted an energy decomposition analysis as described below.
. To obtain a fuller representation of how much energy is required to activate OH to the TS, we have conducted an energy decomposition analysis as described below.
Fig. 7b shows the three main components of the breakdown for top TSs, except Au and Ag which have no top TSs, thus the bridge TSs of these metals were analyzed instead. As a general trend over the whole data set, we note that Eprp(OH) decreases going down the groups, while Eprp(RCO) increases. The values of ETSint decrease down the groups as well, paralleling the decrease of Eprp(OH), but even into negative values.
The OH preparation energy, Eprp(OH), exhibits the largest variation, spanning 15–85 kJ mol−1, and thus also has the largest influence on the barrier Ea, especially for the 3d and 4d metals. Note that Eprp(OH) differs from Eact(OH), as it measures the difference between the energy of OH in the IS and the TS geometries, including the contributions of the metal slab. In contrast, the AS is a stationary adsorption complex at a top/bridge site near the TS where the M–OH distance is typically 10 pm shorter than in the TS. The difference between the two energy quantities is clearly seen when comparing Fig. 7a and b. Although Eact(OH) almost vanishes for the 5d metals, Eprp(OH) remains significant, 20–40 kJ mol−1, and comparable to the other components. Compared to Eact(OH), Eprp(OH) thus more accurately reflects the influence of the hydroxyl moiety in shaping the main trend of the activation energies, e.g., the rapid decrease with decreasing oxophilicity of the metal.
The influence of Eprp(RCO) is relatively smaller, with typical values in the range of 10–50 kJ mol−1. Fe is again found to be an exception, with Eprp(RCO) = 94 kJ mol−1 for the less favored bridge TS (Table 1, Fig. S6†). In contrast to Eprp(OH), the relative and absolute contributions of Eprp(RCO) increase going from the 3d to the 5d metals such that it overtakes Eprp(OH) for the 5d metals. The higher acyl preparation energy Eprp(RCO) might be due to the generally stronger adsorption of acyl groups on the late period transition metals, Table S1 of the ESI.† However, similar to Eprp(OH), the values of Eprp(RCO) mostly decrease across the periods.
Interestingly, the variation in ETSint is also very large, destabilizing the TS by up to 30 kJ mol−1 on Fe, but stabilizing the TS by 30 kJ mol−1 on Pt. Interaction energies are typically destabilizing due to bond competition for the surface;43,44 a negative ETSint hints at a direct interaction between the two fragments, with a small to negligible surface-mediated contribution. We also notice a tendency for the interaction energy to increase (or become less negative) in tandem with the adsorption energy of OH, but not that of acyl (Tables S1 of the ESI†), leading us to postulate that the more strongly OH interacts with the surface, the weaker it binds to the acyl fragment.
This hypothesis was tested by translating the reactants in the TS in the z-direction such that they are closer to (further from) the surface and thus interact more (less) with it. In consequence, ETSint was calculated less positive when either or both of the reactants were lifted from the surface, corroborating our line of reasoning. Shifting OH has a larger effect on the interaction energy as compared to shifting the acyl group. Thus the adsorption energy of OH also contributes indirectly to the barrier Ea by affecting ETSint.
In summary, these findings reinforce the previous conclusion that the main trend of decreasing Ea down the group and across the periods is mainly due to the weaker adsorption of OH. Besides a direct effect by decreasing Eprp(OH), a weaker OH adsorption also correlates with a tendency to greater stabilization of the TS as witnessed by the decreasing ETSint. Increases in Eprp(RCO) fail to reverse this trend; the strong influence of OH adsorption results in 5d metals exhibiting very low barriers, all below 50 kJ mol−1. However, as both Eprp(OH) and Eprp(RCO) decrease across the period, one finds the lowest barriers of each period on the group 11 elements, i.e., for Cu, Ag and Au (Fig. 2).
The decarboxylation pathway in aqueous phase reforming
Knowing how the choice of metal affects the main mode of deoxygenation during APR will be a useful asset for designing new catalysts in a rational fashion. Our results show that insertion of OH into acyl moieties proceeds most rapidly on transition metals towards the lower right-hand corner of the transition metal series, i.e., for Pd, Ag, Ir, Pt, and Au. These metals bind OH weakly, and thus OH is easily activated to the TS geometry where it is able to interact strongly with acyl, thus stabilizing the TS further. In this way, one is able to rationalize the excellent activity of Au for catalyzing the aerobic oxidation of alcohols to acids in the presence of a base,45–47 which follows an APR-like mechanism with a final OH insertion to form the acid.29 However, due to its nobility, Au neither dissociates water well nor is it able to dehydrogenate the starting material. The oxidation will not proceed without adding a base (as a source of OH−) into the reaction mixture.29,47 Additionally, DFT studies show that OH groups are able to activate easily the O–H bond of alcohols on Pt, and that the presence of such groups likely is the main reason for the speed-up in alcohol oxidation rates in the aqueous phase.28 Practical catalysts for decarboxylation in APR thus will also need the ability to dissociate water and cleave C–C bonds, thus ruling out noble metals such as Au and Ag.48 Therefore, Ir, Pt and Pd remain as metals that may show a reasonable APR activity and go through the decarboxylation pathway.More reactive metals such as Ni, Fe, Co and Ru do not insert OH easily because they bind it too strongly. Decarbonylation might be the more favored pathway with these catalysts. Interestingly, in their experiments, Nozawa et al.27 observed acetic acid formation using Ru catalysts. Ru/TiO2 particles with an average diameter of 2.3 nm did not have any activity for producing acetic acid. However, as the particle size was decreased, the turnover frequency of acetic acid formation increased sharply. As a potential rationalization of this finding, one may point to weaker calculated CO binding (for OH this would lead to a more facile insertion) at some sites of Ru57 particles compared to Ru323.49 Similarly, the strength of adsorption of CO was computed to decrease with decreasing Pd cluster size down to about 1 nm.50 This trend of decreasing binding strength with smaller particle size was also observed experimentally.51,52 Smaller Ru clusters were also found to completely reform acetic acid into CO2 and H2,27 and thus show promise as catalysts for decarboxylation.
Bimetallic catalysts such as AuPd and AuPt have shown improved efficiency in catalyzing base-free aerobic oxidation of alcohols to acids as compared to either metal by itself.53 These synergistic effects could be due to combining a metal with good water dissociation ability (Pd) and a metal which excels at catalyzing the insertion of OH (Au). Indeed, when OH is freely available (at pH 9.5), AuPd does not provide any advantage over pure Au catalysts, while pure Pd performed much worse than the Au catalysts.53 It can be envisioned that alloying 3d or 4d metals, which are good at C–C bond scission (e.g., Ni, Ru), with metals facilitating OH insertion (e.g., Pt, Au, Ag) may prove to be useful in designing catalysts for decarboxylation. Such alloys may also reduce the large Eprp(RCO) of 5d metals as 3d and 4d metals bind acyl much weaker.
Regarding the thermodynamics of OH insertion, the reaction is also more exothermic on metals that adsorb both reactants weaker, notably the group 11 metals where also acyl moieties do not bind strongly, Table S1 of the ESI.† For metals where the acid interacts weakly with the surface (with Eads from about −10 kJ mol−1 to −60 kJ mol−1), i.e., Cu, Ag, Au, most of the energy released upon generating the acid is due to the formation energy of the C–OH bond in the gas phase, calculated at 477 kJ mol−1. The energy for forming the acid in the surface-catalyzed reaction thus largely depends on the adsorption energies of the reactants. Hence, metals, that bind the reactants weakly, do not only lead to a kinetically, but also a thermodynamically favorable insertion reaction. This is consistent with the experimental findings regarding minor build-ups of propanoic acid while reforming 1-propanol on Pt catalysts.19,23 In the same spirit, one may also recall that Nozawa et al. witnessed the formation of large quantities of acetic acid while reforming ethanol with Pt and Ir catalysts.27
Experiments showed Pd to be a catalyst for converting alcohols into acids via OH insertion.29 Recall also that on Pd the decarboxylation was determined to be of comparable speed as the decarbonylation.24,25 The latter reaction involves the removal of an OH group from an acid, i.e., the reverse reaction of OH insertion. The ease, with which this dissociation reaction is carried out for the case under study, correlates relatively well with the oxophilicity of the metal catalyst, Fig. S7 of the ESI.† With the present model calculations, very low barriers have been determined for Fe, Ru, Os, and Ir, with activation energies of 55 kJ mol−1 or below (Table 1). Thus, it is likely that even if carboxylic acids can be formed on these oxophilic catalysts, they will be easily converted back into acyl and OH fragments.
Conclusions
The OH moiety plays a major role in the heterogeneous catalysis of forming carboxylic acids via insertion of OH groups into acyl fragments. The OH moiety controls many aspects of the TS, including its energy and geometry. The geometric structure of the TS was found to be determined by the need for activating the OH group to sites of lower valency.By formally splitting the OH insertion into two steps, OH activation and subsequent recombination of the OH and acyl fragments, we arrived at two conclusions regarding the physical origin of the barrier. (i) The adsorption strength of OH on the surface exerts a large influence on the barrier, both directly, by affecting the activation step of OH, and indirectly, by affecting the interaction energy in the TS structure, ETSint, (ii) The strength of acyl adsorption affects the barrier in a rather weak fashion, compared to OH adsorption.
Thus, the list of potential candidates warranting in-depth examination of the decarboxylation (DCX) mechanism of APR, can be notably reduced. To be active in DCX, metals need to be able to dissociate water relatively easily, admit facile C–C bond cleavage, and feature weak OH adsorption. Ir, Pd, and Pt fulfill these criteria and are interesting candidates for further studies.
Ir possesses excellent C–C bond scission activity7 and is very active in OH insertion, as shown in this work. Yet, this metal was reported to have very poor APR activity, possibly due to being inactive for WGS.7 This could easily lead to a buildup of CO, poisoning the catalyst surface. Thus, promoting the DCX mechanism and reducing the CO production by alloying with a metal facilitating OH insertion, e.g., Pt, may substantially improve the biomass reforming capabilities of Ir.
In a similar spirit, one may try to explore bimetallic alloys that combine the excellent ability of Au, Ag, or Pt for producing carboxylic acids with the facile C–C bond scission and H2O dissociation abilities of metals such as Ru, Rh and Ni. The effect of particle size may also be explored, regarding a possible reduction of the OH binding energy, which would promote OH insertion.
Computational
Periodic plane-wave density functional theory (DFT) calculations were carried out with the Vienna ab initio simulation package (VASP).54,55 We used the Perdew–Burke–Ernzerhof (PBE)56,57 implementation of the generalized gradient approximation (GGA), in conjunction with the projector-augmented wave (PAW) representation of the atomic cores.58,59 The cut-off energy of the plane-wave basis set was chosen to be 400 eV for structure relaxations using a fixed unit cell. The Brillouin zone was sampled with a Monkhorst Pack mesh60 of 5 × 5 × 1 k-points. The Fermi surface was treated by second-order Methfessel–Paxton61 smearing with a width of 0.2 eV; the resulting energies were extrapolated to zero width. Dipole corrections were applied perpendicular to the model surfaces; symmetry was turned off.For all metals with fcc and hcp crystal structures, we chose close-packed surfaces. Thus, we used (111) surface models for Ni, Cu, Rh, Pd, Ag, Ir, Pt, and Au, while we employed (0001) surface models for Co, Ru, and Os. For Fe we took the bcc crystal structure and a (110) surface model. The slightly deviating results for Fe may in part be due to the differing surface topology. We carried out spin-polarized calculations when modeling Fe, Co, and Ni which are ferromagnetic materials.
Metal surfaces were approximated by a 3 × 3 supercell containing a slab of five layers of metal atoms. Adsorbates were placed only on the “top” side of the slab models; the “bottom” three layers of the slabs were kept fixed at a structure compatible with the optimized bulk lattice. Adsorbates and the top two layers of the slab models were allowed to relax until the residual force on each atom was below 2 × 10−4 eV pm−1. A space equivalent of at least 10 metal layers (∼2 nm) separated the periodic images of the metal slabs. Gas phase species were calculated in a cubic unit cell of 1.5 nm size, with the Brillouin zone sampled at the Γ point only.
We determined approximate TS structures by the climbing-image nudged-elastic-band (CI-NEB) method62,63 and then refined them by the dimer method.64 All stationary points were confirmed by a normal-mode analysis.
Energy relationships
The adsorption energy Eads(A/M) of adsorbate A on metal M is defined as the reaction energy of the adsorption process, A + M → A/M,| E(A/M) = E(A) + E(M) + Eads(A/M), | (2) |
For establishing Brønsted–Evans–Polanyi (BEP) relationships, it has been found beneficial40 to use an energy reference where the reactants OH and the acyl moiety RCO are in the gas phase, and the surface M is in its bare state, Fig. 5.
| Eref = E(OH) + E(RCO) + E(M) | (3) |
Furthermore, one uses an initial state IS of the surface reaction where the reactants are adsorbed without mutual interaction, i.e., formally at infinite separation (Fig. 5):
| EISads = Eads(OH/M) + Eads(RCO/M) | (4) |
In passing, we note that the total energy EIS(OH,RCO/M) of that initial state can be written as:
| EIS(OH,RCO/M) = Eref + EISads = E(OH/M) + E(RCO/M) − E(M) | (5) |
Here, one has used the definition of the adsorption energy, eqn (2), two times. For the activation energy Ea of the OH insertion, eqn (1), RCO/M + OH/M → RCOOH/M, one has:
| Ea = ETS(RCO–OH/M) − EIS(OH,RCO/M) | (6) |
| = ETSads − EISads | (7) |
The (formal) adsorption energy ETSads of the TS is defined in analogy to eqn (5), Fig. 5:
| ETS(RCO–OH/M) = Eref + ETSads | (8) |
Furthermore, one has for the final state FS of the surface reaction (Fig. 5):
| E(RCOOH/M) = Eref + EFSads | (9) |
Therefore, one can write for the reaction energy Er of the insertion reaction:
| Er = EFSads − EISads | (10) |
| Ereva = ETSads − EFSads = Ea − Er | (11) |
Energy decomposition
We decompose the total energy of the TS in analogy to eqn (2) and (5), thus defining the interaction energy ETSint of the reactants OH and RCO in the TS:44| ETS(RCO–OH/M) = ETS(OH/M) + ETS(RCO/M) − ETS(M) + ETSint | (12) |
Here ETS(OH/M) is the energy of reactant OH in its structure and position as in the TS complex (RCO–OH)TS, but without reactant RCO present. ETS(RCO/M) is defined in analogous fashion and ETS(M) is the energy of the bare slab, but in that same TS geometry. A positive value of ETSint indicates a repulsive interaction. Combining eqn (5) and (6), one obtains:
| Ea = Eprp(OH) + Eprp(RCO) − Eprp(M) + ETSint | (13) |
Eprp(X) = ETS(X/M) − E(X/M), X = OH, RCO, ![[rectangle open, vertical]](https://www.rsc.org/images/entities/char_25af.gif) , , | (14) |
![[rectangle open, vertical]](https://www.rsc.org/images/entities/char_25af.gif) ) into the structure of the slab moiety of the model at the TS. This latter (positive) contribution is counted both in Eprp(OH) and Eprp(RCO), hence has to be subtracted in eqn (14). There is no simple way to correct Eprp(OH) and Eprp(RCO) for this double counting, so that the values of Eprp(OH) and Eprp(RCO) are larger (more positive) than physically justified, but this effect is numerically small for the systems studied.
) into the structure of the slab moiety of the model at the TS. This latter (positive) contribution is counted both in Eprp(OH) and Eprp(RCO), hence has to be subtracted in eqn (14). There is no simple way to correct Eprp(OH) and Eprp(RCO) for this double counting, so that the values of Eprp(OH) and Eprp(RCO) are larger (more positive) than physically justified, but this effect is numerically small for the systems studied.
The value of ETSint comprises “through-bond” and “through-space” interactions. The former contribution reflects the weakening of the adsorption of the two fragments OH and RCO in the TS due to competition for bonding to the surface; the latter contribution mainly represents the direct orbital interaction when forming the bond RCO–OH as well as the direct Pauli repulsion between the two fragments OH and RCO.44
Crystal orbital overlap populations (COOP)
To analyze the bonding properties of the OH and the acyl fragments in the TS structures and in their favored geometries, we carried out a crystal orbital overlap population (COOP)65 analysis, invoking a localized minimal basis set. For this COOP analysis, involving projections onto the plane-wave results, we applied the software package LOBSTER66,67 to the results of a PAW calculation where the semi-core p states were explicitly treated. In this way, the projection resulted in favorable values, below 2%, for the electron density mismatch (“spilling”).66,67 For each system, we selected a right-handed Cartesian coordinate system where the first axis was chosen along the direction of the atom pair under scrutiny; the second axis was determined in the plane containing the analyzed atom pair and an adjacent bonding atom, e.g., Pt–O2–H and Pt–C1–O1. For the bare hydroxyl fragment at a bridge site, we chose the second vector parallel to the surface. In the spirit of a previous analysis,36 we show COOP spectra with orbital interactions decomposed into two contributions: (i) the σ-type components along the first axis (d–pσ), and (ii) the sum the other the two π-type components (d–p⊥) relative to this axis. As a second aspect of this analysis, we compare the COOP spectra of the IS and the corresponding TS; see Fig. 3.Conflict of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Ionut Tranca and Cheng-chau Chiu for helpful discussions. We are grateful to Zhao Weina, Li Wenqing, and Velina Markova for their assistance during the preparation of the manuscript. We acknowledge generous computing resources provided by the A*STAR Computational Resource Centre (A*CRC).References
- G. W. Huber and J. A. Dumesic, Catal. Today, 2006, 111, 119–132 CrossRef CAS.
- D. M. Alonso, J. Q. Bond and J. A. Dumesic, Green Chem., 2010, 12, 1493–1513 RSC.
- J. C. Serrano-Ruiz, R. Luque and A. Sepúlveda-Escribano, Chem. Soc. Rev., 2011, 40, 5266–5281 RSC.
- P. Gallezot, Chem. Soc. Rev., 2012, 41, 1538–1558 RSC.
- X. S. Zhang, G. X. Yang, H. Jiang, W. J. Liu and H. S. Ding, Sci. Rep., 2013, 3, 1120 CrossRef PubMed.
- R. D. Cortright, R. R. Davda and J. A. Dumesic, Nature, 2002, 418, 964–967 CrossRef CAS PubMed.
- R. R. Davda, J. W. Shabaker, G. W. Huber, R. D. Cortright and J. A. Dumesic, Appl. Catal., B, 2003, 43, 13–26 CrossRef CAS.
- J. W. Shabaker, G. W. Huber and J. A. Dumesic, J. Catal., 2004, 222, 180–191 CrossRef CAS.
- J. N. Chheda, G. W. Huber and J. A. Dumesic, Angew. Chem., Int. Ed., 2007, 46, 7164–7183 CrossRef CAS PubMed.
- Y.-C. Lin, Int. J. Hydrogen Energy, 2013, 38, 2678–2700 CrossRef CAS.
- S. Carrettin, P. McMorn, P. Johnston, K. Griffin, C. J. Kiely and G. J. Hutchings, Phys. Chem. Chem. Phys., 2003, 5, 1329–1336 RSC.
- R. R. Davda, J. W. Shabaker, G. W. Huber, R. D. Cortright and J. A. Dumesic, Appl. Catal., B, 2005, 56, 171–186 CrossRef CAS.
- D. M. Alonso, S. G. Wettstein and J. A. Dumesic, Chem. Soc. Rev., 2012, 41, 8075–8098 RSC.
- A. Haryanto, S. Fernando, N. Murali and S. Adhikari, Energy Fuels, 2005, 19, 2098–2106 CrossRef CAS.
- S. Sá, H. Silva, L. Brandão, J. M. Sousa and A. Mendes, Appl. Catal., B, 2010, 99, 43–57 CrossRef.
- D. L. King, L. Zhang, G. Xia, A. M. Karim, D. J. Heldebrant, X. Wang, T. Peterson and Y. Wang, Appl. Catal., B, 2010, 99, 206–213 CrossRef CAS.
- A. Ciftci, D. A. J. M. Ligthart and E. J. M. Hensen, Green Chem., 2014, 16, 853–863 RSC.
- G. W. Huber, J. W. Shabaker, S. T. Evans and J. A. Dumesic, Appl. Catal., B, 2006, 62, 226–235 CrossRef CAS.
- A. Wawrzetz, B. Peng, A. Hrabar, A. Jentys, A. A. Lemonidou and J. A. Lercher, J. Catal., 2010, 269, 411–420 CrossRef CAS.
- D. Basaran, A. Genest and N. Rösch, J. Catal., 2012, 287, 210–213 CrossRef CAS.
- D. Basaran, A. Genest, J. A. Lercher and N. Rösch, ACS Catal., 2013, 3, 1730–1738 CrossRef CAS.
- L. Moskaleva, C.-c. Chiu, A. Genest and N. Rösch, Chem. Rec., 2016, 16, 2388–2404 CrossRef CAS PubMed.
- R. Lobo, C. L. Marshall, P. J. Dietrich, F. H. Ribeiro, C. Akatay, E. A. Stach, A. Mane, Y. Lei, J. Elam and J. T. Miller, ACS Catal., 2012, 2, 2316–2326 CrossRef CAS.
- J. Lu, S. Behtash and A. Heyden, J. Phys. Chem. C, 2012, 116, 14328–14341 CAS.
- J. Lu, S. Behtash, M. Faheem and A. Heyden, J. Catal., 2013, 305, 56–66 CrossRef CAS.
- Z.-Q. Huang, B. Long and C.-R. Chang, Catal. Sci. Technol., 2015, 5, 2935–2944 CAS.
- T. Nozawa, Y. Mizukoshi, A. Yoshida and S. Naito, Appl. Catal., B, 2014, 146, 221–226 CrossRef CAS.
- S. Chibani, C. Michel, F. Delbecq, C. Pinel and M. Besson, Catal. Sci. Technol., 2013, 3, 339–350 CAS.
- B. N. Zope, D. D. Hibbitts, M. Neurock and R. J. Davis, Science, 2010, 330, 74–78 CrossRef CAS PubMed.
- G. M. Mullen, L. Zhang, E. J. Evans, T. Yan, G. Henkelman and C. B. Mullins, Phys. Chem. Chem. Phys., 2015, 17, 4730–4738 RSC.
- M. L. Personick, R. J. Madix and C. M. Friend, ACS Catal., 2017, 7, 965–985 CrossRef CAS.
- S. Sakong and A. Groß, ACS Catal., 2016, 6, 5575–5586 CrossRef CAS.
- S. Sakong and A. Groß, Electrocatalysis, 2017 DOI:10.1007/s12678-017-0370-1.
- A. Michaelides and P. Hu, J. Am. Chem. Soc., 2000, 122, 9866–9867 CrossRef CAS.
- C. J. Zhang and P. Hu, J. Am. Chem. Soc., 2000, 122, 2134–2135 CrossRef CAS.
- R. A. van Santen and I. Tranca, Phys. Chem. Chem. Phys., 2016, 18, 20868–20894 RSC.
- M. T. Koper and R. A. van Santen, J. Electroanal. Chem., 1999, 472, 126–136 CrossRef CAS.
- M. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- R. A. van Santen, M. Neurock and S. G. Shetty, Chem. Rev., 2010, 110, 2005–2048 CrossRef CAS PubMed.
- D. Loffreda, F. Delbecq, F. Vigné and P. Sautet, Angew. Chem., Int. Ed., 2009, 48, 8978–8980 CrossRef CAS PubMed.
- J. Zaffran, C. Michel, F. Auneau, F. Delbecq and P. Sautet, ACS Catal., 2013, 4, 464–468 CrossRef.
- A. Logadottir, T. H. Rod, J. K. Nørskov, B. Hammer, S. Dahl and C. J. H. Jacobsen, J. Catal., 2001, 197, 229–231 CrossRef CAS.
- A. Alavi, P. Hu, T. Deutsch, P. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653 CrossRef CAS.
- Z.-P. Liu and P. Hu, J. Chem. Phys., 2001, 115, 4977–4980 CrossRef CAS.
- L. Prati and M. Rossi, J. Catal., 1998, 560, 552–560 CrossRef.
- S. Biella, L. Prati and M. Rossi, J. Catal., 2002, 206, 242–247 CrossRef CAS.
- S. Carrettin, P. McMorn, P. Johnston, K. Griffin and G. J. Hutchings, Chem. Commun., 2002, 696–697 RSC.
- J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, J. Catal., 2010, 276, 92–100 CrossRef.
- L. Foppa, C. Copéret and A. Comas-Vives, J. Am. Chem. Soc., 2016, 138, 16655–16668 CrossRef CAS PubMed.
- I. V. Yudanov, A. Genest, S. Schauermann, H.-J. Freund and N. Rösch, Nano Lett., 2012, 12, 2134–2139 CrossRef CAS PubMed.
- J. H. Fischer-Wolfarth, J. A. Farmer, J. M. Flores-Camacho, A. Genest, I. V. Yudanov, N. Rösch, C. T. Campbell, S. Schauermann and H.-J. Freund, Phys. Rev. B, 2010, 81, 8–11 CrossRef.
- M. Peter, J. M. Flores Camacho, S. Adamovski, L. K. Ono, K.-H. Dostert, C. P. O'Brien, B. Roldan Cuenya, S. Schauermann and H.-J. Freund, Angew. Chem., Int. Ed., 2013, 52, 5175–5179 CrossRef CAS PubMed.
- M. Comotti, C. D. Pina and M. Rossi, J. Mol. Catal. A: Chem., 2006, 251, 89–92 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B, 1989, 40, 3616–3621 CrossRef CAS.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- H. Jónsson, G. Mills and K. Jacobsen, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. Berne, G. Cicotti and D. Coker, World Scientific, Singapore, 1997, pp. 385–404 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 3528–3537 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional results are provided as supporting information in the online version of this article: structures of TS geometries, additional correlation plots, additional energy data, Cartesian coordinates of pertinent stationary structures. See DOI: 10.1039/c7cy00972k |
| ‡ Present address: Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, Wisconsin 53706, USA. |
| This journal is © The Royal Society of Chemistry 2017 |