Impact of bi-axial strain on the structural, electronic and optical properties of photo-catalytic bulk bismuth oxyhalides†
Sangita
Dutta
,
Tilak
Das‡
* and
Soumendu
Datta
 *
*
S. N. Bose National Centre for Basic Sciences, Department of Condensed Matter Physics and Material Sciences, JD Block, Sector-III, Salt Lake City, Kolkata 700 106, India. E-mail: tilak.iitm@ymail.com; soumendu@bose.res.in
First published on 23rd November 2017
Abstract
The structural, electronic and optical properties of bulk bismuth oxyhalides, BiOX (X = F, Cl, Br, and I), were studied using state-of-the-art density functional theory (DFT)-based calculations. The effects of compressive and tensile strains on the in-plane lattice parameters were analyzed to better understand their good performance in photo-catalytic applications. Our present first-principles calculations show that at least 4% in-plane bi-axial compressive strain over the experimental lattice parameters of BiOF is needed for phonon stability of this material, whereas other BiOX systems can accept up to 2% in-plane bi-axial compressive strain and retain their dynamical stability. On the other hand, 2% in-plane tensile strain breaks the structural stability of all bulk BiOX structures. Tuning the electronic band structures with such external compressive strain indeed helps to enhance the separation of charge carriers due to larger electron–hole effective mass differences in the BiOBr and BiOI structures. The optical properties are discussed from their calculated absorption spectra and optical conductivity within independent particle approximations. The average values of the calculated optical band gaps are in the range of 3.8–3.9 eV, 3.3–3.4 eV, 2.7–2.8 eV and 1.7–1.8 eV for the unstrained and compressive strained structures, respectively, of the BiOF, BiOCl, BiOBr and BiOI materials, which are reasonably good compared to their known experimental ultra-violet visible spectroscopy measured data.
1 Introduction
The search for photo-catalytic inorganic semiconductors that are visible-light-responsive under the solar spectrum is one of the major challenges to date.1–3 Based on their crystallographic bulk geometry, two strategies are widely used: (a) synthesizing ternary or quaternary materials by alloying ns2 elements with nd0 and nd10 elements and (b) doping and co-doping with suitable dopant elements in a wide band-gap host photo-catalyst.4–6 Thus, electronic band-structure engineering of these materials is the key point to understand their activities under the visible range of the solar spectrum.Bismuth oxyhalides BiOX (X = F, Cl, Br, and I), belonging to the class of group V–VII ternary compounds, are a layered semiconductor in their bulk geometry with outstanding optoelectronic properties, which lead to various applications such as photo-catalysts,7,8 gas sensors,9 and medicinal applications.10,11 However, BiOX used as a visible-light-responsive homogeneous12–14 or heterogeneous15–17 photo-catalyst for hydrogen-fuel production through the water-splitting reaction has been of particular research interest in recent times.18–20
A recent work has shown that a controlled synthesis of BiOBr nano-sheets with square and circular geometries leads to different inner strains and hence very different photo-catalytic efficiencies.21,22 In particular, the impact of strain generated in these materials due to different morphologies influences the band symmetry. This is due to the fact that the possible photo-induced optical transitions change from the direct to indirect type, which indeed plays a major role in the context of effective separation of charge carriers for the circular structure. Thereby, even though the circular geometry has a higher band gap (2.82 eV vs. 2.68 eV) and a lower porosity (4.49 m3 g−1vs. 7.03 m3 g−1) than those of square morphology, the former however shows better photo-activities. The role of an applied strain in modifying the opto-electronic properties of the said BiOX system with a reduced dimension has been indicated here.
Thus, in the present work, we have focused primarily on the effects of both in-plane (ab-plane) compressive and tensile bi-axial strains on the bulk crystal structure and the electronic properties of BiOX, using first-principles DFT calculations including the effects of spin-orbital coupling and van der Waals corrections. We have also analyzed the optical absorption spectra and optical conductivity for these unstrained and compressed BiOX systems.
Our electronic band-structure analysis of the bulk phases of BiOX revealed that the valence band (VB) maxima belong to the Z → R path and the conduction band (CB) minima stay at the Z points for BiOF, BiOCl, and BiOBr (Z → Γ for BiOI) in their first Brillouin zone (BZ) in k-space. However, these findings contradict the previous reported literature, where the role of the Bi-5d orbital has been studied systematically within the DFT formalism and a trend was found of a direct band-gap for BiOF at the Z-point, and then gradually the CB minima move away from the Z-points towards Z → Γ for BiOCl, BiOBr and BiOI.23,24 Hence, further studies of the bulk crystal structures of BiOX will be helpful for better understanding their subsequent optoelectronic properties including photo-catalytic activities.
2 Computational details and methodology
First-principles calculations were performed using DFT including spin–orbit (SO) coupling and dispersion energy corrections arising from the van der Waals (vdW)25 interactions solved within DFT-D3 formulations, as implemented through the plane-wave basis Vienna Ab initio Simulation Package (VASP).26,27 The structures were optimized using the Perdew–Burke–Ernzerhof (PBE) formulation of the exchange–correlation potential within the generalized gradient approximation (GGA).28In our plane-wave calculations, the core electrons have been approximated with the projector augmented wave (PAW)29 method and the valence electrons have been treated with the plane-wave basis set with a cut-off of 650 eV. In the valence configuration, we have considered 21 electrons for Bi (5p65d106s26p3), 6 electrons for O (2s22p4) and 7 electrons for halide X (ns2np5) atoms, where n = 2, 3, 4, and 5, respectively, for F, Cl, Br, and I. The energy convergence during the self-consistent cycles using the conjugate gradient algorithm was ensured with an energy convergence threshold of 10−8 eV, and the force convergence was set to 10−3 eV Å−1. The bi-axial tensile and compressive strains were applied with 2% elongation and contraction, respectively, of the in-plane lattice vectors of all the BiOX systems. For BiOF, additional 4% and 6% compressive strains were also considered. The k-mesh used for structural optimization is 12 × 12 × 8 for all BiOX. The internal atomic coordinates of the strained crystal structures were relaxed, keeping the cell volume and crystal symmetry intact. For this purpose, the cell parameters of the strained structures were kept unchanged, which allows the change in the parameters ds, dX and dBi commensurate with the empty-layered space of the bulk structure along the 〈001〉 direction.
The calculated ground-state energies and the electronic density of states from VASP calculations were also cross-checked with the calculations from the all-electron full-potential DFT code, WIEN2K,30 using the PBE-GGA + vdW + SO optimized bulk crystal structures of BiOX. The linearized augmented plane-wave (LAPW) basis set in WIEN2K is used with the following criteria, i.e. multiplying the smallest muffin-tin radii with the plane-wave vector Kmax to be at least 8.0, and the expansion of the wave-function was taken up to lmax = 12. The muffin-tin radius was chosen to be 2.34 for Bi, 1.90 for O, and F = 2.32, Cl = 2.5, Br = 2.5, and I = 2.5 for X in atomic units. In order to understand the impact of missing the correlation effect beyond the ground-state DFT, we have done hybrid calculations with the WIEN2K code using the modified Becke and Johnson exchange potential including spin–orbit coupling (mBJ + SO)31 over their PBE-GGA + vdW + SO optimized ground state structures. For all unstrained and compressive strained cases, the calculations of optical properties were done using the WIEN2K code. A number of unoccupied bands and k-mesh were carefully chosen during the simulations of the optical properties. The dispersion of phonon bands has been calculated within the harmonic approximation with post-processing using the PHONOPY package.32 The dynamical matrices for a given displacement of 0.01 Å on the lattices were estimated from the PBE-GGA + vdW + SO calculations over a super-cell of size 4 × 4 × 3 of the bulk BiOX structures (a total of 288 atoms), using density functional perturbation theory (DFPT) as implemented using the VASP code. Next, the force set and hence phonon DOS and band dispersion were performed using the PHONOPY interface.
3 Results and discussion
3.1 Structural stability from the phonon band dispersion
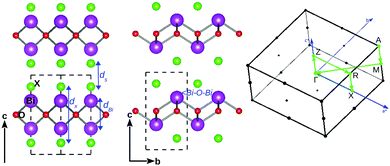
The bulk BiOX systems belong to the matlockite crystal structure23 with a tetragonal space group P4/nmm (No. 129) consisting of [X1−–(Bi2O2)2+–X1−] layers bonded together by strong intra-layer X–Bi–O covalent bonding and inter-layer stacking via the weak vdW interaction along the c-axis. The bulk crystal structure of bismuth oxyhalides, BiOX, is shown in Fig. 1, with its view along the 〈110〉 and 〈100〉 directions, respectively, in the left and middle of the panel. The high symmetry k-points in the first Brillouin zone are connected with the green line, as shown in the right side of the panel. In order to discuss the effect of strain on their bulk geometry, we have focused on some specific geometrical parameters, namely ds: the inter-planar separation of the [X1−–(Bi2O2)2+–X1−] laminae; dX: the width of the lamina sandwiched between two halide X atomic layers, dBi: the separation of Bi–Bi atomic layers, and the in-plane angle ∠Bi–O–Bi within the laminae.The calculated values of the in-plane lattice parameters from our first-principles calculations using the PBE-GGA + vdW + SO formalism, are respectively 3.77, 3.91, 3.94, and 4.02 Å for BiOF, BiOCl, BiOBr and BiOI, which are closer to the corresponding experimental values of 3.76 Å, 3.89 Å, 3.92 Å, and 4.01 Å.33,34 Details of the structural parameters ds, dX, and dBi and ∠Bi–O–Bi, including the Bi–O and Bi–X covalent bond lengths calculated from optimized structures, and their experimental values are tabulated in Section S1 of the ESI† (Table 1). The comparison of the calculated geometry for the bulk structures of BiOX is reasonably good relative to their respective experimental data. Thus, we proceed further to discuss their dynamical, electronic and optical properties using the PBE-GGA + vdW + SO formalism.
| Unstrained structures | ||||||
|---|---|---|---|---|---|---|
| Structure name | d s (Å) | d X (Å) | d Bi (Å) | Bi–X (Å) | Bi–O (Å) | ∠Bi–O–Bi (°) |
| BiOF | 1.80 | 4.39 | 2.61 | 2.81 | 2.29 | 110.5 |
| BiOCl | 2.15 | 5.20 | 2.55 | 3.07 | 2.34 | 113.5 |
| BiOBr | 2.48 | 5.61 | 2.53 | 3.19 | 2.34 | 114.4 |
| BiOI | 2.95 | 6.13 | 2.48 | 3.38 | 2.36 | 116.6 |
| Compressive strained structures | ||||||
|---|---|---|---|---|---|---|
| Structure name | d s (Å) | d X (Å) | d Bi (Å) | Bi–X (Å) | Bi–O (Å) | ∠Bi–O–Bi (°) |
| BiOF | 1.82 | 4.36 | 2.67 | 2.69 | 2.25 | 107.0 |
| BiOCl | 2.10 | 5.26 | 2.60 | 3.02 | 2.31 | 111.8 |
| BiOBr | 2.42 | 5.68 | 2.57 | 3.14 | 2.32 | 112.6 |
| BiOI | 2.89 | 6.21 | 2.53 | 3.34 | 2.34 | 114.7 |
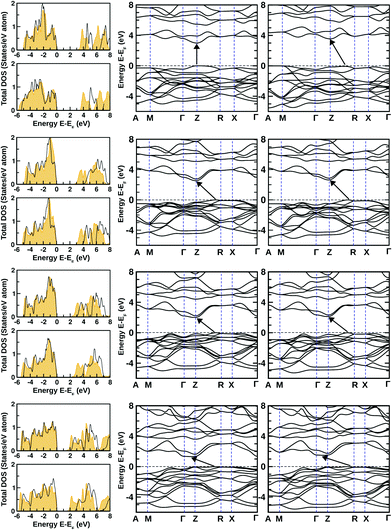
The dynamical stability of these optimized structures was checked, primarily. Here, we have calculated their phonon band dispersion and plotted over the first Brillouin zone of their bulk structure. These phonon band dispersion plots are shown in Fig. 2 for all BiOX bulk structures. They show the clear presence of imaginary phonon modes at the Γ point and also at the Γ → M and M → A regions of the BZ in the case of BiOF, whereas no such effect is observed for the other BiOX, i.e. BiOCl, BiOBr, and BiOI. Thus, the use of experimental lattice parameters or their structural optimization using first-principles calculations may not be a proper approach to further explore the properties of the BiOF bulk phase.
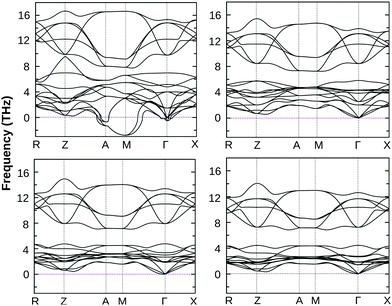 | ||
| Fig. 2 The calculated phonon band dispersion of bulk BiOF (top left), BiOCl (top right), BiOBr (bottom left) and BiOI (bottom right) over their PBE-GGA + vdW + SO optimized crystal structures. | ||
Also, considering a moderate amount of lattice mismatch during the heterostructure formation,35,36 the bulk to film geometry formation37 or the synthesis conditions22 of such layered materials for optoelectronic devices, the application of bi-axial and/or uni-axial strain has been found to be crucial for tuning their electronic, magnetic or optical properties. Therefore, exploring the structures in the potential energy surface around the experimentally reported equilibrium structure of these systems is relevant as the isomers even at a small energy difference may possess exceptionally different properties. Hence, we have applied a small amount of bi-axial strain (±2%) to the in-plane (ab-plane) lattice parameters without too much deviation from their experimental values. Such bi-axial strain is indeed equivalent to the creation of uni-axial pressure along the out-of-plane direction (the c-axis) over the unit cell of BiOX. Details of the lattice parameters before and after strain application are tabulated in Section S2 of the ESI† (Table 2).
| Unstrained structure | ||||
|---|---|---|---|---|
| Structure name | PBE-GGA + vdW + SO (in eV) | mBJ + SO (in eV) | Band-gap type | Experimental values (in eV) |
| BiOF | 3.07 | 4.18 | Direct | 3.5–3.6 |
| BiOCl | 2.63 | 3.72 | Indirect | 2.9–3.4 |
| BiOBr | 2.11 | 2.93 | Indirect | 2.3–2.9 |
| BiOI | 1.46 | 2.11 | Indirect | 1.8–2.1 |
| Compressive strained structure | ||||
|---|---|---|---|---|
| Structure name | PBE-GGA + vdW + SO (in eV) | mBJ + SO (in eV) | Band-gap type | Previous HSE06 + vdW + SO (in eV) |
| BiOF | 3.63 | 4.90 | Indirect | 4.18 |
| BiOCl | 2.75 | 3.84 | Indirect | 3.37 |
| BiOBr | 2.25 | 3.25 | Indirect | 2.82 |
| BiOI | 1.63 | 2.51 | Indirect | 2.00 |
Interestingly, the applied 2% bi-axial compressive strain in fact improves the dynamical stability of BiOF substantially, whereas its structural stability remains unchanged for other BiOX systems under the same amount of compressive strain, which validates our approach and prediction (cf. Section S3 of the ESI,† Fig. S1). The value of compressive strain was further optimized for BiOF in the next step, and we noticed that at least 4% strain to the in-plane lattice parameters is needed for bulk BiOF to be dynamically stable as seen from the calculated phonon band dispersion (cf.Fig. 3). On the other hand, we have seen that as small as 2% tensile strain to the in-plane lattice parameters worsens the situation, giving imaginary frequencies around the Γ point at a low-frequency range of the BZ for all the four systems (cf. Section S3 of the ESI†, Fig. S2). Thus, the impact of tensile strain was omitted from the current scenario because of phonon mode instability in the BiOX bulk phases. We therefore keep using the unstrained and 2% compressive (4% for BiOF) strained structures of BiOX to discuss their electronic and optical properties in the rest of the manuscript.
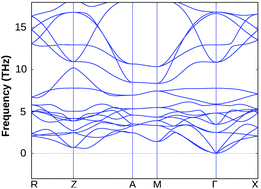 | ||
| Fig. 3 The calculated phonon band dispersion of the bulk BiOF crystal under 4% in-plane bi-axial compressive strain. | ||
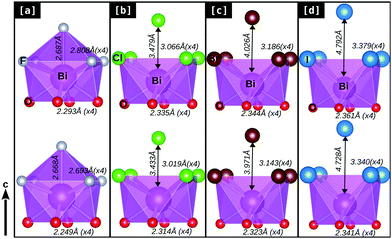
In order to understand such variations in the dynamical stability of these bulk BiOX systems upon strain, we looked at the details of their structural parameters and BiO4X4 polyhedrons affected due to the applied strain, which show different trends for BiOF compared to the other members of the BiOX family. In Fig. 4[a–d], we have represented the details of the BiO4X4 (X = F, Cl, Br, and I) square anti-prismatic polyhedra obtained from the PBE-GGA + vdW + SO optimized bulk structures before (top row) and after (bottom row) the application of compressive strain.
Indeed, notable changes are observed for BiOF, in the sense that the square anti-prism is broken with additional F atoms covalently connected to the out-of-plane direction to the Bi–F facet (cf.Fig. 4[a]). The reverse trend is found for the other BiOX systems, where the out-of-plane halide X atoms remain apart from the chemical bonding range with the Bi–X facet before or after the applied compressive strain (Fig. 4[b]–[d]).
We have noted that the inter-layer spacing ds has the tendency to increase for BiOF but decreases for other BiOX systems and vice versa for the width of the laminar, dX, upon the applied compressive strain (cf.Table 1). This is probably due to the size effect of the smaller F− ions compared to the other larger halide ions Cl−, Br−, and I− and their different chemical affinities with Bi3+. However, the in-plane compressive strain allowed the Bi–X (×4) bond lengths to be compacted differently, and almost the same amount of effect (contraction) is seen on the Bi–O (×4) bond lengths for all BiOX systems. As a result, we have seen that there is a significant change in the in-plane buckling angle ∠Bi–O–Bi for BiOF, which is nearly 4° and almost half or less than 2° for the other BiOX materials. Details of their geometrical parameters are tabulated in Table 1 for the optimized unstrained and compressive strained structures.
An applied 2% compression to the in-plane lattice parameters allows the Bi–X bond lengths to be reduced by ∼0.05 Å for BiOCl, BiOBr and BiOI but they are almost doubled or greater than 0.1 Å for BiOF upon 4% compression. The out-of-plane Bi–F bond length changes by ∼0.02 Å for BiOF and no such bonding is allowed for the other BiOX. So, the kinetic stability observed for the BiOF system upon 4% compressive strain is essentially guided by the modification of in-plane Bi–F and Bi–O bonds, which is directly influenced by chemical covalency rather than the inter-planar weak vdW interactions. Thus, the effect of the vdW interaction gradually decreases due to the increase of the inter-planar spacing, as X changes from F to I. Thus, exfoliation or peeling is possible in the near future of these materials in the form of a mono-layer or few layer geometry with the most favorable order of I > Br > Cl > F, as seen from their geometry. This is indeed in accordance with the reported first-principles prediction of mono-layer binding energies calculated for the family of BiOX.38,39
3.2 Electronic properties and band-gap engineering
The electronic properties of both the unstrained and strained BiOX systems have been studied through the analysis of density of states (DOS) calculated using the PBE-GGA + vdW + SO formalism as shown in Fig. 5. In the left panels of each row, the total DOS values are shown for unstrained (top) and compressive strained structures (bottom) using orange shaded curves. Our estimated band-gaps from these total DOS plots for the unstrained structures are 3.1, 2.6, 2.1 and 1.5 eV, respectively, for BiOF, BiOCl, BiOBr and BiOI bulk phases, which are close to previously reported theoretical values.24 Small changes are noted for our estimated values compared to those reported in ref. 24, which could be possibly due to our additional consideration of vdW corrections.On the other hand, by focusing on the strained systems, we have noted that the band-gap markedly increases due to the additional compressive strain, which is nearly 0.5 eV for BiOF and 0.1–0.2 eV for the other BiOX systems, arising from the quantum size effect. In our cases, the estimated fundamental band-gaps from the electronic DOS plots for unstrained systems are always lower compared to their known experimental limits of 3.5–3.6, 2.9–3.4, 2.3–2.9 and 1.8–2.1 eV, respectively, for the BiOF, BiOCl, BiOBr, and BiOI bulk phases.12,40
Indeed, hybrid potential calculations using the mBJ + SO formulation help to give better accuracy in the estimated values of the band-gaps for the BiOX systems (except BiOF). The related total DOS values from the mBJ + SO calculations are also shown within the respective DOS panels as shown in Fig. 5 using the black solid line curves. The inclusion of the computationally cost-effective hybrid potential calculations improves the calculated band-gap values significantly for Cl, Br and I-based systems.41 The calculated band-gap values are tabulated in Table 2 for all unstrained and compressive strained bulk structures. Note that the estimated indirect band-gaps for their bulk phase from previous first-principles calculations using the hybrid functional (HSE06)42,43 within the DFT formalism were 4.18, 3.37, 2.82, and 2.00 eV, respectively, for the BiOX compounds with X = F, Cl, Br, and I.41
In addition to the total DOS, the corresponding total electronic band structures are plotted for all unstrained and strained structures on the middle and right-side panels of Fig. 5. We have noted that the overall features of the DOS from PBE-GGA + vdW + SO and mBJ + SO calculations are almost the same with a discrete shift of the CB to a higher energy. So, we have shown only the PBE-GGA + vdW + SO data for all of them. Similar to previous theoretically reported data for BiOF, we have seen that the band-gap is direct for the unstrained bulk structure with the VB maximum and the CB minimum at the Z-point in the BZ.24 But, we have noticed that the impact of 4% compressive strain makes it an indirect band-gap system with the band-gap increasing to 3.6 eV, where the VB maximum moves towards the middle of the Z → R region, similar to the other members of this BiOX halide family. This scenario was indeed expected from the known previous experimental measurements and theoretical predictions on this particular family of BiOX systems.41 The CB minima for BiOCl, BiOBr and BiOI tend to move from the Z point towards the Z → Γ path, for both their unstrained and compressive strained structures.
3.3 Effective mass of photo-excited charge carriers
The mobility of charge carriers in a semiconductor is inversely proportional to their effective mass (m*). Thus, the measure of the effective mass indirectly effects the life-times of the photo-excited charge carriers, thus controlling the quantum efficiency of the photo-to-current conversion mechanism in a photo-catalysis process. The effective masses of the charge carriers of electrons and holes are calculated using the following equation: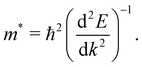 | (1) |
Here, ℏ is the reduced Planck's constant, E is the energy eigenvalue at the VB top and the CB bottom extrema at the point k of the chosen electronic bands in the k-space.
In the case of bulk BiOX, the electronic band structure analysis describes that band-edges predominantly consist of highly dispersive p-states of the constituent Bi, O and X atoms, which could be responsible for the lower effective mass of electrons, thereby inducing better charge separation.41 It is also seen that within their layered structure, a non-uniform charge distribution between the [X1−–(Bi2O2)2+–X1−] layers creates an internal electric-field along the c-axis, which plays a vital role in enhancing photo-activity by promoting faster charge transfer, i.e. longer life-times of the photo-generated excitons.19
To elucidate these predictions, we have calculated the effective mass of photo-excited charge carriers of these pristine and compressive strained BiOX bulk structures. Similar to the previous theoretical estimation of effective mass for unstrained structures, our estimation agreed reasonably with that derived from their band dispersion shown in Fig. 5.41 Here, the VB top belongs to the 〈010〉 direction, i.e. Z → R (except F), and we have noted a similar dispersion for BiOCl and BiOBr, but relatively larger and similar dispersion for BiOF and BiOI. Such a band dispersion in fact implies that the hole effective masses for BiOCl (0.27m0) and BiOBr (0.20m0), which are nearly equal, are also lower compared to BiOF (0.90m0) and BiOI (0.54m0). Here, m0 is the rest mass of an electron. The detailed procedure of our effective mass calculations is given in Section S4 of the ESI.†
The band dispersion plots of unstrained cases show that the CB bottom belongs to the Z point and moves along the 〈001〉 direction, i.e. Z → Γ, moving from F to I. This could be explained as the inter-planar distance ds increases gradually, thus hybridization along the 〈001〉 direction decreases (cf.Fig. 4[a–d]). So, one would expect that the electron motion will be higher to lower and thus the effective mass of the electron will be monotonously higher from the F to I phase in the Z → Γ path. Our calculated values of the electron effective masses were 0.31m0, 0.46m0, 5.68m0 and 6.34m0, respectively, for the F to I systems. So, these calculated values prove that the effective mass difference between the photo-generated holes and electrons is more for BiOBr and BiOI bulk phases, which indirectly indicates that the relative charge separation will be more favorable for these two systems compared to the other two of this family (BiOF and BiOCl).
Indeed, we have seen that the order of effective masses slightly reduces due to compressive strain application with the higher difference value retained for BiOBr (5.42m0) and BiOI (5.55m0). Such minor effects on the effective masses could be explained as the slopes of the VB and CB extrema in their k-space remain unchanged upon the applied compressive strain. On the other hand, if we look into the hole effective masses of BiOBr (0.18m0) and BiOI (0.49m0), this clearly indicates that holes will move faster in BiOBr than in the other one. Thus, in the context of the photo-catalytic application of BiOX bulk phases, it is expected that BiOBr could be the best performing photo-catalyst among all the members of the family due to visible-light-responsive band-gaps and better charge carrier separation.
3.4 Optical properties of bulk bismuth oxyhalides
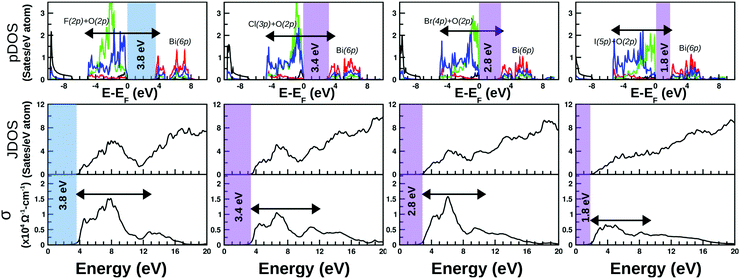
The calculated projected DOS (pDOS) and optical properties (joint density of states, JDOS, and the real part of optical conductivity, σ) of these bulk materials are shown in Fig. 6. The calculations were done over the PBE-GGA + vdW + SO optimized crystal structures. Within the independent particle approximation and the linear optical properties limit, the JDOS is calculated using the following equation,44 as implemented using the WIEN2K code: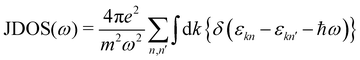 | (2) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i|kn′〉, given as:
i|kn′〉, given as: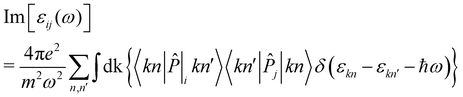 | (3) |
Finally, the diagonal part of the optical conductivity is calculated using the formula:
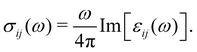 | (4) |
The BiOX bulk phase being a tetragonal structure, with optical anisotropy, is noted for the imaginary part of the dielectric function with light polarization along the in-plane, Im[εxx(ω)], and out-of-plane, Im[εzz(ω)], directions. Details of their plots are given in the ESI† for all unstrained and compressive strained BiOX systems (cf. Section S5, Fig. S4 of ESI†).
As discussed in the previous section, there is no such distinct difference between the total DOS of the unstrained systems and their compressive strained counterpart except a discrete upward shift of the conduction bands, and thus in the subsequent part, we have focused on the optical properties of compressive strained structures and their related pDOS and JDOS analyses. The calculated pDOS, JDOS and optical conductivity for each material are shown in the top, middle and bottom rows of Fig. 6, respectively. The top panels show the plot of pDOS for Bi(6s), Bi(6p), O(2p) and X(np) for each BiOX, as presented with black, red, blue and green solid line curves, respectively. The major contribution in the VB top comes from the occupied O(2p) and halide X(np) states and the minor part from Bi(6s), whereas the bottom of the CB is mostly contributed by the empty Bi(6p) states. The first optical inter-band transition is possibly from the O(2p) valence band to the Bi(6p) empty conduction band, which gradually becomes a transition from a mixed valence state of X(np) and O(2p) moving from F to I. Similarly, JDOS analysis from eigenvalues indicates that the broad lowest energy peak on the optical conductivity plot is related to the possible electronic transitions shown with the schematic arrow over the pDOS plots. The arrow over the −4 eV to 4 eV range of the pDOS is equivalent to the 4–12 eV range on the JDOS or σ plots. A gradual increase in the hybridization from halide X(np) states with O(2p) in the valence band top is probably the reason for having the monotonous flat nature of the optical transitions at the lowest photon energy region of σ of F to I systems.
The optical band-gap is calculated using the tangent at the most linear region of Im[εij(ω)], in a similar way to the experimental Tauc plot. The average values from both of the polarizations and over the unstrained and compressive strained structures are taken to estimate the average value of the optical band-gaps for each of these BiOX bulk phases. The estimated values are printed in the color shaded area of the optical conductivity and pDOS panels, which are 3.8, 3.4, 2.8, and 1.8 eV for BiOF, BiOCl, BiOBr, and BiOI systems, respectively. The applied 4% compressive strain makes BiOF an indirect band-gap system, similar to the other BiOX systems with or without the applied compressive strain, which is denoted with different color shades in Fig. 6.
These calculated band-gap values are indeed directly comparable to the experimentally measured data from ultraviolet-visible optical absorption spectra.20 It is worth mentioning that the previously given band-gap values calculated from the electronic band-structure plots (cf.Table 2) using the PBE-GGA + vdW + SO formalism are lower than the currently estimated values from the optical spectra, which is obvious when considering the average values of both the in-plane and out-of-plane contributions from the theoretical optical absorption spectra.
From the estimated optical band-gap values, it is clear that the F and Cl-based systems are UV-responsive within the solar spectrum, whereas the other two structures consisting of Br and I are expected to be active in the visible part of the spectrum. The calculated optical conductivity is the highest for the F and Br systems with an order of ∼1.5 × 104 Ω−1 cm−1 and an intermediate value for the Cl-based system with an order of ∼1.0 × 104 Ω−1 cm−1 and the lowest for the I-based system with an order of ∼0.5 × 104 Ω−1 cm−1. Thus, it is expected that the BiOBr bulk phase could be the best performing photo-catalyst among all four members that would show better visible-light-responsive photo-catalytic efficiency. Indeed, this is in good agreement with the recent experimental observation.20
4 Conclusions and outlook
In summary, we have studied the dynamical, electronic and optical properties of the crystalline BiOX (X: F, Cl, Br, and I) bulk materials using ground-state DFT as well as hybrid DFT formalisms. Our study shows that a ground-state DFT functional with spin–orbit and vdW corrections is enough in this context to get the same level of accuracy as that of the known experimental data of optical properties if a little compressive strain (less than 2%) is applied to the in-plane lattice vectors without breaking their dynamical stability. This approach may be useful for the future heterostructural modeling of few layered BiOX with other 2D-like materials. Out of the four BiOX systems, the BiOBr bulk phase turns out to be one of the best photocatalysts with moderate band-gap, good optical conductivity and favorable separation of photo-excited charge carriers. Changes in the bandgap and the effective mass of the charge carriers suggest that the optical and electronic properties could be widely tuned by alloying different halides.Finally, we conclude this section by commenting, with caution, that even though ground-state DFT with the PBE-GGA functional lacks the finite temperature effect and an accurate description of electron–hole correlations, a moderate amount of compressive strain introduced through the experimental synthesis process to the structural in-plane lattice parameters of bulk BiOX materials will lead to a quite reasonably calculated band-gap and optical properties due to the exclusion of self-interaction and improper relativistic treatment in such Bi-based ternary compounds. A future study is needed for the exploration of the excitonic role and few layer properties of these materials from both experimental and theoretical approaches.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. D. thanks the Department of Science and Technology, India, for support through the INSPIRE Faculty Fellowship, Grant No. IFA12-PH-27.References
- F. E. Osterloh, Inorganic Materials as Catalysts for Photochemical Splitting of Water, Chem. Mater., 2008, 20(1), 35–54 CrossRef CAS.
- I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Computational Screening of Perovskite Metal Oxides for Optimal Solar Light Capture, Energy Environ. Sci., 2012, 5, 5814–5819 CAS.
- S. Dong, J. Feng, M. Fan, Y. Pi, L. Hu, X. Han, M. Liu, J. Sun and J. Sun, Recent Developments in Heterogeneous Photocatalytic Water Treatment Using Visible Light-responsive Photocatalysts: A Review, RSC Adv., 2015, 5, 14610–14630 RSC.
- X. Chen and S. S. Mao, Titanium Dioxide Nanomaterials: Synthesis, Properties, Modifications, and Applications, Chem. Rev., 2007, 107(7), 2891–2959 CrossRef CAS PubMed.
- A. Kudo and Y. Miseki, Heterogeneous Photocatalyst Materials for Water Splitting, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Semiconductor based Photocatalytic Hydrogen Generation, Chem. Rev., 2010, 110(11), 6503–6570 CrossRef CAS PubMed.
- N. Kijima, K. Matano, M. Saito, T. Oikawa, T. Konishi, H. Yasuda, T. Sato and Y. Yoshimura, Oxidative Catalytic Cracking of N-Butane to Lower Alkenes over Layered BiOCl Catalyst, Appl. Catal., A, 2001, 206, 237–244 CrossRef CAS.
- R. Ghosh, S. Maiti and A. Chakraborty, Facile Catalyzed Acylation of Heteroatoms Using BiCl3 Generated in situ from the Photocatalyst BiOCl and Acetyl Chloride, Tetrahedron Lett., 2004, 45, 6775–6778 CrossRef CAS.
- C. R. Michel, N. L. L. Contreras and A. H. Martínez-Preciado, Gas Sensing Properties of Nanostructured Bismuth Oxychloride, Sens. Actuators, B, 2011, 160, 271–277 CrossRef CAS.
- J. Rotmensch, J. Whitlock, M. Dietz, J. Hines, R. Reba, E. Horwitz and P. Harper, Development of 212-BiOCl as a New Therapeutic Modality Against Microscopic Carcinoma, Abstr. Pap. Am. Chem. Soc., 1998, U926 Search PubMed.
- G. G. Briand and N. Burford, Bismuth Compounds and Preparations with Biological or Medicinal Relevance, Chem. Rev., 1999, 99, 2601–2658 CrossRef CAS PubMed.
- X. Zhang, Z. Ai, F. Jia and L. Zhang, Generalized One-Pot Synthesis, Characterization,and Photocatalytic Activity of Hierarchical BiOX (X = Cl, Br, I) Nanoplate Microspheres, J. Phys. Chem. C, 2008, 112, 747–753 CAS.
- J. Zhang, F. Shi, J. Lin, D. Chen, J. Gao, Z. Huang, X. Ding and C. Tang, Self-Assembled 3-D Architectures of BiOBr as a Visible Light-Driven Photocatalyst, Chem. Mater., 2008, 20, 2937–2941 CrossRef CAS.
- X. Xiao, C. Liu, R. Hu, X. Zuo, J. Na, L. Li and L. Wang, Oxygen-rich Bismuth Oxyhalides: Generalized One-pot Synthesis, Band Structures and Visible-light Photocatalytic Properties, J. Mater. Chem., 2012, 22, 22840–22843 RSC.
- S. Y. Chai, Y. J. Kim, M. H. Jung, A. K. Chakraborty, D. Jung and W. I. Lee, Heterojunctioned BiOCl/Bi2O3, a New Visible Light Photocatalyst, J. Catal., 2009, 262, 144–149 CrossRef CAS.
- X. Chang, J. Huang, C. Cheng, Q. Sui, W. Sha, G. Ji, S. Deng and G. Yu, BiOX (X = Cl, Br, I) Photocatalysts Prepared Using NaBiO3 as the Bi Source: Characterization and Catalytic Performance, Catal. Commun., 2010, 11, 460–464 CrossRef CAS.
- K. Ren, J. Liu, J. Liang, K. Zhang, X. Zheng, H. Luo, Y. Huang, P. Liu and X. Yu, Synthesis of the Bismuth Oxyhalide Solid Solutions With Tunable Band Gap and Photocatalytic Activities, Dalton Trans., 2013, 42, 9706–9712 RSC.
- J. Jiang, K. Zhao, X. Xiao and L. Zhang, Synthesis and Facet-Dependent Photoreactivity of BiOCl Single-Crystalline Nanosheets, J. Am. Chem. Soc., 2012, 134, 4473–4476 CrossRef CAS PubMed.
- J. Li, Y. Yu and L. Zhang, Bismuth Oxyhalide Nanomaterials: Layered Structures Meet Photocatalysis, Nanoscale, 2014, 6, 8473–8488 RSC.
- D. S. Bhachu, S. J. A. Moniz, S. Sathasivam, D. O. Scanlon, A. Walsh, A. M. Bawaked, M. Mokhtar, A. Y. Obaid, I. P. Parkin, J. Tang and C. J. Carmalt, Bismuth Oxyhalides: Synthesis, Structure and Photoelectrochemical Activity, Chem. Sci., 2016, 7, 4832–4841 RSC.
- W. Lin, X. Wang, Y. Wang, J. Zhang, Z. Lin, B. Zhang and F. Huang, Synthesis and Facet-Dependent Photocatalytic Activity of BiOBr Single-Crystalline Nanosheets, Chem. Commun., 2017, 53, 4861 RSC.
- H. Feng, Z. Xu, L. Wang, Y. Yu, D. Mitchell, D. Cui, X. Xu, J. Shi, T. Sannomiya, Y. Du, W. Hao and S. X. Dou, Modulation of Photocatalytic Properties by Strain in 2D BiOBr Nanosheets, ACS Appl. Mater. Interfaces, 2015, 7, 27592–27596 CAS.
- F. A. Bannister and M. H. Hey, The Crystal Structure of the Bismuth Oxyhalides, Mineral. Mag., 1935, 24, 49–58 CAS.
- W. L. Huang and Q. Zhu, DFT Calculations on the Electronic Structures of BiOX (X = F, Cl, Br, I) Photocatalysts With and Without Semicore Bi-5d States, J. Comput. Chem., 2009, 30, 183–190 CrossRef CAS PubMed.
- S. Grimme, Accurate Description of van der Waals Complexes by Density Funcitonal Theory Including Empirical Corrections, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmuller, Efficient Iterative Schemes for Ab-initio Total-energy Calculations Using a Plane-wave Basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmentd-wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augumented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, ed. K. Schwarz, Technische Universitiät Wien, Vienna, 2001 Search PubMed.
- F. Tran and P. Blaha, Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. L. Soubeyroux, S. F. Matar, J. M. Reau and P. Hagenmuller, Etude des Properties Structutales et Electriques de la Solution Solide Pb1−xBixOxF2−x, Solid State Ionics, 1984, 14, 337–345 CrossRef CAS.
- K. G. Keramidas, G. P. Voutsas and P. I. Rentzeperis, The crystal structure of BiOCl Locality: Synthetic, Z. Kristallogr., 1993, 205, 35–40 CAS.
- X. D. Li, S. Yu, S. Q. Wu, Y. H. Wen, S. Zhou and Z. Z. Zhu, Structural and Electronic Properties of Superlattice Composed of Graphene and Monolayer MoS2, J. Phys. Chem. C, 2013, 117, 15347–15353 CAS.
- H.-P. Komsa and A. V. Krasheninnikov, Electronic Structures and Optical Properties of Realistic Transition Metal Dichalcogenides heterostructures from First-principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085318 CrossRef.
- T. Das and T. Saha-Dasgupta, Spin-state Transition in Unstrained & Strained Ultra-thin BiCoO3 Films, Dalton Trans., 2015, 44, 10882–10887 RSC.
- X. Zhang, B. Li, J. Wang, Y. Yuan, Q. Zhang, Z. Gao, L. M. Liu and L. Chen, The Stabilities and Electronic Structures of Single-layer Bismuth Oxyhalides for Photocatalytic Water Splitting, Phys. Chem. Chem. Phys., 2014, 16, 25854–25861 RSC.
- Z. Xu, W. Hao, Q. Zhang, Z. Fu, H. Feng, Y. Du and S. Dou, Indirect-direct Band Transformation of Few-Layer BiOCl under Biaxial Strain, J. Phys. Chem. C, 2016, 120, 8589–8594 CAS.
- H. An, Y. Du, T. Wang, C. Wang, W. Hao and J. Zhang, Photocatalytic properties of BiOX (X = Cl, Br, and I), Rare Met., 2008, 27, 243–250 CrossRef CAS.
- A. M. Ganose, M. Cuff, K. T. Butler, A. Walsh and D. O. Scanlon, Interplay of Orbital and Relativistic Effects in Bismuth Oxyhalides: BiOF, BiOCl, BiOBr, and BiOI, Chem. Mater., 2016, 28, 1980–1984 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- F. Wooten, Optical Properties of Solids, Academic Press, 1972, eBook ISBN: 9781483220765 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp07366f |
| ‡ Present address: Department of Physics, Indian Institute of Science Education and Research, Pune, Dr Homi Bhabha Road, Pashan, 411 008, India. |
| This journal is © the Owner Societies 2018 |