Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Excited-states of a rhenium carbonyl diimine complex: solvation models, spin–orbit coupling, and vibrational sampling effects†
Sebastian
Mai
 a,
Hugo
Gattuso
bc,
Maria
Fumanal
a,
Hugo
Gattuso
bc,
Maria
Fumanal
 d,
Aurora
Muñoz-Losa‡
a,
Antonio
Monari
d,
Aurora
Muñoz-Losa‡
a,
Antonio
Monari
 bc,
Chantal
Daniel
bc,
Chantal
Daniel
 d and
Leticia
González
d and
Leticia
González
 *a
*a
aInstitute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Straße 17, Vienna, 1090, Austria. E-mail: leticia.gonzalez@univie.ac.at
bUniversité de Lorraine Nancy, Theory-Modeling-Simulation SRSMC, Boulevard des Aiguillettes, Vandoeuvre-lès-Nancy, 54500, France. E-mail: antonio.monari@univ-lorraine.fr
cCNRS, Theory-Modeling-Simulation SRSMC, Boulevard des Aiguillettes, Vandoeuvre-lès-Nancy, 54500, France
dLaboratoire de Chimie Quantique, Institut de Chimie Strasbourg, UMR-7177 CNRS/Université de Strasbourg, 1 Rue Blaise Pascal BP 296/R8, Strasbourg, 67008, France. E-mail: c.daniel@unistra.fr
First published on 29th September 2017
Abstract
We present a quantum-chemical investigation of the excited states of the complex [Re(CO)3(Im)(Phen)]+ (Im = imidazole; Phen = 1,10-phenanthroline) in solution including spin–orbit couplings and vibrational sampling. To this aim, we implemented electrostatic embedding quantum mechanics/molecular mechanics (QM/MM) in the Amsterdam Density Functional program suite, suitable for time-dependent density functional calculations including spin–orbit couplings. The new implementation is employed to simulate the absorption spectrum of the complex, which is compared to the results of implicit continuum solvation and frozen-density embedding. Molecular dynamics simulations are used to sample the ground state conformations in solution. The results demonstrate that any study of the excited states of [Re(CO)3(Im)(Phen)]+ in solution and their dynamics should include extensive sampling of vibrational motion and spin–orbit couplings.
1 Introduction
Rhenium(I) carbonyl diimine complexes are a fascinating class of molecules with interesting photochemical and photophysical properties. For example, they are involved in the study of long-range electron transfer processes in proteins across distances longer than 10 Å.1 Such processes were observed in labeled cytochrome C2 or azurins,3,4 where electron transfer takes place from a native Fe or Cu center to the rhenium center of an artificially introduced chromophoric complex. Interestingly, the rate of electron transfer depends sensitively on the surrounding of the metal centers and in particular on the presence or absence of specific amino acids, which could enable a multi-step electron transfer mechanism.5,6The very useful photochemical and photophysical properties7–9 of these complexes partially stem from the different classes of excited states they possess: metal-centered (MC), metal-to-ligand, ligand-to-ligand, ligand-to-metal charge transfer (MLCT, LLCT, LMCT), and intraligand (IL) states. The complexes are strongly absorbing, photostable, exhibit long-lived excited states, and are compatible with supramolecular/biomolecular environments. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequencies depend sensitively on the electronic structure, allowing to easily monitor the excited states with time-resolved infrared spectroscopy.10 Furthermore, the complexes show strong emission spectra that are susceptible to the environment. Consequently, these complexes show a wide range of prospective applications:11 they can be employed as photocatalysts for CO2 reduction,12,13 as phosphorescent labels,14 for sensors,15 for molecular switches,16 and are promising in the development of OLEDs.17
O stretching frequencies depend sensitively on the electronic structure, allowing to easily monitor the excited states with time-resolved infrared spectroscopy.10 Furthermore, the complexes show strong emission spectra that are susceptible to the environment. Consequently, these complexes show a wide range of prospective applications:11 they can be employed as photocatalysts for CO2 reduction,12,13 as phosphorescent labels,14 for sensors,15 for molecular switches,16 and are promising in the development of OLEDs.17
The ultrafast dynamics of rhenium(I) carbonyl diimine complexes has been studied in much detail from an experimental point of view, using time-resolved spectroscopy from the femtosecond to the nanosecond time scale.10,11,18–20 For [Re(CO)3(Im)(Phen)]+ (Im = imidazole; Phen = 1,10-phenanthroline)—which is most similar to the chromophore employed in the azurin electron transfer studies5,6—experiments11 showed that after excitation at 400 nm the complex undergoes ultrafast (about 150 fs) intersystem crossing (ISC), followed by few-ps vibrational relaxation in the triplet states and some solvent dynamics.
Complementary to the experimental work, the excited states of rhenium(I) carbonyl diimine complexes have also been extensively studied theoretically. Pioneering work was performed on the related [Re(CO)3(X)(Phen)] (X = Cl, Br, I) complexes,21–25 in order to decipher the mechanism of ultrafast ISC in third-row transition metal complexes and to explain why ISC counterintuitively is slower for heavier halides (Cl < Br < I).
More recently, these theoretical efforts were extended to the more challenging case of [Re(CO)3(Im)(Phen)]+. Fig. 1 shows the molecular structure of the three most stable conformers,26,27 which differ in the orientation of the Im moiety. Following the notation of ref. 26, the shown structures are labeled as conformers A (CS symmetry) and B (no symmetry, chiral). There is also a third conformer (not considered in ref. 26, but reported in ref. 28), which we label as A′ (also CS symmetry) and where the Im is rotated by 180° relative to conformer A. Conformer B is the one observed in the X-ray structure of [Re(Im)(CO)3(Phen)]2SO4·H2O.29 In aqueous solution, the energy differences between the three conformers were reported to be approximately 0.5 kcal mol−1,28 with a rotation barrier of less than 1 kcal mol−1.28 Hence, a Boltzmann population of all three conformers can be expected in solution, with conformer B predominating.
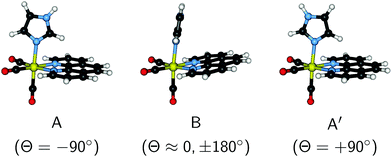 | ||
| Fig. 1 3D depiction of the conformers A, B (following the notation of ref. 26) and A′ of [Re(CO)3(Im)(Phen)]+. The torsion angle Θ (see Fig. S1 in the ESI†) is given in parenthesis. | ||
The excited states of [Re(CO)3(Im)(Phen)]+ were investigated previously with static quantum chemistry using time-dependent density functional theory (TD-DFT) and multi-state complete active space perturbation theory 2nd order (MS-CASPT2) with spin–orbit coupling (SOC) and implicit continuum solvation corrections.26,27,30 Additionally, this complex was also studied with quantum dynamics within a linear vibronic coupling model,31 which included fourteen spin–orbit-coupled states and up to fifteen vibrational modes, considering both vibronic and SOC. Solvent effects on the potential energies were also included by means of an implicit continuum model. As one of the key features of the ISC mechanism, the experimentally observed intermediate state11 was assigned to the lowest triplet IL (3IL, localized on the Phen moiety). It was shown that efficient population transfer occurs from the optically active 1MLCT states to 3IL and to the lowest 3MLCT state (T1; the long-lived, phosphorescent state). The early ultrafast decay together with a 3IL/3MLCT equilibration within 1 ps are fundamental for the photo-luminescent properties of [Re(CO)3(Im)(Phen)]+.
The goal of the present study is to investigate the excited states of [Re(CO)3(Im)(Phen)]+ including explicit solvation, vibrational sampling effects, and SOCs simultaneously. To this end, we report the implementation of electrostatic-embedding quantum mechanics/molecular mechanics (QM/MM)32 for DFT and TD-DFT within the Amsterdam Density Functional (ADF) program.33 This TD-DFT plus electrostatic embedding QM/MM implementation is able to provide excited-state gradients and SOC matrix elements, both of which are crucial for detailed static or dynamical studies of transition metal chromophores in bio-environments. We employ this method to investigate the lower and upper UV part of the absorption spectrum of [Re(CO)3(Im)(Phen)]+, and we compare the results with other theoretical solvation models—COSMO34 (conductor-like screening model) and frozen-density embedding35 (FDE). Moreover, we use molecular dynamics (MD) to sample the configurational space of [Re(CO)3(Im)(Phen)]+ in water, especially the virtually free rotation of the Im ligand. Thereby, it is shown that it is very important to consider multiple conformations when investigating the excited states of such molecules in solution. The ultimate goal of this study is to identify a combination of quantum-chemical methods that is suitable for a full-dimensional description of the excited-state potentials and dynamics of [Re(CO)3(Im)(Phen)]+, in order to go beyond and complement the previous dynamics studies based on a low-dimensional linear vibronic coupling model.31
2 Computational details
The UV absorption spectrum of [Re(CO)3(Im)(Phen)]+ is investigated here with two approaches. Primarily, the absorption spectrum in aqueous solution including vibrational broadening was simulated from an ensemble of geometries taken from a ground state molecular dynamics (MD) simulation. For comparison, the vertical excitation energies were also computed for the three ground state torsional conformers mentioned above. These vertical excitation calculations were also connected through a scan around the Im torsion angle, in order to understand how the torsion affects the excited states.In the following, the computational details of these calculations are given.
2.1 Electronic structure method
In all calculations, except the force field parametrization (see below), we consistently employed the B3LYP functional36 with the ZORA relativistic Hamiltonian,37 in combination with the ZORA-TZP basis set,38 as implemented in the ADF package.33 This combination was shown in several publications21,26,39 to be adequate for the description of the excited states of Re(I) complexes like [Re(CO)3(Im)(Phen)]+. The Becke numerical integration grid (good quality),40 the ZlmFit Coulomb fit method (normal quality),41 and the RI Hartree–Fock scheme (normal quality) of ADF42 were employed, and no electrons were frozen. SCF convergence was in all cases unproblematic, and hence the default SCF settings were used.For the optimization of the ground state minima of the three conformers, we employed the conductor-like screening model (COSMO),34,43 in order to describe solvent (water) effects on the geometry. A linear interpolation in internal coordinates (LIIC) scan was computed based on the three optimized geometries (see the ESI† for coordinates). In order to quantify the torsion angle Θ of the Im ligand, we use the average of the two CIm–NIm–Re–NPhen dihedrals (see Fig. 1 for the Θ values of the conformers and Fig. S1 in the ESI† for details on the definition of Θ).
For the vertical excitation calculation, we applied the Tamm–Dancoff approximation (TDA) to both singlet and triplet states. We computed 30 excited singlet and 30 triplet states at each geometry. In some of the presented results, the considerable SOC effects were taken into account perturbatively,44 using the ZORA spin–orbit operator of ADF.45 For the used set of states, this gives rise to 121 spin–orbit coupled states (30 singlets, plus 3 × 30 triplets, plus the ground state). For vertical excitation calculations with COSMO, linear-response non-equilibrium solvation46 was used, with the dielectric constant at optical frequencies set to 1.77.
2.2 Sampling
In order to realistically simulate the absorption spectrum of [Re(CO)3(Im)(Phen)]+ including vibrational and dynamical effects, a proper sampling of the ground state potential energy surface is necessary, especially because the Im ligand can rotate almost freely around the Re–N axis. The MD simulation for the sampling was carried out with AMBER16.47 The point charges for [Re(CO)3(Im)(Phen)]+ were obtained from a fit of the electrostatic potential employing the usual RESP procedure48 at the B3LYP/6-31G* (LAN2DZ for the rhenium atom) level of theory using the Gaussian09 software.49 Atom types and bond parameters were described using the generalized AMBER force field (GAFF).50,51 The missing bonds, angles and dihedrals involving the Rhenium atom were ad hoc parameterized and refined based on a few-picoseconds QM/MM-MD trajectory (see Fig. S2 and discussion in the ESI†). Moreover, the van der Waals radius and electrostatic non-bonded term for Re were chosen to be 1.47 Å and 0.241, respectively, as suggested in ref. 52.[Re(CO)3(Im)(Phen)]+ was placed in a truncated octahedron box of 12 Å of water (1054 water molecules represented by the TIP3P model53) and the system was neutralized by adding a chloride ion. The system was first minimized for 4000 + 4000 steps (steepest descent and conjugate gradient, respectively) and then thermalized (NVT ensemble) for 200 ps. Equilibration was carried out for 400 ps in the NPT ensemble and followed by a production run of 20 ns in the NPT ensemble. All simulations were carried out with a 2 fs time step and the temperature was kept constant at 300 K using the Langevin thermostat. 100 MD snapshots were taken at equidistant time intervals (every 200 ps) from the entire production run for the calculation of the absorption spectrum.
2.3 Absorption spectrum
The absorption spectrum was computed from vertical excitation calculations at each of the 100 snapshots taken from the MD trajectory. For each geometry, we computed 30 singlet and 30 triplet states, as specified above. From the energies and oscillator strength at all geometries, the spectrum was computed as a sum of Gaussians as,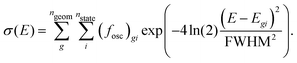 | (1) |
The absorption spectrum was computed with four different solvent models: (i) vacuum, i.e., no solvent; (ii) implicit solvation using the COSMO method; (iii) explicit solvation using electrostatic embedding QM/MM; and (iv) explicit solvation using FDE.35,54 For (i) and (ii), the water and chlorine atoms from the MD snapshots were removed, so that the calculation only used the coordinates of the complex. For (iii), the partial charges of the TIP3P water model53 and the chloride ion were included in the electronic Hamiltonian; to this end, electrostatic embedding was implemented in the development version of ADF, as explained in the next section. For (iv), the electron densities of the water molecules were independently computed (using COSMO), and in a final step, all (frozen) water densities were included in the vertical excitation calculation of the complex. For FDE, we used the PW91K approximant for the non-additive kinetic energy.55
3 Implementation of electrostatic embedding QM/MM
The general implementation of QM/MM methods in ADF is described elsewhere.56,57 The QM/MM Hamiltonian is of the additive type,32i.e.:| Ĥtotal = ĤQM + ĤMM + ĤQM–MM. | (2) |
A more realistic embedding scheme should therefore consider the electrostatic interaction between the charged particles in the MM and QM regions. Therefore, our implementation includes the electrostatic interaction between the MM partial charges and the QM particles in the electronic Hamiltonian:
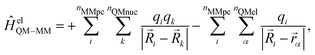 | (3) |
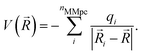 | (4) |
After SCF convergence, the final QM/MM electrostatic interaction energy can be calculated as:
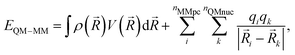 | (5) |
The gradients58 of the QM/MM electrostatic interaction energy can then be computed, for the QM nuclei as:
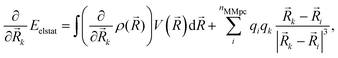 | (6) |
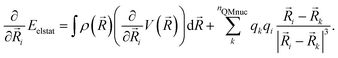 | (7) |
The computation of excitation energies using TD-DFT or TDA does not require any modifications, as only the orbital energies and two-electron integrals enter into the respective equations. Since the orbital energies already incorporate the effect of the MM point charges, no explicit inclusion of V is necessary.59 The same is true for the computation of the relaxed density ρrelaxed of the excited state through the Z-vector equation formalism.60,61 The MM point charges have to be included explicitly only for the actual evaluation of the gradients of the excitation energy.61 This leads to two equations for QM nuclei and MM point charges analogous to eqn (6) and (7), only exchanging Eelstat by ωielstat (i.e., by the electrostatic QM/MM contribution to the excitation energy) and ρ(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) by ρrelaxed(
) by ρrelaxed(![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) (i.e., by the difference between the ground state density and the relaxed excited-state density). The excitation energy gradient for QM nuclei is therefore
) (i.e., by the difference between the ground state density and the relaxed excited-state density). The excitation energy gradient for QM nuclei is therefore
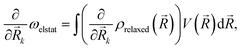 | (8) |
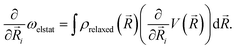 | (9) |
4 Results and discussion
4.1 Molecular dynamics sampling
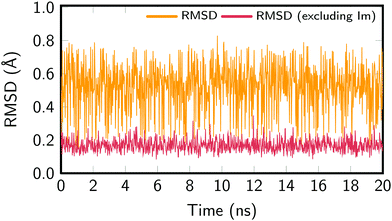
In order to assure the proper sampling of the ground state conformational space and the accuracy of the force field—especially for the Re parameters—we compared the results obtained with the classical MD to those obtained by means of a trajectory resulting from a QM/MM MD run and to the B3LYP-optimized geometries. The computational details of the QM/MM trajectory are given in the ESI† and the results in Fig. S2 (also ESI†), which compares the distribution of relevant geometric parameters. In general, an excellent agreement with the classical MD trajectory was obtained. Slight deviations for the bond lengths of the Phen ligand are due to the fact that the GAFF is not specifically parameterized for this ligand. Most importantly, the parameters defining the Re coordination sphere are correctly reproduced, justifying the use of the cheaper classical MD sampling that allows for a nanosecond time scale propagation. The exhaustive exploration of the potential energy landscape of [Re(CO)3(Im)(Phen)]+ is important for correctly describing its absorption spectrum in aqueous solution.Fig. 2 presents the root-mean-square deviations (RMSD) of the MD snapshots from the optimized geometry of [Re(CO)3(Im)(Phen)]+. To calculate the RMSD, the Re(CO)3(Phen) moiety was aligned with the optimized geometry, whereas the Im ligand was not aligned. The RMSD was then computed for the whole molecule, giving values between 0.15 Å and 0.80 Å, with an average RMSD of 0.54 Å. The RMSD was also computed for the metal complex without the Im ligand, which yielded values between 0.08 Å and 0.35 Å, with an average RMSD of 0.17 Å. These values show that most of the molecular flexibility is due to almost barrierless torsional motion of the Im ligand, whereas the rest of the complex is very rigid.
The torsion of the Im ligand is related to the A, B, and A′ minimum structures mentioned above and reported previously.26,28 As shown in Fig. 3, our MD simulations indicate that of these conformers, B is more stable (maxima at Θ ≈ 0° and ±180°) than conformer A (−90°) or A′ (+90°). Even though our dynamics simulation is probably too short to extract thermodynamic data, it appears that the populations of the conformers are not equal (A: 14%, B: 77%, A′: 9%), indicating that the minima might have different (free) energies, with conformer B having the lowest one. Baranovskii and Maltsev28 reported that in DMF solution conformer B should be 0.5 kcal mol−1 more stable than conformers A and C. It is likely that the energy difference in aqueous solution are similar. Furthermore, due to the extremely small barrier, interconversion between the conformers is very rapid, as evidenced by the time series of the torsion angle reported in Fig. S3 in the ESI.† The effect of the Im torsion on the absorption spectrum and excited state energies will be discussed in the following section.
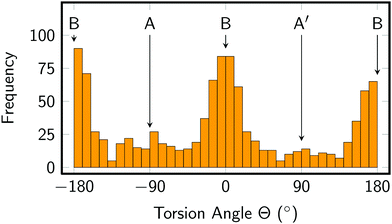 | ||
| Fig. 3 Distribution of imidazole torsion angle in the MD simulation. Angles of 0 and ±180° correspond to conformer B, whereas −90° refers to conformer A and +90° to conformer A′. | ||
4.2 Vertical excitation and imidazole torsion
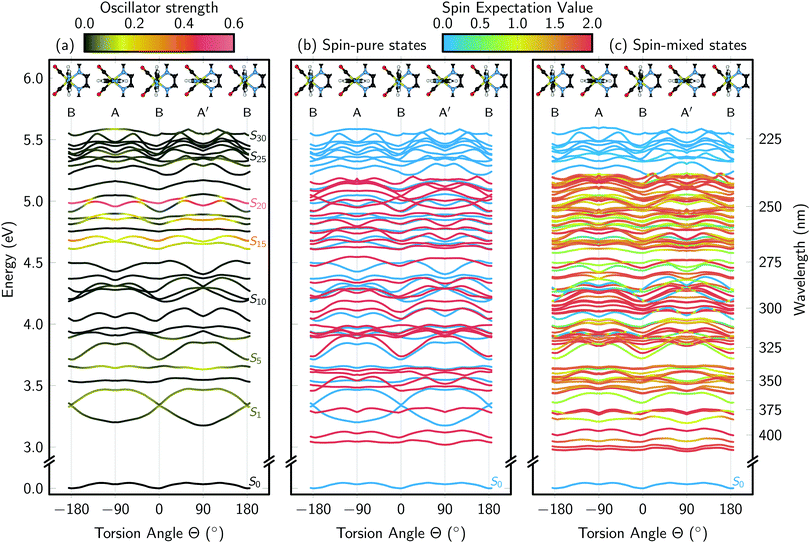
The vertical excitation energies along the Im torsion angle are shown in Fig. 4. The energies, oscillator strengths, and state characters are also compiled in Table S1 in the ESI.† From the ground state potentials, we obtained the energy differences between the three conformers, with A and A′ both approximately 0.8 kcal mol−1 above B. Assuming a simple Boltzmann distribution among the conformers, this translates into a population of B of roughly 80%; this neglects the zero point energy contribution to the free energy, but that contribution is very similar for the three conformers (differences <0.1 kcal mol−1). The computed percentage fits very well with the 77% population obtained in the MD simulation, which is another indicator that the MD force field parametrization reasonably reproduces the ground state potential and allows for a proper sampling of the conformational space.Before discussing the results of the vertical excitation calculations, we note that the values given in Fig. 4(a) and Table S1 (ESI†) are not fully consistent with the calculations in ref. 26 and 27 because the ADF settings are slightly different. Here, we employ the more recent Becke numerical integration grid,40 and the new RI Hartree–Fock scheme of ADF.42 More importantly, here we employ non-equilibrium solvation within the linear-response TD-DFT calculations with a high-frequency dielectric constant of 1.77 for water, in order to describe the instantaneous nature of the vertical excitations. Consequently, there are some small differences in the energies with respect to Table 3 of ref. 26 (conformer B). For the 8 singlet states computed in ref. 26, our computations give energies which are on average 0.08 eV higher (standard deviation 0.02 eV); for the 12 triplets, our energies are 0.04 eV higher (0.04 eV standard deviation). However, for all these 20 states the ordering of the state characters agrees.
One of the purposes of Table S1 (ESI†) and Fig. 4 is to present higher excited states of [Re(CO)3(Im)(Phen)]+ than those published previously.26,27,30 With 30 singlet and 30 triplet states, we extend the previous 3–4 eV (310–410 nm) energy range to 5.5 eV (225 nm). As evidenced by the data (Fig. 4(a)), in this spectral region, there are a number of very bright states, in particular S14, S15, and S20 (at Θ = 0°; at other torsion angles, the state ordering changes and the bright states can be found among the states S14 to S20). These bright states have considerable IL character localized on the Phen ligand, and will likely dominate the UV absorption spectrum of [Re(CO)3(Im)(Phen)]+ below 300 nm. Furthermore, at longer wavelengths, there are MLCT states of moderate oscillator strength (S1, S2, S4, S5), which give rise to the low-energy absorption band of [Re(CO)3(Im)(Phen)]+ previously reported.26,27,30 Besides the bright IL states and the low-lying MLCT states, [Re(CO)3(Im)(Phen)]+ possesses a large number of dark MC states at higher energies, as well as some (dark) excitations involving the Im ligand (see Table S1, ESI†). Some of the higher-energy states are also strongly multi-configurational, with different classes of excitations contributing. This is particularly notable in the highest states in the calculated range, where the density of excited states significantly increases.
Because the MD simulations showed that in solution [Re(CO)3(Im)(Phen)]+ can be found in all three conformers (A, B, A′), a second purpose of Fig. 4 is to scrutinize whether it is necessary to consider all conformers when discussing the excited states. The scan presented in Fig. 4(a) shows that most singlet states are not strongly affected by the Im torsion, with most states shifting less than 0.2 eV during the torsion. For example, the band of very bright states from S14 to S20 stay in the 4.5–5.0 eV window for all torsion angles; this means that the IL absorption band of the spectrum will hardly shift due to the torsional motion of Im. There are a number of states (e.g., S10 to S12), which respond more strongly to the torsion, but since most of them are dark states, they do not affect the absorption spectrum.
Because most experimental studies10,19,20 excite the S1 and S2 states of [Re(CO)3(Im)(Phen)]+, it is particularly interesting to follow the evolution of these two states as a function of the torsion angle. Indeed, we see clearly that for conformers A and A′ these states have a significant energy gap, while for conformer B they are nearly degenerate. This is due to the inversion of the HOMO and HOMO−1 orbitals (both d orbitals) when going from conformer A to conformer B, as discussed in ref. 26. Actually, the shifts of these two states are among the largest shown in Fig. 4(a), at around 0.3 eV. This sensitivity of S1 and S2 to the torsion angle means that torsional motion slightly broadens the MLCT absorption band in the spectrum. However, while the absorption spectrum is not strongly affected by the torsional motion of Im, the strong variation in the S1/S2 energy gap indicates that the dynamics after excitation to S1 and S2 might be very sensitive to the Im torsion angle.
Given the importance of SOC for the excited states of [Re(CO)3(Im)(Phen)]+, Fig. 4(b) and (c) show the singlet and triplet states and the spin–orbit coupled states, respectively. Clearly, the already high density of states increases even more due to SOC. It can also be seen that, generally, almost no pure singlet states are present, as almost every singlet state is coupled to at least one triplet state. The only pure singlet states are two IL and one LLCT states at 4.0–4.3 eV. These states are not strongly spin–orbit coupled to any other state because their excitation is not localized on the Re atom, which is a prerequisite for large SOC matrix elements. On the contrary, there is a significant number of very pure triplet states (indicated by fully red color in panel (c)), which are either not spin–orbit coupled to any other states, or only spin–orbit coupled to other triplet states. The strong modifications of the shapes of the potentials due to SOC, visible in Fig. 4(c), also show that any excited-state dynamics simulation for [Re(CO)3(Im)(Phen)]+ has to take into account SOC.
4.3 Absorption spectra
Fig. 5 presents the simulated absorption spectra of [Re(CO)3(Im)(Phen)]+ in water, using four different solvent models: no solvent (vacuum), frozen-density embedding (FDE), QM/MM with electrostatic embedding (el.stat.), and COSMO. The figure shows also an experimental spectra measured in aqueous solution.29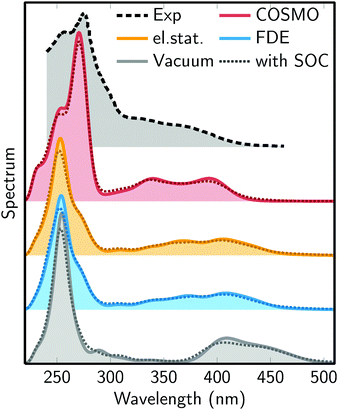 | ||
| Fig. 5 Simulated absorption spectra from the different solvent models: no solvent (Vacuum), frozen-density embedding (FDE), QM/MM with electrostatic embedding (el.stat.), and COSMO. The experimental spectrum (Exp) is from ref. 29. The dotted lines superimposed on each plot show the absorption spectra including SOC. | ||
The figure shows a number of interesting trends. First, in the series vacuum – el.stat./FDE – COSMO, the MLCT absorption band between 300 and 500 nm moves to higher energies. Clearly, the vacuum calculation strongly underestimates the energy of this band. Regarding the three actual solvation models, it is difficult to judge which of them performs best, as they yield similar results. It can also be observed that the three solvent models predict an MLCT band with two maxima, which might correspond to the two shoulders (at 370 nm and 330 nm) of the experimental spectrum.
The simulated spectra also show a second, very intense absorption band between 220 and 300 nm, which is due to the bright IL states (S14 to S20, see above). For this band, the vacuum, FDE, and electrostatic embedding models yield very similar positions of the band maximum (around 255 nm). However, the band is broader for the latter two methods. With COSMO, the absorption maximum is shifted to 270 nm, improving the agreement with the experimental maximum position (275 nm). This could be an indication that this band requires a solvation model which takes into account solvent polarization due to the solute electron density. On the contrary, the close agreement of the vacuum, FDE, and electrostatic embedding QM/MM models shows that the IL band is not very sensitive to hydrogen bonding, consistent with the lack of hydrogen bonding acceptors/donors at the Phen ligand where the IL transitions are localized.
Regarding the effect of SOC, it can be seen in Fig. 5 that the inclusion of SOCs in the computations only has a minor effect on the shape of the absorption spectrum. In particular, SOC leads to a slight smoothing and broadening of the absorption features, as was already previously reported.21,22,26,30 However, SOC does not induce any significant shifts or intensity changes in the spectrum. This is an interesting finding, because Fig. 4 has shown that SOC has a profound effect on the shape of the potential energy surfaces. It appears that each state mixes predominantly with states which are close in energy, and therefore large oscillator strengths stay at approximately the same energy if SOCs are turned on.
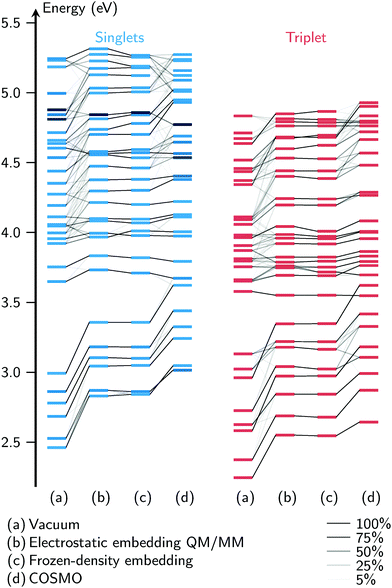
An important methodological conclusion from Fig. 5 is that FDE and electrostatic embedding QM/MM give virtually identical results. This is true for all parts of the spectrum, including both absorption bands. In order to investigate whether this agreement is accidental, and also to compare the four solvent models in general, we apply a wavefunction overlap methodology62,63 to compare the computed excited states. To this end, we treat the excitation vectors from the TDA computations as if they were vectors from a configuration interaction calculation with single excitations. In Fig. 6, for one exemplary geometry (the first snapshot taken from the MD trajectory), we plot the energies of the excited states as horizontal bars, and using the overlaps between the states from different models, we draw correlation lines between the bars. This allows an easy comparison of both the energies and the wavefunctions at the same time.
Several observations can be made from Fig. 6. First, of the four solvent models, the vacuum model tends to produce the lowest excitation energies, followed by FDE and el.stat., followed by COSMO. For the bright singlet states, this was already observed in the spectra in Fig. 5, but the correlation plot shows that the same trend applies to the dark singlet and triplet states. Second, at low excitation energies it is possible to find one-to-one correspondences between the states from different solvent models. For the higher states, the overlaps show that the vacuum calculation produces excitations very different from the FDE and electrostatic embedding models. The states from COSMO overlap moderately well with the states from FDE and electrostatic embedding.
The states of the FDE and electrostatic embedding models overlap almost perfectly (with state reordering for S9/S10 and T25/T26). The RMSD of the excitation energies is smaller than 0.02 eV, with the largest deviation being 0.05 eV (S30). Similar results have been obtained for other MD snapshots, where we consistently find RMSDs of about 0.02 eV and maximum deviations of 0.05 eV. This very strong agreement between the two methods is very unlikely due to coincidence, especially considering that all states agree consistently, and not only some of them. The fact that these two very different methods give very similar results shows that for this molecule, the electrostatic interaction between the solvent and solute is by far the most important effect. More elaborate effects included in FDE—a QM/QM method which is in principle exact54—do not affect the excited states.
4.4 Interaction of spin–orbit coupling and solvation
Until now, the spin–orbit interactions of the excited states of [Re(CO)3(Im)(Phen)]+ have primarily been discussed for specific geometries. While the MD simulations have shown that the Re(CO)3(Phen) moiety is rather rigid in aqueous solution, it is still possible that the excited states are significantly affected by the nuclear motion in the ground state. One of the consequences of this would be that the excited-state characters (i.e., the ordering and mixing of the states) might differ from the ones at the minimum geometries—therefore affecting the way the states are coupled by SOC. Thus, we have investigated the spin–orbit interactions for a number of MD snapshots.Fig. 7 compares the excited-state energies for four snapshots together with a correlation of the spin-free and spin-mixed states. The four diagrams show that the geometry has a dramatic effect on the state energies, state ordering and SOC patterns. For example, it can be seen that the change of geometry from snapshot 1 to 2 leads to a blueshift of approximately 0.4 eV for the S1 and T1 states, with corresponding shifts in the higher states. Similarly, the energy gaps S1/S2 and T1/T2 are notably dependent on the geometry. Hence, it can be expected that the geometry also has a large effect on the wavefunctions of the states, which in turn will affect the SOC matrix elements. This can be seen in snapshots 1 and 2, where the T1 shifts and splits slightly, while for snapshot 3, the T1 mixes strongly with T2 due to their low energy gap; in snapshot 4, the T1 does not split or mix with other states. For higher states, it is even more difficult to discern similarities between the snapshots. This is a clear sign that an analysis of the spin–orbit-induced mixing at one geometry—as is often done in the literature,21,22,26,30e.g., at the Franck–Condon one—is not sufficient to draw general conclusions regarding ISC. Rather, sampling is required, as small geometry changes produce significantly different coupled excited states.
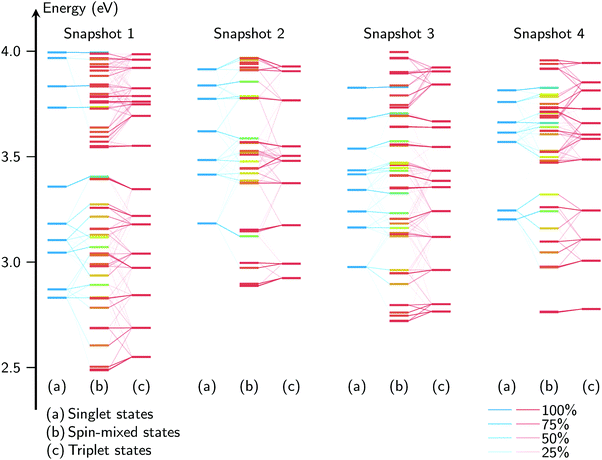 | ||
| Fig. 7 Spin–orbit mixing correlation diagrams of the excited states for four arbitrary MD snapshots, up to 4 eV (for the full figure, see Fig. S4 in the ESI†). For each snapshot, the singlet states are given on the left, the triplets on the right, and the spin–orbit mixed state in the center, with the coloring indicating the total spin expectation value. The thin diagonal lines indicate the contributions of the pure states, with stronger lines indicating a stronger contribution. The vertical axis represents the excitation energy. | ||
5 Conclusions
In this work, we report a comprehensive study of the excited states of [Re(CO)3(Im)(Phen)]+ (Im = imidazole; Phen = 1,10-phenanthroline), considering the effects of vibrational sampling, solvation and spin–orbit coupling.We have performed molecular dynamics simulations to sample the relevant conformers of the complex in aqueous solution. The results show that [Re(CO)3(Im)(Phen)]+ exists in three main conformers, with different orientations of the Im ligand. The energies of the three conformers differ by less than 1 kcal mol−1, with the most stable conformer showing an orientation of Im parallel to the Phen ligand, and the other conformers showing a perpendicular orientation, giving the complex planar symmetry.
Next, we have carried out vertical excitation calculations for different torsional angles of the Im ligand and for different sampled geometries from the dynamics simulations. It was found that in general, the torsion and vibrations have only minor effect on the energies of the bright states and therefore on the shape of the absorption spectrum of [Re(CO)3(Im)(Phen)]+. On the contrary, these motions significantly affect the energy gap between the two lowest MLCT states (S1 and S2), which are the initially populated states in experimental studies. Therefore, it is of high importance to consider the ground state vibration of the molecule in any future ultrafast dynamics study.
In order to incorporate solvent effects in the computation of the excited states by means of TD-DFT, we have implemented electrostatic embedding into the QM/MM module of the Amsterdam Density Functional package. The implementation allows to compute also TD-DFT gradients for the QM and MM parts of the system, and is compatible with the computation of spin–orbit couplings. Using this embedding method, we computed the absorption spectrum of [Re(CO)3(Im)(Phen)]+ based on geometries sampled from the molecular dynamics simulation. We compared the results of the electrostatic embedding computations to results obtained with frozen-density embedding and with the implicit solvation method COSMO, finding very good agreement. The computed spectra reproduce rather well the experimental features of the absorption spectrum of [Re(CO)3(Im)(Phen)]+, which is a prototype molecule for a wide range of Re(I) carbonyls complexes.
We find that the inclusion of spin–orbit couplings does not notably influence the shape of the absorption spectrum. However, the potential energy surfaces are strongly modified by the spin–orbit induced mixing, which might affect the dynamical relaxation pathways. Moreover, the induced spin–orbit mixing is very different depending on the geometries taken from the ground state sampling, and therefore, any analysis of the spin–orbit mixed states should not be restricted to the equilibrium geometry, but should include vibrational sampling.
In conclusion, the results presented here show that QM/MM with electrostatic embedding, together with the chosen functional and basis set, is a suitable method to describe solvent effects in dynamics simulations of the excited states of [Re(CO)3(Im)(Phen)]+. The results also indicate that such simulations must include the effect of spin–orbit coupling and vibrational sampling.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. M., A. M.-L., and L. G. gratefully acknowledge funding from the Austrian Science Fund (FWF) within the project I2883 and generous allocation of computer time on the Vienna Scientific Cluster (VSC3). H. G., M. F., A. M., and C. D. acknowledge funding from the Agence nationale de la recherche (ANR) within project ANR-15-CE29-0027. M. F. and C. D. also thank the FRC and Labex CSC (ANR-10-LABX-0026_CSC). The authors would like to thank the COST action CM1405 (MOLIM) and the universities of Vienna, Lorraine–Nancy, and Strasbourg. Furthermore, Erik van Lenthe, Alexei Yakovlev, and Stan van Gisbergen of SCM are thanked for support related to the implementation of electrostatic embedding QM/MM in ADF. Pedro Sánchez Murcia is acknowledged for help with the QM/MM trajectory computation, Tomasz A. Wesolowski for helpful discussions regarding the frozen-density embedding computations, and Felix Plasser for fruitful discussions.References
- H. B. Gray and J. R. Winkler, Q. Rev. Biophys., 2003, 36, 341–372 CrossRef CAS PubMed.
- D. S. Wuttke, M. J. Bjerrum, J. R. Winkler and H. B. Gray, Science, 1992, 256, 1007–1009 CAS.
- J. R. Winkler and H. B. Gray, Chem. Rev., 1992, 92, 369–379 CrossRef CAS.
- B. R. Crane, A. J. Di Bilio, J. R. Winkler and H. B. Gray, J. Am. Chem. Soc., 2001, 123, 11623–11631 CrossRef CAS PubMed.
- C. Shih, A. K. Museth, M. Abrahamsson, A. M. Blanco-Rodríguez, A. J. Di Bilio, J. Sudhamsu, B. R. Crane, K. L. Ronayne, M. Towrie, A. Vlćek, J. H. Richards, J. R. Winkler and H. B. Gray, Science, 2008, 320, 1760–1762 CrossRef CAS PubMed.
- A. M. Blanco-Rodríguez, A. J. Di Bilio, C. Shih, A. K. Museth, I. P. Clark, M. Towrie, A. Cannizzo, J. Sudhamsu, B. R. Crane, J. Sýkora, J. R. Winkler, H. B. Gray, S. Záliš and A. Vlćek, Chem. – Eur. J., 2011, 17, 5350–5361 CrossRef PubMed.
- D. J. Stufkens and A. Vlćek, Coord. Chem. Rev., 1998, 177, 127–179 CrossRef CAS.
- A. Kumar, S.-S. Sun and A. J. Lees, in Photophysics and Photochemistry of Organometallic Rhenium Diimine Complexes, ed. A. J. Lees, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 29, pp. 37–71 Search PubMed.
- R. A. Kirgan, B. P. Sullivan and D. P. Rillema, in Photochemistry and Photophysics of Coordination Compounds: Rhenium, ed. V. Balzani and S. Campagna, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 45–100 Search PubMed.
- A. Vlćek, in Ultrafast Excited-State Processes in Re(I) Carbonyl-Diimine Complexes: From Excitation to Photochemistry, ed. A. J. Lees, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 115–158 Search PubMed.
- A. El Nahhas, C. Consani, A. M. Blanco-Rodríguez, K. M. Lancaster, O. Braem, A. Cannizzo, M. Towrie, I. P. Clark, S. Záliš, M. Chergui and A. Vlćek, Inorg. Chem., 2011, 50, 2932–2943 CrossRef CAS PubMed.
- H. Takeda and O. Ishitani, Coord. Chem. Rev., 2010, 254, 346–354 CrossRef CAS.
- C. D. Windle and R. N. Perutz, Coord. Chem. Rev., 2012, 256, 2562–2570 CrossRef CAS.
- K. K.-W. Lo, M.-W. Louie and K. Y. Zhang, Coord. Chem. Rev., 2010, 254, 2603–2622 CrossRef CAS.
- A. F. A. Peacock, H. D. Batey, C. Raendler, A. C. Whitwood, R. N. Perutz and A.-K. Duhme-Klair, Angew. Chem., Int. Ed., 2005, 44, 1712–1714 CrossRef CAS PubMed.
- C.-C. Ko, W.-M. Kwok, V. W.-W. Yam and D. L. Phillips, Chem. – Eur. J., 2006, 12, 5840–5848 CrossRef CAS PubMed.
- D. Cleland, G. Irwin, P. Wagner, D. Officer and K. Gordon, Chem. – Eur. J., 2009, 15, 3682–3690 CrossRef CAS PubMed.
- A. Cannizzo, A. M. Blanco-Rodríguez, A. El Nahhas, J. Šebera, S. Záliš, A. Vlćek, Jr. and M. Chergui, J. Am. Chem. Soc., 2008, 130, 8967–8974 CrossRef CAS PubMed.
- A. Vlćek and M. Busby, Coord. Chem. Rev., 2006, 250, 1755–1762 CrossRef.
- A. Vlćek, H. Kvapilová, M. Towrie and S. Záliš, Acc. Chem. Res., 2015, 48, 868–876 CrossRef PubMed.
- C. Daniel, Coord. Chem. Rev., 2015, 282–283, 19–32 CrossRef CAS.
- R. Heydová, E. Gindensperger, R. Romano, J. Sýkora, A. Vlćek, S. Záliš and C. Daniel, J. Phys. Chem. A, 2012, 116, 11319–11329 CrossRef PubMed.
- J. Eng, C. Gourlaouen, E. Gindensperger and C. Daniel, Acc. Chem. Res., 2015, 48, 809–817 CrossRef CAS PubMed.
- Y. Harabuchi, J. Eng, E. Gindensperger, T. Taketsugu, S. Maeda and C. Daniel, J. Chem. Theory Comput., 2016, 12, 2335–2345 CrossRef CAS PubMed.
- C. Gourlaouen, J. Eng, M. Otsuka, E. Gindensperger and C. Daniel, J. Chem. Theory Comput., 2015, 11, 99–110 CrossRef CAS PubMed.
- M. Fumanal and C. Daniel, J. Comput. Chem., 2016, 37, 2454–2466 CrossRef CAS PubMed.
- M. Fumanal and C. Daniel, J. Phys. Chem. A, 2016, 120, 6934–6943 CrossRef CAS PubMed.
- V. Baranovskii and D. Maltsev, Comput. Theor. Chem., 2014, 1043, 71–78 CrossRef CAS.
- W. B. Connick, A. J. D. Bilio, M. G. Hill, J. R. Winkler and H. B. Gray, Inorg. Chim. Acta, 1995, 240, 169–173 CrossRef CAS.
- R. Baková, M. Chergui, C. Daniel, A. Vlček, Jr. and S. Záliš, Coord. Chem. Rev., 2011, 255, 975–989 CrossRef.
- M. Fumanal, E. Gindensperger and C. Daniel, J. Chem. Theory Comput., 2017, 13, 1293–1306 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, O. Baseggio, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Solà, M. Swart, D. Swerhone, G. te Velde, V. Tognetti, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, Amsterdam density functional modeling suite, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2017, http://www.scm.com Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- T. A. Wesolowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050–8053 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- C. Daniel, in Absorption Spectroscopy, Emissive Properties, and Ultrafast Intersystem Crossing Processes in Transition Metal Complexes: TD-DFT and Spin-Orbit Coupling, ed. N. Ferré, M. Filatov and M. Huix-Rotllant, Springer International Publishing, Cham, 2016, pp. 377–413 Search PubMed.
- M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- M. Franchini, P. H. T. Philipsen, E. van Lenthe and L. Visscher, J. Chem. Theory Comput., 2014, 10, 1994–2004 CrossRef CAS PubMed.
- M. Krykunov, T. Ziegler and E. van Lenthe, Int. J. Quantum Chem., 2009, 109, 1676–1683 CrossRef CAS.
- C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408 CrossRef CAS.
- F. Wang and T. Ziegler, J. Chem. Phys., 2005, 123, 154102 CrossRef PubMed.
- F. Wang, T. Ziegler, E. van Lenthe, S. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2005, 122, 204103 CrossRef PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- D. A. Case, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, D. Greene, N. Homeyer, S. Izadi, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER 2017, 2017, http://ambermd.org/ Search PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- B. L. Oliveira, I. S. Moreira, P. A. Fernandes, M. J. Ramos, I. Santos and J. D. G. Correia, J. Mol. Graphics Modell., 2013, 45, 13–25 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- C. R. Jacob, J. Neugebauer and L. Visscher, J. Comput. Chem., 2008, 29, 1011–1018 CrossRef CAS PubMed.
- T. A. Wesolowski, H. Chermette and J. Weber, J. Chem. Phys., 1996, 105, 9182–9190 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- M. Swart, Int. J. Quantum Chem., 2003, 91, 177–183 CrossRef CAS.
- L. Versluis and T. Ziegler, J. Chem. Phys., 1988, 88, 322–328 CrossRef CAS.
- M. R. Provorse, T. Peev, C. Xiong and C. M. Isborn, J. Phys. Chem. B, 2016, 120, 12148–12159 CrossRef CAS PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- M. Seth, G. Mazur and T. Ziegler, Theor. Chem. Acc., 2011, 129, 331–342 CrossRef CAS.
- F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. González, J. Chem. Theory Comput., 2016, 12, 1207 CrossRef CAS PubMed.
- F. Plasser and L. González, J. Chem. Phys., 2016, 145, 021103 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Torsion angle definition, force field validation, vertical excitation data, optimized geometries. See DOI: 10.1039/c7cp05126c |
| ‡ Present address: Área de Química Física, University of Extremadura, Avda. Elvas s/n, Badajoz, 06006 Spain. |
| This journal is © the Owner Societies 2017 |