Giant anisotropic photogalvanic effect in a flexible AsSb monolayer with ultrahigh carrier mobility†
Abstract
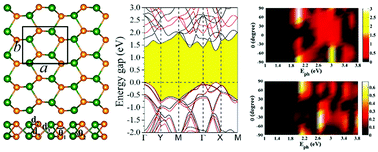
Searching for novel two-dimensional (2D) materials with desirable properties is of great significance for the design of next generation nano-devices. In this work, we address the electronic and optoelectronic properties of monolayer AsSb on the basis of density functional theory (DFT) combined with quantum transport simulations. We find three stable phases of monolayer AsSb, that is, the α, γ and ε phases, and all of them show direct bandgaps, which are beneficial in increasing the transition probability of photon-generated electrons and improving the efficiency of photoelectric conversion. In addition, these systems could attain meaningful strain-induced band engineering and a phase transition from semiconductor to metal occurs. It is highly interesting that the monolayer AsSb has an ultrahigh carrier mobility (∼104 cm2 V−1 s−1), which is evidently larger than most of the reported 2D materials. In light of the nonequilibrium Green's function formalism, a linear photogalvanic effect (PGE) is observed along both the zigzag and armchair directions, suggesting that monolayer AsSb exhibits excellent photoresponse in a broad spectrum ranging from ultraviolet to infrared light, which is favorable for serving as a potential outstanding photovoltaic material. Our results highlight that these monolayer AsSb are promising candidates for future applications in electronics and optoelectronics.
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...