Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The structure of coronene cluster ions inferred from H2 uptake in the gas phase†
Marcelo
Goulart
 a,
Martin
Kuhn
a,
Bilal
Rasul
ab,
Johannes
Postler
a,
Martin
Kuhn
a,
Bilal
Rasul
ab,
Johannes
Postler
 a,
Michael
Gatchell
a,
Michael
Gatchell
 ac,
Henning
Zettergren
c,
Paul
Scheier
ac,
Henning
Zettergren
c,
Paul
Scheier
 *a and
Olof
Echt
*a and
Olof
Echt
 *ad
*ad
aInstitut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstr. 25, A-6020 Innsbruck, Austria. E-mail: marcelo.goulart@uibk.ac.at; Martin.Kuhn@uibk.ac.at; Johannes.Postler@uibk.ac.at; paul.scheier@uibk.ac.at
bDepartment of Physics, University of Sargodha, 40100 Sargodha, Pakistan. E-mail: bilalrasul@uos.edu.pk
cDepartment of Physics, Stockholm University, S-10691 Stockholm, Sweden. E-mail: gatchell@fysik.su.se; henning@fysik.su.se
dPhysics Department, University of New Hampshire, Durham, NH 03824, USA. E-mail: olof.echt@unh.edu
First published on 12th October 2017
Abstract
Mass spectra of helium nanodroplets doped with H2 and coronene feature anomalies in the ion abundance that reveal anomalies in the energetics of adsorption sites. The coronene monomer ion strongly adsorbs up to n = 38 H2 molecules indicating a commensurate solvation shell that preserves the D6h symmetry of the substrate. No such feature is seen in the abundance of the coronene dimer through tetramer complexed with H2; this observation rules out a vertical columnar structure. Instead we see evidence for a columnar structure in which adjacent coronenes are displaced in parallel, forming terraces that offer additional strong adsorption sites. The experimental value for the number of adsorption sites per terrace, approximately six, barely depends on the number of coronene molecules. The displacement estimated from this number exceeds the value reported in several theoretical studies of the bare, neutral coronene dimer.
1. Introduction
Interest in polycyclic aromatic hydrocarbons (PAHs) has many roots, including their role in the formation of soot,1 of H2 in the interstellar medium,2–4 as well as their contribution to the diffuse interstellar bands and aromatic infrared bands.4–6 The highly symmetrical, planar coronene molecule (C24H12, D6h symmetry) is a strong candidate for many unidentified interstellar bands.7 It has also served to model adsorption on graphite and graphene, and intercalation within bilayers of graphene which has ramifications for catalysis, efficient storage of molecular gases, and sensing applications.8–10The interaction between coronene molecules has been investigated to model the interaction between graphene sheets;11–13 clusters of coronene and other PAHs serve as realistic models of carbon grains in interstellar space.14 The Bravais lattice of bulk coronene is monoclinic. In the conventional gamma-herringbone structure coronene molecules are stacked parallel but displaced; columns of molecules are separated from each other by molecules that are tilted by 85°.15 (Another recently discovered stable polymorph,16 the beta-herringbone structure, can be grown in the presence of a magnetic field.) In this phase adjacent molecules are either parallel but displaced, or nearly perpendicular to each other in a T-shaped configuration. Early theoretical work suggested that the coronene dimer is tilted by 42°,17 but more recent studies agree that the molecules are very nearly parallel; the T-shaped configuration is not energetically competitive.12,18–26 Molecules in clusters slightly larger than the dimer are still stacked in a parallel arrangement;12,20,27 handshake and multicolumnar structures start appearing at m ≈ 8.20,26,28–30
However, the exact ground state structure of the coronene dimer is still a matter of debate. The perfectly superimposed stack (or sandwich) does not form a local minimum.20,21,23,25 Using an empirical potential for the repulsion–dispersion interaction, Rapacioli et al. found that the twisted sandwich (TS) represents the most stable structure at −0.98 eV.20 Most other studies conclude that the parallel displaced (PD) dimer constitutes the global energy minimum but do not agree on the direction and magnitude of the horizontal displacement.11,12,18,19,21–26 Published experimental work on neutral or charged coronene clusters does not provide structural information.31–35
Here we study adsorption of molecular hydrogen on positively charged coronene and its clusters. Neutral complexes of hydrogen and coronene are synthesized by passing helium nanodroplets through vapors of C24H12 (abbreviated Cor from now on) and H2; the doped droplets are then ionized by electron impact. Mass spectra predominantly show ions with the composition (H2)nHCorm+ and a weaker series of unprotonated (H2)nCorm+. For the coronene monomer (m = 1) we observe a strong drop in the ion abundance at n = 38, and additional drops at 32 and 36. Guided by previous experimental data36 for HenCor+ and theoretical work involving complexes of coronene with hydrogen,37 helium,38–40 and heavier noble gases41,42 we attribute the anomaly at n = 38 to an abrupt drop in the adsorption energy once all hollow adsorption sites are occupied, completing a solvation shell. As shown in Fig. 1, each face of coronene offers 1 central (c) hollow site, 6 inner (i) hollow sites that surround the c site, and 12 outer (o) hollow sites formed by H–C–C–C–H atoms at the border of the molecule, i.e. a total of 38 hollow sites. The distance between adjacent centers of the carbon rings is only 0.246 nm, less than the minimum in the pair potential between H2–H2 or, for that matter, He–He or Ne–Ne. In a complete commensurate solvation shell these particles would thus be displaced radially outwards as observed in several theoretical studies.37,38,40,41 Quantum mechanical delocalization would exacerbate the outward trend but the D6h symmetry of the substrate would likely be preserved.
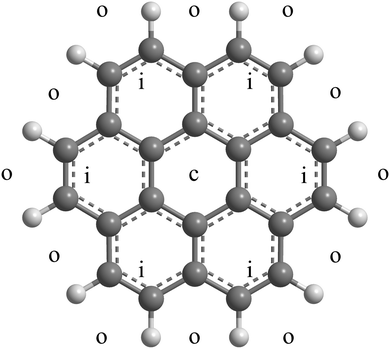 | ||
| Fig. 1 Approximate location of the central (c), inner (i) and outer (o) adsorption sites on one face of (H2)38Cor+. | ||
Interestingly, adsorption of H2 on dimers, trimers, and tetramers of coronene reveal an approximately constant shift of the anomaly by Δn = 11.4 ± 0.6 per added coronene. We attribute this shift to a parallel-displaced structure of the coronene cluster because a displacement opens additional hollow adsorption sites. A cluster with sandwich (or twisted sandwich) structure, i.e. a vertical stack of coronenes, would not offer any additional strong adsorption sites, only more weakly bound peripheral sites on the mantle of the stack. The observed shift Δn thus provides a benchmark for quantum chemical studies of (H2)nHCorm+ or (H2)nCorm+ because the larger the displacement the larger the number of additional strong adsorption sites. We estimate that a minimum displacement of roughly 0.25 nm is needed to account for the observed value of Δn, much larger than the shift computed for bare, neutral coronene dimers.11,12,23–26 Note, however, that adsorption of H2 may enhance and stabilize the displacement because of the large adsorption energy of H2 on coronene.
2. Experiment
Helium nanodroplets were produced by expanding helium (Messer, purity 99.9999%) at a stagnation pressure of 21 bar through a 5 μm nozzle, cooled by a closed-cycle refrigerator to 9.6 K, into vacuum. At these conditions the droplets contain an estimated average number of 4 × 105 helium atoms.43 The expanding beam was skimmed by a 0.8 mm conical skimmer located 8 mm downstream from the nozzle and traversed a differentially pumped pick-up cell filled with coronene vapor produced by heating coronene powder (Sigma-Aldrich, specified purity 97%) to about 135 °C. It then passed through another cell filled with H2 (estimated partial pressure 3.9 × 10−5 mbar).The beam of the doped helium droplets was collimated and crossed by an electron beam with a nominal energy of 70 eV. Cations were accelerated into the extraction region of a reflectron time-of-flight mass spectrometer (Tofwerk AG, model HTOF) with an effective mass resolution m/Δm = 3000 (Δm = full-width-at-half-maximum). Further experimental details have been published elsewhere.44
Mass spectra were evaluated by means of a custom-designed software designed to extract the abundance of specific ions after deconvoluting possible overlapping contributions to particular mass peaks by different ions and isotopologues.45 For example, the mass difference between isotopically pure HCor+ (i.e. H12C24H12+) and pure coronene containing one 13C isotope is only 0.0045 u, 22 times smaller than the instrumental peak width Δm. The software automatically fits mass peaks, subtracts background signals, and explicitly considers isotopic patterns of all ions that are expected to contribute to a given peak. The procedure and significance of accounting for isotope patterns is illustrated in Fig. S1 (ESI†).
3. Results
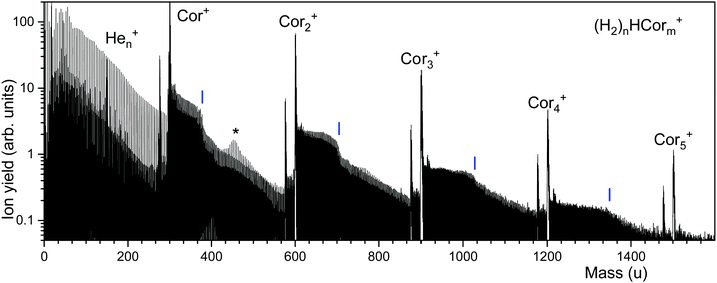
Fig. 2 displays a mass spectrum of helium nanodroplets doped with coronene and hydrogen. Prominent mass peaks are due to bare coronene cluster ions, Corm+, m = 1 through 5. They are preceded by mass peaks due to Corm−1C22H12+, probably arising from a benzo[ghi]perylene impurity in the coronene sample.32,46The most intense ion series that follows Corm+ is due to (H2)nHCorm+ (the notation reflects the fact that the proton affinity of coronene, 8.927 eV, is more than twice that of H2).48 The series exhibits abrupt drops in abundance; their positions are obtained from a nonlinear least square fit (see below for details) and marked by vertical lines. Another, weaker series is due to unprotonated (H2)nCorm+. Although (H2)n13C12C23H12+ and (H2)nH12C24H12+ (and similar ion pairs) remain unresolved, their contributions are disentangled by the analysis software which considers the complete pattern of isotopologues.45 Fig. S1 (ESI†) illustrates the procedure; it also shows expanded sections of the mass spectrum. The prominent ion series below 300 u is due to Hen+. An asterisk at 456.3 u marks a region in which this series is nearly isobaric with the series of protonated coronene ions. The amplitudes of these mass peaks add, giving rise to a volcano-shaped envelope.
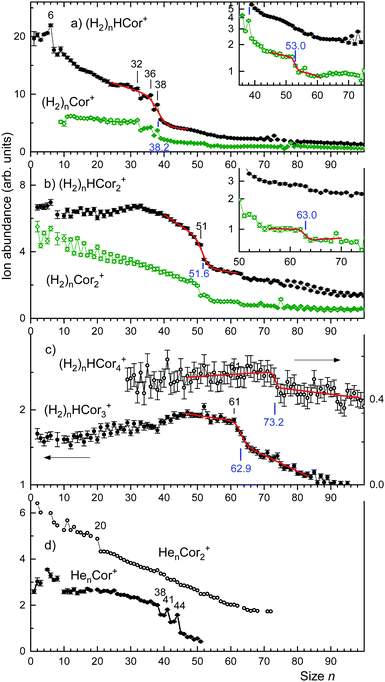
The ion abundances of several ion series, extracted from mass spectra, are displayed in Fig. 3. Data for ions that suffer from strong interference with other ion series or contaminants have been omitted. The abundance of (H2)nHCor+ in panel a exhibits abrupt drops at n = 6, 32, 36, and 38; the unprotonated series of (H2)nCor+ closely tracks these anomalies.
The abundance of (H2)nH(Cor)2+ and (H2)n(Cor)2+ is compiled in Fig. 3b. The protonated series falls off over a broad range; the gradient is strongest at n = 51. The unprotonated series decreases approximately linearly except for an abrupt drop at n = 50. Occasional odd–even oscillations are artifacts caused by interference with ion series containing He.
The abundances of (H2)nH(Cor)3+ and (H2)nH(Cor)4+ are plotted in Fig. 3c; the unprotonated series can no longer be analyzed with confidence in this mass range. The coronene trimer features an enhanced drop that starts at n = 61; the tetramer features a weak drop above n = 70.
In an attempt to obtain unbiased values for the size at which the abundance drops most strongly we have fitted a sigmoidal function to the distributions of protonated coronene ions. The function is the sum of a straight line multiplied by a step function f(n,s,w) which drops rapidly from 1 to 0 at n = s with width w, and another straight line multiplied by 1 − f. The fitted functions are represented in Fig. 3 as red lines; the numerical values of s (at which the gradient is largest) are indicated. In Fig. 4 we plot the values of s (with error bars returned by the fitting routine) versus the number m of coronene molecules. A straight line is fitted to the four data points. Its slope is 11.4 ± 0.6.
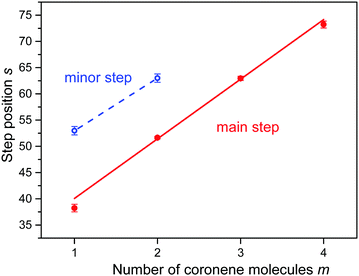 | ||
| Fig. 4 The position s of step functions identified in the abundance distributions shown in Fig. 3versus the number of coronene molecules m. The slope of the straight line equals 11.4 ± 0.6 for major steps (m = 1 to 4). | ||
Close inspection of the data (see the insets in Fig. 3a and b) reveals another abrupt drop in the abundance of (H2)nCor+ and (H2)n(Cor)2+; results of the fitted step functions are included in Fig. 4 and labelled “minor step.” The corresponding protonated ion series feature similar but even weaker steps.
4. Discussion
The most striking feature of the mass spectra of coronene–hydrogen complexes is an abrupt drop in the ion abundance of (H2)nH(Cor)m+ (as well as the unprotonated ion series) at n ≈ 38 for the coronene monomer that shifts approximately linearly as m increases. Increments range from Δn = 10 to 13; the average increment is 11.4 ± 0.6. In the following we present a structural model that accounts for this and other results. The model is classical; it neglects delocalization and zero point energies which have been shown to have significant consequences for the adsorption of helium, hydrogen, and neon on coronene30,37–41 and other carbonaceous systems.49–51 Even so, we expect that the classical structures discussed here will have some bearing on the spatial probability distribution of the actual quantum mechanical system. It has been shown, for example, that a classical description of (neutral or cationic) He32C60 which has a commensurate solvation shell captures essential features of more rigorous quantum mechanical descriptions49–51 although discrepancies become more significant for incomplete and incommensurate shells.37,40,42,49–51The basic assumption is that anomalies in the ion abundance, such as local maxima or abrupt drops, correlate with corresponding features in the adsorption energy (also referred to as dissociation or evaporation energy) of H2.52–54 Pickup of dopants and growth of neutral clusters in a superfluid helium nanodroplet is statistical, resulting in broad, featureless size distributions. Highly metastable configurations such as helium sandwiched between coronene molecules may be formed as well.55 However, a large amount of excess energy is released when dopants solvated inside the helium droplet are ionized, leading to extensive dissociation and annealing of the resulting ions.56
The interaction of H2 with coronene has been the subject of several theoretical studies8,9,37,58–61 but only one (classical) study considers H2 adsorption on cationic coronene which features enhanced adsorption energies,59 and only one (quantum mechanical) study considers adsorption of more than six H2 molecules.37 Therefore our discussion will also resort to theoretical work involving adsorption of other quantum gases on coronene.
The energetically most favorable adsorption site of H2 on neutral coronene is above the central carbon ring (site c, see Fig. 1) with the H2 axis normal to the coronene plane and an adsorption energy of De = 49 meV.60 Adsorption on top of one of the six inner (i) hexagonal rings is about 10% weaker than at c.8,58 The total energy for adsorbing more than one H2 is approximately additive provided the molecules do not occupy adjacent hexagonal rings in which case their interaction would be strongly repulsive.8 (H2)6Cor with its alternating occupation of i-sites on both sides of the molecular plane (symmetry C3v) seems to be particularly stable,8 providing a possible rationale for the enhanced abundance of (H2)6HCor+, see Fig. 3a. However, we note that a theoretical study by Rodriguez-Cantano et al. that includes quantum effects finds enhanced stability for Ar6Cor and Kr6Cor but not Ne6Cor.42
The trio of anomalies in the abundance of (H2)nHCor+ at n = 32, 36, and 38 is reminiscent of a trio of anomalies in the abundance of HenCor+ at n = 38, 41 and 44,36 reproduced in Fig. 3d. In a classical description, n = 38 corresponds to a structure in which all adsorbate particles occupy commensurate sites, i.e. 2 c-sites, 2 × 6 i-sites, and 2 × 12 o-sites with an overall D6h symmetry (see Fig. 1).36–40 Particles at i- and o-sites are pushed radially outwards because their size exceeds the separation (0.246 nm) between the centers of adjacent carbon rings. For helium, 3 or 6 additional atoms can be accommodated at or close to o-sites resulting in anomalies at n = 41 and 44.36,40 H2, however, is larger than He; a monolayer on graphite accommodates 23% fewer H2 than He.62,63 Therefore, rather than accommodating particles beyond n = 38, vacancies at o-sites will help to reduce the repulsive energy in the crowded commensurate (H2)38HCor+, leading to abundance anomalies at (H2)36HCor+ and (H2)32HCor+. The exact structure of these species remains to be determined.
Calvo and Yurtsever have reported path-integral molecular dynamics (PIMD) simulations of neutral coronene complexed with para-H2 and ortho-D2 at 2 K.37 From spatial distributions they calculate an upper bound of n = 42 molecules for para-H2 and 43 molecules for ortho-D2 in the first solvation shell, in reasonable agreement with our value of n = 38.
Our key observation is the approximately constant shift of the step in the ion abundance with increasing number m of coronene molecules (Fig. 4), and the absence of anomalies at or near n = 38 for m > 1. These observations rule out a columnar cluster structure with zero displacement which would still offer 38 strongly bound aromatic adsorption sites at the top and bottom of the stack plus additional sites in the mantle region. The PIMD simulation of hydrogen adsorption on the neutral coronene monomer37 shows that peripheral sites are less tightly bound and more delocalized than aromatic sites. Interaction with and localization at positively charged coronene would be enhanced40,59 but the differences between aromatic and mantle sites would likely remain. Therefore adsorption at vertical columnar coronene clusters would be expected to produce an abrupt drop in the abundance near n = 38, possibly followed by another one when all mantle sites are filled. The weaker steps in the ion abundance of (H2)nCorm+ (m = 1, 2) shown in the insets of Fig. 3 may in fact be due to closure of shells that include the mantle region.
On the other hand, a non-vertical columnar structure offers additional aromatic adsorption sites on newly formed terraces as indicated in Fig. S2 (ESI†). A dimer would feature two identical terraces, one on each coronene. The larger the displacement between the monomers the larger the number of additional adsorption sites (t) on the terrace. Because of the short-range character of the coronene–coronene interaction20 we expect, supported by calculations,18 that the displacement between adjacent coronenes does not change with cluster size m. In other words, each terrace would feature the same number of t-sites, approximately six, and the total number of strong adsorption sites would increase linearly with the number of coronene molecules, as seen in Fig. 4.
The average shift in the steps observed in the ion abundances equals 11.4 ± 0.6 (the statistical error should be taken with a grain of salt; individual shifts range from 10 to 13). Thus each terrace offers 5 to 7 t-sites. A visual inspection of the structures computed for (neutral or cationic) He38Cor38,40 suggests that a displacement by about 0.25 to 0.30 nm would offer that many sites on each terrace (about 4 o and 2 i-sites). The value agrees with a value of 0.27 nm computed for the coronene dimer by Obolensky et al.,21 but several other computed values are significantly smaller, below 0.20 nm.11,12,23–26 For comparison, the displacement between adjacent planes in hexagonal graphite is 0.143 nm, parallel to the long axis of the aromatic rings.12 However, the coronene dimer structures are floppy; an ab-initio calculation by Janowski et al. computes an energy barrier of only 6 meV for planar sliding between one energy minimum and another symmetrically equivalent minimum.25
A direct comparison of displacements computed for neutral dimers and our experimental estimate is complicated by the fact that our value refers to charged systems. Theoretical treatment of cationic dimers will be challenging, last but not least because of charge delocalization.27 Furthermore, H2 adsorption will tend to increase displacements due to the non-negligible adsorption energy. Kocman et al.60 and Gould et al.61 compute adsorption energies of 49 meV for the H2–coronene complex. However, the quantum nature of H2 may reduce these energies by more than 50%.64 In their PIMD study Calvo and Yurtsever find an average adsorption energy of only 11 meV for (H2)38Cor.37
For a comparison between experiment and theory the vibrational temperature will be of relevance. We have no direct way to determine or control the temperature of the ions but the evaporative model pioneered by Klots (in the classical regime) suggests that, for an experimental, mass spectrometric time scale of roughly 10−4 s, the thermal energy kBT equals approximately D/23.5 where D is the activation energy for the most facile dissociation reaction.52,53 An average adsorption energy of 11 meV thus translates to a vibrational temperature of 5 K.
Finally we note that the abundance distributions of (H2)nHCor2+ and HenCor2+ are strikingly different while those of (H2)nHCor+ and HenCor+ are rather similar, see Fig. 3. HenCor2+ shows no anomaly beyond an intriguing (and as yet unexplained) abrupt drop at n = 20. One possible, heuristic explanation would be the existence of several geometrical isomers that differ in the amount and direction of the displacement between the two coronene molecules. Perhaps the lower adsorption energy of helium provides for less stabilization of a distinct coronene dimer structure. Detailed quantum chemical calculations that include the anisotropy of H2 and the effect of the net charge will be required to elucidate details of (H2)nHCorm+ and (H2)nCorm+ cluster ions.
5. Conclusions
In summary, the mass spectra of helium droplets doped with coronene and H2 feature anomalies in the ion abundance that have been traced to particularly stable structures. For the coronene monomer ion features are akin to those in HenCor+ although the larger size of H2 will favor vacancies in an otherwise highly symmetric, commensurate solvation shell of D6h symmetry. For cluster ions containing up to m = 4 coronene molecules a shift of a stepwise decrease in the ion abundance indicates the existence of terraces that offer approximately six additional adsorption sites per terrace. This value provides a benchmark for theoretical studies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was given financial support by the Austrian Science Fund (FWF) Wien (Projects P26635 and M1908-N36), the Swedish Research Council (Contract No. 2016-06625 and 2016-04181), the COST Action CM1204 XLIC, and the European Union's Horizon 2020 research and innovation programme under grant agreement No. 692335.References
- F. Zasada, W. Piskorz, P. Stelmachowski, P. Legutko, A. Kotarba and Z. Sojka, J. Phys. Chem. C, 2015, 119, 6568–6580 CAS.
- E. R. M. Davidson, J. Klimes, D. Alfe and A. Michaelides, ACS Nano, 2014, 8, 9905–9913 CrossRef CAS PubMed.
- S. Cazaux, L. Boschman, N. Rougeau, G. Reitsma, R. Hoekstra, D. Teillet-Billy, S. Morisset, M. Spaans and T. Schlathölter, Sci. Rep., 2016, 6, 19835 CrossRef PubMed.
- G. Vidali, Chem. Rev., 2013, 113, 8762–8782 CrossRef CAS PubMed.
- A. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- S. Kwok, Astron. Astrophys. Rev., 2016, 24, 8 CrossRef.
- S. R. Langhoff, J. Phys. Chem., 1996, 100, 2819–2841 CrossRef CAS.
- T. Heine, L. Zhechkov and G. Seifert, Phys. Chem. Chem. Phys., 2004, 6, 980–984 RSC.
- A. Ferre-Vilaplana, J. Chem. Phys., 2005, 122, 104709 CrossRef CAS PubMed.
- K. Rohini, D. M. R. Sylvinson and R. S. Swathi, J. Phys. Chem. A, 2015, 119, 10935–10945 CrossRef CAS PubMed.
- H. Ruuska and T. A. Pakkanen, J. Phys. Chem. B, 2001, 105, 9541–9547 CrossRef CAS.
- R. Podeszwa, J. Chem. Phys., 2010, 132, 044704 CrossRef PubMed.
- J. C. Sancho-Garcia, A. J. Perez-Jimenez and Y. Olivier, J. Chem. Phys., 2015, 142 Search PubMed.
- M. Rapacioli, F. Calvo, C. Joblin, P. Parneix, D. Toublanc and F. Spiegelman, Astron. Astrophys., 2006, 460, 519–531 CrossRef CAS.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 473–482 CrossRef.
- J. Potticary, L. R. Terry, C. Bell, A. N. Papanikolopoulos, P. C. M. Christianen, H. Engelkamp, A. M. Collins, C. Fontanesi, G. Kociok-Kohn, S. Crampin, E. Da Como and S. R. Hall, Nat. Commun., 2016, 7, 11555 CrossRef CAS PubMed.
- J. H. Miller, W. G. Mallard and K. C. Smyth, J. Phys. Chem., 1984, 88, 4963–4970 CrossRef CAS.
- J. Rodriguez, J. Sanchezmarin, F. Torrens and F. Ruette, J. Mol. Struct., 1992, 86, 429–441 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- M. Rapacioli, F. Calvo, F. Spiegelman, C. Joblin and D. J. Wales, J. Phys. Chem. A, 2005, 109, 2487–2497 CrossRef CAS PubMed.
- O. I. Obolensky, V. V. Semenikhina, A. V. Solov'yov and W. Greiner, Int. J. Quantum Chem., 2007, 107, 1335–1343 CrossRef CAS.
- I. D. Mackie and G. A. DiLabio, J. Phys. Chem. A, 2008, 112, 10968–10976 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. C, 2008, 112, 4061–4067 CAS.
- M. Rapacioli, F. Spiegelman, D. Talbi, T. Mineva, A. Goursot, T. Heine and G. Seifert, J. Chem. Phys., 2009, 130, 244304 CrossRef PubMed.
- T. Janowski, A. R. Ford and P. Pulay, Mol. Phys., 2010, 108, 249–257 CrossRef CAS.
- A. J. Perez-Jimenez and J. C. Sancho-Garcia, Chem. Phys., 2015, 459, 112–124 CrossRef CAS.
- M. Rapacioli and F. Spiegelman, Eur. Phys. J. D, 2009, 52, 55–58 CrossRef CAS.
- R. Khanna, V. Sahajwalla and R. H. Hurt, Carbon, 2005, 43, 67–77 CrossRef CAS.
- T. Heinemann, K. Palczynski, J. Dzubiella and S. H. L. Klapp, J. Chem. Phys., 2015, 143, 174110 CrossRef PubMed.
- J. Hernandez-Rojas, F. Calvo, S. Niblett and D. J. Wales, Phys. Chem. Chem. Phys., 2017, 19, 1884–1895 RSC.
- M. A. Duncan, A. M. Knight, Y. Negishi, S. Nagao, Y. Nakamura, A. Kato, A. Nakajima and K. Kaya, Chem. Phys. Lett., 1999, 309, 49–54 CrossRef CAS.
- M. Schmidt, A. Masson and C. Brechignac, Int. J. Mass Spectrom., 2006, 252, 173–179 CrossRef CAS.
- P. Brechignac, G. A. Garcia, C. Falvo, C. Joblin, D. Kokkin, A. Bonnamy, P. Parneix, T. Pino, O. Pirali, G. Mulas and L. Nahon, J. Chem. Phys., 2014, 141, 164325 CrossRef PubMed.
- F. Gamez, A. R. Hortal, B. Martinez-Haya, J. Soltwisch and K. Dreisewerd, J. Mass Spectrom., 2014, 49, 1127–1138 CrossRef CAS PubMed.
- M. Gatchell and H. Zettergren, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 162001 CrossRef.
- T. Kurzthaler, B. Rasul, M. Kuhn, A. Lindinger, P. Scheier and A. M. Ellis, J. Chem. Phys., 2016, 145, 064305 CrossRef.
- F. Calvo and E. Yurtsever, J. Chem. Phys., 2016, 144, 224302 CrossRef CAS PubMed.
- R. Rodriguez-Cantano, R. P. de Tudela, M. Bartolomei, M. I. Hernandez, J. Campos-Martinez, T. Gonzalez-Lezana, P. Villarreal, J. Hernandez-Rojas and J. Breton, J. Chem. Phys., 2015, 143, 224306 CrossRef PubMed.
- F. Calvo, J. Phys. Chem. A, 2015, 119, 5959–5970 CrossRef CAS PubMed.
- F. Calvo, Comput. Theor. Chem., 2017, 1107, 2–6 CrossRef CAS.
- R. Rodriguez-Cantano, R. P. de Tudela, M. Bartolomei, M. I. Hernandez, J. Campos-Martinez, T. Gonzalez-Lezana, P. Villarreal, J. Hernandez-Rojas and J. Breton, J. Phys. Chem. A, 2016, 120, 5370–5379 CrossRef CAS PubMed.
- R. Rodriguez-Cantano, M. Bartolomei, M. I. Hernandez, J. Campos-Martinez, T. Gonzalez-Lezana, P. Villarreal, R. P. de Tudela, F. Pirani, J. Hernandez-Rojas and J. Breton, J. Chem. Phys., 2017, 146, 034302 CrossRef PubMed.
- L. F. Gomez, E. Loginov, R. Sliter and A. F. Vilesov, J. Chem. Phys., 2011, 135, 154201 CrossRef PubMed.
- H. Schöbel, P. Bartl, C. Leidlmair, S. Denifl, O. Echt, T. D. Märk and P. Scheier, Eur. Phys. J. D, 2011, 63, 209–214 CrossRef.
- S. Ralser, J. Postler, M. Harnisch, A. M. Ellis and P. Scheier, Int. J. Mass Spectrom., 2015, 379, 194–199 CrossRef CAS PubMed.
- The NIST mass spectrum,47 recorded at an electron energy of 70 eV, shows a variety of fragment ion peaks but between 160 and 293 u their intensities do not exceed 0.5% of the parent ion.
- http://webbook.nist.gov/cgi/cbook.cgi?ID=C191071&Units=SI&Mask=2200#Mass-Spec, accessed June 29, 2017.
- E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- C. Leidlmair, Y. Wang, P. Bartl, H. Schöbel, S. Denifl, M. Probst, M. Alcamí, F. Martín, H. Zettergren, K. Hansen, O. Echt and P. Scheier, Phys. Rev. Lett., 2012, 108, 076101 CrossRef PubMed.
- F. Calvo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 060502(R) CrossRef.
- H. Shin and Y. Kwon, J. Chem. Phys., 2012, 136, 064514 CrossRef PubMed.
- C. E. Klots, J. Phys. Chem., 1988, 92, 5864–5868 CrossRef CAS.
- K. Hansen and U. Näher, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1240–1250 CrossRef CAS.
- L. An der Lan, P. Bartl, C. Leidlmair, R. Jochum, S. Denifl, O. Echt and P. Scheier, Chem. – Eur. J., 2012, 18, 4411–4418 CrossRef CAS PubMed.
- F. Calvo, E. Yurtsever and O. Birer, J. Phys. Chem. A, 2016, 120, 1727–1736 CrossRef CAS PubMed.
- Ionization of an embedded dopant proceeds via He+ formation and resonant hole hopping, or via highly mobile He*−.57 Formation of He+ requires about 24.6 eV, much more than ionization of coronene (7.29 ± 0.03 eV). Formation of He*− requires a few eV less.
- A. Mauracher, M. Daxner, J. Postler, S. E. Huber, S. Denifl, P. Scheier and J. P. Toennies, J. Phys. Chem. Lett., 2014, 5, 2444–2449 CrossRef CAS PubMed.
- A. G. Donchev, J. Chem. Phys., 2007, 126, 124706 CrossRef CAS PubMed.
- K. Srinivasu, K. R. S. Chandrakumar and S. K. Ghosh, Phys. Chem. Chem. Phys., 2008, 10, 5832–5839 RSC.
- M. Kocman, P. Jurecka, M. Dubecky, M. Otyepka, Y. Cho and K. S. Kim, Phys. Chem. Chem. Phys., 2015, 17, 6423–6432 RSC.
- T. Gould, S. Lebegue, J. G. Angyan and T. Bucko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- H. Freimuth, H. Wiechert, H. P. Schildberg and H. J. Lauter, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 587–603 CrossRef CAS.
- D. S. Greywall, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 309–318 CrossRef CAS.
- A. Kaiser, M. Renzler, L. Kranabetter, M. Schwärzler, R. Parajuli, O. Echt and P. Scheier, Int. J. Hydrogen Energy, 2017, 42, 3078–3086 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04999d |
| This journal is © the Owner Societies 2017 |