Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantification of f-element covalency through analysis of the electron density: insights from simulation
A.
Kerridge

Department of Chemistry, Faraday Building, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: a.kerridge@lancaster.ac.uk; Web: akresearch.wordpress.com
First published on 26th May 2017
Abstract
The electronic structure of f-element compounds is complex due to a combination of relativistic effects, strong electron correlation and weak crystal field environments. However, a quantitative understanding of bonding in these compounds is becoming increasingly technologically relevant. Recently, bonding interpretations based on analyses of the physically observable electronic density have gained popularity and, in this Feature Article, the utility of such density-based approaches is demonstrated. Application of Bader's Quantum Theory of Atoms in Molecules (QTAIM) is shown to elucidate many properties including bonding trends, orbital overlap and energy degeneracy-driven covalency, oxidation state identification and bond stability, demonstrating the increasingly important role that simulation and analysis play in the area of f-element bond characterisation.
1. Introduction
The f-elements, comprised of the lanthanide (Ln: Z = 57–71) and actinide (An: Z = 89–103) ions, play an increasingly important role in our lives.1 The technological applications of the lanthanides are far-ranging: complexes of gadolinium (and to a lesser extent europium, terbium, dysprosium, thulium and ytterbium) are routinely used as contrast agents in magnetic resonance imaging,2,3 and the optical properties of the lanthanides are exploited more broadly in energy efficient lighting components. Neodymium is the commonly used material in wind turbine magnets and the magnetic properties of other lanthanides, such as praseodymium, dysprosium and thulium, are exploited elsewhere, for example in consumer electronics and in hybrid electric vehicles. The latter also exploit the lanthanides in the context of rechargeable batteries, while vast quantities of ceria (CeO2) is used in catalytic converters by the traditional automotive industry.4In contrast, the majority of technological applications of the actinides are associated with uranium, which is integral to our current approaches to energy production via nuclear fission. The use of uranium in the nuclear power industry leads to the production of other radiotoxic actinides, primarily plutonium, but also the minor actinide (MA) elements, namely neptunium, americium and curium. Separation of neptunium from uranium in the PUREX (Plutonium Uranium Redox EXtraction) process can be problematic and, more broadly, storage of the minor actinides represents a significant health hazard, with their safe management requiring substantial economic commitment and research resources.5 A developing strategy in the management of minor actinide-containing spent fuel is solvent extraction based SANEX (Selective ActiNide EXtraction) and TALSPEAK (Trivalent Actinide Lanthanide Separation by Phosphorus reagent Extraction from Aqueous Komplexation) processes which exploit differences in the thermodynamic stability of analogous Ln and MA complexes to effect separation of the two. It is believed that variation in the covalent contributions to bonding contributes to the effectiveness of this approach,6 although conclusive evidence remains elusive.
Whilst uranium is the dominant actinide from a technological perspective, applications of other members of the series do exist. For example, plutonium is used in the thermoelectric generators which act as power sources for the deep-space Voyager, Curiosity and New Horizons probes, as well as finding utility in human pacemakers. Due to the scarcity of the isotope required for this technology (238Pu), americium and curium are under consideration as alternatives. Americium also finds application in household smoke detectors, where sub-μg quantities are used as ionisation sources.
In addition to their technological relevance, the chemistry of the f-elements is fascinating from a fundamental science perspective: the lanthanides, which exhibit partial population of the high-angular momentum (l = 3) 4f shell, have intriguing magnetic properties that can be modulated by their ligand environments.7 While lanthanide bonding can, with some notable exceptions,8–12 be characterised as ionic in nature, actinide bonding is highly complex: compounds typically exhibit strong relativistic effects, substantial electron correlation and weak crystal fields. Combined, these phenomena result in a poorly-defined valence region in which the 5f, 6d and 7s shells may each play a role in bonding.13 Intriguingly, the 6p shell, which is typically considered to be core-like, can also impact on bonding in a manner that is challenging to characterise.14,15 Deepening our understanding of chemical bonding in complexes of the f-elements and quantifying the nature of this bonding is therefore at the forefront of current f-element research. Opportunities to experimentally investigate the nature of f-element bonding are, however, currently rather limited (see Section 2) and so quantum chemical simulation, combined with appropriate analysis, offers an important and accessible alternative.16,17 In this Feature Article, recent computational progress into the characterisation of f-element bonding and quantitation of its covalent character is reported and contrasted with experimental advances.
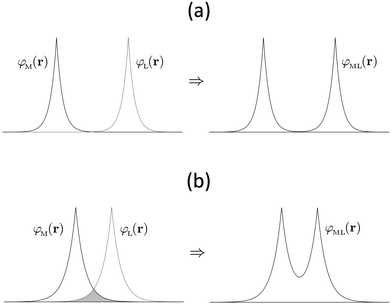
Whilst the meaning of covalency is well-understood from a chemical perspective, there is no formal physical definition. However, from a quantum chemical perspective the manifestation of covalency can be considered in terms of perturbation theory.18 In a molecular orbital description of electronic structure, the mixing of a formally metal-based orbital, φM(r), with a formally ligand-based orbital, φL(r), can be described in terms of a mixing parameter λ, defined as:
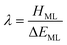 | (1) |
2. Experimental measures of covalency
Numerous spectroscopic approaches have been employed in order to provide evidence of f-element covalency.19 Variation in the relative intensity of photoionization cross-sections has allowed photoelectron spectroscopy (PES) to be employed as a probe of U(VI) and U(IV) 5f-orbital contributions to bonding,20–22 whereas Mössbauer spectroscopy, which can be used to investigate the shielding of s-orbitals by valence orbitals with higher angular momenta, has been used to provide evidence of enhanced Np(IV) covalency in comparison to a Eu(III) analogue.23 More recently, emission spectroscopy has been employed in the identification of unusual bonding in californium-containing compounds, interpreted as being due to Cf(III) 7p covalency.24,25 Two-dimensional 1H, 15N-HMQC (Heteronuclear Multiple Quantum Coherence) Nuclear Magnetic Resonance (NMR) spectroscopy has been used to provide evidence for enhanced covalency in Am(III) compounds in comparison to Lu(III) and Sm(III) analogues,26 whereas 77Se and 125Te NMR has provided evidence of U(VI) 5f-contributions to bonding.27 Electron Paramagnetic Resonance spectroscopy (EPR) has been used to establish 5f contributions to bonding in several complexes of U(V)28,29 and the application of pulsed-EPR has resulted in the quantification of spin-density present on organic ligands coordinating uranium and thorium centres.30Perhaps the most widely-accepted current experimental measure of covalent contributions to f-element bonding comes in the form of X-Ray Absorption Spectroscopy (XAS). Pioneering work by Solomon and co-workers31 established XAS a viable probe of transition metal covalency and this approach has been extended to demonstrate covalent contributions to f-element bonding in uranyl (UO22+),32 U(IV) metallocene dichlorides,33 Ce(IV) and U(IV) halides,9,18 uranocene (U(η8-C8C8)2),34 lanthanide sesquioxides10 and Th(IV) hexacyanoferrate.35
Whilst XAS provides unparalleled spectroscopic insight into the nature of f-element bonding it is unable, as a stand-alone technique, to differentiate between degeneracy- and overlap-driven covalency since, in essence, it probes the metal contribution to formally ligand-based valence p-orbitals that may be present in both situations. Quantum chemical simulations, when appropriately analysed, are able to probe both degeneracy- and overlap-driven covalent interactions and are therefore able to provide increasingly relevant quantitative descriptions of f-element bonding.
3. Analysis of simulated electron structure
Computational molecular-orbital (MO) based simulation methods are focused on the (approximate) solution to the many-electron Schrödinger equation and, invariably, involve the construction of a model Hamiltonian. The eigenfunctions of this Hamiltonian are the (canonical) molecular orbitals. Each occupied MO can be thought of as a quantum mechanical description of a single pair of electrons in a chemical system, but this interpretation is only allowed under the independent particle approximation (IPA), whereby the total many-electron wavefunction can be written as an antisymmetrised product of the occupied MOs. The IPA typically provides a good approximation to the exact wavefunction, however there are numerous situations whereby the approximation breaks down. Structural environments in which this occurs include non-equilibrium geometries and transition states, whereas weak crystal field environments, degenerate ground-states and strong electron correlation provide examples with an electronic origin.Analysis of simulated electron structure can be largely separated into two approaches: those based around analysis of molecular orbitals and those based around analysis of the electron density. Recently, both Kaltsoyannis and Dognon have provided comprehensive summaries of the application of such analysis methods to problems in f-element chemistry.6,36 It should be noted that an alternative approach based on decomposition of the molecular energy into its contributing components, Energy Decomposition Analysis (EDA),37–39 has also been successfully applied to f-element bonding.40,41
3.1 Orbital-based analyses
The simplest of the orbital-based analyses are based on direct examination of the canonical MOs. Such analyses are typically only used to provide qualitative bonding information, although quantitative data can be generated. Examples of this approach include Mulliken42 and Löwdin43 population analyses and Wiberg44 and Mayer45 bond order analyses.Whilst computationally inexpensive, orbital-based analysis approaches are of limited utility. The set of occupied canonical MOs does not provide a unique description of electronic structure, since unitary transformations of this set leave the total energy of the system unchanged. Numerous localisation approaches including the Foster-Boys,46 Edmiston-Ruedenberg47 and Pipek-Mezey48 procedures take advantage of this property, but from a quantitative perspective, orbital-based bonding analyses are prone to ambiguity.
3.2 Density-based analyses
The electron density, in contrast to the electronic wavefunction, is a physical observable and therefore represents a well-defined property to analyse. Numerous density-based approaches exist, including Hirshfeld,49 natural bond orbital50 (NBO) and electron localisation function51,52 (ELF) analyses, however, in recent years, Bader's quantum theory of atoms in molecules53 has gained increasing popularity due to its ability to probe multiple aspects of bonding in a coherent, quantitative and rigorous framework.| ∇ρ(r)·n(r) = 0 | (2) |
| Critical point | (ω, σ) | Character |
|---|---|---|
| Nuclear (NCP) | (3, −3) | Local maximum |
| Bond (BCP) | (3, −1) | 1st-order saddle point |
| Ring (RCP) | (3, +1) | 2nd-order saddle point |
| Cage (CCP) | (3, +3) | Local minimum |
Along with NCPs, bond, ring and cage critical points can be identified and, of these, the bond critical point (BCP) is of most relevance in quantifying bond character. A bond critical point exists if the line of minimum density between two atoms has its minimum point where the corresponding atomic basins share a common surface, since only then is the ∇ρ(r) = 0 condition satisfied. BCPs are most commonly employed to characterise the nature of a chemical interaction and a well-cited rule of thumb states that ρ(r) > 0.2 a.u. with ∇2ρ(r) < 0 is indicative of an open-shell (i.e. covalent) interaction, whereas ρ(r) < 0.1 a.u. with ∇2ρ(r) > 0 represents a closed shell (i.e. ionic, van der Waals or hydrogen bonding) interaction. It should be noted, however, that there is no a priori reason to assume that this rule should hold for f-element bonding.
The lines of minimum density which join the BCPs to the NCPs are known as bond paths and the combination of critical points and bond paths together form the molecular graph of the system, which is visually analogous to the ball-and-stick model of a molecule, see Fig. 2b(v). Characterisation of a chemical system in this manner is a form of topological analysis.
In addition to providing analogies to traditional models of a molecule, QTAIM parameters give quantitative insight into the nature of chemical bonding. Integration over atomic basins allows quantification of the degree of electron sharing between neighbouring atoms, thereby providing insight into both degeneracy- and overlap-driven covalency. The value of the electron density at the BCP, ρBCP, along with its Laplacian, provides complementary data. ρBCP indicates the presence and degree of covalent character in the bond via a direct quantification of charge accumulation in the bonding region and hence provides a measure of overlap-driven covalency (cf.Fig. 1b). The ability of the QTAIM to interrogate both degeneracy- and overlap-driven covalency thus makes it ideally suited to contemporary problems in f-element bonding.
3.3 Bonding trends in the lanthanide and actinide series
Pioneering work by the Kaltsoyannis group represents some of the earliest applications of QTAIM analysis in f-element chemistry. Tassell and Kaltsoyannis investigated covalency in the organometallics AnCp4 (Cp = η5-C5C5) where An = Th–Cm.54 Analysing densities generated using the density functional theory (DFT) approach employing the generalised gradient approximation (GGA) in the form of the PBE exchange–correlation functional, the authors found that, according to the magnitude of ρBCP, An–Cp bonding was highly ionic in character, with greater covalency found near the beginning of the series. This contrasted with Mulliken analysis which suggested increased f-orbital contribution to bonding MOs as the actinide series was traversed. Kirker and Kaltsoyannis performed related studies on AnCp3 where An = Th–Cm, analysing densities generated using both the PBE and hybrid-GGA PBE0 exchange–correlation functionals. The authors came to the same conclusion,55 namely that there is little appreciable charge accumulation in the An–Cp bonds and that what little charge density is present diminishes as the actinide series is traversed. Kerridge investigated the bonding in AnCOT2 (COT = η5-C8C8), where An = Th–Cm, using the complete-active-space self-consistent-field (CASSCF) methodology.56 QTAIM analysis of CASSCF-derived densities again revealed a trend of diminishing covalency, as measured by the magnitude of ρBCP, as the series was traversed (see Fig. 3), with a plateau between Pa and Pu. Kerridge also investigated the delocalisation index, δ(An,C), a measure of the degree of electron-sharing between the actinide and carbon atoms, identifying a similar, though less pronounced trend, thereby demonstrating that in these systems, covalency was more overlap-driven in nature for An = Pa–Pu, as evidenced by ρBCP.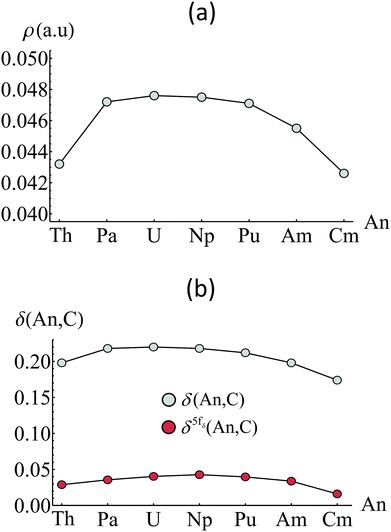 | ||
| Fig. 3 Variation of (a) ρBCP and (b) δ(An,C) in AnCOT2 when the An centred is varied. Adapted from ref. 56 (DOI: 10.1039/c3ra47088a) with permission from the Royal Society of Chemistry. | ||
Reported ρBCP values from these studies are summarised in Table 2. While all values are indicative of predominantly ionic interactions (recall that ρBCP is typically greater than 0.2 a.u. for pronounced covalent bond character), significant variation is found when the ligating species is altered. Interestingly, An interactions with the COT ligand are more covalent than those with the Cp ligand, with ρBCP values ∼50% higher in the former. This is, in part, attributable to the higher charge density on the formally dianionic COT ligand which appears to contribute to the bonding interaction.
Beyond organometallic complexes, Wang et al. analysed PBE-derived densities of AnF4, where An = Th–Cm: similarly to the above, they found larger ρBCP values between Pa and Pu, with the magnitude decreasing for later actinides.58 Huang et al. investigated [AnOn]m+ (n = 1, 2; m = 0–2) where An = Th–Cm59 and, in contrast to previous reports, found pronounced evidence for charge accumulation in the An–O bonds, reporting ρBCP values in excess of 0.2 a.u. and δ(An,O) values close to, and in many cases exceeding, 2. Despite these pronounced covalent interactions, The trend across the series mirrored that previously reported, with Pa, U, Np and Pu exhibiting more pronounced overlap-driven covalency.
The lanthanides are more readily classified as ionically bonded complexes and as a consequence less attention has been paid to Ln bond characterisation. The only systematic study in the literature is that of Fryer-Kanssen et al., who investigated [Ln(H2O)9]3+ and [Ln(BTP)3]3+ (BTP = bis(triazinyl)pyridine) complexes with Ln = Ce–Lu.57 As might be expected, topological analysis of densities generated using the hybrid-GGA exchange–correlation functionals B3LYP and BHLYP revealed low values of ρBCP in all cases and only small (<10%) variation as the series was traversed, indicative of predominantly ionic bonding with little dependence on the nature of the central ion, see Fig. 4.
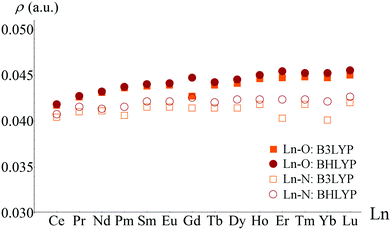 | ||
| Fig. 4 Variation of ρBCP in Ln–O and Ln–N bonds of [Ln(H2O)9]3+ and [Ln(BTP)3]3+, respectively. Adapted from ref. 57. Reprinted with permission from DOI: 10.1021/acs.inorgchem.6b00968. Copyright 2016 American Chemical Society. | ||
3.4 Actinyl bonding
Uranyl, UO22+, is the dominant form of uranium in the +6 oxidation state and is characterised by short strong U–O multiple bonds. Uranyl, along with its Pu analogue, plutonyl, were first investigated via QTAIM by Clark et al. in 2004, although topological properties were not reported.60 QTAIM properties of the U–O bond have been reported by Vallet et al.61 who found strongly covalent interactions with, for example, ρBCP = 0.38 a.u. and a delocalisation index δ(U,0) = 2.29 for densities generated using the hybrid-GGA B3LYP exchange–correlation functional. These results again demonstrate the presence of overlap-driven covalency. The authors also investigated the effect of equatorial complexation on the U–O bond and found that this resulted in reduced covalent character.A related study by Di Pietro and Kerridge62 found similar bonding characteristics: ρBCP = 0.364 a.u. and δ(An,C) = 2.19 for densities generated using the hybrid meta-GGA TPSSh exchange–correlation functional. The authors performed a detailed analysis of the effects of equatorial complexation on the electronic structure of the uranyl unit, concluding that equatorial complexation led to a localisation of electronic charge on the uranyl oxygen centres, reducing the covalent character of the U–O bond and consequently lengthening and weakening it. Charge localisation on the oxygen centres appeared to allow the uranium centre to instead donate charge into equatorial bonds. This quantitative description could also be qualitatively visualised, by investigating the change in charge density distribution induced by equatorial complexation (see Fig. 5).
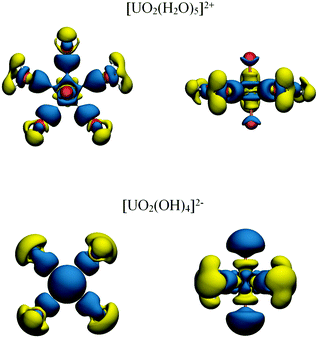 | ||
| Fig. 5 Redistribution of electron density due to uranyl complexation by water and hydroxide. Blue and yellow regions indicate charge accumulation and depletion, respectively. Adapted from ref. 62. Reprinted with permission from DOI: 10.1021/acs.inorgchem.5b01219. Copyright 2016 American Chemical Society. | ||
Du et al. have analysed B3LYP-derived densities of plutonyl, PuO22+, and found covalency of comparable magnitude to that in uranyl,63 with ρBCP = 0.376 a.u. and δ(Pu,O) = 2.37, while equatorial complexation was found to be largely ionic in nature. This latter finding is in contrast to the results of Vallet et al. who found some degree of equatorial charge accumulation when uranyl was coordinated by peroxide and carbonate species.61
Brown et al. have investigated more exotic analogues of uranyl, where one axial oxygen is substituted by a heavier chalcogen, resulting in UOE2+, with E = S or Se. While such analogues do not exist as isolated ions, they can be stabilised via equatorial ligation by, for example, bis(silyl)amide.64 Analysis of PBE-derived densities revealed that substitution by a heavier chalcogen resulted in a reduction of U–O ρBCP values, although this reduction was not pronounced. U–E bonds, however, exhibited significantly less covalent character, with ρBCP values more than 50% lower than corresponding U–O values. This is presumably due to the softer, less electronegative S and Se species providing a poor bonding environment for the uranium centre, which is characterised as a hard acceptor.
3.5 Oxidation state dependency
Few systematic density-based studies investigating the dependency of covalent bond character on metal oxidation state exist. Beekmeyer and Kerridge analysed DFT-, RASSCF and- CASSCF-derived [UCl6]n− (n = 0–3) densities65 and determined that, while only weak covalency, as evidenced by ρBCP and δ(U,Cl) measures, was present, oxidation state dependence was pronounced, see Table 3. The authors found that, irrelevant of the simulation method used, covalent bond character was most pronounced in the highest (+6) oxidation state, with ρBCP values for the lowest (+3) some 60% lower. δ(U,Cl) values gave a similar, albeit less pronounced, trend. Interestingly, while ρBCP values showed little dependence on simulation methodology, it was found that DFT-derived densities gave consistently higher delocalisation indices, thereby demonstrating enhanced degeneracy-driven covalency without a corresponding increase of charge accumulation in the bond.| Metric | CASSCF | RASSCF | B3LYP | PBE | |
|---|---|---|---|---|---|
| U(VI) | ρ BCP | 0.105 | 0.102 | 0.099 | 0.096 |
| δ(U,Cl) | 0.838 | 0.868 | 1.102 | 1.151 | |
| U(V) | ρ BCP | 0.086 | 0.084 | 0.082 | 0.081 |
| δ(U,Cl) | 0.673 | 0.647 | 0.872 | 0.932 | |
| U(IV) | ρ BCP | 0.064 | 0.059 | 0.063 | 0.065 |
| δ(U,Cl) | 0.482 | 0.442 | 0.633 | 0.619 | |
| U(III) | ρ BCP | 0.038 | 0.037 | 0.041 | 0.044 |
| δ(U,Cl) | 0.324 | 0.300 | 0.432 | 0.487 |
Huang et al. have investigated the +2 to +6 oxidation states in a series of actinide oxides, [AnOn]m+ (n = 1, 2; m = 0–2) where An = Th–Cm,59 see Table 4. For uranium and heavier actinides, the same trend as found by Beekmeyer and Kerridge65 was reported, whereas Th and Pa oxides were found to exhibit more complicated behaviour. Covalent bond character was found to be sensitive to the coordination environment of the actinide, with the individual bonds of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes exhibiting less covalent character than analogous 1
1 complexes exhibiting less covalent character than analogous 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, although the cumulative amount of electron sharing was found to be higher in the former.
1 complexes, although the cumulative amount of electron sharing was found to be higher in the former.
| [AnO2]m+ | [AnO]m+ | |||||
|---|---|---|---|---|---|---|
| An(VI) | An(V) | An(IV) | An(IV) | An(III) | An(II) | |
| Th | 0.195 | 0.228 | 0.224 | 0.314 | 0.283 | 0.262 |
| (1.598) | (1.704) | (1.738) | (2.116) | (2.041) | (2.044) | |
| Pa | 0.288 | 0.314 | 0.288 | 0.336 | 0.287 | 0.284 |
| (2.046) | (2.031) | (2.053) | (2.228) | (2.031) | (2.157) | |
| U | 0.377 | 0.325 | 0.290 | 0.346 | 0.284 | 0.259 |
| (2.305) | (2.084) | (2.067) | (2.315) | (2.023) | (2.005) | |
| Np | 0.380 | 0.338 | 0.273 | 0.346 | 0.286 | 0.259 |
| (2.336) | (2.143) | (1.942) | (2.372) | (2.074) | (2.042) | |
| Pu | 0.387 | 0.347 | 0.270 | 0.335 | 0.285 | 0.257 |
| (2.363) | (2.182) | (1.921) | (2.417) | (2.097) | (2.061) | |
| Am | 0.385 | 0.339 | 0.254 | 0.282 | 0.283 | 0.242 |
| (2.360) | (2.175) | (1.864) | (2.248) | (2.079) | (2.011) | |
| Cm | 0.359 | 0.307 | 0.245 | 0.232 | 0.269 | 0.241 |
| (2.266) | (2.026) | (1.745) | (1.827) | (2.081) | (2.029) | |
Whilst the +VI oxidation state of uranium is typically associated with the uranyl structural motif, important exceptions exist. Liddle and coworkers have reported the U(VI) terminal nitride {[U(N)(TrenTIPS)] (TrenTIPS = N(CH2CH2NSiiPr3)3}3−, iPr = CH(CH3)2) and, via analysis of the DFT-generated electron density revealed ρBCP = 0.391 a.u. for the strongly covalent U![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond,66 a value comparable to that of analogous group 6 nitrides as well as the U–Oyl bond of uranyl. Reduction to U(V) significantly reduces this covalent character to ρBCP = 0.252 a.u., while the U
N triple bond,66 a value comparable to that of analogous group 6 nitrides as well as the U–Oyl bond of uranyl. Reduction to U(V) significantly reduces this covalent character to ρBCP = 0.252 a.u., while the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond in the corresponding U(VI) imido complex exhibits ρBCP = 0.16 a.u.67 Substitution of the amido group by phosphinidene and arsenidene again reduces the covalent character of the double bond, with reported values of ρBCP ≤ 0.08 a.u.68,69
N double bond in the corresponding U(VI) imido complex exhibits ρBCP = 0.16 a.u.67 Substitution of the amido group by phosphinidene and arsenidene again reduces the covalent character of the double bond, with reported values of ρBCP ≤ 0.08 a.u.68,69
3.6 d- and f-shell contributions to covalency
Advantage can be taken of the high symmetry of some coordination complexes of the f-elements to resolve the d- and f-contributions to QTAIM metrics. Assuming the Müller approximation,70 the delocalisation index δ(A,B) can be written as: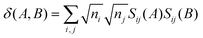 | (3) |
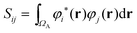 | (4) |
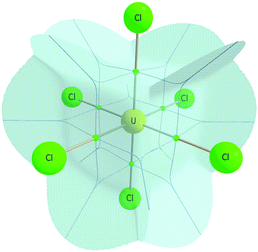 | ||
| Fig. 6 The atomic basin, ΩU, of the uranium centre in UCl6, exhibiting Oh symmetry. Figure reproduced from ref. 65 (DOI:10.3390/inorganics3040482). | ||
Kerridge has used density-based analysis to investigate the dδ and fδ contributions to metal–ligand bonding in AnCOT2, where An = Th–Cm.56 Although it was found that the gerade (dδ) contribution was of greater magnitude than that of the ungerade (fδ) component in each complex, the variation in the total contribution was mirrored by the ungerade component, and was indicative of a reduction as the An series is traversed, commensurate with the 5f shell becoming increasingly compact and core-like.
Beekmeyer and Kerridge have performed the same analysis to identify (n + 1)d and nf bonding contributions in [MCl6]n−, where M = Ce and U.65 Comparing DFT to RASSCF/CASSCF generated densities, they found that the former gave delocalisation indices consistently higher than the latter. However, the majority of this increase could be attributed to the ungerade (i.e. f-shell) contribution, while the (d-shell) gerade component was largely insensitive to the methodology used to simulate the densities (see Fig. 7). The authors suggested that this may be a manifestation of the self-interaction error71 which is inherent to approximate DFT methodologies and would be expected to be more pronounced in more highly correlated systems such as the valence f-shell of actinides and lanthanides.
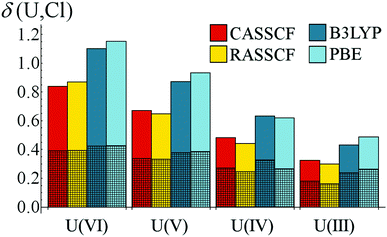 | ||
| Fig. 7 Gerade and ungerade contributions to delocalisation indices in [UCl6]n−. Shaded regions represent gerade contributions. Figure reproduced from ref. 65 (DOI: 10.3390/inorganics3040482). | ||
3.7 U-like covalency in Ce compounds
In contrast to the trivalent lanthanides, which can be almost exclusively classified as exhibiting ionic bonding, recent studies have shown that compounds of cerium, the only lanthanide with an accessible tetravalent oxidation state, can exhibit covalent bond-character of comparable magnitude to that of U(IV) analogues.Motivated by XAS studies indicating detectable covalency in Ce(IV) hexachloride,9,18 Beekmeyer and Kerridge analysed DFT and CASSCF/RASSCF derived densities in order to quantify the covalency in this compound, along with its uranium analogue.65 Remarkably, the magnitude of Ce and U covalency, as evidenced by ρBCP and δ(M,Cl), was almost identical, see Fig. 8. Similar behaviour was found in the carbene complexes M(BIPMTMS)(ODipp)2 (M = Ce, U, Th; BIPMTMS = C(PPh2NSiMe3)2; Dipp = C6H3-2,6-iPr2) by Gregson et al.,11 where the unusually short Ce-C double bond72 was explained in terms of Ce–C covalency of a similar level to that of the U complex, a degree of covalency not present in the Th analogue. The ordering of covalency, Ce ∼ U > Th, was reproduced in experimental exchange reactions with MCl salts. Building on this work, the related bis-carbene M(BIPMTMS)2 (M = Ce, U, Th) complexes were synthesized by the same group.12 The Ce complex exhibits one of the shortest reported Ce–C bond lengths, and represents the first evidence of the inverse-trans-influence (ITI) in tetravalent f-element chemistry. Analysis of CASSCF-derived densities again revealed Ce-covalency to be of the same magnitude as that found in the U–C bond, and the ellipticity of the density at the M–C BCP was indicative of double-bond character.
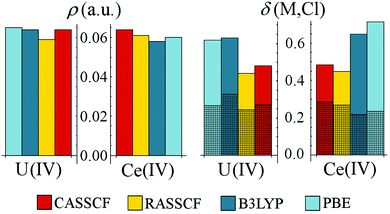 | ||
| Fig. 8 Comparison of U–Cl and Ce–Cl covalency in [MCl6]2−. Figure adapted from ref. 65 (DOI: 10.3390/inorganics3040482). | ||
More recently, Damon et al. have reported a Ce(IV) oxo complex with pronounced covalent bond character.73 Based on analysis of the PBE-derived density, a ρBCP value of 0.196 a.u. was found for the Ce–O bond. This is the largest reported value for a Ce complex in the literature, and is extremely close to the analogous U–O value of 0.199 a.u.
3.8 Correlating covalency with bond strength
Whilst a degree of covalent bond character can be identified in many complexes of the f-elements, relating this to bond strength is a challenging problem, since many other factors including, but not limited to, sterics and electrostatics, contribute to bond stability. Huang et al. have shown that bond strength is closely correlated to the degree of charge transfer upon complexation, as measured by analysis of QTAIM-derived charges.59 Di Pietro and Kerridge have investigated the weakening of axial uranyl bonds to equatorial complexation, and find a strong correlation between axial vibrational frequencies and equatorial QTAIM parameters, see Fig. 9, indicating that it may be possible to probe equatorial bond covalency in related systems using standard spectroscopic techniques.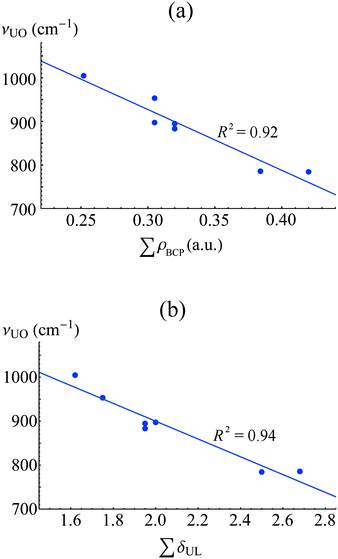 | ||
| Fig. 9 Correlation between equatorial bond covalency, as measured by ρBCP and δ(U,L), and axial vibrational frequencies, for a series of actinyl complexes. Adapted from ref. 62. Reprinted with permission from DOI: 10.1021/acs.inorgchem.5b01219. Copyright 2016 American Chemical Society. | ||
Fryer-Kanssen et al. have investigated the relationship between metal–ligand bond covalency and complex stability in [M(BTP)3]3+ complexes with M = Ln, Am, Cm.57 They considered the exchange reaction:
| [An(H2O)9]3+ + [Ln(BTP)3]3+ → [Ln(H2O)9]3+ + [An(BTP)3]3+ |
3.9 Oxidation state identification
The formal oxidation state of a metal centre in a coordination complex is defined by assuming that any metal charge involved in a bonding interaction is donated entirely to the ligands. This definition lends itself to analysis via the QTAIM, since the electronic population of the atomic basin ΩA, N(A), can be defined in terms of the localisation and delocalisation indices, λ(A) and δ(A,X):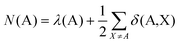 | (5) |
| OSA = ZA − λ(A) | (6) |
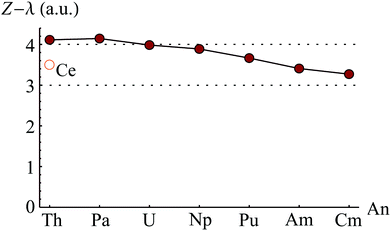 | ||
| Fig. 10 QTAIM-derived oxidation state for the An centre in AnCOT2. Adapted from ref. 56 (DOI: 10.1039/c3ra47088a) with permission from the Royal Society of Chemistry. | ||
The question of oxidation state in cerocene, CeCOT2, has been the subject of debate for several decades. Originally characterised as a Ce(IV) compound,87–89 XANES spectroscopy90 and ab initio calculations91 supported an alternative interpretation, namely that the complex exhibits a multiconfigurational ground state with ∼80% Ce(III) character. This surprising result was investigated by the Kaltsoyannis group,92,93 who reported that the assignment of oxidation state based on configurational admixture was ambiguous. As a result of density based analysis, the authors assigned a +4 oxidation state, but noted significant charge delocalisation which could account for the reported XANES data. These apparently contradictory interpretations have since been shown to both be valid,94 and Kerridge has calculated OSCe to be +3.500 based on analysis of a CASSCF-derived density.95
Table 5 summarises QTAIM-derived oxidation states for a number of simulated compounds. While in all cases rounding these values to the nearest integer yields the formal oxidation state, it remains to be demonstrated if this approach is applicable across the periodic table.
| Complex | Formal OS | OSM |
|---|---|---|
| UO2Ln80–82 | +6 | +5.62–+6.12 |
| [UCl6]n− (n = 0–3)65 | +6, +5, +4, +3 | +5.75, +5.12, +4.25, +3.38 |
| An(E2PL2)4 (An = Th; U, E = S, Se; L= tBu, iPr)83 | +4 | +4.15–+4.29 |
| M(BIPMTMS)(ODipp)2 (M = Ce, Th, U)11 | +4 | +4.26–+4.39 |
| M(BIPMTMS)2 (M = Ce, Th, U)12 | +4 | +4.17–+4.34 |
| {Th-(Cp′′)3}2(μ–η1:η1-P4),84 {Th(Cp′′′)2[κ2-O2C{C5H3-3,3′-(SiMe3)2}]}2(μ-κ2:κ2-C2O4),85 [{Th(Cp′′)3}2{m-(NC5H4)2}], {Th(Cp′′)3}2{m-(NC5H5)2}86 (Cp′′ = {C5H3(SiMe3)2-1,3}) | +4 | +4.20–+4.32 |
| [CeCl6]n− (n = 2,3)65 | +4, +3 | +4.23, +3.29 |
| [MBTP3]3+ (M = Eu, Gd, Am, Cm)57 | +3 | +3.31–+3.50 |
4. Conclusions
In this Feature Article, the utility of Bader's Quantum Theory of Atoms in Molecules (QTAIM) in the understanding of bonding in complexes of the f-elements has been considered and discussed. While significant use of this methodology in the f-element community has only occurred in the last few years, it is already allowing us to quantitatively probe heavy-element bonding at an unprecedented level of detail.Like any analysis method, QTAIM is imperfect, in the sense that it does not always align with our chemical intuition, and may not reproduce all experimentally observed trends (although it should be borne in mind that an analytical method is only as good as the data to which it is applied). However, QTAIM provides a robust, rigorous, unambiguous, quantitative framework in which to interpret simulation and, occasionally, experimental96,97 results. It's applicability to data generated using a variety of simulation methods allows for the straightforward comparison of different systems, a key strength. Perhaps the most important aspect of this (and related) analysis methods though is the fact that they are based on a physical observable, the electron density. This makes any prediction derived from this analysis empirically falsifiable, in principle at least. Few, if any, alternative methods offer such a promise.
Already-realised applications of QTAIM in f-element chemistry include the quantification and nature of bond-covalency and stability, oxidation state identification, and similarities/differences in lanthanide and actinide bonding. Potential future developments might include the ability to analyse spin–orbit coupled densities and more importantly, a rigorous approach to energy decomposition. While a framework for such energy decomposition exists, the Interacting Quantum Atom (IQA) approach of Blanco et al.,98 current implementations are not generally applicable to all exchange–correlation functionals, or to relativistic Hamiltonians. It is the author's belief that as familiarity with the methodology increases, so these developments will be achieved, more applications will be identified, and our understanding of the fundamental properties of f-element bonding will deepen.
Acknowledgements
AK thanks the Engineering and Physical Sciences Research Council for the award of a Career Acceleration Fellowship (EP/J002208/1; EP/J002208/2). AK thanks UCL, Lancaster University and the Nuclear Decommissioning Authority for funding.Notes and references
- J.-C. G. Bünzli, J. Coord. Chem., 2014, 67, 3706–3733 CrossRef.
- K. N. Raymond and V. C. Pierre, Bioconjugate Chem., 2005, 16, 3–8 CrossRef CAS PubMed.
- M. W. Villaraza, A. J. L. Bumb and A. Brechbiel, Chem. Rev., 2010, 110, 2921–2959 CrossRef PubMed.
- L. S. Natrajan and M. H. L. Paden, in RSC Green Chemistry 22: Element Recovery and Sustainability, ed. A. J. Hunt, Royal Society of Chemistry, London, 2013, pp. 140–184 Search PubMed.
- R. C. Ewing, Nat. Mater., 2015, 14, 252–257 CrossRef CAS PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- S. G. Minasian, J. L. Krinsky and J. Arnold, Chem. – Eur. J., 2011, 17, 12234–12245 CrossRef CAS PubMed.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef PubMed.
- A. B. Altman, J. I. Pacold, J. Wang, W. W. Lukens and S. G. Minasian, Dalton Trans., 2016, 45, 9948–9961 RSC.
- M. Gregson, E. Lu, F. Tuna, E. J. L. McInnes, C. Hennig, A. C. Scheinost, J. McMaster, W. Lewis, A. J. Blake, A. Kerridge and S. Liddle, Chem. Sci., 2016, 7, 3286–3297 RSC.
- M. Gregson, E. Lu, D. Mills, F. Tuna, E. McInnes, C. Hennig, A. Scheinost, J. McMaster, W. Lewis, A. Blake, A. Kerridge and S. T. Liddle, Nat. Commun., 2017, 8, 14137 CrossRef CAS PubMed.
- N. Kaltsoyannis, P. J. Hay, J. Li, J.-P. Blaudeau and B. E. Bursten, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein, J. Fuger and J. J. Katz, Springer, Dordrecht, The Netherlands, 3rd edn, 2006, pp. 1893–2012 Search PubMed.
- R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125–4143 CrossRef CAS PubMed.
- E. O’Grady and N. Kaltsoyannis, J. Chem. Soc., Dalton Trans., 2002, 1233–1239 RSC.
- Computational Methods in Lanthanide and Actinide Chemistry, ed. M. Dolg, John Wiley & Sons Ltd, Chichester, 2015 Search PubMed.
- C. E. Kefalidis, L. Castro, L. Perrin, I. Del Rosal and L. Maron, Chem. Soc. Rev., 2016, 45, 2516–2543 RSC.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2012, 134, 5586–5597 CrossRef CAS PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS.
- B. W. Veal, D. J. Lam, W. T. Carnall and H. R. Hoekstra, Phys. Rev. B: Solid State, 1975, 12, 5651–5663 CrossRef CAS.
- J. P. Clark and J. C. Green, Dalton Trans., 1977, 505–508 RSC.
- J. G. Brennan, J. C. Green and C. M. Redfern, J. Am. Chem. Soc., 1989, 111, 2373–2377 CrossRef CAS.
- G. M. Kalvius, J. Less-Common Met., 1986, 353–378 CrossRef CAS.
- M. J. Polinski, E. B. Garner, R. Maurice, N. Planas, J. T. Stritzinger, T. G. Parker, J. N. Cross, T. D. Green, E. V. Alekseev, S. M. Van Cleve, W. Depmeier, L. Gagliardi, M. Shatruk, K. L. Knappenberger, G. Liu, S. Skanthakumar, L. Soderholm, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Chem., 2014, 6, 387–392 CrossRef CAS PubMed.
- S. K. Cary, M. Vasiliu, R. E. Baumbach, J. T. Stritzinger, T. D. Green, K. Diefenbach, J. N. Cross, K. L. Knappenberger, G. Liu, M. A. Silver, A. E. DePrince, M. J. Polinski, S. M. Van Cleve, J. H. House, N. Kikugawa, A. Gallagher, A. A. Arico, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Commun., 2015, 6, 6827 CrossRef CAS PubMed.
- C. Adam, P. Kaden, B. B. Beele, U. Müllich, S. Trumm, A. Geist, P. J. Panak and M. A. Denecke, Dalton Trans., 2013, 42, 14068–14074 RSC.
- D. E. Smiles, G. Wu, P. Hrobárik and T. W. Hayton, J. Am. Chem. Soc., 2016, 138, 814–825 CrossRef CAS PubMed.
- L. A. Seaman, G. Wu, N. Edelstein, W. W. Lukens, N. Magnani and T. W. Hayton, J. Am. Chem. Soc., 2012, 134, 4931–4940 CrossRef CAS PubMed.
- W. W. Lukens, N. M. Edelstein, N. Magnani, T. W. Hayton, S. Fortier and L. A. Seaman, J. Am. Chem. Soc., 2013, 135, 10742–10754 CrossRef CAS PubMed.
- A. Formanuik, A. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. Mcinnes and D. P. Mills, Nat. Chem., 2017, 9, 578–583 CrossRef CAS PubMed.
- E. I. Solomon, B. Hedman, K. O. Hodgson, A. Dey and R. K. Szilagyi, Coord. Chem. Rev., 2005, 249, 97–129 CrossRef CAS.
- R. G. Denning, J. C. Green, T. E. Hutchings, C. Dallera, A. Tagliaferri, K. Giarda, N. B. Brookes and L. Braicovich, J. Chem. Phys., 2002, 117, 8008–8020 CrossRef CAS.
- S. A. Kozimor, P. Yang, E. R. Batista, K. S. Boland, C. J. Burns, D. L. Clark, S. D. Conradson, R. L. Martin, M. P. Wilkerson and L. E. Wolfsberg, J. Am. Chem. Soc., 2009, 131, 12125–12136 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351 RSC.
- T. Dumas, D. Guillaumont, C. Fillaux, A. Scheinost, P. Moisy, S. Petit, D. K. Shuh, T. Tyliszczak and C. Den Auwer, Phys. Chem. Chem. Phys., 2016, 18, 2887–2895 RSC.
- J.-P. Dognon, Coord. Chem. Rev., 2014, 266–267, 110–122 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS.
- T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS.
- G. Frenking and F. M. Bickelhaup, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2014 Search PubMed.
- G. Cavigliasso and N. Kaltsoyannis, Inorg. Chem., 2007, 46, 3557–3565 CrossRef CAS PubMed.
- J.-P. Dognon, C. Clavaguéra and P. Pyykkö, Angew. Chem., Int. Ed. Engl., 2007, 46, 1427–1430 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- I. Mayer, J. Comput. Chem., 2007, 28, 204–221 CrossRef CAS PubMed.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300–302 CrossRef CAS.
- C. Edmiston and K. Ruedenberg, Rev. Mod. Phys., 1963, 35, 457–465 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- M. A. Spackman and P. G. Byrom, Chem. Phys. Lett., 1997, 267, 215–220 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed., 1991, 30, 409–412 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6576–6588 RSC.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
- A. Kerridge, RSC Adv., 2014, 4, 12078–12086 RSC.
- I. Fryer-Kanssen, J. Austin and A. Kerridge, Inorg. Chem., 2016, 55, 10034–10042 CrossRef CAS PubMed.
- C. Wang, C. Cheng, J. Su and P. Huai, Mol. Phys., 2015, 113, 3450–3458 CrossRef CAS.
- Q.-R. Huang, J. R. Kingham and N. Kaltsoyannis, Dalton Trans., 2015, 44, 2554–2566 RSC.
- A. E. Clark, J. L. Sonnenberg, P. J. Hay and R. L. Martin, J. Chem. Phys., 2004, 121, 2563–2570 CrossRef CAS PubMed.
- V. Vallet, U. Wahlgren and I. Grenthe, J. Phys. Chem. A, 2012, 116, 12373–12380 CrossRef CAS PubMed.
- P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583 CrossRef CAS PubMed.
- J. Du, X. Sun and G. Jiang, Int. J. Mol. Sci., 2016, 17, 1–14 Search PubMed.
- J. L. Brown, S. Fortier, G. Wu, N. Kaltsoyannis and T. W. Hayton, J. Am. Chem. Soc., 2013, 135, 5352–5355 CrossRef CAS PubMed.
- R. Beekmeyer and A. Kerridge, Inorganics, 2015, 3, 482–499 CrossRef CAS.
- D. M. King, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2013, 5, 482–488 CrossRef CAS PubMed.
- D. M. King, J. Mcmaster, F. Tuna, E. J. L. Mcinnes, W. Lewis, A. J. Blake and S. T. Liddle, J. Am. Chem. Soc., 2014, 136, 5619–5622 CrossRef CAS PubMed.
- B. M. Gardner, G. Balázs, M. Scheer, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2014, 53, 4484–4488 CrossRef CAS PubMed.
- B. M. Gardner, G. Balázs, M. Scheer, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2015, 7, 582–590 CrossRef CAS PubMed.
- A. M. K. Müller, Phys. Lett. A, 1984, 105, 446–452 CrossRef.
- V. Polo, E. Kraka and D. Cremer, Mol. Phys., 2002, 100, 1771–1790 CrossRef CAS.
- M. Gregson, E. Lu, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed. Engl., 2013, 52, 13016–13019 CrossRef CAS PubMed.
- P. L. Damon, G. Wu, N. Kaltsoyannis and T. W. Hayton, J. Am. Chem. Soc., 2016, 138, 12743–12746 CrossRef CAS PubMed.
- M. Trumm, B. Schimmelpfennig and A. Geist, Nukleonika, 2015, 60, 847–851 CrossRef.
- J. Lan, W. Shi, L. Yuan, Y. Zhao, J. Li and Z. Chai, Inorg. Chem., 2011, 50, 9230–9237 CrossRef CAS PubMed.
- J. H. Lan, W. Q. Shi, L. Y. Yuan, Y. X. Feng, Y. L. Zhao and Z. F. Chai, J. Phys. Chem. A, 2012, 116, 504–511 CrossRef CAS PubMed.
- Y. Yang, J. Liu, L. Yang, K. Li, H. Zhang, S. Luo and L. Rao, Dalton Trans., 2015, 8959–8970 RSC.
- M. Trumm and B. Schimmelpfennig, Mol. Phys., 2016, 114, 876–883 CrossRef CAS.
- L. Petit, L. Joubert, P. Maldivi and C. Adamo, J. Am. Chem. Soc., 2006, 128, 2190–2191 CrossRef CAS PubMed.
- P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583 CrossRef CAS PubMed.
- P. Di Pietro and A. Kerridge, Phys. Chem. Chem. Phys., 2016, 18, 16830–16839 RSC.
- S. D. Woodall, A. N. Swinburne, A. Kerridge, P. Di Pietro, C. Adam, P. Kaden and L. S. Natrajan, Chem. Commun., 2015, 51, 5402–5405 RSC.
- A. C. Behrle, A. Kerridge and J. R. Walensky, Inorg. Chem., 2015, 54, 11625–11636 CrossRef CAS PubMed.
- A. Formanuik, F. Ortu, R. Beekmeyer, A. Kerridge, R. W. Adams and D. P. Mills, Dalton Trans., 2016, 45, 2390–2393 RSC.
- A. Formanuik, F. Ortu, C. J. Inman, A. Kerridge, L. Castro, L. Maron and D. P. Mills, Chem. – Eur. J., 2016, 22, 17976–17979 CrossRef CAS PubMed.
- A. Formanuik, F. Ortu, J. Liu, L. Nodaraki, F. Tuna, A. Kerridge and D. P. Mills, Chem. – Eur. J., 2017, 23, 2290–2293 CrossRef CAS PubMed.
- A. Streitwieser, S. A. Kinsley, J. T. Rigsbee, I. L. Fragala, E. Ciliberto and N. Rosch, J. Am. Chem. Soc., 1985, 107, 7786–7788 CrossRef CAS.
- K. N. Raymond and C. W. Eigenbrot, Acc. Chem. Res., 1980, 13, 276–283 CrossRef CAS.
- A. Streitwieser, S. A. Kinsley, C. H. Jenson and J. T. Rigsbee, Organometallics, 2004, 23, 5169–5175 CrossRef CAS.
- C. Booth, M. Walter, M. Daniel, W. Lukens and R. Andersen, Phys. Rev. Lett., 2005, 95, 267202 CrossRef CAS PubMed.
- M. Dolg, P. Fulde, W. Küchle, C.-S. Neumann and H. Stoll, J. Chem. Phys., 1991, 94, 3011 CrossRef CAS.
- A. Kerridge, R. Coates and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 2896–2905 CrossRef CAS PubMed.
- A. Kerridge and N. Kaltsoyannis, C. R. Chim., 2010, 13, 853–859 CrossRef CAS.
- O. Mooßen and M. Dolg, Chem. Phys. Lett., 2014, 594, 47–50 CrossRef.
- A. Kerridge, Dalton Trans., 2013, 42, 16428–16436 RSC.
- B. B. Iversen, F. K. Larsen, A. A. Pinkerton, A. Martin, A. Darovsky and P. A. Reynolds, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 363–374 Search PubMed.
- V. V. Zhurov, E. A. Zhurova, A. I. Stash, A. Pinkerton and A. Alan, J. Phys. Chem. A, 2011, 115, 13016–13023 CrossRef CAS PubMed.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |