Open Access Article
Open Access ArticleWeak interactions within nitryl halide heterodimers†
David
Quiñonero
*a,
Antonio
Bauzá
a,
Goar
Sánchez-Sanz
 *b,
Cristina
Trujillo
*b,
Cristina
Trujillo
 c,
Ibon
Alkorta
d and
José
Elguero
d
c,
Ibon
Alkorta
d and
José
Elguero
d
aDepartament de Química, Universitat de les Illes Balears, Crta. de Valldemossa km 7.5, 07122 Palma de Mallorca, Spain. E-mail: david.quinonero@uib.es
bSchool of Chemistry, University College Dublin, Belfield, Dublin 4, Ireland. E-mail: goar.sanchez@ucd.ie
cSchool of Chemistry, Trinity Biomedical Sciences Institute, Trinity College Dublin, 152-160 Pearse St., Dublin 2, Ireland
dInstituto de Química Médica, CSIC, Juan de la Cierva, 3, E-28006 Madrid, Spain
First published on 25th July 2016
Abstract
A theoretical study of nitryl halide heterodimers has been carried out using SCS-RI-MP2 and CCSD(T) at the complete basis set (CBS) calculations. For this purpose, 66 heterodimers have been characterized as minima and arranged in six groups depending on the interactions involved and their geometrical arrangements. The CCSD(T)/CBS interaction energies vary between −0.6 and −11.1 kJ mol−1. The heavier the halogen atoms, the larger the interaction energies. Natural bond orbital (NBO) and “atoms-in-molecules” (AIM) theories were then used to analyze the complexes, confirming the presence of halogen, chalcogen, and π-hole interaction bonds. The largest charge-transfer energy contributions were found for halogen bonded complexes (up to 29.1 kJ mol−1). Furthermore, the physical nature of the interactions was studied using symmetry-adapted perturbation theory (SAPT) calculations, and it was concluded that dispersion was the major source of attraction, although electrostatics is important in halogen bonded complexes.
Introduction
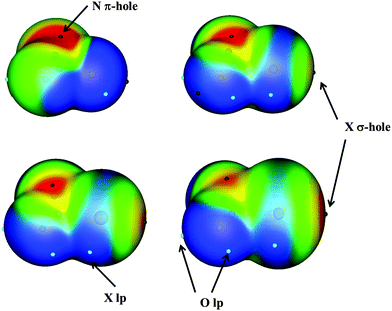
Non-covalent interactions between molecules have been shown to be of great importance in supramolecular chemistry, molecular biology, and even in materials science.1 Among the non-covalent interactions, the hydrogen bond (HB) is probably the most important. However, the number of non covalent interactions (also known as weak interactions) is not only limited to the HB but there is a broad range and type of those interactions including halogen bonds,2 hydride bonds,3 tetrels,4–6 chalcogen–chalcogen interactions7–10 and in the last decade, pnictogen interactions.11–36The electrostatic nature of some of these interactions, in particular halogen, chalcogen and pnictogen interactions, has been explained by the σ-hole concept developed by Politzer.37–39 The term σ-hole refers to the electron-deficient outer lobe of a p orbital involved in forming a covalent bond, in particular when one of the atoms is very electronegative. In the specific cases in which the positive electrostatic potential area is located perpendicular to a portion of a molecular plane, this region is called a π-hole. One example of an intermolecular weak interaction through the π-hole can be found in nitryl derivatives in which the nitrogen atom acts as an electron acceptor and may interact with electron donors. Furthermore, these types of interactions are also simultaneously classified as orthogonal and π-hole interactions.40,41
In recent decades, major interest has been shown towards the so-called reservoir compounds in the atmosphere. A great effort has been devoted to studying and understanding their molecular properties including isomerization processes and the role of their related formation reactions in stratospheric ozone depletion cycles42,43 and tropospheric halogen activation.44 Nitryl halides (XNO2), have been suggested to be examples of such reservoir species.45,46 The potential interactions of the XNO2 with NH3,47 NCH and CNH48 molecules as electron donors in the σ- and π-hole regions have been previously studied with XNO2 and other nitryl derivatives.49,50 Experimental evidence of non-covalent interactions involving nitryl moieties have been recently reported by Roy et al.51 In the present work, the attention has been focused on the nature of the non-covalent interactions found between nitryl halide heterodimers. Thus, the chemical groups attached to the nitryl moiety have been expanded along the halogen series, with bromine (Br), chlorine (Cl), fluorine (F) and iodine (I) atoms.
Computational details
All the geometries of the complexes formed by two XNO2 (X = F, Cl, Br or I) monomers were fully optimized using second order Møller–Plesset perturbation theory (MP2) with the aug-cc-pVTZ basis set.52,53 For heavy atoms, such as I,54 the aug-cc-pVTZ-PP pseudo potential basis set was used. Harmonic vibrational frequencies were computed at the same level used in order to verify that the structures obtained corresponded to local minima.For the preliminary calculations geometry optimizations were carried out using the spin-component scaled MP2 method (SCS-RI-MP2) with the aug-cc-pVTZ basis set and the energies were refined by using the couple cluster single double (triple)/complete basis set CCSD(T)/CBS method. The CCSD(T) technique provides reliable interaction energies only if they are combined with extended atomic orbital (AO) basis sets, and the larger the basis set, the better the interaction energies that result. Because of the rather strong dependence of the interaction energy on the AO basis set size, it is recommended that the relevant calculations be performed at the CBS limit. Different extrapolation schemes have been introduced and the scheme of Helgaker et al.55,56 has become the most widely used. Here, the Hartree–Fock (HF) and correlation (MP2) energies are extrapolated separately as follows:
| EHFX = EHFCBS + A e−αX | (1) |
| EMP2X = EMP2CBS + B X−3 | (2) |
| ECCSD(T)CBS = EHFCBS + EMP2CBS + (ECCSD(T) − EMP2)AVTZ | (3) |
Binding energies were obtained as the difference between the energy of the complex and the energy of the geometry optimized isolated nitryl halides.
The bonding characteristics were analyzed by means of the atoms in molecules (AIM) theory.
For this purpose the most relevant bond critical points (BCP) were located and the electron density at each of them was evaluated, using the AIMALL programs.57 All the interactions were characterized by the formation of a BCP between the atoms involved that are connected by the corresponding bond paths.
The natural bond orbital (NBO) method58 was employed to evaluate the atomic charges using the NBO 3.1 program, included within the Gaussian 09 program, and to analyze charge-transfer interactions between occupied and empty orbitals.
The symmetry adapted perturbation theory (SAPT)59 method allowed for the decomposition of the interaction energy into different terms related to physically well-defined components, such as those arising from electrostatic, exchange, induction, and dispersion terms. The interaction energy (Eint) can be expressed within the framework of the SAPT method as:
| Eint = E(1)el + E(1)exch + E(2)i + E(2)D | (4) |
The density fitting-density functional theory-SAPT (DF-DFT-SAPT) formulation has been used to investigate interaction energies. In this approach, the energies of the interacting monomers are expressed in terms of orbital energies obtained from Kohn–Sham DFT.60,61 In addition to the terms listed in eqn (4), a HF correction term δ(HF), which takes into account higher-order induction and exchange corrections, has been included.62 The DF-DFT-SAPT calculations were performed using the PBE0/aug-cc-pVTZ/aug-cc-pVTZ-PP computational method.63 Asymptotic corrections for this function were considered using the experimental values of the ionization potentials for nitryl fluoride (NO2F),64 and nitryl chloride (NO2Cl).65 In the remaining cases, the calculated values of the MP2/aug-cc-pVTZ computational values have been used. As auxiliary fitting basis set the JK-fitting basis of Weigend66 was employed. The cc-pVQZ JK-fitting basis was used for all atoms. For the intermolecular correlation terms, i.e., the dispersion and exchange-dispersion terms, the related aug-cc-pVTZ MP2-fitting basis of Weigend et al.,67 was employed. All these calculations were carried out using the MOLPRO quantum chemistry software.68
In order to provide a clear nomenclature, the complexes found have been sorted as follows: XYnz, where X and Y (X, Y = F, Cl, Br, or I) correspond to the halogen atoms of the interacting nitryl halides (XNO2 or YNO2), n (n = 1–6) is an ordinal which indicates the type of complex, and z (z = a, b) is an identifier which discriminates between two different configurations in the same type of complex. For example, FCl3a corresponds to a FNO2:ClNO2 complex in which F is the halogen electron donor moiety, whereas in FCl3b, chlorine is the atom interacting in the Lewis base moiety.
Results and discussion
Structure and energetics
Monomers have been extensively studied in the literature,47–50 and therefore will not be discussed in the present paper. However, it is worth mentioning that all the XNO2 present a π-hole over the N atom with molecular electrostatic potential (MEP) values of 154.9, 128.7, 119.5 and 75.4 kJ mol−1 for X = F, Cl, Br, and I, respectively, (Fig. 1).50 An additional σ-hole is observed in the halogen atoms along the X–N axis with MEP values of 64.9, 90.8 and 129.7 kJ mol−1 (X = Cl, Br and I, respectively), with the exception of FNO2 in which it was not found. So those two regions with positive values of MEP will be susceptible to a nucleophile attack. However, negative regions corresponding to halogen and oxygen lone pairs were also described, and therefore, they will act as electron donor regions in the nucleophile attacks.50A total of 66 heterodimer complexes have been found: 10 for each of the FCl, FBr and FI families and another 12 for each of the ClBr, ClI, and BrI families. Their Cartesian coordinates and molecular graphs are summarized in Table S1 (ESI†), and their geometries are depicted in Fig. 2.
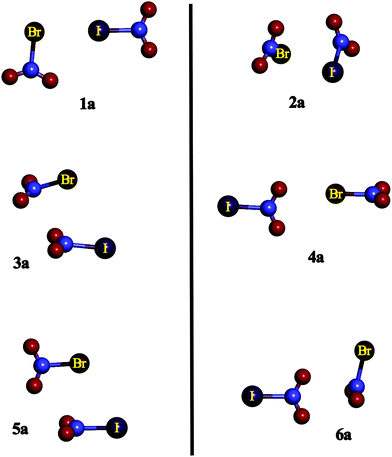 | ||
| Fig. 2 Summary of the geometries of the 1–6 complexes under study exemplified by the BrIa complexes. | ||
Complexes XY1a correspond to those in which an X atom is located pointing towards the σ-hole of Y, whereas in XY1b, the opposite orientation is observed. Complexes XY2a and XY2b show similar structures, in which the halogen atom of one of the molecules is facing the N atom of the other and vice versa. The main difference between both XY2a and XY2b is that in the former complexes, the structures are asymmetrical, whereas in the latter complexes Cs symmetry is found with a plane containing both X–N and Y–N bonds. XY3a corresponds to those structures with both interacting molecules parallel one to each other, i.e., their molecular planes are almost parallel, and X is acting as an electron donor and the N of the YNO2 molecule is acting as a Lewis acid. XY3b is similar to XY3a but in the former complexes Y is the electron donor. XY4a and XY4b complexes show one of the O atoms of the YNO2 moiety (or XNO2) pointing towards the X (or Y) σ-hole, respectively. XY5a and XY5b are similar to XY3a and XY3b but in the former complexes both molecular planes are perpendicular to each other. Finally, complexes XY6a are those in which oxygen atoms belonging to YNO2 are directly over the N π-hole of the XNO2 molecule with both molecular planes perpendicular to each other, whereas in XY6b the opposite is observed. It is worth noting that complexes 1b and 4a were not found for the FCl, FBr and FI families because no σ-hole was found near the F atom in the FNO2 molecule. Similar arrangements of the monomers were also found in the XNO2 homodimers in previous research,50 however, the number and complexity of the heterodimers are much larger than for the homodimers.
The interaction energies, Eb, at CCSD(T)/CBS (see computational details) of all 66 complexes are shown in Table 1. The complex with the highest interaction energy corresponds to BrI4b (−11.1 kJ mol−1) whereas the smallest one is found for FBr4b (−0.6 kJ mol−1). In general, the energy differences between “a” or “b” complexes within the same configuration is relatively small varying from 0.0–0.1 kJ mol−1 (ClBr5a–5b and ClBr3a–3b) up to 2.4 kJ mol−1 in the ClI4a–4b complexes. Considering the interaction energy range for each family of compounds, FCl (−9.0 to −5.2 kJ mol−1), FBr (−4.2 to −0.6 kJ mol−1), FI (−9.4 to −6.4 kJ mol−1), ClBr (−5.5 to −2.1 kJ mol−1), ClI (−10.4 to −7.0 kJ mol−1) and BrI (−11.1 to −9.4 kJ mol−1), the largest interaction energies are observed for iodine containing compounds, whereas those with bromine (with the exception of BrI) present the smallest Eb. In the heterodimers involving fluorine derivatives (FCl, FBr and FI) the strongest interactions correspond to 5b and 6a, in which π-hole interactions through the π-hole over the N atom in FNO2 occurred, the Y or O atom (YNO2) acted as the electron donor. This is consistent with the previously mentioned MEP values which indicate that FNO2 shows the most positive MEP value over the N atom (0.0590 a.u.), and therefore, it should be expected that those complexes involving a donation into the N π-hole would present the largest negative Eb. In the rest of compounds, Eb (ClBr2a) is the most negative (−5.50 kJ mol−1) with ClBr3a–b and ClBr6a at 0.1 kJ mol−1 and 0.2 kJ mol−1, respectively. In ClI and BrI, compounds 3b and 4b present the highest interaction energies. Curiously, compound 3a(b) shows a parallel disposition of the molecules (i.e., both molecular planes are parallel) whereas in 5a(b) both planes are perpendicular. In ClI3b and BrI3b, the molecules interact more strongly (−10.4 kJ mol−1 and −10.8 kJ mol−1) than is observed for ClI5b and BrI5b (−9.2 kJ mol−1 and −9.6 kJ mol−1), with up to 1.2 kJ mol−1 difference, which indicates that parallel structures are favoured.
| Compound | E b/CBS | Compound | E b/CBS | Compound | E b/CBS | Compound | E b/CBS | ||
|---|---|---|---|---|---|---|---|---|---|
| FCl | 1a | −5.2 | 1b | — | ClBr | 1a | −2.8 | 1b | −2.1 |
| 2a | −8.1 | 2b | −7.6 | 2a | −5.5 | 2b | −4.8 | ||
| 3a | −7.9 | 3b | −6.3 | 3a | −5.2 | 3b | −5.1 | ||
| 4a | — | 4b | −4.6 | 4a | −2.4 | 4b | −3.6 | ||
| 5a | −8.4 | 5b | −9.0 | 5a | −5.0 | 5b | −5.0 | ||
| 6a | −8.7 | 6b | −8.0 | 6a | −5.1 | 6b | −4.9 | ||
| FBr | 1a | −1.0 | 1b | — | ClI | 1a | −8.7 | 1b | −7.0 |
| 2a | −3.6 | 2b | −2.5 | 2a | −9.4 | 2b | −9.9 | ||
| 3a | −2.9 | 3b | −2.1 | 3a | −9.2 | 3b | −10.4 | ||
| 4a | — | 4b | −0.6 | 4a | −7.9 | 4b | −10.3 | ||
| 5a | −3.2 | 5b | −4.2 | 5a | −9.4 | 5b | −9.2 | ||
| 6a | −4.1 | 6b | −2.9 | 6a | −10.3 | 6b | −9.3 | ||
| FI | 1a | −6.8 | 1b | — | BrI | 1a | −10.6 | 1b | −9.4 |
| 2a | −7.9 | 2b | −7.5 | 2a | −10.5 | 2b | −10.0 | ||
| 3a | −8.4 | 3b | −6.4 | 3a | −9.8 | 3b | −10.9 | ||
| 4a | — | 4b | −6.9 | 4a | −10.1 | 4b | −11.1 | ||
| 5a | −7.8 | 5b | −8.8 | 5a | −9.8 | 5b | −9.6 | ||
| 6a | −9.4 | 6b | −8.1 | 6a | −10.4 | 6b | −9.7 | ||
Electronic properties
The electron density (ρBCP) of the different complexes was determined using the atoms in molecules (AIM) theory and the molecular graphs which were generated of all the interactions within the complexes are shown in the Table S1 (ESI†). Table S2 (ESI†) summarizes the electron density at the BCP (ρBCP) and the Laplacian (∇2ρBCP) values for each interaction.As observed, four different types of interactions were found within XNO2:YNO2 complexes all of them characterized by the existence of a BCP and a bond path connecting two atoms. These interactions were: halogen bonds between both halogen atoms, X⋯Y, π-hole interactions in which the halogen X or Y atom of one molecule acts as a electron donor and N atom as an acceptor, X⋯N, chalcogen bonds between oxygen atoms of both moieties, O⋯O, X⋯O interactions in which the oxygen is interacting with the X atoms through the σ-hole.
Complexes 1a and 1b are characterized either by a single halogen bond or by a halogen bond plus one X⋯O. However, in those X⋯O interactions found using AIM, X and O atoms are longer than the sum of their van der Waals (vdW) radii, thus these X⋯O contacts cannot be classified as charge transfer interactions. Complexes 2a are stabilized by different type of interactions, FCl2a shows F⋯N, Cl⋯N and additional O⋯O interactions, whereas in FBr2a only F⋯N and O⋯O interactions are present. In the FI2a complex, no π-hole interaction was found but F⋯I and O⋯O interactions were. However, the distance between F and I is 3.592 Å, which is greater than the sum of the vdW radii (3.45 Å).69 The rest of the 2a complexes show a similar number and type of interactions, X⋯N, Y⋯N, X⋯Y and O⋯O interactions. Nevertheless, the X⋯Y interactions found were not classified as stabilizing interactions because the interacting distance is as stated previously, longer that the sum of the vdW radii. In complexes 2b, fluorine derivatives, FCl2b, FBr2b and FI2b present different interactions: FCl (two π-holes X⋯N and Y⋯N), FBr (a single Br⋯N interaction) and FI (F⋯N and F⋯I contacts, and the last one is 0.14 Å longer than the sum of the vdW radii), whereas in ClF, ClI and BrI similar interactions (X⋯N, Y⋯N and X⋯Y) are found to be characterized by the presence of a BCP. Again, as it occurs in complexes 2a, those X⋯Y contacts are not categorized as stabilizing interactions.
Complexes FBr3a and FI3a show F⋯N (π-hole) interactions with a BCP and bond path connecting both atoms, in addition to two parallel O⋯O interactions. However, in FCl3a, ClBr3a, ClI3a and BrI3a complexes, the BCP connecting X and N is not present. Furthermore, those BCPs are not even found in any of the complexes 3b, except for FI3b. Instead X⋯O interactions are revealed.
Complexes 4a and 4b are characterized by the presence of a single BCP between the oxygen atom of moiety X(Y) and the corresponding halogen atom of the opposite monomer Y(X)NO2. For complexes 5a and 5b, similar interactions are found to those in complexes 2a. X⋯N interactions are only present in half of the cases (FCl5a, ClBr5a, FCl5b, FBr5b, ClBr5b and BrI5b). Additionally, bifurcated O⋯O interactions are shown involving two oxygen atoms from one monomer and one oxygen atom from the other moiety.
Finally both complexes 6a and 6b simultaneously exhibit one O⋯N and bifurcated O⋯O interactions. In all cases, O⋯N distances are shorter than the sum of vdW radii and show BCPs between the interacting atoms.
Distance values, ρBCP, ∇2ρ and total electron density energy, H, for all the interactions are summarized in Tables S2–S4 (ESI†) and maxima and minima values are shown in Table 2. As observed, the X⋯Y interaction distance ranges from 2.999 Å (FI1b) to 4.197 Å (BrI2b). In particular, those with shorter X⋯Y distances correspond to 1a and 1b complexes, which present a single X⋯Y interaction through the halogen σ-hole. X⋯N and O⋯N interactions, classified as π-holes, present distances between 2.844–3.757 Å, showing a wider range than in X⋯Y interactions (2.945–3.037 Å). O⋯O and X⋯O interactions show O⋯O and X⋯O distances longer than the sum of the vdW radii, so they are not catalogued as chalcogen interactions, but rather as vdW interactions. For the electron density at the BCPs, the range observed shows that all the interactions correspond to non-covalent interactions. Special attention should be paid to the O⋯O and X⋯O where values relatively close to 0.002 a.u. are observed, indicating such interactions are within the range of vdW interactions. Laplacian values, ∇2ρ, are positive and range from 0.0058 to 0.0271 a.u., indicating close shell interactions.
| X⋯Y | X⋯N | O⋯O | X⋯O | O⋯N | |
|---|---|---|---|---|---|
| R min | 2.999 | 2.844 | 3.066 | 3.064 | 2.945 |
| R max | 4.197 | 3.757 | 3.369 | 3.761 | 3.037 |
| ρ min | 0.0042 | 0.0040 | 0.0030 | 0.0029 | 0.0056 |
| ρ max | 0.0130 | 0.0073 | 0.0058 | 0.0111 | 0.0073 |
| ∇2ρmin | 0.0128 | 0.0158 | 0.0134 | 0.0112 | 0.0271 |
| ∇2ρmax | 0.0485 | 0.0388 | 0.0259 | 0.0436 | 0.0345 |
| H min | 0.0006 | 0.0010 | 0.0006 | 0.0006 | 0.0016 |
| H max | 0.0017 | 0.0022 | 0.0014 | 0.0019 | 0.0020 |
| Exp. R2 (R vs. ρ) | 0.57 | 0.82 | 0.92 | 0.65 | 0.55 |
| Exp. R2 (R vs. ∇2ρ) | 0.71 | 0.96 | 0.93 | 0.82 | 0.78 |
| Exp. R2 (R vs. H) | 0.44 | 0.88 | 0.87 | 0.83 | 0.62 |
In terms of total electron energy density, it has been demonstrated that the sign of the total energy, H, defined as G + V, is an indicator of the amount of covalence in chemical interactions.70–72 Thus, negative H values indicate a significant sharing of electrons. However, H values found within the all complexes are positive which may suggest poor electron sharing between monomers.
Exponential relationships between the Laplacian values, ∇2ρ, at the BCP and the interatomic distance R were found and are shown in Fig. 3 for each family of X⋯N, and O⋯O interactions. The best exponential correlations were found for Cl⋯N and Br⋯N interactions with R2 = 0.99. Similar exponential relationships were found between R versus ρ and R versus ∇2ρ in the XNO2 homodimers and similar non-covalent interactions.8,34,49,73–81 Nevertheless, as observed in Table 2, no fair correlations between ρ and interatomic distance have been found, with the exception of the O⋯O interactions where the correlation coefficient R2 is 0.92.
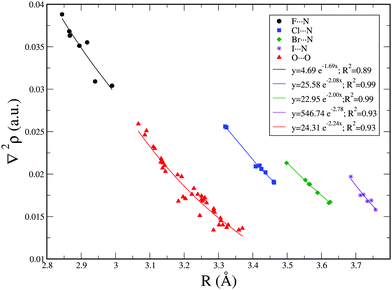 | ||
| Fig. 3 Exponential relationship between X⋯N and O⋯O intermolecular distance (R) and Laplacian of the electron density at the BCP (∇2ρ). | ||
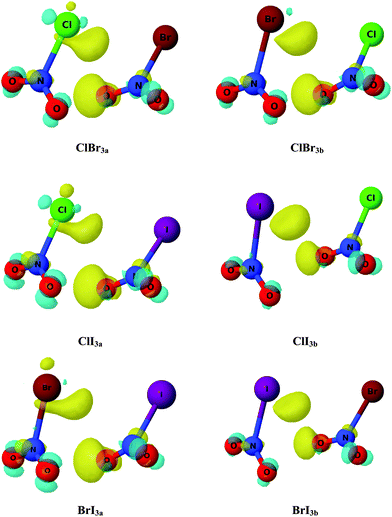
In order to achieve further description of the changes in the electron density upon complexation, electron density shift (EDS) maps were obtained and are shown in Fig. 4 for a set of complexes. The yellow (positive) areas correspond to those regions with an increase of electron density, whereas the cyan (negative) counterparts represent those areas with a loss of electron density upon complexation. As observed in Fig. 3, complexes ClBr3a–b, ClI3a–b and BrI3a–b, in which the AIM results show BCPs between oxygen atoms, exhibit a yellow region around the oxygen atom (right-hand monomer) indicating an increase of the electron density on that atom. Additionally, another yellow area is also observed in the halogen atom (left-hand monomer) which again shows evidence of an increase of the electron density generated by the interaction through the halogen atom. Furthermore, small cyan (negative) areas are found in the rest of the oxygen atoms showing a decrease of the electron density and which are consistent with the AIM predictions. However, it is worth noting that the small areas found in addition to the small isodensity value (0.0005 a.u.) indicate very small changes in the electron density upon complexation and therefore very weak interactions in those particular complexes. It is worth noting that similar EDS maps were also found for XNO2 homodimers, which indicates the same nature of each interaction in both homo- and hetero-dimers.
All possible intermolecular interactions between occupied (donor) Lewis-type NBOs and vacant (acceptor) non-Lewis NBOs for the nitryl halide heterodimers have been examined and their energetic importance was estimated using second-order perturbation theory. In Table 3 only the donor–acceptor interactions with second-order perturbation stabilization energies larger than 0.5 kJ mol−1 have been included.
| System | E(2) | ||||
|---|---|---|---|---|---|
| XYnz | X(Y)lp → σ*N–Y(X) | σN–X(Y) → Ry*Y(X) | |||
| FCl1a | 4.2 | — | |||
| FCl1b | — | — | |||
| FBr1a | 5.8 | — | |||
| FBr1b | — | — | |||
| FI1a | 15.5 (1.0) | — | |||
| FI1b | — | — | |||
| ClBr1a | 10.5 | (1.8) | |||
| ClBr1b | (7.6) | — | |||
| ClI1a | 22.6 (1.5) | (1.5) | |||
| ClI1b | (12.6) | — | |||
| BrI1a | 29.1 (2.0) | (1.6) | |||
| BrI1b | 0.9 (22.7) | 2.7 (2.7) | |||
| X(Y)lp → π*N–O | σN–Y → Ry*X | Olp → Olp | Xlp → Olp | ||
| FCl2a | 1.4 (1.3) | — | 2.1 | — | |
| FCl2b | 1.3 (1.3) | — | — | — | |
| FBr2a | 0.9 (1.1) | — | 1.1 | — | |
| FBr2b | (0.9) | — | — | — | |
| FI2a | 0.8 (1.3) | — | 0.7 | — | |
| FI2b | 1.3 (1.2) | — | — | — | |
| ClBr2a | 0.9 (0.9) | — | — | — | |
| ClBr2b | 0.9 (0.8) | — | — | 0.8 | |
| ClI2a | 0.8 (1.1) | — | — | — | |
| ClI2b | 0.8 (0.9) | — | — | — | |
| BrI2a | 0.8 (1.0) | — | — | — | |
| BrI2b | 0.8 (0.9) | 0.6 | — | — | |
| X(Y)lp → π*N–O | Olp → Olp | Olp → Olp* | Xlp → Olp | Olp → π*Nx(y)–O | |
| FCl3a | — | — | — | — | — |
| FCl3b | — | — | 3.5 | — | — |
| FBr3a | — | — | — | — | — |
| FBr3b | — | — | 1.6 | — | — |
| FI3a | 1.0 | 1.7 | — | — | 0.6 |
| FI3b | — | — | 1.3 | — | — |
| ClBr3a | 1.0 | (1.0 & 1.2) | — | — | (1.8) |
| ClBr3b | (1.0) | 0.8 & 0.9 | — | — | 1.5 |
| ClI3a | 1.2 | — | — | 2.1 | (2.5) |
| ClI3b | (1.1) | 0.6 & 0.6 | — | — | 1.5 |
| BrI3a | 1.0 | — | — | — | (2.3) |
| BrI3b | (1.1) | 0.8 & 0.6 | — | — | 1.5 |
| σN–X(Y) → Ry*O | Olp → σ*N–Y(X) | Olp → X(Y)lp | |||
| FCl4a | — | — | — | ||
| FCl4b | — | 4.2 | — | ||
| FBr4a | — | — | — | ||
| FBr4b | — | 5.6 & 1.7 | — | ||
| FI4a | — | — | — | ||
| FI4b | — | 10.7 | — | ||
| ClBr4a | — | (5.2) | 0.8 | ||
| ClBr4b | (1.3) | 8.2 | — | ||
| ClI4a | — | (6.1) | (1.0) | ||
| ClI4b | (0.9) | 15.6 & 0.9 | — | ||
| BrI4a | 1.4 | (10.9 & 0.7) | 0.7 | ||
| BrI4b | (0.8) | 17.2 & 1.0 | — | ||
| X(Y)lp → π*N–O | Olp → Olp | X(Y)lp → σ*N–Y(X) | Xlp → Olp | ||
| FCl5a | 1.4 | 1.0 | — | — | |
| FCl5b | (0.8) | (2.2) | — | — | |
| FBr5a | — | 2.0 | (0.6) | — | |
| FBr5b | (0.8) | 3.7 (2.6) | — | — | |
| FI5a | — | 0.8 | (1.1) | — | |
| FI5b | (0.9) | (1.5) | — | — | |
| ClBr5a | 0.9 | 1.1 (0.6 & 0.6) | (0.8) | 0.7 | |
| ClBr5b | (0.8) | (1.3) | — | — | |
| ClI5a | 1.0 | 0.9 | (1.5) | — | |
| ClI5b | (0.9) | 1.9 (2.8) | — | — | |
| BrI5a | 0.9 | 0.9 | (1.2) | — | |
| BrI5b | (0.9) | (2.2) | — | — | |
| Olp → π*N–O | Olp → Olp | ||||
| FCl6a | (1.1) | (1.9 & 0.7) | |||
| FCl6b | 1.1 | 2.7 | |||
| FBr6a | (1.3) | (2.0) | |||
| FBr6b | 1.0 | 1.5 & 0.9 | |||
| FI6a | (1.0) | (2.3) | |||
| FI6b | 1.7 | 0.9 & 0.7 | |||
| ClBr6a | (1.6) | (1.0) | |||
| ClBr6b | 1.5 | 2.9 & 0.8 | |||
| ClI6a | (1.7) | (1.5) | |||
| ClI6b | 1.6 | 1.3 & 0.7 | |||
| BrI6a | (1.6) | (1.3) | |||
| BrI6b | 1.7 | 1.4 & 0.8 | |||
According to the NBO analysis, the interaction in 1a and 1b complexes is almost exclusively based on a charge donation from a lone pair of electrons of a halogen atom to the vacant antibonding orbital of the sigma bond between the second halogen and nitrogen atoms, the σ-hole, as derived from the calculated second-order orbital perturbation energies, E(2), listed in Table 3. These σ-hole interactions are characteristic of the halogen bonds, which the molecules are entangled in. In fact, these charge-transfer contributions are very large for most of the cases, with increasing energies from the lightest to the heaviest halogen atoms. For example, when Cl acts as a Lewis acid and F, Br, and I as Lewis bases the E(2) values are 4.2, 7.6, and 12.6 kJ mol−1, respectively. Similarly, when Br acts as a Lewis acid E(2) values are 5.8, 10.5, and 22.7 kJ mol−1 for F, Cl, and I Lewis bases, respectively, which are substantially larger values than those for the electron acceptor Cl. The largest E(2) values (15.5, 22.6, and 29.1 kJ mol−1) are observed for the lp(F, Cl, Br) → σ*(I–N) donor–acceptor contributions, respectively. Complexes with the largest E(2) values correspond to those with the largest binding energies, suggesting that these contributions are significant in such cases. In addition, there are the corresponding back bonding σ-hole interactions in FI1a, ClI1a, BrI1a, and BrI1b, with E(2) values between 0.9 and 2.0 kJ mol−1 and, therefore, these are less relevant than the values of their counterparts because their respective σ-holes are not oriented towards the halogen lone pairs. It is worth mentioning the existence of other charge-transfer contributions of up to 2.7 kJ mol−1 that arise from the charge donation from N–Y sigma bond to the Rydberg unfilled orbital of halogen X (Table 3). The main findings of the NBO results are in agreement with the results of the AIM calculations for 1a and 1b complexes that show the existence of one BCP connecting both halogen atoms, corresponding to the halogen bond. However, NBO calculations do not show X⋯O charge-transfer interactions, a finding which is in agreement with the AIM analysis that shows that the associated BCP is indicative of proximity.
The NBO analysis of the 2a and 2b compounds presents the following general results. Firstly, the main charge-transfer contributions arise from π-hole contacts where a lone pair of a halogen interacts with a π* orbital of an N–O bond (Table 3) and are common in all complexes. In fact there are not one but two π-hole contacts, i.e., one where a halogen atom lone pair of the first nitryl halide interacts with the π*(N–O) orbital of the second nitryl halide, and another one where a halogen atom lone pair of the second nitryl halide interacts with the π*(N–O) orbital of the first nitryl halide (Table 3, values in parentheses). Secondly, the second-order orbital perturbation energies associated with these π-hole contacts are very small in comparison to the ones obtained for the σ-hole halogen bonding interactions in 1a and 1b complexes. Indeed the corresponding E(2) values are around 1 kJ mol−1. It is worth stressing the existence of other small contributions (from 0.6 to 2.1 kJ mol−1) that arise from charge donations from a lone pair of an O atom to a lone pair of another O atom in fluorine-containing complexes, for example, FCl2a, FBr2a, and FI2a, from the σ(N–I) orbital to the Rydberg unfilled orbital of Br in BrI2b, and from a lone pair of Cl to a lone pair of an O atom in ClBr2b. Interestingly, when comparing NBO and AIM results, it was observed that in general both π-hole contacts were identified by the presence of BCP for X⋯N and Y⋯N interactions for 1a and 1b complexes. Furthermore, AIM calculations showed the existence of BCPs between O atoms, as observed in the NBO study. However, the X⋯Y long contacts identified by BCPs were not observed in the NBO analysis thus reaffirming that these interactions cannot be categorized as stabilizing.
Compounds 3 and 5 are characterized by similar charge-transfer interactions because of their geometrical similarity, as derived from the NBO results shown in Table 3. Therefore, these complexes present π-hole interactions between the π*(N–O) orbital and a lone pair of a halogen atom, charge donations from a lone pair of an O atom to a lone pair of another O atom, which are in general reflected in the AIM results by the presence of BCPs. Furthermore, 3 and 5 present a lone pair of Cl interacting with a lone pair of an O atom only in ClI3a and ClBr5a. The AIM results show BCPs for the halogen–oxygen contacts in all complexes suggesting that both atoms are not close enough for charge transfer interactions to occur. In fact only ClI3a and ClBr5a show halogen–oxygen contact distances smaller than the respective sum of their vdW radii. Unlike compounds of 5, compounds of 3, especially those without fluorine, include Olp → π*(N–O) donor–acceptor π-hole contributions. In the same way, compounds of 5 (actually only compound 5a) include Ylp → σ*(N–X) σ-hole contributions that are not present in compounds of 3. In addition, compounds of 5 have more Olp → Olp contributions than compounds of 3 because oxygen atoms in 5 are much closer than in 3. The E(2) values associated with all the previously mentioned interactions are relatively small, around 1 kJ mol−1, except for Olp → π*(N–O) and Olp → Olp donor–acceptor contributions in 3 and 5 that are as large as 2.5 and 3.7 kJ mol−1, respectively. In fact, the latter interactions are slightly larger for 5b complexes than for 5a complexes. In agreement with the NBO results, the AIM analysis reveals BCPs for these contacts.
Similarly, to compounds 1a and 1b, compounds 4a and 4b exhibit typical halogen bond σ-hole interactions based on the charge donation from the lone pair of an oxygen atom to a σ* orbital of a N-halogen bond, as can be inferred from the E(2) values (Table 3). Similarly, these charge-transfer contributions are large, compared to those observed for compounds 2, 3 and 5. The larger the halogen atom acting as a Lewis acid the larger the energy contribution, as also observed in compounds 1a and 1b, although they are larger for the latter than for the former compounds. Thus, the largest E(2) values (15.6 and 17.2 kJ mol−1) are observed mainly when iodine acts as the halogen bond donor (ClI4b and BrI4b, respectively). It is interesting to note the presence of other less important contributions with E(2) values up to 1.4 kJ mol−1. These charge-transfer phenomena are based, firstly, on the N–X(Y) σ bond to a Rydberg unfilled orbital of an oxygen atom donor–acceptor interaction (Table 3) and, secondly, on the oxygen lone pair and a halogen lone pair donor–acceptor interaction, the latter only for complexes of 4a excluding fluorine and the former only for complexes of 4b excluding fluorine and BrI4a. There is a good agreement between the NBO and AIM calculations where the halogen bond is characterized by the presence of a BCP connecting both atoms involved.
The NBO analysis of compounds 6a and 6b shows all the contacts previously noted by the presence of BCPs in the AIM calculations. Therefore, Olp → π*(N–O) π-hole and Olp → Olp charge-transfer interactions are observed for all complexes. The associated E(2) values for these interactions are relatively small, in line with those previously reported for compounds 2, 3, and 5. Thus, E(2) values for the π-hole contribution are approximately 1.5 kJ mol−1, whereas more diverse values are obtained for the Olp → Olp contribution, ranging from 0.9 to 2.9 kJ mol−1.
The total charge transfer was evaluated using NBO methodology (Table S5, ESI†). Complexes 2a and 2b, which exhibit symmetrical interaction between both monomers, do not present charge transfer between them. As expected, the largest charge transfers are observed for complexes with the largest E(2) values, i.e., 1 and 4, with a maximum for BrI1a (−0.04 e). In complexes 3 and 5, a very similar charge transfer occurs which is in agreement with the E(2) orbital interaction energies. Furthermore, charge transfer is larger for 3a and 5a complexes (0.0015–0.0035 e) than for 3b and 5b complexes (0.0001–0.0016 e). This is in agreement with the type of interaction found and the AIM and NBO results. Similarly, complex 6 shows a charger transfer ranging from 0.0002 to 0.0046 e, which is larger for 6a than for 6b.
The physical nature of the interaction in the nitryl halide heterodimers was determined using SAPT-DFT calculations. The energy contributions obtained from the SAPT partitioning scheme are listed in Table 4 and the corresponding attractive terms are shown in Fig. 5. In general, the dispersion component, ED, is the largest attractive contributor to the interaction with values ranging from −6.1 (FBr4b) to −18.1 (BrI2a) kJ mol−1. Of the total attractive forces the dispersion term varies from 37.1% (BrI1a) to 76.6% (FI3b). The electrostatic contribution, Eel, is the second term in importance with values ranging from −2.7 (FBr4b) to −16.5 (BrI1a) kJ mol−1. The relative weight of the electrostatic term within all the attractive forces varies from 18.8% (FI3b) to 47.7% (FCl1a). In fact this term becomes the most important contribution, overcoming the dispersion term, in three σ-hole based complexes that contain iodine as electron acceptor, namely, FI1a, ClI4b and BrI4b. However, the induction term is very small and more or less constant (usually from −0.3 to −1.5 kJ mol−1). Exceptions are the halogen bonded complexes FI4b, BrI1b, FI1a, ClI4b, BrI4b, and BrI1a with induction energies of −2.5, −3.6, −4.0, −5.0, −6.0, −8.2, and −11.9 kJ mol−1 which never overcome either the dispersion or electrostatic terms. All in all, the induction term varies from 1.8% (FCl5a) to 26.3% (BrI1a) of the total attractive forces.
| Family | Comp. | E el | E exch | E i | E D | δ(HF) | E SAPT |
|---|---|---|---|---|---|---|---|
| FCl | 1a(b) | −8.0 | 12.3 | −0.8 | −8.0 | −0.7 | −5.1 |
| 2a(b) | −9.5 (−6.2) | 18.8 (11.0) | −1.1 (−0.7) | −14.9 (−10.1) | −0.5 (−0.4) | −7.2 (−6.5) | |
| 3a(b) | −5.8 (−3.7) | 12.2 (13.0) | −0.7 (−0.6) | −11.8 (−12.3) | −0.2 (−0.3) | −6.4 (−3.9) | |
| 4a(b) | (−3.7) | (8.5) | (−0.5) | (−6.9) | (−0.5) | (−3.2) | |
| 5a(b) | −5.6 (−7.4) | 10.6 (14.9) | −0.3 (−0.6) | −10.6 (−12.6) | −0.7 (−0.5) | −6.5 (−6.2) | |
| 6a(b) | −6.9 (−4.7) | 13.1 (12.1) | −0.7 (−0.5) | −11.1 (−11.6) | −0.4 (−0.3) | −6.0 (−5.0) | |
| FBr | 1a(b) | −4.9 | 8.4 | −0.4 | −6.6 | −1.2 | −4.7 |
| 2a(b) | −7.7 (−10.1) | 12.3 (16.9) | −1.2 (−1.3) | −13.9 (−13.4) | −0.5 (−0.2) | −11.2 (−8.1) | |
| 3a(b) | −5.1 (−4.5) | 9.9 (16.4) | −0.6 (−0.9) | −10.4 (−14.0) | −0.3 (−0.3) | −6.5 (−3.3) | |
| 4a(b) | (−2.7) | (6.5) | (−0.3) | (−6.1) | (−0.8) | (−3.3) | |
| 5a(b) | −8.8 (−6.7) | 17.0 (13.2) | −0.6 (−0.7) | −13.4 (−12.0) | −0.5 (−0.5) | −6.4 (−6.7) | |
| 6a(b) | −5.9 (−4.4) | 11.7 (10.7) | −0.7 (−0.5) | −10.7 (−10.7) | −0.4 (−0.4) | −6.0 (−5.3) | |
| FI | 1a(b) | −12.0 | 12.1 | −4.0 | −10.2 | −0.6 | −14.7 |
| 2a(b) | −7.4 (−8.2) | 17.0 (17.4) | −1.0 (−1.1) | −14.4 (−13.7) | −0.4 (−0.3) | −6.1 (−5.8) | |
| 3a(b) | −8.1 (−3.3) | 15.7 (14.3) | −1.0 (−1.1) | −13.9 (−14.3) | −0.4 (−0.2) | −7.7 (−3.4) | |
| 4a(b) | (−6.9) | (14.2) | (−2.5) | (−9.6) | (−0.0) | (−4.7) | |
| 5a(b) | −7.0 (−7.9) | 13.8 (15.5) | −0.4 (−0.8) | −12.2 (−13.2) | −0.4 (−0.5) | −6.6 (−6.9) | |
| 6a(b) | −9.2 (−5.5) | 15.1 (13.4) | −0.8 (−0.6) | −7.4 (−12.6) | −0.6 (−0.5) | −7.4 (−5.8) | |
| ClBr | 1a(b) | −6.9 (−4.9) | 14.6 (11.8) | −1.0 (−0.5) | −10.1 (−9.0) | −1.8 (−1.5) | −5.2 (−4.1) |
| 2a(b) | −7.4 (−7.1) | 18.9 (16.3) | −0.8 (−0.7) | −16.7 (−14.4) | −0.6 (−0.4) | −6.5 (−6.3) | |
| 3a(b) | −6.7 (−6.1) | 17.6 (17.0) | −1.0 (−0.9) | −15.8 (−15.5) | −0.6 (−0.5) | −6.4 (−5.9) | |
| 4a(b) | −5.1 (−6.7) | 10.3 (12.6) | −0.4 (−0.8) | −7.8 (−8.8) | −1.2 (−1.5) | −4.3 (−5.2) | |
| 5a(b) | −7.0 (−7.0) | 16.2 (16.1) | −0.5 (−0.5) | −14.4 (−14.2) | −0.6 (−0.6) | −6.4 (−6.2) | |
| 6a(b) | −7.2 (−6.5) | 14.8 (14.1) | −0.5 (−0.5) | −12.6 (−12.6) | −0.6 (−0.6) | −6.1 (−6.0) | |
| ClI | 1a(b) | −14.3 (−6.4) | 25.4 (15.6) | −8.2 (−1.5) | −15.1 (−10.8) | 2.1 (−2.0) | −10.0 (−5.1) |
| 2a(b) | −7.1 (−7.1) | 16.7 (19.2) | −1.0 (−1.2) | −15.2 (−17.6) | −0.2 (−0.3) | −6.8 (−7.0) | |
| 3a(b) | −5.5 (−7.9) | 17.2 (18.8) | −1.0 (−1.4) | −16.4 (−17.4) | −0.3 (−0.5) | −6.0 (−8.3) | |
| 4a(b) | −6.5 (−12.5) | 11.4 (20.7) | −0.6 (−5.0) | −8.5 (−12.4) | −1.6 (0.3) | −5.8 (−8.9) | |
| 5a(b) | −7.3 (−7.2) | 17.1 (16.9) | −1.1 (−1.0) | −15.5 (−15.3) | −0.2 (−0.3) | −7.1 (−6.9) | |
| 6a(b) | −8.3 (−6.6) | 15.1 (14.4) | −0.7 (−0.6) | −13.1 (−13.3) | −0.7 (−0.6) | −7.7 (−6.7) | |
| BrI | 1a(b) | −16.5 (−10.7) | 29.3 (23.3) | −11.9 (−3.6) | −16.7 (−13.8) | 4.4 (−2.9) | −11.4 (−7.6) |
| 2a(b) | −7.2 (−7.5) | 19.3 (16.8) | −1.4 (−1.1) | −18.1 (−15.7) | −0.1 (0.0) | −7.4 (−7.4) | |
| 3a(b) | −5.9 (−7.5) | 18.0 (18.8) | −1.1 (−1.4) | −17.3 (−17.8) | −0.2 (−0.3) | −6.5 (−8.2) | |
| 4a(b) | −10.2 (−14.4) | 16.6 (23.0) | −1.3 (−6.0) | −10.6 (−13.4) | −2.6 (0.5) | −8.1 (−10.2) | |
| 5a(b) | −7.0 (−7.2) | 17.0 (17.4) | −1.4 (−1.2) | −15.8 (−15.9) | 0.1 (0.0) | −7.1 (−7.0) | |
| 6a(b) | −8.1 (−7.1) | 15.4 (15.5) | −0.6 (−0.7) | −13.6 (−14.0) | −0.8 (−0.7) | −7.7 (−6.9) | |
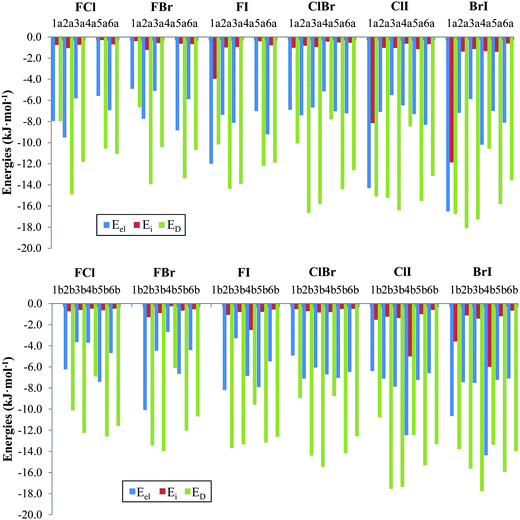 | ||
| Fig. 5 Graphical representation of the attractive energy contributions in a (top) and b (bottom) complexes using the SAPT-DFT partitioning scheme (see text for details). | ||
Next, all the compounds of the series will be considered separately. In the halogen bonded complexes 1 and 4, all three attractive terms have their own importance depending on which complex is being studied. For example, in FY1a, ClI1a, and BrI1a and ClI4b, BrI4a, and BrI4b complexes the electrostatic contribution is very similar to the dispersion contribution. As a general trend the relative importance of the electrostatic contribution increases as the atoms become heavier, leading to cases where the electrostatic term is even somewhat larger than the dispersion term (ClI4b and BrI4b). For the rest of the complexes the dispersion term is always larger than the electrostatic term. However, the induction contribution is generally small except for the previously mentioned cases of FI1a (−4.0 kJ mol−1), ClI4b (−5.0 kJ mol−1), BrI4b (−6.0 kJ mol−1), ClI1a (−8.2 kJ mol−1) and BrI1a (−11.9 kJ mol−1), in other words, for those complexes where the iodine atom (the one with the largest σ-hole) acts as a Lewis acid. Even in the most ideal situation, BrI1a, the induction contribution represents only 26.3% of all the attractive forces.
For the rest of the complexes, 2, 3, 5, and 6, the induction contribution is significantly small, ranging from −0.3 kJ mol−1 to −1.4 kJ mol−1, representing between 1.8% and 5.7% of all the attractive forces, respectively. Because this term is almost negligible it has not been taken into consideration for the following discussion. In compounds 2a and 2b, the dispersion term is twice as large as the electrostatic contribution, with the exception of the FY2b compounds where the electrostatic term is slightly lower than the dispersion one. Similarly, in compounds 5 and 6 the dispersion term is twice the electrostatic contribution, with the exception of FI6a where the latter is slightly lower than the former. Lastly, the most important dispersion contribution is found in the series of 3a and 3b compounds, FY3b, ClI3a, and BrI3a, which is three times as large as the electrostatic term, reaching relative weights of 76.6% for FI3b. For the rest of the compounds of 3, the dispersion contribution is approximately double the value of the electrostatic one. The δ(HF) term in general is very small and only significant values are obtained (>2 kJ mol−1) for ClI1a (2.1 kJ mol−1), BrI1a (4.4 kJ mol−1), and BrI1b (−2.9 kJ mol−1), as would be expected for the complexes with the highest induction contributions.
Conclusions
In summary, the interaction between two units of different nitryl halides have been studied using SCS-RI-MP2 and CCSD(T) calculations. As a result, a total of 66 nitryl halide heterodimers were obtained which were divided into six families of complexes according to the interactions involved and how the molecules were arranged. Initially 72 heterodimers could be expected, 12 for each group. However, six of these complexes where fluorine acts as a halogen bond donor could not be obtained because fluorine lacks the σ-hole in NO2F.XNO2 dimers have shown different types of interactions simultaneously which show the flexibility of XNO2 molecules to adopt different configurations upon complexation. These interactions have been categorized as halogen bonds with different donors X⋯Y and O⋯X, chalcogen bonds O⋯O and π-hole interactions X⋯N.
The binding energy for the series of dimers varies between −0.6 and −11.1 kJ mol−1. In general, the strongest complexes were those exhibiting halogen or π-hole interactions in which the more electronegative atoms are located in the donor and acceptor moiety, respectively. This is explained in terms of the electrostatic nature of the σ-holes (halogen bonds) or π-holes. In the former, the acceptor moiety bears the more polarizable atom (Y) and therefore the σ-hole is deeper than in the donor moiety (X). In the latter, it is the larger electronegativity of the halogen atom (XNO2), which withdraws a larger electron density from the N site, making the π-hole deeper than in YNO2.
In absolute terms complexes FBr and ClBr have the least negative interaction energies and the general trend obtained was that the heavier the halogen atoms, the larger the interactions energies. Therefore, the larger binding energies are found for BrI complexes, specifically for the halogen bonded BrI4b.
The AIM analysis confirmed the four different types of interactions for the series of complexes. In those complexes with only halogen bonds (complexes 1 and 4), Laplacian and electron density at the bond critical points increase with the size of the halogen atom and this was considered to be indicating a relationship between the interaction energies and the electron density at the BCP. For the rest of the complexes similar values were obtained for the X⋯N, Y⋯N, and N⋯O π-hole interactions. No trend was observed for the chalcogen interactions. Furthermore, exponential relationships were found between Laplacian values and interatomic distances for π-hole (R2 = 0.96) and chalcogen (R2 = 0.93) interactions, confirming their non-covalent character.
In general the NBO results were in agreement with the AIM calculations. Thus, the NBO analysis shows that the largest second-order perturbation stabilization energies were observed for the halogen bonds in complexes 1 and 4, ranging from 0.9 to 29.1 kJ mol−1. Within these complexes, the largest E(2) values corresponded to those with the largest binding energies, suggesting that these contributions were significant. Charge transfer between monomers indicated that complexes based on halogen bonds (1 and 4) presented the largest charge transfer of all the complexes studied indicating the electrostatic importance in these types of interactions, which was again in agreement with the mentioned strength.
Furthermore, the energy terms obtained from the SAPT partitioning scheme confirmed that the dispersion is the largest attractive contributor to the interaction, varying from 37.1% (BrI1a) to 76.6% (FI3b) of the attractive forces. These values indicated that despite the fact that the halogen bonds are mainly governed by electrostatic interactions, in those complexes with different types of interactions acting simultaneously, the dispersion played the most important role. This was also supported by the small interaction energies found. However, the electrostatic contribution was the second term of importance varying from 18.8% (FI3b) to 47.7% (FCl1a), and only surpassing the effect of the dispersion term for three halogen-bonding complexes (FI1a, ClI4b and BrI4b) in which pure halogen bonds are governed by electrostatic interactions. The induction term is very small and never overcomes either the dispersion or electrostatic terms.
Acknowledgements
We gratefully acknowledge support from the Ministerio de Economía y Competitividad (MINECO), (projects CONSOLIDER-Ingenio 2010 CSD2010-0065, Fondo Europeo de Desarrollo Regional (FEDER) funds and projects No. CTQ2015-63997-C2-2-P and CTQ2014-57393-C2-1-P) and the Comunidad Autónoma de Madrid (S2013/MIT-2841, Fotocarbon). Goar Sánchez–Sanz thanks the Human Frontier Science Program (Project Reference: LT001022/2013-C) for their support. David Quiñonero thanks the MINECO of Spain for a “Ramón y Cajal” contract. We thank TCHPC (TCD, Ireland), the Irish Centre for High-End Computing (ICHEC), for the provision of computational facilities and support. Thanks are given to the CTI (CSIC), CCC-UAM, and CESGA for the allocation of computer time.References
- K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168 CrossRef.
- Halogen Bonding: Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Springer, Berlin, 2008 Search PubMed.
- I. Rozas, I. Alkorta and J. Elguero, Chem. Phys. Lett., 1997, 275, 423–428 CrossRef CAS.
- I. Alkorta, I. Rozas and J. Elguero, J. Phys. Chem. A, 2001, 105, 743–749 CrossRef CAS.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef PubMed.
- S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824–1834 RSC.
- G. Sánchez-Sanz, C. Trujillo, I. Alkorta and J. Elguero, ChemPhysChem, 2012, 13, 496–503 CrossRef PubMed.
- G. Sánchez-Sanz, I. Alkorta and J. Elguero, Mol. Phys., 2011, 109, 2543–2552 CrossRef.
- L. Azofra, I. Alkorta and S. Scheiner, Theor. Chem. Acc., 2014, 133, 1–8 CrossRef CAS.
- P. Sanz, M. Yáñez and O. Mó, Chem. – Eur. J., 2003, 9, 4548–4555 CrossRef CAS PubMed.
- S. Scheiner, J. Chem. Phys., 2011, 134, 094315 CrossRef PubMed.
- M. Solimannejad, M. Gharabaghi and S. Scheiner, J. Chem. Phys., 2011, 134, 024312 CrossRef PubMed.
- S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem. – Eur. J., 2011, 17, 6034–6038 CrossRef CAS PubMed.
- S. Scheiner, Phys. Chem. Chem. Phys., 2011, 13, 13860–13872 RSC.
- S. Scheiner, CrystEngComm, 2013, 15, 3119–3124 RSC.
- S. Scheiner and U. Adhikari, J. Phys. Chem. A, 2011, 115, 11101–11110 CrossRef CAS PubMed.
- U. Adhikari and S. Scheiner, J. Phys. Chem. A, 2012, 116, 3487–3497 CrossRef CAS PubMed.
- U. Adhikari and S. Scheiner, Chem. Phys. Lett., 2012, 532, 31–35 CrossRef CAS.
- S. Scheiner, Chem. Phys. Lett., 2011, 514, 32–35 CrossRef CAS.
- S. Scheiner, J. Chem. Phys., 2011, 134, 164313 CrossRef PubMed.
- U. Adhikari and S. Scheiner, J. Chem. Phys., 2011, 135, 184306 CrossRef PubMed.
- Q.-Z. Li, R. Li, X.-F. Liu, W.-Z. Li and J.-B. Cheng, J. Phys. Chem. A, 2012, 116, 2547–2553 CrossRef CAS PubMed.
- Q.-Z. Li, R. Li, X.-F. Liu, W.-Z. Li and J.-B. Cheng, ChemPhysChem, 2012, 13, 1205–1212 CrossRef CAS PubMed.
- A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Phys. Chem. Chem. Phys., 2012, 14, 14061–14066 RSC.
- S. Ghosh, S. Biswas, A. Bauzá, M. Barceló-Oliver, A. Frontera and A. Ghosh, Inorg. Chem., 2013, 52, 7508–7523 CrossRef CAS PubMed.
- H. Zhuo, Q. Li, W. Li and J. Cheng, New J. Chem., 2015, 39, 2067–2074 RSC.
- I. Alkorta, G. Sánchez-Sanz, J. Elguero and J. E. Del Bene, J. Chem. Theory Comput., 2012, 8, 2320–2327 CrossRef CAS PubMed.
- J. E. Del Bene, I. Alkorta, G. Sánchez-Sanz and J. Elguero, Chem. Phys. Lett., 2011, 512, 184–187 CrossRef CAS.
- J. E. Del Bene, I. Alkorta, G. Sánchez-Sanz and J. Elguero, J. Phys. Chem. A, 2012, 116, 3056–3060 CrossRef CAS PubMed.
- J. E. Del Bene, G. Sánchez-Sanz, I. Alkorta and J. Elguero, Chem. Phys. Lett., 2012, 538, 14–18 CrossRef CAS.
- J. E. Del Bene, I. Alkorta, G. Sánchez-Sanz and J. Elguero, J. Phys. Chem. A, 2012, 116, 9205–9213 CrossRef CAS PubMed.
- I. Alkorta, G. Sánchez-Sanz, J. Elguero and J. E. Del Bene, J. Phys. Chem. A, 2012, 117, 183–191 CrossRef PubMed.
- J. E. Del Bene, I. Alkorta, G. Sánchez-Sanz and J. Elguero, J. Phys. Chem. A, 2013, 117, 3133–3141 CrossRef CAS PubMed.
- G. Sánchez-Sanz, I. Alkorta, C. Trujillo and J. Elguero, ChemPhysChem, 2013, 14, 1656–1665 CrossRef PubMed.
- I. Alkorta, J. Elguero and J. E. Del Bene, J. Phys. Chem. A, 2013, 117, 10497–10503 CrossRef CAS PubMed.
- S. J. Grabowski, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2013, 117, 3243–3251 CrossRef CAS PubMed.
- J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292 CrossRef CAS.
- A. Mohajeri, A. H. Pakiari and N. Bagheri, Chem. Phys. Lett., 2009, 467, 393–397 CrossRef CAS.
- P. Politzer, J. Murray and M. Concha, J. Mol. Model., 2008, 14, 659–665 CrossRef CAS PubMed.
- J. Murray, P. Lane, T. Clark, K. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS PubMed.
- R. Paulini, K. Müller and F. Diederich, Angew. Chem., Int. Ed., 2005, 44, 1788–1805 CrossRef CAS PubMed.
- M. J. Molina and F. S. Rowland, Nature, 1974, 249, 810–812 CrossRef CAS.
- R. P. Wayne, Chemistry of Atmospheres, Oxford University Press, Oxford, 1991 Search PubMed.
- F. Schweitzer, P. Mirabel and C. George, J. Atmos. Chem., 1999, 34, 101–117 CrossRef CAS.
- S. Fickert, F. Helleis, J. W. Adams, G. K. Moortgat and J. N. Crowley, J. Phys. Chem. A, 1998, 102, 10689–10696 CrossRef CAS.
- R. Lesclaux, F. Caralp, A. M. Dognon and D. Cariolle, Geophys. Res. Lett., 1986, 13, 933–936 CrossRef CAS.
- M. Solimannejad, V. Ramezani, C. Trujillo, I. Alkorta, G. Sánchez-Sanz and J. Elguero, J. Phys. Chem. A, 2012, 116, 5199–5206 CrossRef CAS PubMed.
- M. Solimannejad, N. Nassirinia and S. Amani, Struct. Chem., 2013, 24, 651–659 CrossRef CAS.
- G. Sánchez-Sanz, C. Trujillo, M. Solimannejad, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2013, 15, 14310–14318 RSC.
- C. Trujillo, G. Sanchez-Sanz, I. Alkorta and J. Elguero, New J. Chem., 2015, 39, 6791–6802 RSC.
- S. Roy, A. Bauza, A. Frontera, R. Banik, A. Purkayastha, M. G. B. Drew, B. M. Reddy, S. Balasubramanian, S. Das and S. K. Das, CrystEngComm, 2015, 17, 3912–3916 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446 CrossRef CAS.
- A. Halkier, W. Klopper, T. Helgaker, P. Jørgensen and P. R. Taylor, J. Chem. Phys., 1999, 111, 9157–9167 CrossRef CAS.
- T. A. Keith, Version 15.09.27 edn, 2015, pp. TK Gristmill Software, http://aim.tkgristmill.com.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103 CrossRef PubMed.
- A. Hesselmann and G. Jansen, Phys. Chem. Chem. Phys., 2003, 5, 5010–5014 RSC.
- R. Moszynski, Mol. Phys., 1996, 88, 741–758 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- T. J. Lee, Chem. Phys. Lett., 1993, 216, 194–199 CrossRef CAS.
- D. C. Frost, S. T. Lee, C. A. McDowell and N. P. C. Westwood, J. Electron. Spectrosc. Relat. Phenom., 1975, 7, 331–347 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, M. Schütz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2010.1, a package of ab initio programs.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259–1281 Search PubMed.
- S. Jenkins and I. Morrison, Chem. Phys. Lett., 2000, 317, 97–102 CrossRef CAS.
- W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- G. Sánchez-Sanz, C. Trujillo, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2012, 14, 9880–9889 RSC.
- O. Knop, R. J. Boyd and S. C. Choi, J. Am. Chem. Soc., 1988, 110, 7299–7301 CrossRef CAS.
- I. Alkorta, L. Barrios, I. Rozas and J. Elguero, THEOCHEM, 2000, 496, 131–137 CrossRef CAS.
- O. Knop, K. N. Rankin and R. J. Boyd, J. Phys. Chem. A, 2001, 105, 6552–6566 CrossRef CAS.
- O. Knop, K. N. Rankin and R. J. Boyd, J. Phys. Chem. A, 2002, 107, 272–284 CrossRef.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- I. Alkorta and J. Elguero, Struct. Chem., 2004, 15, 117–120 CrossRef CAS.
- T. H. Tang, E. Deretey, S. J. Knak Jensen and I. G. Csizmadia, Eur. Phys. J. D, 2006, 37, 217–222 CrossRef CAS.
- I. Mata, I. Alkorta, E. Molins and E. Espinosa, Chem. – Eur. J., 2010, 16, 2442–2452 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nj01334a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2016 |