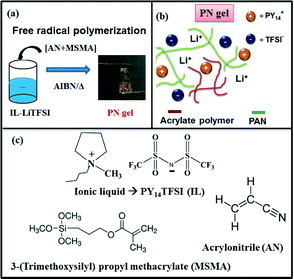
Non-trivial network driven modifications of ion transport in an ionic liquid confined inside a polymer system

Abstract

We discuss here the polymer specificities which completely govern in a non-trivial manner the effective ion transport in polymer gel electrolytes, an important class of soft matter electrolytes. Confinement of a lithium bis(trifluoromethanesulfonyl)imide (LiTFSI)–pyrrolidinium-cation based ionic liquid solution inside a polymer physical network composed of two different polymers with different functionalities is achieved. A physical network of two polymers with different functional groups, viz., one with acrylate and another with acrylonitrile (PAN) leads to multiple interesting consequences. Due to chemical differences between the acrylate-based polymer (formed from (3-trimethoxysilyl)propyl methacrylate (MSMA) monomers) and PAN, the physical knots in the PAN network unlock, leading to a decrease in the elastic modulus with improved mechanical compliance and chain flexibility in the gel. Additionally, ion–polymer interactions increase, resulting in higher free charge carrier density in the gel compared to the unconfined ionic liquid solution. Thus, ion transport is no longer assisted by the ionic liquid and polymer relaxations, as it would be in conventional polymer electrolytes, but fully driven by the chemical characteristics of the polymer physical network. Notably, the polymer matrix significantly influences the anion mobility and transference number. Contrary to the unconfined ionic liquid electrolyte where cations (predominantly due to the pyrrolidinium cation) and anions contribute to the ionic conductivity, the ionic conductivity in PN gels is predominantly due to anions. The gel ionic conductivity is nearly half an order of magnitude higher than that of the unconfined ionic liquid electrolyte and displays good dimensional stability and electrochemical performance in a separator-free battery configuration. Most importantly, this work may revitalize research on single-ion conductors and stimulate new and simple chemical designs of polymer electrolytes displaying high single-ion conductivity.

---

Design, System, Application

Polymer electrolytes exhibit superior mechanical compliance compared to crystalline solid and liquid electrolytes. However, the ionic conductivity of most polymer electrolytes is far inferior to that of liquid electrolytes. Thus, obtaining a high ion conducting, dimensionally stable polymer electrolyte is a grand challenge. Successful achievement of this goal will provide high value opportunities to design safe and high performance electrochemical devices. We demonstrate here a novel design strategy to obtain a gel polymer electrolyte that exhibits high dimensional stability and ionic conductivity comprising an ionic liquid (IL) confined inside a 3-D physically blended polymer system. The different chemical functionalities of the polymers lead to excellent mechanical flexibility. The ion transport in the gel electrolyte is unique as it is completely decoupled from the IL and polymer segmental relaxations and is fully driven by the combined chemical characteristics of the polymer system. Contrary to the unconfined IL electrolyte where the cations and anions are both mobile, gel ionic conductivity is predominantly due to anions. The gel ionic conductivity is higher than that of the unconfined IL electrolyte and displays excellent electrochemical cyclability in a separator-free cell. We strongly feel that this work will also stimulate new and simple chemical designs of single-ion conducting polymer electrolytes.

Introduction

The increasing demand for high performance and safe electrochemical devices has led to extensive focus on strategies aimed at developing both novel materials and device assemblies.^1–5 In the context of rechargeable batteries, a key strategy has been to develop all solid-state devices with solid crystalline or amorphous compounds as electrolytes.⁶ Sustained efforts for several decades, however, have not truly translated into high performance solid-state batteries which can be produced and deployed on the mass scale. While the transition from liquid to solid-state electrolytes does nullify to a great extent the detrimental safety issues associated with liquid electrolytes, the high electrode–solid electrolyte interfacial resistance offsets the gained advantages and leads to poor electrochemical performances. This has been vividly demonstrated in the case of rechargeable batteries based on lithium-ion chemistry. The other major drawback is that both liquid and solid-state electrolytes heavily constrain batteries and other devices to only a few specific geometries. In comparison with the crystalline solid counterparts, “solid-like” soft matter electrolytes show greater versatility and potential in diverse electrochemical devices such as rechargeable batteries, fuel cells, solar cells, sensors and actuators.⁷ The switch in research focus from crystalline solid state to soft matter is due to the fact that the probability of achieving liquid-like conductivity in a highly compliable framework is much higher in comparison with that in a crystalline solid-state matrix.⁸ Additionally, soft matter electrolytes also allow smarter rechargeable battery geometries and may also make the expensive electro-inactive polymer separators redundant. Additionally, the charge transfer kinetics across the electrode–soft matter electrolyte interface will be substantially faster due to lower contact resistance. In this way, employing a soft matter electrolyte will have multiple advantages and lead to long term electrochemical stability and higher operational safety.

Among the various soft matter electrolytes, polymer electrolytes have been explored extensively as a potential alternative to both conventional liquid and solid electrolytes.^9,10 Conventionally, high ionic conductivity in solid polymer electrolytes has been obtained via structural modifications of the polymer matrix leading to lower glass transition temperatures and crystallinity. This results in effective ion transport predominantly assisted by the polymer segmental dynamics. Various design strategies have been adopted to enhance ionic conductivity. One approach has been to design new polymers with optimized architectures and chemical functionalities (e.g. block copolymers, blends).¹¹ However, such approaches are very rigorous and involve several non-trivialities which may not eventually result in a polymer electrolyte with physical properties desired for a practical device. On the other hand, an easier strategy, from the point of view of processability, is the plasticization of polymer matrices. In its simplest form, plasticization has been achieved via incorporation of low molecular weight molecules, such as solvents and chelating agents,¹² into a linear polymer–salt complex. Following such trivial manipulations, several advanced procedures for plasticization of the polymer matrix have been developed. The plasticized polymer electrolytes, termed as gel electrolytes, have been demonstrated as a very promising class of polymer electrolytes for specific applications. The ion transport in gel electrolytes is unique and has been proposed to be determined by both the polymer dynamics and the state of the charged species in the liquid electrolyte confined inside the polymer physical network. Thus, the ion transport characteristics in gel polymer electrolytes are typically governed by the physico-chemical properties of the polymer physical network and by the ion–polymer interactions.

Several strategies have been developed to integrate polymers with an ionic liquid to obtain gel polymer electrolytes with superior physical and electrochemical properties. The integration can be done either via (a) linear addition/swelling of polymer physical networks with ionic liquids or (b) confining the IL into cross-linked polymer physical networks by polymerising monomers in ionic liquid media.^13,14 In this regard, the majority of gel polymer electrolytes comprise of neutral polymers, such as poly-ethylene oxide (PEO), poly-methyl methacrylate (PMMA), poly-vinyl alcohol (PVA), poly-vinylidene difluoride PVDF, poly-acrylonitrile PAN or in the form of block copolymers such as poly-(styrene-block-ethylene oxide-block-styrene) (PS-PEO-PS).¹⁴ Ionic polymer physical network-based gel polymer electrolytes have also attracted enormous research interests in recent times. Ionic liquids functionalised with polymerizable monomers also serve as a polymer matrix, often termed as a poly-ionic liquid (PIL), to obtain ionic liquid integrated gel polymer electrolytes. Beneficial mechanical properties are obtained for the ion gels comprising either a polymer-IL or a poly-(ionic liquid)-IL due to specific interactions of the polymer chain and the polar ionic liquid environment. Cross-linked polymer physical network-based gels are an important subclass of gel polymer electrolytes.¹⁵ Due to higher cross-link network density, they exhibit superior dimensional stability as well as mechanical compliance over the linear polymer-based gel electrolytes. However, higher mechanical strength can be a drawback as this may lead to a drastic decrease in ionic mobility/conductivity and thus, severely limit their electrochemical performance. Therefore, obtaining a (cross-linked) gel electrolyte simultaneously with high dimensional stability and ionic conductivity is a grand challenge. At the fundamental level, this challenge can be overcome if the adopted chemical design approach leads to a gel whose effective ionic conductivity is decoupled from both the liquid and the polymer segmental relaxations without compromising the dimensional stability. In the present study, we demonstrate a gel polymer electrolyte with high dimensional stability and ionic conductivity. The proposed gel polymer electrolyte is a three-dimensional polymer physical network comprising a combination of linear homo- and co-polymer chains.^16,17 It is envisaged that the final gel will be inheriting the beneficial properties of the ionic liquid, viz., high thermal stability, wide potential window and high ionic conductivity. We systematically discuss here the correlation of the key parameters, viz., chain flexibility, elastic modulus and chemical functionalities with the electrolyte physical and electrochemical properties of the dual polymer physical network. Interestingly, this design approach, apart from decoupling long-range ion transport from both the polymer and ionic liquid characteristics, also influences the nature of the predominant charge carriers resulting in almost a single-ion conducting polymer gel electrolyte.

Results and discussion

Three-dimensional cross-linked polymer physical networks not only provide solid mechanical support but also constrain the transport of ions to distinct pathways in gel electrolytes. In polymer physical network (PN)-based gel electrolytes, the polymer network characteristics are key design parameters to achieve higher dimensional stability as well as ionic mobility/conductivity. The ion–ion/ion–polymer interactions and ionic mobilities inside the confined liquid are strongly governed by the polymer physical network characteristics.^18,19 Based on the chemical functionality of the polymer, changes in the polymer network characteristics may also lead to alteration in the nature of the predominant charge carriers in the gel network.¹⁸ The proposed network-based polymer gel electrolyte discussed here is composed of lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) in 1-methyl-1-butyl pyrrolidinium bis(trifluoromethanesulfonyl)imide (PY₁₄TFSI) confined inside a 3-dimensional polymer physical network. The three-dimensional network is proposed to be formed by physical blending of poly-(acrylonitrile) (PAN) with the copolymer of AN and MSMA, P(AN-co-MSMA) (Fig. 1).²⁰ Due to the very high molar percentage of acrylonitrile (>95%), we strongly feel that PAN will coexist with the P(AN-co-MSMA) copolymer to form the overall polymer network. Additionally, the physical appearance of PN-5 and PN-10 are almost similar to that of PN-0. Significant changes are observed only for x > 10 in PN-x gels. So the PAN network is predominantly present for lower values of x. It decreases for higher x due to copolymerisation. The electrolyte synthesis procedure is discussed in detail in the ESI.† The complete polymerisation of MSMA and AN monomers throughout the course of gel preparation is monitored by FTIR spectroscopy. The FTIR spectra of the PN-16 gel and MSMA monomer are shown in Fig. S1.† The MSMA monomer exhibits the characteristic IR stretching frequency of a –C=C bond at 1639 cm⁻¹, which disappears in the PN gel. The absence of the –C=C– band of the vinyl monomer in the gel suggests the MSMA monomer is polymerised completely in the gel network. In the proposed network-based gel, the cross-linked PAN serves as the ion-conducting constituent of the polymer physical network, while the acrylate polymer imparts mechanical support. The overall mechanical strength and degree of flexibility are controlled by the MSMA content in the overall polymer network, formed via physical chain entanglement of PAN with P(AN-co-MSMA). The presence of the linear PMSMA/P(AN-co-MSMA) polymer along with PAN has several advantages. Firstly, acrylate polymers has high chemical compatibility with PAN. This leads to a gel electrolyte with higher mechanical compliance compared to the brittle cross-linked PAN-PY₁₄TFSI (i.e. without P(AN-co-MSMA), denoted as PN-0, vide infra)-based gel electrolyte. Additionally, introduction of a functional group with different polarity, viz., –COOR from MSMA and –CN from AN monomers fine tunes the ion–polymer interactions and also the overall solvation properties of the ionic liquid and the polymers (Fig. 1). Secondly, as will be discussed later, the electrolyte–lithium interface is more stable in the presence of methacrylate polymers. PN gels comprising other methacrylate monomers such as methyl methacrylate (MMA) and poly(ethylene glycol) methyl ether methacrylate (PEGMA) have also been synthesized. However, these gels are not discussed here owing to their low ionic conductivity and unfavourable mechanical strength (such as brittleness with MMA and excessive adhesiveness with PEGMA). PN gels with different elastic moduli are synthesized using different starting weight ratios of MSMA and AN monomers in the polymerization reaction. The varying content of the monomers (i.e. the polymers) in the gels are denoted as PN-x, where x is the weight percentage of MSMA (x: 0–16) with respect to the total weight of the AN and MSMA monomers. The physical and electrochemical properties of PN gels with 0.5 M LiTFSI are studied with respect to the bare PY₁₄TFSI–0.5 M LiTFSI electrolyte (abbreviated to IL–LiTFSI). The ionic conductivity of the ionic liquid–Li-salt solution is appreciably high at this concentration, equal to 2.4 × 10⁻⁴ Ω⁻¹ cm⁻¹. Gels with a LiTFSI concentration greater than 0.5 M possess a very sticky adhesive-like mechanical consistency, which makes it difficult to assemble cells and also to carry out physical property investigations using various characterization tools. Thus, salt concentrations greater than 0.5 M are not discussed here.

Fig. 1 (a) Schematic representation of the synthesis protocol of PN-x (including a photograph showing the gel-like consistency of the PN-x, with the MSMA content, x = (0–16)%, (b) schematic depiction of the morphology of the PN-x (x > 0), and (c) chemical constituents of the ionic liquid (PY₁₄TFSI) and monomers used to prepare PN gels.

Thermal stability and phase characterization of PNs are evaluated by thermo gravimetric analysis (TGA) and differential scanning calorimetry (DSC), as shown in Fig. S2 and S3 (ESI†), respectively. Generally, the thermal stability of the various gels (320–350 °C) is lower compared to that of IL–LiTFSI (≈ 450 °C). However, the thermal stability increases with an increase in x in the PN-x samples (average ≈ 350 °C), these being more stable compared to the PN-0 (≈ 320 °C) sample.

DSC traces of the PN gel clearly indicate complete depression of the crystallization exotherm (at −54.4 °C) and solid–solid phase transition (at −29.8 °C)²¹ of the PY₁₄TFSI ionic liquid when confined inside the polymer matrix (Fig. S3a†). Confinement of IL–LiTFSI in PN-0 results in depression of the melting point, which is shifted to a lower value. With the addition of MSMA (x = 10–13), the melting peak increases, probably implying inappropriate solvation of the IL in the matrix. However, for x > 13 (i.e. x = 16: PN-16) T_m decreases again. Such variations in T_m and the presence of only one depressed melting isotherm at −25.8 °C for PN-16 confirms the absence of any polymer phase separation in the proposed polymer gel as well as good compatibility of the polymers with the entrapped IL–LiTFSI.

The PN gels show only one glass transition temperature (T_g) at −86.5 °C (Fig. S3b†) corresponding to the ionic liquid. The T_g increases from −84.17 °C for PN-10 to −80.3 °C for PN-16 which can be attributed to the confinement of the ionic liquid in a stiffer environment resulting from the entanglement between polymer chains. As the chemical moieties of the monomer/polymer influence the degree of entanglement, the changes in the ionic liquid T_g are thus also indirectly governed by the chemical nature of the polymer physical network.

The elastic modulus (G′) and loss modulus (G′′) of PN gels are obtained as a function of frequency in the frequency range 0.1–650 s⁻¹. In general, for all PN-x, the G′ is observed to be greater than G′′ in the probed frequency range (Fig. S4a†), suggesting formation of a gel. The elastic modulus of PN-x decreases drastically with increasing content of MSMA. Additionally, an increase in MSMA leads to an increase in elasticity. This is observed from the higher degree of elongation (deformation) for PN-16 (approximately 90%) in comparison with 15% for PN-0 (Fig. S4b†).

The presence of an interconnected network in all of the gels is characterised from the steady state shear viscosity versus shear rate plots. The plots are shown in Fig. S5.† The viscosities of all the PN gels exhibit a power law decay with a slope equal to −1, suggesting the presence of a three-dimensional interconnected polymer physical network in all the gels.

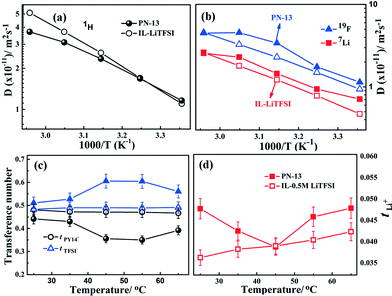
Fig. 3 shows the ionic conductivity as a function of temperature for the PN gels estimated from ac-impedance spectroscopy in the temperature range −20–60 °C. The equivalent circuit fitting of the impedance spectra is shown in Fig. S6.† The ionic conductivity of PN-0 is slightly lower compared to IL–LiTFSI in the measured temperature range. On the contrary, the ionic conductivity of the PNs is greater than those of IL–LiTFSI and PN-0 in the entire temperature range. The room temperature (= 25 °C) ionic conductivity of PN-x (x > 10) is nearly 3–4 times higher than that of PN-0 and 2–3 times that of IL–LiTFSI (Fig. 2 and 3). The increase in room temperature ionic conductivity with the increase in MSMA (x) can be directly correlated to the decrease in elastic modulus of PN gels (Fig. 2). The temperature-dependent ionic conductivity is fitted using the Vogel–Tammann–Fulcher (VTF) equation,²²σ = σ₀ exp[−B/k(T − T₀)], where B has units of energy but is not related to any activation process and T₀ is a reference temperature at which configurational entropy vanishes. The best values of T₀, B and σ₀ are shown in Table ST2.† The best fit T₀ values for IL–LiTFSI and PN-0 are nearly 50 K less than T_g obtained from DSC, implying the validation of the VTF phenomenology. Such validation strongly suggests that ion transport in IL–LiTFSI and PN-0 is determined by the structural relaxation of the ionic liquid. On the other hand, in PN gels, T₀ in general is higher than experimental T_g, except for PN-16 where T₀ ≈ T_g.

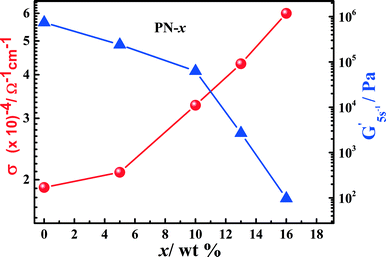Fig. 2 Elastic modulus G′ (blue triangle) at 5 rad s⁻¹ and variations in the room temperature ionic conductivity (red circle) versus the MSMA content, x = (0–16)%.

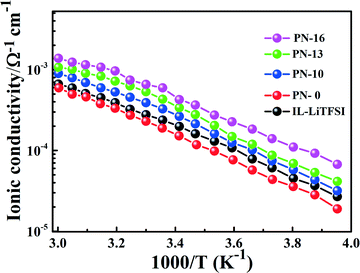Fig. 3 Temperature-dependent ionic conductivity of IL–LiTFSI and PN-x samples (red: PN-0; black: IL–LiTFSI; blue: PN-10; green: PN-13; and magenta: PN-16).

The close proximity in the values of T₀ to T_g in the PN-x strongly suggests that ion transport probably is no longer assisted by the structural relaxation of the ionic liquid and is possibly governed by the characteristics of the polymer physical network. In general, the values of σ₀ for the PN-x gels are higher (cf. Table ST2† for PN-0 and PN-16) than that of IL–LiTFSI. As σ₀ is directly proportional to the attempt frequency for ion mobility, an increase in σ₀ should imply higher mobility. This can take place only when the ions are free i.e. in the dissociated state, which is again linked to the chemical/physical bonds of the ions with their surrounding environment. The ion–polymer interactions increase with x, especially in the range x = (10–16)%. This leads to a higher degree of dissociation, resulting in the increase in free charge carriers. This is an important indicator of the fact that the ion transport mechanism in the gels is altered in comparison with IL–LiTFSI. The pseudo-activation energy (B/k), which is correlated to the critical free volume required for ion conductivity, increases significantly from 931 K (for IL–LiTFSI) to 1042 K (for PN-0). The presence of the P(AN-co-MSMA) polymer in the PAN network initially leads to a decrease in the activation energy to 345 K (for PN-10) compared to IL–LiTFSI and PN-0 gels, implying reduction in the critical free volume required for ion transport with the change in the local environment in the presence of the acrylate functional group in PN-x. Such a decrease can possibly be attributed to the filling up of the free volume in the PAN network by the additional linear chain polymer as well as to the decrease in average size of the mobile charge, which is present in IL–LiTFSI. An increase in x from 10% to 13% results again in an increase in B/k to 715.9 K (for PN-16) which can possibly be only due to the increase in critical free volume. To validate the accuracy and consistency of the fitting parameters, a slight modification of the VTF fitting procedure is done for PN-13 and PN-16, by fixing T₀ to 207 K, as observed in PN-10. A similar improvement in B/k is achieved at higher x (10–13%), followed by a decrease in B/k in PN-16. The increase in the critical free volume at higher x (= 10–13%) is a consequence of the strong interactions between the more polar –COOR group and –CN functional groups, which completely change the local environment of ions. The decrease in B/k in PN-16 indicates an increase in internal flexibility, probably due to the additional chain relaxation associated with the flexible silyl chain end in MSMA. The stronger ionic interaction with acrylate functional groups suggests that the flexible acrylate polymer chain ends may have a contribution to the dynamics and transport of PN-16 gels to some extent (supported also by the reduction in T_m for PN-16 in DSC). The relaxation contribution from the flexible chain ends in the polymer physical network is correlated to slight slope changes in the conductivity data for PN-13 and PN-16 near 20 °C (T_g of PMSMA ∼ 40 °C in its pure form). This results in decoupling of the ion transport from the ionic liquid, leading to an increase in ionic mobility and conductivity. The increase in ionic mobility and ionic conductivity is simultaneously supported by the increase in σ₀ values. Thus, modifications in the ion transport mechanism are due to the increase in charge carriers and mobility.

The degree of salt dissociation in the PN gels (PN-0 to PN-16; Fig. 4b and d) is also studied by Raman spectroscopy at room temperature with reference to IL-X M LiTFSI (X = 0 to 0.5) electrolytes (Fig. 4a and c). Ion association or dissociation, which is typically followed by changes in TFSI⁻ anion conformation in the PN gels, is studied in two different spectral ranges: 720–780 cm⁻¹ (Fig. 4a and b) and 250–450 cm⁻¹ (Fig. 4c and d), respectively. The spectral findings for the PN gels are also compared with the PN-0 gel with a different wt% of the acrylonitrile (AN) monomer (Fig. S9 and S10†). All spectra in Fig. 4a and b have been normalized with respect to the highest intensity band at 742 cm⁻¹ and the bands are fitted with two Lorentzians (Fig. S7 and S8†). The stronger band at 742 cm⁻¹ is characteristic of the free TFSI anion and corresponds to the –CF₃ bending vibrations, δ_s(CF₃) coupled with the asymmetric S–N stretching vibration, ν_s(SNS).²³ An additional weak band appearing at 747 cm⁻¹ is assigned to the ion aggregate (predominantly [Li(TFSI)₂]⁻) formed in the IL–LiTFSI electrolyte.²⁴ The ratio of the intensities of the bands at 747 cm⁻¹ and 742 cm⁻¹ (A₇₄₇/A₇₄₂, inset of Fig. 4a) increases significantly with increasing salt concentration in IL–LiTFSI. Simultaneously, formation of an ionic cluster in IL–LiTFSI leads to changes in the TFSI conformation. This is manifested here via the changes in the rotation of the CF₃ group of the TFSI⁻ anion along with the S–N bond, which results in two types of conformers of the TFSI anion. In the presence of a salt, the area of the band at 397 cm⁻¹ (C₂) decreases with respect to the C₁ band at 408 cm⁻¹ (A₃₉₇/A₄₀₈, Fig. S9†). In comparison with IL–LiTFSI, in the PNs the weak band at 747 cm⁻¹ for the ion pair disappears in PN-10 to PN-16 with increasing MSMA content. Notably, dissociation of ion pairs is not observed in the single polymer network PN-0 gels (Fig. S10†). Indeed, stronger coordination between Li⁺ and –COOR and –CN groups (Fig. S11†) results in dissociation of the [Li(TFSI)₂]⁻ aggregates in the PN gels. The dissociation of [Li(TFSI)₂]⁻ aggregates in the PNs results in the transition from the C₁ conformer to the C₂ conformer within the [Li(TFSI)₂]⁻ cluster. This is confirmed by the increase in the magnitude of the A₃₉₇/A₄₀₈ ratio from 0.4 for PN-0 to 0.8 for PN-16 (Fig. S12†). Thus, the enhanced ion interaction with the polymer chains leads to an increase in the number of free charges in the PN matrices with simultaneous influence on the conformational equilibrium between the C₁ and C₂ conformers of the TFSI⁻. Such dissociation in an ion cluster and TFSI conformational changes in PN gels directly reflects changes in the ionic environment in the presence of acrylate functionality. This also correlates to reduction in free volume and average size of mobile charges in PN-x gels compared to IL–LiTFSI, as proposed from VTF fitting analysis.

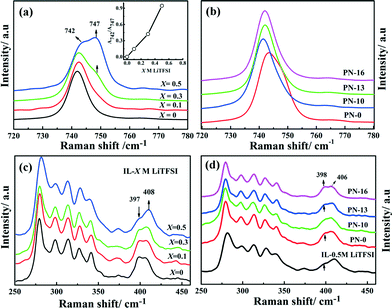Fig. 4 Raman spectroscopic analysis of ion pair formation (a), (b) and TFSI conformational changes (c), (d) in PN gels and IL-X M LiTFSI.

A Brillouin scattering technique is employed here to study the dynamics of an ionic liquid under confinement inside a polymer physical network. The room temperature Brillouin spectra of PN gels with increasing MSMA concentrations are shown in Fig. 5(a). The full width at half maxima and Brillouin shifts are evaluated by fitting the spectra with three Lorentzians (Fig. S13†). No Brillouin modes are seen in the Brillouin spectrum, obtained from the cross-linked PAN without an ionic liquid, which implies an absence of relaxation contributions^25a from PAN. Thus, the spectra obtained should reflect the dynamics and relaxation of the confined ionic liquid. When x increases from 0–10%, only one longitudinal acoustic mode, similar to that of IL-0.5 M LiTFSI (at ∼8.5 GHz), is observed. For higher MSMA concentrations (x > 10%), an additional mode appears at 8.2 GHz. The appearance of an additional mode probably indicates either the changes in the relaxations of a certain fraction of IL molecules as a result of confinement inside the dual polymer physical networks or additional relaxation of a flexible silyl chain end of MSMA. No significant variation in Brillouin shift relating to the propagating sound wave velocity (= fλ₀/(2n sin θ/2), (f: Brillouin frequency shift, λ₀: wavelength of incident light, n: refractive index, θ = scattering angle)²⁵ is observed for PN-0 to PN-13 (the average Brillouin shift is 8.5 ± 0.1 GHz). However, the Brillouin shift increases slightly to 10 GHz for PN-16. Polymer chain entanglement between polymers and interactions of ionic liquid constituent ions, viz., Li⁺ and TFSI⁻, PY₁₄⁺ with the polymer in PN-x may exert some degree of stiffness at the molecular level, which influences the sound velocity propagating through the network. Evidence of increase in stiffness at the molecular level is also highlighted in the context of glass transition and ionic conductivity studies, as was discussed earlier.

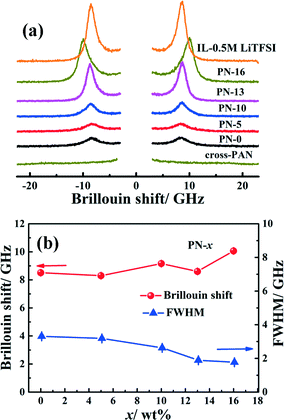Fig. 5 (a) Room temperature Brillouin scattering spectra of PN-x, IL-0.5 M LiTFSI, and PAN and (b) plot of Brillouin shifts and FWHM as a function of MSMA content.

The relaxation of an ionic liquid, correlated to the FWHM of the Brillouin peak, is qualitatively studied as a function of MSMA content (x). Entrapment of the ionic liquid in the PN-0 gel (i.e. with the highest elastic modulus) results in an increase in the FWHM to 3.3 GHz from 1.86 GHz for IL–LiTFSI. As the ion transport is coupled with the ionic liquid, this should lead to faster ionic mobility and hence higher ionic conductivity. With the introduction of PMSMA, the FWHM in general decreases from 3.3 GHz for PN-0 to 1.7 GHz for PN-16. This decrease is attributed to slower relaxation of the ionic liquid with increasing stiffness at the molecular level. Interestingly, the observed FWHM of 1.7 GHz for PN-16 is very similar to the value of 1.86 GHz observed for IL–LiTFSI. In spite of the similar ionic liquid relaxation lifetimes, the ionic conductivity of PN gels is greater than that of IL–LiTFSI, suggesting that ion transport is decoupled from ionic liquid dynamics in PN-x gels. Hence, the relaxation lifetime and sound velocity can indicate the ionic interactions with the polymer physical networks, which in turn determines the ionic conductivity. Thus, the chemical functionality of the polymers has strong influence on the dynamics of the confined ionic liquid inside the polymer matrices, which consequently affects effective ion transport. This can be accounted on the basis of the decoupling of the ion transport from the ionic liquid structural dynamics.

The self-diffusion coefficients, which are also a measure of mobility, of constituent ions viz. PY₁₄⁺, Li⁺, and TFSI⁻ corresponding to the diffusion coefficients of ¹H, ⁷Li and ¹⁹F nuclei, are evaluated independently via multi-nuclear solid state PFG-NMR measurements.²⁶ The self-diffusion coefficients of ¹H (Fig. 6a), ¹⁹F and ⁷Li nuclei (Fig. 6b) for PN-13 are studied as a function of temperature (range: 25–65 °C) with reference to PY₁₄TFSI (IL)–LiTFSI and PN-0 (Fig. S14†). The self-diffusion coefficients of the constituent ions in IL–LiTFSI in the measured temperature range follow the trend D_PY14⁺ (D_H) > D_TFSI⁻ > D_Li⁺. In IL–LiTFSI, the slower diffusion of the smaller Li⁺ ion compared to the bulkier PY₁₄⁺ cation is accounted for on the basis of the presence of ionic clusters as [Li(TFSI)_n]ⁿ⁻¹ (where n = 2 in most cases).²⁷ On the other hand, the PN gels (except PN-0) display a different trend in the self-diffusion coefficients compared to the ¹H, ¹⁹F and ⁷Li nuclei, with the TFSI⁻ anion being the fastest and the Li⁺ ion being the slowest. No significant variation in the self-diffusion coefficient of the PY₁₄⁺ (¹H) cation is observed for PN-0 and PN-13 compared to IL–LiTFSI. However, Li⁺ and TFSI⁻ diffusion coefficients are observed to vary significantly in the PN gels compared to IL–LiTFSI. In PN-0, the various ion diffusion coefficients follow the trend D_PY14⁺ ∼ D_TFSI⁻ > D_Li⁺. The ion transport is mainly due to the PY₁₄⁺ cation and implies that ion transport is predominantly governed by the ionic liquid relaxations. However, the room temperature D_Li in PN-0 increases by almost 2.5 times that of the D_Li in IL–LiTFSI.

Fig. 6 Self-diffusion coefficients of ¹H (black circles) (a) and ¹⁹F (blue triangles) and ⁷Li (red squares) (b) of PY₁₄TFSI–0.5 M LiTFSI (open symbols) and the PN-13 gel (closed symbols) as a function of temperature. The transference numbers of PY₁₄⁺ (black circles) and TFSI⁻ (blue triangles) (c) and Li⁺ (red squares) (d) at various temperatures in the PN-13 gel (closed symbols) with reference to IL–LiTFSI (open symbols), with a 5% error bar.

The enhancement in the Li⁺ diffusion coefficient in the PN-0 gel compared to IL–LiTFSI again strongly suggests the domination of ionic liquid-assisted lithium ion transport and strongly supplements the findings from Brillouin scattering. In spite of the decrease in the elastic modulus, the magnitude of D_Li⁺, however, decreases from PN-0 to PN-13. This is attributed to the stronger coordination of the Li⁺ ion to the -COOR group in the polar acrylate polymer physical network, which leads to dissociation of the ion pairs. However, the D_Li⁺ (= 7.1 × 10⁻¹² m² s⁻¹) and D_TFSI⁻ (= 1.14 × 10⁻¹¹ m² s⁻¹) in PN-13 is 1.5 and 1.2 times higher than that of D_Li⁺ (= 4.7 × 10⁻¹² m² s⁻¹) and D_TFSI⁻ (= 9.4 × 10⁻¹² m² s⁻¹), respectively, in IL–LiTFSI. Contrary to PN-0 where nearly no variation in D_TFSI⁻/D_PY14⁺ is observed, in PN-13 the D_TFSI⁻/D_PY14⁺ ratio (Fig. S15a†) especially at higher temperature significantly increases. This strongly suggests that anion transport completely decoupled from the PY₁₄⁺ cation of the ionic liquid. This again confirms the findings from ionic conductivity and Brillouin scattering measurements. The increase in internal chain flexibility via alteration in polymer network characteristics in PN-x (due to the presence of a flexible silyl chain) influences the TFSI diffusion especially at higher temperatures. Such flexibility, however, does not influence Li⁺ diffusion to a significant extent due to its stronger co-ordination with –COOR and –CN groups.

The ion transport in the unconfined ionic liquid and PN-x can also be accounted by approximately fitting the diffusion data for the various ion species with the Arrhenius equation. The estimated activation energies (E_a) for PY₁₄⁺, Li⁺, and TFSI⁻ are tabulated in Table ST3.† The activation energy for lithium diffusion (38 kJ mol⁻¹) is slightly higher compared to PY₁₄⁺ (32 kJ mol⁻¹) and TFSI⁻ (33 kJ mol⁻¹) in IL–LiTFSI.

This is attributed to ‘structure diffusion’,²⁸ which implies lithium ion hopping between different [Li(TFSI)_n]ⁿ⁻¹ clusters via ligand exchange in the co-ordination shell. Entrapment of IL–LiTFSI electrolytes in PN gel matrices leads to a decrease in activation energy for lithium diffusion from 38 kJ mol⁻¹ in IL–LiTFSI to 30 kJ mol⁻¹ which is comparable to that of TFSI⁻ diffusion (31 kJ mol⁻¹). Interestingly, the activation energy of PY₁₄⁺ cations decreases abruptly from 32 kJ mol⁻¹ in IL–LiTFSI to 24.5 kJ mol⁻¹ in PN gels. The difference in diffusion activation energies between PY₁₄⁺ cations and TFSI anions further supports the decoupled diffusion of the TFSI anion from that of PY₁₄⁺ as discussed earlier. The similarities in activation energies between Li⁺ and TFSI⁻ in PN gels signify the diffusion of Li⁺ and TFSI⁻ as free charges with a diffusion mechanism different from that in IL–LiTFSI. The decrease in E_a for the ion diffusion in PN compared to IL–LiTFSI is attributed to the different chemical nature of the environment and the nature of the mobile ions. Additionally, E_a values from conductivity measurements in PN gels are similar to E_a (D) for ion (Li⁺ and TFSI⁻) diffusion obtained from NMR measurement, while in IL–LiTFSI, E_a (conductivity) is lower than that obtained from NMR measurement. This further signifies that conductivity is much sensitive to ion pairs, mobile ions in the IL rather than in PN gels, with dissociated ionic clusters. Thus, dissociation of ion pairs (as observed from Raman spectroscopy and NMR) leads to a completely different transport mechanism in gels, predominantly due to movement of anions in comparison with the dual ion conductivity in IL–LiTFSI electrolytes.

The transference numbers of Li⁺ (t_Li), PY₁₄⁺ (t_PY14), and TFSI⁻ (t_TFSI) are obtained from the diffusion coefficients for the respective ions using the equation: t_i = x_iD_i/∑x_iD_i,²⁹ where t_i is the transference number of the ith ion, x_i is mole fraction of the ith ion and D_i is the diffusion coefficient of the ith ion. The transference numbers at various temperatures (25–65 °C) are presented in Fig. 6c (for t_PY14 and t_TFSI) and Fig. 6d (for t_Li). In IL–LiTFSI, the constituent ions follow the trend t_PY14 (0.48) ≈ t_TFSI (0.48) > t_Li (0.04) (at 25 °C) suggesting dual ion (PY₁₄⁺, TFSI⁻) transport in the ionic liquid electrolyte. A similar trend is also obtained in the highly cross-linked PN-0 with t_PY14 (0.45) ≈ t_TFSI (0.46) > t_Li (0.08). In contrast to IL–LiTFSI and PN-0, the PN-13 gel shows significant improvement in t_TFSI, (especially at higher temperature) following the trend t_TFSI (0.60) > t_PY14 (0.35) > t_Li (0.05). Decoupling and chain flexibility in PN-13 lead to faster anion diffusion and a higher anion transference number. Thus, the nature of ion transport is completely altered from dual ion (PY₁₄⁺ and TFSI⁻) transport in IL–LiTFSI to anion (TFSI⁻) dominated transport in the PNs. The increase in chain flexibility in PN-13 compared to PN-0 results in faster and decoupled anion transport, leading to a gel with predominantly anion transport. On the other hand, no significant increase in the Li⁺ transference number (≈ 0.05 at 25 °C) is observed in PN-13 compared to that in IL–LiTFSI (0.04 at 25 °C). In fact, the Li⁺ transference number is slightly lower than that of the higher PN-0 gel (t_Li = 0.08 at 25 °C). This can again be interpreted in terms of changes in the ion transport mechanism. In IL–LiTFSI and PN-0, the diffusion is governed by the IL relaxations. In the presence of only PAN (i.e. PN-0), the Li⁺ ions may dissociate from the ion clusters leading to an increase in the t_Li. In the PNs, the Li⁺ ions are solvated differently. Due to stronger interactions with the –COOR and –CN groups, the Li⁺ ions move via coordination with the polymer functional groups. The differences in the t_Li are also supported via the observed differences in the diffusion coefficients as discussed above. Thus, innovative network chemical designs can be employed to tune significantly the conduction mechanism and ion self-diffusion in dual polymer physical network gels.

Ionicity, which denotes the degree of ion dissociation, is obtained from the ratio Λ_imp/Λ_NMR (ref. 30) where Λ_imp and Λ_NMR are the molar conductivities estimated from impedance spectroscopy and PFG-NMR, respectively. The ionicities at various temperatures for IL-0.5 M LiTFSI and PN gel electrolytes are shown in Fig. S15b.†Λ_NMR is calculated from the self-diffusion coefficients of individual ions by using the Nernst–Einstein relation³¹ (Λ_NMR = (Nq²/kT)∑x_iD_i for the i^th ion; D_i is the diffusion coefficient, x_i is the mole fraction). Close proximity of the ionicity towards unity in the PN-13 gel further supports the complete dissociation of ion pairs in the PN gel (as also inferred from Raman spectroscopy and NMR). On the other hand, the ionicity obtained for the PN-0 gel is 0.45, signifying higher salt association and ion transport coupled to the ionic liquid. The higher degree of salt dissociation in the PN-13 gel suggests that, the ion transport is decoupled from the ionic liquid. As a consequence of the two effects, viz., reduction in elastic modulus/increase in chain flexibility and dissociation of ion pairs, TFSI⁻ and Li⁺ diffuse with faster self-diffusion coefficients in the PN gels. The trend in ionicity again highlights the importance of the chemical functionality of the polymer physical network on ionic conductivity. The contribution of Li⁺ (and TFSI⁻) ions towards effective conductivity can be calculated from the Nernst–Einstein relation: σ_Li = Nq²D_i/kT.³¹ In PN-13, the contribution of Li⁺ to effective conductivity is 1.5 times higher than that of Li⁺ in IL–LiTFSI at 25 °C (σ_TFSI(PN-13)/σ_TFSI(IL–LiTFSI) = 1.2 at 25 °C). This is very similar to the ratio of the overall conductivities (σ_imp(PN-13)/σ_imp(IL–LiTFSI) = 1.6 at 25 °C) obtained directly from the ac-impedance measurements. On the other hand, at higher temperature (say 45 °C), the contribution of the TFSI⁻ anion in PN-13 is 1.5 times higher than that of TFSI⁻ in IL–LiTFSI (σ_Li(PN-13)/σ_Li(IL–LiTFSI) = 1.4 at 45 °C). This is again very similar to the ratio of the overall conductivities (σ_imp(PN-13)/σ_imp(IL–LiTFSI) = 1.7 at 45 °C) obtained from the ac-impedance measurement.

Thus, combined enhancements in Li⁺ and TFSI⁻ diffusion contribute to the increase in conductivity in general for PN-x compared to IL–LiTFSI. The simultaneous enhancement in Li⁺ and TFSI⁻ diffusion is not achieved in PN-0 due to the presence of ionic clusters. Thus, the presence of a dual polymer in PN gels influences ionic mobility to a significant extent, which in turn governs the ionic conductivity mechanism in polymer physical network-based gel electrolytes.

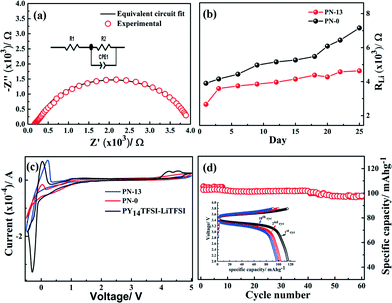
Based on the promising results related to various physical properties, electrochemical performance studies of the PNs are performed. The lithium interfacial stability of PN-0 and PN-13 gels over a period of 25 days is evaluated by ac-impedance spectroscopy in a separator-free Li|PN-x|Li cell. The impedance profile and the equivalent circuit used to fit the impedance profile are shown in Fig. 7a (R₁: bulk resistance, R₂: electrode–electrolyte interface resistance due to formation of a passivation layer at the lithium electrode).³² The interface resistance (R_Li) for PN-13 shows a stable profile up to the 25th day, while PN-0 exhibits an average interfacial resistance (= 5.2 × 10³ Ω) close to that of PN-0 (4.1 × 10³ Ω) within the first 18 days. However, beyond the 18^th day, the resistance increases suddenly to almost 2 times by the 25th day. The stable and lower interfacial resistance in PN-13 compared to PN-0 is attributed to the improved mechanical compliance of the PN-gels. The brittle nature of PN-0 constrains its electrochemical performance. An increase in acrylate content imparts superior mechanical compliance resulting in sustained uniform contact with electrodes and also a stable passivation layer at the electrodes. Additionally, an increase in the ionic conductivity also leads to fast ion transport kinetics across the electrolyte–electrode interface.

Fig. 7 (a) Nyquist plot of a Li|PN|Li symmetrical cell on the 10^th day. (b) Lithium interface resistance versus day of the Li|PN|Li symmetrical cell. (c) Cyclic voltammograms, evaluating the electrochemical potential window of PN-0 (blue), PN-13 (red), and IL–LiTFSI (black) of the Li|PN|SS cell recorded at 0.2 mV s⁻¹. (d) Specific capacity versus cycle number of the PN-13 gel with the LFP-C/MWCNT electrode (inset graph: voltage profile). Filled symbols: discharge capacity, unfilled symbols: charge capacity.

The electrochemical potential windows of PN-13 and PN-0 gels are studied in a Li|PN-x|SS separator-free cell configuration at a scan rate of 0.2 mV s⁻¹, as shown in Fig. 7c. Both electrolytes show a wide potential window of ≈5 V, with no electrolyte degradation. However, the improved mechanical compliance and ionic conductivity of PN-13 result in the improvement of the current response in comparison with PN-0, as observed in the lithium stripping process at 0.5 V. The magnitude of the current with regard to the lithium plating or reduction (at −0.5 V) is also approximately similar. The reversibility and kinetics of lithium stripping/plating clearly improves in PN-13, which correlates well to a more flexible stable interface.

The battery cycling performance of the PN-13 gel is studied in the half cell configuration against an LFP-C/MWCNT electrode at a current density of 50 mA g⁻¹, as shown in Fig. 7d. The inset of Fig. 7d shows the charge–discharge voltage profile signifying the reductive plateau at 3 V and the oxidative one at 3.6 V corresponding to the Fe³⁺/Fe²⁺ redox couple of the LFP cathode. The specific capacity obtained in the 1^st discharge cycle is 105 mA h g⁻¹, followed by a charge capacity of 102 mA h g⁻¹ with a coulombic efficiency of 97%. The coulombic efficiency increases to 98% over successive cycles with a stable specific capacity of 101 mA h g⁻¹ over 100 cycles. A significant variation in coulombic efficiency is obtained as a function of various PN compositions (Fig. S16†). The coulombic efficiency decreases for the PN-0 gel from 90% (discharge capacity of 80 mA h g⁻¹) in the 1^st discharge cycle to 60% (discharge capacity of 45 mA h g⁻¹) in the 100^th cycle. The cycling performance of the polymer physical network-based gel is comparable to previous reports on ionic liquid integrated gel electrolytes with linear chain PEO, a semi-interpenetrating polymer physical network as well as with PIL-based gel electrolytes.³² Coulombic efficiency, which signifies reversibility of the electrochemical process, correlates well with the findings from the mechanical properties, conductivity and the interfacial resistance for the various PN gels. Improved cyclability is attributed to the improved mechanical compliance of the PN-13 gel compared to PN-0. Additionally, the higher conductivity and lower charge transfer resistance improve the current response of the gels, leading to faster charge transfer in both the charge–discharge process. Thus, the process of confining the ionic liquid in a polymer physical network of dual polymers, compared to a single polymer physical network, significantly improves the electrochemical cyclability.

Conclusion

To summarize, a novel polymer gel electrolyte comprising an ionic liquid confined inside polymer networks of dual polymers with dissimilar functional groups has been demonstrated here. The presence of an additional polymer in a physically cross-linked PAN network, which differs in chemical functionality and mechanical properties compared to the others, has absolutely no detrimental effect on structural integrity and ion transport. Systematic investigations carried out as part of this work convincingly reveal that an optimal acrylate polymer content can tune both the flexibility (via unlocking of the cross-links) and solvation of the overall polymer physical network. The ion transport mechanism undergoes a drastic change from solvent-assisted in the unconfined ionic liquid to a polymer physical network-governed ion transport in the PN gels. The consequence of this transition in the ion transport mechanism is vividly demonstrated via changes in terms of both quantum and nature free charge carriers. We envisage that the proposed strategy of the network discussed here will definitely aid in the chemical design of more advanced polymer physical networks with high dimensional stability and ionic conductivity and will provide high value opportunities to diverse fields of energy storage and generation, sensing and stimuli dependent processes.

Acknowledgements

AJB wishes to acknowledge DST-SERB (File Number: EMR/2014/000029) and Indo-Australia Joint Research Project (DST/INT/AUS/P-71/2016) for financial support. SS and SM acknowledge the UGC and India-Taiwan Programme of Cooperation in Science and Technology (GITA/DST/TWN/P-46/2013) for the Senior Research Fellowship (SRF) and Project Assistantship, respectively. SS, SM and AJB thank DST Nano Mission (SR/NM/NS-88/2010) for infrastructure support with regard to rheometry and Mr. Amit Joshi of the Department of Inorganic and Physical Chemistry for Raman Spectroscopy. SS, SM and AJB also thank Mr I. S. Jarali of the Solid State and Structural Chemistry Unit for the thermal and infrared spectroscopy measurements.

References

1. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
2. J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
3. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
4. P. G. Bruce, B. Scrosati and J. M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930–2946.
5. Y. Karatas, N. Kaskhedikar, M. Burjanadze and H. D. Wiemhöfer, Macromol. Chem. Phys., 2006, 207, 419–425.
6. (a) A. R. Rodger, J. Kuwano and A. R. West, Solid State Ionics, 1985, 15, 185–198; (b) A. Kuhn, O. Gerbig, C. Zhu, F. Falkenberg, J. Maier and B. V. Lotsch, Phys. Chem. Chem. Phys., 2014, 16, 14669–14674; (c) V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727.
7. (a) A. S. Arico, P. Bruce, B. Scrosati, J. M. Tarascon and W. V. Schalkwijk, Nat. Mater., 2005, 4, 366–377; (b) M. A. Ratner and D. F. Shriver, Chem. Rev., 1988, 88, 109–124; (c) C. Berthier, W. Gorecki, M. Minier, M. Armand, J. M. Chabagno and P. Rigaud, Solid State Ionics, 1983, 11, 91–95; (d) D. R. Macfarlane, J. Huang and M. Forsyth, Adv. Mater., 2001, 139, 57–96.
8. (a) A. D. Pasquier, P. C. Warren, D. Culver, A. S. Gozdz, G. G. Amatucci and J. M. Tarascon, Solid State Ionics, 2000, 135, 249; (b) K. Fujii, H. Asai, T. Ueki, T. Sakai, S. Imaizumi, U. Chung, M. Watanabe and M. Shibayama, Soft Matter, 2012, 8, 1756–1759.
9. (a) D. T. Hallinan and N. P. Balsara, Annu. Rev. Mater. Res., 2013, 43, 503–525; (b) M. B. Armand, Annu. Rev. Mater. Sci., 1986, 16, 245; (c) S. Lascaud, M. Perrier, A. Vallee, S. Besner, J. Prud'homme and M. Armand, Macromolecules, 1994, 27, 7469–7477.
10. (a) D. E. Fenton, J. M. Parker and P. V. Wright, Polymer, 1973, 14, 589; (b) P. G. Bruce, Solid State Electrochemistry, Cambridge University Press, United Kingdom, 1995; (c) C. Berthier, W. Gorecki, M. Minier, M. B. Armand, J. M. Chabagno and P. Rigaud, Solid State Ionics, 1983, 11, 91–95; (d) S.-I. Lee, M. Schomer, H. Peng, K. A. Page, D. Wilms, H. Frey, C. L. Soles and D. Y. Yoon, Chem. Mater., 2011, 23, 2685–2688.
11. (a) M. Gopinadhan, P. W. Majewski and C. O. Osuji, Macromolecules, 2010, 43, 3286–3293; (b) A. Panday, S. A. Mullin, E. D. Gomez, N. S. Wanakule, V. L. Chen, A. Hexemer, J. A. Pople and N. P. Balsara, Macromolecules, 2009, 42, 4632–4637; (c) B. K. Cho, A. Jain, S. M. Gruner and U. Wiesner, Science, 2004, 305, 1598–1601.
12. G. B. Appetecchi, Y. Aihara and B. Scrosati, Solid State Ionics, 2004, 170, 63–72.
13. (a) A. Fernicola, B. Scrosati and H. Ohno, Ionics, 2006, 12, 95–102; (b) M. A. B. H. Susan, T. Kaneko, A. Noda and M. Watanabe, J. Am. Chem. Soc., 2005, 127, 4976–4983; (c) C. Tiyapiboonchaiya, D. MacFarlane, J. Sun and M. Forsyth, Macromol. Chem. Phys., 2002, 203, 1906–1911.
14. (a) Y. S. Ye, J. Rick and B. J. Hwang, J. Mater. Chem. A, 2013, 1, 2719–2743; (b) A. S. Shaplov, R. Marcilla and D. Mecerreyes, Electrochim. Acta, 2015, 175, 18–34; (c) Y. Gu, S. Zhang, L. Martinetti, K. H. Lee, L. D. McIntosh, C. D. Frisbie and T. P. Lodge, J. Am. Chem. Soc., 2013, 135, 9652–9655.
15. (a) D. F. Miranda, C. Versek, M. T. Tuominen, T. P. Russell and J. J. Watkins, Macromolecules, 2013, 46, 9313–9323; (b) T. Kataoka, Y. Ishioka, M. Mizuhata, H. Minami and T. Maruyama, ACS Appl. Mater. Interfaces, 2015, 7, 23346–23352.
16. (a) L. H. Sperling, in Interpenetrating Polymer physical networks; Advances in Chemistry Series, ed. D. Klempner, L. H. Sperling and L. A. Utrachi, ACS, Washington, DC, 1994, vol. 239; (b) P. L. Kuo, C. A. Wu, C. Y. Lu, C. H. Tsao, C. H. Hsu and S. S. Hou, ACS Appl. Mater. Interfaces, 2014, 6, 3156–3162.
17. (a) L. J. Goujon, A. Khaldi, A. Maziz, C. Plesse, G. T. M. Nguyen, P. H. Aubert, F. Vidal, C. Chevrot and D. Teyssi, Macromolecules, 2011, 44, 9683–9691; (b) Y. Gu, S. Zhang, L. Martinetti, K. H. Lee, L. D. McIntosh, C. D. Frisbie and T. P. Lodge, J. Am. Chem. Soc., 2013, 135, 9652–9655.
18. (a) T. Yamaguchi, R. Matsui and S. Koda, J. Phys. Chem. B, 2013, 117, 7077–7083; (b) N. Boaretto, A. Bittner, C. Brinkmann, B. E. Olsowski, J. Schulz, M. Seyfried, K. Vezzù, M. Popall and V. D. Noto, Chem. Mater., 2014, 26, 6339–6350; (c) S. Seki, M. A. B. H. Susan, T. Kaneko, H. Tokuda, A. Noda and M. Watanabe, J. Phys. Chem. B, 2005, 109, 3886–3892; (d) R. Bhandary and M. Schönhoff, Electrochim. Acta, 2015, 174, 753–761; (e) M. Kunze, A. Schulz, H. D. Wiemhöfer, H. Eckert and M. Schönhoff, Z. Phys. Chem., 2010, 224, 1771–1793; (f) Y. Saito, M. Okano, K. Kubota, T. Sakai, J. Fujioka and T. Kawakami, J. Phys. Chem. B, 2012, 116, 10089–10097.
19. Y. Wei, W. Wang, D. Yang and L. Tang, Chem. Mater., 1994, 6, 1737–1741.
20. (a) A. Martinelli, A. Matic, P. Jacobsson, L. Börjesson, A. Fernicola and B. Scrosati, J. Phys. Chem. B, 2009, 113, 11247–11251; (b) D. R. MacFarlane, P. Meakin, J. Sun, N. Amini and M. Forsyth, J. Phys. Chem. B, 1999, 103, 4164–4170; (c) W. A. Henderson and S. Passerini, Chem. Mater., 2004, 16, 2881–2885.
21. M. B. Armand, P. G. Bruce, M. Forsyth, B. Scrosati and W. Wieczorek, Polymer Electrolytes, in Energy Materials, ed. D. W. Bruce, D. O'Hare and R. I. Walton, John Wiley & Sons, Ltd, Chichester, UK, 2011.
22. (a) K. Fuji, T. Fujimori, T. Takamuku, R. Kanzaki, Y. Umebayashi and S. Ishiguro, J. Phys. Chem. B, 2006, 110, 8179–8183; (b) J. C. Lassègues, J. Grondin, R. Holomb and P. Johansson, J. Raman Spectrosc., 2007, 38, 551–558; (c) J. N. C. Lopes, K. Shimizu, A. A. H. Pádua, Y. Umebayashi, S. Fukuda, K. Fujii and S. Ishiguro, J. Phys. Chem. B, 2008, 112, 1465–1472.
23. (a) I. Nicotera, C. Oliviero, W. A. Henderson, G. B. Appetecchi and S. Passerini, J. Phys. Chem. B, 2005, 109, 22814–22819; (b) J. C. Lassègues, J. Grondin and D. Talaga, Phys. Chem. Chem. Phys., 2006, 8, 5629–5632; (c) R. Arnaud, D. Benrabah and J. Y. Sanchez, J. Phys. Chem., 1996, 100, 10882–10891; (d) Y. Umebayashi, T. Mitsugi, S. Fukuda, T. Fujimori, K. Fujii, R. Kanzaki, M. Takeuchi and S. I. Ishiguro, J. Phys. Chem. B, 2007, 111, 13028–13032.
24. (a) R. Aronsson, H. E. G. Knape and L. M. Torell, J. Phys. Chem., 1982, 77, 677–680; (b) F. Li, Q. Cui, T. Cui, Z. He, Q. Zhou and G. Zou, J. Phys.: Condens. Matter, 2007, 19, 1–9; (c) J. G. Dil, Rep. Prog. Phys., 1982, 45, 286–334.
25. (a) K. Hayamizu, Y. Aihara, S. Arai and C. G. Martinez, J. Phys. Chem. B, 1999, 103, 519–524; (b) B. Fritzinger and U. S. Macromol, Chem. Phys., 2005, 206, 1288–1291.
26. (a) F. Castiglione, E. Ragg, A. Mele, G. B. Appetecchi, M. Montanino and S. Passerini, J. Phys. Chem. Lett., 2011, 2, 153–157; (b) J. C. Lassègues, J. Grondin, C. Aupetit and P. Johansson, J. Phys. Chem. A, 2009, 113, 305–314.
27. F. Castiglione, A. Famulari, G. Raos, S. V. Meille, A. Mele, G. B. Appetecchi and S. Passerini, J. Phys. Chem. B, 2014, 118, 13679–13688.
28. (a) T. Fromling, M. Kunze, M. Schonhoff, J. Sundermeyer and B. Roling, J. Phys. Chem. B, 2008, 112, 12985–12990; (b) Y. Saito, T. Umecky, J. Niwa, T. Sakai and S. Maeda, J. Phys. Chem. B, 2007, 111, 11794.
29. (a) H. Yoon, A. S. Best, M. Forsyth, D. R. MacFarlane and P. C. Howletta, Phys. Chem. Chem. Phys., 2015, 17, 4656–4663; (b) H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600; (c) I. Nicotera, C. Oliviero, W. A. Henderson, G. B. Appetecchi and S. Passerini, J. Phys. Chem. B, 2005, 109, 22814–22819.
30. R. A. McKee, Solid State Ionics, 1981, 5, 133–136.
31. C. Arbizzani, M. Borghini, M. Mastragostino, L. Meneghello and A. Zanelli, Solid State Ionics, 1994, 72, 115–121.
32. (a) A. S. Shaplov, D. O. Ponkratov, P. S. Vlasov, E. I. Lozinskaya, L. V. Gumileva, C. Surcin, M. Morcrette, M. Armand, P. H. Aubert, F. Vidal and Y. S. Vygodskii, J. Mater. Chem. A, 2015, 3, 2188–2198; (b) J. H. Shin, W. A. Henderson, S. Scaccia, P. P. Prosini and S. Passerini, J. Power Sources, 2006, 156, 560–566; (c) M. Li, B. Yang, L. Wang, Y. Zhang, Z. Zhang, S. Fang and Z. Zhang, J. Membr. Sci., 2013, 447, 222–227.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6me00053c

---