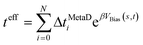Kinetics and mechanism of ionic-liquid induced protein unfolding: application to the model protein HP35†
Hsin-Ju
Tung
and
Jim
Pfaendtner
*
Department of Chemical Engineering, University of Washington, Seattle, Washington 98195, USA. E-mail: jpfaendt@uw.edu
First published on 13th September 2016
Abstract
We demonstrate an approach to quantify protein unfolding times using molecular simulation in a greatly accelerated manner compared to standard MD simulations, showing up to 400 fold speed increases. The approach uses infrequent metadynamics, which has been shown to provide quantitative rates for rare events, accelerated by biasing the RMSD of the protein structure. The results are quantitatively verified against a large benchmark dataset using the model proteins chignolin and villin headpiece (HP35). Following this, we apply the algorithm to protein unfolding in ionic liquids and study the HP35 unfolding time in four different 20% (w/w) IL/water mixtures. An interesting agreement is obtained between the ordering of the anion effects and previously published experiments on anion-induced destabilization of ribonuclease A (RNase A). Additional simulations helped shed light on the molecular mechanisms that lead to accelerated unfolding in ILs that have a chaotropic or hydrophobic anion. Further simulations suggest that, in this case, the tendency of an IL to be structure forming or breaking (kosmotrope vs. chaotrope) in water is unrelated to the unfolding times. Instead, the chaotropic anions, which are also more hydrophobic, more readily bind residues from the hydrophobic core, leading to faster unfolding. This approach should be appropriate for a wide range of protein unfolding simulations in the future and aid in systematic discovery of molecular descriptors for biomolecule function in unique nanostructured environments.
Design, System, ApplicationIn this article we investigate the specific molecular features of ionic liquids (IL) leading to quantitative changes in the structure of biomolecules, specifically, the role of anion hydrophobicity on the rate of protein unfolding. Using a special molecular dynamics method, we relate the anion properties to the unfolding rate, the findings of which are supported by published experimental data. Previously, protein stability and function in ILs have been related in terms of a type of Hofmeister series. We revisit this interpretation through the lens of anion/side chain interactions, which is a departure from the classical view of anion/water interactions suggested by Hofmeister-type designations. Our work suggests that protein/IL interactions may be better predicted and designed by specifically considering the affinity of the ion with the protein hydrophobic core. Since the approach greatly accelerates simulation timescales and is easily used with free software, a future application would be to use the computer algorithm as a screening tool to identify whether a particular IL/protein combination leads to loss of function via denaturing. For example, in the case of enzyme deactivation by ILs, we envision this approach could narrow the design space of the solvent package prior to extensive wet lab experimental efforts. |
Introduction
In the past two decades, ionic liquids (ILs) have emerged as a category of solvents that present unique and interesting effects in biomolecules ranging from selective biomass dissociation,1 to unique enzymatic action,2 to enhanced stability of proteins.3 The specific aspect of IL induced protein stabilization or de-stabilization has generated a lot of interest from groups performing both simulations and experiments due to the highly tunable properties of ILs. Given that there are an estimated ∼106 salts of known anions and cations, many of which are thought to form ILs, the manifold of potential solvent/protein interactions is massive, frustrating efforts at the rational design of new solvent packages for biotechnology applications. For example, work in the area of protein stability in ILs has conclusively shown that IL formulations affecting protein stability in beneficial ways can be obtained.4–8 However, it has thus far proved elusive to obtain a reliable method for predicting a priori whether a given IL will stabilize or destabilize a protein. Commonly, the Hofmeister series has been invoked, which classifies ions either kosmotropes (structure makers) or chaotropes (structure breakers) according to their relative abilities to induce the structuring of water.7,9 The basic concept is that a kosmotrope (usually ions of greater charge and smaller size) can enhance the H-bonding network of the near-surface waters, thus enhancing stability. In contrast, chaotropes (typically ions of smaller charge and larger size) disrupt the structure of water, potentially leading to destabilization.A widely quoted Hofmeister series ranking anions according to their protein-stabilizing efficiency is:10,11 [SO4]2− > [dhp]− > [ac]− > F− > Cl− ‖ > Br− > I− > [SCN]−. The double bar (‖) indicates the crossover from stabilizing to destabilizing behavior (n.b., abbreviations for complex ions are defined in Table 1). However, some work has shown that protein stability in ILs does not always follow the Hofmeister series. For example, there are cases where the Hofmeister series is found to be reversed.12,13 This is a more general example of cases when strong denaturants were found to be acting as stabilizers.14 Such deviations are, at least in part, likely due to the fact that this ranking series does not take into account the complexity of the protein surface, which is known to be a critical determinant of enzymatic activity in ILs.15 The interactions of ribonuclease A (RNase A) and several ILs were characterized in detail with differential scanning calorimetry to systematically characterize the effect of ILs on the thermal denaturation,16 which resulted in the proposal of a specific Hofmeister-like series for anions with the major stability metric being determined as the change in protein melt temperature (Tm): [SO4]2− > [HPO4]2− > Cl− > [EtOSO3]− > [BF4]− ≈ Br− > [MeOSO3]− > [TfO]− > [SCN]− ≈ [DCA]− > [Tf2N]−. Instead of quantifying relative stabilizing or destabilizing effects, this “Hofmeister-like” series instead quantified the relative destabilizing efficiency of various anions (with a fixed cation). This is in line with the general trend that the choice of anion can have a much more consequential effect on protein stability.4,16 Recently, a detailed analysis by Miller et al.17 of myoglobin unfolding in several aqueous solutions of ILs proposed that some ILs function simply by virtue of an ‘ionic strength’ effect whereas some ILs can accelerate unfolding beyond expected ionic strength effects, e.g., an ‘ionic liquid’ effect.
| [BMIM]+ | 1-Butyl-3-methylimidazolium |
| [dhp]− | Dihydrogen phosphate |
| [ace]− | Acetate |
| [EtOSO3]− | Ethylsulfate |
| [DCA]− | Dicyanamide |
| [TfO]− | Trifluoromethanesulfonate |
| [Tf2N]− | Bis(trifluoromethanesulfonyl)imide |
| [SCN]− | Thiocyanate |
| [BF4]− | Tetrafluoroborate |
| [MeOSO3]− (MTS) | Methylsulfate |
Compared to the body of experimental work investigating protein or enzyme structure in ILs, there is comparatively little work using molecular dynamics (MD) simulations to study IL-induced biomolecular structural transitions. Previous work has studied potential IL effects on biocatalysis (including common experimental targets such as lipases18–21 and glycoside hydrolyases22,23), the liquid structure of the IL arising from protein surface charge,24 and some effects of protein structure.5,25 There are now some consensus views emerging about useful analyses and best practices for simulations.26 Unfortunately, ILs, which typically have increased viscosity compared to water, create the need for timescales that are beyond the reach of standard MD simulations in order to study effects like protein folding/unfolding that can take place at least on the microsecond timescale. Moreover, with a few exceptions arising from the use of a special purpose MD computer,27 the use of special methods (so-called enhanced sampling methods) is necessitated for studying long-time conformational changes – either from the perspective of equilibrium thermodynamics or kinetic quantities. To our knowledge, there has not yet been application of enhanced sampling methods to the calculation of IL effects on protein folding free-energies or on the kinetic folding/unfolding transition times, the demonstration of which would bring new capability to IL/protein simulations. We performed these studies on HP35, a 35-residue subdomain of the headpiece of actin-binding protein villin. It has been the target of a wide variety of experimental and computational efforts to characterize its folding and unfolding mechanism, due to its fast-folding properties.28–32 Wild type villin headpiece is known to fold in 4–5 microseconds; a fast-folding mutant exists which folds in under a microsecond.33
There is also a need to further explore the relationship between the properties of an anion within an IL and the propensity of an IL to affect biomolecular structure and dynamics. Deeper knowledge of the anion's role in the mechanism of protein (de)stabilization would assist others in designing new solvents and/or devising new ways to protect or functionalize a biomolecule. Specifically, we set out to apply a recently developed algorithm34 that is a part of the metadynamics (MetaD) family of methods.35 The method, known as “infrequent metadynamics”, provides accurate quantitative measure of the rate of escape from a free-energy basin. This property makes it ideally suited to understanding the role of ILs in changing protein unfolding times. Herein we demonstrate the accuracy of infrequent metadynamics for estimating the unfolding time of a protein and then calculate unfolding rates for a spectrum of different anions in a model 3-helix protein. Following this, we use supplementary simulations and analyses to understand the predicted unfolding times and relate them to a previously proposed Hofmeister-like series.
The rest of this manuscript is organized as follows. The Methods section reviews the infrequent metadynamics algorithm and our application of the algorithm to the calculation of protein unfolding times; this is followed by additional computational details. We next present a validation of our approach by comparison to a detailed benchmark study from a published exhaustive MD calculation that was performed without any accelerated or enhanced sampling on the peptide chignolin and the villin headpiece binding domain (HP35). This miniprotein is ideal as it has been extensively studied with experiments and computations and presents both a three-helix bundle and a hydrophobic core so that key protein secondary structure elements can be studied. The remainder of the results discusses the study of the effects of four ILs of varying anionic strengths on the previously published Hofmeister scale: [BMIM][Cl], [BMIM][DCA], [BMIM][Br], [BMIM][MeOSO3]. In addition to new insights about anion properties and effects on the protein structure, we also show that our approach provides up to a 100-fold increase in efficiency for the accurate calculation of protein unfolding times compared to unbiased MD.
Methods
Infrequent metadynamics
This method34 is an algorithm that is applied to the results of a MetaD simulation that is terminated at the onset of the occurrence of a rare event (i.e., N discrete time points in a biased trajectory passing out of a (meta)stable free-energy basin). The escape time from the basin is calculated through the use of acceleration factors derived from a MetaD simulation. An individual transition time (teff) is calculated as:The MD timestep used in the MetaD simulation (ΔtMetaD) is multiplied by the acceleration factor, which is the exponential of the instantaneous value of the MetaD potential VBias(s,t) at applied to s collective variables (CVs) at the ith point in the transition trajectory. The mean transition time is the ensemble average of a set of individual transition times, the inverse of which is the transition rate. As detailed below, for this study we found it sufficient to calculate 25–50 individual events for each rate calculated. The application of the algorithm relies on two chief assumptions, namely that the biased CVs distinguish between relevant states in the system and that no bias is added in the transition state (TS).36 In practice,37–39 this is achieved through careful selection of the CVs, the use of very large waiting times between deposition of Gaussians in the MetaD bias potential (the common τ value), and the use of a simple and effective Kolmogorov–Smirnov (KS) analysis presented by Salvalaglio et al.36 As in our prior work,39 a bootstrapping sampling method is regularly used to obtain statistical uncertainty of the results. Fig. S1† shows the workflow for conducting a campaign of infrequent MetaD simulations and further details of the bootstrapping are provided in the ESI.† Readers unfamiliar with the MetaD method are referred to any number of recent review articles.35,40,41
MD simulations
All simulations were performed with GROMACS 4.6,42 enabled by the PLUMED plug-in.43 We used two different force fields to describe the protein. The CHARM22*44 model was used for the validation studies described below and the AMBER99SB-ILDN force field45 was used for the studies in ILs. For the solvents, we used the TIP3P46 water model or our previously described procedure47 to obtain systematic IL force fields derived from GAFF.48 The protein structures used (PDB entries in parentheses) in this study included a fast folding mutant of the HP35 (2F4K) protein,49 wild type HP35 (1YRF),29 and the fast folding peptide chignolin (1UAO).50 Systems were energy minimized using the steepest descent method. The use of LINCS enabled freezing bonds with H atoms and use of a 2 fs timestep. Cutoffs of 1.2 nm were used (shift Lennard-Jones potentials) and the particle mesh Ewald summation method was used for electrostatic calculations. Simulations were equilibrated for 1 ns at 1 bar with the Berendsen barostat51 and in all simulations the temperature was controlled with a stochastic global thermostat.52 As described in the Results and discussion section, additional unbiased MD simulations were used to support the results of the MetaD simulations – their parameters remained unchanged compared to those described above.We used the Cα RMSD from the experimental structure as our CV to bias protein unfolding (further details below). From simulations of all systems in the native state, we selected a value of 0.025 nm for σ, the width of the Gaussian ‘hills’ in the MetaD bias potential. To accelerate unfolding, this CV was biased with well-tempered metadynamics53 with a bias factor (γ) of 10 and an initial Gaussian height of 1.0 kJ mol−1. The specific values of τ, the number of steps between depositing successive Gaussians, are discussed below. Infrequent MetaD analyses were performed with an in-house Python code or a bash shell script inspired by the detail in Salvalaglio's work.36 Other analyses were performed with the packaged GROMACS tools or the MDAnalysis Python package.54 Further simulation details for each of the simulated systems are provided in Table S1.†
Results and discussion
Developing infrequent metadynamics for protein unfolding rates
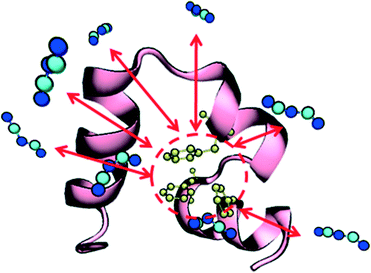
Prior to studying protein unfolding in ionic liquids, we first set out to assess whether the infrequent metadynamics algorithm would provide reliable estimates of protein unfolding times. Lindorff-Larsen et al. recently published an extensive benchmark library of protein folding/unfolding times27 for small fast-folding proteins. Systems were simulated on the 100 μs timescale at temperatures slightly below the protein melting temperature to accelerate observing many folding and unfolding events. On the basis of large ensembles of folding and unfolding events, the authors tabulated folding times, unfolding times, and free-energies of folding. We chose the smallest protein investigated in this study, the mini-protein chignolin, in order to benchmark the method. To provide maximum accuracy in our comparison to these studies, we used identical structure, box size, force field and system temperature. Furthermore, we followed the definition of “folded” vs. “unfolded” by careful inspection of the RMSD values and the fraction of native contacts presented in the unbiased simulation results. Based on their work,27 the protein chignolin can clearly be understood to be unfolded with RMSD values greater than 0.6 nm, which was our cutoff in the infrequent MetaD simulations.As we recently showed,39 the selection of the value of τ requires careful consideration in infrequent metadynamics simulations. Accordingly, we studied different τ values in chignolin unfolding to understand the relationship between the observed unfolding times and the simulation input parameters. Table S2† and Fig. 1 show the details of this calibration study. With p-values above 0.05, the unfolding times quickly converge within an order of magnitude of each other. As seen in the figure, they asymptotically approach some limiting value. However, the simulation times became too long with such long deposition times. Although, the value of τ = 100 ps showed near perfect agreement with the values previously reported (Table 2), we selected the highest value we could computationally afford, τ = 120 ps, to move forward. However, to ensure we were not introducing spurious results, we applied the same parameters to the unfolding of HP35 in water to compare with the published unfolding times.
 | ||
| Fig. 1 Relationship between unfolding times and MetaD Gaussian deposition stride (τ) for chignolin unfolding at T = 340 K. All tested values are in Table S1;† the values shown in the figure represent only those sets that displayed a KS p-value > 0.05. Error bars in the figure were derived from bootstrapping as described in the ESI.† | ||
| Protein | τ MetaD (ps) | T (K) | t MetaDunf (μs) | t MDunf (μs) | p-Value | α | <Biased t> (ns per event) | Aggregate MD tc (μs) |
|---|---|---|---|---|---|---|---|---|
| a Reference unfolding times from the ESI of the Shaw group benchmark data.27 b Alpha is the acceleration factor calculated by the average unfolding time obtained from infrequent metadynamics into the average biased MD time used for the 45 MetaD simulations. c These are the aggregate simulation lengths used to obtain the unbiased unfolding times (tMDunf) from the benchmark data. | ||||||||
| Chignolin (1UAO) | 100 | 340 | 2.1(0.5) | 2.2(4) | 0.48(0.2) | 110 | 10.1 | 106 |
| 120 | 340 | 1.1(0.4) | 2.2(4) | 0.49(0.2) | 110 | 10.2 | 106 | |
| HP35 (2F4K) | 120 | 360 | 0.83(0.2) | 0.9(2) | 0.45(0.2) | 96 | 6.9 | 125 |
To match the prior study and provide more accurate comparison, we used a fast folding mutant of HP35, which substitutes two buried lysine residues with norleucine residues to increase the rates of transition between the folded/unfolded states. Following the details in the benchmark data set,27 we used a cutoff for the folded/unfolded transition of this protein at an RMSD value of 0.4 nm. Using the value of τ = 120 ps, we recorded a large ensemble of unfolding times and calculated the mean transition time. As shown in Table 2, the p-value is excellent and the error bar is quite small. Moreover, with no tuning of parameters, the obtained value of the unfolding time for HP35 is in good quantitative agreement with the benchmark data.
The results from the benchmark studies of these two model proteins unfolding in water using the CHARM22* force field suggest several conclusions. First, using infrequent metadynamics, very good agreement between unbiased protein unfolding times can be obtained with computational cost savings of 200–400 fold (n.b., this estimate is obtained by dividing the unbiased aggregate MD time into the average biased time multiplied times 45). This is a tremendous savings in computational cost; but we note that the unbiased simulation times provided information that our simulations do not – an entire detailed picture that includes folding times and free-energies. However, for cases in which the goal is to quantify solely the unfolding rates, infrequent metadynamics could be an excellent choice. We also note for clarity that our usage of RMSD as a cutoff criteria is an approximation of the benchmark study. That study used a complex definition of the fraction of native contacts, which correlates strongly with RMSD but does vary slightly. Future work might implement this native contact CV into PLUMED and re-evaluate the obtained unfolding times. Overall, the results of this analysis suggest that infrequent metadynamics will provide accurate estimates of protein unfolding times on an accelerated timescale. Using this starting point, we set out to study the effects of ionic liquids on protein unfolding rates.
Unfolding rates of HP35 in different ionic liquids
We used the wild type HP35 at a moderate temperature of 330 K to study the effect of solvents on protein unfolding rates. HP35's structure is stable at this temperature, so the modest increase above room temperature is used only to decrease the total computational cost of the simulations and increase the statistical certainty of the results. Five sets of simulations, each representing HP35 unfolding events, have been carried out in different solvents including, pure water and 20% (w/w) of the ILs [BMIM][Cl], [BMIM][DCA], [BMIM][Br], [BMIM][MeOSO3] as a co-solvent. This choice of concentration was used to be in line with many studies that use aqueous solutions of ILs to study enzyme catalysis. For each solvent tested, 23–29 different unfolding events were recorded. None of the MetaD parameters were changed from the previous HP35 mutant study (i.e., τ = 120 ps, γ = 10, σ = 0.025 nm). For each ensemble of unfolding times, 2000 bootstrapped samples were used to estimate error bars. We also note that for each new simulation we launched, the solvent box was regenerated by randomly placing IL molecules and water molecules. This was an additional step we took in order to ensure the results were not correlated to the initial solvent configuration (in light of the high viscosity of ILs). The unfolding times and other relevant data are summarized in Table 3.| Solution | t MetaDunf (μs) | p-Valuea | Reject rateb | α | <Biased t> (ns per event) | # eventsc |
|---|---|---|---|---|---|---|
| a Mean p-value (KS-test) from 2000 bootstrapped trials and standard deviation of all accepted trials. b Frequency of rejecting a bootstrapped ensemble due to a low p-value. c Total independent number of unfolding events simulated. | ||||||
| Water | 10.0 (2.2) | 0.44 (0.24) | 0.047 | 688 | 12.7 | 26 |
| [BMIM][Cl] | 10.5 (3.7) | 0.35 (0.22) | 0.05 | 701 | 11.6 | 27 |
| [BMIM][Br] | 8.7 (2.2) | 0.41 (0.24) | 0.07 | 571 | 9.72 | 23 |
| [BMIM][MTS] | 8.6 (2.5) | 0.32 (0.22) | 0.15 | 488 | 12.65 | 28 |
| [BMIM][DCA] | 2.6 (0.65) | 0.4 (0.24) | 0.01 | 220 | 12.39 | 29 |
In terms of the predicted unfolding times, the resulting anion series reads: Cl− > Br− > [MeOSO3]− > [DCA]−. This trend follows the experimental measurements (DSC) on melting point depression from the much larger protein RNase A, suggesting that the anions' ability to decrease protein unfolding time shares the same order in HP35 and RNase A. For clarity we note that implicit in this linking is an assumption that a decrease in the melting temperature would correspond to a concomitant decrease in the folding time, i.e., that the effect is due to changes in unfolding, not folding times. While there is no a priori reason to suspect the RNaseA and HP35 would follow the same ‘Hofmeister-like’ trend of protein unfolding, the similarity in ionic effects suggests that there might be more general protein–ion interactions that play a role in the unfolding process.
Anion specific effects on the solvent structure in bulk and at the protein surface
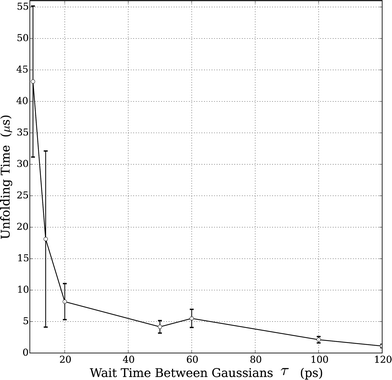
As noted above, the well-known Hofmeister effect for protein structure proposes that the ion-induced changes in the water structure increase or decrease the hydrogen bond networking of water and consequentially affect protein folding and unfolding rates. Increasing structure-breaking (chaotropic) anions tend to have increased hydrophobicity and can destabilize the protein structure. These effects are clearly seen in the trend observed by our simulations in HP35 and the prior experiments on RNase A. Since all the studies were performed with the same BMIM cation, we clearly cannot rule out any potential effects from the positively charged species. However, the assumption of an anion's importance in this case is well supported by prior literature.4,11,55 Accordingly, we sought to understand what aspect of an anion's nature led to the observed changes.We performed supplemental simulations (standard MD) of just the solvent (IL water mixtures) in order to understand the complex solvent structure. Using simulation boxes of size 5 nm, NVT simulations were performed at 330 K. For each of the solvent simulations, 10 independent configurations were generated and simulations were carried out for 2 ns to equilibrate the solvent. The following results are averages of these 10 simulations. The water structure was accessed with radial distribution functions (RDFs) of the water (rO–O); the results are shown in Fig. S2.† As shown in Fig. 2, with the exception of the fact that the pure water simulation has a slightly lower peak in the 1st solvation shell, there is no discernable difference in any of the RDFs. This indicates that any anion-induced changes in the water structure are either not present in the simulation or not detectable with standard measures of the equilibrium liquid structure (i.e., RDF).
 | ||
| Fig. 2 Very small effect on the effect of the water structure when mixed with various ILs (20% w/w) of varying hydrophobicities. WAT refers to a simulation of pure TIP3P water. | ||
The work of Baker and Furbish offers a different explanation on the basis of classical MD simulations of the miniprotein Trp-cage in the IL [C4mpy][Tf2N].5 Simulations of the unfolded protein showed that refolding was possible at elevated temperatures, even with the bulky IL present, but that at lower temperatures the protein did not refold on the MD timescale with ILs. This suggests that protein–IL interactions can block the formation of key intramolecular protein interactions and/or that the IL molecules can frustrate the motion of the protein in the unfolded state. We tried to assess this by studying the solvation structure around the protein in a similar manner to our prior studies of lipase in ILs.24 Short standard MD simulations were performed in triplicate (with different starting structures for the solvent) of each of our systems. The simulations were 5 ns in length and used to study the time average of ions in different shells surrounding the protein. Table 4 shows that DCA, which unfolds HP35 the fastest, has the highest anion number around the protein. The details of the solvent structure around HP35 support the idea that the anions more strongly interfering with the protein structure will cluster more strongly, with DCA and MTS having the most anion molecules located most closely to the protein surface. Note also that since DCA and MTS are larger than Cl and Br, these numbers may be low estimates of the magnitude of the actual physical effect since they are simple number counts not, for example, volume-measured occupancies in the shell. A similar result can be seen by inspecting an anion RDF looking at the anion structure around HP35 (Fig. S3†). Although some studies have shown that high concentration ILs increase the stability of a protein due to their high viscosity,8,56 it is not clear that the comparatively small amount of IL, 20% (w/w), would have such a strong effect hindering the protein motions. This is also supported by prior simulation and experimental studies showing only a very modest increase in viscosity in the regime of 20% (w/w).57,58 In contrast, the order of the occupancy numbers, showing a reverse ordering to that of the unfolding times, suggests that more hydrophobic anions assist in protein unfolding.
| Solvent/distance (nm) | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|
| [BMIM][Cl] | 5.5 | 11.1 | 17.8 | 25.4 |
| [BMIM][DCA] | 10.6 | 15.3 | 21.4 | 28.1 |
| [BMIM][MTS] | 9.6 | 13.9 | 18.9 | 24.8 |
| [BMIM][Br] | 5.4 | 10.0 | 15.4 | 21.8 |
Given the increased tendency for the chaotropic (more hydrophobic) anions to cluster near the protein surface, we hypothesized that these anions could, in addition to their electrostatic effects, more favorably interact with the protein hydrophobic core. This idea is supported by a recent experimental study by Jha and Venkatesu.59 They quantified the transfer free energies between functional groups of the protein and ILs, which are derived from the protein solubility in ILs.60 Within HP35, there are three conserved phenylalanine residues that form a strong core and support stability of the three helices29 as shown in Fig. 3. An increased propensity to interact should be evident in the form of equilibrium free-energies of interaction between the anions and the PHE ring. To test this idea, we performed additional well-tempered MetaD simulations of one anion and one capped (i.e., neutral) phenylalanine residue under vacuum and biased the center-of-mass distance between the anion and the PHE ring. Specific details of the simulations and convergence tests61 are provided in the ESI.† The final free-energy profiles are shown in Fig. 4. The anions DCA and MTS both bind phenylalanine with around 75 kJ mol−1, notably stronger than Br− (∼66 kJ mol−1) and significantly stronger than Cl− (∼46 kJ mol−1). This analysis reveals that 1) protein unfolding rates in ILs could be strongly influenced by the degree to which the anion is able to withdraw hydrophobic residues from the core of the protein and 2) that computationally efficient tests like this pairwise binding energy calculation could be an efficient screening mechanism to support molecular design and engineering approaches. Additionally, we note that within the lens of a Hofmeister-like effect for IL/protein interactions, these results suggest that protein/ion interactions may play a more central role (than water/ion interactions) in the ordering of various anions. Recent work by Miller et al.17 also points to an IL-specific, i.e., not simply due to the ionic strength of the solution, role in opening a protein structure. Due to the high molecular weight of the IL substituents, the actual molar concentration of IL in these simulations is comparatively lower than the other studies that investigated ionic strength effects in protein unfolding,62 in support of the idea that the IL substituents themselves affect the protein in a manner beyond what is recognized as solely changing the solution's ionic strength.
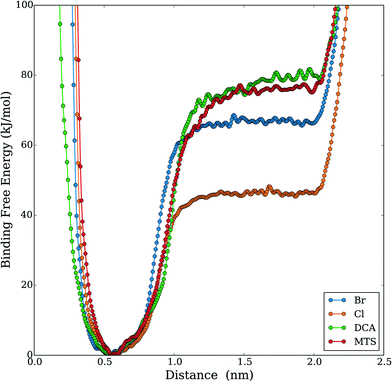 | ||
| Fig. 4 Free energy profile results of MetaD simulation of DCA–phenylalanine binding under vacuum (biased on the distance of the anion's center of mass and the ring structure of phenylalanine). | ||
Conclusions
The understanding of protein dynamics and kinetics in ILs can improve many biomedical and biochemistry applications such as protein stabilization, protein crystalization, and biocatalysis. Our study provides a strategy to guide future experimental efforts to prevent protein denaturation in ILs by providing a quantitative link between unfolding rates, which we show to be calculable in a greatly accelerated manner on a standard computer, and the interaction between hydrophobic anions and protein structural elements. Such knowledge will aid in the computational design of protein/IL pairs for a wide range of applications. For example, although ILs can solubilize cellulosic biomass, maintaining enzyme activity has been a challenge using the traditional pretreatment process.63–66 Our work enables computational screening of the IL design space to search for favorable solvents for both steps (biomass dissolution and biocatalysis). In biomedical applications, ILs also have been used in protein crystallization in order to overcome the problem of kinetic limitations and low yields.67,68 A new application of the work we presented in this aspect would be to study unfolding rates across temperatures and to estimate unfolding barriers based on Arrhenius relationships,34,39 providing a new tunable parameter (e.g., searching design space for ILs that maximize the predicted unfolding barrier).We have quantified and demonstrated the use of the infrequent metadynamics approach to faithfully reproduce the dynamics of protein unfolding processes. The ability to predict protein unfolding times on greatly accelerated timescales should be of great use to a wide range of studies including other IL-based investigations as well as other protein-unfolding processes including protein/surface interactions, which have also been shown to denature or destabilize proteins. Future development of the method should center on testing additional CVs, perhaps the well-defined fraction of native contacts noted above.27 Furthermore in order to enable large scale screening of different solvents or proteins and enable large scale molecular design and optimization studies, it would be beneficial to further optimize the parameters.
From the point of view of the physical chemistry of ion/protein interactions in IL systems, we believe these results call for further investigation of the anion hydrophobicity and interactions with protein hydrophobic cores. Given the large number of small fast-folding proteins and the large number of their variants that have been studied, it should be possible to identify suitable WT/mutant pairs in which some of the hydrophobic residues have been substituted by ALA or other less hydrophobic residues for computational study with a similar approach we outlined above. Further quantification of the solvent properties could be achieved through quantitative analysis of the viscosity B-coefficients for specific water/IL mixtures. Likewise, identifying other anions from the canon of ILs with a wide degree of hydrophobicity should also shed more light on the results presented above. We also note that although our results of using a majority of water as a co-solvent to study IL/protein interactions are consistent with much of the enzyme/IL literature, there are interesting effects to study with respect to understanding if the unfolding rates strongly correlate with the IL content in water, and under what circumstances. Although it is difficult to generalize the IL's effect on protein stability in all types of situations, we expect that our understanding will evolve as the ion–protein interactions become clearer with additional experiments and simulations.
Acknowledgements
The authors would like to thank Dr. Pratyush Tiwary for helpful discussions. Funding from the NSF award CBET-1150596 is acknowledged. This work was enabled through use of the computational resources provided by the Hyak supercomputer system, supported by the University of Washington.References
- H. Miyafuji, J. Wood Sci., 2015, 61, 343 CrossRef CAS.
- M. Naushad, Z. A. Alothman, A. B. Khan and M. Ali, Int. J. Biol. Macromol., 2012, 51, 555 CrossRef CAS PubMed.
- K. Fujita, D. R. MacFarlane and M. Forsyth, Chem. Commun., 2005, 4804 RSC.
- H. Weingartner, C. Cabrele and C. Herrmann, Phys. Chem. Chem. Phys., 2012, 14, 415 RSC.
- J. L. Baker, J. Furbish and G. E. Lindberg, J. Mol. Graphics Modell., 2015, 62, 202 CrossRef CAS PubMed.
- D. Constatinescu, C. Herrmann and H. Weingartner, Phys. Chem. Chem. Phys., 2010, 12, 1756 RSC.
- A. Kumar and P. Venkatesu, Int. J. Biol. Macromol., 2014, 63, 244 CrossRef CAS PubMed.
- F. van Rantwijk and R. A. Sheldon, Chem. Rev., 2007, 107, 2757 CrossRef CAS PubMed.
- N. Galamba, J. Phys. Chem. B, 2012, 116, 5242 CrossRef CAS PubMed.
- K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323 CrossRef CAS PubMed.
- W. Kunz, P. Lo Nostro and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 1 CrossRef CAS.
- M. M. Rieskautt and A. F. Ducruix, J. Biol. Chem., 1989, 264, 745 CAS.
- S. Finet, F. Skouri-Panet, M. Casselyn, F. Bonnete and A. Tardieu, Curr. Opin. Colloid Interface Sci., 2004, 9, 112 CrossRef CAS.
- Y. J. Zhang and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15249 CrossRef CAS PubMed.
- E. M. Nordwald and J. L. Kaar, Biotechnol. Bioeng., 2013, 110, 2352 CrossRef CAS PubMed.
- D. Constantinescu, H. Weingartner and C. Herrmann, Angew. Chem., Int. Ed., 2007, 46, 8887 CrossRef CAS PubMed.
- M. C. Miller, S. L. Hanna, K. G. DeFrates, O. C. Fiebig and T. D. Vaden, Int. J. Biol. Macromol., 2016, 85, 200 CrossRef CAS PubMed.
- M. Klahn, G. S. Lim, A. Seduraman and P. Wu, Phys. Chem. Chem. Phys., 2011, 13, 1649 RSC.
- M. Klahn, G. S. Lim and P. Wu, Phys. Chem. Chem. Phys., 2011, 13, 18647 RSC.
- P. R. Burney and J. Pfaendtner, J. Phys. Chem. B, 2013, 117, 2662 CrossRef CAS PubMed.
- M. Latif, M. Alif, N. M. Micaelo, A. Rahman and M. Basyaruddin, RSC Adv., 2014, 4, 48202 RSC.
- V. W. Jaeger and J. Pfaendtner, ACS Chem. Biol., 2013, 8, 1179 CrossRef CAS PubMed.
- V. Jaeger, P. Burney and J. Pfaendtner, Biophys. J., 2015, 108, 880 CrossRef CAS PubMed.
- P. R. Burney, E. M. Nordwald, K. Hickman, J. L. Kaar and J. Pfaendtner, Proteins: Struct., Funct., Bioinf., 2015, 83, 670 CrossRef CAS PubMed.
- N. M. Micaêlo and C. M. Soares, J. Phys. Chem. B, 2008, 112, 2566 CrossRef PubMed.
- J. P. K. G. Sprenger, Using Molecular Simulation to Study Biocatalysis in Ionic Liquids, in Computational Approaches for Studying Enzyme Mechanism Part A, ed. G. A. Voth, Elsevier, 2016, vol. 577 Search PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517 CrossRef CAS PubMed.
- J. M. Meng, D. Vardar, Y. M. Wang, H. C. Guo, J. F. Head and C. J. McKnight, Biochemistry, 2005, 44, 11963 CrossRef CAS PubMed.
- T. K. Chiu, J. Kubelka, R. Herbst-Irmer, W. A. Eaton, J. Hofrichter and D. R. Davies, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7517 CrossRef CAS PubMed.
- J. K. Chung, M. C. Thielges and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3578 CrossRef CAS PubMed.
- A. Fernandez, M. Y. Shen, A. Colubri, T. R. Sosnick, R. S. Berry and K. F. Freed, Biochemistry, 2003, 42, 664 CrossRef CAS PubMed.
- M. H. Wang, Y. F. Tang, S. S. Sato, L. Vugmeyster, C. J. McKnight and D. P. Raleigh, J. Am. Chem. Soc., 2003, 125, 6032 CrossRef CAS PubMed.
- P. L. Freddolino and K. Schulten, Biophys. J., 2009, 97, 2338 CrossRef CAS PubMed.
- P. Tiwary and M. Parrinello, Phys. Rev. Lett., 2013, 111, 5 CrossRef PubMed.
- O. Valsson, P. Tiwary and M. Parrinello, Annu. Rev. Phys. Chem., 2016, 67, 159 CrossRef CAS PubMed.
- M. Salvalaglio, P. Tiwary and M. Parrinello, J. Chem. Theory Comput., 2014, 10, 1420 CrossRef CAS PubMed.
- P. Tiwary, J. Mondal, J. A. Morrone and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12015 CrossRef CAS PubMed.
- P. Tiwary, V. Limongelli, M. Salvalaglio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E386 CrossRef CAS PubMed.
- K. L. Fleming, P. Tiwary and J. Pfaendtner, J. Phys. Chem. A, 2016, 120, 299 CrossRef CAS PubMed.
- A. Barducci, J. Pfaendtner and M. Bonomi, Tackling Sampling Challenges in Biomolecular Simulations, in Molecular Modeling of Proteins, 2nd edn, 2014 Search PubMed.
- S. Zheng and J. Pfaendtner, Mol. Simul., 2015, 41, 55 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435 CrossRef CAS PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604 CrossRef CAS.
- S. Piana, K. Lindorff-Larsen and D. E. Shaw, Biophys. J., 2011, 100, L47 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950 CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Imprey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882 CrossRef CAS PubMed.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882 CrossRef CAS PubMed.
- J. Kubelka, T. K. Chiu, D. R. Davies, W. A. Eaton and J. Hofrichter, J. Mol. Biol., 2006, 359, 546 CrossRef CAS PubMed.
- S. Honda, K. Yamasaki, Y. Sawada and H. Morii, Structure, 2004, 12, 1507 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 7 CrossRef PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319 CrossRef CAS PubMed.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 24, 247 Search PubMed.
- P. Attri, P. Venkatesu and A. Kumar, Phys. Chem. Chem. Phys., 2011, 13, 2788 RSC.
- A. P. Singh, R. L. Gardas and S. Senapati, Phys. Chem. Chem. Phys., 2015, 17, 25037 RSC.
- M. Anouti, J. Jacquemin and P. Porion, J. Phys. Chem. B, 2012, 116, 4228 CrossRef CAS PubMed.
- I. Jha and P. Venkatesu, Phys. Chem. Chem. Phys., 2015, 17, 20466 RSC.
- P. Attri and P. Venkatesu, Phys. Chem. Chem. Phys., 2011, 13, 6566 RSC.
- P. Tiwary and M. Parrinello, J. Phys. Chem. B, 2015, 119, 736 CrossRef CAS PubMed.
- D. E. Otzen, Biophys. J., 2002, 83, 2219 CrossRef CAS PubMed.
- A. Várnai, M. Siika-aho and L. Viikari, Enzyme Microb. Technol., 2010, 46, 185 CrossRef.
- R. A. Sheldon, R. M. Lau, M. J. Sorgedrager, F. van Rantwijk and K. R. Seddon, Green Chem., 2002, 4, 147 RSC.
- S. Park and R. J. Kazlauskas, Curr. Opin. Biotechnol., 2003, 14, 432 CrossRef CAS PubMed.
- S. Nakagame, R. P. Chandra and J. N. Saddler, Biotechnol. Bioeng., 2010, 105, 871 CAS.
- D. Hekmat, D. Hebel, S. Joswig, M. Schmidt and D. Weuster-Botz, Biotechnol. Lett., 2007, 29, 1703 CrossRef CAS PubMed.
- J. A. Garlitz, C. A. Summers, R. A. Flowers, II and G. E. O. Borgstahl, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1999, 55, 2037 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6me00047a |
| This journal is © The Royal Society of Chemistry 2016 |