Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-universal tracer diffusion in crowded media of non-inert obstacles
Surya K.
Ghosh
a,
Andrey G.
Cherstvy
a and
Ralf
Metzler
 *ab
*ab
aInstitute for Physics & Astronomy, University of Potsdam, 14476 Potsdam-Golm, Germany. E-mail: rmetzler@uni-potsdam.de
bDepartment of Physics, Tampere University of Technology, 33101 Tampere, Finland
First published on 26th November 2014
Abstract
We study the diffusion of a tracer particle, which moves in continuum space between a lattice of excluded volume, immobile non-inert obstacles. In particular, we analyse how the strength of the tracer–obstacle interactions and the volume occupancy of the crowders alter the diffusive motion of the tracer. From the details of partitioning of the tracer diffusion modes between trapping states when bound to obstacles and bulk diffusion, we examine the degree of localisation of the tracer in the lattice of crowders. We study the properties of the tracer diffusion in terms of the ensemble and time averaged mean squared displacements, the trapping time distributions, the amplitude variation of the time averaged mean squared displacements, and the non-Gaussianity parameter of the diffusing tracer. We conclude that tracer–obstacle adsorption and binding triggers a transient anomalous diffusion. From a very narrow spread of recorded individual time averaged trajectories we exclude continuous type random walk processes as the underlying physical model of the tracer diffusion in our system. For moderate tracer–crowder attraction the motion is found to be fully ergodic, while at stronger attraction strength a transient disparity between ensemble and time averaged mean squared displacements occurs. We also put our results into perspective with findings from experimental single-particle tracking and simulations of the diffusion of tagged tracers in dense crowded suspensions. Our results have implications for the diffusion, transport, and spreading of chemical components in highly crowded environments inside living cells and other structured liquids.
I. Introduction
Macromolecular crowding (MMC) abounds in living biological cells, with up to ϕ ≈ 30–35% of the volume of the cytoplasmic fluid being occupied by large biopolymers such as proteins, nucleic acids, ribosomes, as well as membranous structures, and other complexes.1–5 These volume-excluding and often non-inert obstacles alter the diffusion behaviour of cellular components and the rates of biochemical reactions taking place in this highly complex liquid.6–11 These changes occur both due to an enhanced solution viscosity12 and the sheer physical obstruction imposed on particle diffusion due to the presence of the obstacles.The mean squared displacement (MSD) of a tracer particle in such crowded solutions often becomes anomalous13–18
| 〈r2(t)〉 ∼ Dβtβ, | (1) |
Anomalous diffusion of the form (1) is modelled in terms of a wide range of stochastic processes.13–19 These include continuous time random walks (CTRW),13,14,37 fractional Brownian motion16,17,38,39 and the closely related fractional Langevin equation motion,16,17,39–41 as well as diffusion processes with space42–45 and time45–47 dependent diffusion coefficients. CTRW models are closely related to trap models, in which the tracer in the course of diffusion is successively immobilised.13,48–50 Despite advances in simulations29,51 and theoretical approaches,16,17 there is no consensus on the physical understanding of the subdiffusion of passive tracer particles in crowded solutions, that would be directly applicable to the cytoplasm of living cells.15,18 In particular, it is likely that different physical origins dominate for different tracer sizes and shapes, as well as length and time scales of the diffusion. The lack of a consensus picture for diffusion in MMC environments suggests that the observed anomalous diffusion is not universal but depends on specific parameters.
To address such specific origins for deviations from Brownian motion, extensive computer simulations of passive tracer diffusion were performed by several groups. The recent approaches of ref. 52 and 53, for instance, considering the tracer motion in lattices of immobile, randomly positioned obstacles or regularly ordered obstacles jiggling in a confining potential demonstrated that the anomalous diffusion regime is governed by the obstacle volume occupancy, with significant subdiffusive motion observed at higher crowder volume fraction ϕ. This subdiffusion is transient and can be quantified by the dependence of the local anomalous diffusion exponent
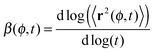 | (2) |
The study of obstructed diffusion by means of simulations was pioneered by Saxton in a series of papers.58–60 In particular, the effects of the fraction of lattice sites occupied by crowders and of their diffusivity were examined. Specifically, effects of tracer–obstacle binding on the anomalous diffusion properties were studied and connected to a binding energy landscape for immobile point-like obstacles positioned at a fixed concentration on the lattice.59 Obstructed diffusion of point-like tracers in a lattice of randomly positioned, static obstacles was investigated in ref. 61 and shown to give rise to a reduction of the tracer diffusivity D with the obstacle concentration. Nonzero values of the diffusivity D even for very densely packed obstacles appear in such a model due to the existence of a percolation structure. True long-time subdiffusion can only be realised at the percolation threshold in such lattices of randomly distributed obstacles.18 On a cubic lattice, the critical percolation thresholds corresponds to 31%.18 For a random walker on the infinite incipient cluster, the scaling exponent of the MSD is β ≈ 0.697.62 The physical reason is the formation of a labyrinthine-like environment,19 in which the tracer needs to escape dead ends and cross narrow causeways present on all scales. For lattices below the percolation transition as well as for regularly positioned obstacles, as in the current study, the anomalous diffusion regime is transient.
An interesting alternative to the modelling of transient anomalous diffusion are Lorentz gas based models which were developed to exploit the localisation transitions on a percolation network of overlapping spherical obstacles.63,64 The scaling relations for the suppression of the tracer diffusivity as the system approaches the critical percolation density ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) was determined, namely D(ϕ) ∼ [(ϕ −
was determined, namely D(ϕ) ∼ [(ϕ − ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) )/
)/![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ]μ, where the percolation exponent is μ ≈ 2.88.63 At the percolation threshold, persistent anomalous diffusion with exponent β = 2/6.25 ≈ 0.32 was found, for even denser systems the particles are eventually localised.63
]μ, where the percolation exponent is μ ≈ 2.88.63 At the percolation threshold, persistent anomalous diffusion with exponent β = 2/6.25 ≈ 0.32 was found, for even denser systems the particles are eventually localised.63
Here, we extend the class of systems considered by Saxton59 based on transient binding of tracer particles to physical obstacles. We perform extensive Monte-Carlo simulations of tracer diffusion on 3D lattices of sticky spherical obstacles of varying radius R. In this obstruction-and-binding diffusion model we examine the trapping time distributions of the tracers, the time averaged MSD—which is a more relevant observable when compared to experimental situations than the ensemble averaged MSD (1)—and the effective tracer diffusivity D. The model parameters are systematically varied, including the crowder radius R and thus the volume fraction of crowders ϕ and the tracer–crowder binding energy εA. A schematic of the system is shown in Fig. 1 along with sample trajectories of a tracer particle. These novel features substantially extend the known simulations results for obstructed tracer diffusion on 2D lattices of reflecting spherical52,53 and cylindrical65 obstacles. Despite the difference of mobile polymer obstacles to our scenario of ordered reactive crowders, our results show interesting similarities with the diffusion of tracer particles in dense solutions of non-inert polymer chains recently reported by the Holm group.66 We discuss the consequences of this similarity below.
The paper is organised as follows. In Section II we introduce the basic notations and the quantities to be analysed. We outline the computational scheme and theoretical concepts. In Section III we report the main simulations results and support them by theoretical scaling arguments. We analyse the effects of the MMC volume fraction and the strength of the obstacle–tracer binding. Moreover, we compute the ensemble and time averaged particle displacements as well as the distributions of particle trapping times to the sticky obstacles. To rationalise the stochastic behaviour and determine the concrete underlying effective diffusion model, we also systematically compute the non-Gaussianity parameter G. In Section IV the conclusions are drawn and possible applications of our results to some experimental systems are discussed.
II. Simulation model and approximations
To mimic the conditions of a crowded environment, we consider a primitive cubic lattice every site of which is occupied by a spherical obstacle, as shown in Fig. 1. The maximal size of the obstacle Rmax for the conditions of close packing is Rmax = a/2 where a is the lattice constant. In the following we will use a = 2 in dimensionless units. The maximal volume occupancy by obstacles on such a static cubic lattice is ϕmax = π/6 ≈ 0.524, compared to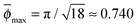 for the densest packing of spheres in 3D.67 The obstacles are considered immobile in our simulations.
for the densest packing of spheres in 3D.67 The obstacles are considered immobile in our simulations.
In the simulations presented below, the point-like tracer starts in the centre of a cage, at the maximal distance from the eight surrounding obstacles. At the very start the tracer particle thus performs free motion, until it encounters the surface of a crowding particle to which it can subsequently bind. The length scale of the spatial heterogeneity l* in the system is of the order of the free path of the tracer between neighbouring obstacles, 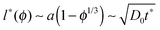 . As we will show such heterogeneities effect subdiffusion at intermediate time scales t*, while at much longer time-scales the diffusion becomes Brownian, as demonstrated in Fig. 3. As many binding–unbinding events take place during the length of the recorded traces in our simulations, the initial particle position does not affect the long time dynamics. The tracer particle becomes adsorbed onto the obstacle surface with the binding energy εA and stays in the bound state for the average adsorption time tads,i. While bound, the tracer diffuses along the spherical obstacle surface with the same diffusion coefficient as in the free unbound state, that is, it moves along the surface of a crowder sphere with Dads = D0. The tracer is considered unbound once it separates from the obstacle for more than the distance 0.1Rmax, see also the definition of the interaction potential below.87 In our simulations we place a single tracer on the crowder lattice and then average over many individual traces. The repeated binding and unbinding events separating the particle motion between surface and bulk diffusion lead to an effective distribution between the modes of tracer motion, which is reflected in the tracer particle MSD and other diffusive characteristics such as average trapping times, see below.
. As we will show such heterogeneities effect subdiffusion at intermediate time scales t*, while at much longer time-scales the diffusion becomes Brownian, as demonstrated in Fig. 3. As many binding–unbinding events take place during the length of the recorded traces in our simulations, the initial particle position does not affect the long time dynamics. The tracer particle becomes adsorbed onto the obstacle surface with the binding energy εA and stays in the bound state for the average adsorption time tads,i. While bound, the tracer diffuses along the spherical obstacle surface with the same diffusion coefficient as in the free unbound state, that is, it moves along the surface of a crowder sphere with Dads = D0. The tracer is considered unbound once it separates from the obstacle for more than the distance 0.1Rmax, see also the definition of the interaction potential below.87 In our simulations we place a single tracer on the crowder lattice and then average over many individual traces. The repeated binding and unbinding events separating the particle motion between surface and bulk diffusion lead to an effective distribution between the modes of tracer motion, which is reflected in the tracer particle MSD and other diffusive characteristics such as average trapping times, see below.
The attractive interactions between the mobile tracer particle and immobile crowder spheres are modelled in terms of the Lennard-Jones 6-12 potential, whose attractive branch is cut off at the distance rcutoff, namely
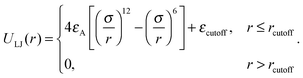 | (3) |
We simulate the motion of the point-like tracer of mass m with coordinate r(t) in the presence of friction based on the Langevin equation
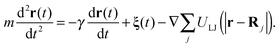 | (4) |
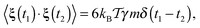 | (5) |
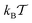 represents the thermal energy. The noise has zero mean and vanishing correlations in the different Cartesian directions. The sum in eqn (4) runs over the positions of all crowding particles Rj. The fact that we consider a point-like particle is not a severe restriction, as a finite size of the tracer particle would correspond to a re-normalisation of the crowder radius, compare also ref. 61. Concurrently the surface diffusivity of the tracer along the crowders would need to be adjusted.
represents the thermal energy. The noise has zero mean and vanishing correlations in the different Cartesian directions. The sum in eqn (4) runs over the positions of all crowding particles Rj. The fact that we consider a point-like particle is not a severe restriction, as a finite size of the tracer particle would correspond to a re-normalisation of the crowder radius, compare also ref. 61. Concurrently the surface diffusivity of the tracer along the crowders would need to be adjusted.
In our simulations we neglect tracer–obstacle hydrodynamic interactions, which can, in principle, affect the long-time behaviour of the system. In particular, because of their long-range 1/r-nature,10 the diffusing particles can feel the obstacles at a finite distance without direct collisions, see e.g.ref. 36. Note however that hydrodynamic interactions have recently also been demonstrated to affect the short-time tracer diffusion dynamics in fluids.69,70
In free space the solution of the Ornstein–Uhlenbeck process (4) without the last term is well known,71
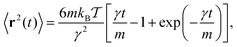 | (6) |
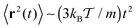 | (7) |
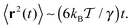 | (8) |
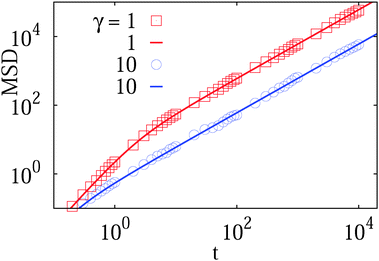 | ||
| Fig. 2 MSD from simulations (dots) of the free underdamped Langevin equation versus the analytical Ornstein–Uhlenbeck solution (6) (solid curves), plotted for different values of the friction coefficient γ, as indicated in the plot. The ballistic regime can be clearly distinguished in the case of lower friction. | ||
The particle mass is m = 1 throughout the paper (we made sure that the code works fine for varying particle mass and solution friction, as shown in Fig. 2). In all figures below, time t is shown in units of the simulation step δt = 0.001 of the Verlet velocity integration scheme, the displacements appear in units of the lattice constant a. The obstacle size below is given in terms of the maximal geometrically allowed radius
| Rmax = a/2 | (9) |
III. Results
We discuss the simulations results with respect to three main observables. In Section IIIA we study the ensemble averaged MSD and the associated effective diffusivity. The trapping times spent by the tracer on the obstacle surface are analysed in Section IIIB, and in Section IIIC we investigate the time averaged MSD based on single trajectory time series.A. MSD, scaling exponent, and effective diffusivity
We study the MSD 〈r2(t)〉 of the tracer particles at varying volume occupancy ϕ of obstacles and the tracer–obstacle affinity εA. The main results are shown in Fig. 3 and 4. Generally, we observe that for small interaction strengths εA the anomalous diffusion exponent β(t) varies along the time evolution of the MSD 〈r2(t)〉. At short times it starts out with the underdamped ballistic motion (7) of the above Ornstein–Uhlenbeck process, as demonstrated in Fig. 2. Such a short time superdiffusive behaviour is due to inertial effects and was indeed observed experimentally, for instance, in single particle tracking studies of fluorescent beads in sucrose solutions;57 see also the detailed studies of ref. 69 and 70 of inertial effects for the particle diffusion in a fluid. Subsequently, Fig. 3 demonstrates that the MSD crosses over to a transient subdiffusive regime with 0 < β(t) < 1. In the long time limit the tracer particle performs Brownian motion with a linear scaling of the MSD and β(t) = 1. Concurrently this regime is characterised by a reduced diffusivity D(ϕ) as compared to unrestricted Brownian motion of the tracer. The dependence of the effective diffusivity D(ϕ) on the MMC volume fraction ϕ is shown for different interaction strengths in Fig. 4. For weakly adhesive obstacles, the diffusion becomes monotonically slower for larger crowders positioned on the lattice.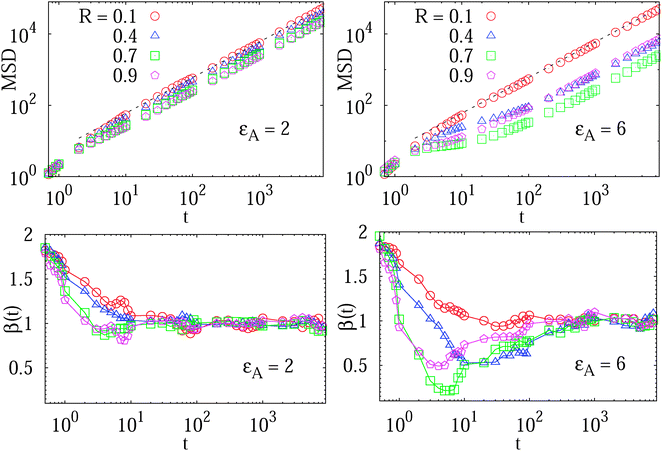 | ||
Fig. 3 MSD 〈r2(t)〉 of the tracer particles and the corresponding scaling exponent β(t), plotted for two trace–crowder attraction strengths, εA = 2 and 6, in units of 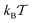 . The result (8) for the MSD of three dimensional Brownian motion is represented by the dashed line in the MSD plots. The number of trajectories used for the averaging is N = 103, and each trajectory consists of 107 steps corresponding to the length T = 104 of the simulated time series r(t) in terms of the simulation step δt = 10−3. Other parameters are as indicated in the plots. The obstacle radius is given in terms of Rmax = a/2. The data sets for varying crowder radius are shown by open symbols. . The result (8) for the MSD of three dimensional Brownian motion is represented by the dashed line in the MSD plots. The number of trajectories used for the averaging is N = 103, and each trajectory consists of 107 steps corresponding to the length T = 104 of the simulated time series r(t) in terms of the simulation step δt = 10−3. Other parameters are as indicated in the plots. The obstacle radius is given in terms of Rmax = a/2. The data sets for varying crowder radius are shown by open symbols. | ||
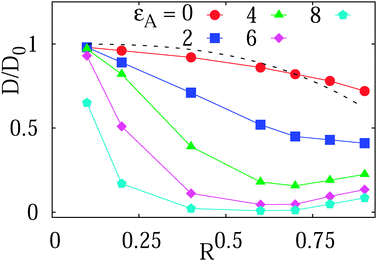 | ||
| Fig. 4 Long-time diffusivity D(ϕ)/D0 in the terminal Brownian regime as function of the obstacle size, plotted for varying tracer–obstacle attraction strengths. Other parameters are the same as in Fig. 3. The dotted line represents the prediction by eqn (10) for inert obstacles. The data sets for varying adsorption strength are shown as filled symbols. | ||
Let us look at these behaviours in some more detail. The variation of the scaling exponent β(t) with the crowding fraction and tracer–crowder attraction strength is shown in Fig. 3. We observe that as both εA and ϕ increase, the transient subdiffusion regime progressively extends over a larger time window. Remarkably, this anomalous diffusion spans up to two decades of time for substantial tracer–obstacle attraction strengths, see the plot of β(t) for 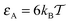 in Fig. 3. For relatively weak tracer–obstacle attraction, at
in Fig. 3. For relatively weak tracer–obstacle attraction, at 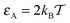 , only marginally anomalous tracer diffusion was detected, with β ∼ 0.85–1. Overall, the subdiffusion regime extends over one to two decades of time, similar to the results for inert static randomly-positioned obstacles61 or for the motion of tracers in a random channel with sticky surfaces.72
, only marginally anomalous tracer diffusion was detected, with β ∼ 0.85–1. Overall, the subdiffusion regime extends over one to two decades of time, similar to the results for inert static randomly-positioned obstacles61 or for the motion of tracers in a random channel with sticky surfaces.72
A physically similar renormalisation of the particle diffusivity was discovered in ref. 73 for glassy states in sticky-particle systems at relatively large volume fractions ϕ. The phase diagram of the hard sphere mixture with a short range inter-particle attraction as well as a self-diffusive MSD dependence were examined, for instance, by simulations in ref. 73. The implications of the square-well sphere-sphere interaction potential εA and volume fraction ϕ of crowders were rationalised in detail. A progressive slowing down of the particle self-diffusion in the attractive hard-sphere mixtures as functions of ϕ and εA observed in Fig. 4 and 5 of ref. 73 is similar to the properties of the tracer diffusion on the lattice of moderately-sticky crowders examined here.
For non-attracting obstacles corresponding to εA = 0 the ratio D(ϕ)/D0 of the diffusing coefficient of the tracer particle versus its value in an un-obstructed environment as function of the obstacle volume occupancy ϕ in a simple mean field approach is predicted to scale as
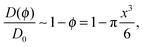 | (10) |
For moderate attraction, 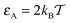 , the decrease of D(ϕ)/D0 with R becomes less pronounced at R ≳ 0.6. For even stronger tracer–obstacle interaction,
, the decrease of D(ϕ)/D0 with R becomes less pronounced at R ≳ 0.6. For even stronger tracer–obstacle interaction, 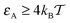 , remarkably the long-time diffusivity D(ϕ) becomes non-monotonic with the crowder size R, as shown in Fig. 4. Physically, at higher ϕ the available space for tracer diffusion becomes effectively reduced from the three dimensional volume to a lower dimensional space. This creates pathways or channels between the “cages” created by the obstacle and can effectively speed up the exploration of space by the tracer particle at higher ϕ fractions. Note that this effect would be modified when the surface diffusivity were considerably smaller than the volume diffusivity. However, as shown in the discussion of the trapping times below, another contribution to this speed up-effect could be that for larger crowder radius R the tracer is in a limbo between vicinal attractive surfaces and thus manoeuvres between obstacles without binding to them.
, remarkably the long-time diffusivity D(ϕ) becomes non-monotonic with the crowder size R, as shown in Fig. 4. Physically, at higher ϕ the available space for tracer diffusion becomes effectively reduced from the three dimensional volume to a lower dimensional space. This creates pathways or channels between the “cages” created by the obstacle and can effectively speed up the exploration of space by the tracer particle at higher ϕ fractions. Note that this effect would be modified when the surface diffusivity were considerably smaller than the volume diffusivity. However, as shown in the discussion of the trapping times below, another contribution to this speed up-effect could be that for larger crowder radius R the tracer is in a limbo between vicinal attractive surfaces and thus manoeuvres between obstacles without binding to them.
We note that in ref. 65 the diffusion coefficient of a tracer on an array of cylindrical obstacles on a static two dimensional square lattice was analysed in terms of the generalised Fick–Jacobs equation and by Brownian dynamics simulations. For the relative diffusivity as function of the crowding fraction ϕ the analogous behaviour D(ϕ)/D0 = 1 − ϕ = 1 − π(R/Rmax)2/4 was found, where π/4 is the maximal surface coverage in this situation.65
B. Statistics of tracer trapping times
The non-monotonic dependence of the long-time tracer particle diffusivity on the crowding fraction is also manifested in the non-monotonic variation of the times that the tracer spends in the obstacle-adsorbed state. In Fig. 5 we present the statistics of individual adsorption times to the crowding particles along a long trajectory containing many binding–unbinding events. In the main graph of Fig. 5 we observe the distribution of tracer–obstacle adsorption times features a peak at short tads, while the tails of the histograms indicates the expected exponential decay. The corresponding mean adsorption time 〈tads〉 is the average over all the binding events encountered in our simulations for a particular set of the model parameters. As we can see, for larger crowders these exponential tails become progressively longer with increasing obstacle size up to some R < 0.6 × a/2, that is, the duration of binding events can become significantly longer. In the inset of Fig. 5 we use a logarithmic abscissa to pronounce the initial peak of the histograms. From this plot it becomes clear that several extremely long binding events can shift the mean 〈tads〉 of the binding time significantly, compare the relative positioning of the maximum of the histograms and the mean values indicated by the coloured dots.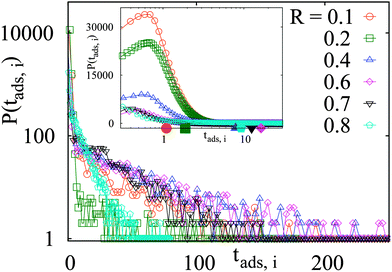 | ||
Fig. 5 Histograms P(tads,i) of individual binding times tads,i spent in the obstacle-adsorbed state by the tracer particles, plotted for the parameters of Fig. 3 with attraction strength 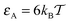 . The mean values 〈tads〉 for each crowder radius are indicated as the dots on the horizontal axis of the inset with the corresponding colour, indicating a non-monotonic behaviour with R. The main graph is shown in log-linear scale to show the exponential tails of the distributions, whereas the inset features a linear-log scale. The total length of the simulated trajectories is 107 steps. The obstacle radius R is given in the legend in terms of Rmax = a/2. . The mean values 〈tads〉 for each crowder radius are indicated as the dots on the horizontal axis of the inset with the corresponding colour, indicating a non-monotonic behaviour with R. The main graph is shown in log-linear scale to show the exponential tails of the distributions, whereas the inset features a linear-log scale. The total length of the simulated trajectories is 107 steps. The obstacle radius R is given in the legend in terms of Rmax = a/2. | ||
Thus, a small number of extremely long binding events govern the corresponding mean adsorption time 〈tads〉. Here, we mention the related study of ref. 75 in which the modes of surface versus bulk diffusion of a tracer in spherical domains were investigated. Also note that a different tracer diffusivity in the obstacle-bound mode as compared to the bulk diffusion can give rise to new interesting effects. In particular, an optimisation of the overall passage times of a tracer in the target-search problems on a lattice of trapping sites (obstacles) with a likely slower diffusivity should be analysed in the future.
Let us now turn to the total time of adsorption tA experience by the tracer particle during a trajectory of duration T generated. We thus sum up all the adsorption times experienced by the tracer,
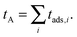 | (11) |
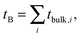 | (12) |
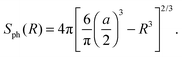 | (13) |
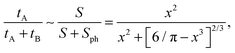 | (14) |
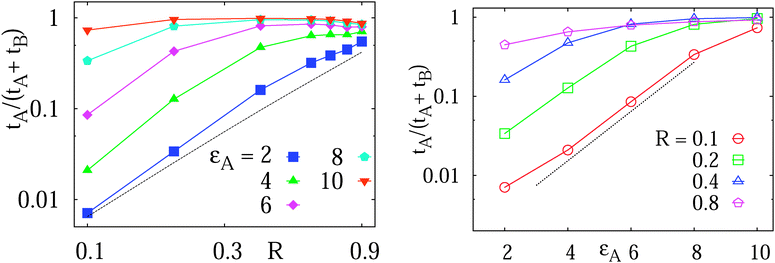 | ||
| Fig. 6 Left: total diffusion time tA in the adsorbed state of the tracer to the obstacle surface versus the obstacle size R, plotted in the log–log scale for varying binding strengths. Data obtained from averages of the histograms as those presented in Fig. 5. The dotted asymptote represents eqn (14). Right: plot of tAversus εA for varying obstacle radius. The dotted line indicates the exponential activation of tA mentioned in the text. At higher εA a saturation of tA is observed. | ||
The ratio tA/T given by eqn (14) is quadratic in the obstacle size R for small volume occupancy by obstacles. This result is in agreement with our simulations results for moderate tracer–obstacle binding, as shown in Fig. 6. In fact, for the attraction strength 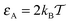 the agreement with result (14) is quite good given the simplicity of our model. In the shown double-logarithmic scale of Fig. 6 over the range R/Rmax = 0.1–0.9 the law (14) in fact only weakly deviates from the quadratic scaling tA/(tA + tB) ∼ (π/6)2/3x2. Naturally, the data for increasing binding affinity progressively deviate from the formula (14), for the strongest binding strength shown the particles move almost exclusively on the obstacle surface, independently of the obstacle size.
the agreement with result (14) is quite good given the simplicity of our model. In the shown double-logarithmic scale of Fig. 6 over the range R/Rmax = 0.1–0.9 the law (14) in fact only weakly deviates from the quadratic scaling tA/(tA + tB) ∼ (π/6)2/3x2. Naturally, the data for increasing binding affinity progressively deviate from the formula (14), for the strongest binding strength shown the particles move almost exclusively on the obstacle surface, independently of the obstacle size.
We observe that for small obstacle sizes and weak tracer–obstacle attraction strengths the total adsorption time tA at fixed R grows exponentially with εA, 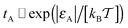 , corresponding to the Boltzmann activation in an equilibrium system. As demonstrated in Fig. 6 on the right, for strong tracer–crowder attraction a saturation in tA(εA) is reached, such that the activation curve for the ratio tA/(tA + tB) is analogous to the expression for a simple two level system,
, corresponding to the Boltzmann activation in an equilibrium system. As demonstrated in Fig. 6 on the right, for strong tracer–crowder attraction a saturation in tA(εA) is reached, such that the activation curve for the ratio tA/(tA + tB) is analogous to the expression for a simple two level system, 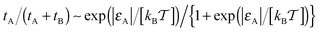 . For larger crowders, when the tracers are confined predominantly to the obstacle surface, the saturation effect at larger attraction strengths is more pronounced, see Fig. 6.
. For larger crowders, when the tracers are confined predominantly to the obstacle surface, the saturation effect at larger attraction strengths is more pronounced, see Fig. 6.
In agreement with the results of Fig. 3 for the MSD, at moderate tracer–obstacle binding the adsorption time progressively increases for more voluminous obstacles on the lattice. In contrast, at strong tracer–crowder adsorption the adsorption time initially increases with the obstacle size
| R = a[3ϕ/(4π)]1/3 | (15) |
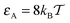 and
and 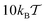 , as well as for the mean values shown in Fig. 5. This decrease of the mean adsorption time and thus a stronger contribution of bulk excursions is consistent with the non-monotonic dependence of D(ϕ)/D0 at large tracer–obstacle binding strengths εA and with the enhanced diffusivity for larger strongly adhesive obstacles, see the curve for
, as well as for the mean values shown in Fig. 5. This decrease of the mean adsorption time and thus a stronger contribution of bulk excursions is consistent with the non-monotonic dependence of D(ϕ)/D0 at large tracer–obstacle binding strengths εA and with the enhanced diffusivity for larger strongly adhesive obstacles, see the curve for 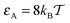 in Fig. 4. We ascribe this small yet somewhat counterintuitive effect to a competition of binding to neighbouring surfaces due to which the tracer particle is in a limbo in the bulk, possibly in conjunction with the reduced effective dimensionality of the environment mentioned above.
in Fig. 4. We ascribe this small yet somewhat counterintuitive effect to a competition of binding to neighbouring surfaces due to which the tracer particle is in a limbo in the bulk, possibly in conjunction with the reduced effective dimensionality of the environment mentioned above.
C. Time averaged MSD and non-Gaussianity parameter
To obtain more insight into the characteristics of the diffusive motion of the tracer particle in the crowded environment, we compute the time averaged MSD15–19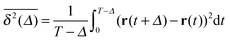 | (16) |
 we also consider the average
we also consider the average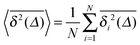 | (17) |
In Fig. 7 we show the time averaged MSD (16) along with the MSD 〈r2(t)〉 of N = 100 individual trajectories. Let us first focus on the case of a moderate tracer–obstacle attraction strength, 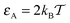 . We observe that the individual time traces
. We observe that the individual time traces 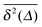 initially grow ballistically and then cross over to normal diffusion, as indicated by the slopes in Fig. 7. The results for individual time traces
initially grow ballistically and then cross over to normal diffusion, as indicated by the slopes in Fig. 7. The results for individual time traces 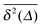 show only minute amplitude variations at different lag times, quantitatively similar to the spread of time traces of regular Brownian particles. Of course, when Δ approaches the measurement time T, the statistics of the time average defining
show only minute amplitude variations at different lag times, quantitatively similar to the spread of time traces of regular Brownian particles. Of course, when Δ approaches the measurement time T, the statistics of the time average defining 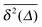 worsen and some amplitude scatter occurs.
worsen and some amplitude scatter occurs.
The average (17) almost perfectly coincides with the ensemble average MSD 〈r2(t)〉, compare the blue and green curves in Fig. 7. The latter observation corroborates the ergodic nature of the tracer motion, that is, the equivalence of ensemble and long time average of physical observables, here 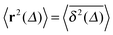 .15–17 The linear long time scaling of the MSD defines the effective diffusion coefficient D(ϕ) we shown in Fig. 4. Note that prolonged adsorption periods of the tracer on obstacle spheres correspond to effective trapping and delays the growth of either 〈x2(Δ)〉 or
.15–17 The linear long time scaling of the MSD defines the effective diffusion coefficient D(ϕ) we shown in Fig. 4. Note that prolonged adsorption periods of the tracer on obstacle spheres correspond to effective trapping and delays the growth of either 〈x2(Δ)〉 or 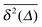 . For more information on the violation of the equivalence between time and ensemble averaged physical observables in anomalous-diffusive stochastic processes we refer to the recent review in ref. 17.
. For more information on the violation of the equivalence between time and ensemble averaged physical observables in anomalous-diffusive stochastic processes we refer to the recent review in ref. 17.
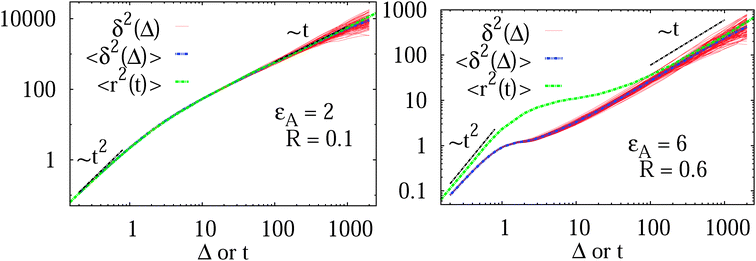 | ||
Fig. 7 MSD 〈r2(t)〉 (green curves) and time averaged MSD 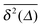 defined in eqn (16) (red curves), as well as the ensemble average defined in eqn (16) (red curves), as well as the ensemble average 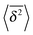 (blue curves) over the simulated trajectories. Parameters are as indicated in the panels, the number of traces used for averaging is N = 100, and the length of the trajectories is T = 104 corresponding to 107 simulation steps. (blue curves) over the simulated trajectories. Parameters are as indicated in the panels, the number of traces used for averaging is N = 100, and the length of the trajectories is T = 104 corresponding to 107 simulation steps. | ||
As shown for the binding time statistics above, the trapping times are exponentially distributed and thus the long time motion converges to regular Brownian motion with a reduced, effective diffusivity D(ϕ). This scenario is therefore fundamentally different from subdiffusive CTRWs,14,37 in which the characteristic trapping time diverges. Our Brownian motion-based physical rationale is consistent with experimental observations of protein diffusion in dense dextran solutions and with Monte-Carlo simulations of tracer diffusion on lattices of immobile inert obstacles as reported in ref. 56. In addition, we checked that the average time averaged MSD features no dependence on the trace length T: the values of 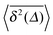 almost perfectly overlap for different trace-lengths T, as demonstrated in Fig. 8 indicating the Brownian nature of the diffusion process.
almost perfectly overlap for different trace-lengths T, as demonstrated in Fig. 8 indicating the Brownian nature of the diffusion process.
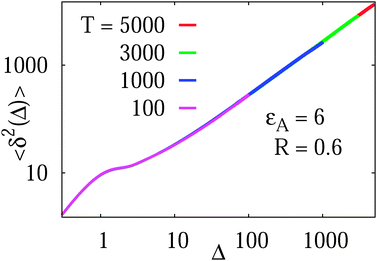 | ||
Fig. 8 Independence of the time averaged MSD 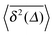 on the length T of the trajectory r(t). Parameters are the same as in Fig. 7. on the length T of the trajectory r(t). Parameters are the same as in Fig. 7. | ||
A different situation is encountered when we consider strong tracer–obstacle attraction, 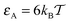 in Fig. 7. We immediately observe that up to t = Δ ≈ 102 the time averaged MSD
in Fig. 7. We immediately observe that up to t = Δ ≈ 102 the time averaged MSD 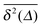 significantly differs from the corresponding ensemble average 〈r2(t)〉. That is, on these time scales the systems exhibits the disparity
significantly differs from the corresponding ensemble average 〈r2(t)〉. That is, on these time scales the systems exhibits the disparity 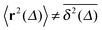 . For times exceeding t = Δ ≈ 102 the agreement between both quantities becomes excellent, the system is asymptotically ergodic. Individual curves
. For times exceeding t = Δ ≈ 102 the agreement between both quantities becomes excellent, the system is asymptotically ergodic. Individual curves 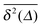 for single time traces show a somewhat increased spread around their mean
for single time traces show a somewhat increased spread around their mean 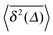 , however, this is still within the range expected for (asymptotically) ergodic processes,76 and is significantly different from weakly non-ergodic processes such as subdiffusive CTRWs15–17,19,77 or heterogeneous diffusion processes.17,42 For diffusion processes of the subdiffusive CTRW type the spread of individual time averaged MSD traces is expected to be finite even for vanishing lag times.16,17 This kind of behaviour is definitely not observed in our simulations. Here a very narrow spread of
, however, this is still within the range expected for (asymptotically) ergodic processes,76 and is significantly different from weakly non-ergodic processes such as subdiffusive CTRWs15–17,19,77 or heterogeneous diffusion processes.17,42 For diffusion processes of the subdiffusive CTRW type the spread of individual time averaged MSD traces is expected to be finite even for vanishing lag times.16,17 This kind of behaviour is definitely not observed in our simulations. Here a very narrow spread of 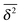 in the whole range of tracer–obstacle affinities and obstacle sizes is observed, see, e.g., Fig. 7. The transient non-ergodic features observed here imply that the relaxation time towards ergodic behaviour is increased for longer trapping times when the tracer–obstacle attraction is more pronounced. The fact that the disparity
in the whole range of tracer–obstacle affinities and obstacle sizes is observed, see, e.g., Fig. 7. The transient non-ergodic features observed here imply that the relaxation time towards ergodic behaviour is increased for longer trapping times when the tracer–obstacle attraction is more pronounced. The fact that the disparity 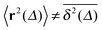 is most pronounced around the turnover from initial ballistic to terminal Brownian motion is consistent with observations of confined stochastic processes driven by correlated Gaussian noise.17,79
is most pronounced around the turnover from initial ballistic to terminal Brownian motion is consistent with observations of confined stochastic processes driven by correlated Gaussian noise.17,79
We now address a quantity that is based on the fourth order moment of the time trace 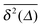 . This non-Gaussianity parameter G(Δ) was shown to be a sensitive experimental indicator of the type of effective stochastic process driving the tracer particle in crowded complex fluids.57 The non-Gaussianity parameter in three dimensions is defined by18
. This non-Gaussianity parameter G(Δ) was shown to be a sensitive experimental indicator of the type of effective stochastic process driving the tracer particle in crowded complex fluids.57 The non-Gaussianity parameter in three dimensions is defined by18
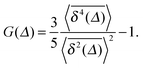 | (18) |
We observe that for the simulated diffusion process in the presence of attractive obstacles the non-Gaussianity parameter shown in Fig. 9 is close to zero for almost the entire length of the traces, apart from the initial regime of the motion including inertial effects. These short time deviations from G ≈ 0 are particularly pronounced for relatively large obstacles with strong tracer–obstacle attraction, as shown for the different parameters analysed in Fig. 9. The fact that G ≈ 0 together with the equivalence of the ensemble and time averaged MSDs at sufficiently long times are, of course, a mirror for the Brownian nature of the observed motion. The smaller non-zero values of G detected in the long-time limit in Fig. 9 are due to small discrepancies between the ensemble and time averaged MSDs.
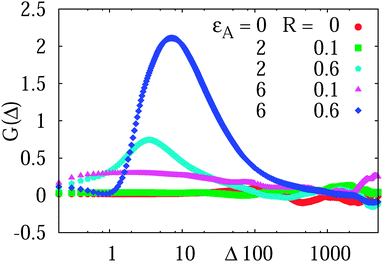 | ||
| Fig. 9 Non-Gaussianity parameter (18) computed for the tracer diffusion on a lattice of sticky obstacles, the parameters are indicated. As a reference for almost perfect Gaussian behaviour G = 0, we present the non-Gaussianity parameter for vanishingly small, inert obstacles. The length of individual simulated trajectories is T = 104. | ||
At short to moderate times the non-Gaussianity parameter substantially deviates from the zero value characteristic of Brownian motion for strongly adhesive and relatively large crowders, see, e.g., the blue curve in Fig. 9. The deviations of G(Δ) occur at time scales of t ∼ 1–30 when the tracer diffusion is inherently non-ergodic, as we see from the right panel of Fig. 7 plotted for the same parameters (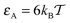 and R/Rmax = 0.6). At very short times, t ≪ 1, on which the MSD and time averaged MSD coincide, the non-Gaussianity parameter respectively assumes very small values. Otherwise, the deviations from G = 0 we observe are within the range typically measured in experiments57 for asymptotically ergodic stationary-increment processes.
and R/Rmax = 0.6). At very short times, t ≪ 1, on which the MSD and time averaged MSD coincide, the non-Gaussianity parameter respectively assumes very small values. Otherwise, the deviations from G = 0 we observe are within the range typically measured in experiments57 for asymptotically ergodic stationary-increment processes.
IV. Conclusions
We studied the passive motion of a tracer particle in an ordered, stationary array of attractive spherical crowders. Based on a truncated attractive Lennard Jones interaction between tracer and crowding obstacles, we simulate long individual trajectories of the tracer based on the Langevin equation. The resulting motion features a transition from initial ballistic flights corresponding to the inertial particle motion to a long time Brownian diffusion behaviour. The magnitude of the effective diffusion coefficient of this terminal Brownian motion is reduced for increasing obstacle volume filling fraction and tracer–obstacle attraction. However, a distinct non-monotonicity in this behaviour for large obstacle radii and high attraction strength is observed, likely due to competing attraction from multiple obstacles for which the tracer particle is in a limbo in the bulk. The same effect also leads to a decrease of the time tA(ϕ) spent adsorbed to the obstacle surfaces during a long trajectory. The long time Brownian dynamics was consistently shown to be associated with approximately vanishing non-Gaussianity parameter. These dynamic features point out the crucial role of varying tracer–obstacle binding strengths in the analysis of crowded systems, as performed here. To put these qualitative statements on a more physical foundation, additional simulations will be necessary. In particular, we will study the time averaged van Hove cross-correlation functions78 for the tracer motion.At intermediate times the tracer particle motion is anomalous, with a distinctly time-dependent scaling exponent β(t). In this regime the trapping to the obstacles becomes the dominant mechanism. According to our results the time and ensemble averaged MSDs are equivalent for moderate tracer–obstacle attraction strength, however, a transient non-ergodic disparity between the two observables is observed over a range of some 2.5 orders of magnitude for stronger tracer–crowder binding. This transient form of weakly non-ergodic behaviour was previously observed for correlated Gaussian processes under confinement34,79 of the otherwise ergodic process.39 This behaviour should be kept in mind when precise diffusive properties are to be analysed from measured or simulated time traces of our system.
Extensions of the current model should consider a range of surface diffusivities of tracer particles bound to obstacles. Moreover, the arrangement of crowders should release the static, ordered arrangement on a lattice. Thus, off-lattice simulations could include the motion of crowders around their equilibrium positions, similarly to the analysis in ref. 53. Differences in the sizes of individual crowders and a certain randomness in the tracer–obstacle affinity would be additional relevant generalisations of the current system. Mobile obstacles were shown to profoundly reduce the time range of the transient subdiffusive motion compared to immobile crowders.53 However, the generality of these findings needs to be explored in a broader parameter range. Currently, it remains elusive to arrive at realistic models capturing the richness of real MMC effects in living biological cells with their wide variety of crowder shapes, surface properties, persistence length and degree of branching as well as a poly-disperse size distribution, in addition to cellular structural elements, as well as charge effects.5 Finally, active processes such as energy-consuming transport in living cells35,80,81 needs to be added to achieve a closed picture of all facets of cellular dynamics.
Our study complements several other recent analyses of tracer motion in crowded environments. Thus, tracer diffusion in a system of relaxed and stretched polymer chains in the presence of tracer–polymer attraction was studied by Langevin dynamics simulations with the Espresso package.82 We observe that such obstructed diffusion with sticky obstacles resembles our current results. For instance, the evolution of the time-dependent MSD scaling exponent β (see Fig. 4 in ref. 82) shows a transition from the initial ballistic regime to a subdiffusive regime at intermediate times, and further to Brownian motion in the long-time limit. The anomalous diffusion regime was shown to span a larger time window for the relaxed as compared to the stretched self-avoiding chains.82 Higher polymer densities and stronger tracer–polymer interactions yield wider regions of tracer subdiffusion.82 A continuation of this study for tracer diffusion in a cylindrical pore with surface-grafted polymer brushes of varying density showed that the subdiffusive regime is more pronounced for weak-to-moderate tracer–polymer interaction.66
We also mention an experimental study of impeded colloidal diffusion in transient polymer networks with varying colloid–polymer binding interactions.83 For the diffusion of an inert tracer in a responsive elastic network system, when the tracer size is of the same order as the unit cell of this gel, transient subdiffusion was reported and shown to involve characteristic collective dynamics of tracer and gel.78 The transient subdiffusion in this study is in contrast to the experimentally observed long-tailed distribution of trapping times of sub-micron tracers in semi-flexible, inherently dynamic networks of cross-linked actin84 and thus further underlines the non-universal character of the dynamics in crowded systems. We finally mention that diffusion in two-dimensional, oriented fibrous networks in the presence of repulsive and attractive particle–obstacle interactions was in fact studied experimentally in connection with hydrogel-like structures of the extracellular matrix.85
Is crowding in cells merely an effect of cramming a rich multitude of different bio-molecules into a minimal volume, or does it have an evolutionary purpose in giving rise to dynamic phenomenon such as (transient) subdiffusion?21,86 The combination of advanced single particle technology and other experimental methods along with improved in silico studies will lead to significant advances in the understanding of these still elusive questions.
Acknowledgements
The authors acknowledge funding from the Academy of Finland (FiDiPro scheme to RM), the German Research Foundation (DFG Grant CH 707/5-1 to AGC), and the German Ministry of Education and Research (BMBF Grant to SG).References
- S. B. Zimmerman and S. O. Trach, J. Mol. Biol., 1991, 222, 599 CrossRef CAS PubMed.
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27 CrossRef CAS PubMed.
- D. Hall and A. P. Minton, Biochim. Biophys. Acta, 2003, 1649, 127 CrossRef CAS.
- H. X. Zhou, J. Mol. Recognit., 2004, 17, 368 CrossRef CAS PubMed.
- A. R. McGuffee and A. H. Elcock, PLoS Comput. Biol., 2010, 6, e1000694 Search PubMed.
- R. J. Ellis, Curr. Opin. Struct. Biol., 2001, 11, 114 CrossRef CAS PubMed.
- A. P. Minton, J. Biol. Chem., 2001, 276, 10577 CrossRef CAS PubMed.
- A. P. Minton, Biopolymers, 1981, 20, 2093 CrossRef CAS.
- H. X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375 CrossRef CAS PubMed.
- C. Echeverria and R. Kapral, Phys. Chem. Chem. Phys., 2012, 14, 6755 RSC.
- E. Spruijt, E. Sokolova and W. T. S. Huck, Nat. Nanotechnol., 2014, 9, 406 CrossRef CAS PubMed.
- J. Shin, A. G. Cherstvy and R. Metzler, New J. Phys., 2014, 16, 053047 CrossRef.
- J. P. Bouchaud and A. Georges, Phys. Rep., 1990, 195, 127 CrossRef.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1 CrossRef CAS.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65(8), 29 CrossRef CAS.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128 RSC.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- I. M. Sokolov, Soft Matter, 2012, 8, 9043 RSC.
- M. Wachsmuth, W. Waldeck and J. Langowski, J. Mol. Biol., 2000, 298, 677 CrossRef CAS PubMed.
- I. Golding and E. C. Cox, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed; S. C. Weber, A. J. Spakowitz and J. A. Theriot, Phys. Rev. Lett., 2010, 104, 238102 CrossRef PubMed.
- I. Bronstein, et al. , Phys. Rev. Lett., 2009, 103, 018102 CrossRef CAS PubMed; K. Burnecki, E. Kepten, J. Janczura, I. Bronshtein, Y. Garini and A. Weron, Biophys. J., 2012, 103, 1839 CrossRef PubMed.
- M. Platani, I. Goldberg, A. I. Lamond and J. R. Swedlow, Nat. Cell Biol., 2002, 4, 502 CrossRef CAS PubMed.
- J.-H. Jeon, et al. , Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed; M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed.
- G. Seisenberger, et al. , Science, 2001, 294, 1929 CrossRef CAS PubMed.
- C. Brauchle, et al. , ChemPhysChem, 2002, 3, 299 CrossRef CAS PubMed.
- M. R. Horton, F. Höfling, J. O. Rädler and T. Franosch, Soft Matter, 2010, 6, 2648 RSC.
- J. Ehrig, E. P. Petrov and P. Schwille, Biophys. J., 2011, 100, 80 CrossRef CAS PubMed.
- J.-H. Jeon, H. M. S. Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef CAS PubMed; G. R. Kneller, K. Baczynski and M. Pasienkewicz-Gierula, J. Chem. Phys., 2011, 135, 141105 CrossRef PubMed; M. Javanainen, H. Hammaren, L. Monticelli, J.-H. Jeon, R. Metzler and I. Vattulainen, Faraday Discuss., 2013, 161, 397 RSC.
- E. Yamamoto, T. Akimoto, M. Yasui and K. Yasuoka, Sci. Rep., 2014, 4, 4720 Search PubMed.
- A. S. Kozlov, D. Andor-Ardo and A. J. Hudspeth, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2896 CrossRef CAS PubMed.
- D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960 CrossRef CAS PubMed.
- G. Guigas, C. Kalla and M. Weiss, Biophys. J., 2007, 93, 316 CrossRef CAS PubMed; W. Pan, L. Filobelo, N. D. Q. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef PubMed.
- J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
- D. Robert, Th.-H. Nguyen, F. Gallet and C. Wilhelm, PLoS One, 2010, 4, e10046 Search PubMed; I. Goychuk, V. O. Kharchenko and R. Metzler, PLoS One, 2014, 9, e91700 Search PubMed; I. Goychuk, V. O. Kharchenko and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 16524 RSC.
- O. Chepizhko and F. Peruani, Phys. Rev. Lett., 2013, 111, 160604 CrossRef PubMed.
- E. W. Montroll and G. H. Weiss, J. Math. Phys., 1969, 10, 753 CrossRef CAS; H. Scher and E. W. Montroll, Phys. Rev. B: Solid State, 1975, 12, 2455 CrossRef.
- B. B. Mandelbrot and J. W. van Ness, SIAM Rev., 1968, 10, 422 CrossRef.
- W. Deng and E. Barkai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef.
- E. Lutz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051106 CrossRef CAS.
- I. Goychuk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046125 CrossRef CAS; I. Goychuk, Adv. Chem. Phys., 2012, 150, 187 CrossRef.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, New J. Phys., 2013, 15, 083039 CrossRef CAS; A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2013, 15, 20220 RSC.
- P. Massignan, C. Manzo, J. A. Torreno-Pina, M. F. Garca-Parako, M. Lewenstein and G. L. Lapeyre, Jr., Phys. Rev. Lett., 2014, 112, 150603 CrossRef CAS PubMed.
- A. G. Cherstvy and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012134 CrossRef CAS.
- A. Fulinski, J. Chem. Phys., 2013, 138, 021101 CrossRef CAS PubMed; A. Fulinski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061140 CrossRef.
- S. C. Lim and S. V. Muniandy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021114 CrossRef CAS.
- F. Thiel and I. M. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012115 CrossRef CAS; J.-H. Jeon, A. V. Chechkin and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 15811 RSC.
- J. P. Bouchaud, A. Comtet, A. Georges and P. le Doussal, Ann. Phys., 1990, 201, 285 CAS.
- J. W. Haus and K. W. Kehr, Phys. Rep., 1987, 150, 263 CrossRef CAS.
- E. Bertin and J.-P. Bouchaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 026128 CrossRef CAS; C. Monthus and J.-P. Bouchaud, J. Phys. A: Math. Gen., 1996, 29, 3847 CrossRef; S. Burov and E. Barkai, Phys. Rev. Lett., 2007, 98, 250601 CrossRef PubMed.
- A. Sikorski and P. Polanowski, Soft Matter, 2014, 10, 3597 RSC.
- H. Berry and H. Chaté, arXiv:1103.2206.
- H. Berry and H. Chaté, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022708 CrossRef CAS; H. Soula, B. Caré, G. Beslon and H. Berry, Biophys. J., 2013, 105, 2064 CrossRef PubMed.
- Moreover, in ref. 52 the distribution of particle trapping times in dynamical cages formed between the crowders was shown to be inconsistent with the CTRW model, as observed in simulations for mobile crowders, crowders confined in a potential, and static obstacles. Namely, the power-law distribution of trapping times ψ(τ) ∼ τ−γ was shown to range between γ = 3.5–4, in contrast to the range γ = 1–2 expected for subdiffusive CTRW processes with diverging characteristic waiting time15–17.
- T. K. Piskorz and A. Ochab-Marcinek, J. Phys. Chem. B, 2014, 118, 4906 CrossRef CAS PubMed.
- J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed.
- D. Ernst, J. Koehler and M. Weiss, Phys. Chem. Chem. Phys., 2014, 16, 7686 RSC.
- M. J. Saxton, Biophys. J., 1987, 52, 990 CrossRef.
- M. J. Saxton, Biophys. J., 1996, 70, 1250 CrossRef CAS PubMed.
- M. J. Saxton, Biophys. J., 2010, 99, 1490 CrossRef CAS PubMed.
- P. A. Netz and T. Dorfmuller, J. Chem. Phys., 1997, 107, 9221 CrossRef CAS.
- Y. Meroz, I. M. Sokolov and J. Klafter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 010101(R) CrossRef.
- F. Höfling, T. Franosch and E. Frey, Phys. Rev. Lett., 2006, 96, 165901 CrossRef.
- M. Spanner, et al. , J. Phys.: Condens. Matter, 2011, 23, 234120 CrossRef PubMed.
- L. Dagdug, M. V. Vazquez, A. M. Berezhkovskii, V. Yu. Zitserman and S. M. Bezrukov, J. Chem. Phys., 2012, 136, 204106 CrossRef PubMed.
- R. Chakrabarti, S. Kesselheim, P. Kosovan and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062709 CrossRef.
- N. A. Mahynski, A. Z. Panagiotopoulos, D. Meng and S. K. Kumar, Nat. Commun., 2014, 5, 4472 CAS.
- M. A. Lomholt, I. M. Zaid and R. Metzler, Phys. Rev. Lett., 2007, 98, 200603 CrossRef PubMed; A. V. Chechkin, I. M. Zaid, M. A. Lomholt, I. M. Sokolov and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041101 CrossRef.
- R. Huang, I. Chavez, K. M. Taute, B. Lukic, S. Jeney, M. G. Raizen and E.-L. Florin, Nat. Phys., 2011, 7, 576 CrossRef CAS.
- D. S. Grebenkov, M. Vahabi, E. Bertseva, L. Forro and S. Jeney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 040701(R) CrossRef.
- W. T. Coffey and Y. P. Kalmykov, The Langevin equation, World Scientific, Singapore, 2012 Search PubMed.
- M. Bauer, A. Godec and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 6118 RSC.
- E. Zaccarelli and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15203 CrossRef CAS PubMed.
- J. Balbo, P. Mereghetti, D. P. Herten and R. C. Wade, Biophys. J., 2013, 104, 1576 CrossRef CAS PubMed.
- J.-F. Rupprecht, O. Benichou, D. S. Grebenkov and R. Voituriez, J. Stat. Phys., 2012, 147, 891 CrossRef CAS.
- J.-H. Jeon and R. Metzler, J. Phys. A: Math. Gen., 2010, 43, 252001 CrossRef.
- A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef CAS PubMed; Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef PubMed.
- A. Godec, M. Bauer and R. Metzler, New J. Phys., 2014, 16, 092002 CrossRef.
- J.-H. Jeon and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021147 CrossRef.
- A. Caspi, R. Granek and M. Elbaum, Phys. Rev. Lett., 2000, 85, 5655 CrossRef CAS PubMed.
- S. Leitmann and T. Franosch, Phys. Rev. Lett., 2013, 111, 190603 CrossRef PubMed.
- F. Tabatabaei, O. Lenz and C. Holm, Colloid Polym. Sci., 2011, 289, 523 CAS.
- J. Sprakel, J. van der Gucht, M. A. Cohen-Stuart and A. M. Besseling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061502 CrossRef.
- I. Y. Wong, et al. , Phys. Rev. Lett., 2004, 92, 178101 CrossRef CAS PubMed.
- O. Lieleg, R. M. Baumgartel and A. R. Bausch, Biophys. J., 2009, 97, 1569 CrossRef CAS PubMed.
- G. Guigas and M. Weiss, Biophys. J., 2008, 94, 90 CrossRef CAS PubMed; M. Hellmann, D. W. Heermann and M. Weiss, Europhys. Lett., 2011, 94, 18002 CrossRef; L. E. Sereshki, M. A. Lomholt and R. Metzler, Europhys. Lett., 2012, 97, 20008 CrossRef.
- To map the exchange between the bulk and a reactive surface (here defined via the attractive part of the potential (3)) onto a random walk picture, compare ref. 68.
| This journal is © the Owner Societies 2015 |